Interferometry in an Atomic Fountain with Ytterbium Bose–Einstein Condensates
Abstract
:1. Introduction
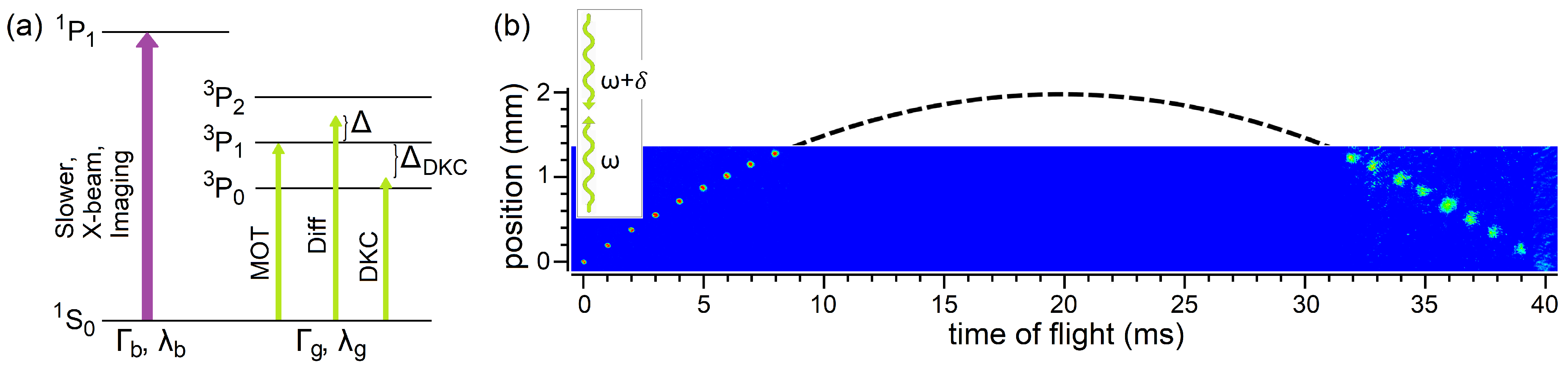
2. Yb BEC Fountain
2.1. BEC Source and Atom Optics
2.2. Vertical Fountain Launch
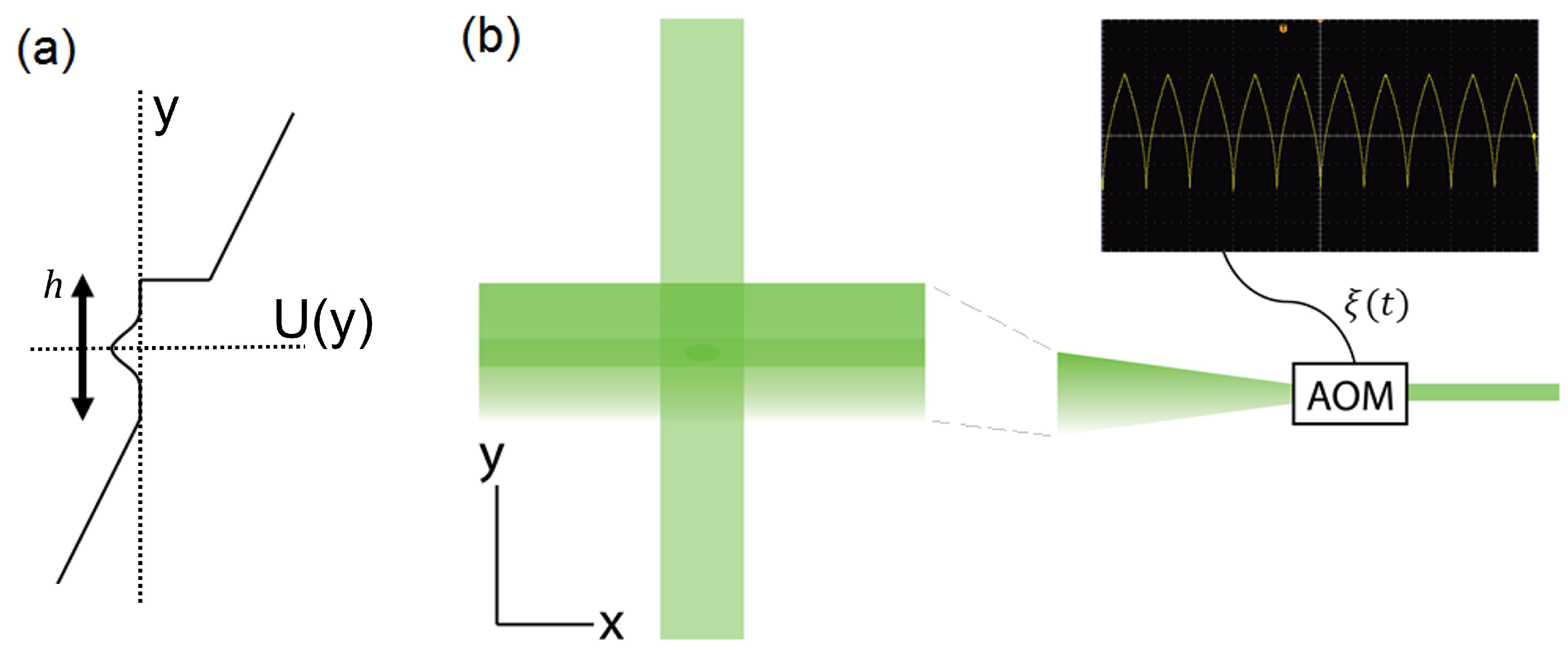
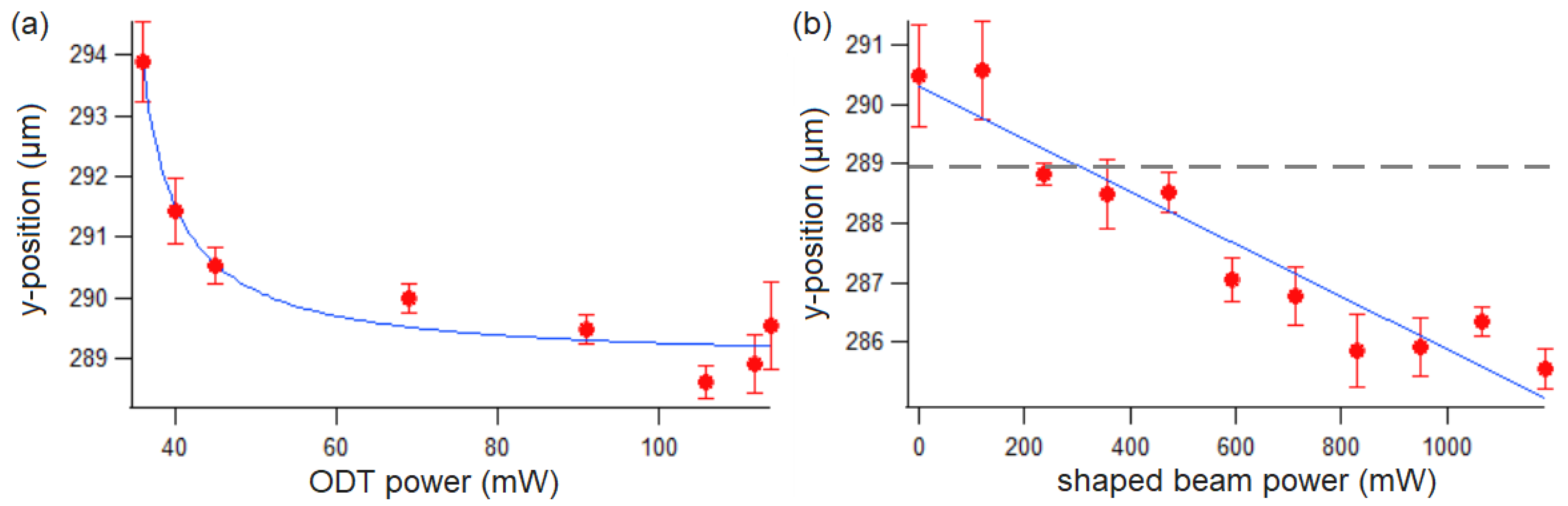
3. Gravity Compensation by Shaped Optical Beam
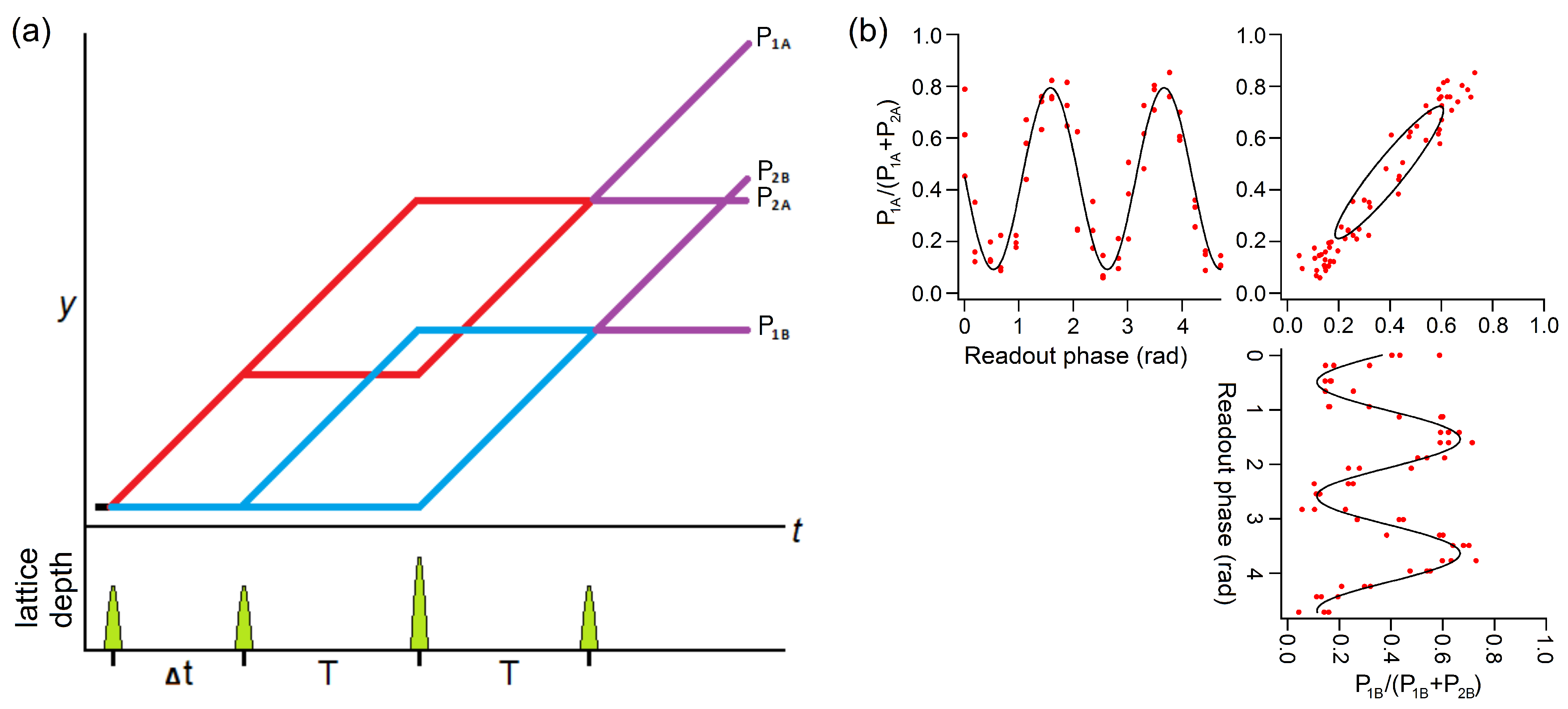
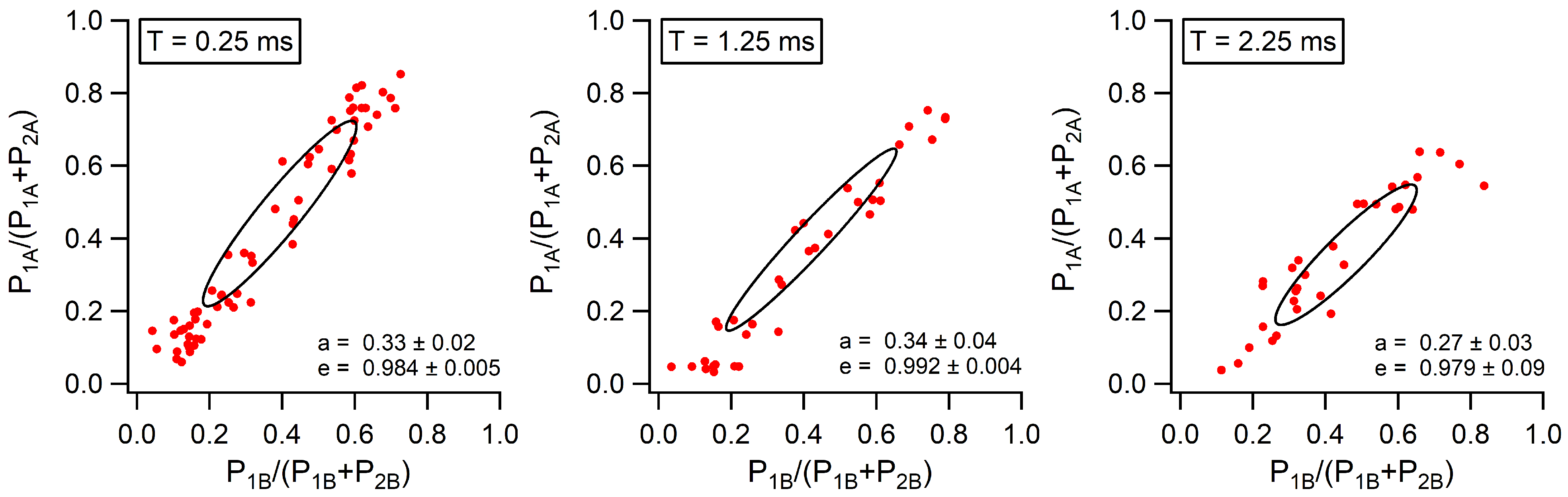
4. Double Mach–Zehnder Interferometer
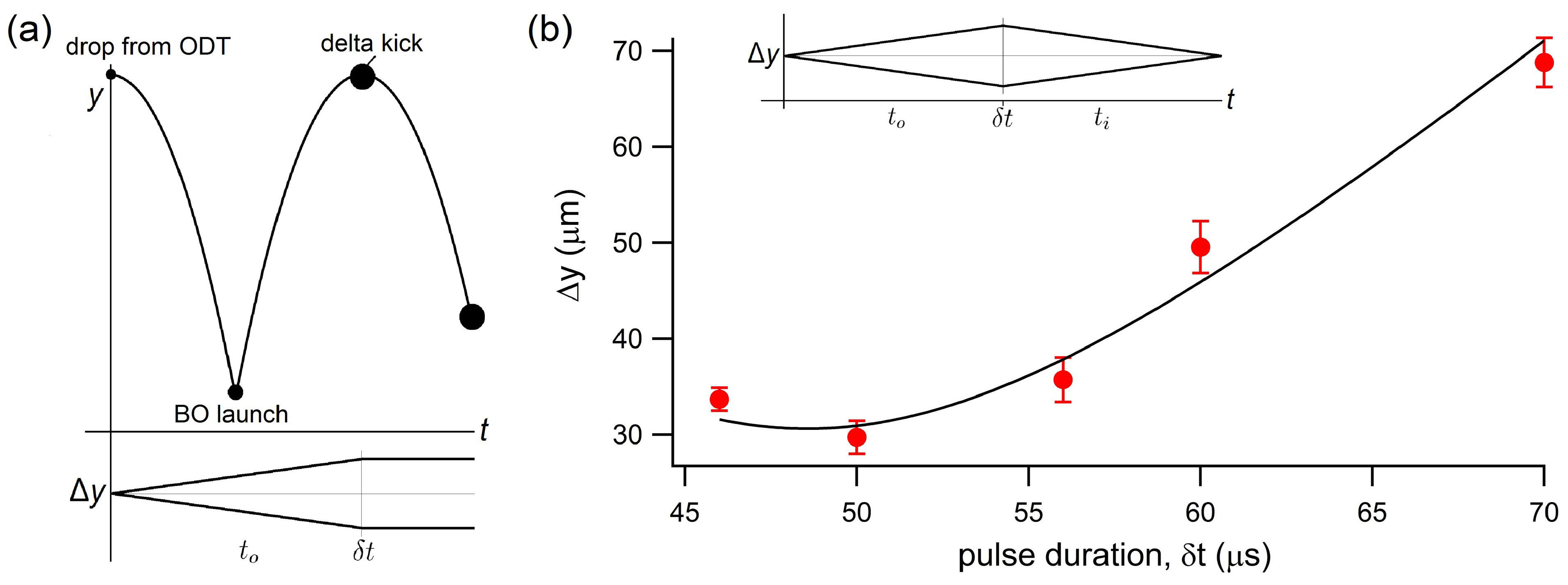
5. Delta-Kick Collimation of Yb for Vertical AI
5.1. Delta-Kick Collimation
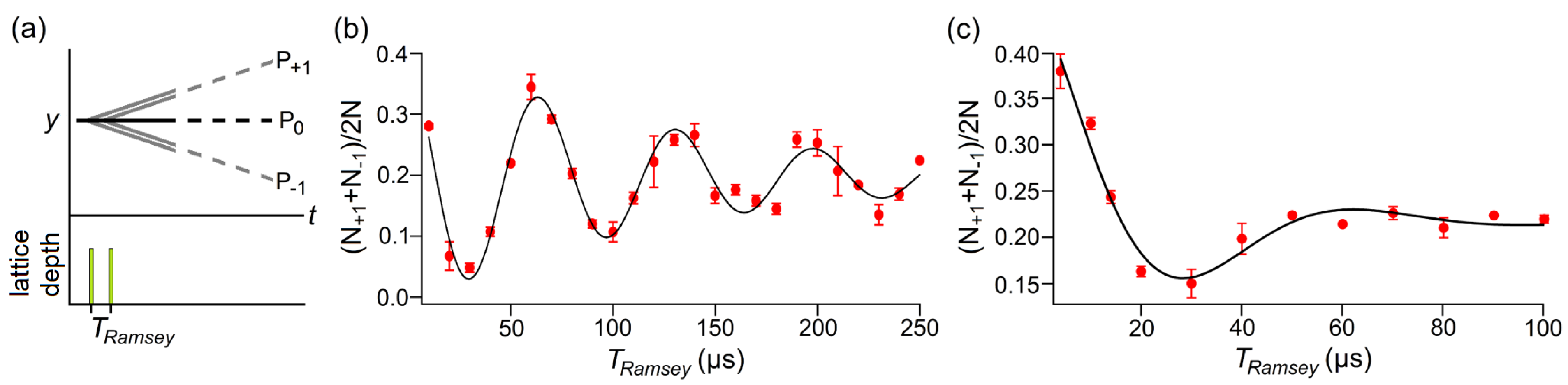
5.2. Ramsey Interferometry and Coherence Time Measurements
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bouchendira, R.; Clade, P.; Guellati-Khelifa, S.; Nez, F.; Biraben, F. New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef] [Green Version]
- Mazzoni, T.; Zhang, X.; Del Aguila, R.; Salvi, L.; Poli, N.; Tino, G. Large-momentum-transfer Bragg interferometer with strontium atoms. Phys. Rev. A 2015, 92, 053619. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Poli, N.; Salvi, L.; Tino, G. Atom Interferometry with the Sr Optical Clock Transition. Phys. Rev. Lett. 2017, 119, 263601. [Google Scholar] [CrossRef] [Green Version]
- Parker, R.H.; Yu, C.; Estey, B.; Zhong, W.; Muller, H. Measurement of the fine-structure constant as a test of the Standard Model. Science 2018, 360, 191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asenbaum, P.; Overstreet, C.; Kovachy, T.; Brown, D.; Hogan, J.; Kasevich, M. Phase Shift in an Atom Interferometer due to Spacetime Curvature across its Wave Function. Phys. Rev. Lett. 2017, 118, 183602. [Google Scholar] [CrossRef] [Green Version]
- Jamison, A.O.; Plotkin-Swing, B.; Gupta, S. Advances in Precision Contrast Interferometry with Yb Bose–Einstein condensates. Phys. Rev. A 2014, 90, 063606. [Google Scholar] [CrossRef] [Green Version]
- Rudolph, J.; Wilkason, T.; Nantel, M.; Swan, H.; Holland, C.; Jiang, Y.; Garber, B.; Carman, S.; Hogan, J. Large Momentum Transfer Clock Atom Interferometry on the 689 nm Intercombination Line of Strontium. Phys. Rev. Lett. 2020, 124, 083604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plotkin-Swing, B.; Gochnauer, D.; McAlpine, K.; Cooper, E.; Jamison, A.; Gupta, S. Three-Path Atom Interferometry with Large Momentum Separation. Phys. Rev. Lett. 2018, 121, 133201. [Google Scholar] [CrossRef] [Green Version]
- Gochnauer, D.; McAlpine, K.; Plotkin-Swing, B.; Jamison, A.; Gupta, S. Bloch-band picture for light-pulse atom diffraction and interferometry. Phys. Rev. A. 2019, 100, 043611. [Google Scholar] [CrossRef] [Green Version]
- McAlpine, K.; Gochnauer, D.; Gupta, S. Excited-band Bloch oscillations for precision atom interferometry. Phys. Rev. A. 2020, 101, 023614. [Google Scholar] [CrossRef] [Green Version]
- Plotkin-Swing, B. Large Momentum Separation Matter Wave Interferometry. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2018. [Google Scholar]
- Plotkin-Swing, B.; Wirth, A.; Gochnauer, D.; Rahman, T.; McAlpine, K.; Gupta, S. Crossed-beam slowing to enhance narrow-line ytterbium magneto-optic traps. Rev. Sci. Instrum. 2020, 91, 093201. [Google Scholar] [CrossRef] [PubMed]
- Castin, Y.; Dum, R. Bose–Einstein Condensates in Time Dependent Traps. Phys. Rev. Lett. 1996, 77, 5315. [Google Scholar] [CrossRef] [PubMed]
- Jamison, A.O.; Kutz, J.N.; Gupta, S. Atomic Interactions in Precision Interferometry Using Bose–Einstein Condensates. Phys. Rev. A. 2011, 84, 043643. [Google Scholar] [CrossRef] [Green Version]
- Shibata, K.; Ikeda, H.; Suzuki, R.; Hirano, T. Compensation of gravity on cold atoms by a linear optical potential. Phys. Rev. Res. 2020, 2, 013068. [Google Scholar] [CrossRef] [Green Version]
- McGuirk, J.M.; Foster, G.T.; Fixler, J.B.; Snadden, M.J.; Kasevich, M.A. Sensitive absolute-gravity gradiometry using atom interferometry. Phys. Rev. A 2002, 65, 033608. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Leanhardt, A.E.; Cronin, A.D.; Pritchard, D.E. Coherent Manipulation of Atoms with Standing Light Waves. C. R. Acad. Sci. IV-Phys. 2001, 2, 479. [Google Scholar] [CrossRef]
- Foster, G.T.; Fixler, J.B.; McGuirk, J.M.; Kasevich, M.A. Method of phase extraction between coupled atom interferometers using ellipse-specific fitting. Opt. Lett. 2002, 27, 951. [Google Scholar] [CrossRef] [PubMed]
- Stockton, J.K.; Wu, X.; Kasevich, M.A. Bayesian estimation of differential interferometer phase. Phys. Rev. A 2007, 76, 033613. [Google Scholar] [CrossRef]
- Bertoldi, A.; Lamporesi, G.; Cacciapuoti, L.; de Angelis, M.; Fattori, M.; Petelski, T.; Peters, A.; Prevedelli, M.; Stuhler, J.; Tino, G. Atom interferometry gravity-gradiometer for the determination of the Newtonian gravitational constant G. Eur. Phys. J. D 2006, 40, 271–279. [Google Scholar] [CrossRef]
- Chiow, S.; Herrmann, S.; Chu, S.; Muller, H. Noise-Immune Conjugate Large-Area Atom Interferometers. Phys. Rev. Lett. 2009, 103, 050402. [Google Scholar] [CrossRef] [Green Version]
- Chu, S.; Bjorkholm, J.; Ashkin, A.; Gordon, J.; Hollberg, L. Proposal for optically cooling atoms to temperatures of the order of 10−6 K. Opt. Lett. 1986, 11, 73. [Google Scholar] [CrossRef] [PubMed]
- Kovachy, T.; Hogan, J.; Sugarbaker, A.; Dickerson, S.; Donnelly, C.; Overstreet, C.; Kasevich, M. Matter Wave Lensing to Picokelvin Temperatures. Phys. Rev. Lett. 2015, 114, 143004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muntinga, H.; Ahlers, H.; Krutzik, M.; Wenzlawski, A.; Arnold, S.; Becker, D.; Bongs, K.; Dittus, H.; Duncker, H.; Gaaloul, N.; et al. Interferometry with Bose–Einstein Condensates in Microgravity. Phys. Rev. Lett. 2013, 110, 093602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagley, E.W.; Deng, L.; Kozuma, M.; Trippenbach, M.; Band, Y.B.; Edwards, M.; Doery, M.; Julienne, P.S.; Helmerson, K.; Rolston, S.L.; et al. Measurement of the Coherence of a Bose–Einstein Condensate. Phys. Rev. Lett. 1999, 83, 3112. [Google Scholar] [CrossRef] [Green Version]
- Dzuba, V.; Flambaum, V.; Schiller, S. Testing physics beyond the standard model through additional clock transitions in neutral ytterbium. Phys. Rev. A 2018, 98, 022501. [Google Scholar] [CrossRef] [Green Version]
- Hinkley, N.; Sherman, J.; Phillips, N.; Schioppo, M.; Lemke, N.; Beloy, K.; Pizzocaro, M.; Oates, C.; Ludlow, A. An Atomic Clock With 10−18 Instability. Science 2013, 341, 1215–1218. [Google Scholar] [CrossRef] [Green Version]
- Hartwig, J.; Abend, S.; Schubert, S.; Schlippert, D.; Ahlers, H.; Posso-Trujillo, K.; Gaaloul, N.; Ertmer, W.; Rasel, E. Testing the universality of free fall with rubidium and ytterbium in a very large baseline atom interferometer. New J. Phys. 2015, 17, 035011. [Google Scholar] [CrossRef] [Green Version]
- Niederriter, R.; Schlupf, C.; Hamilton, P. Cavity probe for real-time detection of atom dynamics in an optical lattice. Phys. Rev. A 2020, 102, 051301(R). [Google Scholar] [CrossRef]
- Roura, A.; Schubert, C.; Schlippert, D.; Rasel, E. Measuring gravitational time dilation with delocalized quantum superpositions. arXiv 2020, arXiv:2010.11156. [Google Scholar]
- Takasu, Y.; Maki, K.; Komori, K.; Takano, T.; Honda, K.; Kumakura, M.; Yabuzaki, T.; Takahashi, Y. Spin-singlet Bose–Einstein Condensation of Two-Electron Atoms. Phys. Rev. Lett. 2002, 91, 040404. [Google Scholar] [CrossRef] [Green Version]
- See Toh, J.; McCormick, K.; Tang, X.; Su, Y.; Luo, X.; Zhang, C.; Gupta, S. Observation of Many-body Dynamical Delocalization in a Kicked Ultracold Gas. arXiv 2021, arXiv:2106.13773. [Google Scholar]
- Pagano, G.; Mancini, M.; Cappellini, G.; Lombardi, P.; Schäfer, F.; Hu, H.; Liu, X.; Catani, J.; Sias, C.; Inguscio, M.; et al. A one-dimensional liquid of fermions with tunable spin. Nat. Phys. 2014, 10, 198–201. [Google Scholar] [CrossRef]
- Scazza, F.; Hofrichter, C.; Höfer, M.; De Groot, P.; Bloch, I.; Fölling, S. Observation of two-orbital spin-exchange interactions with ultracold SU(N)-symmetric fermions. Nat. Phys. 2014, 10, 779–784. [Google Scholar] [CrossRef] [Green Version]
- Ono, K.; Kobayashi, J.; Amano, Y.; Sato, K.; Takahashi, Y. Antiferromagnetic interorbital spin-exchange interaction of 171Yb. Phys. Rev. A 2019, 99, 032707. [Google Scholar] [CrossRef] [Green Version]
- Stock, R.; Babcock, N.; Raizen, M.; Sanders, B. Entanglement of group-II-like atoms with fast measurement for quantum information processing. Phys. Rev. A 2008, 78, 022301. [Google Scholar] [CrossRef] [Green Version]
- Saskin, S.; Wilson, J.; Grinkemeyer, B.; Thompson, J. Narrow-Line Cooling and Imaging of Ytterbium Atoms in an Optical Tweezer Array. Phys. Rev. Lett. 2019, 122, 143002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Covey, J.; Sipahigil, A.; Szoke, S.; Sinclair, N.; Endres, M.; Painter, O. Telecom-Band Quantum Optics with Ytterbium Atoms and Silicon Nanophotonics. Phys. Rev. App. 2019, 11, 034044. [Google Scholar] [CrossRef] [Green Version]
- Schlippert, D.; Hartwig, J.; Albers, H.; Richardson, L.; Schubert, C.; Roura, A.; Schleich, W.; Ertmer, W.; Rasel, E. Quantum Test of the Universality of Free Fall. Phys. Rev. Lett. 2014, 112, 203002. [Google Scholar] [CrossRef] [Green Version]
- Asenbaum, P.; Overstreet, C.; Kim, M.; Curti, J.; Kasevich, M. Atom-Interferometric Test of the Equivalence Principle at the 10−12 Level. Phys. Rev. Lett. 2020, 125, 191101. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gochnauer, D.; Rahman, T.; Wirth-Singh, A.; Gupta, S. Interferometry in an Atomic Fountain with Ytterbium Bose–Einstein Condensates. Atoms 2021, 9, 58. https://doi.org/10.3390/atoms9030058
Gochnauer D, Rahman T, Wirth-Singh A, Gupta S. Interferometry in an Atomic Fountain with Ytterbium Bose–Einstein Condensates. Atoms. 2021; 9(3):58. https://doi.org/10.3390/atoms9030058
Chicago/Turabian StyleGochnauer, Daniel, Tahiyat Rahman, Anna Wirth-Singh, and Subhadeep Gupta. 2021. "Interferometry in an Atomic Fountain with Ytterbium Bose–Einstein Condensates" Atoms 9, no. 3: 58. https://doi.org/10.3390/atoms9030058
APA StyleGochnauer, D., Rahman, T., Wirth-Singh, A., & Gupta, S. (2021). Interferometry in an Atomic Fountain with Ytterbium Bose–Einstein Condensates. Atoms, 9(3), 58. https://doi.org/10.3390/atoms9030058





