Abstract
The O I 777-nm triplet transition is often used for plasma density diagnostics. It is also employed in nonlinear optics setups for producing quasi-comb structures when pumped by a near-resonant laser field. Here, we apply computer simulations to situations of the radiating atom subjected to the plasma microfields, laser fields, and both perturbations together. Our results, in particular, resolve a controversy related to the spectral line anomalously broadened in some laser-produced plasmas. The importance of using time-dependent density matrix is discussed.
1. Introduction
The plasma Stark broadening of the O I 777-nm triplet (individual components at 777.19, 777.42, and 777.54 nm [1]) appears to be a controversial topic. The theoretical values, among the plasma broadening parameters of many other neutral and singly ionized atoms were published in the monograph of Griem [2] and later updated [3]. On the experimental side, Baronets and Bykova [4] reported about excess of the measured width of the line and attributed it to an unknown mechanism, perhaps related to chemical activity of oxygen, and suggested more studies would be needed to resolve the issue. Bernhardt et al. [5] observed a much larger, 6.7× discrepancy in their experiment. Notably, in that study a plasma filament was formed by a femtosecond Ti:sapphire () laser pulse in air. On the other hand, a very recent experimental study of Sainct et al. [6] found a fair agreement in the density determined from the Stark broadening of the O I 777-nm line and that of hydrogen Balmer- and - in pulsed discharges at atmospheric pressure. The typical electron density in this case was 1–2 orders of magnitude higher than in [4,5], though.
Although disagreements between theoretical and experimental plasma Stark-broadening coefficients of so called isolated lines [3] are not unheard of, they typically increase with the charge of the radiator species but still do not exceed a factor of two or so [7]. The 6–7-times disagreement, especially for a neutral radiator, is truly outstanding and calls for a resolution. This is of particular concern since new studies, using the Stark-broadening constant inferred in [5] for plasma diagnostics, continue to be published (e.g., [8,9]).
Recently, Ilyin et al. [10] suggested that the significantly larger broadening observed in [5] might, in fact, be caused by the laser field (after the main pulse) that happened to be nearly resonant with the transition investigated. Indeed, very pronounced sideband features of this line in laser-generated microplasmas were reported by Compton et al. [11]. It should be noted that in [10], the calculations were approximate (readily acknowledged by the authors) due to a rather complex interplay between the plasma electron impacts, laser fields, and the spin–orbit atomic interaction, requiring a fairly advanced modeling for accurate treatment.
The objective of the present work is twofold: first, to calculate the plasma Stark broadening of the 777-nm line using modern techniques, namely, a computer simulation (CS) modeling [12] and second, to investigate the influence of the laser field on the shape of this line using the same CS.
Our results of the plasma Stark broadening closely match those of [3]. It is also confirmed that a moderate laser radiation causes a noticeable shift of all triplet components and, with an appropriate distribution of the magnitudes, may result in effective broadening and shift that could be misattributed to a higher plasma density.
In addition, we find out that the 1064-nm radiation of a Nd:YAG laser, which is also frequently used in various applications, can affect the shape of the 777-nm transition in a similar way due to a different nearly resonant atomic-level interaction. Furthermore, our calculations show a minor effect of the magnetic component of the laser electromagnetic field.
2. Method
We use a variant of CS described in [13] and extended to account for the laser electromagnetic fields [14]. Briefly, the Hamiltonian of the atomic system of the radiator is a sum of the unperturbed Hamiltonian and a time-dependent perturbation V:
where the perturbation is due to the simulated plasma electric field and the laser electric and magnetic fields acting on the dipole electric and magnetic moments of the radiator:
The simulation follows the reduced-mass model [15] using a spherical volume with a static radiator fixed at its center and radius of several times the electron Debye length to ensure convergence [16]. The Debye potential is used to calculate the electric field acting on the radiator. The motion of Debye quasiparticles is, in general, obtained by accounting for monopole interactions between them and the radiator using a velocity Verlet algorithm [17]. For the present calculations, however, the radiators are neutral and, therefore, the trajectories of all plasma particles were assumed straight. Such very fast Debye-quasiparticle molecular dynamic simulations provide rather accurate results for weakly-to-moderately coupled plasmas, as follows from comparisons with fully interacting N-body simulations [18,19].
The time-dependent Schrödinger equation (2) is numerically solved by introducing the time-development operator in the interaction representation:
(here and below, is assumed). The time evolution of the dipole operator is then obtained:
and its Fourier transform,
is used to calculate the line spectrum in the dipole approximation:
Here, the i and f indices run over the initial and final levels, respectively, is the level-energy difference, and the angle brackets denote an averaging over several runs of the code (which corresponds to an averaging over a statistically-representative ensemble of radiators). The density matrix is assumed to be diagonal and independent of time, as is customary in line-shape broadening calculations [3].
The atomic Hamiltonian includes, in addition to the initial and final levels of the transition of interest, six other close levels with strong dipole couplings to either or ; namely, , , , , , and (here and further on, the common electronic configuration core is omitted). The level energies and the dipole oscillator strengths are taken from the NIST database [1]. The quadrupole contribution to the line broadening is neglected, since it was shown, by several independent calculations, to have a minor effect on the isolated-line widths and shifts [20].
3. Results and Discussion
We begin with plasma-broadening calculations, without the laser field. The results are shown in Figure 1, with the previously calculated data [3] given for comparison. As seen, our results are in a very good agreement with [3] as far as the width is concerned. The shifts differ notably. It is worth noting that, contrary to the width that is mostly affected by electrons, the shift is significantly influenced by the plasma ions, too. The lighter (faster) the ions, the larger their effect is. Therefore, assuming a proton–electron plasma (with oxygen as a minority), as is done in our calculations, gives the upper bound on the effect of singly charged ions of any kind.
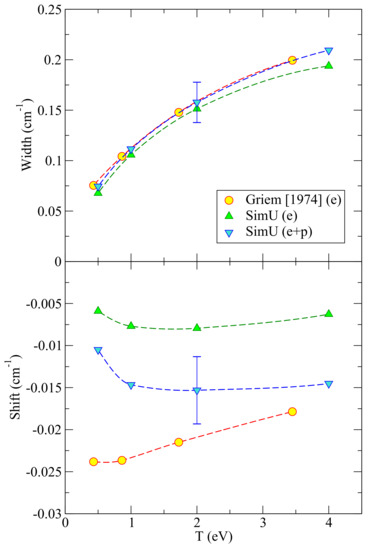
Figure 1.
The Stark width (FWHM) and shift of the O I 777-nm line assuming a plasma with . Shown are results for a one-component electron plasma (“e”) and those for a proton-electron one (“e+p”). “Griem [1974]” stands for [3], “SimU” labels our results. The error bars indicate estimated uncertainties of our calculations.
In Figure 2 we demonstrate the effect of the nearly resonance radiation on the shape of this transition. It is seen that a modest intensity of is sufficient to cause a noticeable shift of about of the triplet as a whole (there is also a minor broadening of the two stronger components). However, for the stronger fields corresponding to , the structure of the line pattern changes significantly. Here, the electric-field-induced perturbation becomes comparable to the spin–orbit interaction and largely breaks it. The left group of the transition components originate mostly from the upper-level states with , while the right one from those with . Consequently, their radiation are predominantly - and -polarized, respectively. It should be noted that, although the nearly resonant – interaction is responsible for the major part of the effect, there are other levels that contribute to it, too. These in particular are and , spaced in the wavelength units from by 1130 nm and 926 nm, respectively; that is, their contribution is also “resonantly enhanced”, but to a lesser degree. A rather counterintuitive feature is that these levels cause a shift that is additive to that of the pure two-level ( and ) model—in spite of being above the level with which they interact. This can be understood in the second-order approximation within the Floquet formalism, yielding the energy shift of level i due to a harmonic perturbation (e.g., [21,22])
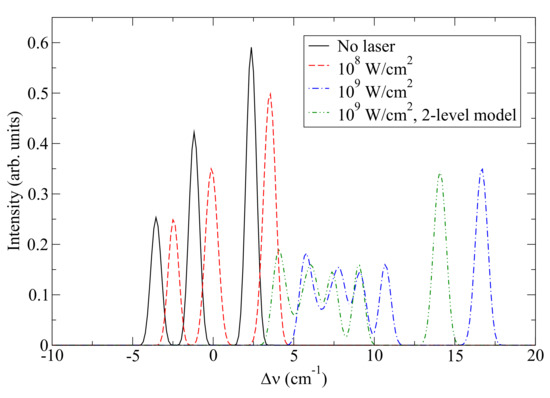
Figure 2.
Effect of the nearly resonant laser field on the lineshape. A 805-nm laser radiation (as in [5]) is assumed. All spectra are area-normalized.
One can readily see that, depending on the relative values of and , the sign of the resonant term(s) in Equation (7) may flip. This is indeed the case with and .
Finally, we investigate the influence on the transition pattern of the radiation of another widely used laser type, Nd:YAG, with the fundamental wavelength of 1064 nm. In this case, the and levels become nearly resonant with and their contributions, respectively, increase, while the – interaction loses its dominance. Compared to the 805-nm case, the effect is weaker, because the perturbation largely affects only one of the levels of the transition and the detuning is larger (also, the – oscillator strength is smaller). As a result, an order-of-magnitude stronger laser intensity is required to achieve a comparable effect—see Figure 3. For comparison, we also show results of a similar modeling but assuming the second-harmonic generation of the same laser. In this non-resonant case, the effect is significantly weaker, as one would expect. We again draw reader’s attention to the non-trivial signs of the transition shifts (and their change when switching the perturbation frequency) resulting from the complicated interplay of multiple terms in Equation (7).
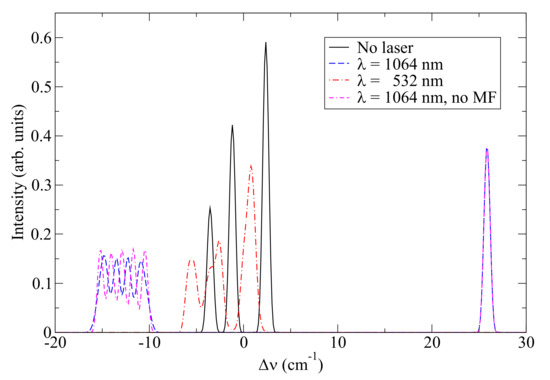
Figure 3.
Comparison of the effect of nearly resonant () and non-resonant () laser fields on the lineshape. Laser irradiation intensity of is assumed. All spectra are area-normalized.
A very interesting feature of the 1064-nm-affected spectrum in this figure is influence of the magnetic component of the laser field, seen in the “red”-shifted part of the spectrum. The magnetic-field magnitude in the - intensity is about one tesla, corresponding to ∼ on the energy scale. Indeed, the differences between the spectra calculated with and without the magnetic-field perturbation are of the same order of magnitude. What is surprising, though, is that it is observed in a highly dynamic regime, with the frequency of the perturbation (∼) exceeding its magnitude (∼) by many orders of magnitude. This is quite contrary to the findings of [14], where the effect of the magnetic component was found in the quasistatic regime. The apparent solution of this paradox is the resonant nature of the perturbation in the present case: in the rotating “frame” of the dipole matrix element, the perturbation is almost stationary.
The results presented above are based on the assumption of a stationary diagonal density matrix, see Equation (6). This is, however, not necessarily the case with nearly resonant laser pumping of sufficient magnitude. Indeed, in Figure 4 we show time-dependent population of the O I and states under the influence of a Gaussian laser pulse alone and under joint action of the same laser pulse and a rather dense, , plasma (since the perturbation significantly exceeds the spin–orbit coupling, the spin degree of freedom was neglected in this case). We obtain the density matrix in the same framework of computer simulations; namely,
with being defined in 3.
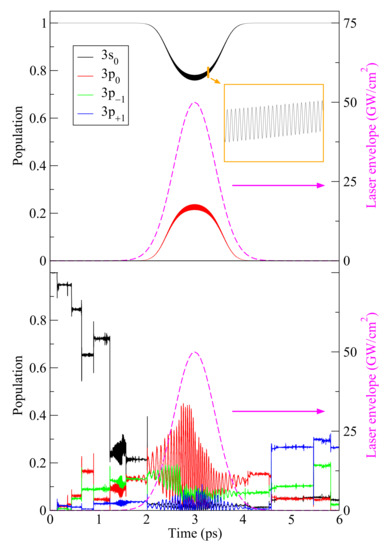
Figure 4.
Time-dependent populations (i.e., the diagonal density-matrix elements) of the O I and states under influence of a picosecond, laser pulse (upper panel) and under joint action of the same laser pulse and a plasma with and (lower panel). The laser envelope is shown by the dashed line. The quantization axis is parallel to the electric field of the laser.
We assume the atom is initially in the metastable state. As seen in the upper panel of the figure, the laser pulse with a 1-ps Gaussian envelope gradually transfers the population to and then back to , while the states remain practically unpopulated (there is a tiny, population due to the magnetic component of the laser field). Note the high-frequency (about ) modulation of the graphs, shown in the inset, which is due to the non-resonant interaction term [corresponding to the second term in Equation (7)]. This minor feature is absent in the “rotating-wave” approximation (compare to Figure 1 in [23]).
In the presence of plasma, the picture looks quite different (the lower panel of Figure 4). We see that the plasma strongly mixes the states on the time scale of about 1 ps, mainly due to the so called “strong” electron collisions [3] causing nearly instantaneous jumps of the state populations. Contrary to the adiabatic smooth pumping in the previous case, now we observe strong fast oscillations at the generalized (or detuned) Rabi frequency (e.g., [24]) that depends on the amplitude of the laser field (compare to Figure 2 in [23]). We note that the population histories given here are obtained in a single run of the code. After having averaged over many runs, one would observe familiar smooth relaxation curves establishing statistical equilibrium. Additionally, note that the populations of the and levels do not add up to unity, since the electron collisions also result in the population of the other atomic levels included in the Hamiltonian.
Evidently, the spectra under these two scenarios should differ notably. Although line-shape calculations employing true time dependence of the density matrix have not been implemented by us yet (it is a work in progress), we show results based on an approximate approach, where the density matrix varies from run to run [recall that the angle brackets in Equation (7) denote averaging over many, typically hundreds or thousands runs], but is constant over duration of each run, taken as an average over its period.
The spectra thus obtained are given in Figure 5. One immediately recognizes the so called Rabi sideband on the blue side of the unperturbed-line position, strictly -polarized when no plasma perturbation is assumed. When the latter is added, several phenomena are observed. First, the separate peaks in the Rabi sideband become broadened and less “contrast”. Second, a -polarized emission, having a qualitatively similar structure, but with differently placed minima and maxima, appears. Finally, a single strongly -polarized red-shifted peak emerges. We stress that the approach used to calculate spectra in Figure 5 is approximate in the treatment of the atomic density matrix. However, we believe that the qualitative features are correct. In particular, the plasma-caused smoothing of the Rabi sideband quasi-comb structures was observed experimentally—see Heck et al. [25] and references therein.
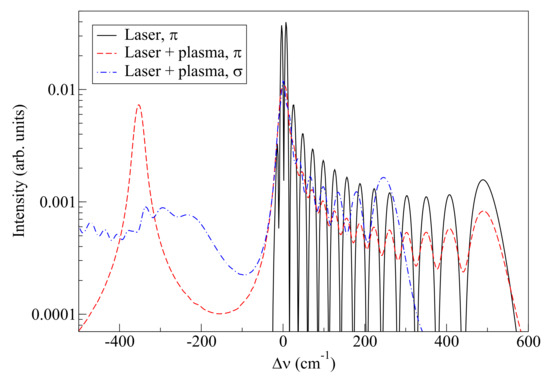
Figure 5.
Spectra calculated under two scenarios: only laser perturbation and laser and plasma fields together. and polarizations are shown separately. The settings assumed are the same as in Figure 4.
4. Conclusions
Computer simulations were used to calculate Stark effect of the O I 777-nm line in plasma, and under the influence of laser field. Our results of the plasma Stark broadening closely match those of Griem [3], while the shift is significantly smaller. We also observe that a moderately intense radiation of near-visible IR laser radiation causes a noticeable Stark shift and/or splitting. More generally, similar phenomena likely exist in other neutral or weakly ionized species where transitions between various levels separated by 1–2 eV are rather common. Given the ever growing use of powerful lasers for producing plasma in fundamental research and various applications, care should be exercised to avoid possible misinterpretation of the laser-field-induced effects of pre- or post-pulses in Stark-based plasma density diagnostics.
On the other hand, the observation of the Stark-affected pattern under the laser field can be used for determination of the areal power density of laser radiation at the level of 10–10 W/cm—for example, prepulses of intense femtosecond beams.
Author Contributions
Calculations and original draft preparation by E.S.; E.S., E.K., Y.M. and V.M. contributed to the analysis, discussions, and the final shaping of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the U.S. National Science Foundation and the U.S.–Israel Binational Science Foundation (joint grant number 2017669), Israel Science Foundation (grant number 1426/17), and by research grants from the Wolfson Foundation and from Dita and Yehuda L. Bronicki.
Acknowledgments
We thank Ramy Doron for drawing our attention to the controversial results of [5].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.7.1). Available online: http://physics.nist.gov/asd/ (accessed on 1 October 2020).
- Griem, H.R. Plasma Spectroscopy; McGraw-Hill Book Company: New York, NY, USA, 1964. [Google Scholar]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic: New York, NY, USA, 1974. [Google Scholar]
- Baronets, P.N.; Bykova, N.G. Diagnostics of the plasma in a high power induction plasmatron by the intensity and broadening of spectral lines. J. Appl. Spectrosc. 1991, 54, 399–403. [Google Scholar] [CrossRef]
- Bernhardt, J.; Liu, W.; Théberge, F.; Xu, H.L.; Daigle, J.F.; Châteauneuf, M.; Dubois, J.; Chin, S.L. Spectroscopic analysis of femtosecond laser plasma filament in air. Opt. Commun. 2008, 281, 1268–1274. [Google Scholar] [CrossRef]
- Sainct, F.P.; Urabe, K.; Pannier, E.; Lacoste, D.A.; Laux, C.O. Electron number density measurements in nanosecond repetitively pulsed discharges in water vapor at atmospheric pressure. Plasma Sources Sci. Technol. 2020, 29, 025017. [Google Scholar] [CrossRef]
- Ralchenko, Y.V.; Griem, H.R.; Bray, I. Electron-impact broadening of the 3s-3p lines in low-Z Li-like ions. J. Quant. Spectrosc. Radiat. Transf. 2003, 81, 371–384. [Google Scholar] [CrossRef][Green Version]
- Finney, L.A.; Skrodzki, P.J.; Burger, M.; Xiao, X.; Nees, J.; Jovanovic, I. Optical emission from ultrafast laser filament-produced air plasmas in the multiple filament regime. Opt. Express 2018, 26, 29110–29122. [Google Scholar] [CrossRef] [PubMed]
- Burger, M.; Skrodzki, P.J.; Jovanovic, I.; Phillips, M.C.; Harilal, S.S. Laser-produced uranium plasma characterization and Stark broadening measurements. Phys. Plasmas 2019, 26, 093103. [Google Scholar] [CrossRef]
- Ilyin, A.A.; Golik, S.S.; Shmirko, K.A.; Mayor, A.Y.; Proschenko, D.Y.; Kulchin, Y.N. Broadening and shift of emission lines in a plasma of filaments generated by a tightly focused femtosecond laser pulse in air. Quantum Electron. 2018, 48, 149. [Google Scholar] [CrossRef]
- Compton, R.; Filin, A.; Romanov, D.A.; Levis, R.J. Dynamic Rabi sidebands in laser-generated microplasmas: Tunability and control. Phys. Rev. A 2011, 83, 053423. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Zeeman effect induced by intense laser light. Phys. Rev. Lett. 2014, 113, 083002. [Google Scholar] [CrossRef] [PubMed]
- Seidel, J.; Stamm, R. Effects of radiator motion on plasma-broadened hydrogen Lyman-β. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 499–503. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Ideal Coulomb plasma approximation in line shape models: Problematic issues. Atoms 2014, 2, 253–258. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Stambulchik, E.; Fisher, D.V.; Maron, Y.; Griem, H.R.; Alexiou, S. Correlation effects and their influence on line broadening in plasmas: Application to Hα. High Energy Density Phys. 2007, 3, 272–277. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.Á.; González-Herrero, D.; Lara, N.; et al. Ion dynamics effect on Stark broadened line shapes: A cross comparison of various models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Stambulchik, E.; Dimitrijević, M.S.; Alexiou, S.; Duan, B.; Bonifaci, N. The Third and Fourth Workshops on Spectral Line Shapes in Plasma Code Comparison: Isolated lines. Atoms 2018, 6, 30. [Google Scholar] [CrossRef]
- Rosenbusch, P.; Ghezali, S.; Dzuba, V.A.; Flambaum, V.V.; Beloy, K.; Derevianko, A. AC Stark shift of the Cs microwave atomic clock transitions. Phys. Rev. A 2009, 79, 013404. [Google Scholar] [CrossRef]
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 92. [Google Scholar] [CrossRef]
- Svidzinsky, A.A.; Eleuch, H.; Scully, M.O. Rabi oscillations produced by adiabatic pulse due to initial atomic coherence. Opt. Lett. 2017, 42, 65–68. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Heck, G.; Filin, A.; Romanov, D.A.; Levis, R.J. Decoherence of Rabi oscillations in laser-generated microplasmas. Phys. Rev. A 2013, 87, 023419. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).