Hydrogen Line Shapes in Plasmas with Large Magnetic Fields

Abstract

We report on hydrogen line shape calculations in the presence of an external magnetic field, at conditions such that the quadratic Zeeman effect is important. The latter is described through a term proportional to B² in the Hamiltonian, accounting for atomic diamagnetism. It provides a shift and an asymmetry on Lorentz triplets, and it leads to the occurrence of forbidden components. Motivated by investigations performed at the fifth edition of the Spectral Line Shape in Plasmas (SLSP5) code comparison workshop, we perform new calculations of hydrogen Lyman line profiles. Field values representative of magnetized white dwarf atmosphere conditions are taken. The calculations are done using a computer simulation technique, designed for Stark broadening modeling. A discussion of the results is done in the framework of plasma diagnostics.

1. Introduction

A significant number of white dwarfs contain a high magnetic field, with values up to 10 kT [1,2]. For such high values, the atoms emitting and absorbing radiation are subject to the quadratic Zeeman effect, which yields a perturbation of the energy levels proportional to B² in addition to the linear Zeeman perturbation. A feature of the quadratic Zeeman effect is that the Lorentz triplets observed in spectra are strongly shifted and are no longer symmetric; furthermore, the spectral lines exhibit additional components corresponding to forbidden transitions. The quadratic Zeeman effect has already been investigated in the literature, in particular for hydrogen; e.g., see [3] for a comprehensive review. Recent works have been devoted to the modeling of the combined action of the quadratic Zeeman effect and the Stark effect associated with the plasma microfield, for applications to the diagnostic of magnetized white dwarf atmospheres [4,5]. In 2019, this topic was selected as a case problem at the Spectral Line Shape in Plasmas code comparison workshop (SLSP [6], fifth edition). We here report on new line shape calculations performed in the conditions close to those considered at the workshop. The first hydrogen Lyman lines are considered.

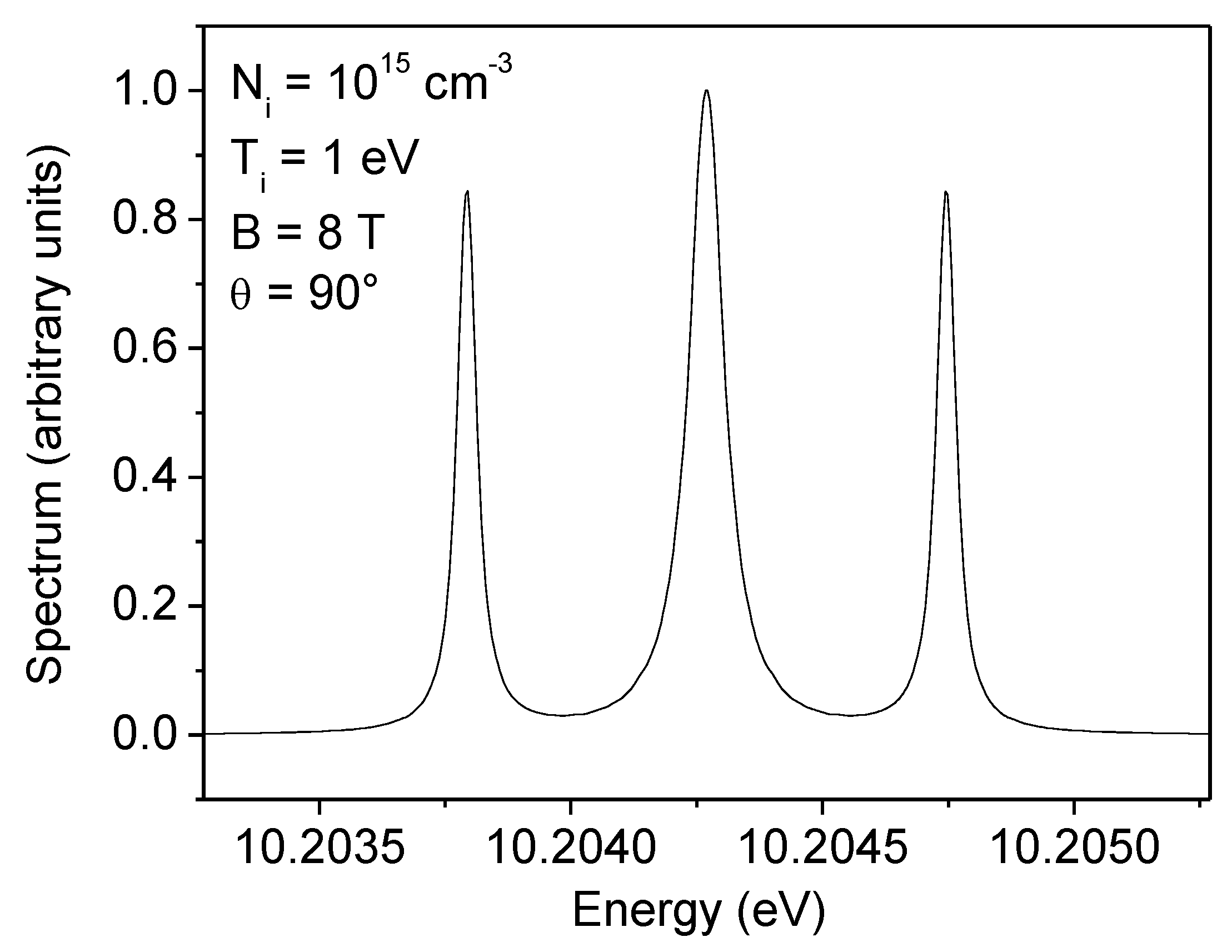
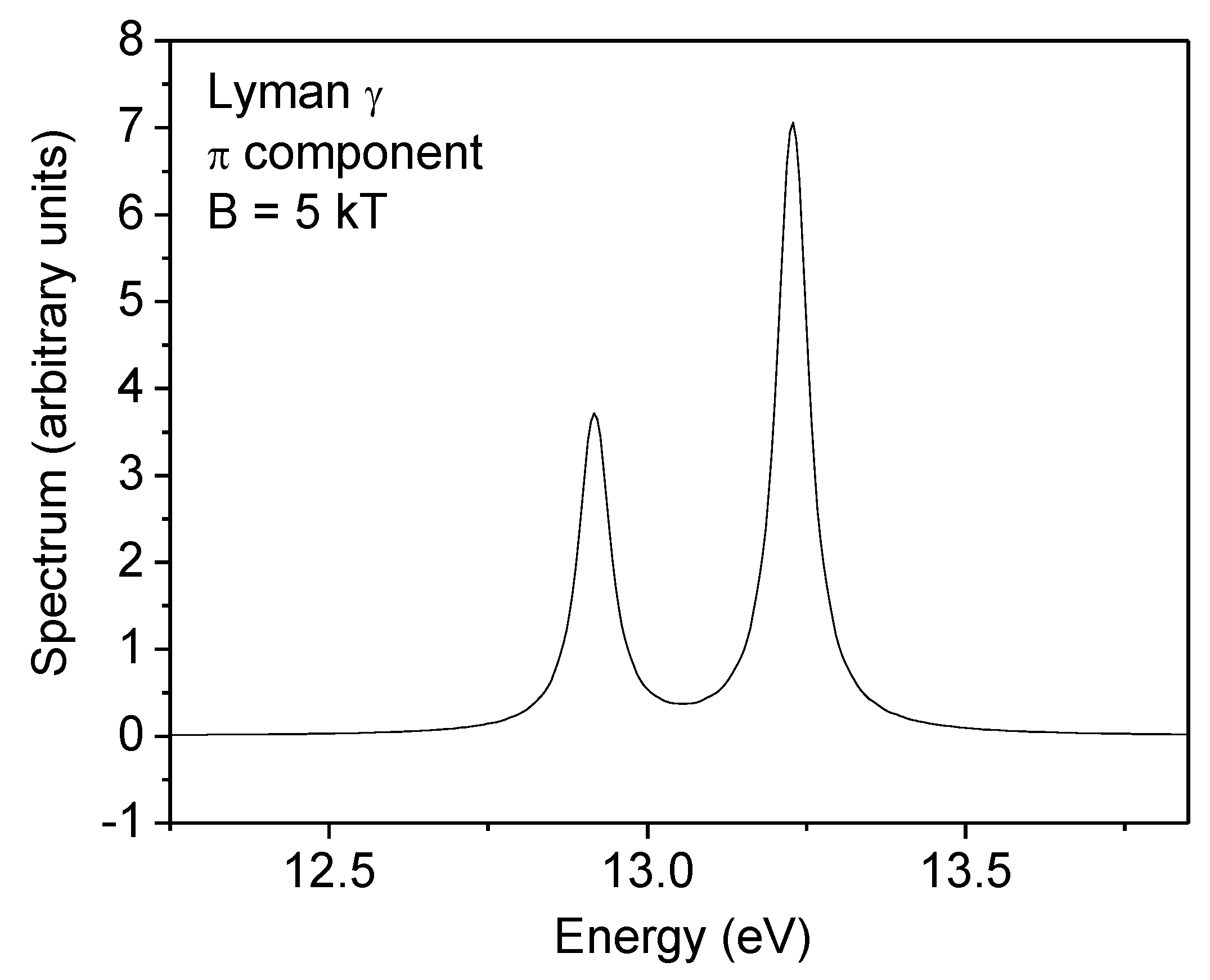
2. Line Broadening Modeling

We first give a summary of the formalism involved in line shape calculations. Consider an atom that emits or absorbs a photon (for the sake of clarity in discussions, it will always be referred to as the “emitter”) in the presence of charged particles located at its vicinity. The electric field they generate modifies the energy level structure of the emitter (Stark effect), and the resulting spectral lines are broader. The spectrum of a Stark-broadened line is proportional to the Fourier transform of the dipole autocorrelation function [7]:

$$I\left(\omega \right)=\frac{1}{\pi }\mathrm{Re}{\int }_0^{\infty }dt\left\{Tr\left[\rho \mathbf{d}\left(0\right)·\mathbf{d}\left(t\right)\right]\right\}{e}^{i\omega t}.$$

(1)

Here, d(t) denotes the atomic dipole operator expressed in the Heisenberg picture, ρ is the density operator, Tr(...) denotes a trace over the atomic states and the brackets {...} correspond to an average over the perturbers. The dipole at time t is related to its initial value through $\mathbf{d}\left(t\right)= U^{+}\left(t\right)\mathbf{d}\left(0\right)U\left(t\right)$, where $U\left(t\right) \equiv U\left(t,0\right)$ is the evolution operator from time 0 to t. The latter obeys the time-dependent Schrödinger equation:

$$i\hslash \frac{dU}{dt}\left(t\right)=\left[H_0+V\left(t\right)\right]U\left(t\right).$$

(2)

Here, H₀ is the Hamiltonian corresponding to the unperturbed atom and $V\left(t\right)=-\mathbf{d}·\mathbf{E}\left(t\right)$ is the Stark effect term; E(t) is the electric field generated at the emitter’s location by the perturbers. In the framework of the so-called standard model, the ions are assumed motionless and the electrons are described within a collisional picture in terms of a relaxation operator K_e. In practice, these two assumptions yield the substitution $-\mathbf{d}·\mathbf{E}\left(t\right)\to -\mathbf{d}·{\mathbf{E}}_i\left(0\right)-i{K}_e$ in the Stark effect term; the Schrödinger equation has an exponential solution and the line shape is obtained from a matrix inversion (e.g., [7] for details). The standard model provides a good estimate of the line broadening but it can be inaccurate in regimes such that the ions move significantly during the characteristic decorrelation time for the dipole (usually referred to as the “time-of-interest”; it is of the order of the inverse line width). More elaborate techniques using dedicated models and codes can be used (e.g., see reports of previous SLSP workshops [8,9]). In the following, we report on computer simulations performed using a code developed previously for tokamak plasma spectroscopy applications [10,11]. The Zeeman effect is retained by adding the term $-\mathsf{\mu }·\mathbf{B}$ (with μ being the magnetic moment) to H₀. An illustration is provided in Figure 1. The Lyman α line shape has been calculated in high-density tokamak divertor plasma conditions [12]. A magnetic field of 8 T has been assumed and the observation direction has been set perpendicular to B. The spectrum in the atomic frame of reference is shown, i.e., Doppler broadening due to the thermal motion of emitters is not retained. For the sake of clarity, only the contribution due to ions has been included here in the Stark broadening calculation. A density of 10¹⁵ cm⁻³ and a temperature of 1 eV have been assumed for the ions. The triplet structure visible in the spectrum is a feature of the Zeeman effect. The separation between components is proportional to B. The central component (π) is polarized parallel to the magnetic field and the lateral components (σ) are polarized perpendicular to the magnetic field. In the next section, we report on spectra calculations in magnetic white dwarf conditions. A focus is put on the case of large magnetic fields, such that the Zeeman splitting becomes a function nonlinear in B.

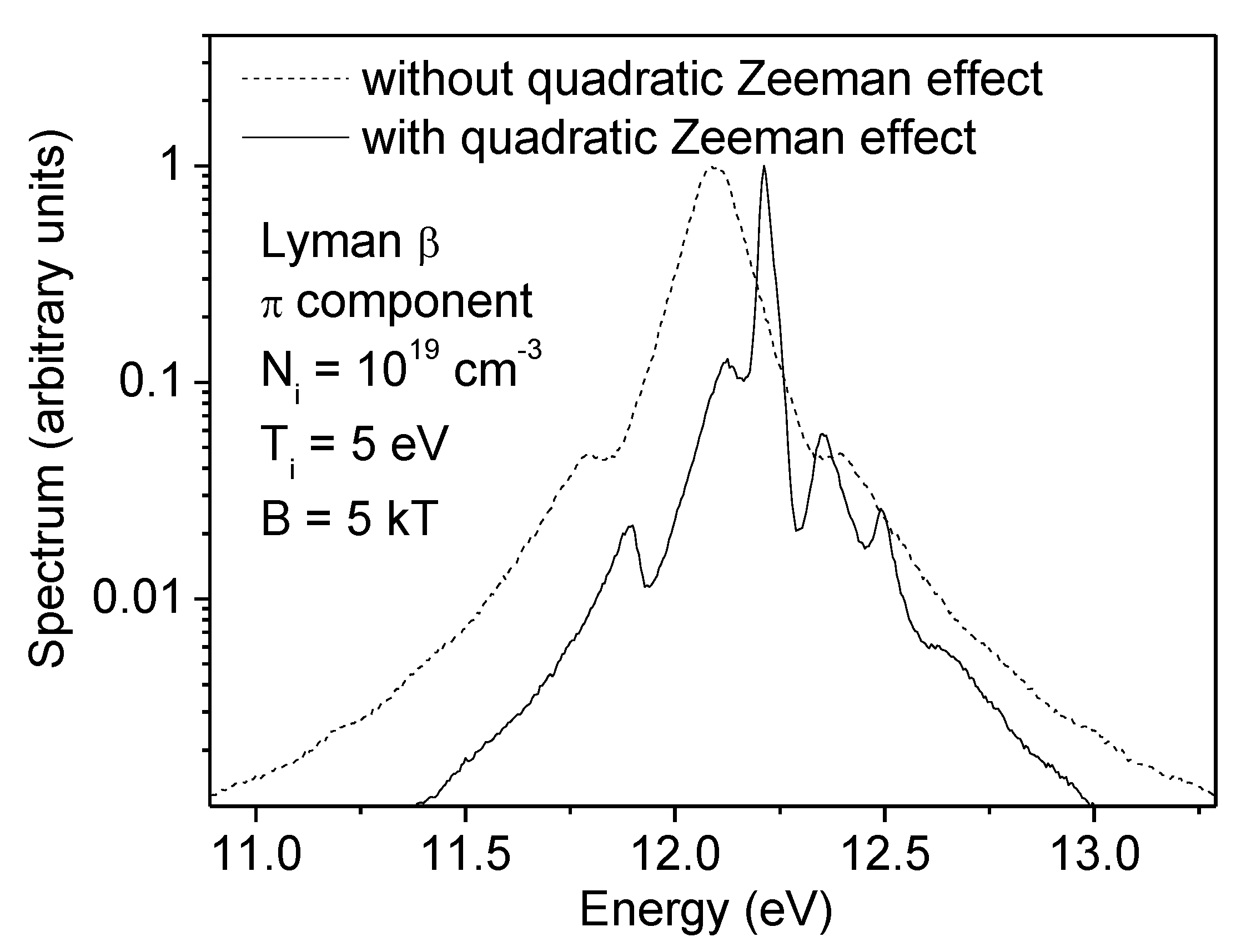
3. Investigation of Quadratic Zeeman Effect

A significant amount of white dwarf spectra exhibit lines with an asymmetric triplet structure, which is a feature of the presence of strong magnetic fields [1,2]. Simple estimates based on the separation between the components indicate that the magnetic field can attain several kiloteslas. The asymmetry stems from the contribution of the quadratic Zeeman effect to the energy level structure. This effect is retained by adding the term e²(B × r)²/8m_e (atomic diamagnetism) to the Hamiltonian H₀ [3]. An estimate based on perturbation theory indicates that the Zeeman π and σ components are not equidistant and are shifted. The energy level correction due to the quadratic Zeeman effect is given by the following diagonal matrix element

$$\langle nlm\left|\frac{e^2}{8m_e}{\left(\mathbf{B}\times \mathbf{r}\right)}^2\right|nlm\rangle =\frac{e^2{B}^2{a}_0^2}{8m_e}\frac{n^2\left[5n^2+1-3l\left(l+1\right)\right]\left(l^2+l-1+m^2\right)}{\left(2l-1\right)\left(2l+3\right)}.$$

(3)

Applying this relation to the π and σ components, one obtains, for Lyman lines,

$$\Delta E_n^{\pi }=\frac{e^2{B}^2{a}_0^2}{8m_e}\left[n^4-n^2-2\right],$$

(4)

$$\Delta E_n^{{\sigma }^{\pm }}=\pm \frac{eB}{2m_e}+\frac{e^2{B}^2{a}_0^2}{4m_e}\left[n^4-n^2-1\right],$$

(5)

where $\Delta E_n^{\pi }$ and $\Delta E_n^{{\sigma }^{\pm }}$ refer to the position of the π and σ^± components, respectively, with respect to the energy level E_n of the unperturbed atom. These relations serve as an indicator of global shift (directly through Equation (4)) and asymmetry (by noting that the energy differences $\Delta E_n^{{\sigma }^{+}}-\Delta E_n^{\pi }$ and $\Delta E_n^{\pi }-\Delta E_n^{{\sigma }^{-}}$ are different). The diagonal matrix element (3) does not provide a complete description of the quadratic Zeeman effect because the operator (B × r)² involves couplings between states with different quantum numbers n and l. A consequence is the occurrence of forbidden components, violating the |Δl| = 1 selection rule. Figure 2 gives an illustration of this property. The π component of the hydrogen Lyman γ line shape has been calculated assuming a magnetic field of 5 kT. Couplings between different n have been neglected but couplings between different l have been retained. The resulting spectrum exhibits two components, which correspond to the 4p₀-1s transition (allowed) and the 4f₀-1s transition (forbidden). A homogeneous Lorentz broadening has been assumed for each component. The numerical value for the width has been set up in order to get clean components; in particular, it does not rely on any physical mechanism here. Furthermore, for the sake of clarity, the overlap with neighboring lines has not been retained in the calculation.

The quadratic Zeeman effect is currently the subject of investigations for the design of accurate line shape models. A part of the fifth edition of the SLSP workshop was dedicated to this issue. A cross-check between line shape codes simultaneously accounting for Stark broadening and the Zeeman effect has been performed. Two test cases have been defined in the following way: (i) H Lyman α line with N_e = 10¹⁹ cm⁻³, T = 5 eV, B = 0, 0.5, 2, 5 kT; (ii) H Lyman β with the same parameter set. A pure hydrogen plasma is considered in each case, and no couplings between different n are considered. We show in Figure 3 an example of the result. The π component of Lyman β, obtained assuming Stark broadening due to ions only, is plotted. The two curves visible in the figure correspond to one calculation done retaining the linear Zeeman effect only and one calculation done retaining both linear and quadratic Zeeman effects. The overlap with neighboring lines has not been retained, again for the sake of clarity. As can be seen in the figure, the spectrum is split in many components when the quadratic Zeeman is retained. These components are a consequence of the simultaneous action of the magnetic field and the plasma’s microscopic electric field on the atomic energy levels. Presently, no analytical formula is applicable to the modeling of such a spectrum in a general case. New calculations are presently underway in order to have a better understanding of this structure. They will involve both codes and models based on specific approximations (such as the standard model discussed above).

4. Conclusions

New hydrogen line shape calculations have been performed with the assumption that a high magnetic field is present. A focus has been put on the quadratic Zeeman effect. This effect is accounted for through an additional term, proportional to B², in the atomic Hamiltonian. It provides a shift and an asymmetry on Lorentz triplets, and it leads to the occurrence of forbidden components. We have illustrated these properties through calculations of Lyman lines in ideal cases. In the framework of plasma spectroscopy modeling, we have shown that the simultaneous action of Stark and Zeeman effects results in spectra presenting a complex structure, with many components. New calculations are presently underway in order to have a better understanding of this issue. Applications to the diagnostic of magnetic white dwarf atmospheres will be performed. An additional issue that will be addressed is the modification of the particle trajectories due to the magnetic field, and how this alters spectral line shapes. New investigations will be done along the lines of previous works [13,14,15].