Study of Electron and Positron Elastic Scattering from Hydrogen Sulphide Using Analytically Obtained Static Potential
Abstract
1. Introduction
2. Theory
2.1. Scattering Amplitude and Cross Sections
2.2. Complex Optical Potential
3. Results and Discussion
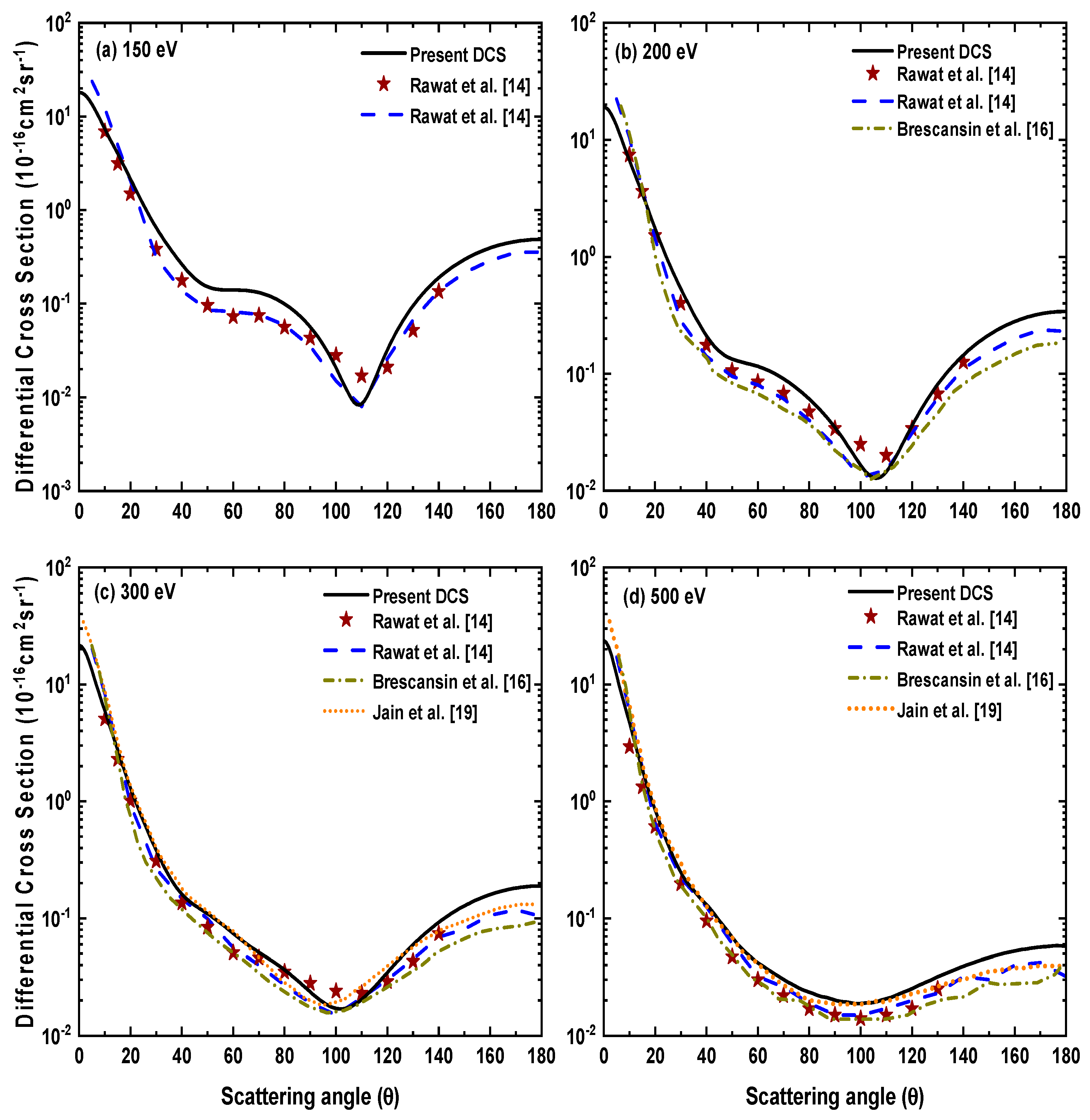
3.1. Electron-H2S Differential Cross Sections
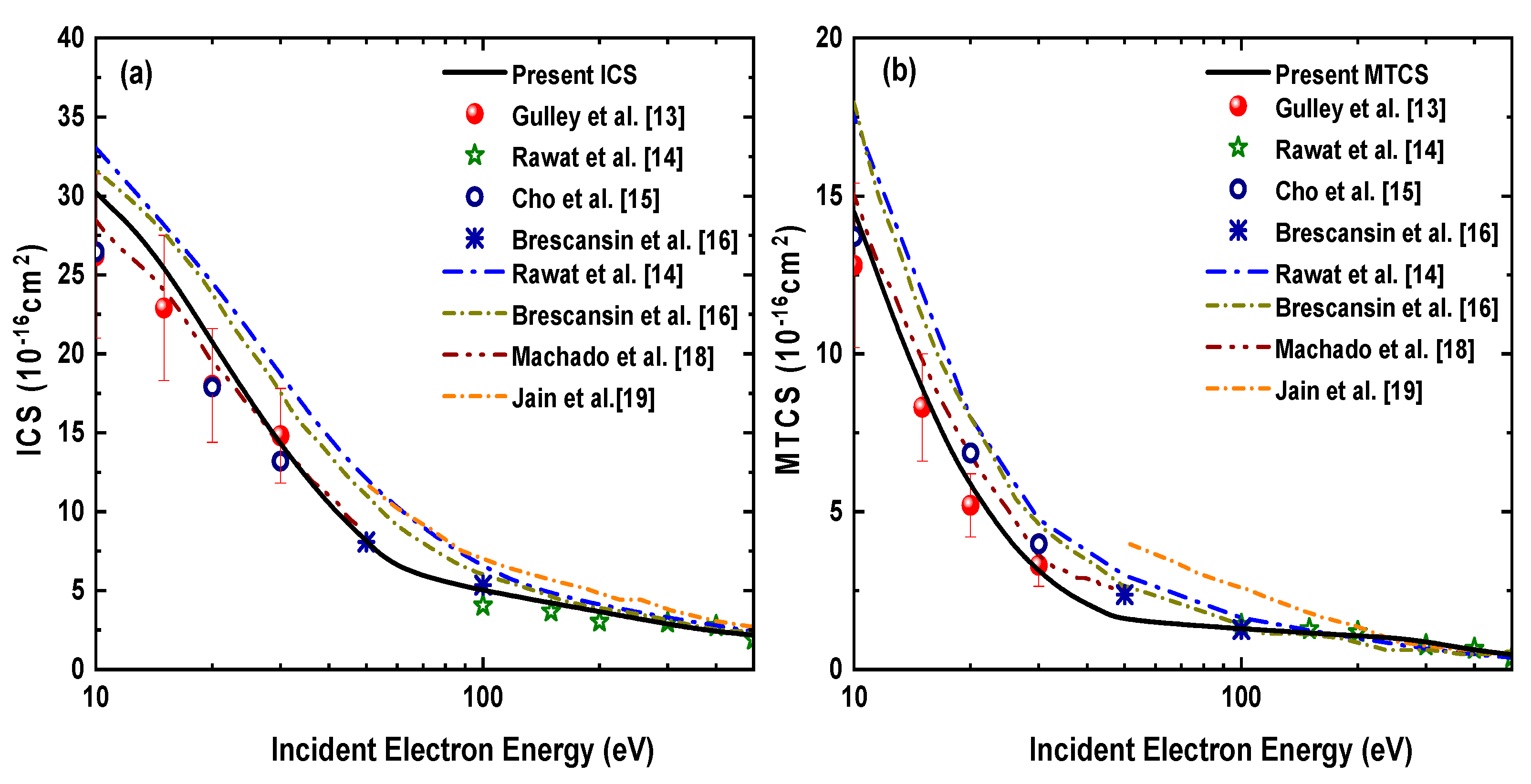
3.2. Electron-H2S Integral and Momentum Transfer Cross Section
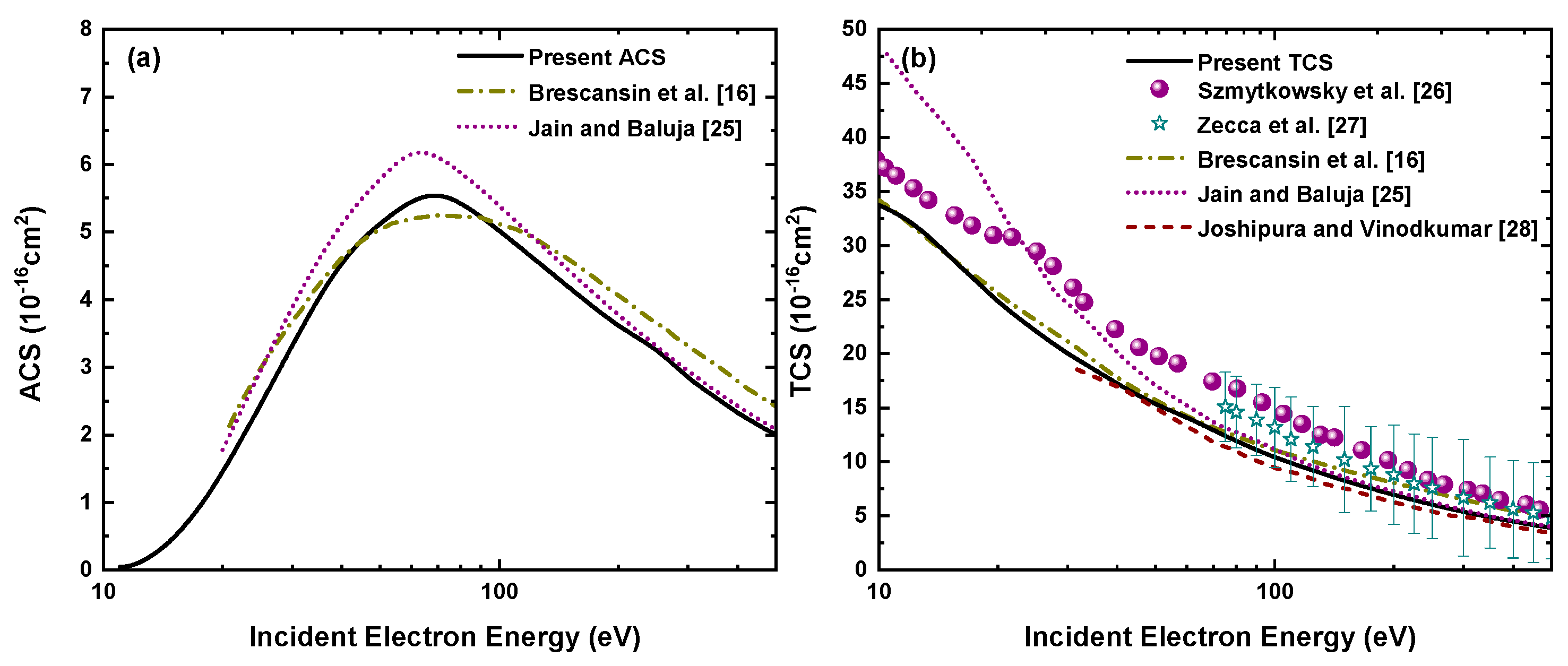
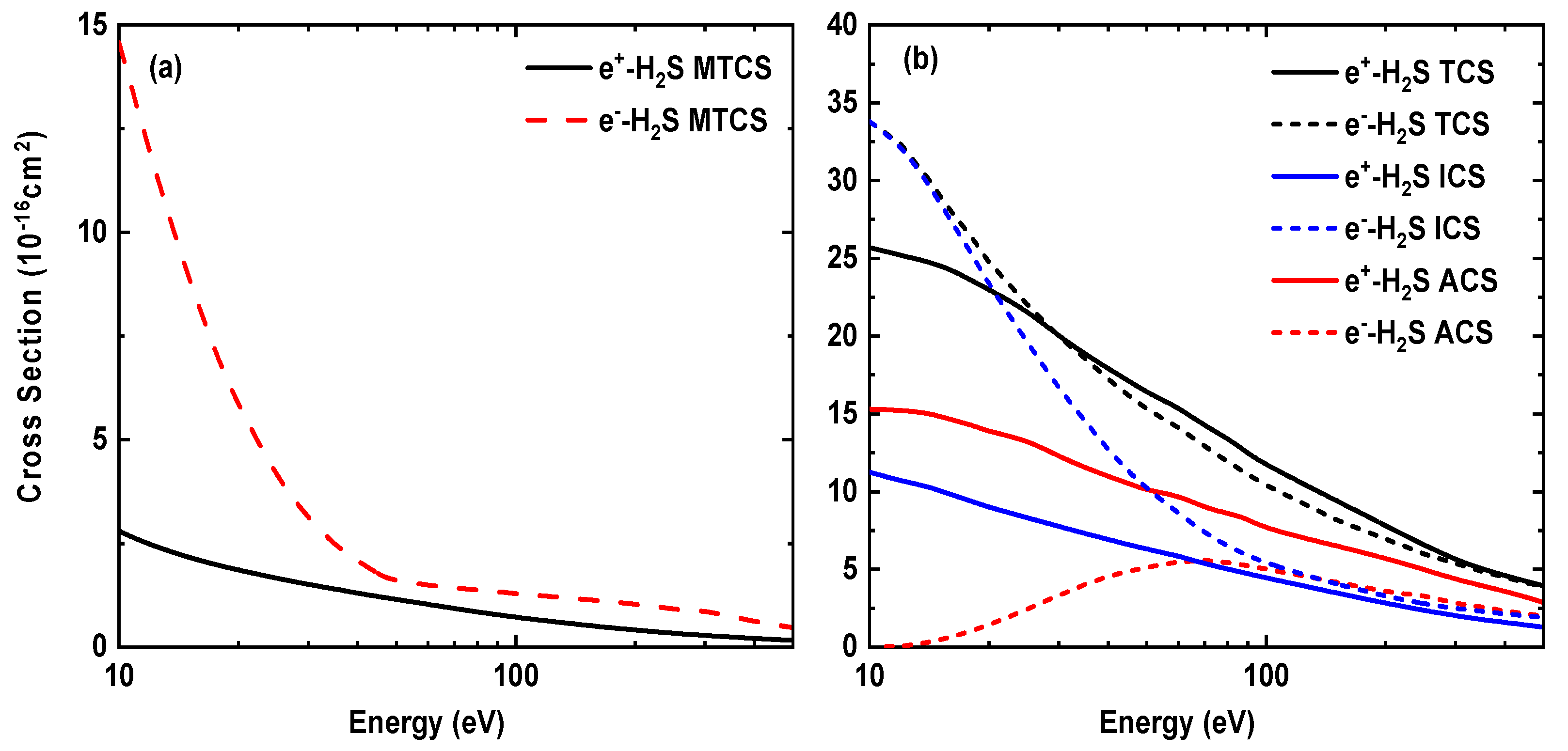
3.3. Electron-H2S Absorption and Total Cross Section
3.4. Positron-H2S Differential Cross Section
3.5. Positron-H2S Elastic, Momentum, Absorption and Total Cross Section
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bockelée-Morvan, D.; Colom, P.; Crovisier, J.; Despois, D.; Paubert, G. Microwave detection of hydrogen sulphide and methanol in comet Austin (1989c1). Nature 1991, 350, 318–320. [Google Scholar] [CrossRef]
- Irwin, P.G.J.; Toledo, D.; Garland, R.; Teanby, N.A.; Fletcher, L.N.; Orton, G.A.; Bézard, B. Detection of hydrogen sulfide above the clouds in Uranus’s atmosphere. Nat. Astron. 2018, 2, 420–427. [Google Scholar] [CrossRef]
- Phuong, N.T.; Chapillon, E.; Majumdar, L.; Dutrey, A.; Guilloteau, S.; Piétu, V.; Wakelam, V.; Diep, P.N.; Tang, Y.-W.; Beck, T.; et al. First detection of H2S in a protoplanetary disk. Astron. Astrophys. 2018, 616, L5. [Google Scholar] [CrossRef]
- Chupp, E.L.; Forrest, D.J.; Higbie, P.R.; Suri, A.N.; Tsai, C.; Dunphy, P.P. Solar Gamma Ray Lines observed during the Solar Activity of August 2 to August 11, 1972. Nature 1973, 241, 333–335. [Google Scholar] [CrossRef]
- Leventhal, M.; MacCallum, C.J.; Stang, P.D. Detection of 511 keV positron annihilation radiation from the galactic center direction. Astrophys. J. 1978, 225, L11–L14. [Google Scholar] [CrossRef]
- Trajmar, S.; Register, D.F.; Chutjian, A. Electron scattering by molecules II. Experimental methods and data. Phys. Rep. 1983, 97, 219–356. [Google Scholar] [CrossRef]
- Wang, R.; Fan, Q.; Zhang, J.; Zhang, X.; Kang, Y.; Wang, Z. Hydrogen Sulfide Demonstrates Promising Antitumor Efficacy in Gastric Carcinoma by Targeting MGAT5 1,2. Transl. Oncol. 2018, 11, 900–910. [Google Scholar] [CrossRef]
- Wen, Y.-D.; Wang, H.; Zhu, Y.-Z. The Drug Developments of Hydrogen Sulfide on Cardiovascular Disease. Oxid. Med. Cell. Longev. 2018, 2018, 4010395. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Baró, J.; Sempau, J.; Fernández-Varea, J.M.; Salvat, F. PENELOPE: An algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl. Instrum. Methods Phys. Res. B 1995, 100, 31–46. [Google Scholar] [CrossRef]
- Blanco, F.; Muñoz, A.; Almeida, D.; da Silva, F.F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Ruset, C.; Bloyce, A.; Bell, T. Plasma nitrocarburising with nitrogen, hydrogen, and hydrogen sulphide gas mixtures. Surf. Eng. 1995, 11, 308–314. [Google Scholar] [CrossRef]
- Gulley, R.J.; Brunger, M.J.; Buckman, S.J. The scattering of low energy electrons from hydrogen sulphide. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 2913–2925. [Google Scholar] [CrossRef]
- Rawat, P.; Iga, I.; Lee, M.-T.; Brescansin, L.M.; Homem, M.G.P.; Machado, L.E. Cross sections for elastic electron–hydrogen sulfide collisions in the low- and intermediate-energy range. Phys. Rev. A 2003, 68, 052711. [Google Scholar] [CrossRef]
- Cho, H.; Park, S.J.; Park, Y.S. Measurements of elastic electron scattering by hydrogen sulfide extended to backward angles. J. Korean Phys. Soc. 2005, 46, 431–434. [Google Scholar]
- Brescansin, L.M.; Machado, L.E.; Lee, M.-T.; Cho, H.; Park, Y.S. Absorption effects in intermediate-energy electron scattering by hydrogen sulphide. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 185201. [Google Scholar] [CrossRef]
- Varella, M.T.d.N.; Bettega, M.H.F.; Lima, M.A.P.; Ferreira, L.G. Low-energy electron scattering by H2O, H2S, H2Se, and H2Te. J. Chem. Phys. 1999, 111, 6396–6406. [Google Scholar] [CrossRef]
- Machado, L.E.; Leal, E.P.; Mu-Tao, L.; Brescansin, L.M. Low energy elastic scattering of electrons by hydrogen sulphide molecules. J. Mol. Struct. THEOCHEM 1995, 335, 37–43. [Google Scholar] [CrossRef]
- Jain, A.K.; Tripathi, N.; Jain, A. Elastic scattering ofelectrons by H2S at 50—1000 eV. Phys. Rev. A 1990, 42, 6912–6915. [Google Scholar] [CrossRef]
- Gianturco, F.A. Ab initio model calculations to treat electron scattering from polar polyatomic targets: H2S and NH3. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 4627–4648. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, Z. Electron scattering with H2S and PH3 molecules. Zeitschrift Für Phys. D Atoms Mol. Clust. 1993, 28, 207–214. [Google Scholar] [CrossRef]
- Nishimura, T.; Itikawa, Y. Vibrationally elastic and inelastic scattering of electrons by hydrogen sulphide molecules. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4213–4226. [Google Scholar] [CrossRef]
- Gupta, M.; Baluja, K.L. Application of R-matrix method to electron-H2S collisions in the low energy range. Eur. Phys. J. D 2007, 41, 475–483. [Google Scholar] [CrossRef]
- Aouchiche, H.; Medegga, F.; Champion, C. Doubly differential and integral cross sections for electron elastic scattering by hydrogen sulfide. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2014, 333, 113–119. [Google Scholar] [CrossRef]
- Jain, A.; Baluja, K.L. Total (elastic plus inelastic) cross sections for electron scattering from diatomic and polyatomic molecules at 10—5000 eV: H2, Li2, HF, CH4, N2, CO, C2H2, HCN, O2, HC1, H2S, PH3, SiH4, and CO2. Phys. Rev. A 1992, 45, 202–218. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Mozejko, P.; Krzysztofowicz, A. Measurements of absolute total cross sections for electron scattering from triatomic polar molecules: SO2 and H2S. Radiat. Phys. Chem. 2003, 68, 307–311. [Google Scholar] [CrossRef]
- Zecca, A.; Karwasz, G.P.; Brusa, R.S. Total-cross-section measurements for electron scattering by NH3, SiH4, and H2S in the intermediate-energy range. Phys. Rev. A 1992, 45, 2777–2783. [Google Scholar] [CrossRef]
- Joshipura, K.N.; Vinodkumar, M. Total cross sections of electron collisions with S atoms; H2S, OCS and SO2 molecules (E i ≥ 50 eV). Z. Phys. D 1997, 41, 133–137. [Google Scholar] [CrossRef]
- Limbachiya, C.; Vinodkumar, M.; Mason, N. Calculation of electron-impact rotationally elastic total cross sections for NH3, H2S, and PH3 over the energy range from 0.01 eV to 2 keV. Phys. Rev. A 2011, 83, 042708. [Google Scholar] [CrossRef]
- Joachain, C.J. Quantum Collision Theory, 3rd ed.; North Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Schiff, L.I. Quantum Mechanics, 3rd ed.; Tata McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Milisavljević, S.; Šević, D.; Chauhan, R.K.; Pejčev, V.; Filipović, D.M.; Srivastava, R.; Marinković, B.P. Differential and integrated cross sections for the. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2371–2384. [Google Scholar] [CrossRef]
- Tennyson, J. Electron-molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347–425. [Google Scholar] [CrossRef]
- Sanna, N.; Baccarelli, I.; Morelli, G. SCELib3.0: The new revision of SCELib, the parallel computational library of molecular properties in the Single Center Approach. Comput. Phys. Commun. 2009, 180, 2544–2549. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Scialla, S. Local approximations of exchange interaction in electron-molecule collisions: The methane molecule. J. Phys. B At. Mol. Phys. 1987, 20, 3171–3189. [Google Scholar] [CrossRef]
- O’Connell, J.K.; Lane, N.F. Nonadjustable exchange-correlation model for electron scattering from closed-shell atoms and molecules. Phys. Rev. A 1983, 27, 1893–1903. [Google Scholar] [CrossRef]
- Padial, N.T.; Norcross, D.W. Parameter-free model of the correlation-polarization potential for electron-molecule collisions. Phys. Rev. A 1984, 29, 1742–1748. [Google Scholar] [CrossRef]
- Staszewska, G.; Schwenke, D.W.; Thirumalai, D.; Truhlar, D.G. Quasifree-scattering model for the imaginary part of the optical potential for electron scattering. Phys. Rev. A. 1983, 28, 2740–2751. [Google Scholar] [CrossRef]
- Jain, A. Low-energy positron-argon collisions by using parameter-free positron correlation polarization potentials. Phys. Rev. A 1990, 41, 2437–2444. [Google Scholar] [CrossRef]
- Reid, D.D.; Wadehra, J.M. A quasifree model for the absorption effects in positron scattering by atoms. J. Phys. B At. Mol. Opt. Phys. 1996, 29, L127–L133. [Google Scholar] [CrossRef]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules, 2nd ed.; Prentice Hall Pearson: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Das, T.; Stauffer, A.D.; Srivastava, R. A method to obtain static potentials for electron-molecule scattering. Eur. Phys. J. D 2014, 68, 102. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Stauffer, A.D.; Srivastava, R. Electron impact elastic scattering from methane and silane molecules. Eur. Phys. J. D 2019, 73, 189. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Srivastava, R. An approach to study electron and positron scattering from NH3 and PH3 using the analytic static potential. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 225204. [Google Scholar] [CrossRef]
- Tóth, I.; Campeanu, R.I.; Chiş, V.; Nagy, L. Screening effects in the ionization of molecules by positrons. Phys. Lett. A 2006, 360, 131–134. [Google Scholar] [CrossRef]
- Tóth, I.; Campeanu, R.I.; Nagy, L. Ionization of NH3 and CH4 by electron impact. Eur. Phys. J. D 2015, 69, 2. [Google Scholar] [CrossRef]
- Stevens, D.; Babij, T.J.; Machacek, J.R.; Buckman, S.J.; Brunger, M.J.; White, R.D.; García, G.; Blanco, F.; Ellis-Gibbings, L.; Sullivan, J.P. Positron scattering from pyridine. J. Chem. Phys. 2018, 148, 144308. [Google Scholar] [CrossRef]
- Olney, T.N.; Cann, N.M.; Cooper, G.; Brion, C.E. Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum-rules. Chem. Phys. 1997, 223, 59–98. [Google Scholar] [CrossRef]
- Lias, S.G. NIST Chemistry WebBook, NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020. [Google Scholar]
- Lidez, D.R. CRC Handbook of Physics and Chemistry, 74th ed.; Chemical Rubber Company, Ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Da Paixo, F.J.; Lima, M.A.P.; McKoy, V. Spin exchange in elastic e-O2 collisions. Phys. Rev. Lett. 1992, 68, 1698–1701. [Google Scholar] [CrossRef]
- Makochekanwa, C.; Sueoka, O.; Kimura, M. Similarities and differences between electron and positron scattering from molecules. J. Phys. Conf. Ser. 2007, 80, 012012. [Google Scholar] [CrossRef]




| Energy Eigenvalues (eV) | −91.82436 | −8.62558 | −6.31578 | −6.31354 | −6.31008 | −0.88948 | −0.50648 | −0.39461 | −0.28071 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1s | 0.99783 | −0.35478 | 0.00000 | −0.00731 | 0.00000 | 0.08458 | 0.00000 | 0.04775 | 0.00000 | |
| S | 2s | 0.00649 | 1.04753 | 0.00000 | 0.02175 | 0.00000 | −0.28399 | 0.00000 | −0.14345 | 0.00000 |
| 2px | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.98740 | 0.00000 | 0.00000 | 0.00000 | −0.30318 | |
| 2py | 0.00000 | 0.00000 | 0.98494 | 0.00000 | 0.00000 | 0.00000 | −0.18896 | 0.00000 | 0.00000 | |
| 2pz | −0.00017 | −0.01711 | 0.00000 | 0.98503 | 0.00000 | 0.05106 | 0.00000 | −0.22009 | 0.00000 | |
| 3s | −0.00087 | 0.04782 | 0.00000 | −0.01091 | 0.00000 | 0.79115 | 0.00000 | 0.61998 | 0.00000 | |
| 3px | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.04632 | 0.00000 | 0.00000 | 0.00000 | 1.03186 | |
| 3py | 0.00000 | 0.00000 | 0.05717 | 0.00000 | 0.00000 | 0.00000 | 0.54074 | 0.00000 | 0.00000 | |
| 3pz | 0.00016 | −0.00875 | 0.00000 | 0.05621 | 0.00000 | −0.12548 | 0.00000 | 0.68194 | 0.00000 | |
| H1 | 1s | 0.00021 | −0.01041 | −0.01140 | 0.01169 | 0.00000 | 0.21629 | 0.48298 | −0.33510 | 0.00000 |
| H2 | 1s | 0.00021 | −0.01041 | 0.01140 | 0.01169 | 0.00000 | 0.21629 | −0.48298 | −0.33510 | 0.00000 |
| Atom | Orbital | Exponent | Coefficient |
|---|---|---|---|
| S | 1s | 0.5529038289E + 04 | 0.9163596281E − 02 |
| 0.1013743118E + 04 | 0.4936149294E − 01 | ||
| 0.2836087927E + 03 | 0.1685383049E + 00 | ||
| 0.9742727471E + 02 | 0.3705627997E + 00 | ||
| 0.3783386178E + 02 | 0.4164915298E + 00 | ||
| 0.1558207360E + 02 | 0.1303340841E + 00 | ||
| 2s | 0.3455896791E + 03 | −0.1325278809E − 01 | |
| 0.6840121655E + 02 | −0.4699171014E − 01 | ||
| 0.2125904712E + 02 | −0.3378537151E − 01 | ||
| 0.8179121699E + 01 | 0.2502417861E + 00 | ||
| 0.3552198128E + 01 | 0.5951172526E + 00 | ||
| 0.1628232301E + 01 | 0.2407061763E + 00 | ||
| 2p | 0.3455896791E + 03 | 0.3759696623E − 02 | |
| 0.6840121655E + 02 | 0.3767936984E − 01 | ||
| 0.2125904712E + 02 | 0.1738967435E + 00 | ||
| 0.8179121699E + 01 | 0.4180364347E + 00 | ||
| 0.3552198128E + 01 | 0.4258595477E + 00 | ||
| 0.1628232301E + 01 | 0.1017082955E + 00 | ||
| 3s | 0.1294439442E + 02 | −0.7943126362E − 02 | |
| 0.3466625105E + 01 | −0.7100264172E − 01 | ||
| 0.1300021248E + 01 | −0.1785026925E + 00 | ||
| 0.5819134077E + 00 | 0.1510635058E + 00 | ||
| 0.2879592903E + 00 | 0.7354914767E + 00 | ||
| 0.1484042983E + 00 | 0.2760593123E + 00 | ||
| 3p | 0.1294439442E + 02 | −0.7139358907E − 02 | |
| 0.3466625105E + 01 | −0.1829277070E − 01 | ||
| 0.1300021248E + 01 | 0.7621621429E − 01 | ||
| 0.5819134077E + 00 | 0.4145098597E + 00 | ||
| 0.2879592903E + 00 | 0.4889621471E + 00 | ||
| 0.1484042983E + 00 | 0.1058816521E + 00 | ||
| H | 1s | 0.3552322122E + 02 | 0.9163596281E − 02 |
| 0.6513143725E + 01 | 0.4936149294E − 01 | ||
| 0.1822142904E + 01 | 0.1685383049E + 00 | ||
| 0.6259552659E + 00 | 0.3705627997E + 00 | ||
| 0.2430767471E + 00 | 0.4164915298E + 00 | ||
| 0.1001124280E + 00 | 0.1303340841E + 00 |
| DCS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Angle (deg) | 15 eV | 20 eV | 50 eV | 100 eV | 150 eV | 200 eV | 300 eV | 500 eV |
| 0 | 25.1610 | 26.6501 | 34.0321 | 17.0130 | 18.1060 | 19.0440 | 21.5230 | 23.6450 |
| 5 | 24.1281 | 25.2460 | 29.9162 | 13.9210 | 13.5510 | 13.2680 | 13.1140 | 11.9590 |
| 10 | 21.2822 | 21.6572 | 21.4790 | 8.6657 | 7.3693 | 6.7151 | 5.9198 | 4.7034 |
| 15 | 17.5680 | 17.2411 | 14.1612 | 5.1474 | 4.0113 | 3.4772 | 2.7449 | 1.8663 |
| 20 | 13.8621 | 13.1460 | 9.0720 | 3.0349 | 2.1488 | 1.7617 | 1.2962 | 0.8442 |
| 30 | 8.0617 | 7.2216 | 2.9852 | 0.9611 | 0.6514 | 0.5354 | 0.3810 | 0.2470 |
| 40 | 4.3292 | 3.5418 | 0.5673 | 0.3287 | 0.2632 | 0.2117 | 0.1607 | 0.1305 |
| 50 | 2.0106 | 1.3875 | 0.0237 | 0.1466 | 0.1517 | 0.1334 | 0.1095 | 0.0689 |
| 60 | 0.7741 | 0.3847 | 0.0513 | 0.1302 | 0.1403 | 0.1156 | 0.0743 | 0.0419 |
| 70 | 0.2951 | 0.1135 | 0.1489 | 0.1692 | 0.1316 | 0.0905 | 0.0512 | 0.0302 |
| 80 | 0.2221 | 0.2033 | 0.2148 | 0.1839 | 0.0994 | 0.0608 | 0.0364 | 0.0236 |
| 90 | 0.2801 | 0.3758 | 0.2378 | 0.1484 | 0.0563 | 0.0348 | 0.0236 | 0.0201 |
| 100 | 0.3250 | 0.4784 | 0.2183 | 0.0799 | 0.0207 | 0.0165 | 0.0171 | 0.0189 |
| 110 | 0.3303 | 0.4674 | 0.1603 | 0.0174 | 0.0085 | 0.0145 | 0.0204 | 0.0207 |
| 120 | 0.3491 | 0.3908 | 0.0879 | 0.0037 | 0.0321 | 0.0358 | 0.0347 | 0.0252 |
| 130 | 0.4512 | 0.3237 | 0.0362 | 0.0692 | 0.0953 | 0.0811 | 0.0596 | 0.0318 |
| 140 | 0.6762 | 0.3374 | 0.0357 | 0.2189 | 0.1894 | 0.1444 | 0.0925 | 0.0391 |
| 150 | 1.0033 | 0.4515 | 0.0898 | 0.2462 | 0.2968 | 0.2150 | 0.1279 | 0.0464 |
| 160 | 1.3501 | 0.6156 | 0.1789 | 0.6397 | 0.3949 | 0.2796 | 0.1596 | 0.0527 |
| 170 | 1.6156 | 0.7661 | 0.2539 | 0.7997 | 0.4634 | 0.3249 | 0.1814 | 0.0569 |
| 180 | 1.7216 | 0.8306 | 0.2913 | 0.8589 | 0.4881 | 0.3415 | 0.1889 | 0.0579 |
| ICS | 25.50 | 20.73 | 8.15 | 4.97 | 4.13 | 3.68 | 2.86 | 2.19 |
| MTCS | 8.91 | 5.83 | 1.51 | 1.15 | 1.07 | 1.07 | 0.88 | 0.47 |
| ACS | 0.55 | 1.44 | 5.12 | 5.02 | 4.18 | 3.59 | 2.83 | 1.99 |
| TCS | 28.61 | 24.76 | 15.33 | 10.41 | 8.19 | 6.94 | 5.42 | 3.89 |
| DCS | ||||
|---|---|---|---|---|
| Angle (deg) | 20 eV | 50 eV | 100 eV | 500 eV |
| 0 | 16.7280 | 15.7601 | 15.0310 | 16.439 |
| 5 | 14.3860 | 10.8720 | 7.0699 | 1.0818 |
| 10 | 9.3056 | 4.2009 | 1.4995 | 2.3921 |
| 15 | 5.0222 | 1.3262 | 0.4113 | 2.2818 |
| 20 | 2.4881 | 0.3603 | 0.5887 | 1.1657 |
| 30 | 0.4157 | 0.3904 | 0.8018 | 0.2895 |
| 40 | 0.1007 | 0.5507 | 0.5577 | 0.1292 |
| 50 | 0.2471 | 0.4176 | 0.1975 | 0.0648 |
| 60 | 0.3645 | 0.2342 | 0.1214 | 0.0384 |
| 70 | 0.3504 | 0.1311 | 0.0982 | 0.0227 |
| 80 | 0.2744 | 0.0956 | 0.0778 | 0.0171 |
| 90 | 0.1868 | 0.0862 | 0.0584 | 0.0119 |
| 100 | 0.1259 | 0.0799 | 0.0447 | 0.0095 |
| 110 | 0.0927 | 0.0711 | 0.0364 | 0.0078 |
| 120 | 0.0796 | 0.0616 | 0.0311 | 0.0064 |
| 130 | 0.0785 | 0.0532 | 0.0275 | 0.0059 |
| 140 | 0.0817 | 0.0472 | 0.0248 | 0.0049 |
| 150 | 0.0852 | 0.0434 | 0.0229 | 0.0047 |
| 160 | 0.0870 | 0.0416 | 0.0219 | 0.0043 |
| 170 | 0.0889 | 0.0398 | 0.0208 | 0.0041 |
| 180 | 0.0893 | 0.0394 | 0.0206 | 0.0048 |
| ICS | 9.01 | 6.30 | 4.45 | 1.28 |
| MTCS | 1.86 | 1.15 | 0.72 | 0.17 |
| ACS | 14.03 | 10.09 | 7.24 | 2.66 |
| TCS | 23.04 | 16.39 | 11.69 | 3.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahato, D.; Sharma, L.; Srivastava, R. Study of Electron and Positron Elastic Scattering from Hydrogen Sulphide Using Analytically Obtained Static Potential. Atoms 2020, 8, 83. https://doi.org/10.3390/atoms8040083
Mahato D, Sharma L, Srivastava R. Study of Electron and Positron Elastic Scattering from Hydrogen Sulphide Using Analytically Obtained Static Potential. Atoms. 2020; 8(4):83. https://doi.org/10.3390/atoms8040083
Chicago/Turabian StyleMahato, Dibyendu, Lalita Sharma, and Rajesh Srivastava. 2020. "Study of Electron and Positron Elastic Scattering from Hydrogen Sulphide Using Analytically Obtained Static Potential" Atoms 8, no. 4: 83. https://doi.org/10.3390/atoms8040083
APA StyleMahato, D., Sharma, L., & Srivastava, R. (2020). Study of Electron and Positron Elastic Scattering from Hydrogen Sulphide Using Analytically Obtained Static Potential. Atoms, 8(4), 83. https://doi.org/10.3390/atoms8040083







