Magic Wavelengths for Optical-Lattice Based Cs and Rb Active Clocks
Abstract
1. Introduction
2. Method of Evaluation
3. Results
3.1. Static Polarizabilities
3.2. Magic Wavelengths
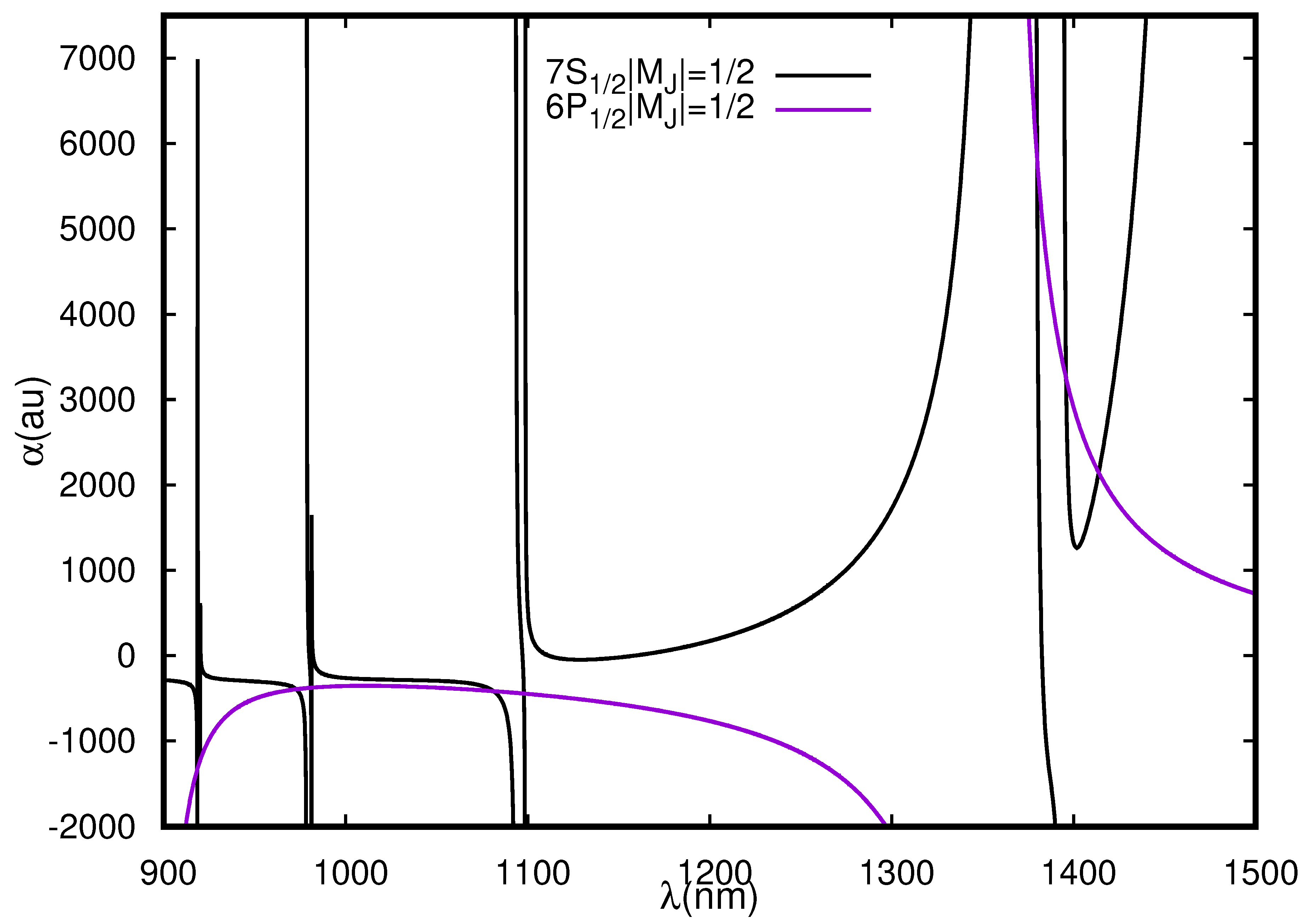
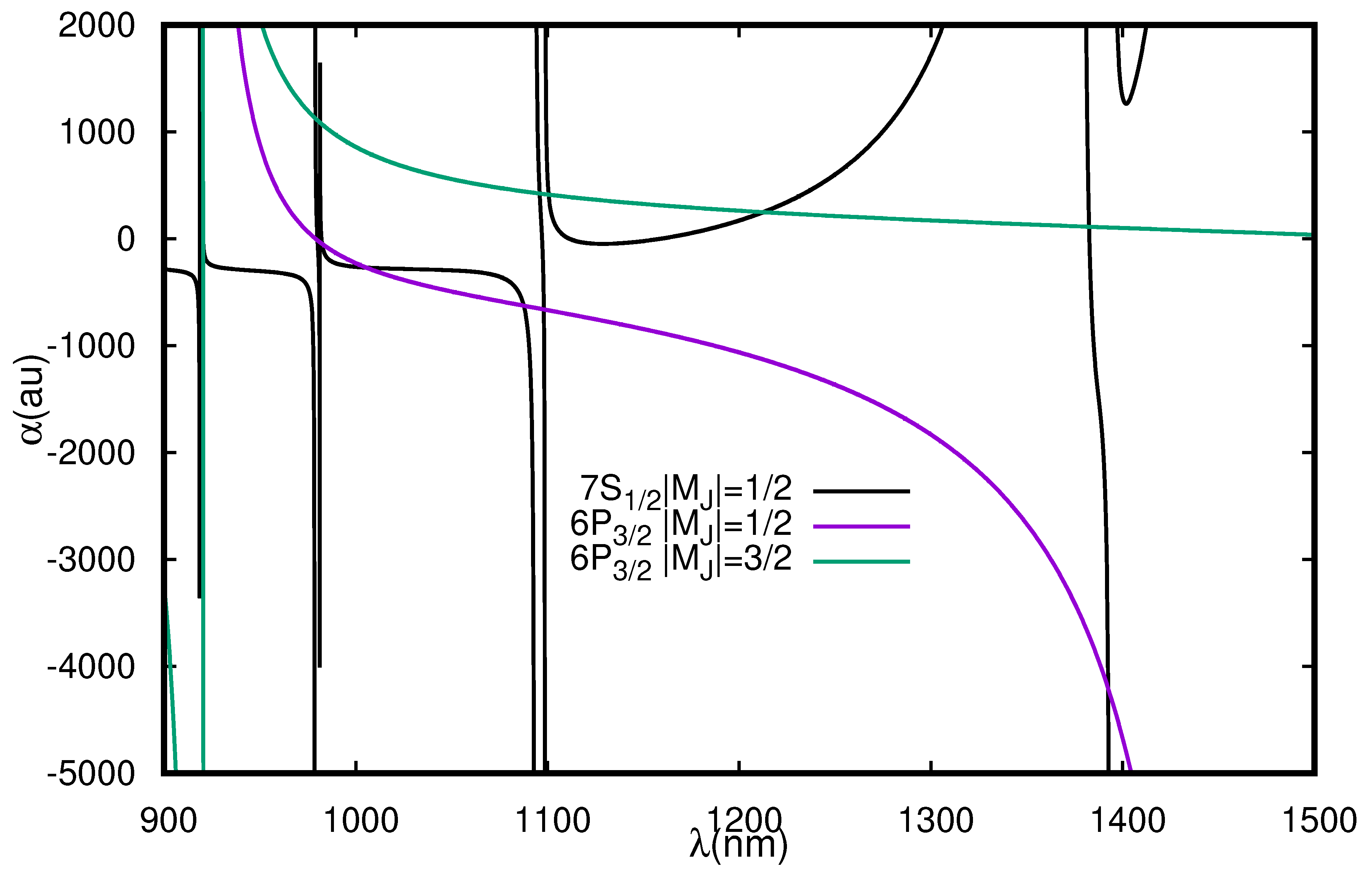
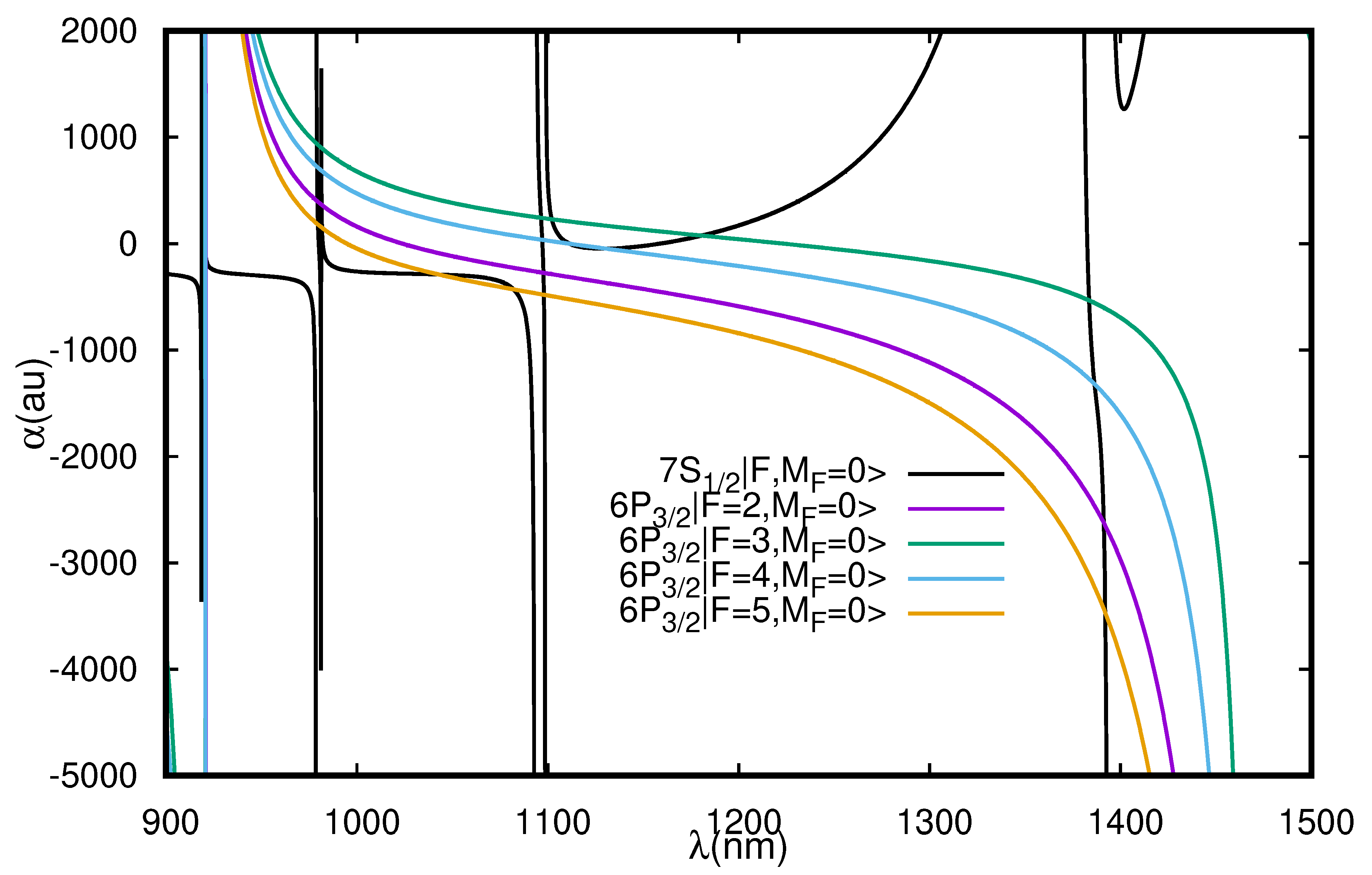
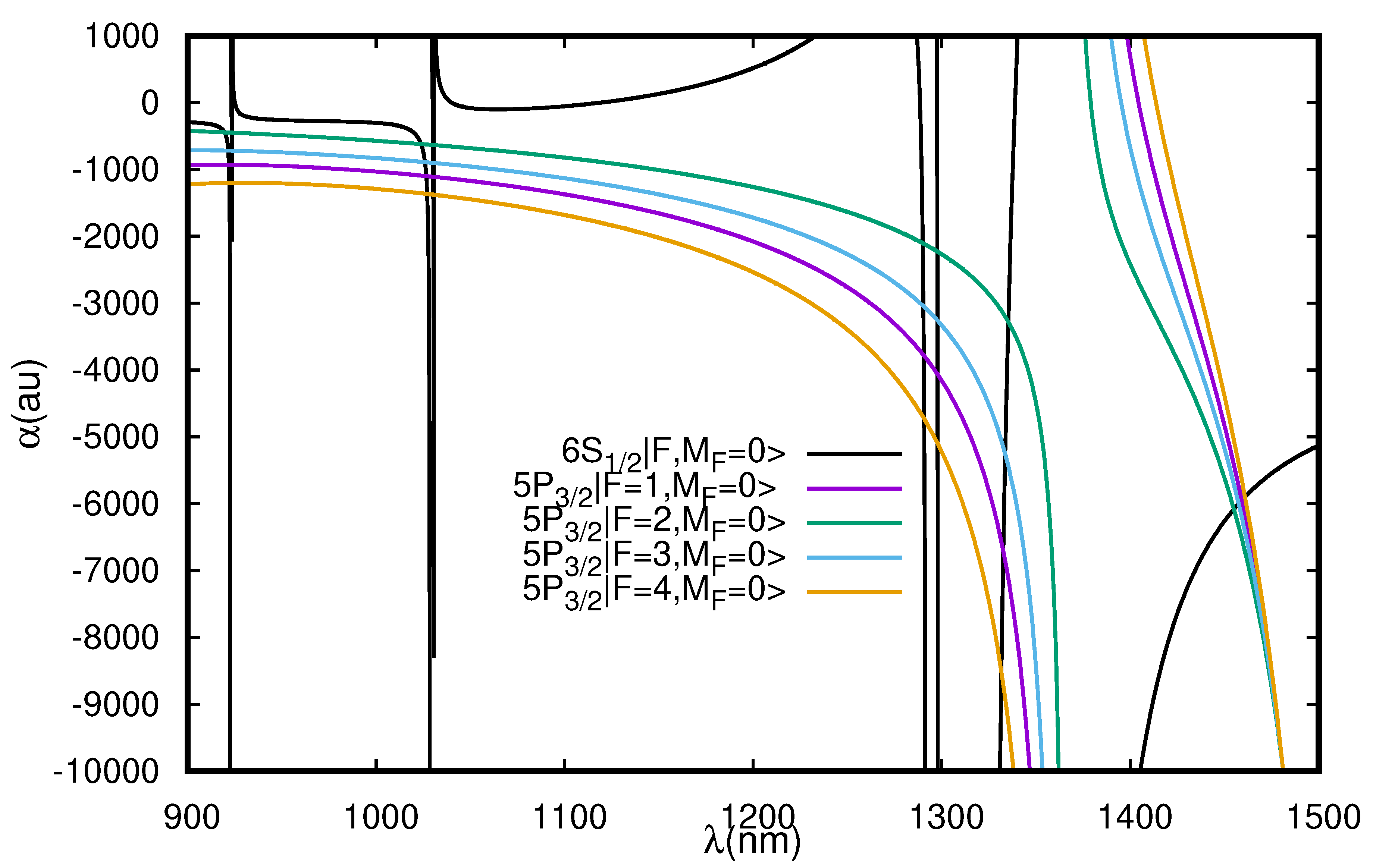
3.2.1. Cs Atom
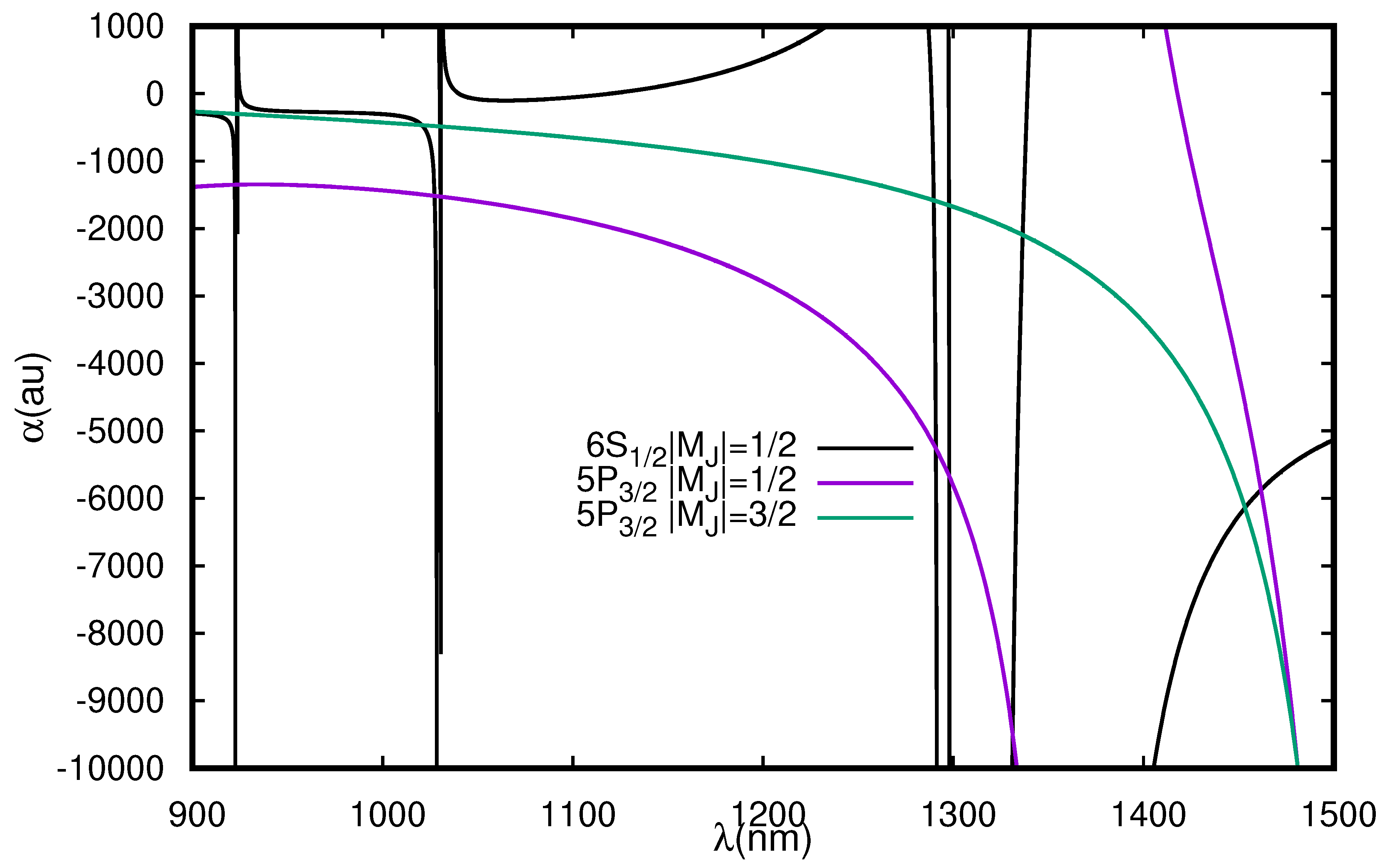
3.2.2. Rb Atom
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Norcia, M.A.; Winchester, M.N.; Cline, J.R.K.; Thompson, J.K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2016, 2, e1601231. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X. Optical lattice laser. In Frequency Control Symposium and Exposition; IEEE: Vancouver, BC, Canada, 2005; p. 3. [Google Scholar]
- Yu, D.; Chen, J. Optical clock with millihertz linewidth based on a phase-matching effect. Phys. Rev. Lett. 2007, 98, 050801. [Google Scholar] [CrossRef]
- Meiser, D.; Ye, J.; Carlson, D.R.; Holland, M.J. Prospects for a millihertz-linewidth laser. Phys. Rev. Lett. 2009, 102, 163601. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Active optical clock. Chin. Sci. Bull. 2009, 54, 348–352. [Google Scholar]
- Major, F.G. The Quantum Beat: Principles and Applications of Atomic Clocks; Springer: New York, NY, USA, 2015. [Google Scholar]
- Schawlow, A.L.; Devlin, G.E. Intermediate State of Superconductors: Influence of Crystal Structure. Phys. Rev. 1958, 110, 1011. [Google Scholar] [CrossRef]
- Kuppens, S.J.; van Exter, M.P.; Woerdman, J.P. Quantum-limited linewidth of a bad-cavity laser. Phys. Rev. Lett. 1994, 72, 3815. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Zang, X.; Zhuang, W.; Chen, J. Active optical clock based on four-level quantum system. Chin. Sci. Bull. 2013, 58, 2033–2038. [Google Scholar] [CrossRef]
- Bohnet, J.G.; Chen, Z.; Weiner, J.M.; Cox, K.C.; Thompson, J.K. Relaxation oscillations, stability, and cavity feedback in a superradiant Raman laser. Phys. Rev. Lett. 2012, 109, 253602. [Google Scholar] [CrossRef]
- Bohnet, J.; Chen, Z.; Weiner, J.; Cox, K.; Thompson, J. Linear-response theory for superradiant lasers. Phys. Rev. A 2014, 89, 013806. [Google Scholar] [CrossRef]
- Christensen, B.T.R.; Henriksen, M.R.; Schaffer, S.A.; Westergaard, P.G.; Ye, J.; Holland, M.; Thomsen, J.W. Non-linear Spectroscopy of Sr Atoms in an Optical Cavity for Laser Stabilization. Phys. Rev. A 2015, 92, 053820. [Google Scholar] [CrossRef]
- Kazakov, G.; Schumm, T. Stability analysis for bad cavity lasers using inhomogeneously boradened spin −1/2 atoms as a gain medium. Phys. Rev. A 2017, 95, 023839. [Google Scholar] [CrossRef]
- Weiner, J.M.; Cox, K.C.; Bohnet, J.G.; Thompson, J.K. Phase synchronization inside a superradiant laser. Phys. Rev. A 2017, 95, 033808. [Google Scholar] [CrossRef]
- Kazakov, G.; Bohnet, J.; Schumm, T. Prospects for a bad-cavity laser using a large ion crystal. Phys. Rev. A 2017, 96, 023412. [Google Scholar] [CrossRef]
- Norcia, M.A.; Thompson, J.K. Cold-Strontium Laser in the Superradiant Crossover Regime. Phys. Rev. X 2016, 6, 011025. [Google Scholar] [CrossRef]
- Norcia, M.A.; Cline, J.R.K.; Muniz, J.A.; Robinson, J.M.; Hutson, R.B.; Goban, A.; Marti, G.E.; Ye, J.; Thompson, J.K. Frequency measurements of superradiance from the strontium clock transition. Phys. Rev. X 2018, 8, 021036. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Y.; Zhang, X.; Yuan, B.; Han, C.; Xue, F. Superradiant Laser with Ultra-Narrow Linewidth Based on 40Ca. Chin. Phys. Lett. 2012, 29, 73202. [Google Scholar]
- Xu, Z.; Zhuang, W.; Wang, Y.; Wang, D.; Zhang, X.; Xue, X.; Pan, D.; Chen, J. Lasing of Cesium four-level active optical clock. In Proceedings of the European Frequency and Time Forum & International Frequency Control Symposium, Prague, Czech Republic, 21–25 July 2013; p. 395. [Google Scholar]
- Pan, D.; Xu, Z.; Xue, X.; Zhuang, W.; Chen, J. Lasing of cesium active optical clock with 459 nm laser pumping. In Proceedings of the Internatinal Frequency Control Symposium, Taipei, Taiwan, 19–22 May 2014; p. 1. [Google Scholar]
- Pan, D.; Arora, B.; mei Yu, Y.; Sahoo, B.K.; Chen, J. Optical-lattice based Cs active clock with continual superradiant lasing signal. arXiv 2020, arXiv:2008.11397. [Google Scholar]
- Katori, H.; Ido, T.; Kuwata-Gonokami, M. Optimal design of dipole potentials for efficient loading of Sr atoms. J. Phys. Soc. Jpn. 1999, 68, 2479–2482. [Google Scholar] [CrossRef]
- Takamoto, M.; Hong, F.L.; Higashi, R.; Katori, H. An optical lattice clock. Nature 2005, 435, 321–324. [Google Scholar] [CrossRef]
- Ovsiannikov, V.D.; Pal’chikov, V.G.; Taichenachev, A.V.; Yudin, V.I.; Katori, H.; Takamoto, M. Magic-wave-induced S 0 1- P 0 3 transition in even isotopes of alkaline-earth-metal-like atoms. Phys. Rev. A 2007, 75, 020501. [Google Scholar] [CrossRef]
- Arora, B.; Safronova, M.S.; Clark, C.W. Magic wavelengths for the np–ns transitions in alkali-metal atoms. Phys. Rev. A 2007, 76, 052509. [Google Scholar] [CrossRef]
- Singh, S.; Kaur, K.; Sahoo, B.K.; Arora, B. Comparing magic wavelengths for the 6s2S1/2-6p2P1/2,3/2 transitions of Cs using circularly and linearly polarized light. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 145005. [Google Scholar] [CrossRef]
- Kaur, J.; Nandy, D.K.; Arora, B.; Sahoo, B.K. Properties of alkali-metal atoms and alkaline-earth-metal ions for an accurate estimate of their long-range interactions. Phys. Rev. A 2015, 91, 1012705. [Google Scholar] [CrossRef]
- Schäffer, S.A.; Christensen, B.T.R.; Rathmann, S.M.; Appel, M.H.; Henriksen, M.R.; Thomsen, J.W. Towards passive and active laser stabilization using cavity-enhanced atomic interaction. In Proceedings of the International Conference on Spectral Line Shapes, Torun, Poland, 19–24 June 2016. [Google Scholar]
- Topcu, T.; Derevianko, A. Possibility of triple magic trapping of clock and Rydberg states of divalent atoms in optical lattices. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 144004. [Google Scholar] [CrossRef]
- Iskrenova-Tchoukova, E.; Safronova, M.S.; Safronova, U.I. High-precision study of Cs polarizabilities. J. Comp. Meth. Sci. Eng. 2007, 7, 521. [Google Scholar] [CrossRef]
- Bonin, K.D.; Kresin, V.V. Electric-Dipole Polarizabilities of Atoms, Molecules and Clusters; World Scientific: Singapore, 1997. [Google Scholar]
- Manakov, N.L.; Ovsiannikov, V.D.; Rapoport, L.P. Atoms in a laser field. Phys. Rep. 1986, 141, 319. [Google Scholar] [CrossRef]
- Singh, S.; Sahoo, B.K.; Arora, B. Magnetic-sublevel-independent magic wavelengths: Application to Rb and Cs atoms. Phys. Rev. A 2016, 93, 063422. [Google Scholar] [CrossRef]
- Blundell, S.A.; Johnson, W.R. Sapirstein J Relativistic all-order calculations of energies and matrix elements in cesium. Phys. Rev. A 1991, 43, 3407. [Google Scholar] [CrossRef]
- Johnson, W.R.; Idrees, M. Sapirstein, J Second-order energies and third-order matrix elements of alkali-metal atoms. Phys. Rev. A 1987, 35, 8. [Google Scholar] [CrossRef]
- Blundell, S.; Johnson, W.; Liu, Z.; Sapirstein, J. Relativistic all-order calculations of energies and matrix elements for Li and Be+. Phys. Rev A 1989, 40, 2233. [Google Scholar] [CrossRef]
- Safronova, M.S.; Johnson, W.R. All-Order Methods for Relativistic Atomic Structure Calculations. Adv. At. Mol. Opt. Phys. 2007, 55, 191. [Google Scholar]
- Safronova, M.S. High-Precision Calculation of Atomic Properties and Parity Nonconservation in Systems with One Valence Electron. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2001. [Google Scholar]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST Atomic Spectra Database; Version 5; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012. Available online: http://physics.nist.gov/asd (accessed on 12 December 2012).
- van Wijngaarden, W.; Li, J. Polarizabilities of cesium S, P, D, and F states. Quant. Spectrosc. Radiat. Transf. 1994, 52, 555. [Google Scholar] [CrossRef]
- Bates, D.R.; Damgaard, A. The calculation of the absolute strengths of spectral lines. Philos. Trans. R. Soc. 1949, 242, 101. [Google Scholar]
- Hunter, L.R.; Krause, D.; Miller, K.E.; Berkeland, D.J.; Boshier, M.G. Precise measurement of the Stark shift of the cesium D1 line. Opt. Commun. 1992, 94, 210. [Google Scholar] [CrossRef]
- Tanner, C.E.; Wieman, C.E. Precision measurement of the Stark shift in the 6P1/2–6P2/3 cesium transition using a frequency-stabilized laser diode. Phys. Rev. A 1988, 38, 162. [Google Scholar] [CrossRef]
- van Wijngaarden, W. Scalar and tensor polarizabilities of low lying S, P, D, F and G states in rubidium. J. Quant. Spectrosc. Radiat. Transf. 1997, 57, 275. [Google Scholar] [CrossRef]
- Zhu, C.; Dalgarno, A.; Porsev, S.G.; Derevianko, A. Dipole polarizabilities of excited alkali-metal atoms and long-range interactions of ground- And excited-state alkali-metal atoms with helium atoms. Phys. D At. Mol. Clust. 1997, 41, 229. [Google Scholar] [CrossRef]
- Miller, K.E.; Krause, D.; Hunter, L.R. Precise measurement of the Stark shift of the rubidium and potassium D1 lines. Phys. Rev. A 1994, 49, 5128. [Google Scholar] [CrossRef]
- Krenn, C.; Scherf, W.; Khaitm, O.; Musso, M.; Windholz, L. Stark effect investigations of resonance lines of neutral potassium, rubidium, europium and gallium Z. Phys. D At. Mol. Clust. 1997, 41, 229–233. [Google Scholar] [CrossRef]
- Bennett, S.C.; Roberts, J.L.; Wieman, C.E. Measurement of the dc Stark shift of the 6S→7S transition in atomic cesium. Phys. Rev. A 1999, 59, 16(R). [Google Scholar] [CrossRef]
- Kaur, J.; Singh, S.; Arora, B.; Sahoo, B.K. Annexing magic and tune-out wavelengths to the clock transitions of the alkaline-earth-metal ions. Phys. Rev. A 2017, 95, 042501. [Google Scholar] [CrossRef]
- Xiao, Z.; Tong, Z.; Jing, C. Magic wavelengths for a lattice trapped rubidium four-level active optical clock. Chin. Phys. Lett. 2012, 29, 090601. [Google Scholar]

| State | State | State | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Transition | Transition | Transition | |||||||
| 4.25(9) | −179(8) | 4.489(7) | −131.9(4) | 6.324(7) | −124.7(3) | 124.7(3) | |||
| 10.33(5) | 2415(23) | 4.25(9) | 180(8) | 6.49(8) | 226(5) | −226(5) | |||
| 0.929(9) | 8.8(2) | 1.0(1) | 6(1) | 1.5(1) | 6(1) | −6(1) | |||
| 0.356(7) | 1.02(4) | 0.55(6) | 1.4(3) | 0.77(8) | 1.4(3) | −1.4(3) | |||
| 0.185(5) | 0.25(1) | 0.36(4) | 0.57(9) | 0.51(5) | 0.6(1) | −0.6(1) | |||
| 6.49(8) | −453(11) | 7.02(2) | 1084(7) | 3.17(2) | 133(1) | 106(1) | |||
| 14.34(5) | 4413(31) | 4.3(4) | 121(2) | 2.1(2) | 15(3) | 12(3) | |||
| 1.64(1) | 27.3(5) | 2.1(2) | 21(4) | 1.0(1) | 2.5(5) | 2.0(4) | |||
| 0.70(1) | 3.9(1) | 1.3(1) | 7(1) | 0.61(6) | 0.8(2) | 0.7(1) | |||
| 0.388(8) | 1.08(4) | 0.93(9) | 3.6(7) | 0.43(4) | 0.40(8) | 0.32(6) | |||
| 0.71(7) | 2.0(4) | 0.33(3) | 0.22(4) | 0.18(4) | |||||
| 9.59(8) | 1174(20) | −235(4) | |||||||
| 6.3(6) | 132(26) | −26(5) | |||||||
| 2.9(3) | 22(4) | −4.3(9) | |||||||
| 1.8(2) | 7(1) | −1.5(3) | |||||||
| 1.3(1) | 3.5(7) | −0.7(1) | |||||||
| 1.0(1) | 2.0(4) | −0.40(8) | |||||||
| Main() | 6238(41) | Main() | 1295(12) | Main() | 1602(33) | −256(9) | |||
| Tail() | 4(2) | Tail() | 28(14) | Tail() | 30(9) | −6(2) | |||
| −0.47 | ∼0 | ∼0 | ∼0 | ||||||
| 15.8(3) | 15.8(3) | 15.8(3) | |||||||
| Total | 6257(41) | Total | 1339(18) | Total | 1648(35) | −262(9) | |||
| Others | 6238(41) [30] | Others | 1338 [25] | Others | 1650 [25] | −261 [25] | |||
| 6140 [40] | 1290 [40] | 1600 [40] | −233 [40] | ||||||
| Experiment | 6238(6) [48] | Experiment | 1328.4(6) [42] | Experiment | 1641(2) [43] | −262(2) [43] | |||
| State | State | State | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Transition | Transition | Transition | |||||||
| 4.15(3) | −167(2) | 4.231(3) | −104.1(1) | 5.977(4) | −102.0(1) | 102.0(1) | |||
| 9.68(6) | 1915(24) | 4.15(3) | 167(2) | 6.05(3) | 183(2) | −183(2) | |||
| 0.999(6) | 9.5(1) | 0.953(2) | 4.83(1) | 1.350(2) | 4.94(2) | −4.94(2) | |||
| 0.393(4) | 1.2(2) | 0.502(2) | 1.120(7) | 0.708(2) | 1.129(7) | −1.129(7) | |||
| 6.05(3) | −366(4) | 8.05(7) | 700(12) | 3.63(3) | 74(1) | 59(1) | |||
| 13.6(1) | 3693(54) | 1.35(6) | 10(1) | 0.66(3) | 1.3(1) | 1.01(9) | |||
| 1.54(1) | 22.4(3) | 1.1(1) | 5(1) | 0.51(5) | 0.6(1) | 0.5(1) | |||
| 0.628(7) | 2.967(7) | 0.79(6) | 2.6(4) | 0.37(3) | 0.29(4) | 0.23(3) | |||
| 0.61(4) | 1.4(2) | 0.28(2) | 0.16(2) | 0.13(2) | |||||
| 10.90(9) | 665(11) | −133(2) | |||||||
| 1.98(9) | 11(1) | −2.2(2) | |||||||
| 1.5(1) | 5(1) | −1.1(2) | |||||||
| 1.10(8) | 2.5(4) | −0.51(7) | |||||||
| 0.8(5) | 1.4(2) | −0.28(3) | |||||||
| Main() | 5112(59) | Main() | 788(12) | Main() | 849(11) | −163(2) | |||
| Tail() | 3(2) | Tail() | 16(8) | Tail() | 17(9) | −5(3) | |||
| −0.26 | ∼0 | ∼0 | ∼0 | ||||||
| 9.08(45) | 9.08(45) | 9.08(45) | |||||||
| Total | 5124(59) | Total | 813(14) | Total | 875(14) | −168(4) | |||
| Others | 5110 [44] | Others | 805 [25] | Others | 867 [25] | −167 [25] | |||
| 807 [45] | 870 [45] | −171 [45] | |||||||
| Experiment | 810.6(6) [46] | Experiment | 857(10) [47] | −163(3) [47] | |||||
| Resonance | Resonance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 894.59 | 917.48 | |||||||||
| 918.46(2) | −1335 | |||||||||
| 918.671 | 918.671 | |||||||||
| 920.101(4) | −1225 | 918.677(3) | 35,277 | |||||||
| 920.141 | 920.141 | |||||||||
| 973(3) | −393 | 921.0(9) | −147 | 920.3(3) | 56 | |||||
| 978.651 | 921.11 | |||||||||
| 980.86(5) | −376 | 978.651 | ||||||||
| 981.231 | 980.1(7) | −14 | 979.01(8) | 1126 | ||||||
| 1081(5) | −415 | 981.231 | ||||||||
| 1093.356 | 982(2) | −46 | 981.33(3) | 1088 | ||||||
| 1097.92(6) | −444 | 1005(5) | −269 | |||||||
| 1098.723 | 1088(3) | −625 | ||||||||
| 1359.201 | 1093.356 | |||||||||
| 1378.173 | 1098.09(9) | −661 | 1095.9(3) | 424 | ||||||
| 1379.9(1) | 5830 | 1098.723 | ||||||||
| 1394.057 | 1100.6(8) | 413 | ||||||||
| 1395.8(2) | 3248 | 1213(6) | 249 | |||||||
| 1413(2) | 2145 | 1359.201 | ||||||||
| 1469.892 | 1378.173 | |||||||||
| 1392.4(1) | −4207 | 1382.4(5) | 113 | |||||||
| 1394.057 | ||||||||||
| 1469.892 | ||||||||||
| 920.8(1) | −119 | 920.5(3) | −35 |
| 979.3(3) | 398 | 979.1(1) | 938 |
| 981.5(2) | 366 | 981.35(4) | 901 |
| 1097.7(2) | −274 | 1096.5(4) | 243 |
| 1102(3) | 229 | ||
| 1181(8) | 73 | ||
| 1391.2(5) | −2623 | 1383.5(9) | −533 |
| 920.6(1) | −81 | 920.9(1) | −136 |
| 979.1(1) | 722 | 979.6(6) | 180 |
| 981.38(7) | 687 | 982(1) | 150 |
| 1043(9) | −290 | ||
| 1082(3) | −430 | ||
| 1097.1(4) | 36 | 1097.9(1) | −480 |
| 1112(5) | −1 | ||
| 1130(7) | −47 | ||
| 1386(2) | −1320 | 1392.0(2) | −3469 |
| Resonance | Resonance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 867.95 | 867.95 | ||||||||
| 921.96(2) | −917 | 922.281(9) | −1351 | ||||||
| 922.71 | 922.71 | ||||||||
| 923.533(3) | −917 | 923.569(2) | −1350 | 923.414(6) | −301 | ||||
| 923.67 | 923.67 | ||||||||
| 1026.58(9) | −1090 | 1027.31(5) | −1516 | 1020.6(6) | −467 | ||||
| 1028.67 | 1028.67 | ||||||||
| 1030.336(9) | −1102 | 1030.395(7) | −1526 | 1030.20(1) | −487 | ||||
| 1030.67 | 1030.67 | ||||||||
| 1290.85(3) | −5597 | 1290.80(3) | −5259 | 1289.70(7) | −1583 | ||||
| 1292.28 | 1292.28 | ||||||||
| 1297.867(7) | −6606 | 1297.841(7) | −5671 | 1297.67(1) | −1655 | ||||
| 1298.28 | 1298.28 | ||||||||
| 1323.88 | 1323.88 | ||||||||
| 1342.4(2) | 2609 | 1331.2(1) | −9501 | 1336.5(2) | −2095 | ||||
| 1366.87 | 1366.87 | ||||||||
| 1421.8(7) | −7909 | 1461.7(7) | −5872 | 1453.3(8) | −6139 | ||||
| 1475.65 | 1529.26 | ||||||||
| 2732.18 | 1529.37 | ||||||||
| 2771.1(3) | 1132 | 2732.18 | |||||||
| 2791.29 | 2771.0(3) | 1501 | 2771.1(3) | 1000 | |||||
| 2791.29 | |||||||||
| 921.98(2) | −930 | 919.6(4) | −446 |
| 923.534(3) | −930 | 923.455(5) | −451 |
| 1026.60(8) | −1100 | 1023.9(3) | −621 |
| 1030.337(9) | −1110 | 1030.24(1) | −635 |
| 1290.49(4) | -3781 | 1289.94(6) | −2103 |
| 1297.786(8) | −4063 | 1297.71(1) | −2228 |
| 1332.7(1) | −6714 | 1335.3(2) | −3279 |
| 1459.1(9) | −5950 | 1455(1) | −6082 |
| 2771.1(3) | 1300 | 2771.1(3) | 1071 |
| 923.507(3) | −720 | 923.559(2) | −1201 |
| 1025.9(1) | −891 | 1027.12(5) | −1367 |
| 1030.30(1) | −902 | 1030.377(9) | −1377 |
| 1290.28(4) | −3045 | 1290.70(3) | -4731 |
| 1297.753(9) | −3259 | 1297.823(7) | −5097 |
| 1333.7(2) | −5258 | 1331.7(1) | −8520 |
| 1457.5(6) | −6000 | 1460.9(9) | −5897 |
| 2771.1(3) | 1201 | 2771.0(3) | 1429 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Jyoti; Arora, B.; Sahoo, B.K.; Yu, Y.-m. Magic Wavelengths for Optical-Lattice Based Cs and Rb Active Clocks. Atoms 2020, 8, 79. https://doi.org/10.3390/atoms8040079
Singh S, Jyoti, Arora B, Sahoo BK, Yu Y-m. Magic Wavelengths for Optical-Lattice Based Cs and Rb Active Clocks. Atoms. 2020; 8(4):79. https://doi.org/10.3390/atoms8040079
Chicago/Turabian StyleSingh, Sukhjit, Jyoti, Bindiya Arora, B. K. Sahoo, and Yan-mei Yu. 2020. "Magic Wavelengths for Optical-Lattice Based Cs and Rb Active Clocks" Atoms 8, no. 4: 79. https://doi.org/10.3390/atoms8040079
APA StyleSingh, S., Jyoti, Arora, B., Sahoo, B. K., & Yu, Y.-m. (2020). Magic Wavelengths for Optical-Lattice Based Cs and Rb Active Clocks. Atoms, 8(4), 79. https://doi.org/10.3390/atoms8040079






