Multiple Sequential Ionization of Valence n = 4 Shell of Krypton by Intense Femtosecond XUV Pulses
Abstract
1. Introduction
- (i)
- The photon energy of the FEL is high enough to eject an electron from an inner shell. Within a few femtoseconds the hole is filled by an electron originating from an outer shell, through a single or cascaded Auger decay mechanism. The ultrafast dynamics of the Auger decay competes with the absorption by the target ion of another photon from the same femtosecond FEL pulse. Therefore, ionization of the target often proceeds through a chain of consecutive photoionization and Auger decay events [2]. Usually, the ion yields of the different charge states are measured in the experiment as a function of the FEL pulse parameters and they are compared with the corresponding predictions of theoretical models [3,4]. So far, only a limited number of electronic spectra in this regime have been reported in the literature [2,5].
- (ii)
- The photon energy is not enough for creating a hole in an inner shell and therefore, the Auger process is energetically forbidden, if multiphoton ionisation is neglected. The atom is then ionized only by sequential absorption of photons by valence electrons as far as it is energetically allowed. Sequential photoionization in this regime was observed in noble gases [6,7,8,9,10] and the experimental results were compared with theoretical predictions [11,12,13,14]. For these processes, in addition to the ion yield and photoelectron spectra, also the angular distribution and even angular correlation [6,12,15,16] of two emitted electrons were studied both experimentally and theoretically. The important role of autoionizing resonances was also investigated [10,17,18]. To the best of our knowledge, no studies investigating multiple ionization beyond triple charged ions in the (ii) regime has been reported so far, except a general theoretical formulation for the photoelectron angular distributions in [19].
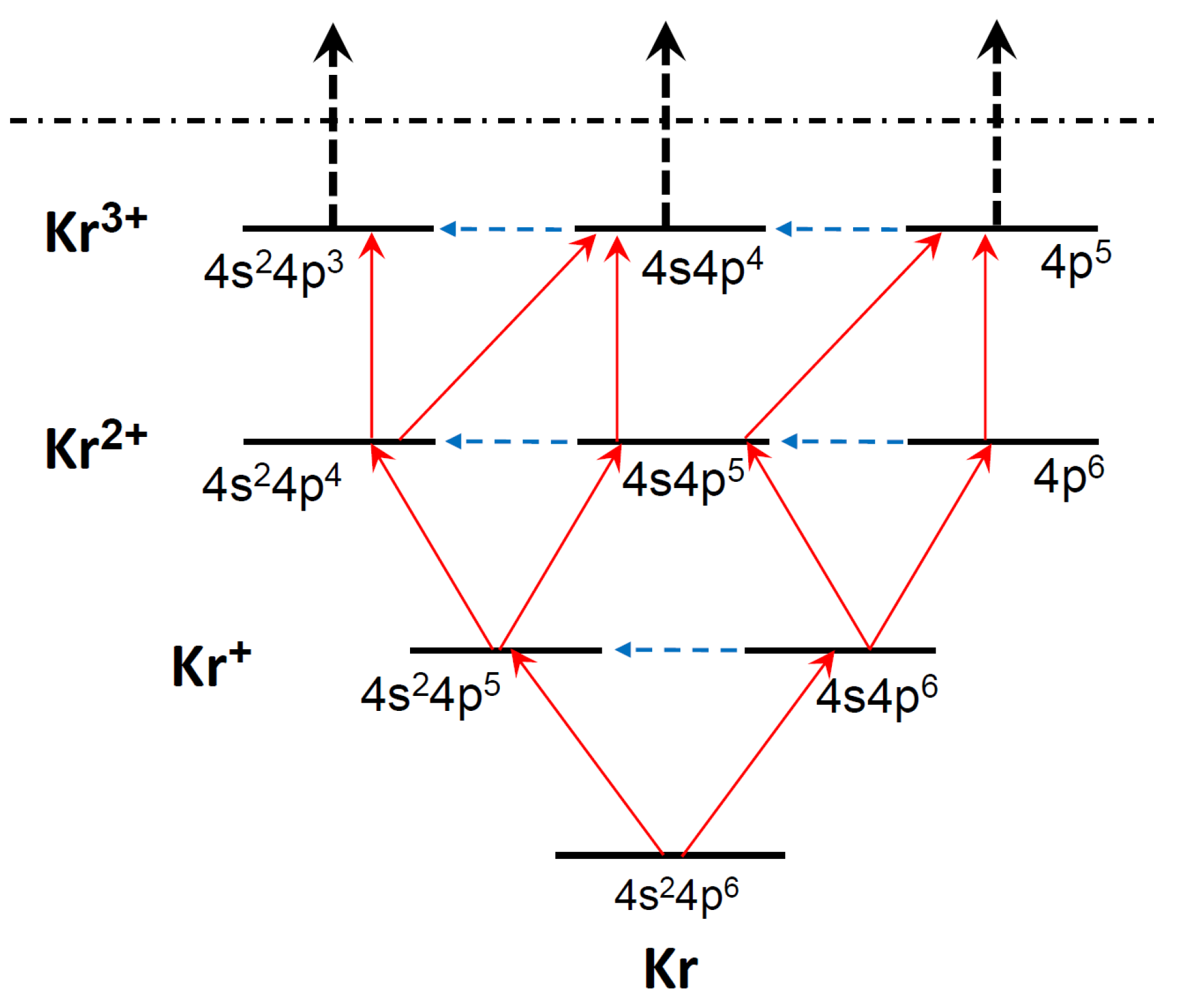
2. Process Description
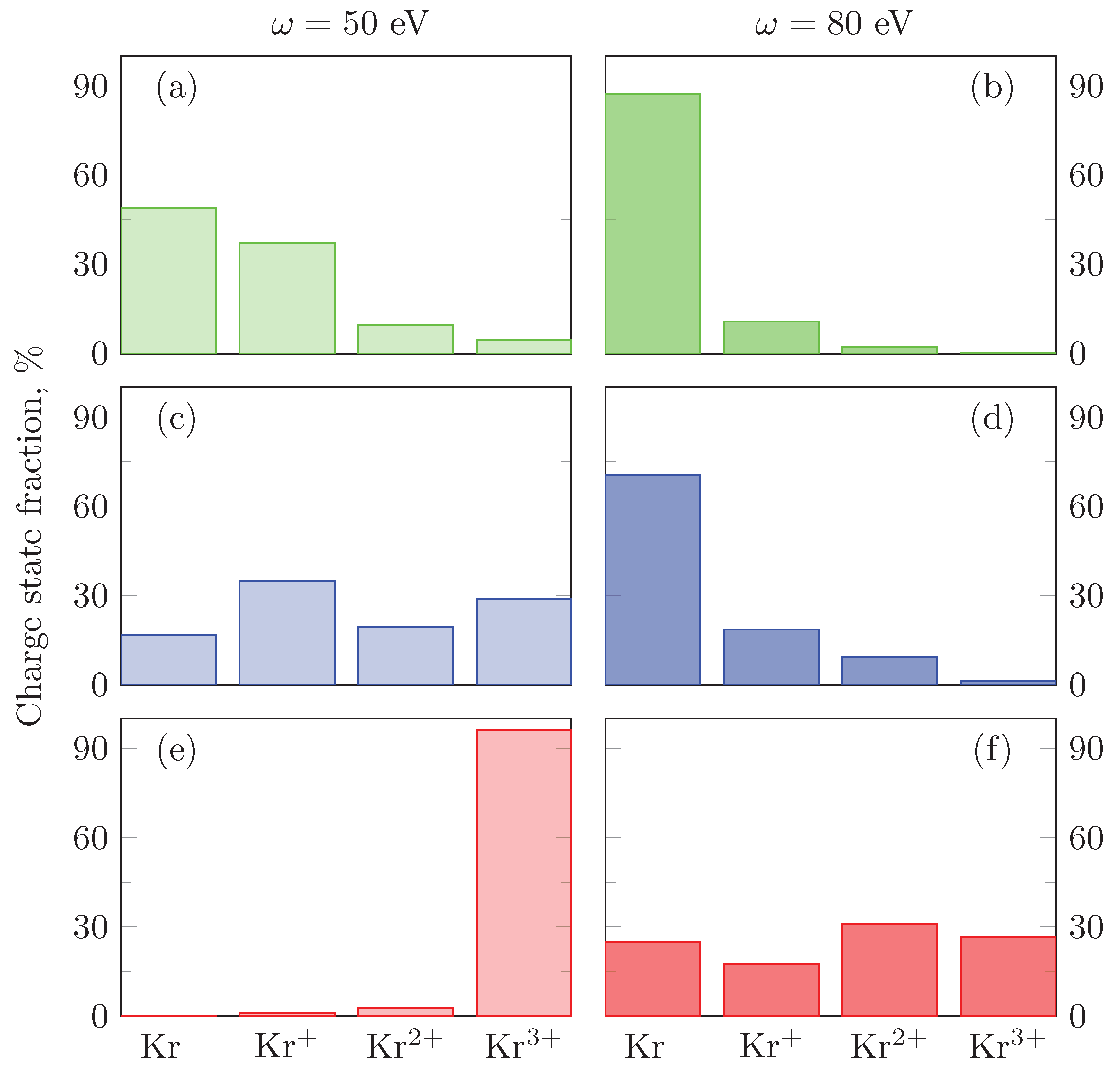
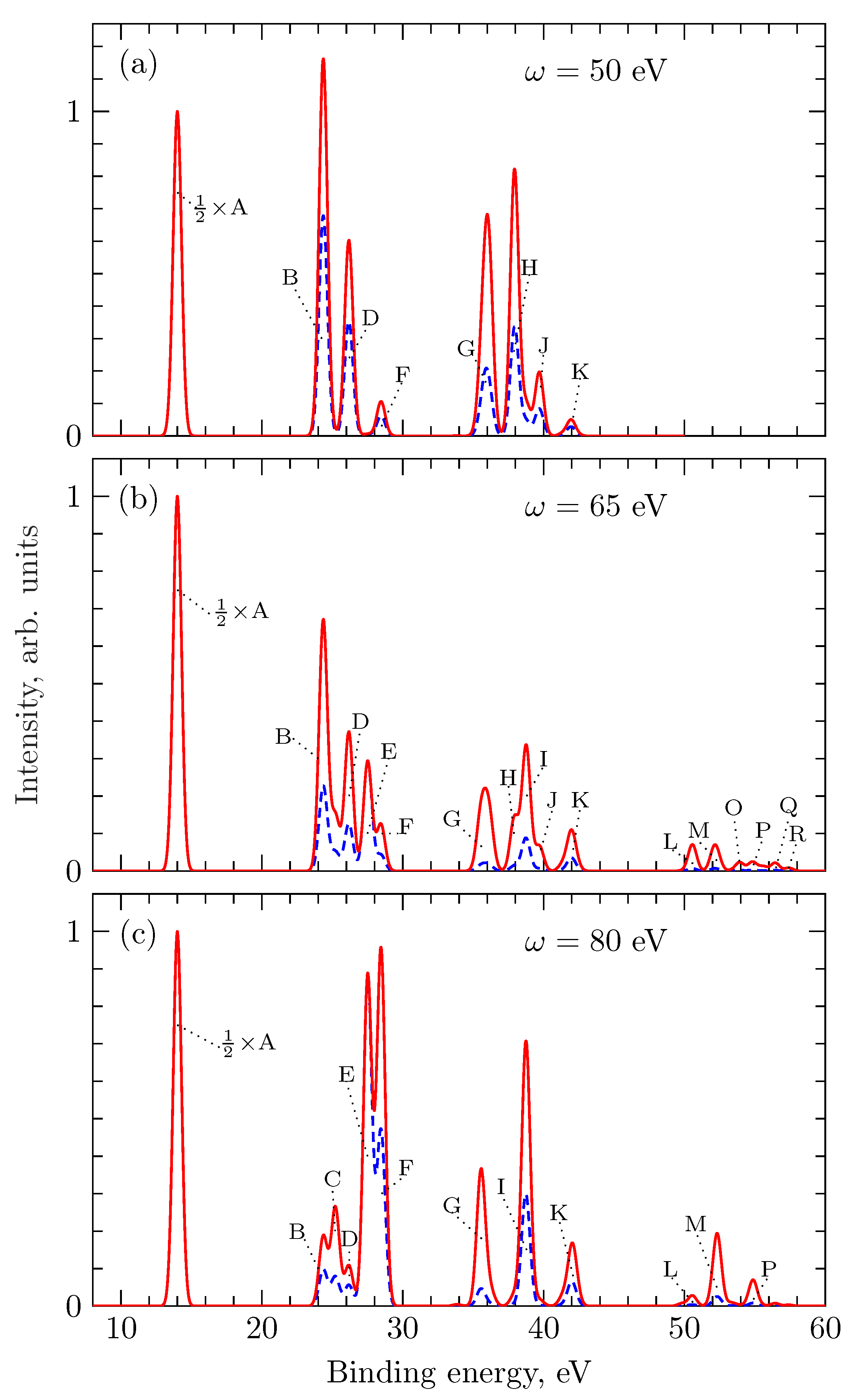
3. Results and Discussion
3.1. Time Evolution of Population
3.2. Photoelectron Spectra
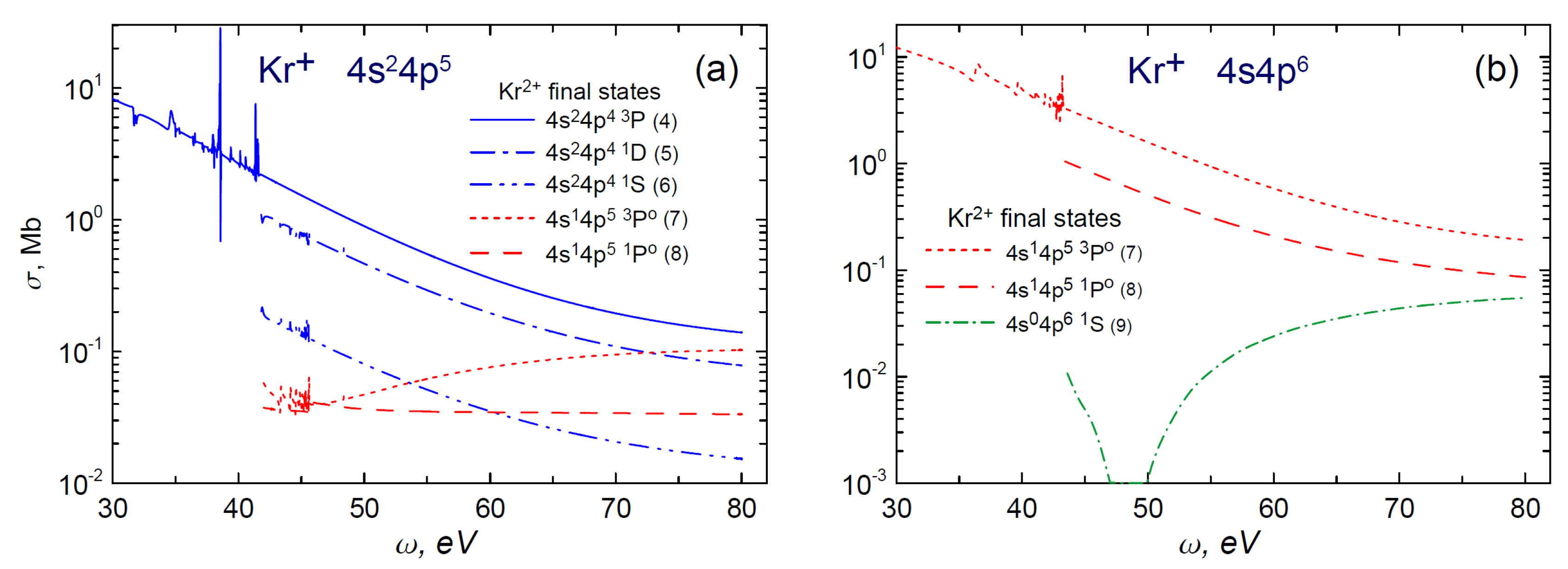
4. Method of the Cross Section Calculations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sorokin, A.A.; Bobashev, S.V.; Feigl, T.; Tiedtke, K.; Wabnitz, H.; Richter, M. Photoelectric Effect at Ultrahigh Intensities. Phys. Rev. Lett. 2007, 99, 213002. [Google Scholar] [CrossRef]
- Young, L.; Kanter, E.P.; Krässig, B.; Li, Y.; March, A.M.; Pratt, S.T.; Santra, R.; Southworth, S.H.; Rohringer, N.; DiMauro, L.F.; et al. Femtosecond electronic response of atoms to ultra-intense X-rays. Nature 2010, 466, 56–61. [Google Scholar] [CrossRef]
- Southworth, S.H.; Dunford, R.W.; Ray, D.; Kanter, E.P.; Doumy, G.; March, A.M.; Ho, P.J.; Krässig, B.; Gao, Y.; Lehmann, C.S.; et al. Observing pre-edge K-shell resonances in Kr, Xe, and XeF2. Phys. Rev. A 2019, 100, 022507. [Google Scholar] [CrossRef]
- Berrah, N.; Fang, L.; Osipov, T.; Murphy, B.; Bostedtc, C.; Bozek, J. Multiphoton ionization and fragmentation of molecules with the LCLSX-ray FEL. J. Electron Spectrosc. Relat. Phenom. 2014, 196, 34–37. [Google Scholar] [CrossRef]
- Fushitani, M.; Sasaki, Y.; Matsuda, A.; Fujise, H.; Kawabe, Y.; Hashigaya, K.; Owada, S.; Togashi, T.; Nakajima, K.; Yabashi, M.; et al. Multielectron-Ion Coincidence Spectroscopy of Xe in Extreme Ultraviolet Laser Fields: Nonlinear Multiple Ionization via Double Core-Hole States. Phys. Rev. Lett. 2020, 124, 193201. [Google Scholar] [CrossRef]
- Kurka, M.; Rudenko, A.; Foucar, L.; Kühnel, K.U.; Jiang, Y.H.; Ergler, T.; Havermeier, T.; Smolarski, M.; Schössler, S.; Cole, K.; et al. Two-photon double ionization of Ne by free-electron laser radiation: A kinematically complete experiment. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 141002. [Google Scholar] [CrossRef]
- Mondal, S.; Ma, R.; Motomura, K.; Fukuzawa, H.; Yamada, A.; Nagaya, K.; Yase, S.; Mizoguchi, Y.; Yao, M.; Rouzée, A.; et al. Photoelectron angular distributions for the two-photon sequential double ionization of xenon by ultrashort extreme ultraviolet free electron laser pulses. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 164022. [Google Scholar] [CrossRef]
- Braune, M.; Hartmann, G.; Ilchen, M.; Knie, A.; Lischke, T.; Reinköster, A.; Meissner, A.; Deinert, S.; Glaser, L.; Al-Dossary, O.; et al. Electron angular distributions of noble gases in sequential two-photon double ionization. J. Mod. Opt. 2016, 63, 324. [Google Scholar] [CrossRef]
- Ilchen, M.; Hartmann, G.; Gryzlova, E.V.; Achner, A.; Allaria, E.; Beckmann, A.; Braune, M.; Buck, J.; Callegari, C.; Coffee, R.N.; et al. Symmetry breakdown of electron emission in extreme ultraviolet photoionization of argon. Nat. Commun. 2018, 8, 4659. [Google Scholar] [CrossRef]
- Carpeggiani, P.A.; Gryzlova, E.V.; Reduzzi, M.; Dubrouil, A.; Faccialá, D.; Negro, M.; Ueda, K.; Burkov, S.M.; Frassetto, F.; Stienkemeier, F.; et al. Complete reconstruction of bound and unbound electronic wavefunctions in two-photon double ionization. Nat. Phys. 2019, 15, 170–177. [Google Scholar] [CrossRef]
- Kheifets, A.S. Sequential two-photon double ionization of noble gas atoms. J. Phys. B At. Mol. Opt. 2007, 40, F313–F318. [Google Scholar] [CrossRef][Green Version]
- Fritzsche, S.; Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Kabachnik, N.M. Angular distributions and angular correlations in sequential two-photon double ionization of atoms. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 165601. [Google Scholar] [CrossRef]
- Fritzsche, S.; Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Kabachnik, N.M. Sequential two-photon double ionization of Kr atoms. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 145602. [Google Scholar] [CrossRef]
- Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Meyer, M. Non-dipole effects in the angular distribution of photoelectrons in sequential two-photon atomic double ionization. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215602. [Google Scholar] [CrossRef]
- Rouzee, A.; Johnsson, P.; Gryzlova, E.; Fukuzawa, H.; Yamada, A.; Siu, W.; Huismans, Y.; Louis, E.; Bijkerk, F.; Holland, D.; et al. Angle-resolved photoelectron spectroscopy of sequential three-photon triple ionization of neon at 90.5 eV photon energy. Phys. Rev. A 2011, 83, 031401(R). [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Grum-Grzhimailo, A.N.; Fritzsche, S.; Kabachnik, N.M. Angular correlations between two electrons emitted in the sequential two-photon double ionization of atoms. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 225602. [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Ma, R.; Fukuzawa, H.; Motomura, K.; Yamada, A.; Ueda, K.; Grum-Grzhimailo, A.N.; Kabachnik, N.M.; Strakhova, S.I.; Rouzée, A.; et al. Doubly resonant three-photon double ionization of Ar atoms induced by an EUV free-electron laser. Phys. Rev. A 2011, 84, 063405. [Google Scholar] [CrossRef]
- Augustin, S.; Schulz, M.; Schmid, G.; Schnorr, K.; Gryzlova, E.V.; Lindenblatt, H.; Meister, S.; Liu, Y.F.; Trost, F.; Fechner, L.; et al. Signatures of autoionization in the angular electron distribution in two-photon double ionization of Ar. Phys. Rev. A 2018, 98, 033408. [Google Scholar] [CrossRef]
- Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Fritzsche, S.; Kabachnik, N.M. Photoelectron angular distributions and correlations in sequential double and triple atomic ionization by free electron lasers. J. Mod. Opt. 2016, 60, 334–357. [Google Scholar] [CrossRef]
- King, G.C.; Tronc, M.; Read, F.H.; Bradford, R.C. An investigation of the structure near the L2,3 edges of argon, the M4,5 edges of krypton and the N4,5 edges of xenon, using electron impact with high resolution. J. Phys. B At. Mol. Phys. 1977, 10, 2479–2495. [Google Scholar] [CrossRef]
- NIST Atomic Spectra Database (Version 5.7.1); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. Available online: https://physics.nist.gov/asd (accessed on 9 November 2020).
- Nakajima, T.; Nikolopoulos, L.A.A. Use of helium double ionization for autocorrelation of an xuv pulse. Phys. Rev. A 2002, 66, 041402R. [Google Scholar] [CrossRef]
- Makris, M.G.; Lambropoulos, P.; Mihelič, A. Theory of Multiphoton Multielectron Ionization of Xenon under Strong 93-eV Radiation. Phys. Rev. Lett. 2009, 102, 033002. [Google Scholar] [CrossRef] [PubMed]
- Son, S.K.; Santra, R. Impact of hollow-atom formation on coherent x-ray scattering at high intensity. Phys. Rev. A 2011, 83, 033402. [Google Scholar] [CrossRef]
- Son, S.K.; Santra, R. Monte Carlo calculation of ion, electron, and photon spectra of xenon atoms in x-ray free-electron laser pulses. Phys. Rev. A 2012, 85, 063415. [Google Scholar] [CrossRef]
- Lorenz, U.; Kabachnik, N.M.; Weckert, E.; Vartanyants, I.A. Impact of ultrafast electronic damage in single-particle x-ray imaging experiments. Phys. Rev. E 2012, 86, 051911. [Google Scholar] [CrossRef] [PubMed]
- Lunin, V.Y.; Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Sinitsyn, D.O.; Petrova, T.E.; Lunina, N.L.; Balabaev, N.K.; Tereshkina, K.B.; Stepanov, A.S.; Krupyanskii, Y.F. Efficient calculation of diffracted intensities in the case of nonstationary scattering by biological macromolecules under XFEL pulses. Acta Cryst. D 2015, 71, 293–303. [Google Scholar] [CrossRef]
- Serkez, S.; Geloni, G.; Tomin, S.; Feng, G.; Gryzlova, E.V.; Grum-Grzhimailo, A.N.; Meyer, M. Overview of options for generating high-brightness attosecond x-ray pulses at free-electron lasers and applications at the European XFEL. J. Opt. 2018, 20, 024005. [Google Scholar] [CrossRef]
- Buth, C.; Beerwerth, R.; Obaid, R.; Berrah, N.; Cederbaum, L.S.; Fritzsche, S. Neon in ultrashort and intense X-rays from free electron lasers. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 055602. [Google Scholar] [CrossRef]
- Ilchen, M.; Mazza, T.; Karamatskos, E.T.; Markellos, D.; Bakhtiarzadeh, S.; Rafipoor, A.J.; Kelly, T.J.; Walsh, N.; Costello, J.T.; O’Keeffe, P.; et al. Two-electron processes in multiple ionization under strong soft-X-ray radiation. Phys. Rev. A 2016, 94, 013413. [Google Scholar] [CrossRef]
- Rudek, B.; Son, S.K.; Foucar, L.; Epp, S.W.; Erk, B.; Hartmann, R.; Adolph, M.; Andritschke, R.; Aquila, A.; Berrah, N.; et al. Ultra-efficient ionization of heavy atoms by intense X-ray free-electron laser pulses. Nat. Photonics 2012, 6, 858–865. [Google Scholar] [CrossRef]
- Rudek, B.; Rolles, D.; Son, S.K.; Foucar, L.; Erk, B.; Epp, S.; Boll, R.; Anielski, D.; Bostedt, C.; Schorb, S.; et al. Resonance-enhanced multiple ionization of krypton at an x-ray free-electron laser. Phys. Rev. A 2013, 87, 023413. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Finetti, P.; Höppner, H.; Allaria, E.; Callegari, C.; Capotondi, F.; Cinquegrana, P.; Coreno, M.; Cucini, R.; Danailov, M.B.; Demidovich, A.; et al. Pulse Duration of Seeded Free-Electron Lasers. Phys. Rev. X 2017, 7, 021043. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Ivanov, V.K.; Cherepkov, N.A.; Chernysheva, L.V. Interference effects in photoionization of noble gas atoms outer s-shells. Phys. Lett. 1972, 40A, 361–362. [Google Scholar] [CrossRef]
- Lynch, M.J.; Gardner, A.B.; Codling, K.; Marr, G.V. The photoionization of the 3s subshell of argon in the threshold region by photoelectron spectroscopy. Phys. Lett. 1973, 43A, 237–238. [Google Scholar] [CrossRef]
- Amusia, M.; Chernysheva, L.; Yarzhemsky, V. Handbook of Theoretical Atomic Physics: Data for Photon Absorption, Electron Scattering, and Vacancies Decay; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Tulkki, J.; Aksela, S.; Aksela, H.; Shigemasa, E.; Yagishita, A.; Furusawa, Y. Krypton 4p, 4s, and 3d partial photoionization cross sections below a photon energy of 260 eV. Phys. Rev. A 1992, 45, 4640–4645. [Google Scholar] [CrossRef]
- Sukhorukov, V.L.; Lagutin, B.M.; Petrov, I.D.; Schmoranzer, H.; Ehresmann, A.; Schartner, K.H. Photoionization of Kr near 4s threshold. II. Intermediate-coupling theory. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 241–256. [Google Scholar] [CrossRef]
- Huang, K.N.; Johnson, W.; Cheng, K. Theoretical photoionization parameters for the noble gases argon, krypton, and xenon. At. Data Nucl. Data Tables 1981, 26, 33–45. [Google Scholar] [CrossRef]
- Ehresmann, A.; Vollweiler, F.; Schmoranzer, H.; Sukhorukov, V.L.; Lagutin, B.M.; Petrov, I.D.; Mentzel, G.; Schartner, K.H. Photoionization of Kr 4s: III. Detailed and extended measurements of the Kr 4s-electron ionization cross section. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 1489–1496. [Google Scholar] [CrossRef]
- Berrah, N.; Farhat, A.; Langer, B.; Lagutin, B.M.; Demekhin, P.V.; Petrov, I.D.; Sukhorukov, V.L.; Wehlitz, R.; Whitfield, S.B.; Viefhaus, J.; et al. Angle-resolved energy dependence of the 4p4nd(2S1/2) (n = 4–7) correlation satellites in Kr from 38.5 to 250 eV: Experiment and theory. Phys. Rev. A 1997, 56, 4545–4553. [Google Scholar] [CrossRef]
- Aksela, S.; Aksela, H.; Levasalmi, M.; Tan, K.H.; Bancroft, G.M. Partial photoionization cross sections of Kr 3d, 4s, and 4p levels in the photon energy range 37–160 eV. Phys. Rev. A 1987, 36, 3449–3450. [Google Scholar] [CrossRef] [PubMed]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Samson, J.A.R.; Gardner, J.L. Photoionization Cross Sections of the Outer s-Subshell Electrons in the Rare Gases. Phys. Rev. Lett. 1974, 33, 671–673. [Google Scholar] [CrossRef]
- Johnson, W.R.; Cheng, K.T. Photoionization of the outer shells of neon, argon, krypton, and xenon using the relativistic random-phase approximation. Phys. Rev. A 1979, 20, 978–988. [Google Scholar] [CrossRef]
- Kiselev, M.D.; Carpeggiani, P.A.; Gryzlova, E.V.; Burkov, S.M.; Reduzzi, M.; Dubrouil, A.; Facciala, D.; Negro, M.; Ueda, K.; Frassetto, F.; et al. Photoelectron spectra and angular distribution in sequential two-photon double ionization in the region of autoionizing resonances of ArII and KrII. J. Phys. B At. Mol. Phys. 2020. accepted. [Google Scholar] [CrossRef]




| N | Initial State | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Final State | |||||||||||
| 1 | - | - | - | - | - | - | - | - | - | ||
| 2 | A, 14.0 | - | - | - | - | - | - | - | - | ||
| 3 | E, 27.5 | - | - | - | - | - | - | - | - | ||
| 4 | - | B, 24.4 | - | - | - | - | - | - | - | ||
| 5 | - | D, 26.2 | - | - | - | - | - | - | - | ||
| 6 | - | F, 28.5 | - | - | - | - | - | - | - | ||
| 7 | - | I, 38.7 | C, 25.2 | - | - | - | - | - | - | ||
| 8 | - | K, 42.0 | F, 28.4 | - | - | - | - | - | - | ||
| 9 | - | - | K, 42.1 | - | - | - | - | - | - | ||
| 10 | - | - | - | G, 35.8 | - | - | - | - | - | ||
| 11 | - | - | - | I, 38.0 | G, 36.1 | 33.8 | - | - | - | ||
| 12 | - | - | - | J, 39.7 | H, 37.9 | G, 35.6 | - | - | - | ||
| 13 | - | - | - | L, 50.6 | - | - | G, 35.5 | - | - | ||
| 14 | - | - | - | O, 53.9 | M, 52.1 | 49.8 | I, 38.8 | G, 36.3 | - | ||
| 15 | - | - | - | R, 57.4 | 55.6 | 53.3 | K, 42.3 | J, 39.8 | - | ||
| 16 | - | - | - | Q, 56.4 | P, 54.6 | M, 52.3 | K, 41.4 | I, 38.8 | - | ||
| 17 | - | - | - | - | - | - | P, 54.9 | M, 52.3 | I, 38.7 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gryzlova, E.V.; Kiselev, M.D.; Popova, M.M.; Zubekhin, A.A.; Sansone, G.; Grum-Grzhimailo, A.N. Multiple Sequential Ionization of Valence n = 4 Shell of Krypton by Intense Femtosecond XUV Pulses. Atoms 2020, 8, 80. https://doi.org/10.3390/atoms8040080
Gryzlova EV, Kiselev MD, Popova MM, Zubekhin AA, Sansone G, Grum-Grzhimailo AN. Multiple Sequential Ionization of Valence n = 4 Shell of Krypton by Intense Femtosecond XUV Pulses. Atoms. 2020; 8(4):80. https://doi.org/10.3390/atoms8040080
Chicago/Turabian StyleGryzlova, Elena V., Maksim D. Kiselev, Maria M. Popova, Anton A. Zubekhin, Giuseppe Sansone, and Alexei N. Grum-Grzhimailo. 2020. "Multiple Sequential Ionization of Valence n = 4 Shell of Krypton by Intense Femtosecond XUV Pulses" Atoms 8, no. 4: 80. https://doi.org/10.3390/atoms8040080
APA StyleGryzlova, E. V., Kiselev, M. D., Popova, M. M., Zubekhin, A. A., Sansone, G., & Grum-Grzhimailo, A. N. (2020). Multiple Sequential Ionization of Valence n = 4 Shell of Krypton by Intense Femtosecond XUV Pulses. Atoms, 8(4), 80. https://doi.org/10.3390/atoms8040080






