Abstract
A scattering process can be a natural process or a process carried out in a laboratory. The scattering of particles from targets has resulted in important discoveries in physics. We discuss various scattering theories of electrons and positrons and their applications to elastic scattering, resonances, photoabsorption, excitation, and solar and stellar atmospheres. Among the most commonly employed approaches are the Kohn variational principle, close-coupling approximation, method of polarized orbitals, R-matrix formulation, and hybrid theory. In every formulation, an attempt is made to include exchange, long-range and short-range correlations, and to make the approach variationally correct. The present formulation, namely, hybrid theory, which is discussed in greater detail compared to other approximations, includes exchange, long-range correlations, and short-range correlations at the same time, and is variationally correct. It was applied to calculate the phase shifts for elastic scattering, the resonance parameters of two-electron systems, photoabsorption in two-electron systems, excitation of atomic hydrogen by an electron and positron impact, and to study the opacity of the Sun’s atmosphere. Calculations of polarizabilities, Rydberg states, and bound states of atoms are also discussed.
1. Introduction
In 1897, the electron was discovered by J. J. Thompson, which helped the development of physics beyond classical physics. In 1911, elastic scattering of alpha particles from a foil led to the discovery of the nucleus by Rutherford, which further led to the development of a planetary model of the atomic structure. He called the nucleus of the hydrogen atom a proton, which means “the first one” in the Greek language (very appropriate). He also deduced the well-known formula for the differential cross-section, , where is the angle of scattering of the alpha particle. Rutherford showed from this experiment that the number of electrons = A/2, where A is the atomic number. This holds for all atoms. J. J. Thomson initially thought that the number of electrons = 1000A, as seen in his model of the atom. In 1912, Bohr proposed a model of the hydrogen atom in which new laws were formulated. He assumed that the electron in a hydrogen atom moves in a circular orbit due to the Coulomb force between the electron and the nucleus (Rutherford’s planetary model), and the electron’s angular momentum is quantized. Radiation is emitted only when a transition from a state of a higher quantum number to a lower quantum number state takes place. Emission is monochromatic radiation. He also proposed the correspondence principle, which implies that at large quantum numbers, predictions based on quantum concepts must agree with the predictions based on classical concepts. In 1923, an experiment on the scattering of X-rays by electrons by Compton [1] led to the confirmation of the existence of photons. This confirmation also came from experiments by Bothe and Geiger [2], who developed coincidence counters and showed that the electron moved from its position in about 10−7 s. A wave would have taken much longer to move the electron. We also know that diffraction and interference are explained by invoking a wave picture of radiation. According to Bohr, the picture ought to be regarded not as contradictory but as complementary. Further experiments by Compton and Simon [3] showed that energy is conserved at every step of the process. This brought an end to the theory of Bohr, Kramers, and Slater (BKS) [4], where they proposed that energy conservation need not hold in atomic processes. In 1926, Erwin Schrödinger [5] formulated the wave equation to determine the wave function of a quantum mechanical system. In 1932, Chadwick [6] discovered the neutron by bombarding beryllium with alpha particles. This brought an end of theories that postulated the existence of electrons in a nucleus. After this, it was clear that a nucleus consists of a number of protons and neutrons, depending on the charge of the nucleus. Forces acting in atomic processes are Coulomb forces, which are well-understood. Therefore, it is possible to infer the various quantities occurring in most processes accurately. However, there are other forces or potentials (Vdp) due to the distortion of the target by the incident particle [7]; the attractive potential (1/r2) [8] due to the degeneracy of the 2s and 2p levels; the potential between neutral atoms, which is proportional to 1/r6 and becomes proportional to 1/r7 when the neutral atoms are separated by distances larger than 137a0, where is the Bohr radius (Casimir and Polder [9]). It was pointed out by Kelsey and Spruch [10] that the attractive polarization potential between an electron interacting with a polarizable atom experiences a repulsive potential (VKS) at distances greater than 137a0. These variations in potentials were discussed by Lundeen [11]. These potentials are in the ratio:
We see that the Coulomb potential dominates in all cases. We will discuss some of these potentials in various sections. First, we will discuss interactions of electrons with atoms and ions and then those of positrons. We use Rydberg units: e2 = 2, me = 1/2, and ħ = 1.
In this article, we will discuss the scattering of electrons and positrons from various targets, photoabsorption, resonances, Rydberg states, the relativistic and retardation corrections to such states, and their polarizabilities. We will compare our results with the results of other calculations, whenever possible. We use some of the results obtained here to calculate the opacity in the atmosphere of the Sun and stellar objects due to electrons and positrons.
2. Calculations Involving Electrons
Our aim is to calculate the scattering cross-section for a particle incident on a target. For this purpose, various approximations or theories have been developed. We mention a few of them. We discuss scattering by hydrogenic systems only because the target function is known exactly, and therefore, we can test various approximations. For targets with many electrons, configuration–interaction type wave functions have to be used, where such functions provide accurate eigenvalues which are, however, not exact. An easy calculation of phase shifts of electron–hydrogen scattering can be carried out by using a simple wave function of the form:
In the above equation, is the scattering function and is the target function. However, the exchange between the two electrons must be included (due to the Pauli exclusionprinciple). Such a calculation was carried out by Morse and Allis [12] in 1933. The wave function is of the form:
The plus sign refers to singlet states and the minus sign refers to triplet states. In Equation (2):
where the angle , measured in steradians, is the solid angle defined in terms of the spherical polar angles and . The ground state wave function is given by:
The scattering function of the incident electron is obtained from:
where and are the distances of the incident and bound electrons, respectively. H is the Hamiltonian of electron–hydrogen system and E is the energy of the system. We assume that the target is of infinite mass compared to the mass of the electron; therefore, it is assumed fixed.
k2 is the kinetic energy of the incident electron and Z is the nuclear charge. Equation (5) gives the following equation to determine the scattering function :
where = 1 for l = 0 only. The direct or Hartree potential is:
and the nonlocal potentials are:
The phase shifts (radians) are obtained from the asymptotic value of the scattering function:
The main aim of most approximations is to include various correlations to get accurate results. We, therefore, try various approximations to infer the scattering parameters. In a target, the orbital of the electron is distorted when the incident electron creates an electric field Ec, resulting in a change of energy of the target given by , where is the polarizability of the target, which is equal to 4.5 for a hydrogen atom. For a slowly moving incident electron, this distortion can be taken into account using the method of polarized orbitals of Temkin [7], assuming that the atom follows the instantaneous motion of the scattered electron (adiabatic hypothesis), and the incident electron is slow. He proved that for an incident electron at a distance from the nucleus, the polarized orbital of the target electron is of the form:
where is the angle between and . The function depends on both coordinates and , is a step function that is equal to 1.0 for r1 greater than r2 and zero otherwise. This gives rise to an attractive polarization potential . In this method, the scattering function is obtained from:
The scattering function obtained from Equation (14) is not the same as that obtained from Equation (5) since the one obtained from Equation (14) includes the effect of the polarization of the target. The phase shifts obtained from Equations (5) and (14) are not expected to be the same. The resulting integro-differential equation for , including corrections for l > 0, is given by Sloan [13], where the polarizability as a function of x is given by:
where and . Singlet and triplet phase shifts for the scattering of electrons from hydrogen atoms have been calculated using this method. The method of polarized orbitals has been used extensively for various atomic and molecular targets, even though the method is not variationally correct. There are other methods to solve for the scattering functions. One of them is the close-coupling method. Electron–hydrogen scattering calculations were carried out by Burke and Smith [14]. In 1987, the R-matrix method was introduced in atomic physics by Burke and Robb [15]. Electron–hydrogen scattering phase shifts were calculated by Burke et al. [16]. This method has been extensively employed in solving problems in atomic and molecular physics. A calculation using the Kohn variational method was carried out by Schwartz [17]. This method does not provide any bounds on the phase shifts. However, the scatterings lengths obtained are upper bounds on the exact scattering lengths. Calculations have been carried out using the projection operator formalism of Feshbach [18] in which we divide the space into two parts using projection operators P and Q such that in the limit:
where represents a scattering state and for . These operators are idempotent (,) and orthogonal (). Phase shifts were calculated by Bhatia and Temkin [19] for electron–hydrogen scattering. There is another approach, namely, the exterior complex scaling method [20], which was applied to calculate electron–hydrogen scattering, spin-flip cross-sections in hydrogen, and the photoionization of helium. We have briefly mentioned some of the methods, although each one deserves a separate article. Next, we will discuss the hybrid approximation.
3. Hybrid Theory
We want to reduce a many-body Schrödinger equation, with all the correlations, to a one-body Schrödinger equation. The above method (projection operator formalism) cannot be generalized to also include long-range correlations because it is difficult to write a projection operator in terms of , instead of the ground state function . An improved method, which includes exchange and long-range and short-range correlations at the same time, is called a hybrid theory [21]. In this method, the polarization of the target takes place whether the incident electron is outside or inside the target. The wave function for scattering, including the polarized orbital of the target electron, as well as short-range correlations, is given by:
The correlation function is of the Hylleraas type and for any angular momentum L, it is given by:
The functions ( = +1, −1) are the rotational harmonics [22]. The and are the generalized “radial” functions, which depend upon the three residual coordinates to define the two vectors and , where these are Hylleraas-type functions. The function in Equation (18) is a cutoff function. In order to replace a many-particle Schrödinger equation with a single-particle equation, we define the correlation term with unknown coefficients :
Since is an eigenfunction of the Hamiltonian, the equation for the scattering function is obtained from:
To include the polarization of the target, is replaced by in Equation (21a). The equation for the scattering function is now obtained from:
Details are given in [21] and various quantities, not given here, are also given in [21]. Definitive results were obtained using this method. In Table 1 and Table 2, we present the singlet and triplet phase shifts for the scattering of electrons from hydrogen atoms obtained using the above methods. The scattering length a is defined as:

Table 1.
Electron–hydrogen 1S phase shifts (radians) obtained with different methods.

Table 2.
Electron–hydrogen 3S phase shifts (radians) obtained with different methods.
The scattering length is calculated at a distance R. However, there is a correction due to the long-range polarization potential [23] and the corrected scattering length is given by:
In the above equation, is the polarizability of a hydrogen atom. At R = 117.3088, the singlet S scattering length value is a(R) = 5.96554. The corrected scattering length a, using Equation (23), is 5.96611. The triplet S scattering length value is 1.781542 at R = 349.0831. Using Equation (23), the corrected scattering length value is 1.900. These scattering lengths agree with those calculated by Schwartz [17]. The scattering lengths are also given in Table 1 and Table 2. In the Kohn variational method [17], the scattering lengths are upper bounds on the exact scattering lengths, while there are no bounds on the phase shifts.
Hybrid theory was also used to calculate phase shifts for e–He+, given in Table 3 and Table 4 and e–Li2+ scattering phase shifts [25], given Table 5.

Table 3.
Comparison 1S phase shifts (radians) for electron—He+ scattering with those obtained using close-coupling (CC) [24], the hybrid theory [25], those obtained by Gien [26,27] using the Harris–Nesbet method, and Feshbach projection operator formalism (OP) [28].

Table 4.
Comparison 3S phase shifts (radians) for electron—He+ scattering with those obtained using OP [28], CC [26], and obtained by Gien [26] using the Harris–Nesbet method.

Table 5.
Comparison of the 1S and 3S calculated phase shifts (radians) for electron—Li2+ scattering [25] with those obtained by Gien [27] using the Harris–Nesbet method.
4. Photoabsorption
Wildt [29] suggested that an important source of opacity in the atmosphere of the Sun is the photodetachment of negative hydrogen ions:
The cross-section for this process in the length form and in the dipole approximation is given by:
In the above equation, is the fine structure constant, I is the ionization potential and are the dipole transition operators, and k is the momentum of the outgoing electron. If the target is in the S state, then the outgoing electron is in the P state. The bound S-state wave function is of the Hylleraas type and the final state wave function is of the form given in Equation (13). An earlier calculation of the photodetachment cross-section of H− was carried out by Chandrasekhar [30] in 1945. These were also calculated using the Feshbach formalism [31]. The present results [32] are given in Table 6 and are compared with those obtained using the Feshbach formalism [31]. The agreement is good. They are also compared with those obtained by Wishart [33] using a close-coupling pseudostate expansion.

Table 6.
Photodetachment cross-sections (Mb) of the ground state of H−. The outgoing electron has momentum k. The number of terms in the Hylleraas wave function for the bound state is 364. These results are compared with those obtained by Wishart [33].
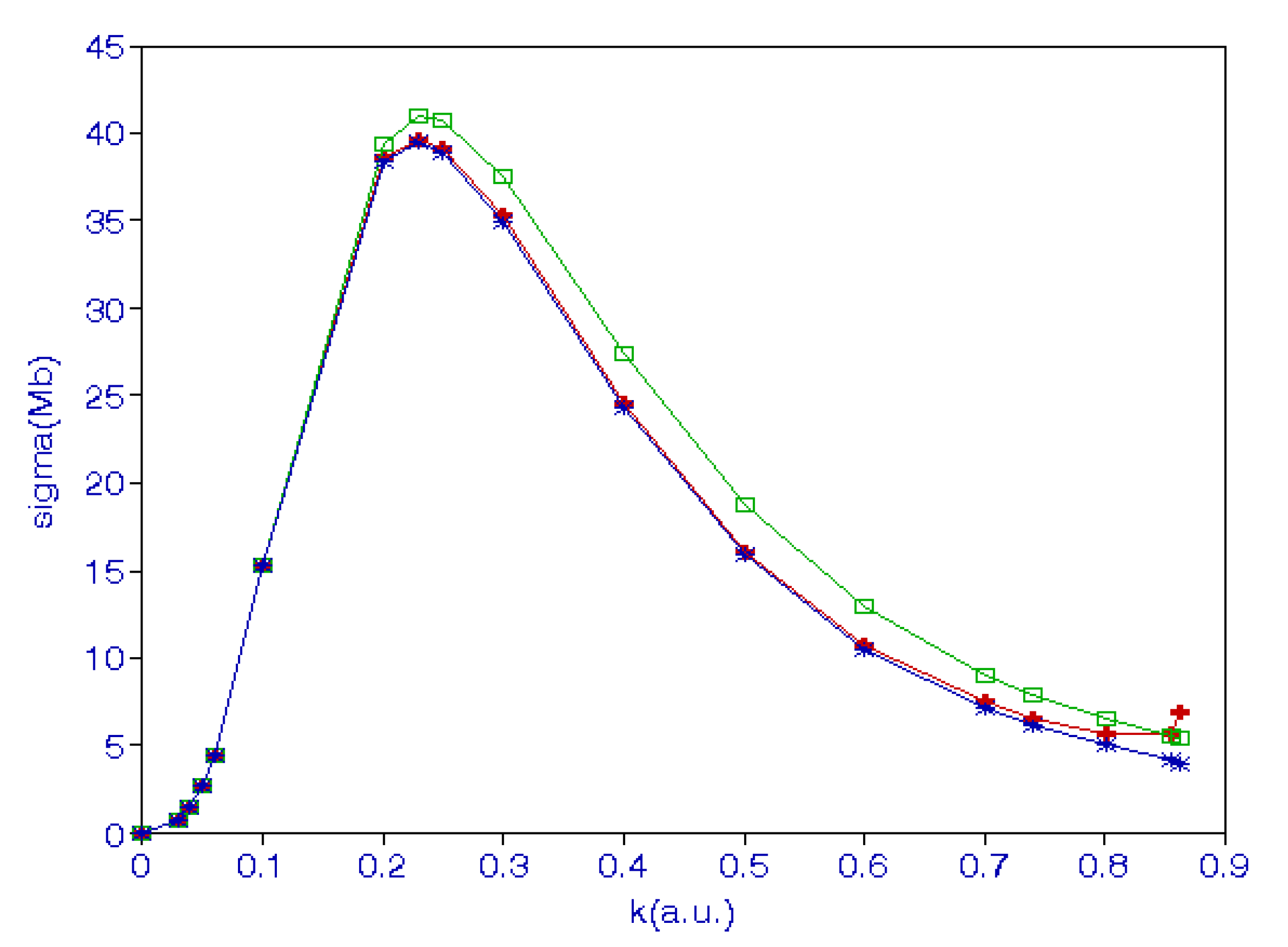
Photodetachment cross-sections have a maximum around k = 0.23, which corresponds to a photon wavelength of 8406.3 Å (using Å). The calculated cross-sections are close to the experimental results of Branscomb and Smith [34]. They found a maximum close to 8000 Å. Ohmura and Ohmura [35], using the effective range theory and the loosely bound structure of a hydrogen ion, calculated the photodetachment cross-section of H− at the outgoing momentum k:
where and is the effective range. The binding energy of the hydrogen ion is . The cross-sections obtained from Equation (26) are in good agreement with those obtained using the hybrid theory [32]. The cross-sections in various approximations are shown in Figure 1. The lowest curve is obtained when only long-range correlations are included, the middle curve is obtained when the short-range correlations are also included. The top curve represents the cross-sections obtained using Equation (26). We also calculated the photoionization cross-sections [32] of He using a Hylleraas function with 220 terms in the S-state wave function and compared these with those obtained using the R-matrix approach [36] and also with experimental results [37].
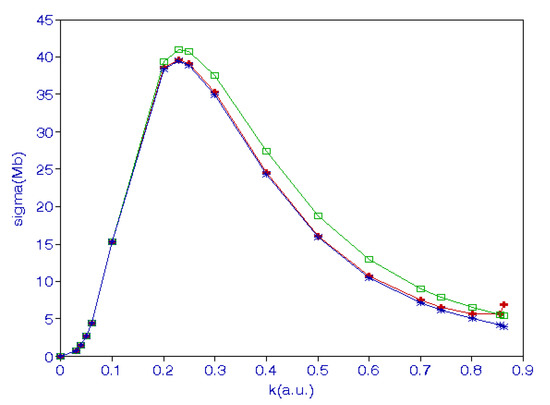
Figure 1.
(Color online) Photodetachment cross-sections of a negative hydrogen ion in various approximations. The lowest curve is obtained when only long-range correlations are included, the middle curve is obtained when the short-range correlations are also included. The top curve represents the cross-sections obtained using Equation (26).
The photoionization cross-sections of He given in Table 7 and of Li+, given in Table 8, were calculated using the hybrid theory [32] and also by using the method of polarized orbitals by Daskhan and Ghosh [38]. These results are also given in Table 8.

Table 7.
Photoionization cross-section (Mb) of He.

Table 8.
Photoionization cross-section (Mb) of Li+ using 165 terms in the Hylleraas wave function for the bound state wave function. The outgoing momentum of the electron is k.
It can be seen from Table 6 that as k tends to zero, the photodetachment cross-sections of H− tend to zero because the final scattering state wave function behaves like the Bessel function , which is finite at k = 0. Equation (25) has k outside the square of the matrix element, which makes the cross-section equal to zero at k = 0. However, in the case when the remaining target is charged, the outgoing electron sees a Coulomb field, which makes the scattering function behave like k−0.5, which cancels the k outside the square of the matrix element. It can be seen from Table 7 that the cross-sections for He do not go to zero as k goes to zero.
While calculating the photoionization cross-sections of Li+, we [32] also calculated the 3P and 1P phase shifts for electron–Li2+. Calculations of the photoionization of metastable states (1s2s) 1S and 3S states of He and Li+ were carried out using the hybrid theory [32].
The photoionization of atoms with more than two electrons was calculated using the method of polarized orbitals [7]. Phase shifts for the scattering of electrons from Li+ and Na+ were also calculated at the same time. The photoionization cross-sections of Li and Na are given in [39] and [40], respectively.
5. Recombination Rates
In Equation (24), we provided the photodetachment of H−. There is a reverse process, namely, radiative attachment or recombination:
which further helps in the formation of hydrogen molecules:
Since the process in Equation (27a) is invariant under charge conjugation, the recombination rate for a positron combining with antihydrogen :
is the same as for Equation (27a).
The radiative attachment plays an important role in solar and astrophysical problems. The attachment cross-section is , where g(i) and g(f) are the statistical weights of the initial and final states. This result follows from the principle of detailed balance. These cross-sections are much smaller than the photoabsorption cross-sections. The radiative rate coefficients averaged over the Maxwellian distribution is given by:
where S is the spin of the final state and kB is the Boltzmann constant. Rate coefficients of (1s1s) 1S states of H−, He, and Li+ are calculated using the photoabsorption cross-sections given in Table 6, Table 7 and Table 8, and the results are given in [32].
6. Photoejection with Excitation
Up to now, we have considered the photoabsorption of two-electron systems when the final state is (1s) 2S. It is possible to have a final state that is (2p) 2P. This state can decay to the (1s) 2S state, giving a Lyman- radiation at 1216 Å in the case of a hydrogen atom:
Now, the outgoing electron can be in a p state or a d state. The cross-section for this process is given by:
and for the 2S state:
The matrix M is defined as:
In the above equation, and are the dipole transition operators. Bhatia and Drachman [41] calculated the total photoabsorption cross-section for two 2S and two 2P states. Their results are given in [41]. Photoionization with excitation can take place due to electron–electron correlations only. Therefore, it can test the quality of different approximations. Recombination rate coefficients at various temperatures are also given in [41]. Cross-section and recombination rate coefficients are required in the investigation of astrophysical objects, the upper atmosphere, and laboratory plasmas.
7. Excitation by Electron Impact
The excitation cross-sections of the 2S state of atomic hydrogen at low incident electron energies (10.30 to 54.5 eV) were calculated using the variational polarized method (hybrid theory) [42]. Nine partial waves were used to get the converged results. The total cross-section, calculated using the plane waves in the final state wave function, which is simpler than using coupled state approximation, is:
The transition matrix element is given by:
The initial wave function, assumed to be exact, is given in Equation (22) and the final state wave function (plane wave approximation) is given by:
The excited state wave function of the target is:
The cross-section for the excitation is given by:
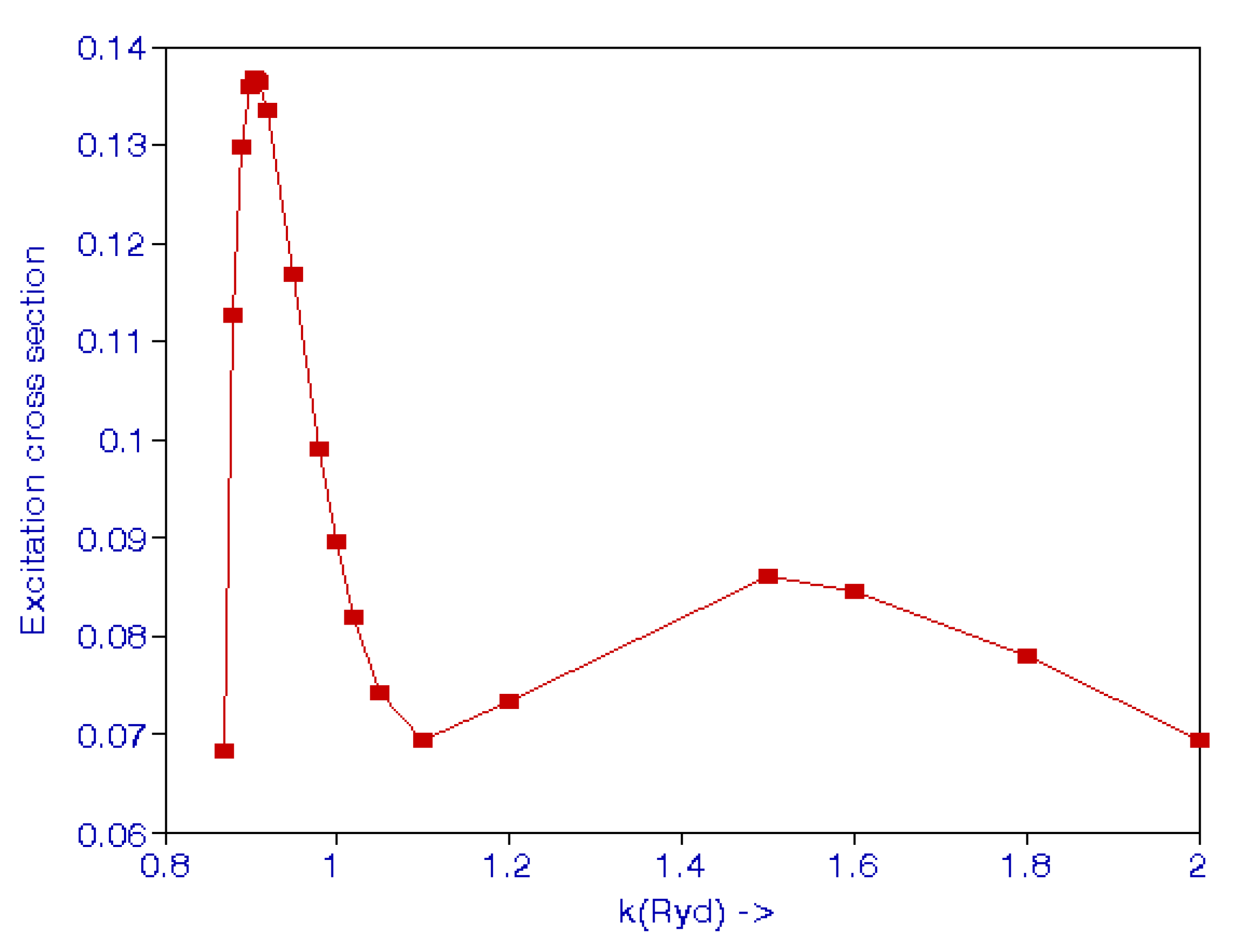
In the above expression, ki and kf are the initial and final momenta, and is the angle between the initial and final electron directions. Callaway [43] calculated the cross-sections for excitation in the range 12 to 54 eV using an 11-state expansion, including 7 pseudostates. Burke et al. [44] also carried out a close-coupling calculation to calculate excitation cross-sections. Scott et al. [45] used the standard R-matrix close-coupling method using a nine-state basis consisting of three eigenstates and six pseudostates. These results are given in [42]. The excitation cross-sections are shown in Figure 2. There is a maximum at k = 0.907 and another maximum at k = 1.50.
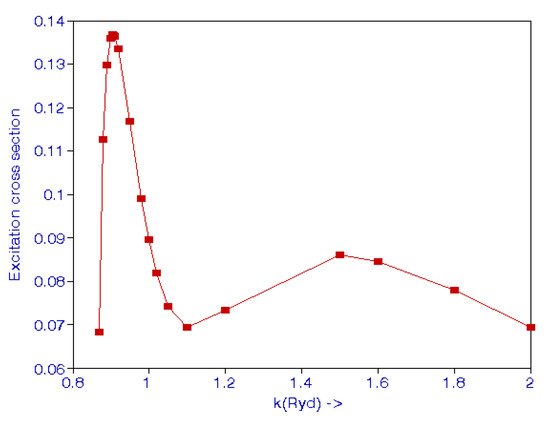
Figure 2.
(Color online). Cross-sections (Mb) for the 2S state excitation of atomic hydrogen from the 1S state by an electron impact.
8. Resonances
In a scattering experiment, when the measured cross-sections are plotted against the incident energy of the electron, sometimes there are peaks instead of a smooth curve. In such situations, the electron is caught by the target for a short time and then the electron is ejected. Such a state is called an autoionization state, a doubly excited state, or a Feshbach resonance. These states are formed below the various excited states of the target. The states formed below the n = 2 state of the hydrogen atom are (2s2s) 1S and 3S. Moreover, resonance states for L > 0 exist below the threshold. States with an angular momentum of L = 1 can also be formed by photoabsorption. These resonance states are like bound states; however, they are embedded in the continuum. Therefore, there is an interaction with the continuum that makes the state short-lived. These states were calculated using various approaches, namely, the stabilization method, the complex rotation method, and the Feshbach projection operator formalism [18]. We calculated the discrete energy of a resonance state using the Ritz variational principle using bound state projected functions :
The energy of the resonance state is given by , where is the shift due to the interaction of the bound state with the continuum. In the narrow region of the width, the scattering phase shift increases by π radians. There is an upper bound on the calculated discrete energy , but that bound is lost when the shift is added to it. For the state (2s2s) 1S in He, eV, = 0.02112 eV, giving = 57.8435 eV for the position of the autoionization state with respect the ground state of He with a width = 0.125 eV.
An accurate photoabsorption experiment to determine the position and width of the (2s2p) 1P resonance was carried out by Madden and Codling [46], which obtained a position = 60.186 ± 0.015 eV relative to the ground state of He and a width = 0.038 ± 0.004 eV. Bhatia et al. [47] carried calculations for this state using the Feshbach formalism [18] and a pseudostate nonresonant continuum, obtaining 60.1449 eV and 0.0369 eV for the position and width, respectively. The agreement of their calculated results with the experimental results is good.
Using the hybrid theory [42], phase shifts are calculated in the resonance region and resonance parameters are calculated by fitting these phase shifts to the Breit–Wigner form:
In the above expression, E = k2 is the incident energy; are the calculated phase shifts; , A, , and ER are the fitting parameters in the resonance region. Fitting the phase shifts to Equation (39), we find ER = 57.8481 eV relative to the He ground state and a width Γ = 0.1233 eV. These resonance parameters compare well with those mentioned above. Similarly, for Li+, we find = 70.5904 eV and Γ = 0.1657 eV, which compares well with the = 70.5837 eV and Γ = 0.157 eV obtained using the Feshbach formalism [48].
Drake [49] carried out extensive calculations using Ritz’s variational principle for such states, obtaining very accurate results for the 4He atom. However, Drachman [50] showed that it is much easier if perturbation theory is used, in which all the multipoles are calculated to obtain an asymptotic expansion for the effective potential, as indicated below:
The energy of any (1sNL) state can be calculated using unperturbed He wavefunctions. In Table 9, we compare the variational method with the asymptotic method for a few values of N and L. The energies are given in MHz (1 Ry = 3.289 × 109 MHz). We see that the agreement between the energies obtained using the two methods is very good. An advantage of having Equation (40) is that once it has been obtained, it can be used for any state (NL), while in a variational calculation, every state has to be calculated starting from the beginning.

Table 9.
Comparison of the asymptotic expansion obtained by Drachman [50] with the variational method of Drake [49]. Energies are in megahertz.
Accurate measurements [51] were carried out of the fine-structure intervals in excited lithium atoms. Using the perturbation theory described above and including relativistic corrections and the retardation (Casimir) effect, Bhatia and Drachman [52] computed several fine-structure intervals. The addition of a radiative (Lamb shift) correction [52] produces an essentially exact agreement with the measurements [51]. We show a comparison with measurements in Table 10. We see that the perturbation theory, with corrections, gives very accurate results.

Table 10.
Comparison level energy difference in megahertz between theory and measurements.
The polarization model was also used to calculate the fine-structure intervals in C IV, O VI, and Ne VIII [53].
9. Polarizabilities
In the above calculation, we used the polarizabilities of a Li ion. They are required in scattering calculations, as well as to calculate the fine-structure intervals in Rydberg states. Polarizabilities for two-electron systems were calculated by Bhatia and Drachman [54] using the pseudostate method. They include the effect of finite mass corrections. For Li+, they are given below:
The multipole polarizabilities of other two-electron systems were also calculated in the above reference [54].
10. Optical Properties of Helium Gas
Bhatia and Drachman [55] calculated the polarizabilities of a He atom as a function of frequency, including relativistic corrections using the Breit–Pauli operator, to calculate the refractive index n and Verdet constant, which measures the rotation of the plane of polarization in the Faraday effect.
The index of refraction is given by:
The Verdet constant is given by:
We compared these results at for the refractive index and Verdet constant at with experimental values and found significant discrepancies. Perhaps, there is a need to redo the experiment.
11. Lamb Shift
We mentioned above that the Lamb shift was included in the calculation of the fine-structure intervals in the Rydberg states of Li. It requires a calculation of the Bethe logarithm term given by:
where are pseudostates having L = 1, both bound and continuum, of the two-electron Hamiltonian, and:
Because of the term , the convergence of the numerator and denominator in Equation (44) is very slow. Using the pseudostate method of Bhatia and Drachman [56] and also using the method of Dalgarno and Steward [57], the summation over n could be extended to infinity. For a two-electron system, results for ln(K) are given in Table 11. These results agree well with those of Goldman and Drake [58].

Table 11.
Results of ln(K) for two-electron systems.
These results can be fitted to:
12. Retardation Correction (Casimir)
In the calculation of Rydberg states of Li that was mentioned above, we needed to take the retardation corrections into account, which arise when the Rydberg electron is at a distance much greater than the radius of the core. This is due to the finite time light propagation taken between the Rydberg electron and the core. By the time the signal from the Rydberg electron arrives at the core, the electron in the core moves away in time t = a0/v. The effective potential is proportional to x−5. Au et al. [59] showed that there is an energy shift due to the modification of the potential. Using the equations given in [59], Bhatia and Drachman [60] evaluated this correction, where the results for N = 10 are given in Table 12.

Table 12.
Retardation corrections (MHz) for lithium for N = 10.
13. Hyperfine Structure of Li
The hyperfine structure of Li was calculated by Larsson [61] using a 100-term Hylleraas wavefunction to obtain a hyperfine splitting = 2.906. The hyperfine splitting is proportional to
Here, is the eigenfunction of the non-relativistic Hamiltonian . We replace by the global operator ; then, .
We see that improved results are obtained if is replaced by a global identity given above, which was proposed by Hiller et al. [62]. Bhatia and Sucher [63], using a 40-term configuration type wavefunction (CI) and the global identity for the function, obtained a hyperfine splitting of 2.9014, which compares favorably with the experimental value of 2.9062 [64]. We show the results in Table 13 as the number of terms in the CI functions is increased.

Table 13.
Values of the energy and Fermi contact terms for various values of N in the calculation of the energy of a Li atom.
14. Parity-Violating Electric-Dipole Transitions in Helium
The party-violating transitions [65] between the n =2 levels in He are:
The matrix element for this transition is:
Again, improved results were obtained using simple wave functions instead of Hylleraas functions when using the global identity in place of the function.
15. Positron–Hydrogen Scattering
It might appear that positron calculations should be easier because there is no exchange between electrons and positrons. However, the possibility of positronium formation makes calculations more difficult. Furthermore, in electron–hydrogen scattering, electrons arrange themselves on either side of the nucleus because of the repulsion between them. On the other hand, positrons and electrons tend to be on the same side of the nucleus because of the attraction between a positron and an electron. It is clear that correlations are more important in this case. Positron–hydrogen interaction is repulsive but the polarization of the target produces an attractive potential. The two tend to cancel each other, making it harder to get meaningful results. In 1971, Bhatia at al. [66] carried out calculations for positron–hydrogen scattering using the Feshbach formalism [18] and using a generalized Hylleraas type wave function:
The nonlinear parameters are and , and the Cs are the linear parameters. The component in the above wave function takes into account the virtual positronium atom contribution. Phase shifts for this scattering system were calculated by Schwartz [17] using the Kohn variational principle, which does not have any bounds on the calculated phase shifts. In [66], long-range interactions could not be added at the same time. Such interactions could be taken into account using hybrid theory [67] and a shorter expansion of the wave function is enough to obtain converged results. In the positron scattering, Equation (11) is replaced by:
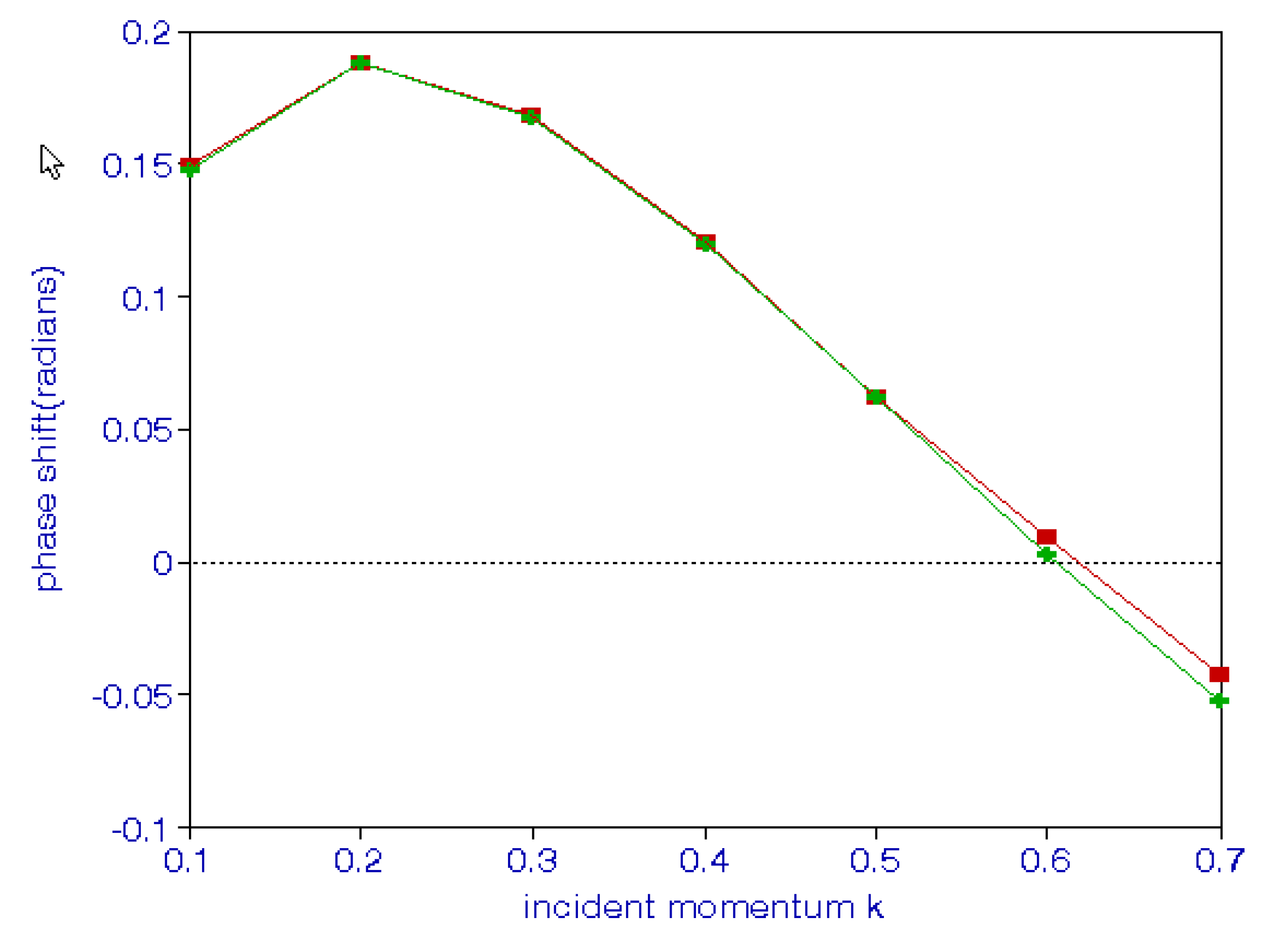
It should be noted that we need a plus sign in positron–hydrogen scattering, as indicated above. A comparison of results obtained using thee different approaches is given in Table 14. A comparison of the phase shifts for positron–hydrogen scattering using hybrid theory and the Feshbach projection operator formalism is shown in Figure 3. Fewer terms are needed in the hybrid theory compared to the 84 terms used in the Feshbach formalism.

Table 14.
Comparison of S-wave and P-wave phase shifts (radians).
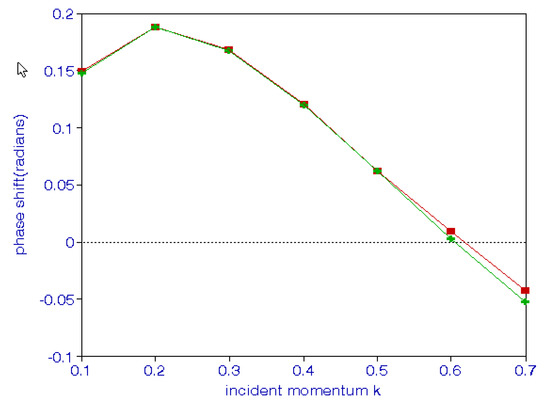
Figure 3.
(Color online). The upper curve represents phase shifts for positron–hydrogen scattering using hybrid theory and the lower curve represents those obtained using the Feshbach formalism.
In [67], the scattering length “a” was calculated. Using 56 terms in the Hylleraas wave function, we found a = −2.10074. Correcting for the long-range interaction, namely, Equation (23), we found a = −2.10158 − 0.002424 = −2.104004. This agrees well with the scattering length of −2.10036 ± 0.0004 obtained by Houston and Drachman [68] using the Kohn and Harris methods. In the Kohn variational method, the scattering length has an upper bound. The scattering length obtained in [68] can be less than that obtained by them. The result for the scattering length obtained in [67] is then consistent with their result [68]. Bhatia et al. [69] also carried out P-wave calculations using the Feshbach formalism [18], while Bhatia [70] used hybrid theory to obtain P-wave phase shifts. These results are also compared in Table 14.
16. Zeff
An atomic electron can annihilate with an incident positron, emitting two gamma rays. Ferrell [71] calculated the cross-section for this process:
where ki is the momentum of the incident positron, and:
For L > 1, we used plane wave normalization:
Then, we obtain:
Zeff for the partial waves L = 0 and L = 1, obtained in [67,70] using hybrid theory, are given in Table 15. Zeff was calculated by Humberston and Wallace [72] using the Kohn variational principle, and by Green and Gribakin [73] using diagrammatic many-body theory.

Table 15.
Zeff for positron–hydrogen scattering.
17. Positronium Formation
Positronium, the bound state of an electron and a positron, was predicted by Mohorovocic [75] to explain the spectra of nebulae. Positronium formation takes place when an incident positron captures an electron in a hydrogen atom before annihilation:
Experimental determination of the cross-section of positronium formation was carried by Zhou et al. [76]. The differential cross-section for this rearrangement is given by:
In the above expression, ki and kPs are the momenta of the initial positron and the positronium atom, and are the initial and final reduced masses. T is the transition matrix given by Khan and Ghosh [77]:
where:
The ground state wave function of the positronium atom is given by:
The interaction in the final state is given by:
We can write:
where the first term represents the matrix element without polarization and the second term is with polarization n. Such calculations have also been carried out by Cheshire [78]. The function Ψf was obtained using hybrid theory [70]. The integral occurring in this calculation can be solved using the Fourier transforms [77,78,79]. In Table 16, the cross-sections for the positronium formation are given and compared with the results obtained in other calculations.

Table 16.
Comparison of the cross-sections () obtained using the hybrid theory with those obtained in other calculations.
18. Resonances in Systems Involving Positrons
Resonances formed with electrons are very common in atomic and molecular systems. However, this is not so with positrons. Mittleman [8] showed that in the equation for the positron–hydrogen system, there is an attractive 1/r2 potential due to the degeneracy of the 2s and 2p states of the hydrogen atom. This implies that there should be infinite resonance states in this case also, as in the electron–hydrogen system. The S-wave resonance of a positron–hydrogen system was calculated successfully for the first time by Doolen et al. [82] using a sparse matrix technique in the complex rotation method [83], in which the radial coordinates are rotated by an angle ,, transforming the Hamiltonian:
The wave function used in their calculation was:
where α is the nonlinear parameter, is a Laguerre polynomial, and:
Only one resonance was found with complex energy:
We look for stationary paths as the angle is varied. The resonance parameters converge as the number of terms in the trial function is increased below the n = 2 threshold of the hydrogen atom, as indicated in Table 17.

Table 17.
Position and width of the resonance in Rydberg units.
We see that the resonance position is at −0.2573741 Ry with a width of 0.00001354 Ry. We also see that a large number of terms is required to calculate the resonance parameters. This is the reason that previous attempts failed to calculate resonance parameters.
19. Resonances in Positronium Ion
The positronium ion is obtained by replacing the proton in the hydrogen ion with a positron. Now that the nucleus has the same mass as an electron, the mass polarization term in the Hamiltonian becomes important:
Resonances in the singlet and triplet states of Ps− were calculated by Ho [84], where he used 364 terms in the singlet states and 455 terms in the triplet states in the Hylleraas trial wave function. Using the complex rotation method, he obtained resonances below the n = 2, 3, 4, and 5 thresholds of Ps. His results are shown in Table 18.

Table 18.
Resonance positions (eV) are relative to the ground state of Ps−.
Triplet P even parity doubly-excited states below n = 2, 3, 4, 5, and 6 were calculated by Ho and Bhatia [85]. The resonance parameters are given in Table 19.

Table 19.
Doubly-excited or Feshbach-type 3Pe resonances in Ps−.
Odd parity triplet and singlet P states were calculated in [86,87]. Their results are given in Table 20 and Table 21. The lowest odd parity P state was observed by Michishio et al. [88] using laser beams of 2285 and 2297 Å. The observed position and width agree with the calculated values.

Table 20.
Odd parity triplet P states of a Ps− ion.

Table 21.
Odd parity singlet P states of a Ps− ion.
20. Positron Impact Excitation
In Section 7, we described the theory for electron-impact excitation of atomic hydrogen. Using the details given there, Bhatia [89,90,91] carried out excitation of nS, nP, and nD (n = 2, 3, 4, 5, and 6) states of a hydrogen atom due to an impact of a positron. Thirty partial waves were used to get the converged results. Convergence with partial waves and comparison with the results of other calculations for the 2S state are given in [89]. The minimum of 2S cross-sections is at k = 0.87 and they increase smoothly up to k = 1.0, then they start decreasing. Wigner [92] emphasized the importance of long-range forces in a threshold region, which were included in these calculations. In the threshold region, the cross-sections are proportional to [93]. The 2S cross-sections in the threshold region can be fitted to the form:
In [91], we gave the total cross-sections for the n = 2 to 6 states at various positron energies.
21. High-Energy Cross-Sections
Only the static potential remains at high energies. According to the first Born approximation, the total cross-sections for electron–He and positron–He scattering should be the same. Kauppila et al. [94] verified this fact experimentally. We show their results in Table 22. We see that the cross-sections tend to be equal as the incident energy increases.

Table 22.
Measured cross-sections () for e–He and e+–scattering.
22. Photodetachment of a Positronium Ion
We mentioned a calculation of the photodetachment of a hydrogen ion by Ohmura and Ohmura [35] in Section 6. Following Ohmura and Ohmura, Bhatia and Drachman [95] calculated the photodetachment of the positronium ion in the length and velocity form, obtaining:
The binding energy is 1.5, where = 0.12651775 and k is the momentum of the outgoing electron. Photodetachment was observed by Michishio et al. [88].
The Lyman- radiation at 1216 Å due to the transition of a 2P state to a 2S state in the hydrogen atom was observed using Voyager measurements [96]. Similarly, it may be possible to observe the Lyman- radiation at 2432 Å due to the transition of 2P to 2S in the positronium atom when in the photodetachment of the Ps−, the remaining positronium is left in a 2P state. Following Ohmura and Ohmura [37], photodetachment cross-sections were calculated when the remaining atom is in the 2p, 3p, 4p, 5p, 6p, and 7p states [97].
23. Opacity of the Atmosphere of the Sun
The opacity of the atmosphere of the sun is due to various processes, where among them are bound–bound transitions, Thomson scattering, and photodetachment (bound–free) transitions due to the absorption of photons in negative hydrogen ions and negative positronium ions. Photodetachment was suggested by Wildt [29] as an important source of opacity, which is the absorption of photons (Equation (24)).
Chandrasekhar and Elbert [98] calculated the cross-sections for this process. These transitions explain the opacity of the atmosphere of the Sun between 4000 to 16,000 Å. Beyond this range, the opacity is due to free–free transitions involving electrons:
In the free–free transition indicated in Equation (71), an electron with energy absorbs photon energy and the final electron energy is . Both the initial and final states of the electron are in the continuum. The change in energy is .
The cross-sections calculated by Chandrasekhar and Breen [99], when averaged over the Maxwell distribution of the initial velocities, give the absorption coefficient:
In the above, and the multiplying factor is due to stimulated emission. Ohmura and Ohmura [100] showed that:
Ohmura and Ohmura [100] also showed that the Ms depend only on S-wave scattering phase shifts:
Phase shifts and are the triplet and singlet phase shifts, respectively, for the scattering of an electron with momentum k from a hydrogen atom. They were accurately calculated in the hybrid theory and are given in Table 1 and Table 2, respectively. Free–free transitions involving positrons are:
The S-wave positron hydrogen scattering phase shifts are given in Table 14. Equation (74) now becomes:
In Table 23, we give the Maxwellian averaged absorption coefficients (cm4/dyne) for free–free transitions involving electrons and hydrogen atoms, as well as for positrons and hydrogen atoms. The wavelength is given by 911.3/.

Table 23.
Maxwellian averaged absorption coefficients (cm4/dyne) for free–free transitions involving electrons and hydrogen atoms, and positrons and hydrogen atoms.
In Table 24, we compare the present results for the absorption coefficients with those obtained by Ohmura and Ohmura [100] and with those obtained by Chandrasekhar and Breen [99]. It should be noted that at the time of Chandrasekhar and Breen, only the Hartree potential could be used when carrying out the numerical calculations precisely because of the non-availability of computers at that time. The resulting absorption coefficients were overestimated. Nevertheless, Chandrasekhar set the stage for further investigations.

Table 24.
Comparison of the presently calculated absorption coefficients (1025 cm4/dyne) with those obtained in [99] and [100].
In Table 25, we compare the photodetachment cross-sections for H− and Ps−. The photoabsorption cross-sections are not averaged over the Maxwellian distribution because the emitted electron has a definite velocity. We also compare the free–free transition coefficients for electrons and positrons. From this table, we conclude that at longer wavelengths, the photodetachment cross-sections do not contribute to the opacity, while free–free transitions contribute at longer wavelengths. Furthermore, positrons almost contribute equally. Free–free transitions involving a positron and Ps are also possible. The phase shifts for e+–Ps were calculated by Ward et al. [101].

Table 25.
Comparison of bound–free () and free–free (Cf.) absorption coefficients for electrons and positrons and hydrogen atoms at T = 6300 K.
From the charge conjugation theorem, these two processes have the same absorption coefficient. The absorption coefficients for Equation (77) are also given in Table 25 at a temperature of 6300 K, where the temperatures of typical cool stars range between 3000 K and 7000 K. Furthermore, this temperature was used in previous publications on this subject.
All the processes mentioned above are also possible with He, He+, Li+, Li2+, etc. However, their abundance decreases as we consider elements beyond hydrogen atoms. Long ago, it was pointed out by Cecilia Payne Goposchkin (student of Eddington) that hydrogen is the most abundant in the universe.
24. Conclusions
The interactions of electrons, positrons, the radiation field, atoms, and ions have been discussed in this article. Scattering functions were calculated using different approaches. We described in detail the calculations for various processes using the hybrid theory because it is the most recent one and we have used it extensively. We have discussed scattering from hydrogenic targets because the wave functions for them are known exactly. This allowed us to judge the approach and accuracy of results. The present theory described above takes into account exchange and short-range and long-range interactions at the same time and is variationally correct. Accurate resonance parameters were obtained using the hybrid theory and these were compared with those obtained using the Feshbach formalism, where the shifts and widths have to be calculated separately. The photoabsorption cross-sections obtained using the present theory agree well with the results obtained using other theories and experimental results. We have calculated the photodetachment of a Ps− ion leaving Ps in various excited states, pointing out the possibility of observing positronium Lyman- radiation at 2432 Å. Phase shifts and photoabsorption cross-sections were used to calculate the opacity of the atmosphere of the Sun and also of stellar atmospheres, pointing out that the contribution of positrons is comparable to that of electrons.
Funding
This research work received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Compton, A.H. A Quantum Theory of the scattering of X-rays by light. Elements. Phys. Rev. 1923, 21, 152. [Google Scholar] [CrossRef]
- Bothe, W.; Geiger, H. Uber das Wesen des Compton effects ein experimenteller Breitrag Theorie der Strahlung. Zeits für Phys. 1925, 22, 639. [Google Scholar] [CrossRef]
- Compton, A.H.; Simon, A.W. Directed Quanta of Scattered X-rays. Phys. Rev. 1925, 26, 289. [Google Scholar] [CrossRef]
- Bohr, N.; Kramers, H.A.; Slaters, J.C. The quantum theory of radiation. Phil. Mag. J. Science. 1924, 47, 785. [Google Scholar] [CrossRef]
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049. [Google Scholar] [CrossRef]
- Chadwick, J. Possible Existence of a neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Temkin, A. A note on Scattering of Electrons from Atomic Hydrogen. Phys. Rev. 1959, 116, 358. [Google Scholar] [CrossRef]
- Mittleman, M.H. Resonances in Proton-Hydrogen and Positron-Hydrogen. Phys. Rev. 1966, 152, 76. [Google Scholar] [CrossRef]
- Casimir, H.B.G.; Polder, D. The influence of Radiation on the London-van der Waals Forces. Phys. Rev. 1948, 73, 360. [Google Scholar] [CrossRef]
- Kelsey, E.J.; Spruch, L. Radiation effects on high Rydberg States. A retarded R−5polarization potential. Phys. Rev. A 1978, 18, 15. [Google Scholar] [CrossRef]
- Lundeen, S.R. Experimental Studies of High-L High Rydberg States in Helium in Long-Range Casimir Forces Theory and Experiments on Atomic Systems; Levin, F.S., Micha, D.A., Eds.; Plenum Press: New York, NY, USA, 1993; p. 73. [Google Scholar]
- Morse, P.M.; Allis, W.P. The effect of Exchange on the scattering of Slow Electrons from Atoms. Phys. Rev. 1933, 44, 269. [Google Scholar] [CrossRef]
- Sloan, I.H. The method of polarized orbitals for the elastic scattering of slow electrons by ionized helium and atomic hydrogen. Proc. Roy. Soc. 1961, 281, 151. [Google Scholar]
- Burke, P.G.; Smith, K. The Low-Energy Scattering of Electrons and Positrons by Hydrogen Atoms. Rev. Mod. Phys. 1962, 34, 458. [Google Scholar] [CrossRef]
- Burke, P.G.; Robb, W.D. The R-Matrix Theory of Atomic Processes. Adv. Atom. Mole. Phys. 1976, 11, 143. [Google Scholar]
- Burke, P.G.; Noble, C.J.; Scott, M.P. Electron-hydrogen atom scattering at intermediate energies. Proc. Roy. Soc. A 1987, 410, 289. [Google Scholar]
- Schwartz, C. Electron Scattering from hydrogen. Phys. Rev. 1961, 124, 1468. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions II. Ann. Phys. (NY.) 1962, 19, 287. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A. Complex-correlation Kohn T-matrix method of calculating total cross sections: Electron-hydrogen elastic scattering. Phys. Rev. A 2001, 64, 032709. [Google Scholar] [CrossRef]
- McCurdy, C.W.; Baertschy, M.; Rescigno, T.N. Solving the three-body Coulomb breakup problem. J. Phys. B 2004, 37, R137. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of electron-hydrogen elastic scattering. Phys. Rev. A 2007, 75, 032713. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A. Symmetric Euler-Angle Decomposition of the Two-Electron Fixed-Nucleus Problem. Rev. Mod. Phys. 1964, 36, 1050. [Google Scholar] [CrossRef]
- Temkin, A. Polarization and the Triplet-Electron Hydrogen Scattering Length. Phys. Rev. Lett. 1961, 6, 354. [Google Scholar] [CrossRef]
- Oza, D.H. Phase shifts and resonances for electron scattering by He+ below N = 2 threshold. Phys. Rev. A 1986, 33, 824. [Google Scholar] [CrossRef]
- Bhatia, A.K. Applications of the hybrid theory to the scattering of electrons from He+ and Li2+. Phys. Rev. A 2008, 77, 052707. [Google Scholar] [CrossRef]
- Gien, T.T. Accurate calculation of phase shifts for electron-He+ collisions. J. Phys. B 2002, 35, 4475. [Google Scholar] [CrossRef]
- Gien, T.T. Accurate calculation of phase shifts for electron-Li2+ collisions. J. Phys. B 2003, 36, 2291. [Google Scholar] [CrossRef]
- Bhatia, A.K. Electron-He+ elastic Scattering. Phys. Rev. A 2002, 66, 06472. [Google Scholar] [CrossRef]
- Wildt, R. Electron Affinity in Astrophysics. Astrophys. J. 1939, 89, 295. [Google Scholar] [CrossRef]
- Chandrasekhar, S. On the Continuous Absorption Coefficient of the negative Hydrogen Ion. Astrophys. J. 1945, 102, 223. [Google Scholar] [CrossRef]
- Bhatia, A.K. Electron-He+ P-wave elastic scattering and photoabsorption in two-electron systems. Phys. Rev. A 2006, 73, 012705. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of P-wave electron-Li2+elastic scattering and photoabsorption in two electron systems. Phys. Rev. A 2013, 87, 042705. [Google Scholar] [CrossRef]
- Wishart, A.W. The bound—free photodetachment of H. J. Phys. B 1979, 12, 3511. [Google Scholar] [CrossRef]
- Branscomb, L.M.; Smith, S.J. Experimental Cross Sections for Photodetachment of Electrons from H- and D. Phys. Rev. 1955, 98, 1028. [Google Scholar] [CrossRef]
- Ohmura, T.; Ohmura, H. Electron-Hydrogen scattering at low energies. Phys. Rev. 1960, 118, 154. [Google Scholar] [CrossRef]
- Nahar, S.N. The Ultraviolet Properties of Evolved Stellar Populations. In New Quests in Stellar Astrophysics II; Chavez, M., Bertone, E., Rosa-Gonzalez, D., Rodriguez-Merino, L.H., Eds.; Springer: New York, NY, USA, 2009; p. 245. [Google Scholar]
- Samson, J.A.; He, Z.X.; Yin, L.; Haddad, G.N. Precision measurements of the absolute photoionization cross sections of He. J. Phys. B 1994, 27, 887. [Google Scholar] [CrossRef]
- Daskhan, M.; Ghosh, A.S. Photoionization of He and Li+. Phys. Rev. A 1984, 86, 032713. [Google Scholar]
- Bhatia, A.K.; Temkin, A.; Silver, A. Photoionization of Li. Phys. Rev. A 1975, 12, 2044. [Google Scholar] [CrossRef]
- Dasgupta, A.; Bhatia, A.K. Photoionization of Sodium Atoms and Electron scattering from Ionized Sodium Atoms. Phys. Rev. A 1985, 31, 759. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.K.; Drachman, R.J. Photoejection with excitation in H- and other systems. Phys. Rev. A 2015, 91, 012702. [Google Scholar] [CrossRef]
- Bhatia, A.K. Application of P-wave hybrid theory for the scattering of electrons from He+and resonances in He and H. Phys. Rev. A 2007, 86, 032713. [Google Scholar] [CrossRef]
- Callaway, J. Scattering of electrons by atomic hydrogen at intermediate energies. Elastic Scattering and n = 2 excitation from 12 to 54 eV. Phys. Rev. A 1985, 32, 775. [Google Scholar] [CrossRef]
- Burke, P.G.; Schey, H.M.; Smith, K. Collisions of slow Electrons and Positrons with Atomic Hydrogen. Phys. Rev. 1963, 129, 1258. [Google Scholar] [CrossRef]
- Scott, M.P.; Scholz, T.T.; Walters, H.R.; Burke, P.G. Electron scattering by atomic hydrogen at intermediate energies: Integrated elastic 1s-2s and 1s-2p cross sections. J. Phys. B 1989, 22, 3055. [Google Scholar] [CrossRef]
- Madden, R.P.; Codling, K. Two-Electron Excitation States of Helium. Ap. J. 1965, 141, 364. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Burke, P.G.; Temkin, A. Calculation of (2s2p) 1P Autoionization State of He with a Pseudostate Nonresonant Continuum. Phys. Rev. A 1973, 8, 21. [Google Scholar] [CrossRef]
- Bhatia, A.K. Autoionization and quasibound states of Li+. Phys. Rev. A 1977, 15, 1315. [Google Scholar] [CrossRef]
- Drake, G.W.F. High-Precision Calculations for The Rydberg States of Helium in Long-Range Casimir Forces Theory and Experiments on Atomic Systems; Levin, F.S., Micha, D.A., Eds.; Plenum Press: New York, NY, USA, 1993; p. 107. [Google Scholar]
- Drachman, R.J. High Rydberg States of Two-Electron Atoms in Perturbation Theory in Long-Range Casimir Forces Theory and Experiments on Atomic Systems; Levin, F.S., Micha, D.A., Eds.; Plenum Press: New York, NY, USA, 1993; p. 219. [Google Scholar]
- Rothery, N.E.; Storry, C.H.; Hessel, E.A. Precision radio-frequency measurements of the high-L Rydberg states of lithium. Phys. Rev. A 1995, 51, 2919. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.K.; Drachman, R.J. Relativistic, retardation, and radiative corrections in Rydberg states in lithium. Phys. Rev. A 1997, 55, 1842. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Energy levels of C IV. The polarization model. Phys. Rev. A 1999, 60, 2848. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Properties of two-electron systems in an electric field. Can. J. Phys. 1997, 75, 11. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Optical properties of helium including relativistic corrections. Phys. Rev. A 1998, 58, 4470. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Another way to calculate the Lamb Shift in two-electron systems. Phys. Rev. A 1998, 57, 4301. [Google Scholar] [CrossRef]
- Dalgarno, A.; Stewart, A.L. The screening approximation for the helium sequence. Proc. Phys. Soc. Lond. 1960, 70, 49. [Google Scholar] [CrossRef]
- Goldman, S.P.; Drake, G.W.F. 1/Z expansion calculation of the Bethe logarithm for the ground state Lamb-shift of two-electron ions. J. Phys. B 1983, 16, L183. [Google Scholar] [CrossRef]
- Au, C.K.; Feingberg, G. Sucher, Retarded Long-Range Interaction in He Rydberg States. J. Phys. Rev. Lett. 1984, 53, 1145. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. A new way to calculate the Lamb shift in Two-electron systems. Phys. Rev. A. 1997, 55, 1842B. [Google Scholar] [CrossRef]
- Larsson, S. Calculations on the 2S Ground State of of the Lithium Atom Using Wave Functions of Hylleraas type. Phys. Rev. 1968, 169, 49. [Google Scholar] [CrossRef]
- Hiller, J.; Feinberg, G.; Sucher, J. New technique for revaluating parity-conserving and parity violating contact term. Phys. Rev. A 1978, 18, 2399. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Sucher, J. New approach to hyperfine structure: Application to the Li ground state. J. Phys. B 1980, 13, L409. [Google Scholar] [CrossRef]
- Kusch, P.; Taub, H. On the gJ Values of the Alkali Atoms and the Hyperfine structure of the Alkali Atoms. Phys. Rev. 1949, 78, 1477. [Google Scholar] [CrossRef]
- Hiller, J.; Sucher, J.; Bhatia, A.K.; Feinberg, G. Parity-violating electric-dipole transitions in helium. Phys. Rev. A 1980, 21, 1082. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A.; Drachman, R.J.; Eiserike, H. Generalized Hylleraas Calculation of Positron-Hydrogen Scattering. Phys. Rev. A 1971, 3, 1328. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron-Hydrogen Scattering, Annihilation, and Positronium Formation. Atoms 2016, 4, 27. [Google Scholar] [CrossRef]
- Houston, S.K.; Drachman, R.J. Positron-Atom Scattering by Kohn and Harris Methods. Phys. Rev. A 1971, 3, 1335. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A.; Eiserike, H. Rigorous Precision P-wave Positron-Hydrogen scattering Calculations. Phys. Rev. A 1974, 9, 219. [Google Scholar] [CrossRef]
- Bhatia, A.K. P-wave Positron-Hydrogen Scattering, Annihilation, and Positronium formation. Atoms 2017, 5, 17. [Google Scholar] [CrossRef]
- Ferrell, R. Theory of Positron Annihilations in Solids. Rev. Mod. Phys. 1956, 28, 308. [Google Scholar] [CrossRef]
- Humberston, J.W.; Wallace, J.B.G. Positronium formation in S-wave positron-hydrogen scattering. J. Phys. B 2001, 5, 1138. [Google Scholar] [CrossRef]
- Green, D.G.; Gribakin, G.F. Positron scattering and annihilation in hydrogen like ions. Phys. Rev. A 2013, 88, 032708. [Google Scholar] [CrossRef]
- Houston, S.K.; Drachman, R.J. Positron-Atom Scattering by the Kohn and Harris Methods. (unpublished).
- Mohorovocic, S. Possibility of new elements and their meaning in astrophysics. Asron. Nahr. 1934, 253, 93. [Google Scholar]
- Zhou, S.; Li, H.; Kauppila, W.E.; Kwan, C.K.; Stein, T.S. Measurements of total and positronium formation cross sections for positrons and electrons scattered by hydrogen atoms and molecules. Phys. Rev. A 1997, 55, 361. [Google Scholar] [CrossRef]
- Khan, A.; Ghosh, A.S. Positronium formation in positron-hydrogen scattering. Phys. Rev. A 1983, 27, 1904. [Google Scholar] [CrossRef]
- Cheshire, I.M. Positronium formation by fast positrons in atomic hydrogen. Proc. Phys. Soc. 1964, 83, 227. [Google Scholar] [CrossRef]
- Direnzi, J.; Drachman, R.J. Re-examination of a Simplified Model for Positronium-Helium Scattering. J. Phys. B 2003, 36, 2409. [Google Scholar] [CrossRef]
- Humberston, J.W. Positronium formation in a s-wave positronium-hydrogen scattering. Can. J. Phys. 1982, 60, 591. [Google Scholar] [CrossRef]
- Kvitsky, A.A.; Wu, A.; Hu, C.Y. scattering of electrons and positrons on hydrogen using Faddev equations. J. Phys. B 1995, 28, 275. [Google Scholar] [CrossRef]
- Doolan, G.D.; Nuttal, J.; Wherry, C.J. Evidence of a Resonance in a e+-H S-wave scattering. Phys. Rev. Lett. 1978, 40, 313. [Google Scholar] [CrossRef]
- Balslev, E.B.; Combes, J.W. Spectral properties of many-body Schrödinger Operators with Dialation-analytic interactions. Comm. Math. Phys. 1971, 22, 280. [Google Scholar] [CrossRef]
- Ho, Y.K. Doubly-excited resonances of positronium negative ion. Phys. Rev. A 1984, 102, 348. [Google Scholar] [CrossRef]
- Ho, Y.K.; Bhatia, A.K. Doubly excited 3Peresonant states in Ps−. Phys. Rev. A 1992, 45, 62688. [Google Scholar]
- Bhatia, A.K.; Ho, Y.K. Complex-coordinate calculation of 1,3P resonances in Ps-using Hylleraas functions. Phys. Rev. A 1990, 42, 1119. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.K.; Bhatia, A.K. P-wave shape resonances I positronium ion. Phys. Rev. A 1993, 47, 1497. [Google Scholar] [CrossRef]
- Michishio, K.; Katani, T.; Kuma, S.; Azuma, T.; Wade, K.; Mochizuka, I.; Hydo, T.; Yogishita, A.; Ngashima, Y. Observation of shape resonance. Nat. Artic. 2016, 7, 11060. [Google Scholar]
- Bhatia, A.K. Positron Impact Excitation of the 2S State of Atomic Hydrogen Atoms. Atoms 2019, 7, 69. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron Impact Excitation of the nS State of Atomic Hydrogen Atoms. Atoms 2019, 8, 9. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron Impact of Excitation of the nS, nP, and nD States of Atomic Hydrogen. Mod. Concepts Mater. Sci. 2020, 3, 1. [Google Scholar]
- Wigner, E.P. On the behavior of cross sections near thresholds. Phys. Rev. 1948, 71, 100. [Google Scholar] [CrossRef]
- Sadegpour, H.R.; Bohn, J.L.; Covagnero, M.L.; Esry, B.D.; Fabrikant, I.I.; Macek, J.H.; Rao, A.R.P. Collision near threshold in atomic and molecular physics. J. Phys. B 2000, 33, R93. [Google Scholar] [CrossRef]
- Kauppila, W.E.; Stein, T.S.; Smart, J.H.; Debabneh, H.Y.K.; Dawning, J.P.; Pol, V. Measurements of total cross sections for intermediate-energy positrons and electrons colliding with helium, neon, and argon. Phys. Rev. A 1981, 24, 308. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Photodetachment of the positronium negative ion. Phys. Rev. A 1985, 32, 3745. [Google Scholar] [CrossRef]
- Lailement, R.; Quemerais, E.; Bertaux, J.-L.; Sandel, B.R.; Izamodenov, V. Voyager Measurements of Hydrogen Lyman-αDiffuse Emission from Milky Way. Science 2011, 334, 1665. [Google Scholar] [CrossRef]
- Bhatia, A.K. Photodetachment of the Positronium Negative ion with Excitation in the Positronium Atom. Atoms 2018, 7, 2. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Elbert, D.D. On continuous absorption coefficient of the negative hydrogen ion. Ap. J. 1958, 128, 633. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Breen, F.H. On continuous absorption coefficient of the negative hydrogen ion. Ap. J. 1946, 104, 430. [Google Scholar] [CrossRef]
- Ohmura, T.; Ohmura, H. Continuous Absorption Due to Free-Free Transitions in Hydrogen. Phys. Rev. 1961, 121, 513. [Google Scholar] [CrossRef]
- Ward, S.J.; Humberston, J.W.; McDowell, M.R.C. Elastic scattering of electrons (or positrons) from positronium and photodetachment of positronium negative ion. J. Phys. B 1987, 20, 127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).