Abstract
The interaction between Be4+ and hydrogen atom is studied using the three-body classical trajectory Monte Carlo method (CTMC) and the quasiclassical trajectory Monte Carlo method of Kirschbaum and Wilets (QTMC-KW). We present total cross sections for target ionization, target excitation, and charge exchange to the projectile bound states. Calculations are carried out in the projectile energy range between 10 and 1000 keV/au, relevant to the interest of fusion research when the target hydrogen atom is in the ground state. Our results are compared with previous theoretical results. We found that the classical treatment describes reasonably well the cross sections for various final channels. Moreover, we show that the calculations by the QTMC-KW model significantly improve the obtained cross sections.
1. Introduction
The currently used energy production methods will not be able to satisfy the energy needs of humanity in the long run. One of the best solutions in the future would be the implementation of fusion power plants. Beryllium is typically considered as the armor material for plasma facing components (PFCs) of fusion devices and it is the first wall of the international thermonuclear experimental reactor (ITER) [1]. Chemical and physical erosion of the first wall releases beryllium atoms and several molecular species, which eventually lead to the presence of fully-stripped beryllium ions in the plasma core. Beryllium is attractive as a plasma facing reactor material because of its low atomic number (i.e., low potential for radiative plasma power losses), excellent gettering properties concerning oxygen (unavoidably present in any fusion plasma), and adequate thermo-mechanical and erosion properties when exposed to plasma energy and particle fluxes. The inelastic collision processes between Beq+ ions and H are particularly important when energetic neutral hydrogen is injected into the plasma for heating and diagnostic purposes [2]. Therefore, the accurate description and knowledge of these interactions are extremely important for fusion research.
The calculation of cross section in collision Be4+ and hydrogen atom for ionization, charge exchange and excitation channels have been studied using different theoretical approaches such as:
- i.
- Atomic-orbital close-coupling (AOCC) [3,4]
- ii.
- Adiabatic superpromotion model [5]
- iii.
- The molecular orbital expansion of the solution of the time-dependent Schrodinger equation [6]
- iv.
- Symmetric Eikonal approximation [7]
- v.
- Classical methods [8]
In the last two decades, there has been a great revival of the classical trajectory Monte Carlo (CTMC) calculations applied in atomic collisions involving three or more particles. This approximation is useful in treating atomic collisions where the quantum mechanical ones become very complicated or unfeasible [8]. One of the advantages of the CTMC method is that many-body interactions are exactly taken into account during the collisions on a classical level. The CTMC method is a non-perturbative method, where classical equations of motions are solved numerically [9,10,11]. The quasiclassical trajectory Monte Carlo method of Kirschbaum and Wilets model represents one step further towards a better description of the classical atomic collisions. In particular, it is desirable to have a method that consistently treats electron transfer and ionization as well as multiplicities and combinations of these processes. For atoms, a necessary condition for stability is that the electrons are not allowed to collapse to the symmetry point, i.e., to the nucleus. The effective potential enforcing this condition is motivated by the Heisenberg uncertainty principle , where r and p are the distance and momentum of an electron with respect to a nucleus and is a constant. This condition is equivalent to the de Broglie description of the hydrogen atom. In addition, the Pauli constraint classically means that any two electrons having the same spins cannot occupy the same volume of phase space. We effect this by requiring that , where , is the relative position and , is the relative momentum of the ith and jth identical electrons, respectively, and is another dimensionless constant which must be determined.
Up to now, the QTMC-KW [12] has been applied to a variety of problems [13]. The method and its extensions [14,15,16,17,18] use momentum-dependent effective potentials in a Hamiltonian model to stabilize realistic atomic and molecular structures, which would otherwise autoionize classically. In this work, the interaction between Be4+ and ground state hydrogen atom is studied using the three-body CTMC and QTMC-KW in the projectile energy range between 10 and 1000 keV/au.
2. Theory
2.1. CTMC Method
In the present work, the CTMC simulations were made in the three-body approximation. The three particles (p; projectile, e; electron, T; target) are characterized by their masses and charges. For the description of the interaction among the particles, Coulomb potential is used. Figure 1 shows the relative position vectors of the three-body collision system.
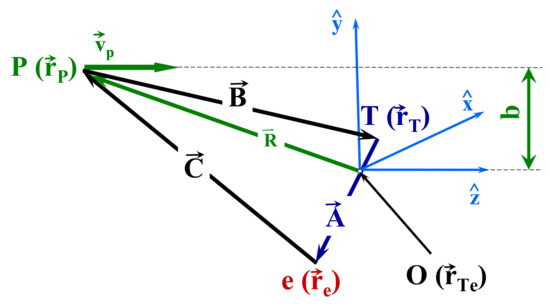
Figure 1.
The relative position vectors of the particles involved in 3-body collisions. , and , in such way that . Also, is the position vector of the center-of-mass of the target system, R is the position vector of the projectile and b is the impact parameter.
The Hamiltonian equation for the three particles can be written as:
where
and
where T and Vcoul are total kinetic energy and the potential energy term., , Z, and m are the position vector, momentum vector, the charge and the mass of the corresponding particles, respectively. The equations of motion taking into account the Hamiltonian mechanics is given as follows:
Introducing the relative position vectors , and , in such a way that as well as the definition of , the Equations (4)–(6) are reduced to the following:
The initial conditions of the collisions system, i.e., the coordinates and the velocities of the internal motion of (T,e) atomic system and the relative projectile and atomic center-of-mass motion were selected randomly. Equations (7) and (8) were integrated considering the time as an independent variable by the standard Runge–Kutta method for a given set of initial conditions as described by Tőkési and Kövér [19].
The total cross-sections were computed with the following formula:
The statistical uncertainty of the cross sections is given by:
where TN is the total number of trajectories calculated for impact parameters less than bmax, is the number of trajectories that satisfy the criteria for the corresponding final channels (ionization, excitation, charge exchange) and bj(i) is the actual impact parameter for the trajectory corresponding to ionization, excitation or charge exchange processes.
In the CTMC calculations, the energy level E of an electron after the excitation is determined simply by calculating its binding energy U = −E. A classical principal quantum number is assigned according to:
where is the reduced mass of the target nucleus and the target electron. The classical values of nc are “quantized” to a specific level n [20] if they satisfy the relation:
The classical orbital angular momentum is defined by
where x, y, and z are the Cartesian coordinates of the electron relative to the nucleus. Since lc is uniformly distributed for a given n level [21], the quantal statistical weights are reproduced by choosing bin sizes such that
where l is the quantum-mechanical orbital-angular-momentum. The choice of bins in classical microcanonical ensemble and by a principle of proportionality of classical and quantal weights is discussed in detail by Becker and Mackellar [20].
2.2. QTMC-KW Method
For the more accurate classical simulation results, we must also consider the constrains of Heisenberg and Pauli principles. This approach was proposed by Kirschbaum and Wilets (KW) [12] in the dominant of the fermion molecular dynamic model (FMD). They added effective potentials, VH and VP, motivated by the Heisenberg and Pauli principles, to the pure Coulomb inter-particle potentials describing the atom. Thus,
where H0 is the usual Hamiltonian containing the total kinetic energy of all bodies and Coulomb potential terms between all pairs of electrons and between the nucleus and electrons, respectively. The extra terms are
and
where a and b denote the nuclei, while i and j index the electrons. Also, and relative momenta are:
and if the spins of the ith and jth electrons are the same and if they are different. The constraining potentials are chosen of the form
In this work, in the case of hydrogen as a one electron target we just take into account the Heisenberg constrain and the parameters universally used = 4 and = 0.9428, respectively. Also, the Heisenberg potential between electron and both target and projectile nucleus is as follows:
According to Figure 1, the equations of motion taking into account the Hamiltonian mechanics besides the extra potential is given by:
3. Results and Discussion
To study the collision between Be4+ and hydrogen atoms, we used both the standard three-body classical trajectory Monte Carlo and quasiclassical trajectory Monte Carlo method of Kirschbaum and Wilets methods. We performed a classical simulation with an ensemble of 1×106 primary trajectories for each energy. The calculations are carried out in the projectile energy range between 10 and 1000 keV/au, relevant to the interest of the fusion research when the target hydrogen atom is in the ground state. We estimate uncertainties in our calculation of 0.6% obtained by the standard statistical error in (see Equation (10)). Furthermore, we note that, according to our knowledge, this is the first time to present cross section data using the QTMC-KW method for the Be4+ + H(1s) system.
3.1. Ionization
For the illustration of the ionization channel, defined by Equation (24), Figure 2 shows typical trajectories in the y–z coordinate system (a) and y position as a function of time (b) for three bodies (projectile, electron, and target) in the lab frame, respectively. The trajectories were obtained at 900 keV/au projectile impact.
Be4+ + H(1s) → Be4++ H+ + e-
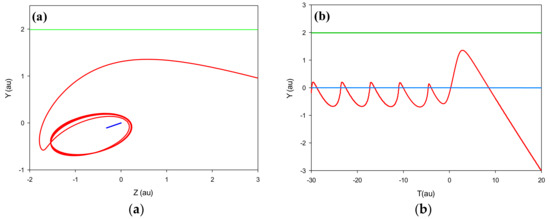
Figure 2.
(a) Trajectories in the y-z lab frame, (b) y position as a function of time for the electron (red line), projectile (green line) and target (blue line) for ionization channel and for Be4+ with E = 900 keV/au.
Figure 3 shows the ionization cross section obtained by both the CTMC and QTMC-KW methods as a function of projectile energy in the energy range between 10 and 1000 keV/au. The results of the present CTMC models are compared with the previous results. Our results with CTMC method match the data of Olson [9] for the entire energy range. At the same time, our results show lower cross section data than that obtained by Krstic and Radmilovic [5] for lower projectile energies. Applying the effective potentials, VH, to mimic the Heisenberg principles in our simulations, the cross section data are a little increased compared to the standard CTMC results.
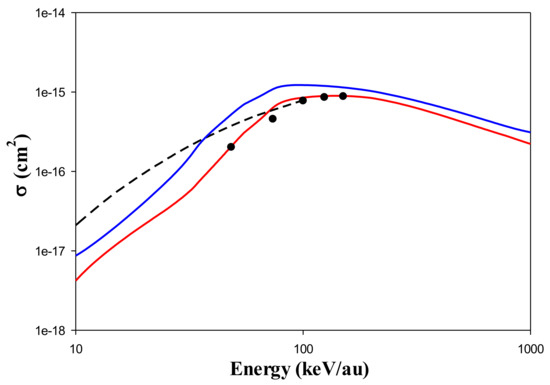
Figure 3.
Cross section for ionization of H(1s) by Be4+ as a function of projectile energy. CTMC (red solid line), QTMC-KW (blue solid line), Reference [5] (dash line), Reference [9] (●).
3.2. Charge Exchange (CX)
The accurate knowledge of the charge exchange cross sections in fusion plasma is very important. For example, the charge exchange recombination spectroscopy (CXRS) measurements using Be4+ provide a high-quality determination of the plasma parameters. The quality of such concentration measurements relies on the accuracy of the charge exchange cross sections.
Figure 4 shows typical classical trajectories for the charge exchange channel. The trajectory calculations were performed at 900 keV/au impact energy. Furthermore, we have calculated the total cross section of CX to the projectile bound state according to CTMC and QTMC-KW methods for the process:
Be4+ + H(1s) → Be3+(nl)+ H+
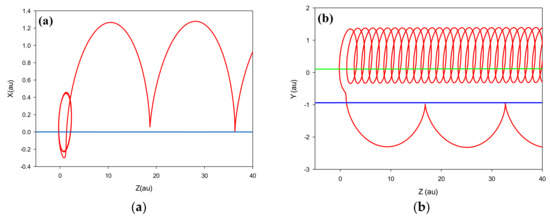
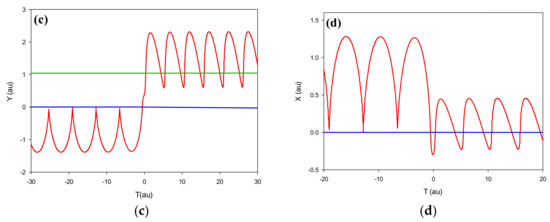
Figure 4.
(a) Trajectories in the x-z projectile frame, (b) Trajectories in the y-z center-of-mass frame, (c) y position as a function of time in the lab frame, (d) x position as a function of time in the projectile frame for the electron (red line), projectile (green line) and target (blue line) for charge exchange channel for a typical Be4+ with E = 900 keV/au.
The comparisons were made with all available methods such as the solution of time-dependent Schroedinger equations, molecular-orbital-close coupling (MOCC), and atomic-orbital-close coupling (AOCC) calculations (see Figure 5).
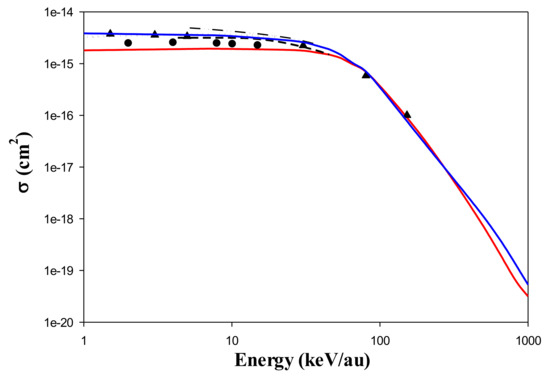
Figure 5.
Total cross section for charge exchange in Be4+ + H(1s) collision, as a function of the impact energy. CTMC (solid red line), QTMC-KW (solid blue line), Reference [22] (dash line), Reference [23] ( -..-.. ), Reference [24] (…), Reference [6] (●), Reference [4] (▴).
We found a significant improvement in the cross section using the QTMC-KW method compared to the standard CTMC model. We also found excellent agreement between our QTMC-KW results and the previous data by Qu et al. [4], Ludde et al. [22], Bransden et al. [23], and Harel et al. [24].
3.3. Excitation
In the following, we show cross sections for Be4+ induced and transitions in atomic hydrogen by using CTMC and QTMC-KW methods. The excitation process is given as follows:
Be4+ + H(1s) → Be4+ + H(n,l,m)*
We considered the excitation of hydrogen atom by beryllium from 1s state to 2s and 2p excited states. Hence, the hydrogen’s electron is then described by the quantum numbers n = 2 and l = 0,1 which corresponds to spherical (s) or polar (p) orbital-angular-momentum, respectively.
Figure 6a,b show the y position as a function of time and 3D trajectory in the lab frame, using the CTMC method for three bodies (projectile, electron and target), respectively. These figures correspond to a projectile with the energy of 900 keV/au.
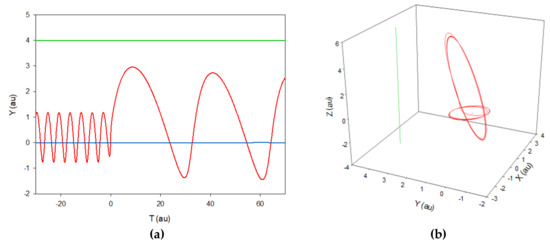
Figure 6.
(a) y position trajectory as a function of time in the lab frame, (b) 3D trajectory in the lab frame for the electron (red line), projectile (green line) and target (blue line) for the excitation channel 1s → 2s,2p and for Be4+ with E = 900 keV/au.
Figure 7 shows the excitation cross section in Be+4 + H(1s) collisions as a function of projectile energy for (see Figure 7a) and (see Figure 7b) transition states, respectively. The comparisons were made with the corresponding results based on adiabatic superpromotion model [5], symmetric Eikonal approximation [7] as well as AOCC calculations [25].
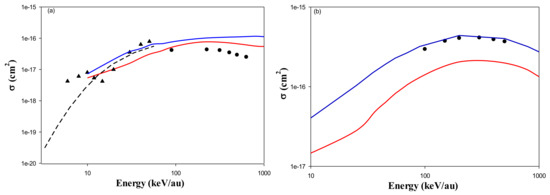
Figure 7.
Cross section for the excitation of (a) nl = 2s and (b) nl = 2p hydrogen subshells in Be4+ + H(1s).collision, as a function of the impact energy. CTMC (solid red line), QTMC-KW (solid blue line), Reference [5] (dash line), Reference [25] (▴), Reference [7] (●).
We note that, while in the previous works, the obtained excitation cross sections are from H(1s) to H(n = 2), in this work we show cross sections into H(2s) and H(2p) subshells. As shown in Figure 7, both CTMC and QTMC-KW methods are useful to describe the excitation cross section for H(1s) to H(2s) transition state. Furthermore, using the QTMC-KW model it is seen that the cross sections are shifted to higher values compared to the CTMC data. It is noticeable that the data obtained by the QTMC-KW model are in good agreement with the data reported by the symmetric Eikonal approximation results [7].
4. Conclusions
Cross sections for ionization, charge exchange, and low-level excitation channels were simulated for a Be4++H(1s) collision system using the classical trajectory Monte Carlo method and quasiclassical trajectory Monte Carlo method of Kirschbaum and Wilets. To increase the calculation’s accuracy, we considered one million trajectories for each impact parameter. We estimate uncertainties of 0.6%. We draw the conclusion that the classical treatment can describe the cross sections reasonably. Since there is no experimental data for the mentioned collision system, we compared our results with the previous literature based on other methods, such as AOCC, MOCC, adiabatic superpromotion model, and Symmetric Eikonal approximation. We found that our calculations are in good agreement with previous results.
Author Contributions
I.Z. and K.T. discussed the results and contributed to the final manuscript. I.Z.: development of CTMC code, performance of analytical and numerical calculations. K.T.: development of CTMC code, performance of analytical calculations and supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
The work was support by the National Research, Development and Innovation Office (NKFIH) Grant KH126886.
Acknowledgments
The work was support by the National Research, Development and Innovation Office (NKFIH) Grant KH126886. This work has been carried out within the framework of the EURO fusion Consortium and has received funding from the Euratom research and training program 2014-2018 under grant agreement No 633053. The views and opinions expressed herein do not necessarily react to those of the European Commission.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pitts, R.; Carpentier, S.; Escourbiac, F.; Hirai, T.; Komarov, V.; Kukushkin, A.; Lisgo, S.; Loarte, A.; Merola, M.; Mitteau, R.; et al. Physics basis and design of the ITER plasma-facing components. J. Nucl. Mater. 2011, 415, S957–S964. [Google Scholar] [CrossRef]
- Hackman, J.; Uhlenbusch, J. Test of a beryllium limiter in the tokamak unitor. J. Nucl. Mater. 1984, 128/129, 418–421. [Google Scholar] [CrossRef]
- Igenbergs, K.; Schweinzer, J.; Aumayer, F. Charge exchange in Be4+ -H(n=1,2) collision studied systematically by atomic-orbital close-coupling calculations. J. Phys. B: At. Mol. Opt. Phys. 2009, 42, 1–8. [Google Scholar] [CrossRef]
- Qu, Y.Z.; Liu, L.; Liu, C.H.; Li, T.C.; Wang, J.G.; Janev, R.K. Charge transfer cross section calculation and evaluation for Beq+ + H collisions. In Proceedings of the Eighth International Conference on Atomic and Molecular Data and Their Applications, NIST, Cambridge, MA, USA, 30 September –4 October 2012; pp. 232–241. [Google Scholar]
- Krstic, P.S.; Radmilovic, M. Charge exchange, excitation and ionization in slow Be4+ + H and B5+ + H collisions. J. Nuclear Fusion. 1992, 3, 113–125. [Google Scholar]
- Kimura, M.; Thorson, W.R. Molecular-state studies of charge transfer in Li3+-H, Be4+-H and B5+-H collisions. J. Phys. B At. Mol. Phys. 1983, 16, 1471–1480. [Google Scholar] [CrossRef]
- Olivera, G.H.; Ramirez, C.A.; Rivarola, R.D. Cross-Sections for Excitation and Ionization of Helium and Hydrogen by Be4+ and B6+ Ions. Physica Scripta. 1996, T62, 84–87. [Google Scholar] [CrossRef]
- Olson, R.E.; Reinhold, C.O.; Schultz, D.R. High-Energy Ion-Atom Collisions. In Proceedings of the IVth Workshop on High-Energy Ion-Atom Collision Processes, Debrecen, Hungary, 17–19 September 1990. [Google Scholar]
- Olson, R.E.; Salop, A. Charge-transfer and impact-ionization cross sections for fully and partially stripped positive ions colliding with atomic hydrogen. Phys. Rev. A 1977, 16, 531–541. [Google Scholar] [CrossRef]
- Tőkési, K.; Hock, G. Versatility of the exit channels in the three-body CTMC method. Nucl. Instrum Meth. Phys. Res. B 1994, 86, 201–204. [Google Scholar] [CrossRef]
- Tőkési, K.; Hock, G. Double electron capture in collision up to 1500 keV/amu projectile impac. J. Phys. B 1996, 29, L119–L125. [Google Scholar] [CrossRef]
- Kirschbaun, C.L.; Wilet, L. Classical many-body model for atomic collisions incorporating the Heisenberg and Pauli principles. Phys. Rev. A 1980, 21, 834–841. [Google Scholar] [CrossRef]
- Wilet, L.; Cohen, J.S. Fermion molecular dynamics in atomic, molecular and optical Physics. Contemp. Phys. 1998, 39, 163–175. [Google Scholar] [CrossRef]
- Cohen, J.S. Molecular effects on antiproton capture by H2 and the states of pp formed. Phys. Rev. A. 1997, 56, 3583–3596. [Google Scholar] [CrossRef]
- Cohen, J.S. Extension of quasiclassical effective Hamiltonian structure of atoms through Z=94. Phys. Rev. A 1998, 57, 4964–4966. [Google Scholar] [CrossRef]
- Cohen, J.S. Multielectron effects in capture of antiprotons and muons by helium and neon. Phys. Rev. A 2000, 62, 022512. [Google Scholar] [CrossRef]
- Jorge, A.; Illescas, C.; Mendez, L.; Pons, B. Switching classical trajectory Monte Carlo method to describe two-active-electron collisions. Phys. Rev. A 2016, 94, 022710. [Google Scholar] [CrossRef]
- Nicolas, B.; Otranto, S. Evaluation of differential cross sections using classical two-active electron models for He. Eur. Phys. J. D. 2019, 73, 1–6. [Google Scholar]
- Tőkési, K.; Kövér, Á. Electron capture to the continuum at 54.4 eV positron-argon atom collisions. J. Phys. B 2000, 33, 3067–3077. [Google Scholar] [CrossRef]
- Becker, R.L.; Mackellar, A. Theoretical initial l dependence of ion-Rydberg-atom collision cross sections. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 3923–3942. [Google Scholar] [CrossRef]
- Tőkési, K.; Mukoyama, T. Theoretical Investigation of ECC Peak for Charged Particles with the CTMC Method. Bull Ins Chem Res Kyoto Univ. 1994, 72, 62–68. [Google Scholar]
- Ludde, H.J.; Dreizler, R.M. Electron capture with He2+, Li3+, Be4+ and B5+ projectiles from atomic hydrogen. J. Phys. B At. Mol. Phys. 1982, 15, 2713–2720. [Google Scholar] [CrossRef]
- Bransden, B.H.; Newby, C.W.; Noble, C.J. Electron capture by fully stripped ions of helium, lithium, beryllium and boron from atomic hydrogen. J. Phys. B At. Mol. Phys. 1980, 13, 4245–4255. [Google Scholar] [CrossRef]
- Harel, C.; Salin, A. Charge exchange in collision of highly ionised ions and atoms. J. Phys. B At. Mol. Phys. 1977, 10, 3511–3522. [Google Scholar] [CrossRef]
- Fritsch, W.; Lin, C.D. Atomic-orbital-expansion studies of electron transfer in bare-nucleus Z (Z=2,4-8)-hydrogen-atom collision. Phys. Rev. A 1984, 29, 3039–3051. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).