Abstract
The excitation cross sections of the nS states, n = 2 to 6, of atomic hydrogen at various incident positron energies (10.23 to 300 eV) were calculated using the variational polarized-orbital method. Nine partial waves were used to obtain converged cross sections. The present results should be useful for comparison with results obtained from other theories and approximations. The positron-impact cross section was found to be higher than the electron-impact cross sections. Experimental and other theoretical results are discussed. The threshold law of excitation is discussed and the cross sections in this region were seen to obey the threshold law proportional to . Cross sections were calculated in the Born approximation also and compared to those obtained using the variational polarized orbital method.
1. Introduction
Dirac [1] in 1928 formulated the well-known relativistic wave equation and predicted an antiparticle of spin ħ/2. This antiparticle, later on called the positron, was detected experimentally by Anderson [2] by observing, in a cloud chamber, decay of cosmic ray pions into positrons and neutrinos. Over the years, research has been carried out to study its interaction with matter. For example, positronium annihilation has been observed from the center of the galaxy and also in solar flares. Positron annihilation can be used to study metallic defects [3]. They are essential in the formation of antihydrogen and in understanding of positron binding to neutral systems. Resonances in electron-atoms and electron-ions are ubiquitous but not in the case of positrons. However, some resonances have been calculated in positron-atom systems. Positrons are also used to detect diseases in a body by observing the positronium decay, called positron emission tomography.
The static potential between an incoming positron and a fixed target and the polarization potential are of opposite signs. The resultant potential is attractive but not attractive enough to bind a positron to atomic hydrogen. Total cross sections for positrons colliding with hydrogen atoms have been measured by Zhou et al. [4] in the energy range 1 to 1000 eV. Their measured cross sections include elastic scattering, excitation to all the higher levels, and perhaps ionization, but not annihilation and positronium cross sections. Total cross sections have been calculated by Gien [5] using the modified Glauber approximation, and by Walters [6] using a multi-pseudostate approximation, supplemented by the second Born approximation. He has calculated elastic and excitation of 1S to 2S and 2P cross sections, 2P cross sections being much larger than the 2S cross sections. Total cross sections calculated by him are the sum of elastic and excitation cross sections to all levels above n = 1. In a previous publication [7], results for positron-impact excitation cross sections for the excitation of the 2S state of atomic hydrogen were given for the incident positron energies (10.30 to 300 eV). It was shown that at high-incident energies cross sections are very close to those obtained using the Born approximation. In that calculation [7], there was a misprint in the computer program for scattering, found recently, affecting results for higher partial waves. For example, for k = 0.90 the cross section changes from previous value of 0.247 to 0.246, at k = 1.2 it changes from 0.338 to 0.317, and at the highest k = 4.696 it changes from 0.0128 to 0.0151. After correcting, the same calculation was repeated and extended to the excitation of higher states up to n = 6. Previous results were not much affected. Nine partial waves were used to obtain converged cross sections. The results of the previous calculation were compared with the close-coupling results of Burke et al. [8] and of Morgan [9] for the 2S excitation. A close-coupling calculation was carried out by Sarkar and Ghosh [10] with two basis sets of hydrogen and positronium states. The agreement is good with all these calculations and the comparison is not repeated here. There are various approximations to calculate excitation cross sections. The aim of this calculation is to provide another method for comparison of results obtained from various theories and approximations. Rydberg units are used and cross sections are in units of π.
2. Theory and Calculations
The present calculations were carried out using the variational polarized-orbital method [11], using the expression for the cross section:
where and are the initial and final momenta of the positron, respectively, and the transition matrix is:
The positions of the incident positron and target electron is given by and , . The nucleus is assumed to be of infinite mass and the incident wave function is , which, in principle, is an exact solution of the Schrödinger equation. It is given by:
The scattering function in the plane wave normalization for a partial wave L is given by:
The plane wave normalization is:
Other quantities in Equation (3) are given in [7] and the parameter in Equation (8) of [7] is generally equal to 0.5. The final state wave function for a partial wave L is given by:
are the excited S state functions. Using Equations (3) and (6) in Equation (2), we find that the cross section is given by:
where
and
is the spherical Bessel function, and are the radial functions for the nS and 1S states.
In the expression (7), we used:
Total cross sections converge when L is equal to 8 or less and it is given by:
3. Born Approximation
The Born approximation is obtained by replacing the scattering function in Equation (3) by an incident plane wave :
It can be shown that:
Cross section is given by:
In the above equations, , a = 3/2, and is given in Equation (7) of [7].
4. Results
Results for various cross sections, calculated in the variational polarized approximation [11], are given in Table 1 from ki = 0.867 to ki = 4.696. The higher excited state cross sections are small compared to the n = 2 excitation cross sections. However, they increase as the incident energy increases. Walters [6] has calculated elastic and excitation to 2S and 2P cross sections at k = 2.0, 2.711, 3.834, and 4.696 corresponding to 54.4, 100, 200, and 300 eV. In Table 2, results for elastic and total excitation cross sections obtained in this calculation are given and are compared to those obtained by Walters [6]. He has calculated elastic and excitation to 2S and 2P states, but not for higher states. The sum of these three cross sections does not add up to his total cross sections, which agree with those obtained by Gien [5] and the experimental results obtained by Zhou et al. [4]. It seems there is a substantial contribution from higher-excited nP, nD, and nF states. These calculations will be carried out in the near future.

Table 1.
Excitation cross sections of nS states, n = 1 to 6, of atomic hydrogen using the variational polarized orbital method with lmax = 8.

Table 2.
Elastic and total excitation cross sections and those obtained by Walters.
In Figure 1, total excitation cross sections for 2S to 6S are shown. We added cross sections at ki = 0.867, 0.8675, 0.868, and 0.869, close to the threshold. In the present calculation, very close to the threshold kf tends to zero and the Bessel function is close to 1, making cross sections large in the threshold region.
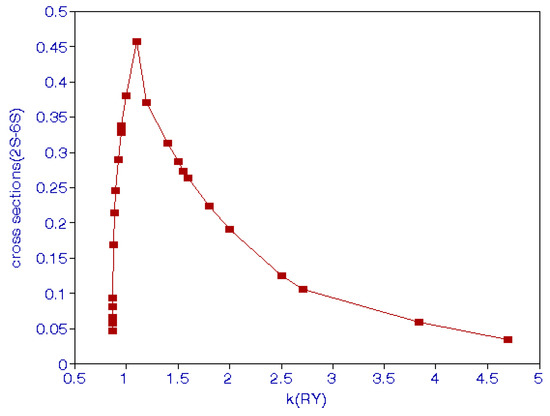
Figure 1.
(Color online) Total excitation cross sections as a function of the incident k to nS states, n = 2 to 6.
The minimum is at k = 0.87 and the cross sections increase smoothly up to k = 1.0, then they start decreasing. The cross sections in the threshold region are shown in Figure 2. Wigner [12] has emphasized the importance of the long-range forces near the threshold region. The long-range force has been included in the present calculation, as indicated in [7,11]. In the threshold region the cross sections are proportional to [13]. The cross sections calculated here in the threshold region can be fitted to , as shown by the solid line in Figure 2. Threshold behavior can be a useful diagnostic of the long-range potential [13].
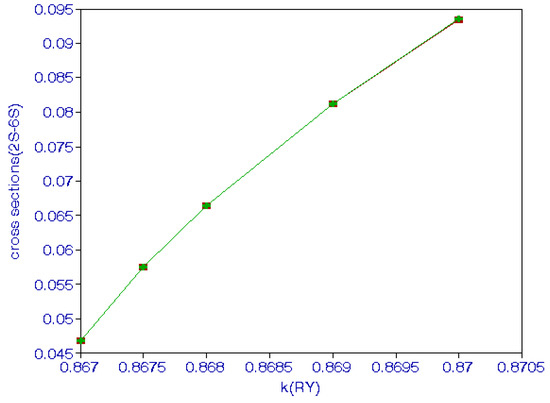
Figure 2.
(Color online) 2S excitation cross sections as a function of the incident k in the threshold region, the solid line represents the fit to the squares (calculated cross sections).
No scaling law between the cross sections proportional to the power of n, the quantum number of the excited state, could be discerned. The cross sections including polarization of the target obtained in the Born approximation are given Table 3. In general the Born approximation is valid at high-incident energies. However, the agreement is quite good even at low-incident energies.

Table 3.
2S excitation cross sections in the Born approximation.
A comparison of positron-impact excitation cross sections and electron-impact cross sections to the excited 2S is shown in Figure 3, which was given in the previous publication [7] and is repeated again because results at higher energies are not the same as before, as explained above. The positron-impact cross sections are higher than the electron-impact cross sections.
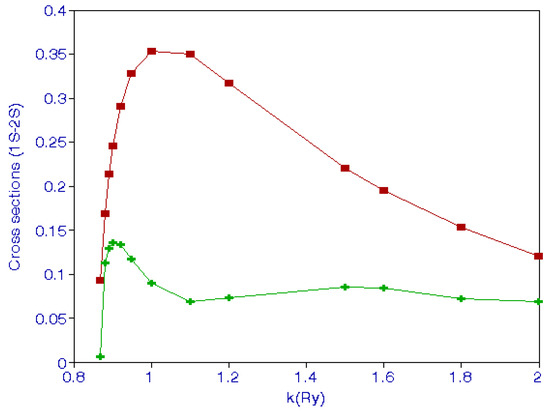
Figure 3.
(Color online) Comparison of the 2S excitation cross sections as a function of the incident k of positron (upper curve) and electron impacts (lower curve).
5. Conclusions
We applied the variational polarized method to calculate excitation cross sections by positron impact for 2S state to 6S states. Results of this calculation were compared to the results obtained using other theories and approximations. The positron-impact cross sections were found to be higher than the electron-impact cross sections. Cross sections in the threshold region were proportional and they were fitted to a form depending on and . The present results were also compared with those obtained using the Born approximation.
Funding
The research received no external funding.
Acknowledgments
Thanks are extended to R. J. Drachman for helpful discussions and for critical reading of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dirac, P.A. In the Development of Quantum Theory; Gordon and Breach Science Publications: London, UK, 1971; p. 59. [Google Scholar]
- Anderson, C.D. The positive electron. Phys. Rev. 1933, 43, 1933. [Google Scholar] [CrossRef]
- Mackenzie, K.; Khooo, T.L.; McDonald, A.B.; Mckee, B.T.A. Temperature dependence of positron mean lives in metals. Phys. Rev. Lett. 1967, 19, 946. [Google Scholar] [CrossRef]
- Zhou, S.; Kauppila, W.E.; Kwan, C.K.; Stein, T.S. Measurements of total cross sections for positrons and electrons colliding with atomic hydrogen. Phys. Rev. Lett. 1994, 72, 1443. [Google Scholar] [CrossRef] [PubMed]
- Gien, T.T. Total cross sections for positron-hydrogen scattering. J. Phys. B 1995, 28, L321. [Google Scholar] [CrossRef]
- Walters, H.R.J. Positron scattering by atomic hydrogen at intermediate energies: 1s to is, is to 2s and 1s to 2p transitions. J. Phys. B 1988, 21, 1893. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron impact excitation of the 2S state of atomic hydrogen. Atoms 2019, 7, 69. [Google Scholar] [CrossRef]
- Burke, P.G.; Schey, H.M.; Smith, K. Collision of slow electrons and positrons with atomic hydrogen. Phys. Rev. 1963, 129, 1258. [Google Scholar] [CrossRef]
- Morgan, L.A. Positron impact excitation of the n = 2 level of hydrogen. J. Phys. B At. Mol. Phys. 1982, 15, L25–L29. [Google Scholar] [CrossRef]
- Sarkar, N.K.; Ghosh, A.S. Positron hydrogen scattering at low and medium energies using CCA. J. Phys. B 1994, 27, 759–779. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of electron-hydrogen scattering. Phys. Rev. A 2007, 75, 032713. [Google Scholar] [CrossRef]
- Wigner, E.P. On the behavior of cross sections near thresholds. Phys. Rev. 1948, 73, 1002. [Google Scholar] [CrossRef]
- Sadeghpour, H.R.; Bohn, J.L.; Cavagnero, M.J.; Esry, B.D.; Fabrikant, I.I.; Macek, J.H.; Rau, A.R.P. Collisions near threshold in atomic and molecular physics. J. Phys. B 2000, 33, R93. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).