Differential Study of Projectile Coherence Effects on Double Capture Processes in p + Ar Collisions
Abstract
1. Introduction
2. Experiment
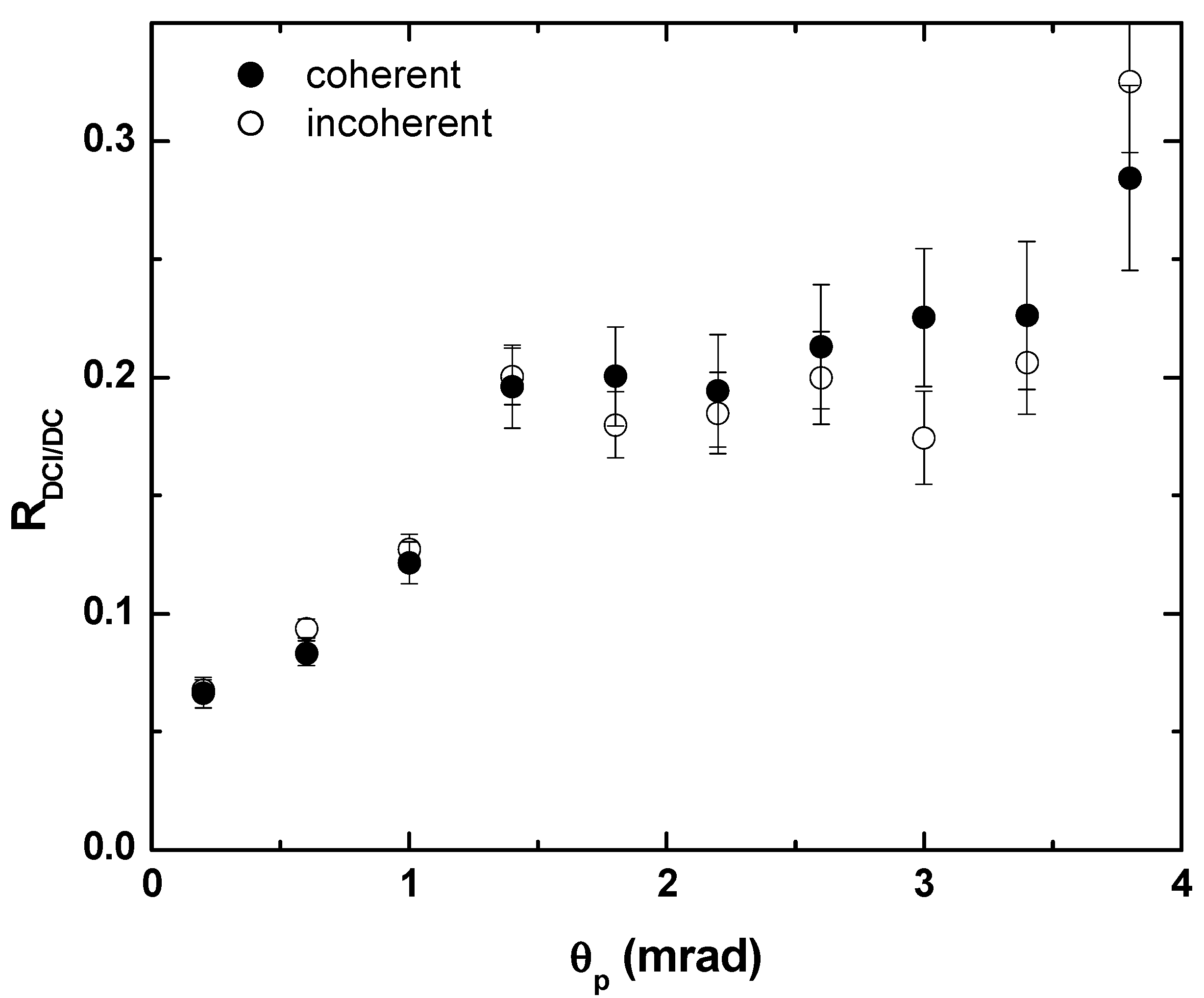
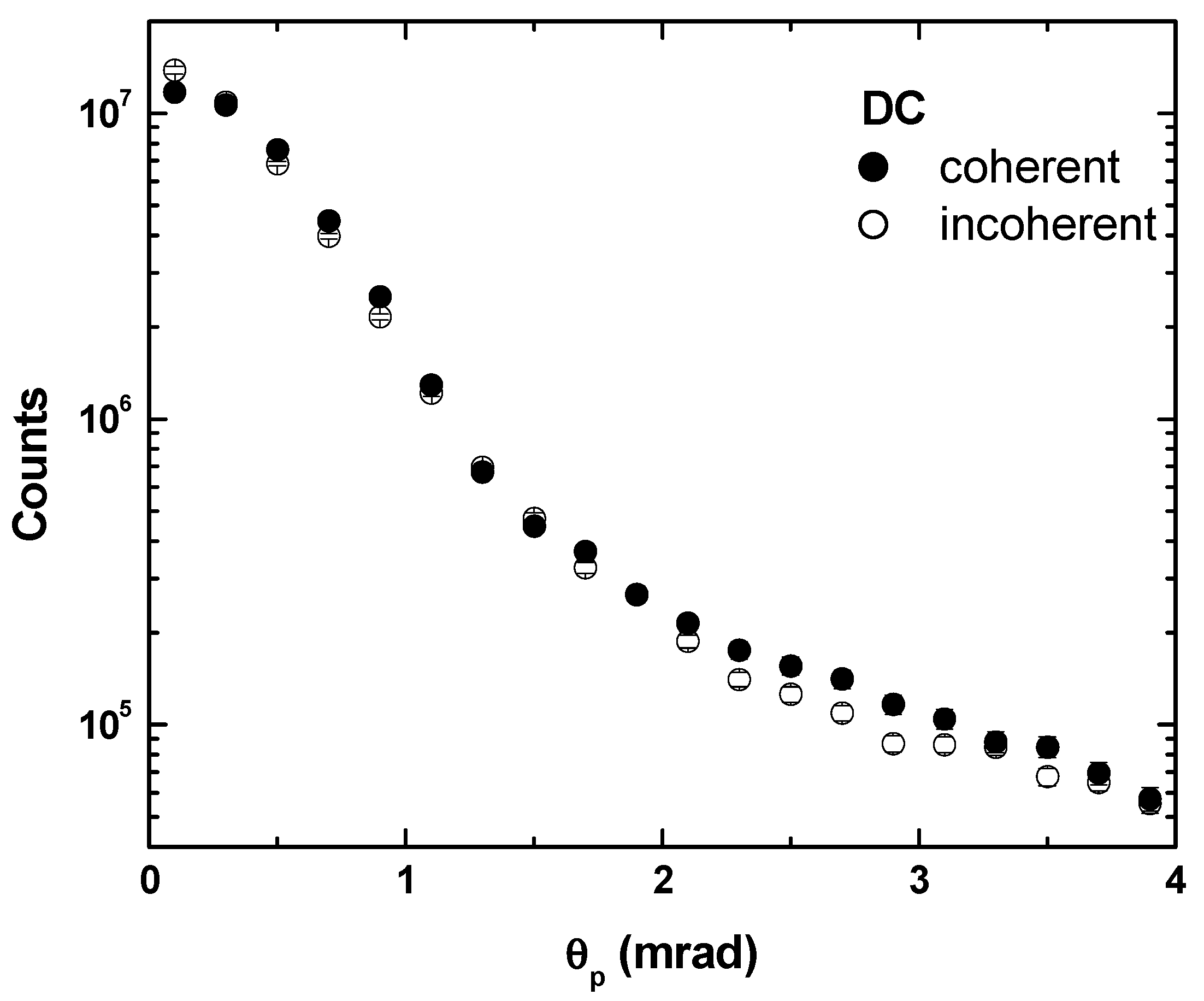
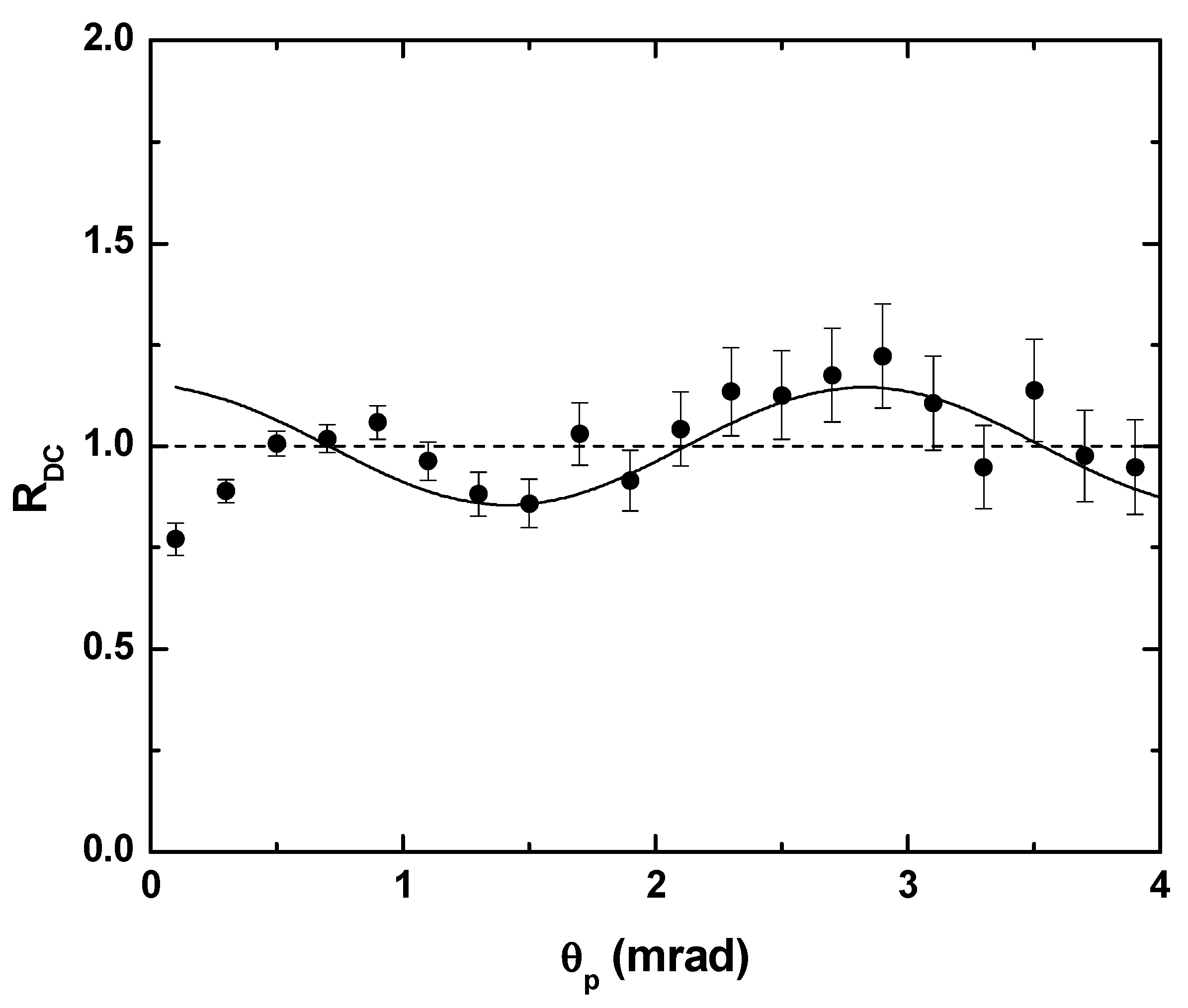
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schulz, M.; Moshammer, R.; Fischer, D.; Kollmus, H.; Madison, D.H.; Jones, S.; Ullrich, J. Three-dimensional imaging of atomic four-body processes. Nature 2003, 422, 48. [Google Scholar] [CrossRef] [PubMed]
- Schulz, M.; Madison, D.H. Studies of the few-body problem in atomic break-up processes. Int. J. Mod. Phys. A 2006, 21, 3649. [Google Scholar] [CrossRef]
- Taylor, J.R. Scattering Theory: The Quantum Theory of Nonrelativistic Collisions; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Rescigno, T.N.; Baertschy, M.; Isaacs, W.A.; McCurdy, C.E. Collisional breakup in a quantum system of three charged particles. Science 1999, 286, 2474. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Bray, I.; Fursa, D.V.; Colgan, J.; Pindzola, M.S.; Pflüger, T.; Senftleben, A.; Xu, S.; Dorn, A.; Ullrich, J. Electron-impact ionization of helium: A comprehensive experiment benchmarks theory. Phys. Rev. A 2011, 83, 52711. [Google Scholar] [CrossRef]
- Colgan, J.; Foster, M.; Pindzola, M.S.; Bray, I.; Stelbovis, A.T.; Fursa, D.V. Triple differential cross sections for the electron-impact ionization of helium at 102 eV incident energy. J. Phys. B 2009, 42, 145002. [Google Scholar] [CrossRef]
- McGovern, M.; Whelan, C.T.; Walters, H.R.J.; McGovern, M.; Whelan, C.T.; Walters, H.R.J. C6+-impact ionization of helium in the perpendicular plane: Ionization to the ground state, excitation-ionization, and relativistic effects. Phys. Rev. A 2010, 82, 32702. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Pindzola, M.S.; Colgan, J. Fully differential cross section for O8+-impact ionization of Li. Phys. Rev. A 2013, 87, 42706. [Google Scholar] [CrossRef]
- Abdurakhmanov, I.B.; Bailey, J.J.; Kadyrov, A.S.; Bray, I. Wave-packet continuum-discretization approach to ion-atom collisions including rearrangement: Application to differential ionization in proton-hydrogen scattering. Phys. Rev. A 2018, 97, 32707. [Google Scholar] [CrossRef]
- Baxter, M.; Kirchner, T.; Engel, E. Time-dependent spin-density-functional-theory description of He+-He collisions. Phys. Rev. A 2017, 96, 32708. [Google Scholar] [CrossRef]
- McGuire, J.H.; Eichler, J. Exact second Born calculations for electron capture for systems with various projectile and target charges. Phys. Rev. A 1983, 28, 2104. [Google Scholar] [CrossRef]
- Voitkiv, A.B.; Najjari, B.; Ullrich, J. On the higher-order effects in target single ionization by bare ions in the perturbative regime. J. Phys. B 2003, 36, 2591. [Google Scholar] [CrossRef]
- Chuluunbaatar, O.; Zaytsev, S.A.; Kouzakov, K.A.; Galstyan, A.; Shablov, V.L.; Popov, Y.V. Fully differential cross sections for singly ionizing 1-MeV p+ He collisions at small momentum transfer: Beyond the first Born approximation. Phys. Rev. A 2017, 96, 42716. [Google Scholar] [CrossRef]
- Madison, D.H.; Fischer, D.; Foster, M.; Schulz, M.; Moshammer, R.; Jones, S.; Ullrich, J. Probing scattering wave functions close to the nucleus. Phys. Rev. Lett. 2003, 91, 253201. [Google Scholar] [CrossRef] [PubMed]
- Pedlow, R.T.; O’Rourke, S.F.C.; Crothers, D.S.F. Fully differential cross sections for 3.6 MeVu−1 AuZP++ He collisions. Phys. Rev. A 2005, 72, 62719. [Google Scholar] [CrossRef]
- Voitkiv, A.B. Single ionization of helium by 1−MeV protons. Phys. Rev. A 2017, 95, 32708. [Google Scholar] [CrossRef]
- Dhital, M.; Bastola, S.; Silvus, A.; Hasan, A.; Lamichhane, B.R.; Ali, E.; Ciappina, M.F.; Lomsadze, R.A.; Cikota, D.; Boggs, B.; et al. Few-body dynamics underlying postcollision effects in the ionization of H2 by 75-keV proton impact. Phys. Rev. A 2019, 99, 62710. [Google Scholar] [CrossRef]
- Dhital, M.; Bastola, S.; Silvus, A.; Lamichhane, B.R.; Ali, E.; Ciappina, M.F.; Lomsadze, R.; Hasan, A.; Madison, D.H.; Schulz, M. Target dependence of postcollision interaction effects on fully differential ionization cross sections. Phys. Rev. A 2019, 100, 32707. [Google Scholar] [CrossRef]
- Egodapitiya, K.N.; Sharma, S.; Hasan, A.; Laforge, A.C.; Madison, D.H.; Moshammer, R.; Schulz, M. Manipulating atomic fragmentation processes by controlling the projectile coherence. Phys. Rev. Lett. 2011, 106, 153202. [Google Scholar] [CrossRef]
- Sharma, S.; Hasan, A.; Egodapitiya, K.N.; Arthanayaka, T.P.; Schulz, M. Projectile coherence effects in electron capture by protons colliding with H2 and He. Phys. Rev. A 2012, 86, 22706. [Google Scholar] [CrossRef]
- Schneider, K.; Schulz, M.; Wang, X.; Kelkar, A.; Grieser, M.; Krantz, C.; Ullrich, J.; Moshammer, R.; Fischer, D. Role of projectile coherence in close heavy ion-atom collisions. Phys. Rev. Lett. 2013, 110, 113201. [Google Scholar] [CrossRef]
- Sharma, S.; Arthanayaka, T.P.; Hasan, A.; Lamichhane, B.R.; Remolina, J.; Smith, A.; Schulz, M. Complete momentum balance in ionization of H2 by 75-keV-proton impact for varying projectile coherence. Phys. Rev. A 2014, 89, 52703. [Google Scholar] [CrossRef]
- Sharma, S.; Arthanayaka, T.P.; Hasan, A.; Lamichhane, B.R.; Remolina, J.; Smith, A.; Schulz, M. Fully differential study of interference effects in the ionization of H2 by proton impact. Phys. Rev. A 2014, 90, 52710. [Google Scholar] [CrossRef]
- Arthanayaka, T.P.; Sharma, S.; Lamichhane, B.R.; Hasan, A.; Remolina, J.; Gurung, S.; Schulz, M.J. Separation of single-and two-center interference in ionization of H2 by proton impact. J. Phys. B 2015, 48, 71001. [Google Scholar] [CrossRef]
- Arthanayaka, T.P.; Sharma, S.; Lamichhane, B.R.; Hasan, A.; Remolina, J.; Gurung, S.; Sarkadi, L.; Schulz, M. Influence of the post-collision interaction on interference effects in ionization of H2 by proton impact. J. Phys. B 2015, 48, 175204. [Google Scholar] [CrossRef]
- Arthanayaka, T.; Lamichhane, B.R.; Hasan, A.; Gurung, S.; Remolina, J.; Borbély, S.; Járai-Szabó, F.; Nagy, L.; Schulz, M. Fully differential study of wave packet scattering in ionization of helium by proton impact. J. Phys. B 2016, 49, 13LT02. [Google Scholar] [CrossRef]
- Lamichhane, B.R.; Arthanayaka, T.; Remolina, J.; Hasan, A.; Ciappina, M.F.; Navarrete, F.; Barrachina, R.O.; Lomsadze, R.A.; Schulz, M. Fully differential study of capture with vibrational dissociation in p+ h2 collisions. Phys. Rev. Lett. 2017, 119, 83402. [Google Scholar] [CrossRef]
- Lamichhane, B.R.; Hasan, A.; Arthanayaka, T.; Dhital, M.; Koirala, K.; Voss, T.; Lomsadze, R.A.; Schulz, M. Fully differential study of dissociative single capture and Coulomb explosion through double capture in p + H2 collisions. Phys. Rev. A 2017, 96, 42708. [Google Scholar] [CrossRef]
- Schulz, M.; Hasan, A.; Lamichhane, B.; Arthanayaka, T.; Dhital, M.; Bastola, S.; Nagy, L.; Borbély, S.; Járai-Szabó, F. Projectile Coherence Effects in Simple Atomic Systems. J. Phys. Conf. Proc. 2020. accepted for publication. [Google Scholar]
- Gassert, H.; Chuluunbaatar, O.; Waitz, M.; Trinter, F.; Kim, H.-K.; Bauer, T.; Laucke, A.; Müller, C.; Voigtsberger, J.; Weller, M.; et al. Agreement of experiment and theory on the single ionization of helium by fast proton impact. Phys. Rev. Lett. 2016, 116, 73201. [Google Scholar] [CrossRef]
- Schulz, M. The Role of Projectile Coherence in the Few-Body Dynamics of Simple Atomic Systems. Ad. At. Mol. Opt. Phys. 2017, 66, 508. [Google Scholar]
- Jarai-Szabo, F.; Nagy, L. Theoretical investigations on the projectile coherence effects in fully differential ionization cross sections. Eur. Phys. J. D 2015, 69, 4. [Google Scholar] [CrossRef]
- Karlovets, D.V.; Kotkin, G.L.; Serbo, V.G. Scattering of wave packets on atoms in the Born approximation. Phys. Rev. A 2015, 92, 52703. [Google Scholar] [CrossRef]
- Sarkadi, L.; Barrachina, R. Loss of wave-packet coherence in ion-atom collisions. Phys. Rev. A 2016, 93, 32702. [Google Scholar] [CrossRef]
- Fabre, I.; Navarrete, F.; Sarkadi, L.; Barrachina, R.O. Free evolution of an incoherent mixture of states: A quantum mechanical approach to the van Cittert–Zernike theorem. Eur. J. Phys. 2018, 39, 15401. [Google Scholar] [CrossRef]
- Gulyás, L.; Egri, S.; Igarashi, A. Theoretical investigation of the fully differential cross sections for single ionization of He in collisions with 75-keV protons. Phys. Rev. A 2019, 99, 32704. [Google Scholar] [CrossRef]
- Keever, W.C.; Everhart, E. Resonant Electron-Capture Measurements of Close He++—He and He++—H Collisions. Phys. Rev. 1966, 150, 43. [Google Scholar] [CrossRef]
- Schuch, R.; Justiniano, E.; Vogt, H.; Deco, G.; Grün, N. Double electron capture of He2+ from He at high velocity. J. Phys. B 1991, 24, L133. [Google Scholar] [CrossRef]
- Dörner, R.; Mergel, V.; Spielberger, L.; Jagutzki, O.; Ullrich, J.; Schmidt-Böcking, H. State-selective differential cross sections for double-electron capture in 0.25–0.75-MeV He2+-He collisions. Phys. Rev. A 1998, 57, 312. [Google Scholar] [CrossRef]
- Schulz, M.; Vajnai, T.; Brand, J.A. Differential double capture cross sections in p+ He collisions. Phys. Rev. A 2007, 75, 22717. [Google Scholar] [CrossRef]
- Bross, S.W.; Bonham, S.M.; Gaus, A.D.; Peacher, J.L.; Vajnai, T.; Schmidt-Böcking, H.; Schulz, M. Differential transfer ionization cross sections for 50–175-keV proton-helium collisions. Phys. Rev. A 1994, 50, 337. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voss, T.; Lamichhane, B.R.; Dhital, M.; Lomsadze, R.; Schulz, M. Differential Study of Projectile Coherence Effects on Double Capture Processes in p + Ar Collisions. Atoms 2020, 8, 10. https://doi.org/10.3390/atoms8020010
Voss T, Lamichhane BR, Dhital M, Lomsadze R, Schulz M. Differential Study of Projectile Coherence Effects on Double Capture Processes in p + Ar Collisions. Atoms. 2020; 8(2):10. https://doi.org/10.3390/atoms8020010
Chicago/Turabian StyleVoss, Trevor, Basu R. Lamichhane, Madhav Dhital, Ramaz Lomsadze, and Michael Schulz. 2020. "Differential Study of Projectile Coherence Effects on Double Capture Processes in p + Ar Collisions" Atoms 8, no. 2: 10. https://doi.org/10.3390/atoms8020010
APA StyleVoss, T., Lamichhane, B. R., Dhital, M., Lomsadze, R., & Schulz, M. (2020). Differential Study of Projectile Coherence Effects on Double Capture Processes in p + Ar Collisions. Atoms, 8(2), 10. https://doi.org/10.3390/atoms8020010