Charge Exchange Cross Sections for Noble Gas Ions and N2 between 0.2 and 5.0 keV
Abstract
1. Introduction
2. Charge Exchange with N
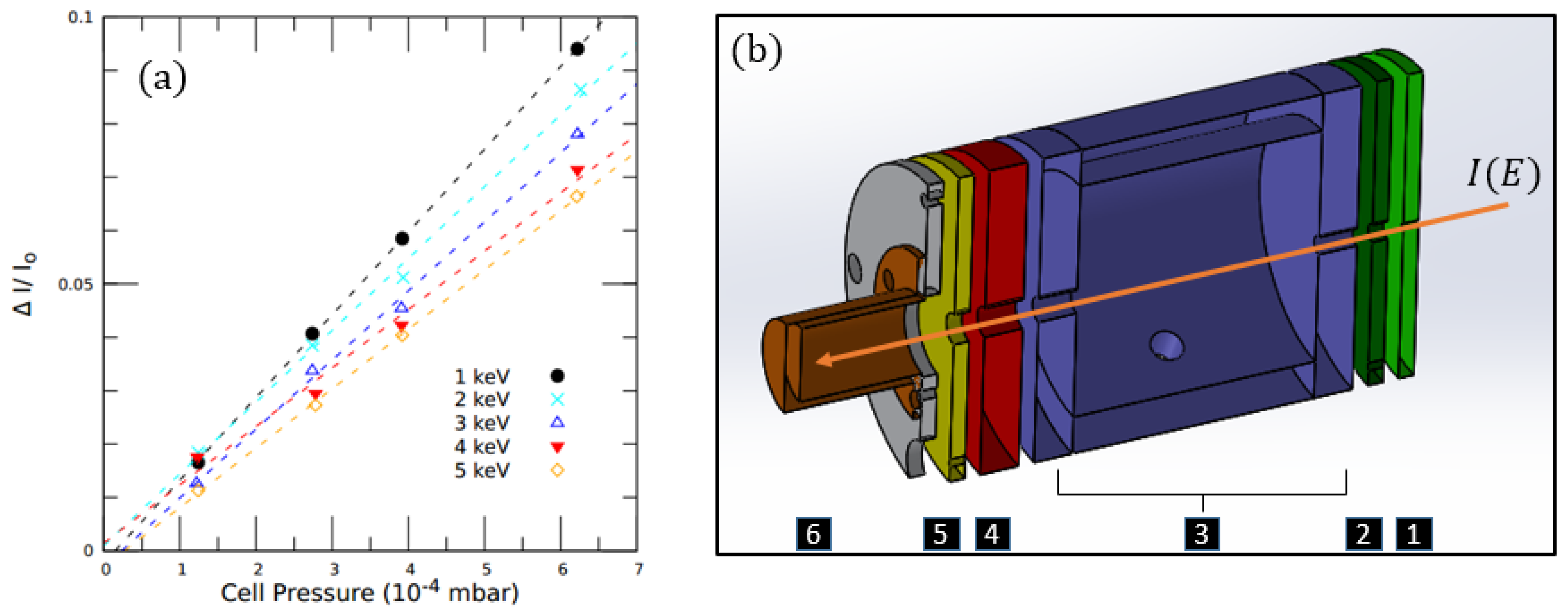
2.1. Experimental Details
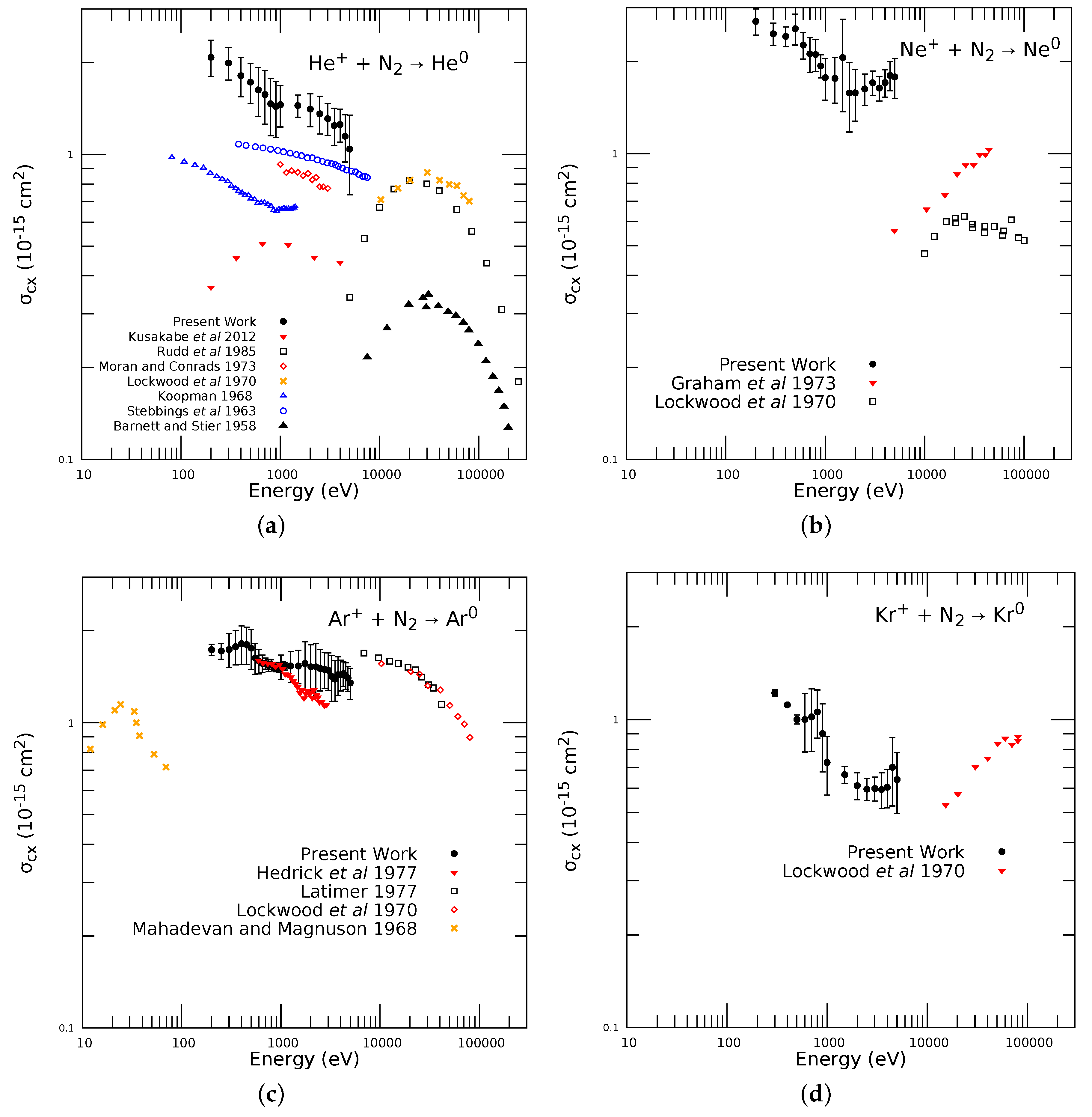
2.2. N Results
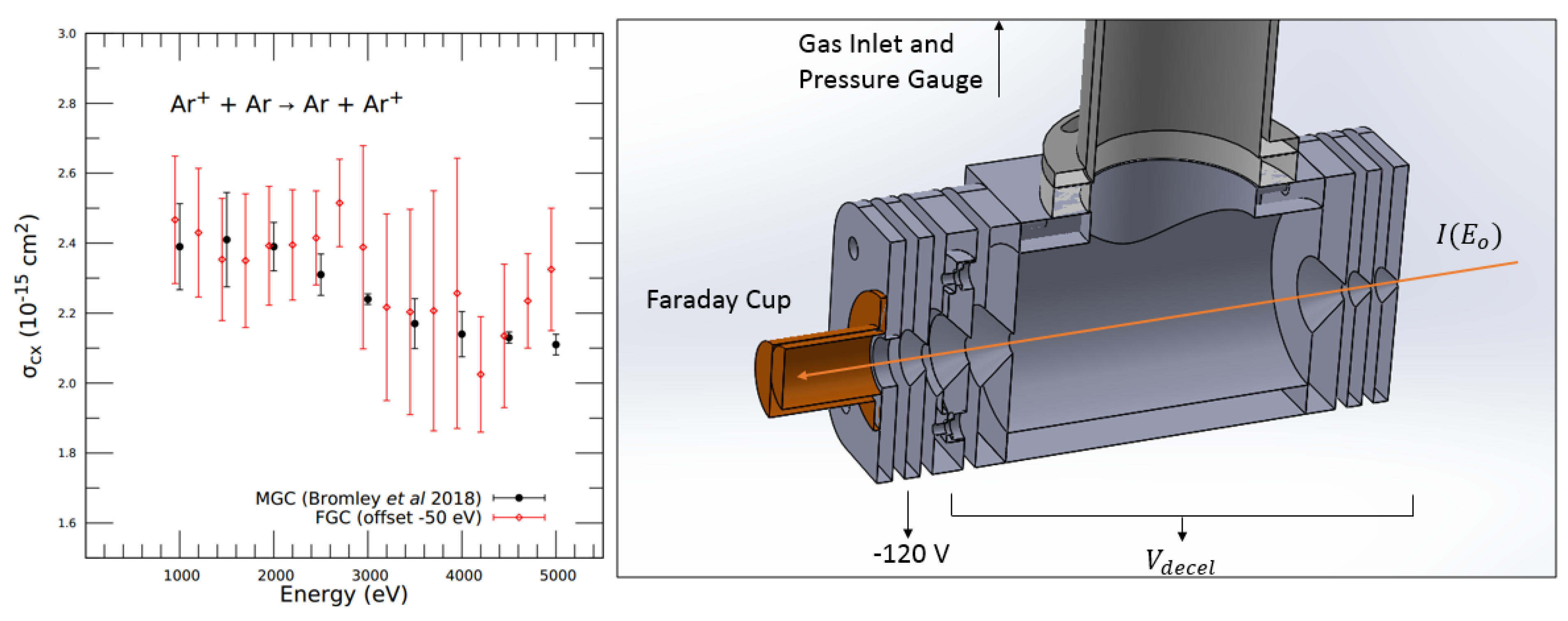
3. Floating Gas Cell
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CX | charge exchange |
| FGC | Floated Gas Cell |
| MGC | Manipulator Gas Cell |
References
- Janev, R.; Harrison, M.; Drawin, H. Atomic and molecular database for fusion plasma edge studies. Nucl. Fusion 1989, 29, 109. [Google Scholar] [CrossRef]
- Schwadron, N.A.; Cravens, T.E. Implications of Solar Wind Composition for Cometary X-rays. Astrophys. J. 2000, 544, 558. [Google Scholar] [CrossRef]
- Fabian, A.C.; Sanders, J.S.; Williams, R.J.R.; Lazarian, A.; Ferland, G.J.; Johnstone, R.M. The energy source of the filaments around the giant galaxy NGC 1275. Mon. Not. R. Astron. Soc. 2011, 417, 172–177. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Dhanya, M.B.; Alok, A.; Barabash, S.; Wieser, M.; Futaana, Y.; Wurz, P.; Vorburger, A.; Holmström, M.; Lue, C.; et al. A new view on the solar wind interaction with the Moon. Geosci. Lett. 2015, 2, 10. [Google Scholar] [CrossRef]
- Mullen, P.D.; Cumbee, R.S.; Lyons, D.; Gu, L.; Kaastra, J.; Shelton, R.L.; Stancil, P.C. Line Ratios for Solar Wind Charge Exchange with Comets. Astrophys. J. 2017, 844, 7. [Google Scholar] [CrossRef]
- Roble, R.G.; Ridley, C.C. An auroral model for the NCAR thermospheric general circulation model (TGCM). Ann. Geophys. A 1987, 5, 369–382. [Google Scholar]
- Lindsay, B.G.; Stebbings, R.F. Charge transfer cross sections for energetic neutral atom data analysis. J. Geophys. Res. 2005, 110, A12213. [Google Scholar] [CrossRef]
- Larsson, M.; Geppert, W.D.; Nyman, G. Ion chemistry in space. Rep. Prog. Phys. 2012, 75, 066901. [Google Scholar] [CrossRef]
- Bodewits, D.; Hoekstra, R.; Seredyuk, B.; McCullough, R.W.; Jones, G.H.; Tielens, A.G.G.M. Charge Exchange Emission from Solar Wind Helium Ions. Astrophys. J. 2006, 642, 593. [Google Scholar] [CrossRef]
- Werbowy, S.; Pranszke, B. Charge-exchange processes in collisions of H+, , , He+, and ions with CO and CO2 molecules at energies below 1000 eV. Phys. Rev. A 2016, 93, 022713. [Google Scholar] [CrossRef]
- Kusakabe, T.; Kitamuro, S.; Nakai, Y.; Tawara, H.; Sasao, M. Charge-Transfer Cross Sections of Ground State He+ Ions in Collisions with He Atoms and Simple Molecules in the Energy Range below 4.0 keV. Plasma Fusion Res. 2012, 7, 2401062. [Google Scholar] [CrossRef]
- Rapp, D.; Francis, D.E. Charge Exchange between Gaseous Ions and Atoms. J. Chem. Phys. 1962, 37, 2631–2645. [Google Scholar] [CrossRef]
- Hodgkinson, D.P.; Briggs, J.S. Resonant charge exchange at low velocities. J. Phys. B At. Mol. Phys. 1976, 9, 255. [Google Scholar] [CrossRef]
- Massey, H.S.W. Collisions between atoms and molecules at ordinary temperatures. Rep. Prog. Phys. 1949, 12, 248. [Google Scholar] [CrossRef]
- Friedman, B.; DuCharme, G. Semi-empirical scaling for ion-atom single charge exchange cross sections in the intermediate velocity regime. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 115202. [Google Scholar] [CrossRef]
- Rudd, M.E.; Goffe, T.V.; Itoh, A. Cross sections for ionization of gases by 10–2000 keV He+ ions and for electron capture and loss by 5–350 keV He+ ions. Phys. Rev. A 1985, 32, 829–835. [Google Scholar] [CrossRef]
- Moran, T.F.; Conrads, R.J. Charge neutralization of He+ ion beams. J. Chem. Phys. 1973, 58, 3793–3799. [Google Scholar] [CrossRef]
- Lockwood, G.J. Total Cross Section for Charge Transfer of Noble-Gas Ions N2. Phys. Rev. A 1970, 2, 1406–1410. [Google Scholar] [CrossRef]
- Koopman, D.W. Light-Ion Charge Exchange in Atmospheric Gases. Phys. Rev. 1968, 166, 57–62. [Google Scholar] [CrossRef]
- Stebbings, R.F.; Smith, A.C.H.; Ehrhardt, H. Dissociative Charge Transfer in He+–O2 and He+–N2 Collisions. J. Chem. Phys. 1963, 39, 968–971. [Google Scholar] [CrossRef]
- Barnett, C.F.; Stier, P.M. Charge Exchange Cross Sections for Helium Ions in Gases. Phys. Rev. 1958, 109, 385–390. [Google Scholar] [CrossRef]
- Bromley, S.J.; Fox, D.C.; Sosolik, C.E.; Harriss, J.E.; Marler, J.P. A gas cell apparatus for measuring charge exchange cross sections with multicharged ions. Rev. Sci. Instrum. 2018, 89, 073107. [Google Scholar] [CrossRef] [PubMed]
- Graham, W.G.; Latimer, C.J.; Browning, R.; Gilbody, H.B. Ionization of fragmentation of diatomic molecular gases by 5–45 keV Ne+ and Na+ ions and Ne atoms. J. Phys. B At. Mol. Phys. 1973, 6, 2641–2652. [Google Scholar] [CrossRef]
- Hedrick, A.F.; Moran, T.F.; McCann, K.J.; Flannery, M.R. Charge transfer cross sections in argon ion–diatomic molecule collisions. J. Chem. Phys. 1977, 66, 24–31. [Google Scholar] [CrossRef]
- Latimer, C.J. Near-resonant charge transfer in collisions of rare-gas ions with simple molecules within the energy range 4–45 keV. J. Phys. B At. Mol. Phys. 1977, 10, 515–522. [Google Scholar] [CrossRef]
- Mahadevan, P.; Magnuson, G.D. Low-Energy (1- to 100-eV) Charge-Transfer Cross-Section Measurements for Noble-Gas-Ion Collisions with Gases. Phys. Rev. 1968, 171, 103–109. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bromley, S.; Ahl, C.; Sosolik, C.; Marler, J. Charge Exchange Cross Sections for Noble Gas Ions and N2 between 0.2 and 5.0 keV. Atoms 2019, 7, 96. https://doi.org/10.3390/atoms7040096
Bromley S, Ahl C, Sosolik C, Marler J. Charge Exchange Cross Sections for Noble Gas Ions and N2 between 0.2 and 5.0 keV. Atoms. 2019; 7(4):96. https://doi.org/10.3390/atoms7040096
Chicago/Turabian StyleBromley, Steven, Corey Ahl, Chad Sosolik, and Joan Marler. 2019. "Charge Exchange Cross Sections for Noble Gas Ions and N2 between 0.2 and 5.0 keV" Atoms 7, no. 4: 96. https://doi.org/10.3390/atoms7040096
APA StyleBromley, S., Ahl, C., Sosolik, C., & Marler, J. (2019). Charge Exchange Cross Sections for Noble Gas Ions and N2 between 0.2 and 5.0 keV. Atoms, 7(4), 96. https://doi.org/10.3390/atoms7040096




