Abstract
Collisions of low energy electrons with molecules are important for understanding many aspects of the environment and technologies. Understanding the processes that occur in these types of collisions can give insights into plasma etching processes, edge effects in fusion plasmas, radiation damage to biological tissues and more. A radical update of the previous expert system for computing observables relevant to these processes, Quantemol-N, is presented. The new Quantemol Electron Collision (QEC) expert system simplifyies the user experience, improving reliability and implements new features. The QEC graphical user interface (GUI) interfaces the Molpro quantum chemistry package for molecular target setups, and the sophisticated UKRmol+ codes to generate accurate and reliable cross-sections. These include elastic cross-sections, super elastic cross-sections between excited states, electron impact dissociation, scattering reaction rates, dissociative electron attachment, differential cross-sections, momentum transfer cross-sections, ionization cross sections, and high energy electron scattering cross-sections. With this new interface we will be implementing dissociative recombination estimations, vibrational excitations for neutrals and ions, and effective core potentials in the near future.
1. Introduction
Electron collisions drive many processes both in the natural world and industrial processes. Compilations of electron collision cross sections, see for example [1,2,3,4], are becoming increasingly reliant on theory. Indeed the difficulty of measuring cross sections for chemically unstable species (radicals) has led to the suggestion that computed cross sections represent the solution for many problems involving technological plasmas [5,6]. Computed cross sections sets for key species are beginning to become available [7,8]. Computing such data sets, especially for low-energy collisions, requires sophisticated computer programs capable of treating both the electronic structure of the target molecule and the details of the electron collision process.
The R-matrix method [9] has proved very powerful for computing cross sections for a whole range of atomic and molecular problems [9]. For electron–molecule collisions the method has been implemented in a series of codes [10,11,12,13], generically known as the UK Molecular R-matrix (UKRmol) codes. These codes are powerful and can be used to tackle a variety of problems [14] but they are far from straightforward to run, as they require specialist knowledge on both molecular structure and electron scattering as well as experience on how to build sophisticated and balanced models, see [15,16,17] for example.
To address this problem Quantemol Ltd. developed an expert system, known as Quantemol-N (QN) [18], to run the UKRmol codes of Carr et al. [12]. Over time this code was developed to include not only the normal facilities of the UKRMol code to compute elastic and electronically inelastic cross sections but also to compute differential, momentum transfer and rotational excitation cross sections using code POLYDCS [19], ionization cross sections using the BEB (binary encounter Bethe) method of Kim and Rudd [20], and an especially developed dissociative electron attachment (DEA) estimator [21]. More recent developments involved the extension of calculations to high energies using the so-called BEf procedure of Kim [22] and the spherical complex optical potential (SCOP) method [23,24,25]. Recent releases of QN also feature an implementation of the UKRMol photoionization model [26].
Recently Benda, Mašín, Gorfinkiel and co-workers have developed a significantly updated and improved version of the UK Molecular R-matrix codes known as UKRmol+ [13]. New features in UKRMol+ include the implementation of new integrals package [27] which allows the use of Gaussian (GTO) [28] and B-spline (BTO) [29,30] type orbitals to represent the continuum. This new package facilitates the treatment of electron collisions with significantly larger molecules than was possible with UKRmol [31] and hence QN. UKRmol+ also features a greatly improved procedure for construction and diagonalization of the inner region Hamiltonian matrix [32], which is the rate-limiting step in most R-matrix calculations, as well as a number of other improvements.
Previous implementations of these codes essentially contained a quantum chemistry code at their heart. In order to construct the Hamiltonian matrix on the basis of configurations, a unique set of molecular orbitals describing the target molecule are needed. Previous implementations of the codes contained programs that allowed generation of these orbitals using simple approaches. UKRmol+ uses a different philosophy whereby the target molecular orbitals and the atomic GTO basis are read in from a file in the Molden format [33]. Although the Molden file is general and can be generated by a range of quantum chemistry software, most calculations actually use the general-purpose quantum chemistry program package Molpro [34,35]. This gives UKRmol+ access to orbitals generated using a wide range of sophisticated methods including state-averaged complete active space self-consistent field (CASSCF).
To take advantage of the improvements offered by the new UKRmol+ code, we decided to build a new expert system, known as Quantemol Electron Collisions or QEC for short. QEC incorporates all the features of QN discussed above plus new functionality made possible by UKRmol+ and closer integration with Molpro. The purpose of this paper is to describe the QEC expert system.
2. The R-Matrix Method
The R-matrix method is an example of an embedding method which divides space into different regions. In this case the method uses an inner region which is a sphere of radius a and an outer region. In its most general form the inner region wave functions are represented by the close-coupling expansion:
In this equation represents the target wave function. In QEC this wave function is generated using GTOs from the Molpro basis set library and orbital imported from Molpro generated with one of two models: either HF (Hartree–Fock) or MC-SCF (multi-configuration self consistent field) as discussed below. The are orbitals used to represent the continuum for which QEC has a library of GTO functions based on those of Faure et al. [28]. Functions with (i.e., up to g wave) are explicitly included. The antisymmetriser, , ensures that the product of the target wave function and continuum orbital obeys the Pauli principle.
The second sum in Equation (1) runs over configurations so-called where all electrons are place in target orbitals. The precise configurations chosen depends on the model used for a particular calculation. QEC implements three distinct scattering models which are selected by the user.
Static exchange (SE) is the simplest model implemented; it uses HF target wave function and the configurations are given simply by placing the scattering electron in unoccupied target (virtual) orbitals.
Static exchange plus polarization (SEP) builds on the SE model by also including configurations which involve promoting an electron from the HF target wave function to a virtual orbital while also placing the scattering electron in a target virtual orbital. This provides a good representation of low-lying resonances which are the route to DEA. The SEP model is therefore recommended for computing DEA cross sections.
Close-coupling (CC) expansions involve including several target states in the inner region expansion, Equation (1). This model normally uses a complete active spaces (CAS) description of these states [15] for which it employs MCSCF orbitals (this is an improvment of QN which used HF orbitals for this step). Studies of electron-impact electronic excitation and dissociation (which goes via electronic excitation) must be performed at the CC level; this is also recommended for studies of Feshbach resonances. CC calculations are computationally more demanding than SE or SEP ones.
There is a fourth possible model for studying electron molecule collisions with UKRMol/UKRmol+, which is the R-matrix with pseudostates (RMPS) method [36,37]. The RMPS method is a generalization of the CC method which allows for the inclusion of target continuum states in the CC expansion. RMPS calculations have very useful properties in terms of extending the energy range of the calculations and converging polarization effects [38], but are computationally very demanding [16,39] so as yet have not been implemented in QEC.
Solving the problem in the outer region is performed in two steps. First the R-matrix is propagated from the boundary given by to some large [40], where is chosen such that the non-Coulombic potential can be neglected for asymptotic region defined by ; QEC assumes a and beyond this uses an asymptotic expansion due to Gailitis [41,42]. The K-matrices so calculated are used by QEC to automatically detect and fit resonances [43] and to construct the corresponding T-matrices. The resonance parameters form the main input to the DEA estimator [21]. The T-matrices are used to compute elastic and electronically inelastic cross sections, and provide the input to code POLYDCS [19] which computes differential, momentum transfer and rotational-excitation cross sections. For molecules with a permanent dipole moment it is necessary to correct for partial waves higher than [44]; this done either using POLYDCS or code BornCross [45]. Finally, the elastic and electronically inelastic cross sections are turned into rates assuming Maxwellian distribution for the electron energies.
3. The QEC Interface
QEC runs through a graphical user interface (GUI) which guides the user through the calculations. The first inputs come on a screen which provides the molecule set up, see Figure 1. The geometry of the molecule can be put in by hand or via an xyz file. If the precise geometric parameters are not known, an approximate geometry can be guessed and is automatically optimized by Molpro. This is requested using the “Optimise” tab and results in a rapid Hartree–Fock level calculation. The figure illustrates the geometry of methane which has been optimized in this fashion.
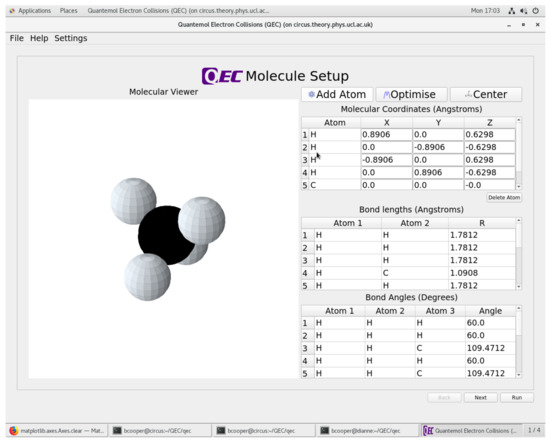
Figure 1.
Screenshot of the molecular set-up page in the Quantemol Electron Collision (QEC) graphical user interface (GUI) showing methane as an example. The screenshot was taken after the geometry had been optimized using Molpro and the coordinates automatically shifted to the center of mass.
It is a requirement of the R-matrix method that the origin of the coordinate system is the molecular center of mass. QEC automatically shifts the geometry to this center of mass; it stores a library of main-isotope atomic masses for this purpose. Note that for molecular ions, the choice of center of mass is important for obtaining the correct target dipole moment [46]; the effect of isotopic substitution on the center of mass can be controlled via an advanced option.
Both Molpro and QEC only use Abelian symmetry groups i.e., ones which contain no degenerate representations. Molpro contains the facility to automatically classify molecules to a point group. QEC exploits this facility once the geometry has been determined. The resulting point group is illustrated using the appropriate mirror planes in the QEC molecular viewer which forms part of second input page of the GUI. Figure 2 shows this for the example of methane. Note that while methane in its equilibrium geometry has point-group symmetry T, Molpro and QEC only use the C subgroup.
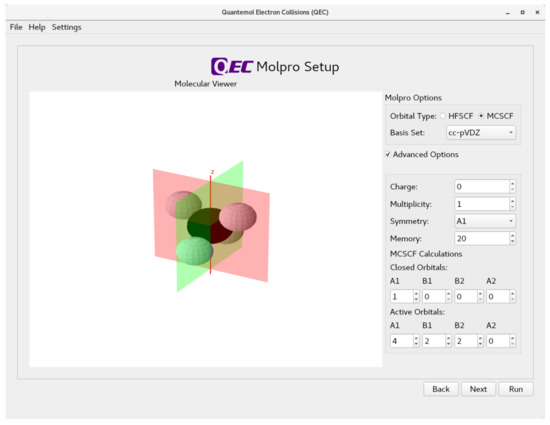
Figure 2.
Screenshot of the page in the QEC GUI which sets up the molecular target calculation which is performed using Molpro.
The second input page also allows the user to choose a target basis set from a number of standard GTO sets. The level of calculation used to generate the target orbitals and wave functions must be chosen at this point: HF orbitals are used for SE and SEP calculations, while MCSCF orbitals are required for CC calculations. Here, and elsewhere, there are a number of advanced user options which allow the experienced user to change the standard QEC defaults. Figure 2 shows the choice of MCSCF orbitals computed using a standard cc-pVDZ basis set. The advanced user options displayed are actually the default ones. However, we note that calculations on ionic targets require the charge of the target molecule to be selected as non-zero at this point. The default active space used for the MCSCF calculations is the standard one used by Molpro; it is the valence space, comprising all the orbitals of the highest n quantum number that are occupied, that are active, so for methane that means 2s2p for C and 1s for H, with the 1s orbital of C treated as a core orbital. For large molecules with many active electrons it may be necessary to reduce this space.
Input page 3 of the GUI sets up the R-matrix and parameters for scattering calculation. The methane example shown in Figure 3 uses QEC defaults. At this stage the parameters of the calculations are now fully determined.
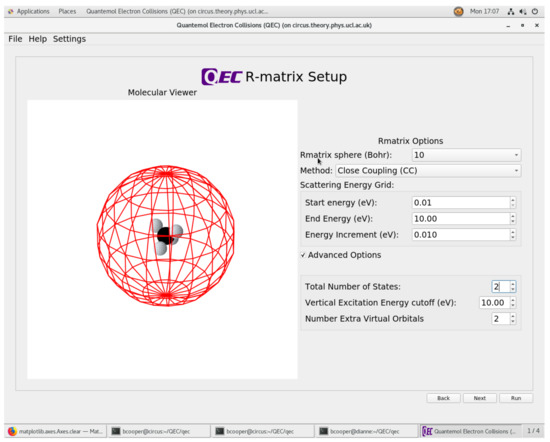
Figure 3.
Screenshot of the page in the QEC GUI which set the parameters for the scattering calculation.
The final input page of the GUI, see Figure 4, allows the user to specify what results are required. Only outputs consistent with the chosen model (SE, SEP or CC) are allowed. Optionally the user can choose to compute differential, momentum transfer and rotational-excitation cross sections using code POLYDCS. Since POLYDCS only allows for electronically-elastic cross sections, these cross sections are only computed up to the first electronic excitation threshold in CC calculations. Choice of the DEA estimator requires the user to provide further information such as an estimated vibrational frequency of the dissociating mode and an estimated dissociation energy. We plan to use Molpro to provide these data automatically in the future. QEC already contains a library of electron affinities for standard atomic and molecular fragments.
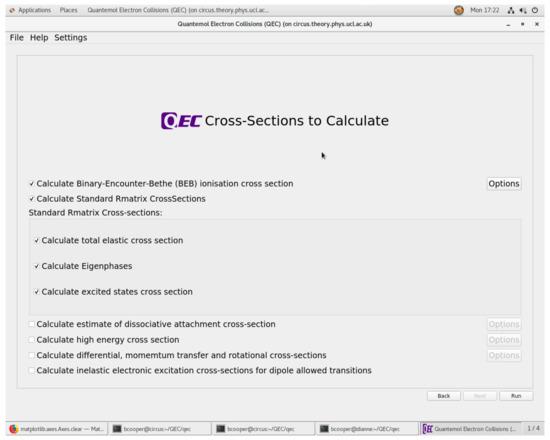
Figure 4.
Sample screen for a close-coupling (CC) calculation on methane showing the outputs selected to be total cross section, the eigenphase sums for each symmetry, the rate of elastic scattering as a function of temperature and the ionization cross section computed using the binary encounter Bethe (BEB) method.
The final two optional cross sections are the SCOP and BEf high energy approximations. SCOP calculations provide high energy estimates of the total elastic and inelastic (including ionization, etc.) cross section. SCOP calculations employ charge distributions provided by Molpro but are rather slow so should only be used if the user actually wants the results. Finally the BEf method is used to estimate high energy electronic excitation cross sections. The BEf method works using a dipole approximation [22] and only dipole-allowed electronic excitations are actually considered; this is consistent with the fact that excitations cross sections which are not dipole allowed go rapidly to zero at higher energies. Parameters for both BEB (ionization) and BEf calculations are fully provided by Molpro. For BEB the user has the option to change the ionization potential, which Molpro determines using Koopman’s theorem, if they wish. Note that selecting BEB only at this stage will run only a BEB calculation which is very quick even for large systems.
QEC provides a variety of results. Figure 5 illustrates some of the graphs automatically generated for the methane example considered above. Note that the B and B eigenphases are degenerate which is a usual occurrence when C symmetry is used as a proxy for a higher-symmetry point group. These eigenphases have been smoothed to remove arbitrary jumps by . Note that the illustrated results for methane use a very simple SE model; a comprehensive R-matrix study of this problem is available [47].
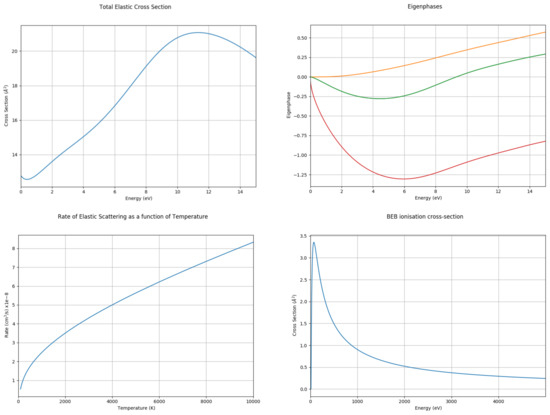
Figure 5.
Examples of graphical outputs produced by QEC for a static exchange (SE) calculation on methane showing total cross sections, eigenphase sums, rates and ionization (BEB) cross sections.
Finally Figure 6 shows examples of plots displaying differential cross sections for CO as a function of both electron collision energy and angle. The results are for an SEP calculation with eight virtual orbitals, using a cc-pVDZ target GTO basis. The results are plotted as single angle–energy dependent contour plots or, alternatively, as cuts through the DCS at a single angle or energy. Illustrated are the cross sections as a function of energy for a scattering angle of 126. Figure 7 shows examples plots displaying differential cross sections for CO.
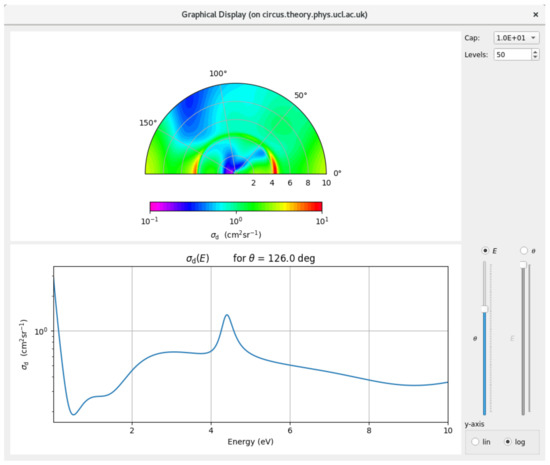
Figure 6.
Differential cross sections for CO as displayed by the QEC GUI.
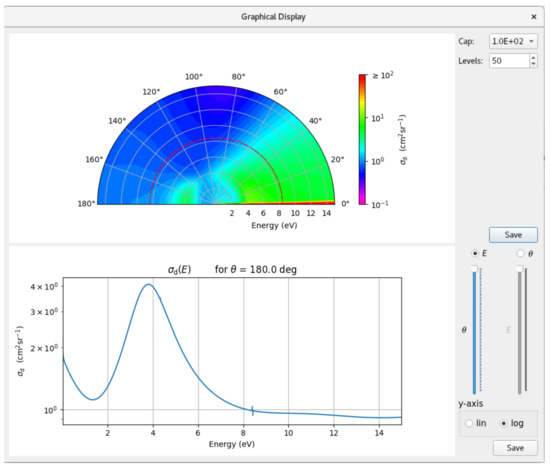
Figure 7.
Differential cross sections for CO as displayed by the QEC GUI.
All the graphical results are also available as data spreadsheets. QEC also provides parameters for the resonances it detects and a theory model file gives details of the calculations performed plus appropriate references to quote when preparing the results for publication.
QEC is provided with a comprehensive manual and associated help facility. It also has a library of about a dozen previously run example which users can try and, if appropriate, adapt; this library is being systematically added to.
4. Concluding Remarks
The present article describes a new expert system designed for an easy and rapid generation of low-energy electron scattering data using the Quantemol Electron Collision (QEC) expert system. QEC runs an integrated versions of the Molpro ab initio molecular electronic structure code [34,35] and the newly developed UKRmol+ R-matrix electron molecule scattering code [13]. QEC exploits this close coupling of the codes in a number of ways such as automated geometry optimization and symmetry determination, and the direct provision of inputs for SCOP, BEB and BEf calculations. However there are a number of other places where this coupling will be exploited further in the future such as the automated provision of parameters for the DEA estimator.
Future releases of QEC will further increase its functionality. Plans include the implementation of a dissociative recombination estimator [48], automated electron-impact vibrational calculations, and the use of effective core potentials for heavy atoms.
Author Contributions
B.C. and M.T. were lead developers for QEC and were assisted by S.M., A.O., M.H., A.D. and J.T.; J.D.G., J.B., Z.M., A.F.A.-R. and J.T. developed UKRmol+; P.J.K. advised on the Molpro integration; J.T. and B.C. drafted the paper which was read and approved by all co-authors.
Funding
This work funded by UK research councils STFC and EPSRC grants numbers ST/R005133/1, EP/R029342/1, EP/G055556/1, EP/G055599/1, EP/P022146/1, EP/N509577/1 and EP/R513143/1, as well as eCSE projects eCSE01-13 and eCSE08-7.
Conflicts of Interest
QEC is distributed by Quantemol Ltd; Maria Tudorovskaya and Sebastian Mohr work for Quantemol while Anna Dzarasova and Jonathan Tennyson are company Directors. Aran O’Hare and Martin Hanicinec receive partial support for their studentships from Quantemol. Peter Knowles acts as a consultant to TTI GmbH, the owner of Molpro. None of the other authors are conflicted.
References
- Song, M.Y.; Yoon, J.S.; Cho, H.; Itikawa, Y.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Cross sections for electron collisions with methane. J. Phys. Chem. Ref. Data 2015, 44, 023101. [Google Scholar] [CrossRef]
- Song, M.Y.; Yoon, J.S.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Cross sections for electron collisions with acetylene. J. Phys. Chem. Ref. Data 2017, 46, 013106. [Google Scholar] [CrossRef]
- Song, M.Y.; Yoon, J.S.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Hamilton, J.R.; Tennyson, J. Cross sections for electron collisions with NF3. J. Phys. Chem. Ref. Data 2017, 46, 043104. [Google Scholar] [CrossRef]
- Song, M.Y.; Yoon, J.S.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Electron collision cross sections with NO, N2O and NO2. J. Phys. Chem. Ref. Data 2019, in press. [Google Scholar]
- Winstead, C.; McKoy, V. Electron-molecule collisions in low-temperature plasmas—The role of theory. Adv. At. Mol. Phys. 2000, 43, 111–145. [Google Scholar]
- Bartschat, K.; Kushner, M.J. Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology. Proc. Natl. Acad. Sci. USA 2016, 113, 7026–7034. [Google Scholar] [CrossRef] [PubMed]
- Blanco, F.; Roldan, A.M.; Krupa, K.; McEachran, R.P.; White, R.D.; Marjanovic, S.; Petrovic, Z.L.; Brunger, M.J.; Machacek, J.R.; Buckman, S.J.; et al. Scattering data for modelling positron tracks in gaseous and liquid water. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 145001. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Tennyson, J.; Huang, S.; Kushner, M.J. Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 2017, 26, 065010. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions: Application to Atomic, Molecular and Optical Processes; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gillan, C.J.; Tennyson, J.; Burke, P.G. The UK molecular R-matrix scattering package: A computational perspective. In Computational Methods for Electron-Molecule Collisions; Huo, W., Gianturco, F.A., Eds.; Plenum: New York, NY, USA, 1995; pp. 239–254. [Google Scholar]
- Gillan, C.J.; Tennyson, J.; McLaughlin, B.M.; Burke, P.G. Low energy electron impact excitation of the nitrogen molecule: optically forbidden transitions. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 1531–1547. [Google Scholar] [CrossRef]
- Carr, J.M.; Galiatsatos, P.G.; Gorfinkiel, J.D.; Harvey, A.G.; Lysaght, M.A.; Madden, D.; Mašín, Z.; Plummer, M.; Tennyson, J. The UKRmol program suite. Eur. Phys. J. D 2012, 66, 58. [Google Scholar] [CrossRef]
- Benda, J.; Mašín, Z.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling of electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2019, in press. [Google Scholar]
- Tennyson, J. Electron-molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Tennyson, J. R-matrix calculation of Rydberg states of CO. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 6185–6201. [Google Scholar] [CrossRef]
- Halmová, G.; Gorfinkiel, J.D.; Tennyson, J. Low and intermediate energy electron collisions with the molecular anion. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 155201. [Google Scholar] [CrossRef]
- Little, D.A.; Tennyson, J. Singlet and triplet ab initio Rydberg states of N2. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 145102. [Google Scholar] [CrossRef]
- Tennyson, J.; Brown, D.B.; Munro, J.J.; Rozum, I.; Varambhia, H.N.; Vinci, N. Quantemol-N: An expert system for performing electron molecule collision calculations using the R-matrix method. J. Phys. Conf. Ser. 2007, 86, 012001. [Google Scholar] [CrossRef]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering for polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3945. [Google Scholar] [CrossRef]
- Munro, J.J.; Harrison, S.; Tennyson, J.; Fujimoto, M.M. A dissociative electron attachment cross-section estimator. J. Phys. Conf. Ser. 2012, 388, 012013. [Google Scholar] [CrossRef]
- Kim, Y.K. Scaling of plane-wave Born cross sections for electron-impact excitation of neutral atoms. Phys. Rev. A 2001, 64, 032713. [Google Scholar] [CrossRef]
- Calogero, F. Variable Phase Approach to Potential Scattering; Academic: New York, NY, USA, 1954. [Google Scholar]
- Jain, A. Elastic scattering of electrons and positrons by CH4 at 25–800 eV. J. Chem. Phys. 1983, 78, 6579–6583. [Google Scholar] [CrossRef]
- Jain, A.; Baluja, K.L. Total (elastic plus inelastic) cross sections for electron scattering from diatomic and polyatomic molecules at 10–5000 eV: H2, Li2, HF, CH4, N2, CO, C2H2, HCN, O2, HCl, H2S, PH3, SiH4, and CO2. Phys. Rev. A 1992, 45, 202–218. [Google Scholar] [CrossRef] [PubMed]
- Brigg, W.J.; Harvey, A.G.; Dzarasova, A.; Mohr, S.; Brambila, D.S.; Morales, F.; Smirnova, O.; Tennyson, J. Calculated photoionization cross sections using Quantemol-N. Jpn. J. Appl. Phys. 2015, 54, 06GA02. [Google Scholar] [CrossRef][Green Version]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D. GBTOlib: A library for evaluation of molecular integrals in the basis of multicentric Gaussian and single-centre B-spline orbitals. In preparation.
- Faure, A.; Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. GTOBAS for fitting Gaussian Type Orbitals to Bessel and Coulomb functions. Comput. Phys. Commun. 2002, 144, 224–241. [Google Scholar] [CrossRef]
- Bachau, H.; Cormier, E.; Decleva, P.; Hansen, J.E.; Martin, F. Applications of B-splines in atomic and molecular physics. Rep. Prog. Phys. 2001, 64, 1815–1943. [Google Scholar] [CrossRef]
- Darby-Lewis, D.; Mašín, Z.; Tennyson, J. R-Matrix Calculations of electron-impact electronic excitation of BeH. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 175201. [Google Scholar] [CrossRef]
- Loupas, A.; Gorfinkiel, J.D. Shape and core-excited resonances in electron scattering from alanine. J. Chem. Phys. 2019, 150, 064307. [Google Scholar] [CrossRef]
- Al-Refaie, A.F.; Tennyson, J. A parallel algorithm for Hamiltonian matrix construction in electron-molecule collision calculations: MPI-SCATCI. Comput. Phys. Commun. 2017, 214, 216–224. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput.-Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Györffy, W.; Kats, D.; Korona, T.; Lindh, R.; et al. MOLPRO, Version 2019.2, a Package of ab Initio Programs. 2019. Available online: https://www.molpro.net (accessed on 14 October 2019).
- Gorfinkiel, J.D.; Tennyson, J. Electron- collisions at intermediate energies. J. Phys. B At. Mol. Opt. Phys. 2004, 37, L343–L350. [Google Scholar] [CrossRef]
- Gorfinkiel, J.D.; Tennyson, J. Electron impact ionisation of small molecules at intermediate energies: The R-matrix with pseudostates method. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 1607–1622. [Google Scholar] [CrossRef][Green Version]
- Jones, M.; Tennyson, J. On the use of pseudostates to calculate molecular polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 045101. [Google Scholar] [CrossRef]
- Zhang, R.; Galiatsatos, P.G.; Tennyson, J. Positron collisions with acetylene calculated using the R-matrix with pseudo-states method. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 195203. [Google Scholar] [CrossRef]
- Morgan, L.A. A generalized R-matrix propagation program for solving coupled 2nd-order differential-equations. Comput. Phys. Commun. 1984, 31, 419–422. [Google Scholar] [CrossRef]
- Gailitis, M. New forms of asymptotic expansions for wavefunctions of charged-particle scattering. J. Phys. B At. Mol. Opt. Phys. 1976, 9, 843. [Google Scholar] [CrossRef]
- Noble, C.J.; Nesbet, R.K. CFASYM, a program for the calculation of the asymptotic solutions of the coupled equations of electron collision-theory. Comput. Phys. Commun. 1984, 33, 399. [Google Scholar] [CrossRef]
- Tennyson, J.; Noble, C.J. RESON: For the automatic detection and fitting of Breit-Wigner resonances. Comput. Phys. Commun. 1984, 33, 421–424. [Google Scholar] [CrossRef]
- Norcross, D.W.; Padial, N.T. The Multipole-Extracted Adiabatic-Nuclei Approximation for Electron-Molecule collisions. Phys. Rev. A 1982, 25, 226–338. [Google Scholar] [CrossRef]
- Baluja, K.L.; Mason, N.J.; Morgan, L.A.; Tennyson, J. Electron scattering from ClO using the R-matrix method. J. Phys. B At. Mol. Opt. Phys. 2000, 33, L677–L684. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Faure, A.; Tennyson, J. Electron-impact excitation of diatomic hydride cations: HeH+, CH+, ArH+. Mon. Not. R. Astron. Soc. 2016, 455, 3281–3287. [Google Scholar] [CrossRef]
- Brigg, W.J.; Tennyson, J.; Plummer, M. R-Matrix calculations of low-energy electron collisions with Methane. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 185203. [Google Scholar] [CrossRef]
- Fonseca dos Santos, S.; Douguet, N.; Kokoouline, V.; Orel, A.E. Scattering matrix approach to the dissociative recombination of HCO+ and N2H+. J. Chem. Phys. 2014, 140, 164308. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).