Abstract
Orthogonal operators can successfully be used to calculate eigenvalues and eigenvector compositions in complex spectra. Orthogonality ensures least correlation between the operators and thereby more stability in the fit, even for small interactions. The resulting eigenvectors are used to transform the pure transition matrix into realistic intermediate coupling transition probabilities. Calculated transition probabilities for close lying levels illustrate the power of the complete orthogonal operator approach.
1. Introduction
Since its first introduction [1], the orthogonal operator technique has appeared to be a powerful tool in reducing the deviations between calculated and experimental energy values in complex spectra (Z > 20). Due to its orthogonality, the operator set is stable enough to introduce small (thus far neglected) higher-order magnetic and electrostatic effects in the fitting procedure. By this extension, deviations between calculated and experimental energy values frequently approach experimental accuracy [2]. More recent use is found in the FERRUM project [3] and in the analysis of 5d-spectra [4]. Origin and subsequent developments underlying the method are discussed. The operator inner product is shown to be a property of operators rather than of its accidental matrix elements by a general progression formula as a function of the number of electrons. Linear algebra can now fruitfully be used to project a variety of contributions onto the orthogonal operator set, both analytically and numerically. The actual construction of an orthogonal operator set is illustrated for configurations. Also, the orthogonal operator method is positioned (as to overlap and differences) with respect to other approaches for describing complex spectra, such as large-scale use of Cowan’s code or Multi-Configuration Dirac-Hartree-Fock (MCDHF) calculations. The description of the odd and even spectra of Fe VI are used as a running example, but other regions of application are mentioned. Ab initio calculations as well as conversion of operator sets are considered, and the interplay between explicit and implicit configuration interaction is discussed. Possibly controversial issues such as (over)completeness, term dependency and a truncation of the model space are reviewed. The accurate description of the energy structure is expected to result in optimally calculated eigenvector compositions. Naturally, this property can be exploited to calculate accurate electric dipole (E1), magnetic dipole (M1) and electric quadrupole (E2) transition probabilities. How polarization, core and valence excitations and full relativity are presently implemented and can be improved in the near future, will be discussed. We recently reinstalled our original database with transition arrays of the 3d and 5d shell [5]. We intend to cooperate with other groups and increase the accessibility of the method.
2. Applications
Why should one use orthogonal operators when a conventional Slater–Condon approach such as Cowan’s code [6,7] is so easy-to-use as a universal tool? Cowan’s code has been a blessing for the experimental atomic physicist for the last 50 years, and it will no doubt continue to be so for many years to come. The orthogonal operator approach may be considered as both an extension and a refinement of the conventional least-squares fitting (LSF) approach, but it also raises the need of finding physically acceptable initial estimates for quite a number of small parameters, especially with an incomplete spectrum. The stability of a parameter versus change or addition of others, on the other hand, is a great asset of the method. Figure 1 provides a clear picture of this aspect [8].
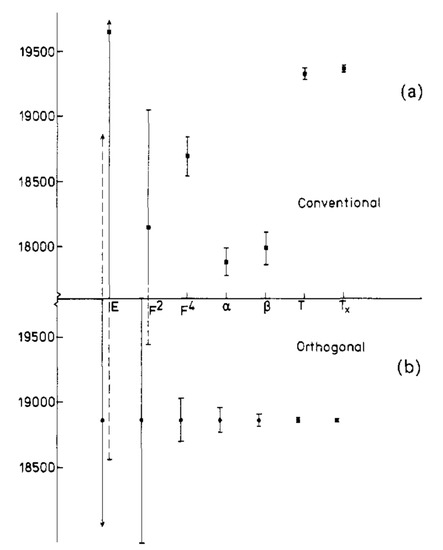
Figure 1.
(a) The values of the parameter in a number of LSF to the 3d configuration in Cr IV.
In the first fit (from left to right) only the parameter was allowed to vary with all other parameters fixed at zero while in subsequent fits the parameter indicated on the abscissa was added. (b) The values of the parameter using the same procedure as in (a), but using a set of orthogonal equivalents.
Both the conventional and the orthogonal operator approaches are based on semiempirical LSF of physical parameters. The mean error can be interpreted as the ’blobsize’ used by painters (Seurat and others) of the art-movement ’Pointillism’ [9]. They used blobs for their paintings and could not represent details smaller than the blobsize. In the same way we cannot describe level structures in detail when the spacing between levels is smaller or comparable to the mean error.
In quite a number of cases, the mean error of an orthogonal operator LSF is smaller by an order of magnitude w.r.t. a conventional LSF. In principle, this leads to better eigenvector compositions and thus better transition probabilities. In some cases, refinements are expedient and they will be discussed below. In Table 1, some of the characteristics of both methods are set side by side.

Table 1.
Characteristics of the conventional and the orthogonal operator LSF methods.
The term analysis of complex spectra like Mn IV [10], Re III [11] and Os III [12] only came within reach by the accuracy of orthogonal operator predictions. Such predictions concern both energy levels and electric dipole intensities.
In addition, reliable calculations of forbidden magnetic dipole and electric quadrupole intensities are enabled by the accurate eigenvectors from an orthogonal operator LSF of the pertinent system. On a more theoretical level, use of orthogonal operators allows establishing small and thus far neglected interactions that reflect many-body, relativistic and correlation effects. Fully relativistic ab initio perturbation or Configuration Interaction (CI) calculations can subsequently be compared to the parameter values found.
2.1. Oscillator Strengths Involving Close Lying Levels
To illustrate the importance of accurate eigenvectors, two examples in the spectra of Fe III and Fe II are given below. The effect is especially striking for close lying levels, when the actual separation may be smaller than the mean error of the fit: the ’blobsize’ is here too large for a reliable calculation.
First, the eigenvectors of the conventional and the orthogonal method in the Fe III case are compared in Table 2 [13]:

Table 2.
Two close lying levels in the matrix of the 3d4p configuration of Fe III calculated by the conventional and the orthogonal method.
With deviations lower by an order of magnitude, it is seen that the eigenvector composition changes appreciably. Next, the corresponding transition probabilities (-values) are compared to experiment in Table 3:

Table 3.
Transition probabilities () in Fe III calculated by the conventional (Conv.) and the orthogonal (Orth.) method, compared to experiment [14]: B. are estimates of photographic blackening on a logarithmic scale, Int. are scaled intensities calculated from B.
The conventional method calculates two equally strong lines and then two equally weaker lines, while the experiment shows a strong line, a weaker line, a little bit weaker line and then again a stronger line but not as strong as the first line. This pattern is exactly described by the orthogonal operator approach.
Another striking example of the impact of the mixing percentages, i.e. the eigenvector accuracy, on the oscillator strengths is given by Hibbert [15,16] in the spectrum of Fe II. Two lines at 2507 Å and 2509 Å originating from the same (even) lower level are considered; the two close (odd) upper levels are given in Table 4:

Table 4.
Mixings in levels of Fe II.
In Table 5, the eigenvector percentages are from our original calculation [17], a calculation of Corrégé and Hibbert [15] fine-tuned to the experimental energy levels, and our present contribution with a similar manipulation of the parameter. The effect of the fine-tuning is obvious: the level percentages are seen to approach each other very closely and turn out to be quite sensitive to the eigenvalue calculation, even at the sub- cmlevel.

Table 5.
Oscillator strengths of the 2507, 2509 Å lines in Fe II.
The corresponding oscillator strengths are given in Table 5, together with the result of a conventional calculation [18]. As to be expected, the oscillator strengths are accordingly sensitive to the eigenvector composition, and finally turn out to become about equal. This result is consistent with an earlier successful modeling of the emission spectrum of Carinae [19].
2.2. Interplay with ab initio Calculations
The inner product of two operators t and u is defined as:
where the summation runs over all states of the system; it is basically the (double) contraction of the two matrices. The inner product is commutative by definition.
Taking magnetic degeneracy into account, it can be reduced to:
or, in the case of electrostatic operators:
Equating to zero is used to define a set of orthogonal operators to be used in a LSF procedure: as a result, each parameter is now equipped with its own unique ’behavior’. However, use of the concept of operator inner product does not stop there. The resulting linear algebra allows the definition of an operator projection and this opens up new possibilities that can fruitfully be exploited in ab initio calculations. Let the operator space be spanned by a set of orthogonal operators with , where the angular operators form an orthogonal set and the radial factors are treated as parameters. Any arbitrary operator can now be expressed in terms of the complete basis set of orthogonal operators:
The expression for the individual contribution of a single operator U to a parameter and (when summed over all possible contributing operators U) its complete ab initio calculation follows:
Moreover, the projection of any physical operator on a finite (and possibly incomplete) basis is complete if and only if the magnitude of the operator equals the sum of the magnitudes of its projections:
The simple projection formula (3) can be used to derive analytical expressions, e.g. for the contribution of a variety of two-particle effects, relativistic and perturbative, to the spin-orbit parameter [20]. Analytic expressions for the important [4] orthogonal operators (3-body electrostatic) and (2-body magnetic) were derived in this way as well [2,21].
Alternatively, equation (3) is readily programmed to allow numerical projections, e.g., of Slater integrals or perturbative effects onto the orthogonal operator set to calculate the contributions to any parameter of your choice.
Earlier ab initio calculations of parameters, whether analytical or numerical, could only take into account contributions that are directly proportional to the operator concerned. Equation (3), on the other hand, allows us to calculate all ab initio contributions with a non-zero inner product.
This is exemplified in Table 6 by an ab initio calculation of the Trees operator in Fe VI (3d). Nominally, ’only’ accounts for and excitations. Using Equation (3), one finds that there are also non-zero contributions from excitations with a different spin-angular character. A second example of this method is the ab initio calculation of and in Fe VI (3d4s), given in Table 7.

Table 6.
Second-order contributions to the three-particle Trees parameter in Fe VI (3d).

Table 7.
Calculated contributions to and in Fe VI (3d4s) compared with experiment.
Another fruitful strategy is fitting to MCDHF calculated energy levels (single configuration). Keeping the parameters associated with effective operators fixed to zero, the mean error of such fits is generally well below 1 cm. This demonstrates the completeness of the orthogonal operator description in the case of full relativity. The resulting parameter values may be compared to a direct ab initio calculation from wavefunction integration. The results turn out to be completely equivalent, as illustrated by the below example of Fe VI (3d).
The general relativistic form of the traditional Slater integral [21]:
is straightforwardly integrated with the MCDHF wavefunctions of Fe VI (3d) to yield: . On the other hand, a fit of orthogonal operators to the corresponding Dirac energy levels gives: and , from which . The closeness of the results demonstrates the ability of the orthogonal operator method to retrieve the correct physical information from the data.
This property may also be used to obtain initial values for two-body magnetic parameters. Two-body magnetic parameters describe mutual spin-orbit (MSO) and electrostatic spin-orbit (EL-SO) interactions. These interactions are both included in a MCDHF calculation: the first in the (Dirac-)Breit interaction and the second by the fact that single electron excitations of the type are to a large extent included in the Hartree-Fock potential (Brillouin’s theorem) [6]. In addition, there are two-body magnetic operators for spin-spin effects (included in the Breit interaction) as well.
The impact of the values of the one- and two-body magnetic parameters on the mean error of the fit is shown in Table 8 for Fe VI (3d).

Table 8.
Values of one- and two-body magnetic operators in Fe VI 3d.
The operators associated with to have spin-orbit character while and describe spin-spin effects. In each case, all other (electrostatic) parameters were left free to vary. In the column Fit(1), the two-body parameters were fixed to zero. The values of a pure Dirac-Fock (DF) calculation only deteriorate the fit: it can be concluded that addition of the Breit interaction (DF+Breit) is essential for improvement; the DF and DF+Breit calculations are carried out with the GRASP92 package [22].
In the column headed B-splines, a complete first and second order Hartree-Fock (HF) calculation of and the parameters is carried out; the channel for the excitations is calculated with a B-splines program developed in Amsterdam [23,24]. This program employs the effective completeness of B-splines to calculate channels of one-electron excitations from a frozen HF core potential. All values can be compared with the results of the final fit Fit(2).
2.3. Configuration Interaction
It is well known that the central field model is flawed by configuration interaction (CI). This is particularly relevant in the spectra of doubly ionized, singly ionized and neutral atoms, where the single configuration model is increasingly breaking down. For the iron group elements, this is mainly due to energetically favorable substitutions. More specifically, effective parameters that account for weak configuration interactions with large numbers of high-lying configurations, are not able to do a reliable job in the spectra with a lower degree of ionization. Higher order electrostatic and magnetic effects (described by effective orthogonal operators) can only be determined reliably if the first order model is reasonably accurate. Evidently, the model space has to be expanded to include nearby configurations. Yet, in the balance between (perturbative) effective parameters and (variational) explicit interactions, with orthogonal operators we like to retain the first and limit the second to the ones most necessary. Still, in Fe II, this implies already at least 6 configurations of the same parity for the lower even and odd systems.
The orthogonal operator approach is at its best for operators with many diagonal matrix elements, so the inherent off-diagonal character of CI admittedly reduces the strength of the approach. To obtain consistent iso-electronic parameter extrapolations, it is necessary to keep the same configurations in the model space over the entire sequence [4] or to subtract the explicit configuration-interaction from the effective parameter. Proceeding in this way, we conclude that it is possible to meaningfully combine perturbation theory (using effective parameters) and a diagonalization approach (using interaction integrals) into one orthogonal operator description of an atomic system. The convincing comparison of recent branching fractions and measurements to our calculations in Co II [25] illustrates this point.
Another case of strong CI occurs for higher ionization in the odd system, when the p-shell opens up. The resulting wide 3p3d configurations seem to be a problem for any atomic physics approach [26], even for the impressive large scale MCDHF calculations that have recently been undertaken [27,28]. We are presently developing orthogonal operators suited for those systems, with special attention to the particularly large magnetic configuration interactions involving .
2.4. Transition Probabilities Improved
To obtain relatively accurate transition probabilities, both the eigenvectors to be used in the intermediate coupling transformation and the transition integrals should be optimized. While an orthogonal operator LSF is already optimized to produce satisfactory eigenvectors, work has to be done to obtain reliable transition integrals and to incorporate the most important core and valence excitations. To achieve this, several steps are taken:
- Use of core-polarization to account for the induced dipole moment, which is particularly important in the case of large, loosely bound (lower ionization stages) ionic cores.This usually decreases the E1-integral by 5-10%: where the dipole polarizability (in terms of ) is either taken from literature or calculated ab initio. A cutoff radius is introduced here to avoid divergence at .For E2 transitions, the electric quadrupole polarization is used.
- Use of MCDHF calculated transition integrals.
- Inclusion of essential configurations in the model space for full diagonalization.
- Use of perturbation theory: let and refer to the full odd and even states of the system, to be approximated by the model states and respectively, and far-lying configurations to be summed over. The first order expression of the dipole operator can be corrected to second order by linking the virtual configurations to the model configurations with the Coulomb operator V:
To elaborate further on the last two points: with orthogonal operators, energy effects of unobserved configurations are accounted for by effective operators, while the number of strongly interacting configurations required in the model space is limited. Effects of unobserved configurations on the transition probabilities, however, are not automatically included in this way. This means that core-polarization effects are not absorbed by orthogonal operators and have to be included as corrections to the transition integrals. Also, second order corrections to the transition matrix elements may be added to take into account the valence effects of large numbers of far-away configurations [29]. The new radial factors entering this approach involve complete channels of single electron orbitals and can effectively be calculated with a B-splines program based on a frozen HF core [23,24].
Below, we use the excitation as a example: , and :
The above expression turns out to give good agreement with a full diagonalization approach:
Another important example of this point concerns the excitations and within the Layzer complex : especially for higher ionization they should be included [30] either explicitly or by the above perturbative approach of equation (6).
3. Origin
To get a feel for the increased stability of orthogonal operators in a LSF and why they are least correlated, one may look at the simple high school project of Figure 2 for comparison.

Figure 2.
Determining the center of mass of a bicycle: orthogonal lines are the most accurate.
To find the center of mass of an extended object like a bicycle, one may suspend this object under various angles, determine the plumb line in each case and preserve them like the yellow lines in the picture. The intersection of the plumb lines is the center of mass. Mathematically, this means finding the best intersection of a number of straight lines, a problem to be solved with least squares. Orthogonal plumb lines (being most independent) do the most accurate job.
We recall a little linear algebra to describe the fitting process in a simplified way. Let be one parameter of a vector of parameters and one energy of a vector of energies. All energy operators will be contained in the matrix A.
To solve for , multiply with the transpose from the left and invert:
The matrix is now the matrix of the inner products of all operators: . For orthogonal operators, this matrix is diagonal and even orthonormal if . Thus, the final solution in the orthogonal case becomes:
As there is no reference in the solution of to any other parameter , they turn out to be completely uncorrelated! Actually, this derivation only holds for diagonal matrix elements, which explains why orthogonal operators are least correlated instead of uncorrelated.
Orthogonal operators are normalized in batches of operators of the same type (2-body magnetic, 3-body electrostatic, etc.), which means that is the same for all operators in the batch. From the formula for the LSF error on the parameter :
it can now be understood, why parameter errors are equal (and minimal) for all parameters in the same batch.
3.1. Construction of an Orthogonal Set
First, let us make a subdivision of possible energy operators, to be able to survey the field:
- There are three subspaces of operators that are orthogonal by their tensorial character: expressed as double tensors with ranks in separate spin- and orbital spaces [31], one distinguishes: electrostatic, spin-orbit and spin-spin.
- Operators acting on different electrons belong in different orthogonal subspaces as well. The and interactions are described, for example, by separate orthogonal operators.
- In addition, each operator has a unique particle character, i.e., the number of electrons it acts on (only the average energy is a 0-particle operator). We distinguish in the electrostatic space, in the spin-orbit space and in the spin-spin space. An operator may have different particle characters in different shells: the Trees operator has a three-particle character in the d-shell, while the operator has a two-particle character in the d-shell and a 1-particle character in the s-shell.
- A further classification is the order of perturbation theory: preferably, we describe first- and second (or higher) order effects by different operators. In line with the previous point: n-body operators occur in the order of perturbation.
There are some useful properties of inner products that help defining a set of orthogonal operators. First, the inner product is independent of the coupling scheme.
Second, the behavior of the inner product as a function of the number of electrons in the shell is well-defined. If operators and occur together in the shell for the first time, then their inner product in the shell is closely related:
The coefficients and only depend on N and on the particle characters of the two operators: and are independent of the operators in question. In an orthogonal operator set, only the average energy operator has a non-zero trace. As a result, once operators are orthogonal in their parent configuration, i.e. the shell(s) where they first make their appearance, then they automatically remain orthogonal in all other configurations. This statement is equivalent to the below group theoretical result [32]:
If and belong to different irreducible representations and (differing symmetries) of a group ánd does not contain the identity representation of , then .
This property has been used notably by Brian Judd to construct orthogonal operators based on Lie groups such as , , and [33,34].
Except building operators with well-defined group-theoretical properties, one may also start from elementary building blocks for inequivalent electrons that are orthogonal due to the well-known properties of -symbols. To build a first orthogonal basis, we use annihilation and creation tensor operators [31] with ranks and k in spin- and orbital spaces, coupled to a total rank t:
In the electrostatic case, this simplifies to yielding a number of basic orthogonal operators in [35].
Such a first orthogonal basis of six electrostatic operators is given in Table 9 for the dp configuration as an example:

Table 9.
Matrix elements of operators for dp.
In order to avoid square roots in the entries, the common normalization factors are given below each column: .
The next step is to find linear combinations of these operators to distinguish between first order direct and exchange Coulomb interactions and higher order effects. The Coulomb parameters are named and the distinct higher order parameters (Sack), respectively [36,37]. Operators are always written lower case to distinguish them from the corresponding parameters, e.g., the operator is associated with the parameter .
The below example describes the route from the original orthogonal basis given in Table 9 towards the final orthogonal operator set used for configurations [37] and may serve as a blueprint for any configuration.
Properties: and .
Immediate use: and . Property: applies to all exchange operators.
Use: we combine the remaining operators: , and to: and its orthogonal counterpart . To check the whole procedure afterwards, we verify the inner products:
and .
Final results:
First order Coulomb: , and
Higher order: ), and .
These final results are summarized in Table 10.

Table 10.
Matrix elements of the and operators for dp.
All entries in a column are to be divided by the factors to ensure common normalization:
.
3.2. Completeness
An issue sometimes raised in connection with orthogonal operators is the comparatively large number of parameters M versus the number of observed energy levels N. Usually N is equal or larger than M, and ideally maybe even much larger. As each orthogonal operator describes an independent physical effect, however, it may quickly be seen that with a small number of parameters, many effects are inevitably omitted and one can not hope to obtain a physically reliable fit. On the other hand, for each configuration with one electron outside closed shells, we have two operators and and therefore: : for this case we seem to be used to a complete set already!
In fact, each complete set of operators may be shown to yield a unique joint solution to level energies and level compositions. Consequently, an operator set that consists of more operators than the number of levels in the configuration is actually not overcomplete. In principle there is, in addition to the level energies, sufficient physical information dependent on the level compositions (Landé g-factors, line strengths) to determine all parameter values unambiguously. In many cases the experimental information is far from complete, but theoretical or empirical knowledge of the parameters can readily be used to reduce the number of parameters to be varied. For a Hamiltonian consisting of angular operators and associated radial parameters to yield correct energies and level compositions, a complete operator set should be used as a fact of principle, even though the number of operators may exceed the number of fitted energy levels. Noble-gas configurations , using Landé g-factors for additional information on the level compositions, have been used to substantiate this point [38]. The fit with and yielded physically realistic parameter values in line with ab initio results. In practice, however, one can always neglect the smaller effects, or add them as non-variable quantities derived from empirical or theoretical knowledge.
4. Outlook and Summary
The orthogonal operator approach is briefly reviewed and compared to the conventional LSF approach. The increased stability of orthogonal operators creates room to meaningfully include two-body magnetic operators and higher order effective electrostatic operators. The mean LSF error is thereby substantially reduced, which should give better eigenvector compositions and improved transition probabilities. However, ’orthogonal operators’ is certainly no plug-and-play method: the initial estimates require iso-ionic/iso-electronic extrapolations, preliminary ab initio calculations or both. Experience with neighboring spectra obviously helps. Little experience has been gained in the open and the shells yet, though we recently implemented orthogonal operators for both cases; applications for configurations with are planned in the near future.
While large-scale calculations with Cowan’s code (including many individual configurations) certainly lead in a quick and reliable way to satisfactory results, important magnetic effects are left out and this may constitute a problem for close lying levels. Orthogonal operators (including many effective operators) are more perturbative than variational in nature. As to higher order electrostatic effects, it is not easy to compare the impact of a large number of unobserved, scaled configurations (that indeed act as effective operators) to the effective 3- and 4-body orthogonal operators: they probably represent the same effects only partially. When strong configuration interaction comes into play, the orthogonal model space is extended with a limited number of configurations. The LSF mean error is still clearly smaller but closer to the mean error of the conventional approach in these cases.
We look forward to cooperate both with experimental groups to support their work and with theoretical groups to be able to implement more advanced ab initio methods. In the course of doing this, we hope to make the method of orthogonal operators more generally accessible.
Author Contributions
Both authors contributed to all aspects of this work. Writing–original draft, P.U. and T.R.; Writing–review and editing, P.U. and T.R.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Judd, B.; Hansen, J.; Raassen, A. Parametric fits in the atomic d shell. J. Phys. B At. Mol. Phys. 1982, 15, 1457–1472. [Google Scholar] [CrossRef]
- van het Hof, G.; Raassen, A.; Uylings, P. Parametric Description of 3dN4s Configurations using Orthogonal Operators. Phys. Scr. 1991, 44, 343–350. [Google Scholar]
- Hartmann, H.; Nilsson, H.; Engström, L.; Lundberg, H. The FERRUM project: Experimental lifetimes and transition probabilities from highly excited even 4d levels in Fe II. Astron. Astrophys. 2015, 584, 1–6. [Google Scholar] [CrossRef]
- Azarov, V. Parametric study of the 5d3, 5d2 6s and 5d2 6p configurations in the Lu I isoelectronic sequence (Ta III-Hg X) using orthogonal operators. At. Data Nucl. Data Tables 2018, 119, 193–217. [Google Scholar] [CrossRef]
- Raassen, A.; Uylings, P. 2019. Available online: https://personal.sron.nl/ tonr/atomphys/levtext.html (accessed on 11 November 2019).
- Cowan, R. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kramida, A. Cowan Code: 50 Years of Growing Impact on Atomic Atomic Physics. Atoms 2019, 7, 64. [Google Scholar] [CrossRef]
- Hansen, J.; Uylings, P.; Raassen, A. Parametric Fitting with Orthogonal Operators. Phys. Scr. 1988, 37, 664–672. [Google Scholar] [CrossRef]
- Hautecoeur, L. De Impressionisten, Georges Seurat; Atrium: Alphen aan den Rijn, The Netherlands, 1972. [Google Scholar]
- Tchang-Brillet, W.Ü.; Artru, M.C.; Wyart, J.F. The 3d4-3d34p Transitions of Triply Ionized Manganese (Mn IV). Phys. Scr. 1986, 33, 390–400. [Google Scholar] [CrossRef]
- Azarov, V.; Gayasov, R. The third spectrum of rhenium (Re III): Analysis of the (5d5 + 5d46s)–(5d46p + 5d36s6p) transition array. At. Data Nucl. Data Tables 2018, 121, 306–344. [Google Scholar] [CrossRef]
- Azarov, V.; Tchang-Brillet, W.Ü.; Gayasov, R. Analysis of the spectrum of the (5d6 +5d56s) − (5d56p+5d46s6p) transitions of two times ionized osmium (Os III). At. Data Nucl. Data Tables 2018, 121, 345–377. [Google Scholar] [CrossRef]
- Raassen, A.; Uylings, P. The Use of Complete Sets of Orthogonal Operators in Spectroscopic Studies. Phys. Scr. 1996, T65, 84–87. [Google Scholar] [CrossRef]
- Ekberg, J. Wavelengths and transition probabilities of the 3d6-3d54p and 3d54s-3d54p transition arrays of Fe III. Astron. Astrophys. Suppl. Ser. 1993, 101, 1–36. [Google Scholar]
- Corrégé, G.; Hibbert, A. The Oscillator Strengths of Fe II λλ2507,2509. Astrophys. J. 2005, 627, L157–L159. [Google Scholar] [CrossRef]
- Hibbert, A. Successes and Difficulties in Calculating Atomic Oscillator Strengths and Transition Rates. Galaxies 2018, 6, 77. [Google Scholar] [CrossRef]
- Raassen, A.; Uylings, P. Critical evaluation of calculated and experimental transition probabilities and lifetimes for singly ionized iron group elements. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 3137–3146. [Google Scholar] [CrossRef]
- Kurucz, R. 2017. Available online: http://kurucz.harvard.edu/atoms/2601/gf2601.pos (accessed on 1 June 2019).
- Verner, E.; Gull, T.; Bruhweiler, F.; Johansson, S.; Ishibashi, K.; Davidson, K. THE origin of Fe II and [Fe II] emission lines in the 4000–10000 Å range in the BD weigelt blobs of η CARINAE. Astrophys. J. 2002, 581, 1154–1167. [Google Scholar] [CrossRef]
- Uylings, P. Extended theory of the spin-orbit interaction. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 2947–2961. [Google Scholar] [CrossRef]
- Uylings, P. Applications of second quantization in the coupled form. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 4391–4407. [Google Scholar] [CrossRef]
- Parpia, F.; Froese Fischer, C.; Grant, I. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Comm. 1996, 94, 249–271. [Google Scholar] [CrossRef]
- Hansen, J.; Bentley, M.; van der Hart, H.; Landtman, M.; Lister, G.; Shen, Y.T.; Vaeck, N. The Introduction of B-Spline Basis Sets in Atomic Structure Calculations. Phys. Scr. 1993, T47, 7–17. [Google Scholar] [CrossRef]
- Bachau, H.; Corbier, E.; Decleva, P.; Hansen, J.; Martín, F. Applications of B-splines in atomic and molecular physics. Rep. Prog. Phys. 2001, 64, 1815–1942. [Google Scholar] [CrossRef]
- Lawler, J.; Feigenson, T.; Sneden, C.; Cowan, J.; Nave, G. Transition Probabilities of Co II Weak Lines to the Ground and Low Metastable Levels. Astron. Astrophys. Suppl. Ser. 2018, 238, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Ryabtsev, A. Survey of Some Recent Experimental Analysis of 3p53dN+1 Configurations and of Rh I-like Spectra. Phys. Scr. 1996, 1996, 23–30. [Google Scholar] [CrossRef]
- Li, Y.; Xu, X.; Li, B.; Jönsson, P.; Chen, X. Multiconfiguration Dirac–Hartree–Fock calculations of energy levels and radiative rates of Fe VII. Mon. Not. R. Astron. Soc. 2018, 479, 1260–1266. [Google Scholar]
- Li, B.; Xu, X.; Chen, X. Relativistic large scale CI calculations of energies, transition rates and lifetimes in Ca-like ions between Co VIII and Zn XI. At. Data Nucl. Data Tables 2019, 127, 131–139. [Google Scholar] [CrossRef]
- Uylings, P.; Raassen, A. Accurate calculation of transition probabilities using orthogonal operators. J. Phys. B At. Mol. Opt. Phys. 1995, 28, L209–L212. [Google Scholar] [CrossRef]
- Quinet, P.; Hansen, J. The influence of core excitations on energies and oscillator strengths of iron group elements. J. Phys. B At. Mol. Opt. Phys. 1995, 28, L213–L220. [Google Scholar] [CrossRef]
- Judd, B. Second Quantization and Atomic Spectroscopy; John Hopkins Press: Baltimore, MD, USA, 1967. [Google Scholar]
- Judd, B. Operator Averages and Orthogonalities; Springer: Berlin, Germany, 1984; Volume 201. [Google Scholar]
- Judd, B.; Leavitt, R. Many-electron orthogonal scalar operators in atomic shell theory. J. Phys. B At. Mol. Phys. 1986, 19, 485–499. [Google Scholar] [CrossRef]
- Dothe, H.; Judd, B. Orthogonal operators applied to term analysis residues for Fe VI 3d24p. J. Phys. B At. Mol. Phys. 1987, 20, 1143–1151. [Google Scholar] [CrossRef]
- Dothe, H.; Judd, B.; Hansen, J.; Lister, G. Orthogonal scalar operators for pNd and pdN. J. Phys. B At. Mol. Phys. 1985, 18, 1061–1080. [Google Scholar] [CrossRef]
- Klinkenberg, P.; Uylings, P. The 5f2-Configuration in Doubly Ionized Thorium, Th III. Phys. Scr. 1986, 34, 413–422. [Google Scholar] [CrossRef]
- Uylings, P.; Raassen, A. High Precision Calculation of Odd Iron-group Systems with Orthogonal Operators. Phys. Scr. 1996, 54, 505–513. [Google Scholar] [CrossRef]
- van het Hof, G.; Uylings, P.; Raassen, A. On the necessity and meaning of complete sets of orthogonal operators in atomic spectroscopy. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 1161–1173. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).