Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials
Abstract
1. Introduction
2. Quantum Defect Theory and the Universal Model
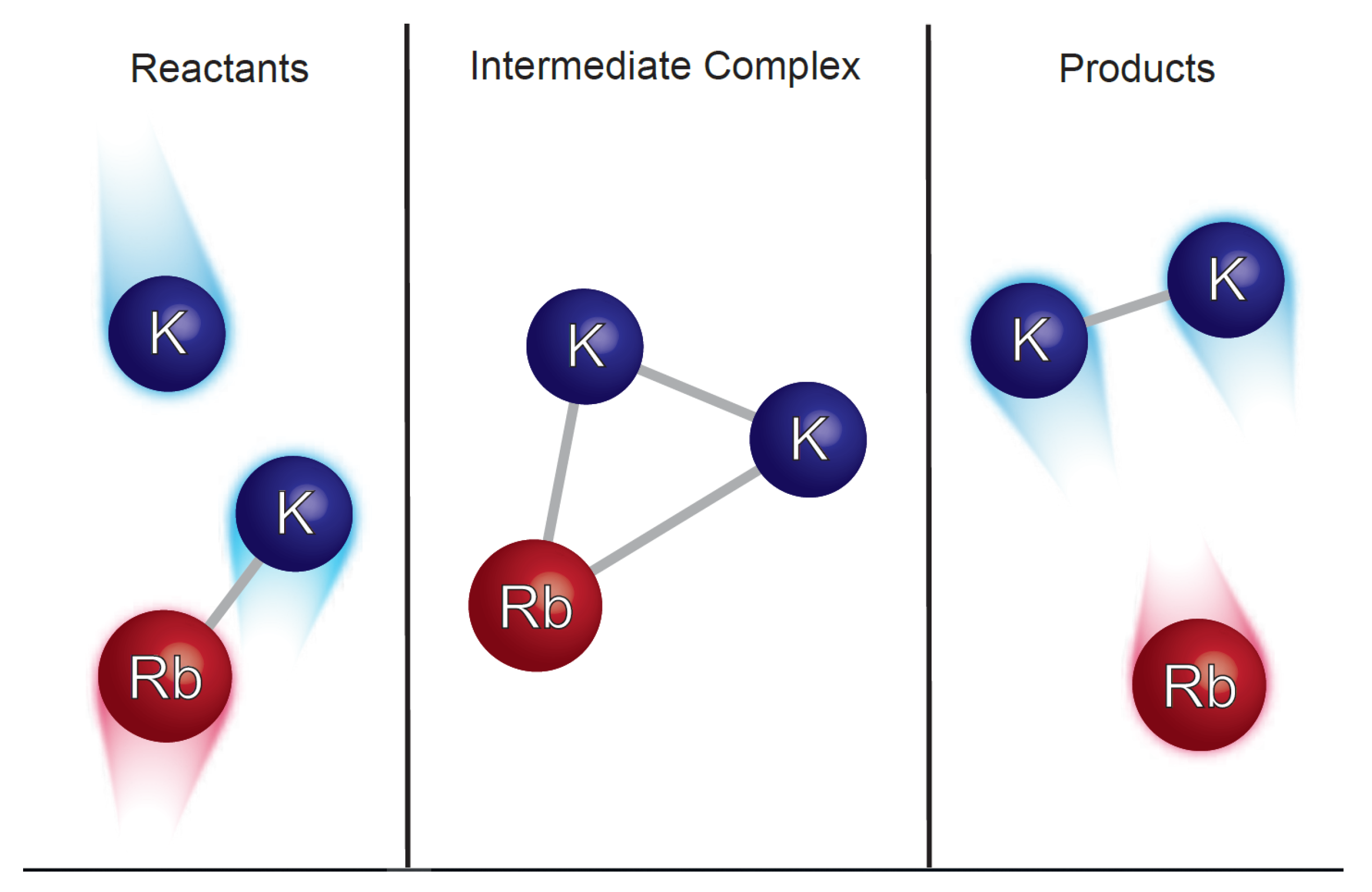
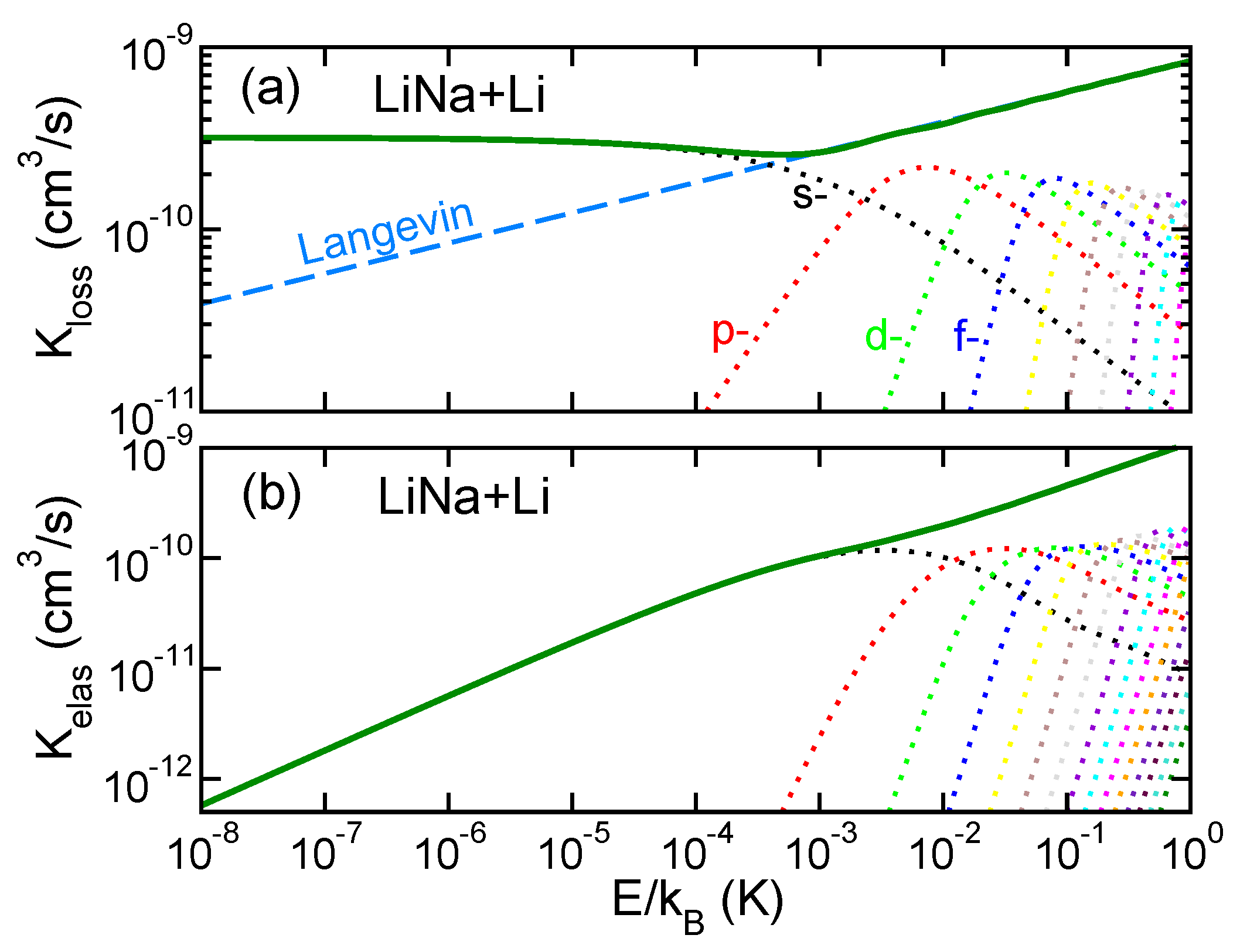
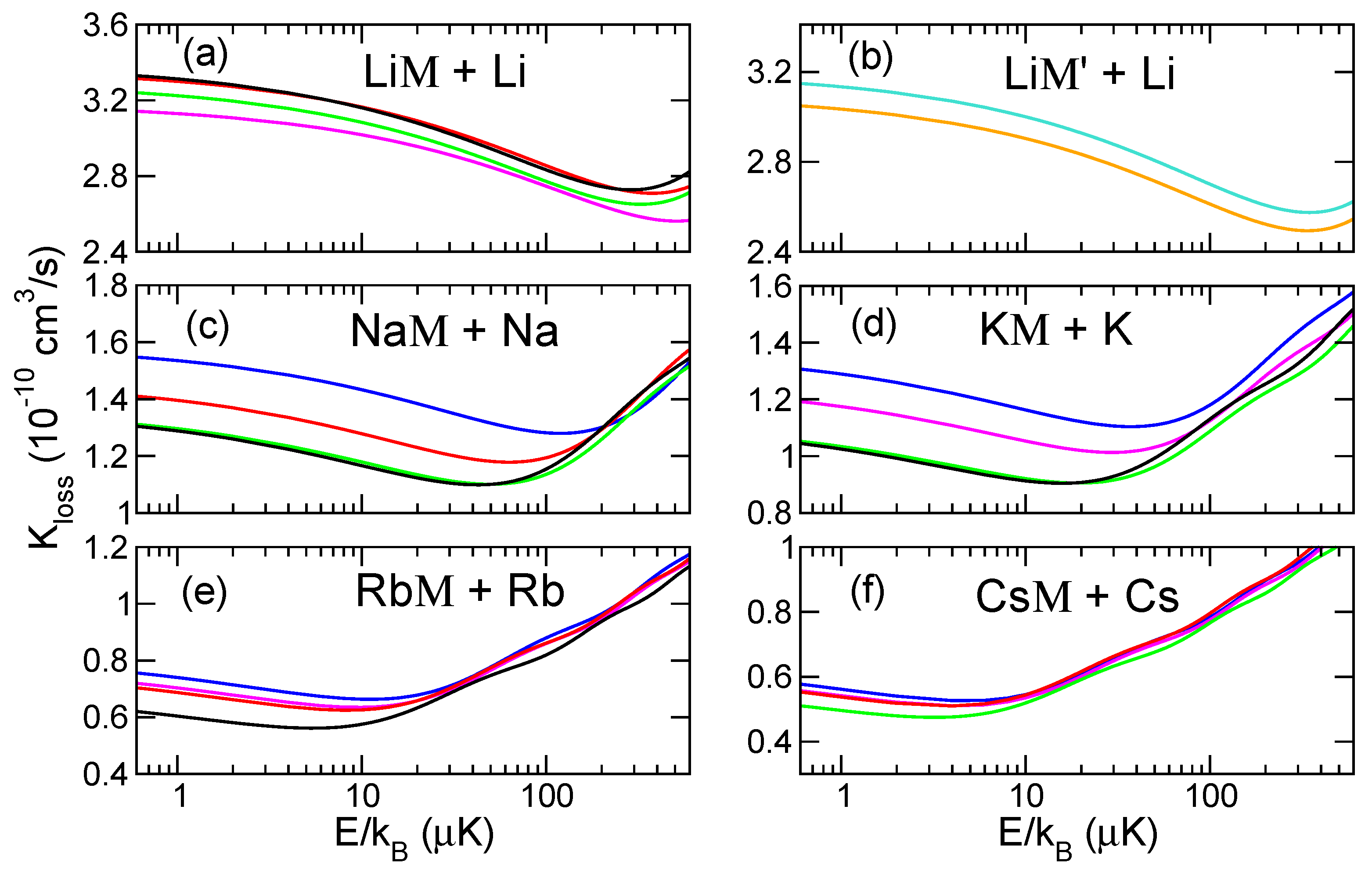
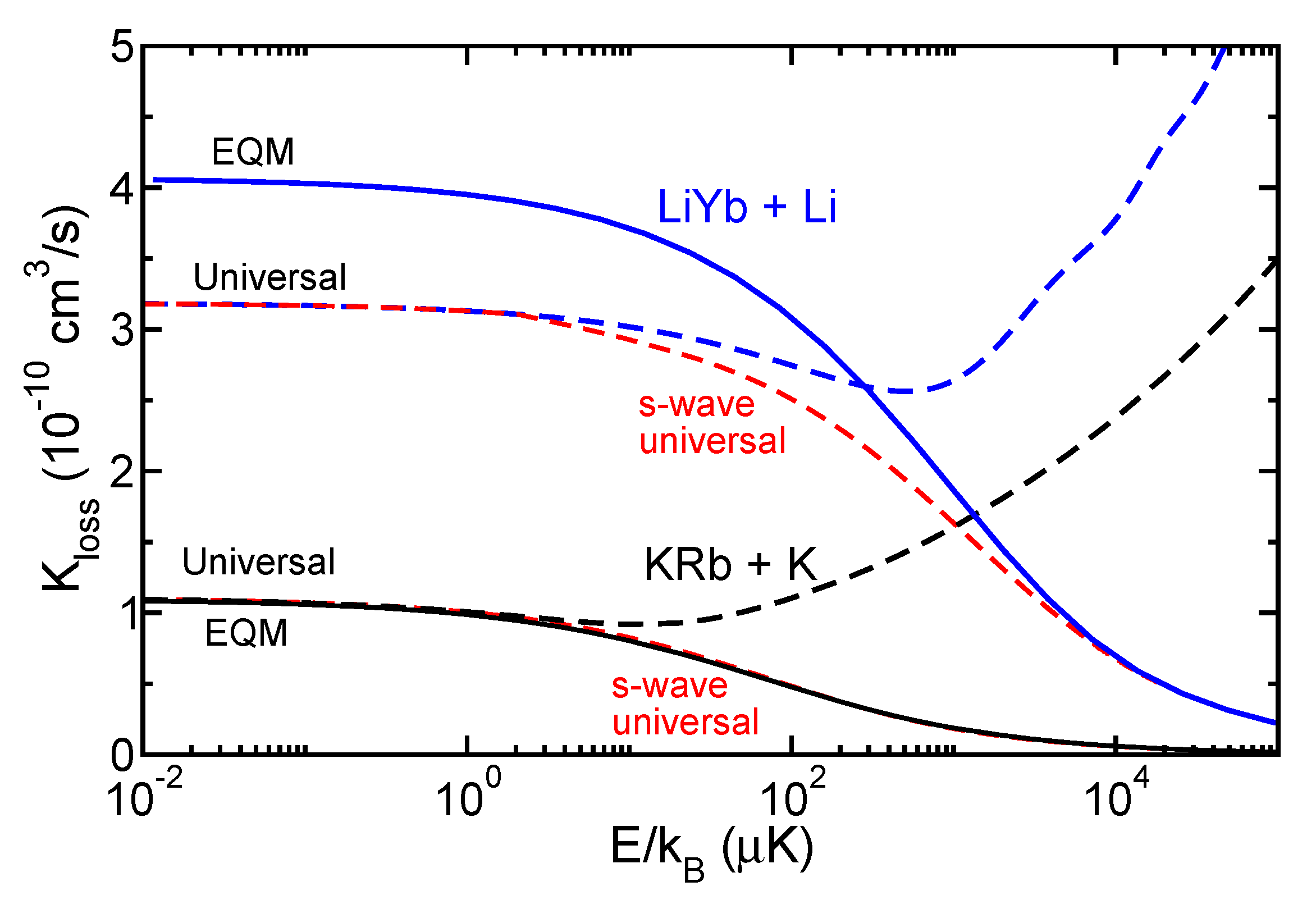
3. Comparisons of Inelastic Rate Coefficients for Atom-Molecule Collisions
4. Molecular Dynamic Polarizability and Van Der Waals Coefficients
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ni, K.K.; Ospelkaus, S.; de Miranda, M.H.G.; Pe’er, A.; Neyenhuis, B.; Zirbel, J.J.; Kotochigova, S.; Julienne, P.S.; Jin, D.S.; Ye, J. A High Phase-Space-Density Gas of Polar Molecules. Science 2008, 322, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Takekoshi, T.; Reichsöllner, L.; Schindewolf, A.; Hutson, J.M.; Le Sueur, C.R.; Dulieu, O.; Ferlaino, F.; Grimm, R.; Nägerl, H.C. Ultracold Dense Samples of Dipolar RbCs Molecules in the Rovibrational and Hyperfine Ground State. Phys. Rev. Lett. 2014, 113, 205301. [Google Scholar] [CrossRef]
- Molony, P.K.; Gregory, P.D.; Ji, Z.; Lu, B.; Köppinger, M.P.; Le Sueur, C.R.; Blackley, C.L.; Hutson, J.M.; Cornish, S.L. Creation of Ultracold 87Rb133Cs Molecules in the Rovibrational Ground State. Phys. Rev. Lett. 2014, 113, 255301. [Google Scholar] [CrossRef] [PubMed]
- Park, J.W.; Will, S.A.; Zwierlein, M.W. Ultracold Dipolar Gas of Fermionic 23Na40K Molecules in Their Absolute Ground State. Phys. Rev. Lett. 2015, 114, 205302. [Google Scholar] [CrossRef] [PubMed]
- Seeßelberg, F.; Buchheim, N.; Lu, Z.K.; Schneider, T.; Luo, X.Y.; Tiemann, E.; Bloch, I.; Gohle, C. Modeling the adiabatic creation of ultracold polar 23Na40K molecules. Phys. Rev. A 2018, 97, 013405. [Google Scholar] [CrossRef]
- Guo, M.; Zhu, B.; Lu, B.; Ye, X.; Wang, F.; Vexiau, R.; Bouloufa-Maafa, N.; Quéméner, G.; Dulieu, O.; Wang, D. Creation of an Ultracold Gas of Ground-State Dipolar 23Na87Rb Molecules. Phys. Rev. Lett. 2016, 116, 205303. [Google Scholar] [CrossRef] [PubMed]
- Rvachov, T.M.; Son, H.; Sommer, A.T.; Ebadi, S.; Park, J.J.; Zwierlein, M.W.; Ketterle, W.; Jamison, A.O. Long-Lived Ultracold Molecules with Electric and Magnetic Dipole Moments. Phys. Rev. Lett. 2017, 119, 143001. [Google Scholar] [CrossRef] [PubMed]
- Ospelkaus, S.; Ni, K.K.; Wang, D.; de Miranda, M.H.G.; Neyenhuis, B.; Quéméner, G.; Julienne, P.S.; Bohn, J.L.; Jin, D.S.; Ye, J. Quantum-State Controlled Chemical Reactions of Ultracold Potassium-Rubidium Molecules. Science 2010, 327, 853–857. [Google Scholar] [CrossRef] [PubMed]
- de Miranda, M.H.G.; Chotia, A.; Neyenhuis, B.; Wang, D.; Quéméner, G.; Ospelkaus, S.; Bohn, J.; Ye, J.; Jin, D. Controlling the quantum stereodynamics of ultracold bimolecular reactions. Nat. Phys. 2011, 7, 502. [Google Scholar] [CrossRef]
- Julienne, P.S.; Hanna, T.M.; Idziaszek, Z. Universal ultracold collision rates for polar molecules of two alkali-metal atoms. Phys. Chem. Chem. Phys. 2011, 13, 19114–19124. [Google Scholar] [CrossRef] [PubMed]
- Quéméner, G.; Julienne, P.S. Ultracold molecules under control! Chem. Rev. 2012, 112, 4949–5011. [Google Scholar] [CrossRef]
- Zuchowski, P.; Hutson, J.M. Reactions of ultracold alkali-metal dimers. Phys. Rev. A 2010, 81, 060703(R). [Google Scholar] [CrossRef]
- Idziaszek, Z.; Julienne, P.S. Universal Rate Constants for Reactive Collisions of Ultracold Molecules. Phys. Rev. Lett. 2010, 104, 113202. [Google Scholar] [CrossRef]
- Kotochigova, S. Dispersion interactions and reactive collisions of ultracold polar molecules. New J. Phys. 2010, 12, 073041. [Google Scholar] [CrossRef]
- Quéméner, G.; Bohn, J.L.; Petrov, A.; Kotochigova, S. Universalities in ultracold reactions of alkali-metal polar molecules. Phys. Rev. A 2011, 84, 062703. [Google Scholar] [CrossRef]
- Mayle, M.; Ruzic, B.P.; Bohn, J.L. Statistical aspects of ultracold resonant scattering. Phys. Rev. A 2012, 85, 062712. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, D.C.; Liu, L.; Liu, Y.X.; Nan, J.; Zhao, B.; Pan, J.W. Observation of magnetically tunable Feshbach resonances in ultracold 23Na40K + 40K collisions. Science 2019, 363, 261–264. [Google Scholar] [CrossRef] [PubMed]
- Hudson, E.R.; Gilfoy, N.B.; Kotochigova, S.; Sage, J.M.; DeMille, D. Inelastic Collisions of Ultracold Heteronuclear Molecules in an Optical Trap. Phys. Rev. Lett. 2008, 100, 203201. [Google Scholar] [CrossRef]
- Deiglmayr, J.; Repp, M.; Wester, R.; Dulieu, O.; Weidemüller, M. Inelastic collisions of ultracold polar LiCs molecules with caesium atoms in an optical dipole trap. Phys. Chem. Chem. Phys. 2011, 13, 19101–19105. [Google Scholar] [CrossRef]
- De Marco, L.; Valtolina, G.; Matsuda, K.; Tobias, W.G.; Covey, J.P.; Ye, J. A degenerate Fermi gas of polar molecules. Science 2019. [Google Scholar] [CrossRef]
- Li, Z.; Gong, T.; Ji, Z.; Zhao, Y.; Xiao, L.; Jia, S. A dynamical process of optically trapped singlet ground state 85Rb133Cs molecules produced via short-range photoassociation. Phys. Chem. Chem. Phys. 2018, 20, 4893–4900. [Google Scholar] [CrossRef]
- Ye, X.; Guo, M.; González-Martínez, M.L.; Quéméner, G.; Wang, D. Collisions of ultracold 23Na87Rb molecules with controlled chemical reactivities. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef]
- Makrides, C.; Hazra, J.; Pradhan, G.B.; Petrov, A.; Kendrick, B.K.; González-Lezana, T.; Balakrishnan, N.; Kotochigova, S. Ultracold chemistry with alkali-metal–rare-earth molecules. Phys. Rev. A 2015, 91, 012708. [Google Scholar] [CrossRef]
- Croft, J.; Makrides, C.; Li, M.; Petrov, A.; Kendrick, B.; Balakrishnan, N.; Kotochigova, S. Universality and chaoticity in ultracold K + KRb chemical reactions. Nat. Commun. 2017, 8, 15897. [Google Scholar] [CrossRef]
- Frye, M.D.; Julienne, P.S.; Hutson, J.M. Cold atomic and molecular collisions: Approaching the universal loss regime. New J. Phys. 2015, 17, 045019. [Google Scholar] [CrossRef]
- Gao, B. Universal Model for Exoergic Bimolecular Reactions and Inelastic Processes. Phys. Rev. Lett. 2010, 105, 263203. [Google Scholar] [CrossRef]
- Żuchowski, P.S.; Kosicki, M.; Kodrycka, M.; Soldán, P. van der Waals coefficients for systems with ultracold polar alkali-metal molecules. Phys. Rev. A 2013, 87, 022706. [Google Scholar] [CrossRef]
- Julienne, P.S.; Mies, F.H. Collisions of ultracold trapped atoms. J. Opt. Soc. Am. B 1989, 6, 2257–2269. [Google Scholar] [CrossRef]
- Orzel, C.; Walhout, M.; Sterr, U.; Julienne, P.S.; Rolston, S.L. Spin polarization and quantum-statistical effects in ultracold ionizing collisions. Phys. Rev. A 1999, 59, 1926–1935. [Google Scholar] [CrossRef]
- Quéméner, G.; Honvault, P.; Launay, J.M.; Soldán, P.; Potter, D.E.; Hutson, J.M. Ultracold quantum dynamics: Spin-polarized K + K2 collisions with three identical bosons or fermions. Phys. Rev. A 2005, 71, 032722. [Google Scholar] [CrossRef]
- Stone, A.J. The Theory of Intermolecular Forces; Clarendon Press: London, UK, 1996. [Google Scholar]
- Derevianko, A.; Porsev, S.G.; Babb, J.F. Electric dipole polarizabilities at imaginary frequencies for hydrogen, the alkali–metal, alkaline–earth, and noble gas atoms. At. Data Nucl. Data Tables 2010, 96, 323–331. [Google Scholar] [CrossRef]
- Monkhorst, H.J. Calculation of properties with the coupled-cluster method. Int. J. Quantum Chem. 1997, 12, 421–432. [Google Scholar] [CrossRef]
- Dalgaard, E.; Monkhorst, H.J. Some aspects of the time-dependent coupled-cluster approach to dynamic response functions. Phys. Rev. A 1983, 28, 1217–1222. [Google Scholar] [CrossRef]
- Koch, H.; Jörgensen, P. Coupled cluster response functions. J. Chem. Phys. 1990, 93, 3333–3344. [Google Scholar] [CrossRef]
- Kobayashi, R.; Koch, H.; Jörgensen, P. Calculation of frequency-dependent polarizabilities using coupled-cluster response theory. Chem. Phys. Lett. 1994, 219, 30–35. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Harding, M.E.; Szalay, P.G. Computer Code CFOUR: A Program Package to Perform High-Level Quantum Chemical Calculations on Atoms and Molecules; University of Texas: Austin, TX, USA, 2011. [Google Scholar]
- Watts, J.D.; Gauss, J.; Bartlett, R.J. Coupled-cluster methods with noniterative triple excitations for restricted open-shell Hartree–Fock and other general single determinant reference functions. Energies and analytical gradients. J. Chem. Phys. 1993, 98, 8718. [Google Scholar] [CrossRef]
- Prascher, B.P.; Woon, D.E.; Peterson, K.A.; Dunning, T.H.; Wilson, A.K. Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg. Theor. Chem. Acc. 2011, 128, 69–82. [Google Scholar] [CrossRef]
- Lim, I.S.; Schwerdtfeger, P.; Metz, B.; Stoll, H. All-electron and relativistic pseudopotential studies for the group 1 element polarizabilities from K to element 119. J. Chem. Phys. 2005, 122, 104103. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Neyenhuis, B.; Yan, B.; Moses, S.A.; Covey, J.P.; Chotia, A.; Petrov, A.; Kotochigova, S.; Ye, J.; Jin, D.S. Anisotropic Polarizability of Ultracold Polar 40K87Rb Molecules. Phys. Rev. Lett. 2012, 109, 230403. [Google Scholar] [CrossRef]
- Gregory, P.D.; Blackmore, J.A.; Aldegunde, J.; Hutson, J.M.; Cornish, S.L. ac Stark effect in ultracold polar 87Rb133Cs molecules. Phys. Rev. A 2017, 96, 021402. [Google Scholar] [CrossRef]

| LiNa + Li | 2112 | NaLi + Na | 2241 | KLi + K | 5341 | RbLi + Rb | 6478 | CsLi + Cs | 9455 |
| LiK + Li | 3179 | NaK + Na | 3592 | KNa + K | 5698 | RbNa + Rb | 6896 | CsNa + Cs | 9879 |
| LiRb + Li | 3505 | NaRb + Na | 3948 | KRb + K | 6905 | RbK + Rb | 7696 | CsK + Cs | 11,237 |
| LiCs + Li | 4192 | NaCs + Na | 4631 | KCs + K | 8473 | RbCs + Rb | 9506 | CsRb + Cs | 11,414 |
| LiSr + Li | 3137 | ||||||||
| LiYb + Li | 3086 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, M.; Makrides, C.; Petrov, A.; Kotochigova, S. Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms 2019, 7, 36. https://doi.org/10.3390/atoms7010036
Li H, Li M, Makrides C, Petrov A, Kotochigova S. Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms. 2019; 7(1):36. https://doi.org/10.3390/atoms7010036
Chicago/Turabian StyleLi, Hui, Ming Li, Constantinos Makrides, Alexander Petrov, and Svetlana Kotochigova. 2019. "Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials" Atoms 7, no. 1: 36. https://doi.org/10.3390/atoms7010036
APA StyleLi, H., Li, M., Makrides, C., Petrov, A., & Kotochigova, S. (2019). Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms, 7(1), 36. https://doi.org/10.3390/atoms7010036




