On the Time Scales of Optical Variability of AGN and the Shape of Their Optical Emission Line Profiles
Abstract
:1. Introduction
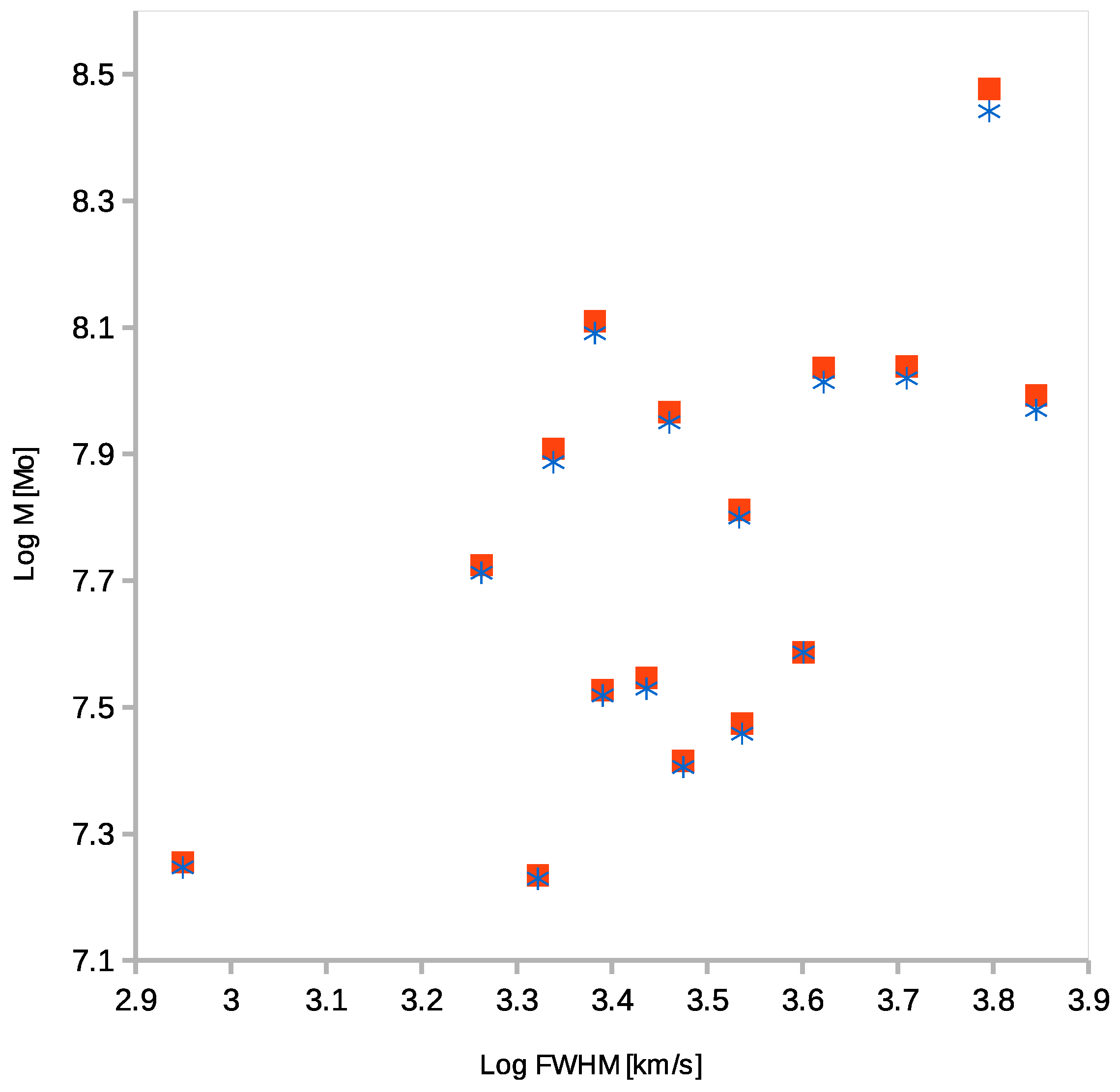
1.1. Variability Time Scales and Amplitudes
1.2. Periodic Variability of AGN
1.3. Supermassive Black Hole Binaries
1.4. Broad Emission Line Shape Connection with the Variability Time Scales
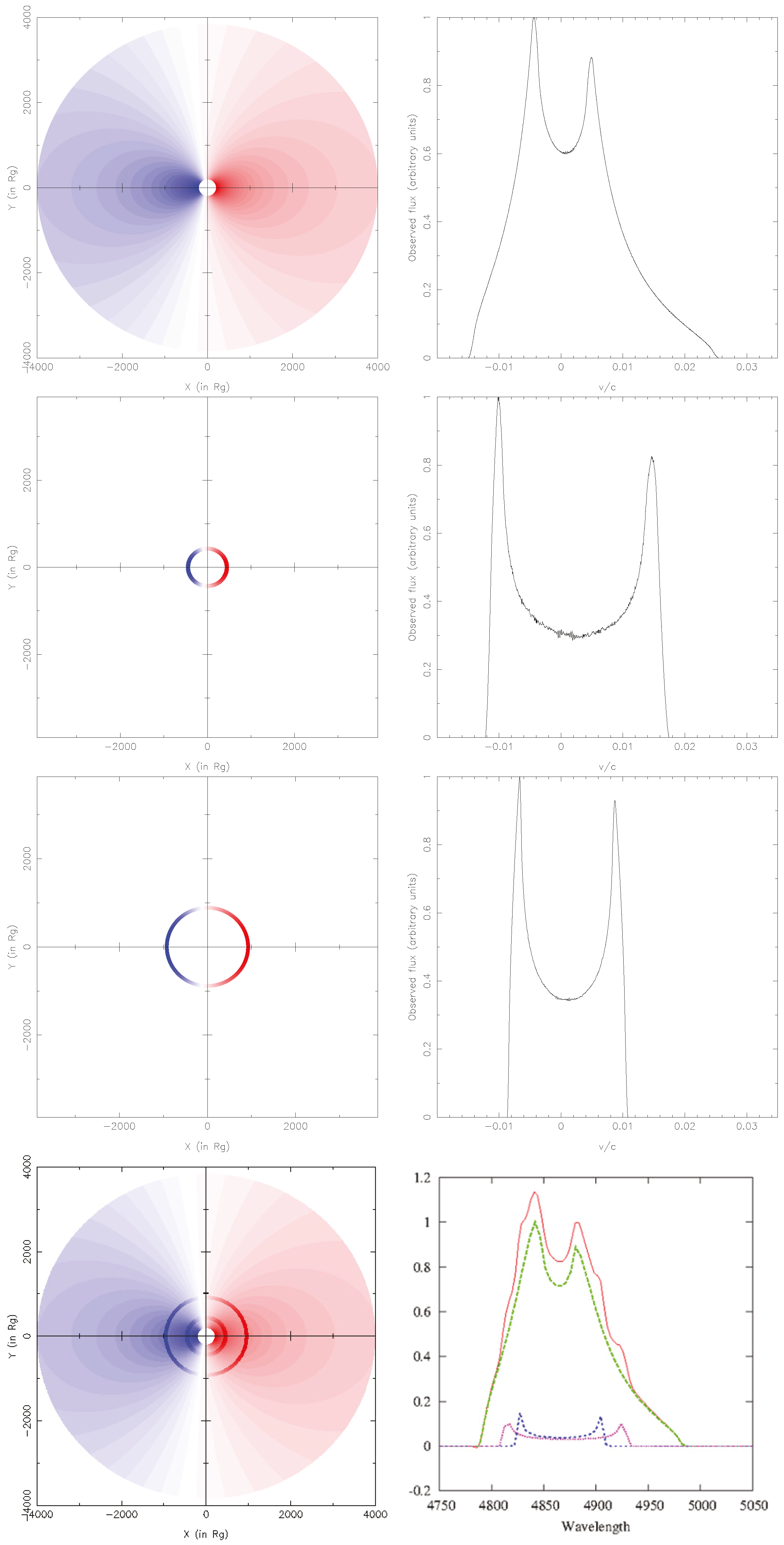
2. Method
Model of AD with Amplified Thin Ring Emission
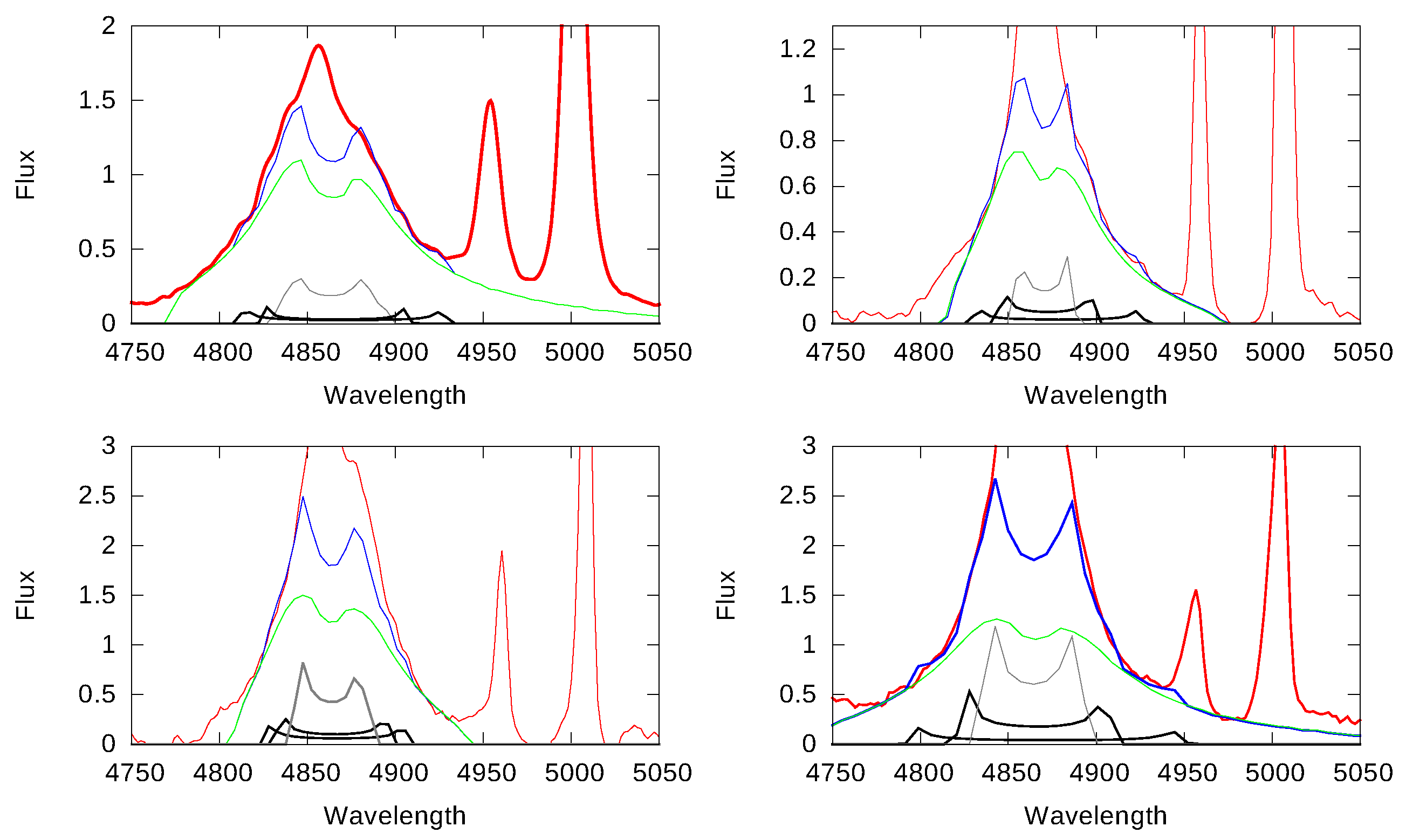
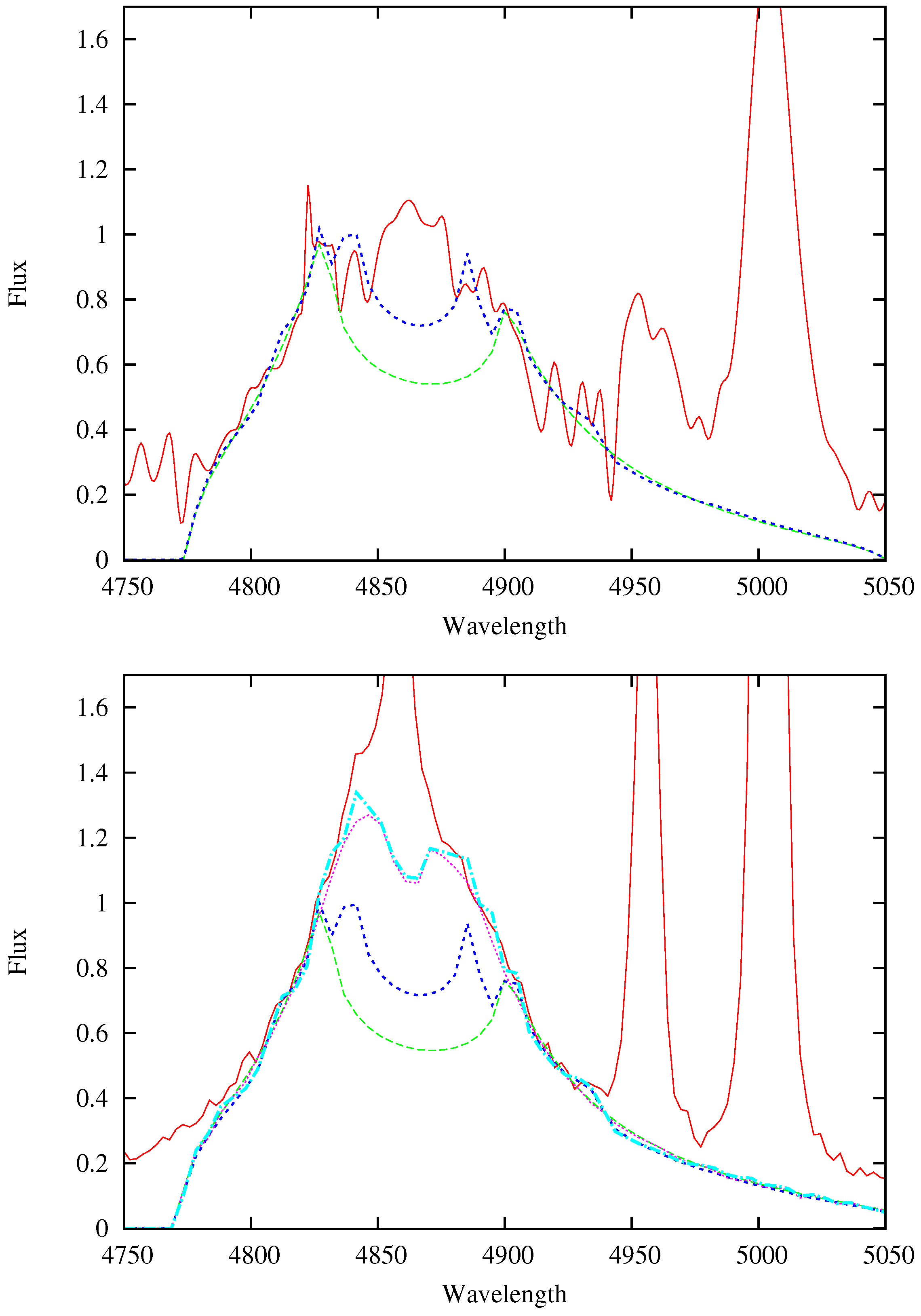
3. Results
4. Possible Interpretations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaskell, C.M.; Klimek, E.S. Variability of Active Galactic Nuclei from Optical to X-ray Regions. Astron. Astrophys. Trans. 2003, 22, 661–679. [Google Scholar] [CrossRef]
- Vaughan, S.; Uttley, P. Detecting X-ray QPOs in active galaxies. Adv. Space Res. 2006, 38, 1405–1408. [Google Scholar] [CrossRef]
- Vaughan, S.; Uttley, P.; Markowitz, A.G.; Huppenkothen, D.; Middleton, M.J.; Alston, W.N.; Scargle, J.D.; Farr, W.M. False periodicities in quasar time-domain surveys. Mon. Not. R. Astron. Soc. 2016, 461, 3145–3152. [Google Scholar] [CrossRef]
- Bhatta, G.; Zola, S.; Ostrowski, M.; Winiarski, M.; Ogłoza, W.; Dróżdż, M.; Siwak, M.; Liakos, A.; Kozieł-Wierzbowska, D.; Gazeas, K.; et al. Detection of Possible Quasi-periodic Oscillations in the Long-term Optical Light Curve of the BL Lac Object OJ 287. Astrophys. J. 2016, 832, 47. [Google Scholar] [CrossRef]
- Sillanpaa, A.; Haarala, S.; Valtonen, M.J.; Sundelius, B.; Byrd, G.G. OJ 287-Binary pair of supermassive black holes. Provided by the SAO/NASA Astrophysics Data System. Astrophys. J. 1988, 325, 628–634. [Google Scholar] [CrossRef]
- Oknyanskij, V.; Lyuty, V. Optical Variability of NGC 4151 During 100 Years. Peremennye Zvezdy Prilozhenie 2007, 28, 7. [Google Scholar]
- Bon, E.; Jovanović, P.; Marziani, P.; Shapovalova, A.I.; Bon, N.; Jovanović, V.B.; Borka, D.; Sulentic, J.; Popović, L.Č. The First Spectroscopically Resolved Sub-parsec Orbit of a Supermassive Binary Black Hole. Astrophys. J. 2012, 759, 118. [Google Scholar] [CrossRef]
- Guo, D.-F.; Hu, S.-M.; Tao, J.; Yin, H.X.; Chen, X.; Pan, H.J. Optical monitoring of the Seyfert galaxy NGC 4151 and possible periodicities in its historical light curve. Res. Astron. Astrophys. 2014, 14, 923. [Google Scholar] [CrossRef]
- Bon, E.; Zucker, S.; Netzer, H.; Marziani, P.; Bon, N.; Jovanović, P.; Shapovalova, A.I.; Komossa, S.; Gaskell, C.M.; Popović, L.Č.; et al. Evidence for Periodicity in 43 year-long Monitoring of NGC 5548. Astrophys. J. Suppl. 2016, 225, 29. [Google Scholar] [CrossRef]
- Li, Y.R.; Wang, J.M.; Ho, L.C.; Lu, K.-X.; Qiu, J.; Du, P.; Hu, C.; Huang, Y.-K.; Zhang, Z.-X.; Wang, K.; et al. Spectroscopic Indication of a Centi-parsec Supermassive Black Hole Binary in the Galactic Center of NGC 5548. Astrophys. J. 2016, 822, 4. [Google Scholar] [CrossRef]
- Li, Y.-R.; Wang, J.-M.; Zhang, Z.-X.; Wang, K.; Huang, Y.-K.; Lu, K.-X.; Hu, C.; Du, P.; Ho, L.C.; Bai, J.-M.; et al. A Possible 20-Year Periodicity in Long-term Variations of the Nearby Radio-Quiet Active Galactic Nucleus Ark 120. arXiv, 2017; arXiv:1705.07781. [Google Scholar]
- Yuan, Y.-H.; Fan, J.H.; Tao, J.; Qian, B.-C.; Costantin, D.; Xiao, H.-B.; Pei, Z.-Y.; Lin, C. Optical monitoring of BL Lac object S5 0716+714 and FSRQ 3C 273 from 2000 to 2014. Astron. Astrophys. 2017, 605, A43. [Google Scholar] [CrossRef]
- Babadzhanyants, M.K.; Belokon, E.T. New evidence of the reality of a 13-year period in the optical variability of the quasar 3C 273 and its correlation with observed parameters of the parsec-scale radio jet. Astron. Rep. 1993, 37, 127. [Google Scholar]
- Artymowicz, P.; Lubow, S.H. Dynamics of binary-disk interaction. 1: Resonances and disk gap sizes. Astrophys. J. 1994, 421, 651–667. [Google Scholar] [CrossRef]
- Roedig, C.; Sesana, A.; Dotti, M.; Cuadra, J.; Amaro-Seoane, P.; Haardt, F. Evolution of binary black holes in self gravitating discs. Dissecting the torques. Astron. Astrophys. 2012, 545, A127. [Google Scholar] [CrossRef]
- D’Orazio, D.J.; Haiman, Z.; MacFadyen, A. Accretion into the central cavity of a circumbinary disc. Mon. Not. R. Astron. Soc. 2013, 436, 2997–3020. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Milosavljević, M. An Eccentric Circumbinary Accretion Disk and the Detection of Binary Massive Black Holes. Astrophys. J. 2008, 672, 83. [Google Scholar] [CrossRef]
- Netzer, H. The Physics and Evolution of Active Galactic Nuclei; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Marziani, P.; Bon, E.; Grieco, A.; Bon, N.; Dultzin, D.; Del Olmo, A.; D’Onofrio, M. Optical variability patterns of radio-quiet and radio-loud quasars. In New Frontiers in Black Hole Astrophysics, Proceedings of the International Astronomical Union, IAU Symposium, Baton Rouge, LA, USA, 16 October 2017; Cambridge University Press: Ljubljana, Slovenia, 2017; Volume 324, p. 243. [Google Scholar] [CrossRef]
- MacLeod, C.L.; Ross, N.P.; Lawrence, A.; Goad, M.; Horne, K.; Burgett, W.; Chambers, K.C.; Flewelling, H.; Hodapp, K.; Kaiser, N.; et al. A systematic search for changing-look quasars in SDSS. Mon. Not. R. Astron. Soc. 2016, 457, 389–404. [Google Scholar] [CrossRef]
- Oknyansky, V.L.; Gaskell, C.M.; Huseynov, N.A.; Lipunov, V.M.; Shatsky, N.I.; Tsygankov, S.S.; Gorbovskoy, E.S.; Mikailov, K.M.; Tatarnikov, A.M.; Buckley, D.A.H.; et al. The curtain remains open: NGC 2617 continues in a high state. Mon. Not. R. Astron. Soc. 2017, 467, 1496–1504. [Google Scholar] [CrossRef]
- Oknyansky, V.L.; Malanchev, K.L.; Gaskell, C.M. Changing-look Narrow-Line Seyfert 1s? In Proceedings of the POS: Revisiting Narrow-Line Seyfert 1 Galaxies and Their Place in the Universe, Padova, Italy, 9–13 April 2018. [Google Scholar]
- Bon, N.; Bon, E.; Marziani, P. Exploring possible relations between optical variability time scales and broad emission line shapes in AGN. Front. Astron. Space Sci. 2018, 5, 3. [Google Scholar] [CrossRef]
- Pei, L.; Fausnaugh, M.M.; Barth, A.J.; Peterson, B.M.; Bentz, M.C.; De Rosa, G.; Denney, K.D.; Goad, M.R.; Kochanek, C.S.; Korista, K.T.; et al. Space Telescope and Optical Reverberation Mapping Project. V. Optical Spectroscopic Campaign and Emission-line Analysis for NGC 5548. Astrophys. J. 2017, 837, 131. [Google Scholar] [CrossRef]
- Komossa, S.; Burwitz, V.; Hasinger, G.; Predehl, P.K.J.S.; Kaastra, J.S.; Ikebe, Y. Discovery of a Binary Active Galactic Nucleus in the Ultraluminous Infrared Galaxy NGC 6240 Using Chandra. Astrophys. J. Lett. 2003, 582, L15. [Google Scholar] [CrossRef]
- Komossa, S. Observational evidence for binary black holes and active double nuclei. Mem. Soc. Astron. Ital. 2006, 77, 733. [Google Scholar]
- Bogdanović, T.S.; Britton, D.; Sigurdsson, S.; Eracleous, M. Modeling of Emission Signatures of Massive Black Hole Binaries. I. Methods. Astrophys. J. Suppl. 2008, 174, 455. [Google Scholar] [CrossRef]
- Bogdanović, T.; Eracleous, M.; Sigurdsson, S. Emission lines as a tool in search for supermassive black hole binaries and recoiling black holes. New Astron. Rev. 2009, 53, 113–120. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Glikman, E.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Larson, S.; Christensen, E. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 2015, 518, 74. [Google Scholar] [CrossRef] [PubMed]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Glikman, E.; Larson, S.; Christensen, E. A systematic search for close supermassive black hole binaries in the Catalina Real-time Transient Survey. Mon. Not. R. Astron. Soc. 2015, 453, 1562–1576. [Google Scholar] [CrossRef]
- Popović, L.Č. Super-massive binary black holes and emission lines in active galactic nuclei. New Astron. Rev. 2012, 56, 74–91. [Google Scholar] [CrossRef]
- Komossa, S. Tidal disruption of stars by supermassive black holes: Status of observations. J. High Energy Astrophys. 2015, 7, 148–157. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Bon, E.; Marziani, P.; Bon, N. Periodic optical variability of AGN. New Front. Black Hole Astrophys. 2017, 324, 176–179. [Google Scholar] [CrossRef]
- Charisi, M.; Bartos, I.; Haiman, Z.; Goad, M.; Horne, K.; Burgett, W.; Chambers, K.C.; Flewelling, H.; Hodapp, K.; Kaiser, N.; et al. A population of short-period variable quasars from PTF as supermassive black hole binary candidates. Mon. Not. R. Astron. Soc. 2016, 463, 2145–2171. [Google Scholar] [CrossRef]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307. [Google Scholar] [CrossRef]
- Iwasawa, K.; Miniutti, G.; Fabian, A.C. Flux and energy modulation of redshifted iron emission in NGC 3516: Implications for the black hole mass. Mon. Not. R. Astron. Soc. 2004, 355, 1073–1079. [Google Scholar] [CrossRef]
- Bon, N.; Bon, E.; Marziani, P.; Jovanović, P. Gravitational redshift of emission lines in the AGN spectra. Astrophys. Space Sci. 2015, 360, 41. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. 2015, 813, L41. [Google Scholar] [CrossRef]
- Kun, E.; Karouzos, M.; Gabányi, K.É.; Britzen, S.; Kurtanidze, O.M.; Gergely, L.Á. Flaring radio lanterns along the ridge line: Long-term oscillatory motion in the jet of S5 1803+784. Mon. Not. R. Astron. Soc. 2018, 478, 359–370. [Google Scholar] [CrossRef]
- Kun, E.; Frey, S.; Gabányi, K.É.; Britzen, S.; Cseh, D.; Gergely, L.Á. Constraining the parameters of the putative supermassive binary black hole in PG 1302–102 from its radio structure. Mon. Not. R. Astron. Soc. 2015, 454, 1290–1296. [Google Scholar] [CrossRef]
- Kun, E.; Gabányi, K.É.; Karouzos, M.; Britzen, S.; Gergely, L.Á. A spinning supermassive black hole binary model consistent with VLBI observations of the S5 1928 + 738 jet. Mon. Not. R. Astron. Soc. 2014, 445, 1370–1382. [Google Scholar] [CrossRef]
- Britzen, S.; Roland, J.; Laskar, J.; Kokkotas, K.; Campbell, R.M.; Witzel, A. On the origin of compact radio sources-The binary black hole model applied to the gamma-bright quasar PKS 0420-014. Astron. Astrophys. 2001, 374, 784–799. [Google Scholar] [CrossRef]
- Farris, B.D.; Duffell, P.; MacFadyen, A.I.; Haiman, Z. Characteristic signatures in the thermal emission from accreting binary black holes. Mon. Not. R. Astron. Soc. 2015, 446, L36–L40. [Google Scholar] [CrossRef]
- Cuadra, J.; Armitage, P.J.; Alexander, R.D.; Begelman, M.C. Massive black hole binary mergers within subparsec scale gas discs. Mon. Not. R. Astron. Soc. 2009, 393, 1423–1432. [Google Scholar] [CrossRef]
- Miranda, R.; Muñoz, D.J.; Lai, D. Viscous hydrodynamics simulations of circumbinary accretion discs: Variability, quasi-steady state and angular momentum transfer. Mon. Not. R. Astron. Soc. 2017, 466, 1170–1191. [Google Scholar] [CrossRef]
- Hayasaki, K.; Saito, H.; Mineshige, S. Binary Black Hole Accretion Flows From a Misaligned Circumbinary Disk. Aesthetic. Surg. J. 2013, 65, 86. [Google Scholar] [CrossRef]
- Jovanović, P.; Popović, L.Č.; Stalevski, M.; Shapovalova, A.I. Variability of the Hβ Line Profiles as an Indicator of Orbiting Bright Spots in Accretion Disks of Quasars: A Case Study of 3C 390.3. Astrophys. J. 2010, 718, 168. [Google Scholar] [CrossRef]
- Gezari, S.; Halpern, J.P.; Eracleous, M. Long-Term Profile Variability of Double-peaked Emission Lines in Active Galactic Nuclei. Astrophys. J. Suppl. 2007, 169, 167. [Google Scholar] [CrossRef]
- Newman, J.A.; Eracleous, M.; Filippenko, A.V.; Halpern, J.P. Measurement of an Active Galactic Nucleus Central Mass on Centiparsec Scales: Results of Long-Term Optical Monitoring of Arp 102B. Astrophys. J. 1997, 485, 570. [Google Scholar] [CrossRef]
- Chen, K.; Halpern, J.P. Structure of line-emitting accretion disks in active galactic nuclei—ARP 102B. Astrophys. J. 1989, 344, 115–124. [Google Scholar] [CrossRef]
- Chen, K.; Halpern, J.P.; Filippenko, A.V. Kinematic evidence for a relativistic Keplerian disk—ARP 102B. Astrophys. J. 1989, 339, 742–751. [Google Scholar] [CrossRef]
- Eracleous, M.; Halpern, J.P. Doubled-peaked emission lines in active galactic nuclei. Astrophys. J. Suppl. 1994, 90, 1–30. [Google Scholar] [CrossRef]
- Gavrilović, N.; Bon, E.; Popović, L.Č.; Prugniel, P. Determination of Accretion Disc Parameters in the Case of Five AGN with Double-peaked Lines. AIP Conf. Proc. 2007, 938, 94–97. [Google Scholar] [CrossRef]
- Jovanović, P.; Popović, L.Č. Observational effects of strong gravity in vicinity of supermassive black holes. Fortschritte der Physik 2008, 56, 456–461. [Google Scholar] [CrossRef]
- Bon, E.; Popović, L.Č.; Ilić, D.; Mediavilla, E. Stratification in the broad line region of AGN: The two-component model. New Astron. Rev. 2006, 50, 716–719. [Google Scholar] [CrossRef]
- Bon, E. The Disk Emission in Single Peaked Lines for 12 AGNs. Serb. Astron. J. 2008, 177, 9–13. [Google Scholar] [CrossRef]
- Bon, E.; Popović, L.Č.; Gavrilović, N.; La Mura, G.; Mediavilla, E. Contribution of a disc component to single-peaked broad lines of active galactic nuclei. Mon. Not. R. Astron. Soc. 2009, 400, 924–936. [Google Scholar] [CrossRef]
- Bon, E.; Gavrilović, N.; La Mura, G.; Popović, L.Č. Complex broad emission line profiles of AGN - Geometry of the broad line region. New Astron. Rev. 2009, 53, 121–127. [Google Scholar] [CrossRef]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Bertone, G.; Bon, E.; Blas, D.; Brito, R.; et al. Black holes, gravitational waves and fundamental physics: A roadmap. arXiv, 2018; arXiv:1806.05195. [Google Scholar]
- Kaspi, S.; Smith, P.S.; Netzer, H.; Maoz, D.; Jannuzi, B.T.; Giveon, U. Reverberation Measurements for 17 Quasars and the Size-Mass-Luminosity Relations in Active Galactic Nuclei. Astrophys. J. 2000, 533, 631. [Google Scholar] [CrossRef]
- Fanton, C.; Calvani, M.; de Felice, F.; Cadez, A. Detecting Accretion Disks in Active Galactic Nuclei. Publ. Astron. Soc. Jpn. 1997, 49, 159–169. [Google Scholar] [CrossRef]
- Čadež, A.; Fanton, C.; Calvani, M. Line emission from accretion discs around black holes: The analytic approach. New Astron. 1998, 3, 647–654. [Google Scholar] [CrossRef]
- Popović, L.Č.; Mediavilla, E.; Bon, E.; Ilić, D. Contribution of the disk emission to the broad emission lines in AGNs: Two-component model. Astron. Astrophys. 2004, 423, 909–918. [Google Scholar] [CrossRef]
- Popović, L.Č.; Mediavilla, E.G.; Bon, E.; Stanić, N.; Kubičela, A. The Line Emission Region in III Zw 2: Kinematics and Variability. Astrophys. J. 2003, 599, 185. [Google Scholar] [CrossRef]
- Strateva, I.V.; Strauss, M.A.; Hao, L.; Schlegel, D.J.; Hall, P.B.; Gunn, J.E.; Li, L.-X.; Ivezić, Ž.; Richards, G.T.; Zakamska, N.L. Double-peaked Low-Ionization Emission Lines in Active Galactic Nuclei. Astron. J. 2003, 126, 1720. [Google Scholar] [CrossRef]
- Jovanović, P. The broad Fe Kα line and supermassive black holes. New Astron. Rev. 2012, 56, 37–48. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Zamanov, R.; Calvani, M.; Dultzin-Hacyan, D.; Bachev, R.; Zwitter, T. An Optical Spectroscopic Atlas of Low-Redshift Active Galactic Nuclei. Astrophys. J. Suppl. 2003, 145, 199. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Wiita, P.J. Variable emission lines as evidence of spiral shocks in accretion disks around active galactic nuclei. Astrophys. J. 1994, 434, 518–522. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Czerny, B.; Hryniewicz, K. The origin of the broad line region in active galactic nuclei. Astron. Astrophys. 2011, 525, L8. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Kocsis, B.; Lyra, W.; Winter, L.M. Intermediate-mass black holes in AGN discs - II. Model predictions and observational constraints. Mon. Not. R. Astron. Soc. 2014, 441, 900–909. [Google Scholar] [CrossRef]
- Lin, D.N.C. Star/Disk Interaction in the Nuclei of Active Galaxies. In Emission Lines in Active Galaxies: New Methods and Techniques, Proceedings of the IAU Colloquium 159: Emission Lines in Active Galaxies: New Methods and Techniques, Shanghai, China, 17–20 June 1996; Astronomical Society of the Pacific: San Francisco, CA, USA, 1997; Volume 113, p. 64. [Google Scholar]
- Lin, D.N.C.; Papaloizou, J.C.B. Theory of Accretion Disks II: Application to Observed Systems. Annu. Rev. Astron. Astrophys. 1996, 34, 703–747. [Google Scholar] [CrossRef]
- McKernan, B.; Ford, K.E.S.; Kocsis, B.; Haiman, Z. Ripple effects and oscillations in the broad Fe Kα line as a probe of massive black hole mergers. Mon. Not. R. Astron. Soc. 2013, 432, 1468–1482. [Google Scholar] [CrossRef]
| 1. | |
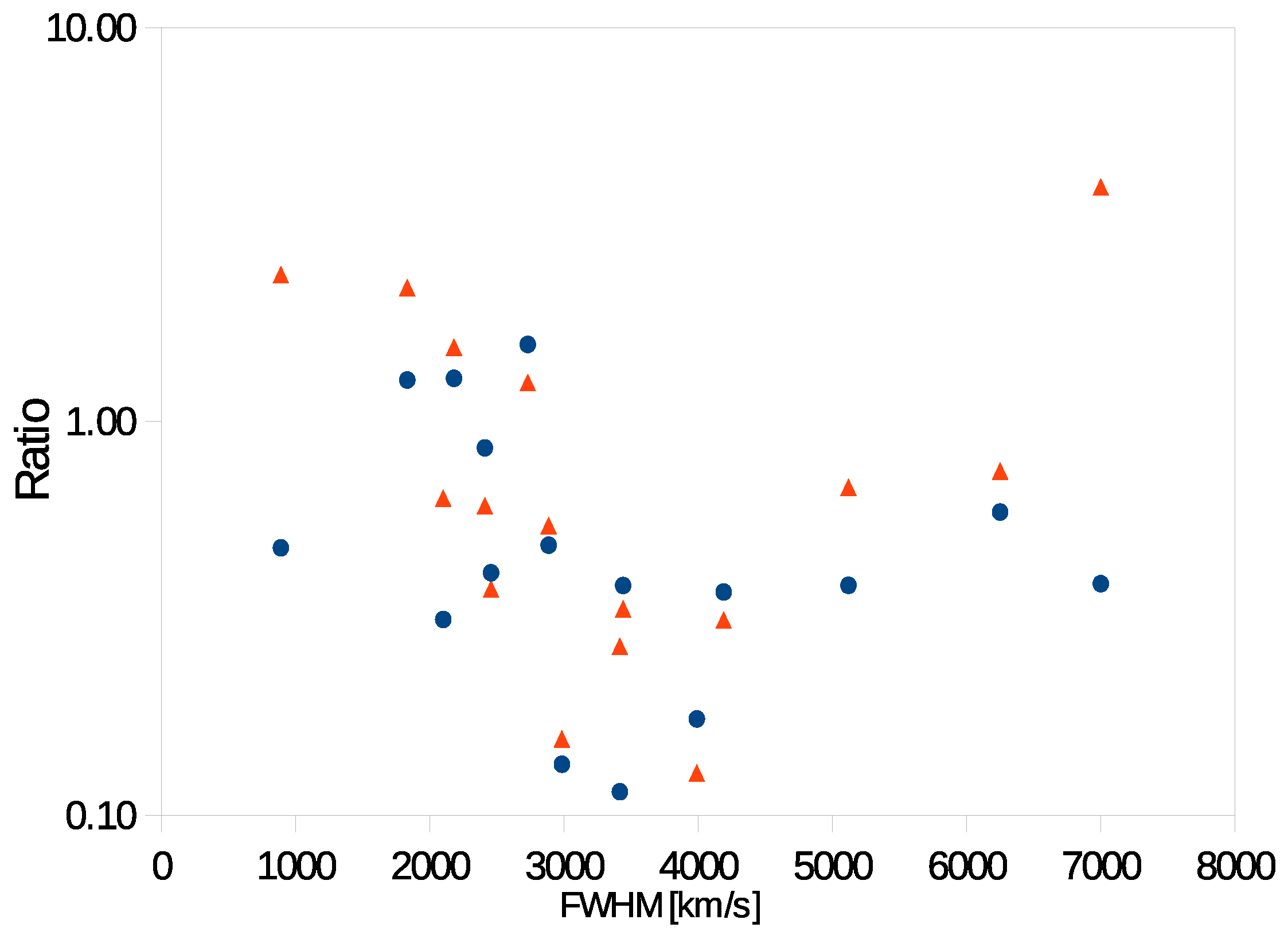
| 2. | This outer contribution would correspond to much longer period that we could not be able to detect with such short monitoring intervals of several years, in case it could be connected to any periodicity. These distant radii are probably excited due to reverberation processes. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bon, E.; Marziani, P.; Jovanović, P.; Bon, N. On the Time Scales of Optical Variability of AGN and the Shape of Their Optical Emission Line Profiles. Atoms 2019, 7, 26. https://doi.org/10.3390/atoms7010026
Bon E, Marziani P, Jovanović P, Bon N. On the Time Scales of Optical Variability of AGN and the Shape of Their Optical Emission Line Profiles. Atoms. 2019; 7(1):26. https://doi.org/10.3390/atoms7010026
Chicago/Turabian StyleBon, Edi, Paola Marziani, Predrag Jovanović, and Nataša Bon. 2019. "On the Time Scales of Optical Variability of AGN and the Shape of Their Optical Emission Line Profiles" Atoms 7, no. 1: 26. https://doi.org/10.3390/atoms7010026
APA StyleBon, E., Marziani, P., Jovanović, P., & Bon, N. (2019). On the Time Scales of Optical Variability of AGN and the Shape of Their Optical Emission Line Profiles. Atoms, 7(1), 26. https://doi.org/10.3390/atoms7010026





