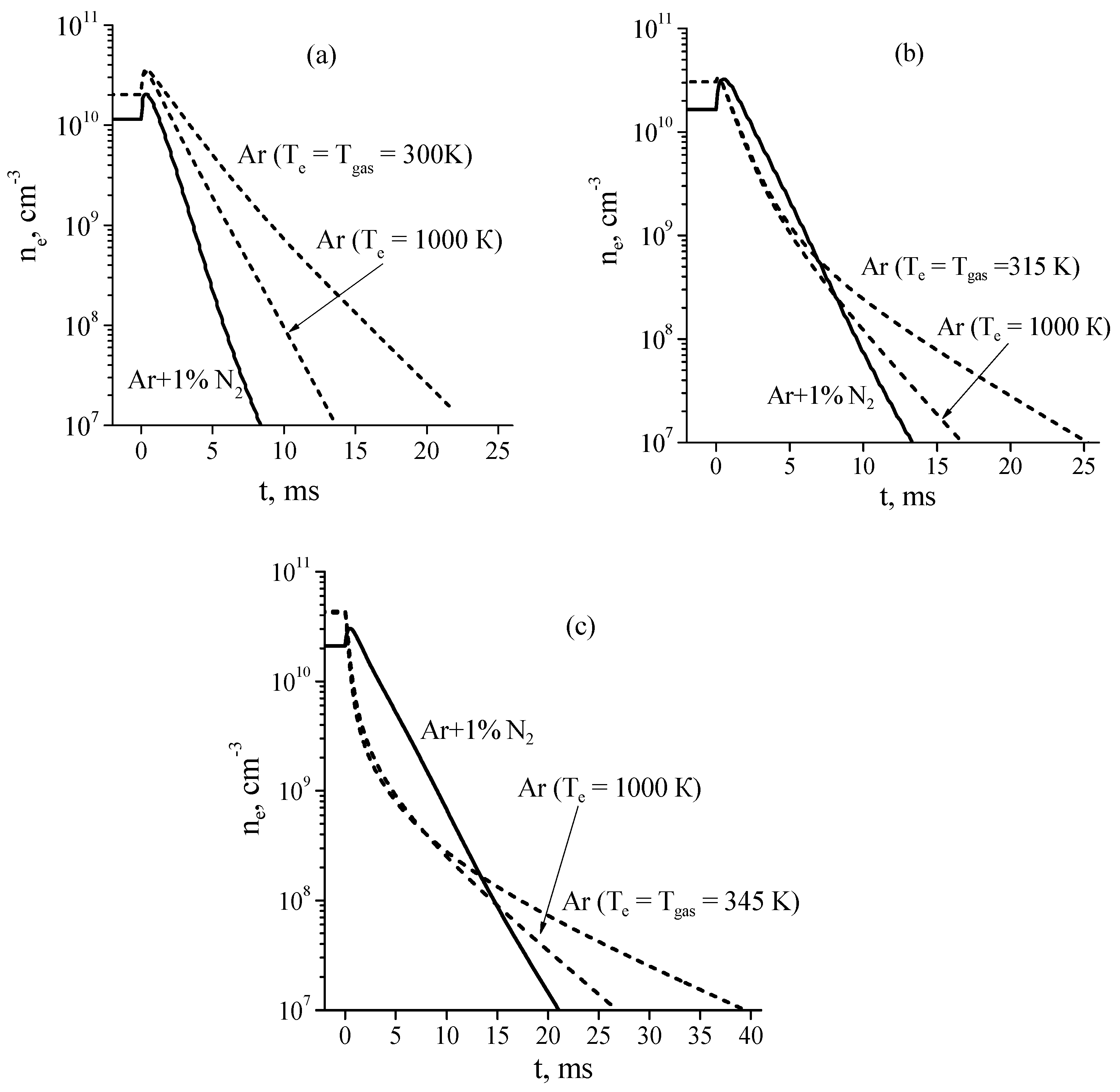2. Influence of N2 Admixture on the Current–Voltage Characteristic of a Diffuse Glow Discharge in Ar
In glow discharges in pure rare gases the main ionization process is stepwise ionization from the lower metastable states (except for the case of very low pressures and discharge currents). The effect of molecular admixture on discharge characteristics depends, in particular, on the ratio of the ionization energy of the admixture molecules and the energy of the lower metastable state of rare gas atoms. If the ionization energy of molecules is lower than the energy of atoms, then a small admixture of a molecular gas can lead to a reduction in both the breakdown voltage and the discharge operating voltage. Such a situation occurs in discharges in He and Ne (see, e.g., [
28,
29,
30] and references therein), because the energy of the lower metastable states of He* (19.8 eV) and Ne* (16.6 eV) is higher than the ionization energy of any molecular admixture. The effect of discharge voltage and breakdown voltage reduction is partially due to the low ionization energy of molecules, but is mainly caused by the processes of the Penning ionization (He* + M → He + M+ + e, Ne* + M → Ne + M+ + e). If the percentage of admixture is relatively high, the situation is more complicated. On the one hand, the admixture can appreciably change the electron energy balance in the plasma due to losses of the electron energy going to the excitation of vibrational and lower electronic levels of molecules. This effect leads to an increase in the voltage required to sustain the discharge. On the other hand, as the admixture concentration increases, a new ionization mechanism can occur (related directly to molecules), which may lead to a reduction in the discharge voltage. In general, the resulting change in the discharge characteristics depends on the experimental conditions: the sort of rare gas, the percentage of admixture, the sort of molecular gas and the gas pressure. This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn.
If the rare gas is argon and the molecular admixture is nitrogen, the Penning ionization mechanism is absent, since the energy of the lower metastable level of Ar atom (11.6 eV) is lower than the ionization energy of nitrogen molecules (15.58 eV). The ionization energy of Ar atoms (15.76 eV) is close to the ionization energy of nitrogen molecules, therefore nitrogen is not an easily ionized additive. Cross sections for the excitation of vibrational levels of N
2 molecules by electron impact are rather high in the energy range 2–3.5 eV (i.e., at energies below the energy of the lower argon metastable state), so in Ar:N
2 discharge plasma the electron energy losses due to excitation of vibrational levels can be significant. Moreover, in Ar:N
2 plasma metastable states of Ar atoms are effectively quenched in collisions with N
2 molecules [
31]
In addition, it is also well known that, for the same conditions (discharge tube geometry, gas pressure, and discharge current) the electric field in the positive column (or the discharge voltage) required to sustain a dc diffuse glow discharge in pure nitrogen is much higher than that in pure argon [
32].
Given the above arguments, one would expect that the addition of nitrogen would lead to an increase in the electric field in the positive column of the dc discharge in argon. Indeed, this is exactly what happens at relatively low gas pressures (
P~1–2 Torr for a tube radius of
R~1–2 cm; see, for example, [
14,
33]). This is illustrated in
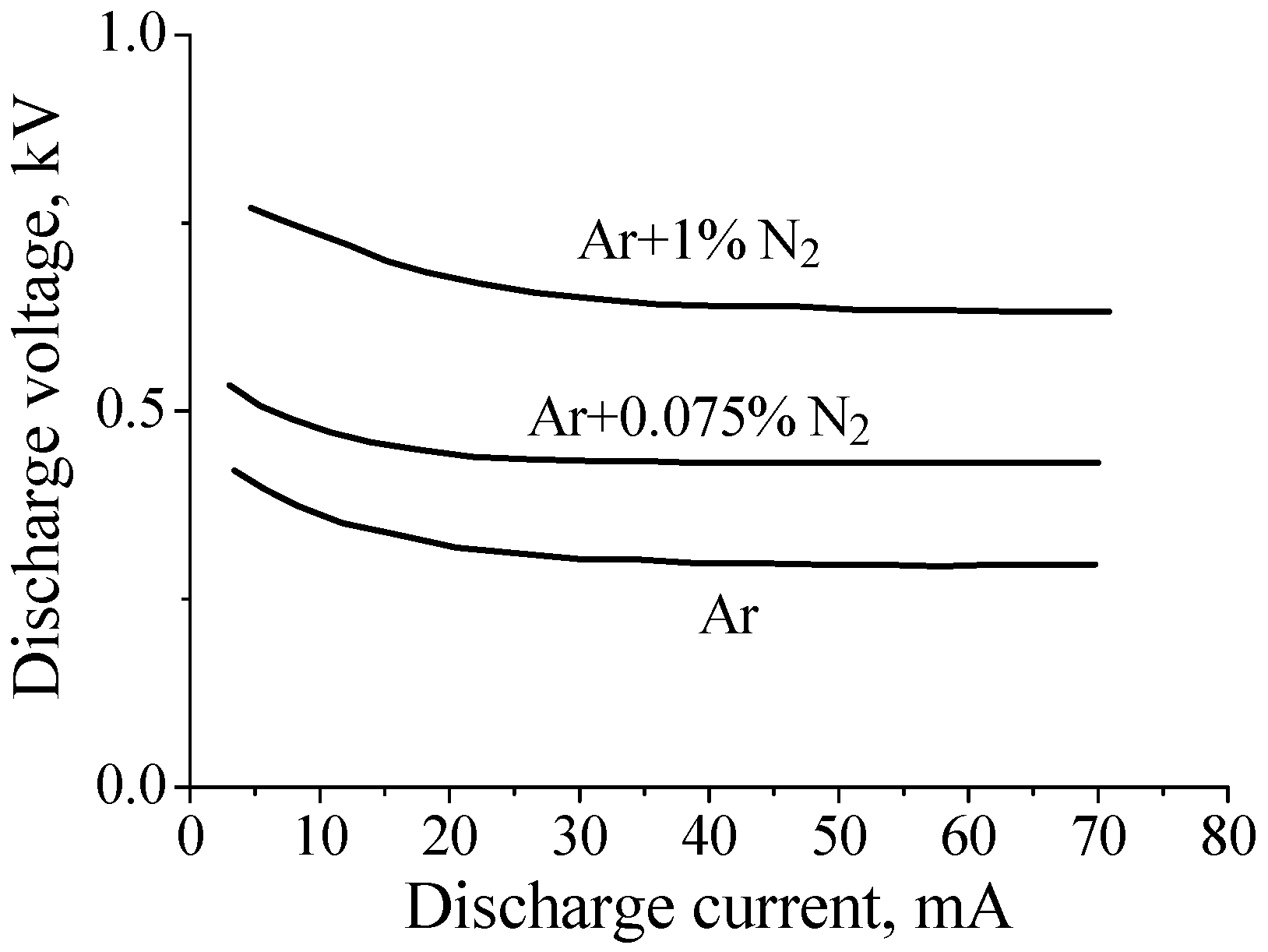
Figure 1, which shows current–voltage characteristic of discharges in pure argon and in Ar + 0.075%N
2 and Ar + 1%N
2 gas mixtures at gas pressure
P = 2 Torr (
R = 1.4 cm, interelectrode distance ≈ 75 cm). One can see that the discharge voltage increases with a factor 2 when 1% of nitrogen is added to argon.
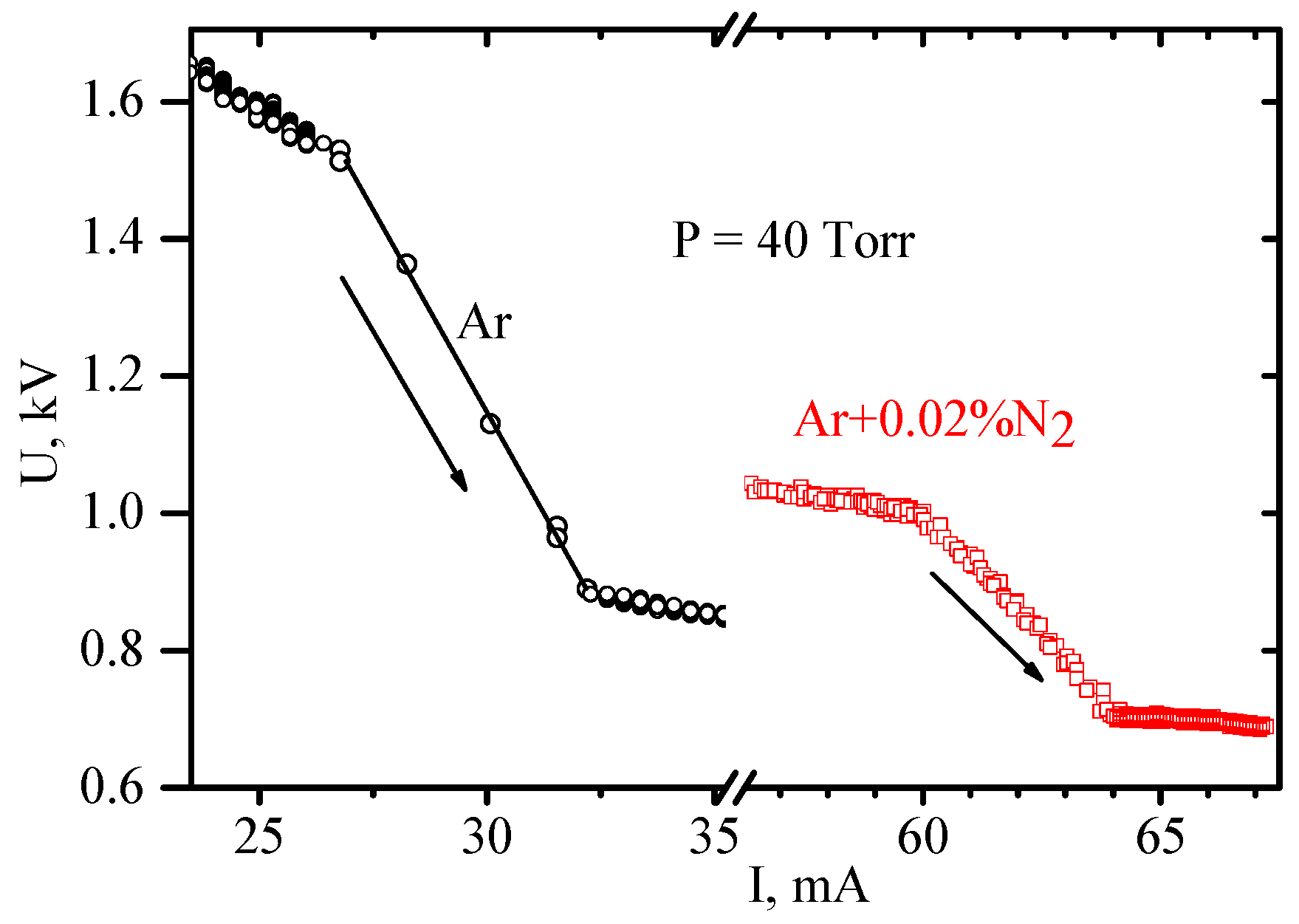
However, at intermediate pressures (tens of Torr), the situation changes dramatically. It was observed that at intermediate pressures a small additive of nitrogen to argon resulted in a noticeable decrease in the discharge voltage of a diffuse dc discharge. This effect was discovered in experiments with partially constricted discharges in Ar:N
2 mixtures [
15,
16,
34].
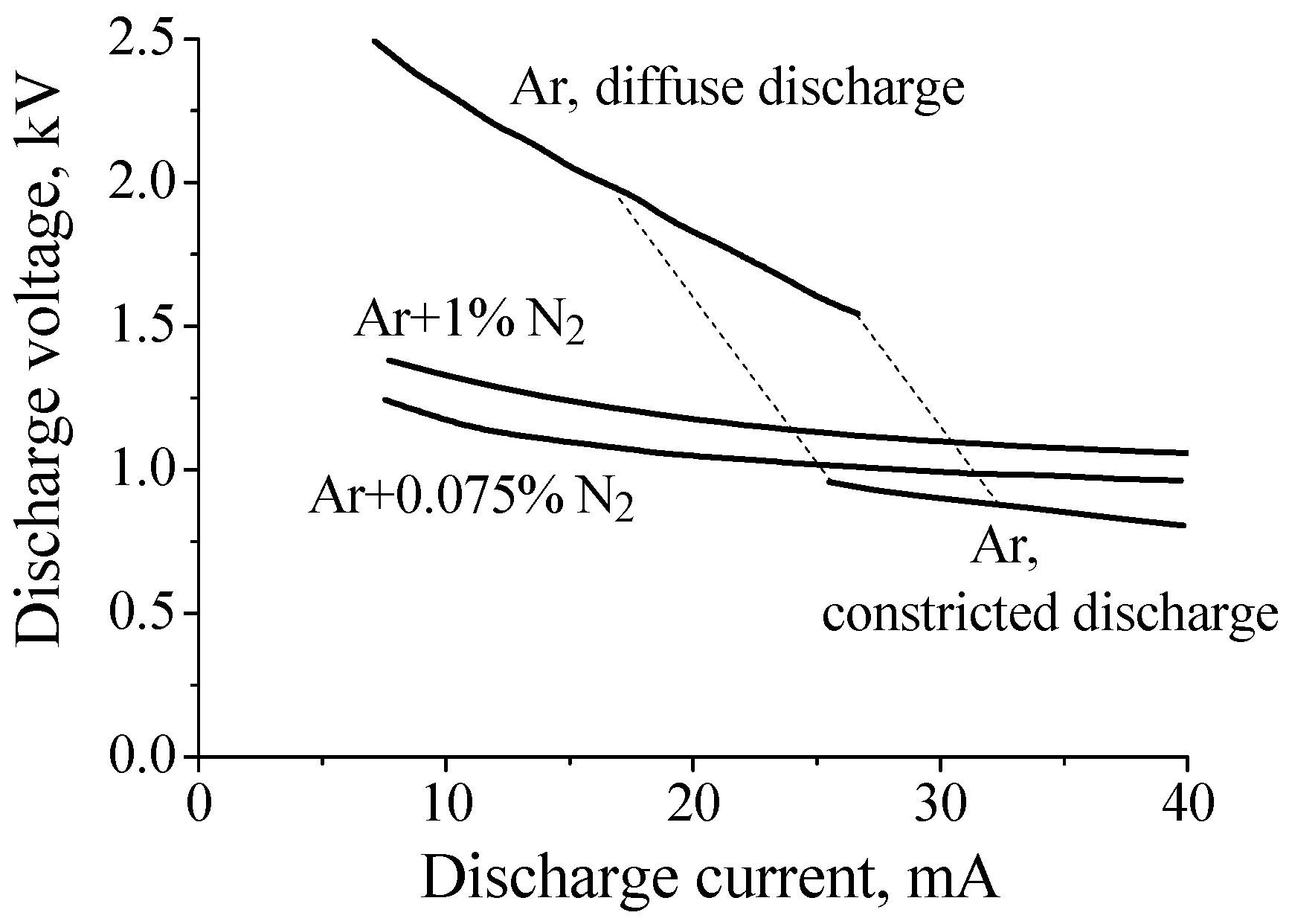
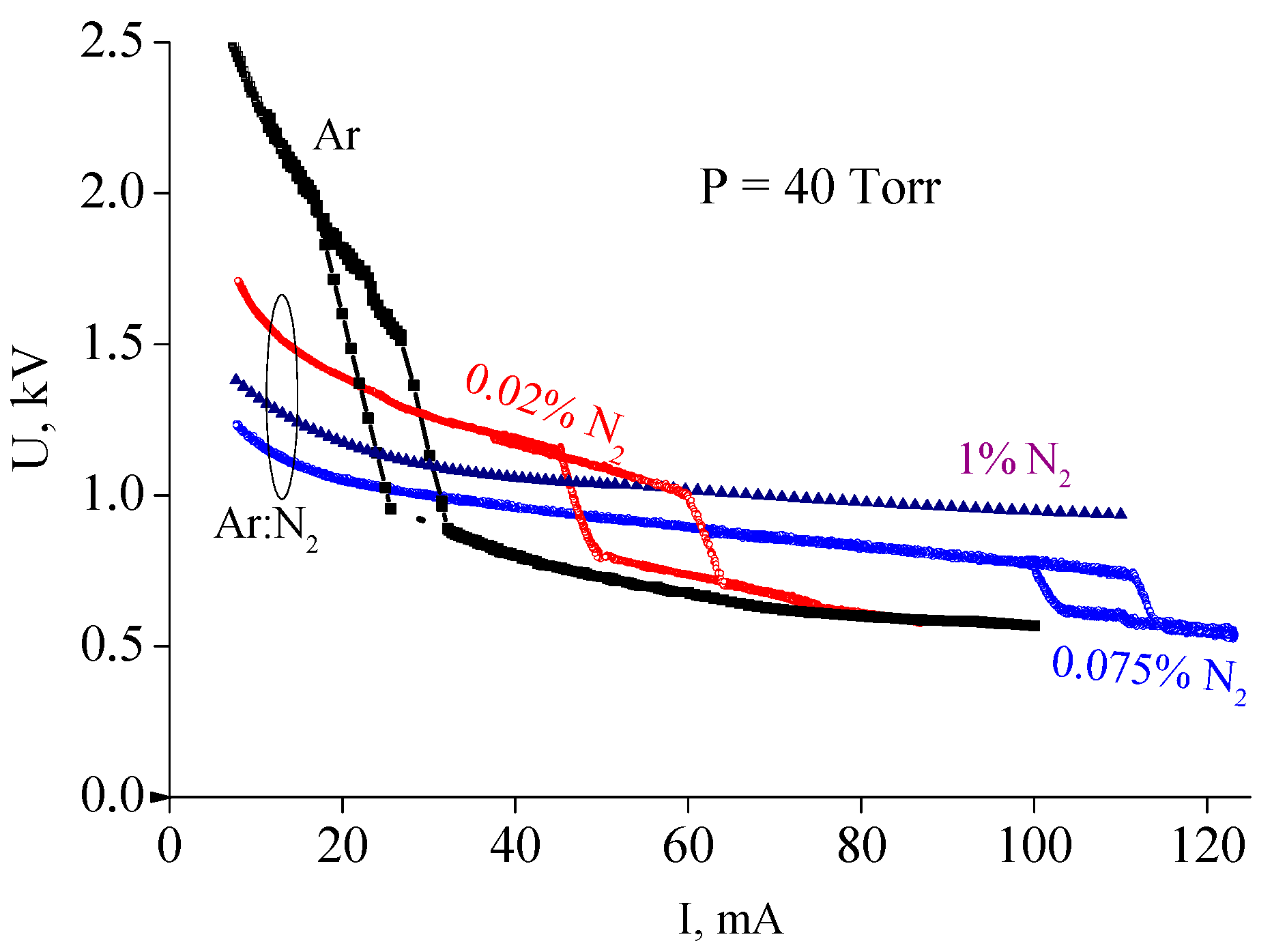
Figure 2 shows current–voltage characteristics measured in pure argon and in Ar + 0.75%N
2 and Ar + 1%N
2 gas mixtures at gas pressure
P = 40 Torr (
R = 1.4 cm, interelectrode distance ≈ 75 cm). As can be seen from
Figure 2, the discharge voltage of a diffuse discharge decreases by 2–1.5 times (depending on discharge current value) when 0.75% of nitrogen is added to argon. In the case of 1% of nitrogen the effect is slightly less pronounced.
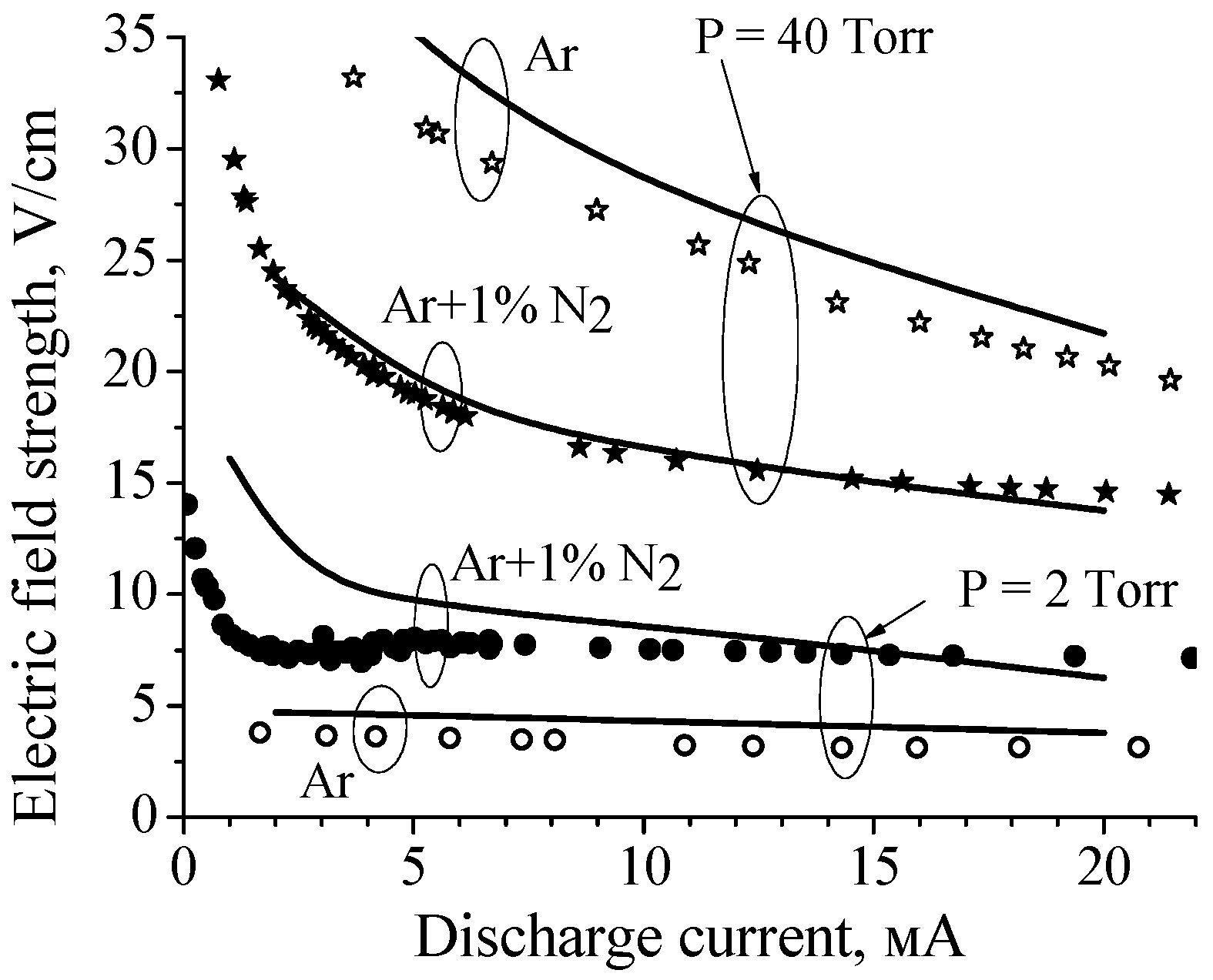
The explanation of the observed effect was given in paper [
17], in which characteristics of discharge plasma in pure argon and Ar + 1%N
2 mixture were studied both experimentally and theoretically (
R = 1.4 cm, interelectrode distance ≈ 75 cm). To reproduce in the calculations the current–voltage characteristics measured at various pressures (2 Torr, 40 Torr and 80 Torr, see
Figure 3), a rather complex (complete) zero-dimensional kinetic model was elaborated [
17]. The model included kinetics of excited states of Ar atoms (four lower levels and the higher states combined into three lumped levels), the kinetics of electronic levels of N
2 (N
2(A
), N
2(B
3Π
g), N
2(B’
), N
2(a’
), N
2(a
1Π
g), N
2(w
1Δ
u), and N
2(C
3Π
u)), the vibrational kinetics of nitrogen molecules in the ground state N
2(X
,
v) (45 vibrational levels), the kinetics of electronic states of N atoms (N(
4S), N(
2D), and N(
2P)), and the kinetics of electrons and Ar
+,
, N
+,
,
, and
ions. Electron transport coefficients and rate constants for electron induced processes were calculated by solving the electron Boltzmann equation in parallel with the system of kinetic equations. Besides, the model included the equation for the electric circuit.
The gas temperature on the tube axis was evaluated from the experimental data and used in the model as a parameter. Naturally, the radial temperature profile was not taken into account within 0D model. The temperature value that was used in the calculations corresponded to the gas temperature on the tube axis. It was estimated as follows. First, for given experimental data on the electric field strength, E, and the discharge current, I, the power deposited per unit length of the discharge, Q = IE, was calculated. Then, a one-dimensional (along the tube radius) thermal balance equation with a given heat source was solved numerically and the radial profile of the gas temperature was calculated. It was assumed that the wall temperature was 300 K and the radial profile of the deposited energy was Besselian.
The gas temperature in a glow discharge under the conditions close to the experimental conditions [
17] was measured in [
35] (Ar, Ar + 1%N
2, pressure of 50 Torr, tube diameter of 3.8 cm, and currents of 5–50 mA). In that paper, the gas temperature was also estimated using the procedure described above. It was shown that for the case of gas mixture the calculated values of the gas temperature agreed quite well with the measured ones. For pure Ar discharge the estimated gas temperatures were lower than measured. This was explained by the fact that, under considered conditions, the discharge in argon contracted at approximately 35 mA whereas the discharge in mixture remained diffuse even at 200 mA. In pure Ar, at discharge currents relatively close to 35 mA the radial profile of the deposited energy is noticeably narrower than the Besselian profile and, as a result, the measured temperature profile is narrower than the calculated one (for example, at
I = 20 mA, see comments in [
35]). Naturally, with decreasing current, the radial profile of the discharge current density becomes wider, and the theoretical estimate of the gas temperature becomes more reliable. In [
17], the relatively low discharge currents were considered (≤20 mA), so it can be expected that the performed estimation of the gas temperature was rather correct.
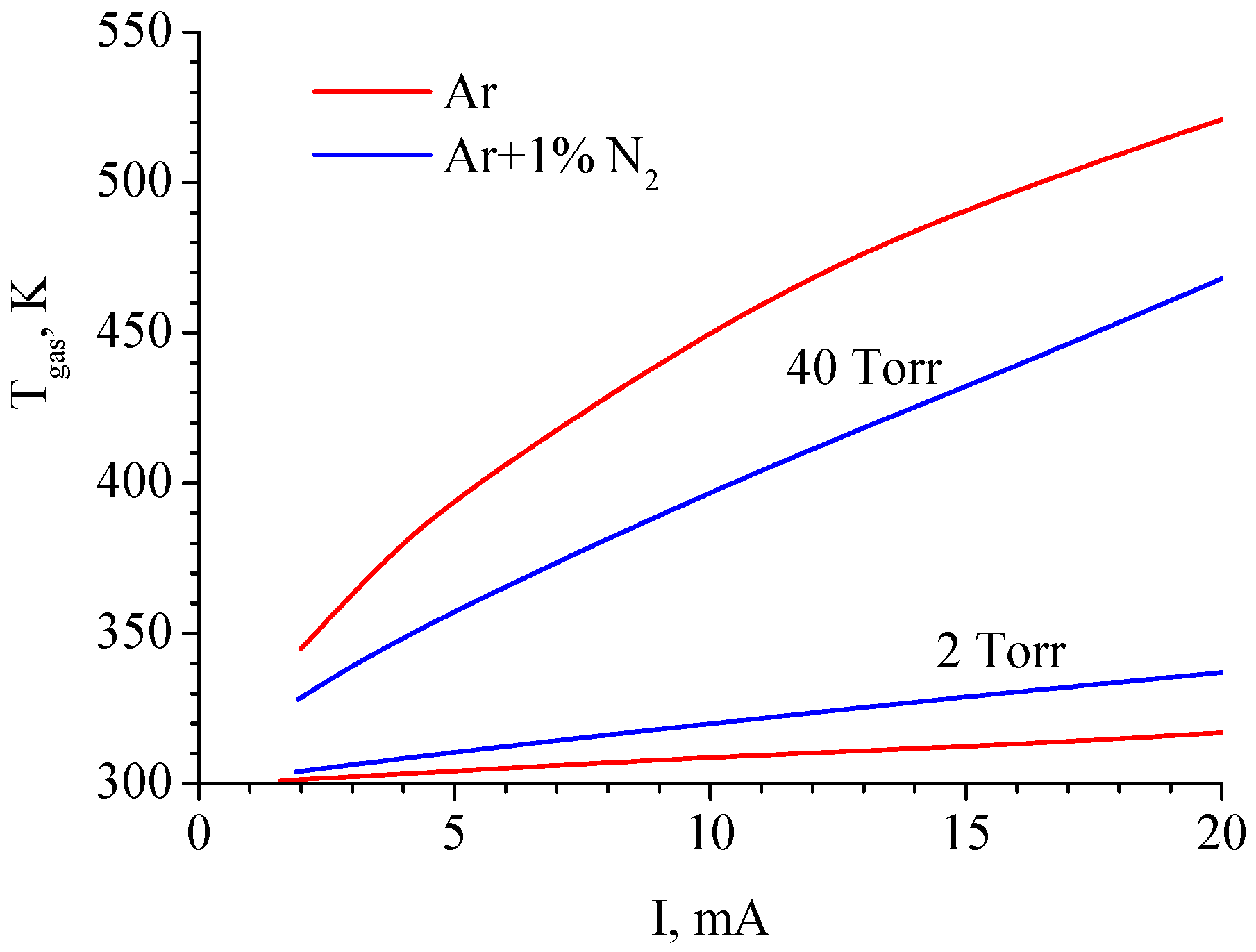
Gas temperatures at the axis of the discharge tube calculated in pure argon and the Ar + 1%N
2 mixture for
P = 2 Torr and 40 Torr are shown in
Figure 4. According to calculations, at
P = 40 Torr, the gas temperature in pure Ar discharge is higher than in Ar + 1%N
2 mixture discharge, which is consistent with experimental data [
35].
The calculated
E(
I) characteristics were in a reasonable agreement with the experimental data (see
Figure 3). As for the reduced electric field (
E/
N,
N is the gas number density), in the case of
P = 40 Torr the calculated
E/
N value varies from 3.9 Td to 3.3 Td (in pure Ar) and from 2.1 Td to 1.6 Td (in Ar + 1%N
2 mixture) with discharge current increase from 2 mA to 20 mA. That is, in argon, the reduced electric field is two times higher than in the mixture. At low pressure (2 Torr) the
E/
N value varies from 7.59 Td to 6.6 Td (in pure Ar) and from 22.5 Td to 10.9 Td (in Ar + 1%N
2 mixture) with discharge current increase from 2 mA to 20 mA.
The performed analysis showed that, in pure argon at intermediate pressures (e.g., 40 Torr) the stepwise ionization from the lower excited electronic states of Ar atoms was the dominant ionization process. The excitation of these states was provided by electron impact from the ground state, the energy of the lower state is about 11.6 eV. Due to ion conversion reaction the main ion in plasma was Ar2+. Losses of electrons were mainly provided by recombination with Ar2+ ions and, partially, by ambipolar diffusion.
According to calculations [
17], in the Ar + 1%N
2 mixture at intermediate pressures, a very effective ionization mechanism was realized. The ionization was mainly provided by processes of associative ionization of excited nitrogen atoms
and (to a lesser extent) by processes of associative ionization of excited nitrogen molecules
It was also shown that, at intermediate pressures, the degree of vibrational excitation of nitrogen was very high and the processes involving vibrationally excited molecules substantially contributed to the production of N atoms
and N
2(a’) molecules
Due to charge transfer and ion conversion processes
the major ion in discharge appeared to be Ar
2+, i.e., the same as in pure Ar discharge.
Note that the energies of N(2D) and N(2P) states are 2.38 eV and 3.57 eV, respectively. Nitrogen atoms are produced in processes (5) with the participation of vibrationally excited molecules N2(X, 14 ≤ v ≤ 19) and electronically excited N2(A) molecules. Lower vibrational levels of N2 molecules (v ≤ 8) are excited by electron impact, the threshold for the excitation of the first vibrational level is about 0.29 eV. The upper vibrational levels are populated due to V–V exchange processes. The lower metastable state N2(A3Σu) is excited by electron impact from the ground electronic state N2(X, v), the energy of the N2(A3Σu) state is about 6.17 eV. One can see that the energies of key species, which provide ionization in Ar + 1%N2 mixture at intermediate pressures, are essentially lower than 11.6 eV. For this reason, the ionization mechanism in Ar + 1%N2 mixture is realized at E/N values noticeably lower than those in pure Ar.
Therefore, at intermediate gas pressures, the addition of N2 to Ar leads to more effective ionization processes, while the major ion in plasma and, thus, the mechanisms of electron losses remain the same. As a result, the electric field in Ar + 1%N2 discharge (and the reduced electric field) is lower than that in the pure argon discharge.
At low gas pressures (e.g., 2 Torr) the losses of electrons and ions in discharges in pure argon and in Ar + 1%N
2 mixture are due to ambipolar diffusion, the rate of losses is noticeably higher than that at intermediate pressures (e.g., 40 Torr). For this reason, the reduced electric field
E/
N in the plasma increases [
17], because, in order to preserve ionization balance in the discharge plasma, it is necessary that the ionization rate be sufficiently high. In pure argon discharge, the required rate of ionization is provided, as before, mainly by stepwise ionization processes. In Ar + 1%N
2 discharge at low pressures the Processes (3) and (4) cannot provide the required rate of ionization and the ionization processes involving argon atoms (ionization by electron impact from the ground state, stepwise ionization and chemoionization) contribute substantially to electron production [
17]. At that, the value of
E/
N (and, accordingly, the value of
E) in Ar + 1%N
2 mixture is appreciably higher than that in pure argon. This is related, in particular, to the fact that, in the mixture, excited argon atoms are efficiently quenched by nitrogen molecules (Processes (1) and (2)).
Naturally, the results of the calculations depend on the used values of the rate constants. The choice of the rate constants for the processes included in the model is discussed in detail in paper [
17]. Here we briefly discuss the situation with rate constants for the key ionization Processes (3) and (4). The rate constant of Process (3a) is known only approximately. Estimate performed in [
36] yield a value of ~10
−12 cm
3 s
−1, which is lower by one order of magnitude than the estimate given in [
37]. The rate constant used in the model [
17] was taken from [
36]. As for the Process (3b), it was shown in [
38] that the use of this process in the model of the afterglow nitrogen plasma allows one to adequately describe specific features of the experimentally observed plasma decay dynamics. According to estimates [
38], the rate constant of this process is 2 × 10
−11 cm
3 s
−1, it is this value that was used in the model [
17]. The rate constants of Reactions (4a) and (4b) used in different studies differ by one to two orders of magnitude. In the model [
17] rate constants of these processes were chosen in accordance with recommendations made in [
39]: 10
−11 cm
3 s
−1 and 5 × 10
−11 cm
3 s
−1, respectively.
It is also worth noting that, in contrast to argon, the addition of nitrogen (1%, for example) to neon or helium leads to an increase in the electric field (discharge voltage) in a dc glow discharge even at intermediate gas pressures. The explanation of this effect is as follows [
18]. Addition of N
2 to Ne also leads to changing the ionization mechanism in dc discharge plasma, ionization processes in Ne + 1%N
2 discharge are similar to that in Ar + 1%N
2 discharge. On the other hand, in contrast to argon atoms, the ionization energy of Ne atoms is essentially higher than that of N
2 molecules, therefore the charge transfer process from N
2+ ion to Ne atom is absent Ne + 1%N
2 plasma. For this reason, the addition of N
2 to Ne leads to the replacement of Ne
2+ (major ion in plasma in pure Ne) with N
4+ in Ne + 1%N
2 mixture. The rate constant for the process of electron recombination with N
4+ ion is one order of magnitude higher than that with Ne
2+ ion. The increase in the rate of electron losses due to recombination with N
4+ ions appears to be more significant factor than the new ionization mechanism, so the electric field needed for the glow discharge maintenance increases with the addition of N
2 to Ne. In the case of He, the situation is similar to that in Ne.
3. Effect of Nitrogen Addition to Argon on the Rate of Plasma Decay in the Afterglow
It is shown in [
17] that, in a dc glow discharge in Ar + 1%N
2 mixture, a very high degree of vibrational excitation of nitrogen molecules is achieved. In the afterglow of such a discharge, the electrons gain energy in superelastic (second kind) collisions with vibrationally excited molecules, so the effective electron temperature (
Te = 2/3
um, where
um is the mean electron energy) in the afterglow plasma can be quite high for some time (about the relaxation time of the vibrational distribution function). In turn, the high electron temperature provides the high rate of plasma decay due to ambipolar diffusion process.
It should be noted that the evolution of the electron energy distribution function (EEDF) in nitrogen afterglow plasma was a subject of a large body of studies within the past 30 years (see [
40,
41] and references therein). It was ascertained that, in the afterglow plasma, the EEDF form was governed by heating of electrons in superelastic collisions with vibrationally excited molecules. As a consequence, there was a strong coupling between the degree of the vibrational excitation of nitrogen and the electron temperature. The EEDF and the effective electron temperature in pure nitrogen afterglow plasma were studied in a large number of papers (see [
40,
41] and references therein), though there are a few works, in which similar studies were performed in gas mixtures of a rare gas with nitrogen [
3,
26,
42,
43,
44].
In particular, in paper [
43] the EEDF in the afterglow of a pulsed direct current discharge was measured in an Ar + 1%N
2 mixture. The vibrational temperature,
Tv, of N
2 molecules was also experimentally estimated. The discharge was maintained in a cylindrical glass tube of 3 cm internal diameter at gas pressures of 0.5 Torr and 1 Torr. The pulse duration was 40 µs and the pulse repetition frequency was 1 kHz. The estimated vibrational temperature was about 4000–5000 K, and the electron temperature, calculated by the measured EEDFs, was varied in the range 4000–6000 K (depending on the gas pressure and the discharge current). In [
3], the electron temperature in the afterglow of Ar:N
2 power-pulsed microwave plasma was measured. Measurements were performed in a quartz tube with an inner radius of 0.3 cm in mixtures with N
2 percentage of 1–20% at a total gas pressure of 8–30 Torr. It was shown that in mixtures with a relatively low N
2 percentage (for example, 1%) the electron temperature in the afterglow plasma can be as high as 0.8 eV, which indicates that the degree of vibrational excitation of nitrogen is high.
Actually, the vibrational distribution function in the afterglow plasma (as well as in the discharge plasma) is not the Boltzmann function, i.e., is not characterized by only the temperature
Tv. Calculations of the vibrational distribution function and the EEDF in the afterglow of a dc glow discharge in Ar + 1%N
2 were presented in conference paper [
44]. In calculations the kinetic model [
17] was used, and the procedure of simulation was as follows. Firstly, time–evolution of plasma parameters was calculated up to approaching steady-state discharge conditions which were characterized by the discharge current value. Then, the applied voltage (the electric field in plasma) was switched off, and the time-variation of plasma parameters in the post-discharge was calculated. The following conditions were considered: discharge tube radius
R = 1.5 cm, gas pressure
P = 5 Torr, gas temperature
Tgas = 350 K, discharge current
I = 20 mA.
According to simulations in [
44], the reduced electric field in the steady-state discharge is about
E/
N = 4.7 Td, the electron number density is
ne = 2.0 × 10
10 cm
–3. Vibrational distribution functions in discharge and afterglow plasma are shown in
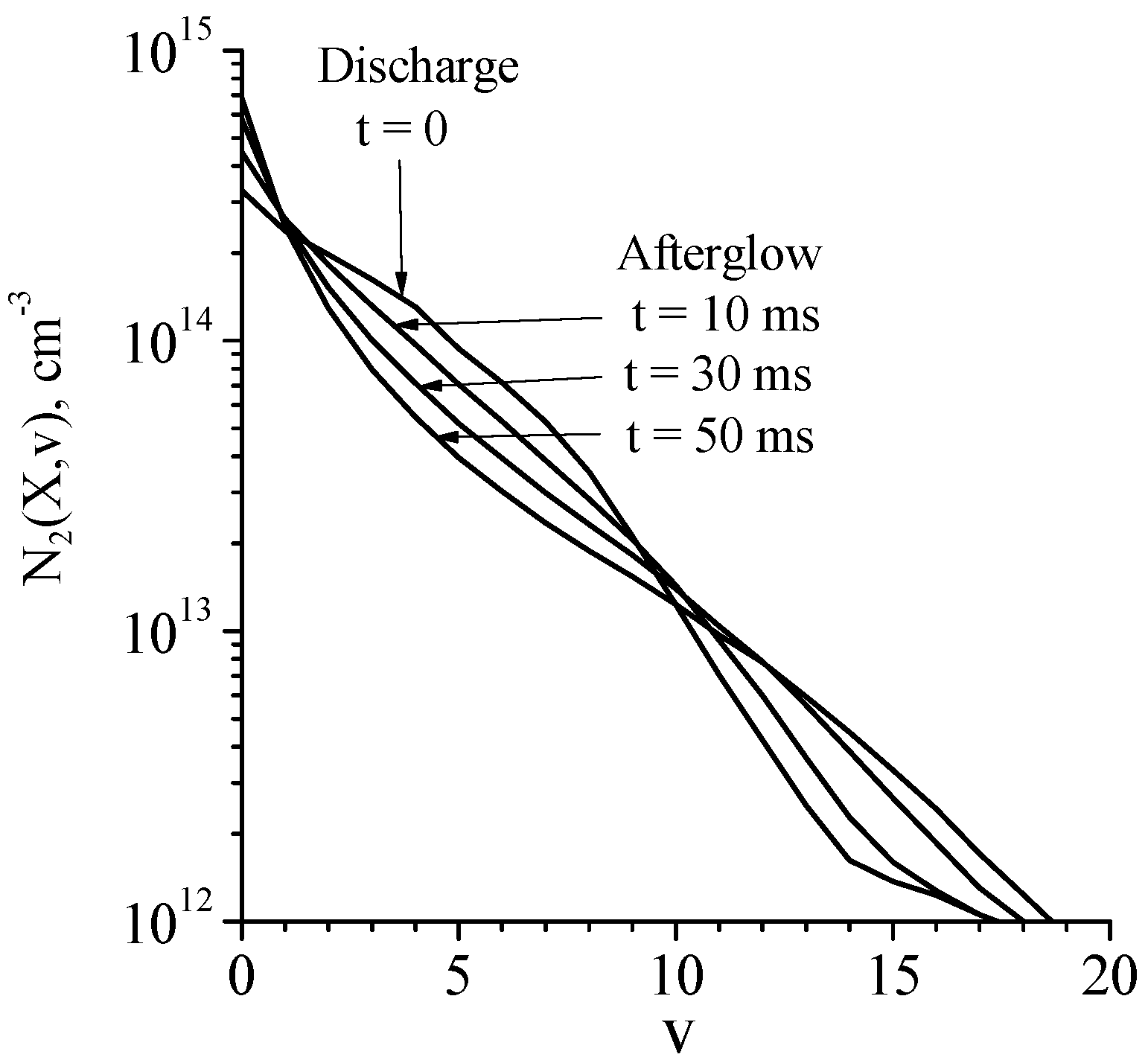
Figure 5. The shape of the distribution function (and the degree of the vibrational excitation) can be characterized by ‘local’ vibrational temperatures,
Tvi,i+1, calculated using the populations of two successive vibrational levels,
i and
i + 1. In the discharge plasma the vibrational temperature
Tv0,1 is as high as 10,580 K and in the afterglow, it decreases down to 3300 K during 50 ms (see
Table 1). Note also that
Tvi,i+1 values (
i = 1, 2, 3, 4, see
Table 1) are noticeably higher than
Tv0,1 values.
The high degree of the vibrational excitation of nitrogen molecules leads to high effective electron temperatures in the afterglow plasma (see
Table 1). At
t = 10 ms, the electron temperature is as high as
Te ≈ 8520 K, and the further decrease in
Te value is explained by the decrease in the degree of vibrational excitation of nitrogen molecules, which is illustrated in
Figure 5 by growth of N
2(X,
v = 0) population. At that, even at
t = 30 ms the electron temperature is rather high
Te ≈ 6590 eV. It is worth noting that the calculated
Te values agree with those measured in the afterglow of a pulsed microwave discharge in the Ar + 1%N
2 mixture [
3].
It was mentioned in [
44] that, under the considered conditions, the rate of plasma decay due to ambipolar diffusion process was high because of the high electron temperature in the afterglow. However, no comparison with plasma decay rate in pure argon afterglow was performed. Such a comparison was presented in paper [
26], in which the time variation of the electron concentration in the afterglow of dc glow discharges in pure Ar and Ar + 1%N
2 mixture was numerically studied. As in work [
44], the kinetic model [
17] was used in simulations. The following conditions were considered: discharge tube radius
R = 1.4 cm, gas pressures
P = 1, 2, and 5 Torr, discharge currents
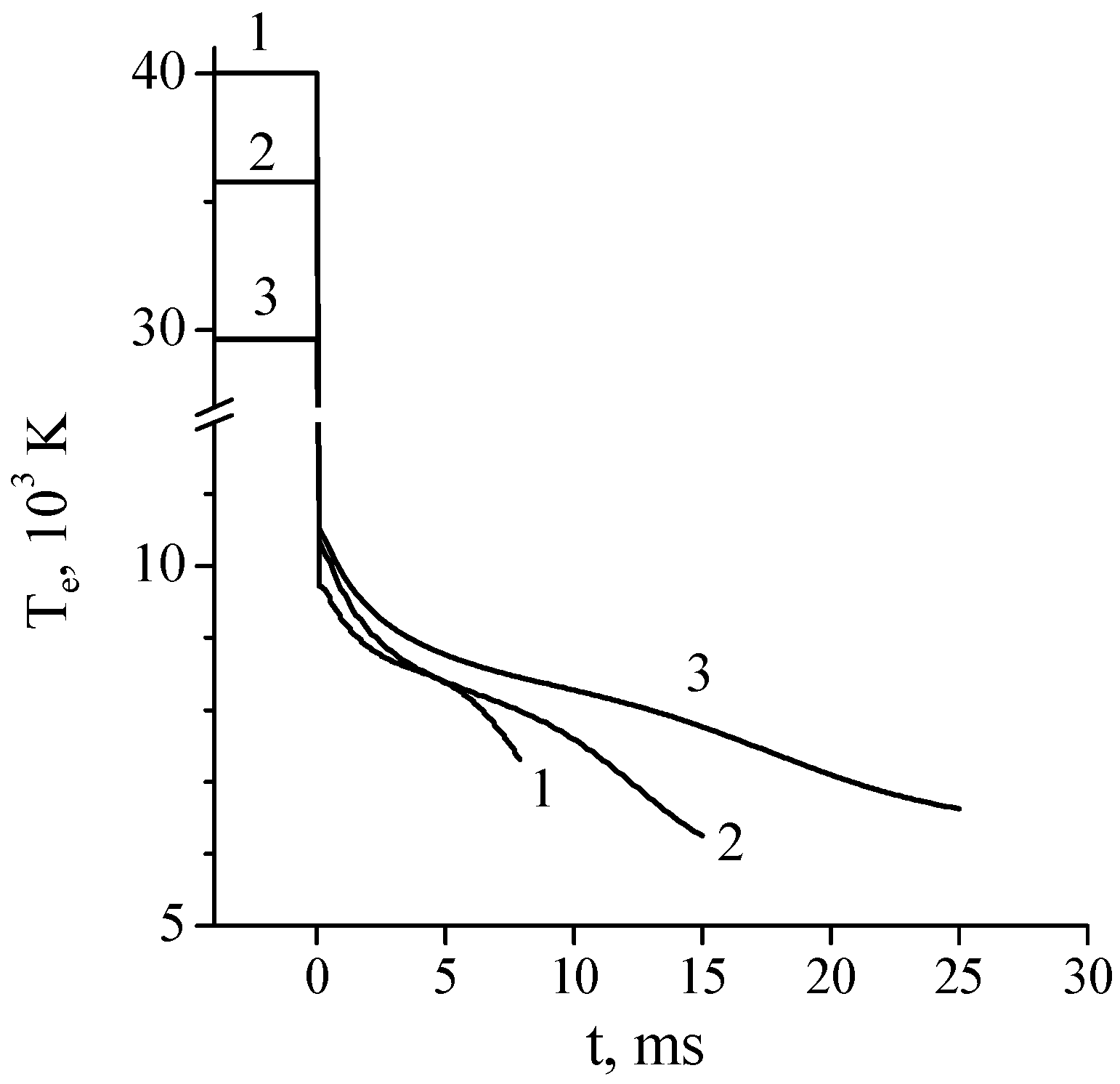
I = 20 mA and 56 mA. Time variation of the effective electron temperature in Ar + 1%N
2 afterglow calculated at fixed discharge current
I = 20 mA and various gas pressures is shown in
Figure 6. As follows from the calculations, the lower the gas pressure, the faster the electron temperature decreases in the discharge afterglow. In the afterglow of a discharge in pure argon, electrons are heated in superelastic collisions with electronically excited atoms. In addition, fast electrons appear in chemoionization processes Ar* + Ar* = Ar + Ar
+ + e (≈7.6 eV). In [
26], the electron temperature in the pure argon afterglow was not calculated because of the problem of accounting for the letter process in the Boltzmann equation. On the other hand, it was observed in [
3,
45] that the electron temperature in the argon afterglow plasma dropped rapidly (during ~100 μs at pressures of 6–30 Torr) to
Te~1200 K. Therefore, in calculations [
26], the electron energy distribution function in pure argon afterglow was assumed to be Maxwellian with the temperature
Te = 1000 K or
Te =
Tgas (for comparison).
Electron densities in the discharge and their time evolution in the afterglow calculated for pure Ar and Ar + 1%N
2 mixture at a discharge current of
I = 20 mA are shown in
Figure 7a–c. From
Figure 7 it follows that in some cases an increase in the electron concentration is observed at the very beginning of the afterglow. According to calculations, in steady state Ar + 1%N
2 discharge plasma under considered conditions, production of electrons is mainly due to associative ionization (3) and (4) and chemoionization (Ar* + Ar* → Ar
+ + Ar + e) processes and losses of electrons are due to ambipolar diffusion process. After turning off the electric field, the mean electron energy instantaneously (within the model used) decreases. The decrease in the mean electron energy leads to the decrease in the rate of electron losses due to ambipolar diffusion process while the rate of electron production remains near the same, since the rates of the ionization processes mentioned above do not depend on the electron temperature. As a result, this leads to an increase in the electron concentration at the very beginning of the afterglow.
In pure Ar discharge under considered conditions losses of electrons are also due to ambipolar diffusion process. At that, at pressure 1 Torr, production of electrons is partially due to chemoionization processes. As a result, an increase in the electron concentration at the very beginning of the afterglow is observed in simulations. It follows from simulations that, with increasing pressure, the contribution of chemoionization processes to ionization rate decreases and the production of electrons is almost completely provided by stepwise ionization processes. In this case, the decrease in the electron temperature in the afterglow leads to significant decrease in the rate constant of stepwise ionization and, accordingly, the rate of electron production. As a result, the concentration of electrons monotonously decreases in the afterglow.
As
Figure 7a shows, at
P = 1 Torr, the afterglow plasma of a discharge in the Ar + 1%N
2 mixture decays noticeably faster than that of a discharge in pure Ar. In this case, the decay of plasma (both in pure argon and in a gas mixture) is governed by the ambipolar diffusion process, the rate of which in Ar + 1%N
2 afterglow plasma is high due to the high electron temperature (see
Figure 6).
However, the situation changes significantly with the pressure increase. At
P = 5 Torr (
Figure 7c), at the beginning of the afterglow (during 1 ms) the electron density in the Ar + 1%N
2 mixture decreases much slower than in pure argon, although the rate of ambipolar diffusion in argon is significantly lower. As a result, even at
t = 13 ms after the end of the discharge, the electron density in Ar + 1%N
2 mixture remains slightly higher than that in pure Ar. In contrast, at
t > 15 ms, the electron density in pure argon is significantly higher with respect to that in Ar + 1%N
2 mixture. This result is explained by two main effects [
26]. The first effect consists in the following: at the beginning of the afterglow in pure argon, the Ar
+ ions (dominant ions in the discharge plasma) are quickly (~0.3 ms) converted in molecular ions Ar
2+ (see comments in [
26]). At the beginning of the afterglow, the rate of plasma decay due to recombination of electrons with molecular ions is higher than that due to the ambipolar diffusion process. The rate of the recombination process decreases with the electron (and ion) concentration decrease, so that, at
t > 15 ms, the plasma decay is governed by the ambipolar diffusion only.
The second reason is that, according to calculations, in Ar + 1%N2 afterglow the high rate of plasma decay due to ambipolar diffusion process is balanced (to a large extent) by the high rate of electron production via associative ionization of excited nitrogen atoms and molecules (3) and (4). As a result, the plasma decay rate during 1 ms after the end of the discharge is appreciably lower than in the Ar afterglow plasma.
The above described results of simulations were used in [
26] for the qualitative explanation of the experimental data on the influence of a nitrogen admixture on the anomalous memory effect in the breakdown of low-pressure argon in a long discharge tube.