Transverse Momentum Transfer Distributions Following Single Ionization in 3.6 MeV/amu Au53+ + He Collisions: A 4-Body Classical Treatment
Abstract
:1. Introduction
2. Results
2.1. Classical Method
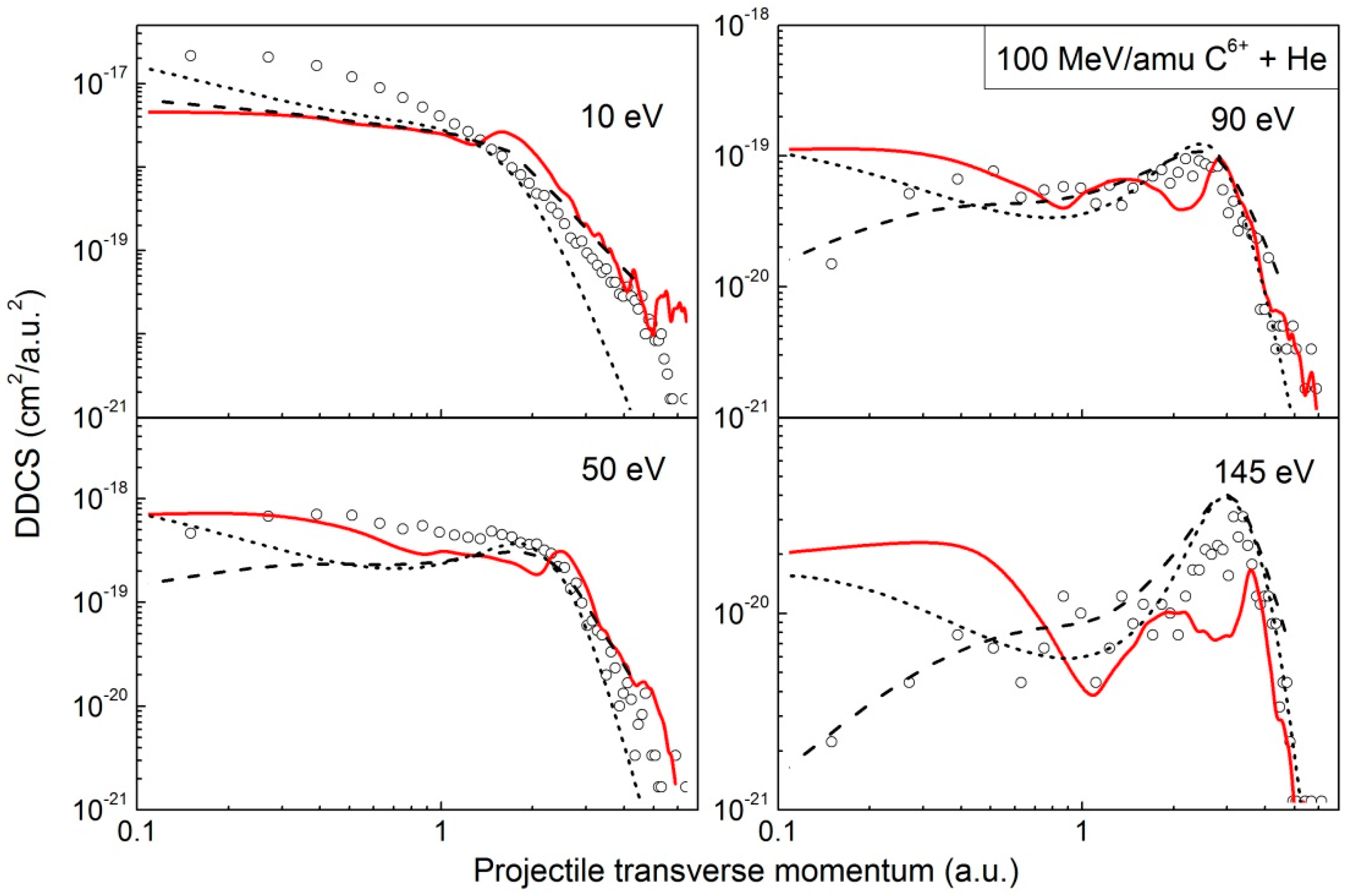
2.2. C6+ + He Collisions
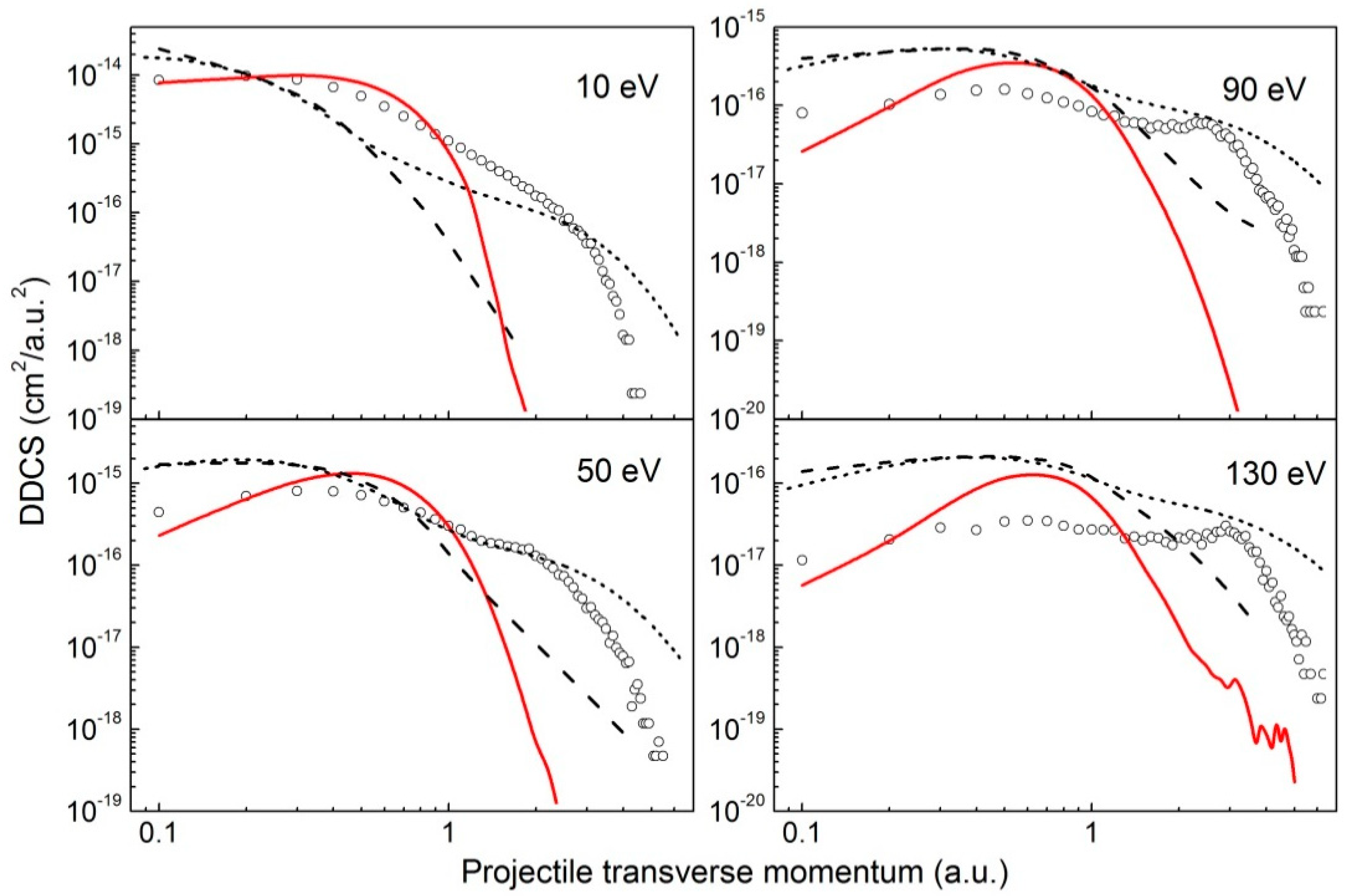
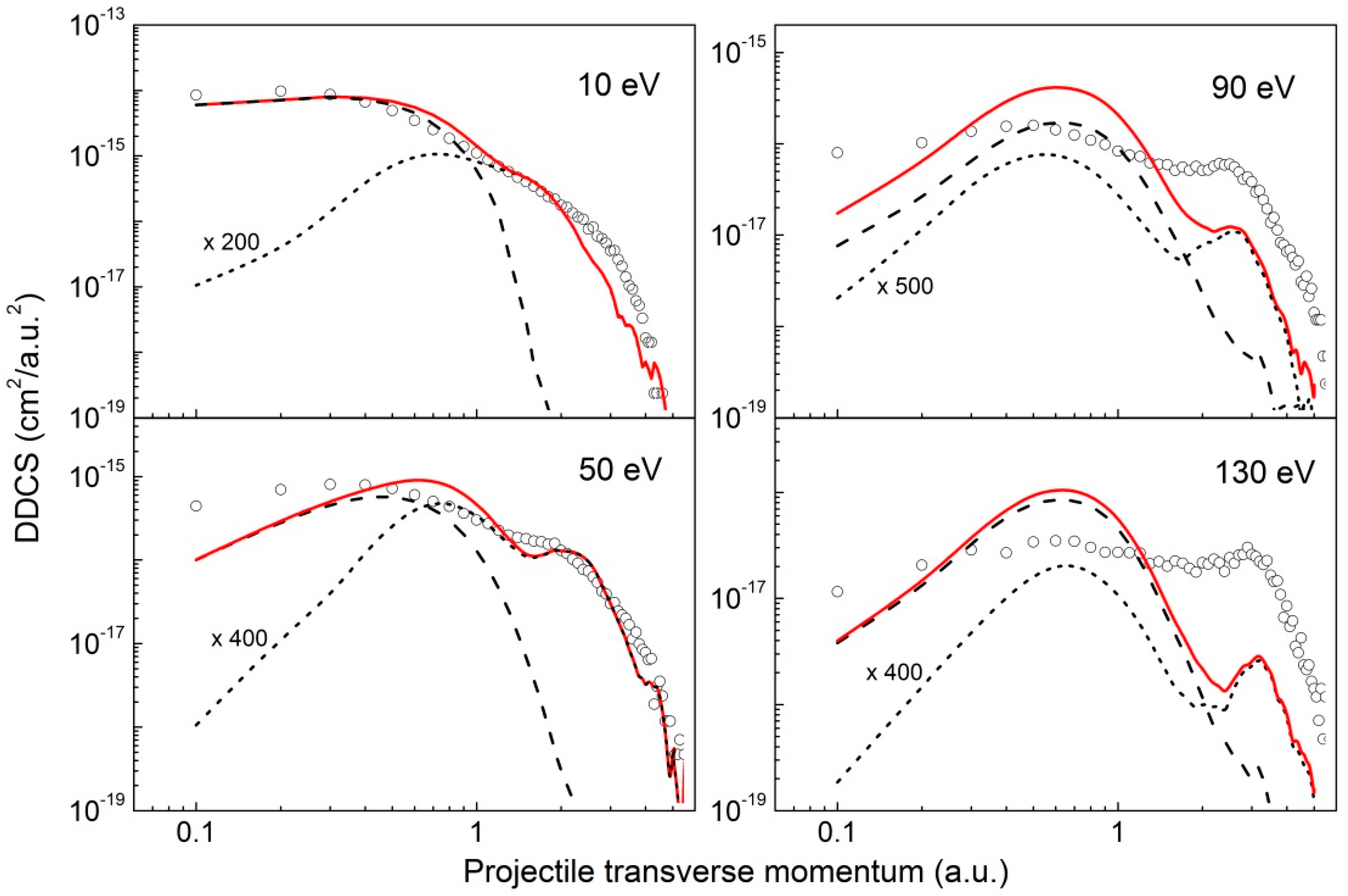
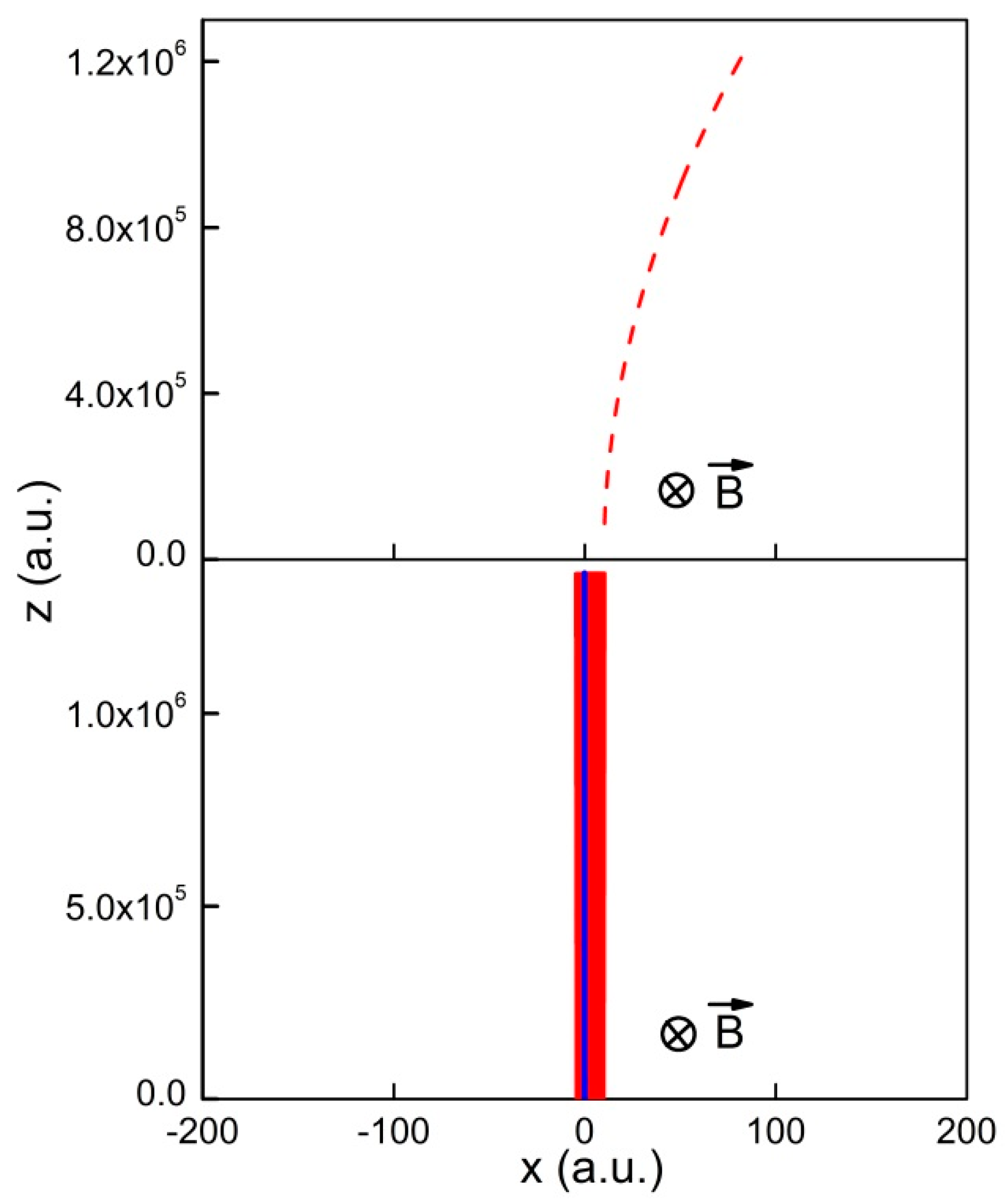
2.3. Au53+ + He Collisions
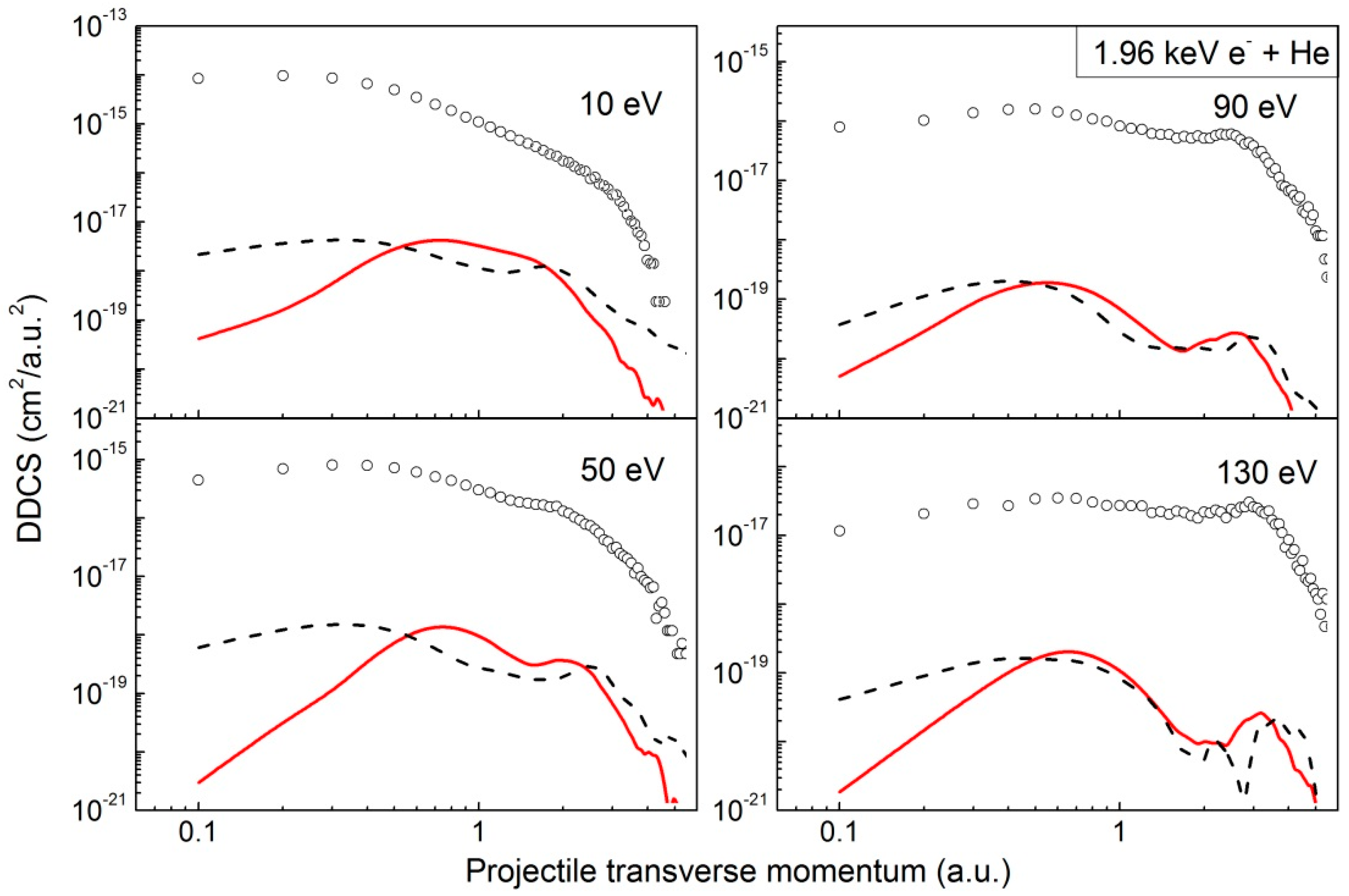
2.4. Contribution of 1.96 keV e− + He Collisions
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmitt, W.; Moshammer, R.; O’Rourke, F.S.C.; Kollmus, H.; Sarkadi, L.; Mann, R.; Hagmann, S.; Olson, R.E.; Ullrich, J. Ultra-low energy electrons from fast heavy-ion helium collisions : the "target cusp". Phys. Rev. Lett. 1998, 81, 4337. [Google Scholar] [CrossRef]
- Moshammer, R.; Perumal, A.N.; Schulz, M.; Rodriguez, V.D.; Kollmus, H.; Mann, R.; Hagmann, S.; Ullrich, J. Three-body Coulomb problem probed by mapping the Bethe surface in ionizing ion-atom collisions. Phys. Rev. Lett. 2001, 87, 223201. [Google Scholar] [CrossRef] [PubMed]
- Schulz, M.; Moshammer, R.; Madison, D.H.; Olson, R.E.; Marshalant, P.; Whelan, C.T.; Walters, H.R.J.; Jones, S.; Foster, M.; Kollmus, H.; et al. Triply differential single-ionization cross sections in coplanar and non-coplanar geometry for fast heavy ion-atom collisions. J. Phys. B At. Mol. Phys. 2001, 34, L305. [Google Scholar] [CrossRef]
- Olson, R.E.; Fiol, J. Mapping of the Bethe surface in single-ionization ion-atom collisions. J. Phys. B At. Mol. Phys. 2001, 34, L625. [Google Scholar] [CrossRef]
- Schulz, M.; Moshammer, R.; Perumal, A.N.; Ullrich, J. Triply differential single-ionization cross sections in fast ion-atom collisions at large perturbation. J. Phys. B At. Mol. Phys. 2002, 35, L161. [Google Scholar] [CrossRef]
- Madison, D.; Schulz, M.; Jones, S.; Foster, M.; Moshammer, R.; Ullrich, J. Comparison of theoretical and absolute experimental fully differential cross sections for ion-atom impact ionization. J. Phys. B At. Mol. Phys. 2002, 35, 3297. [Google Scholar] [CrossRef]
- Rodriguez, V.D. CDW-EIS theoretical calculations of projectile deflection for single ionization in highly charged ion-atom collisions. Nucl. Instrum. Methods Phys. Res. B 2003, 205, 498. [Google Scholar] [CrossRef]
- Fiol, J.; Olson, R.E. Three- and four-body dynamics in fast heavy ion-atom ionization. J. Phys. B At. Mol. Phys. 2004, 37, 3947. [Google Scholar] [CrossRef]
- Foster, M.; Madison, D.H.; Peacher, J.L.; Ullrich, J. Highly charged particle impact ionization of He. J. Phys. B At. Mol. Phys. 2004, 37, 3797. [Google Scholar] [CrossRef]
- Fainstein, P.D.; Gulyás, L. Three- and four-body dynamics in single ionization of He by swift highly charged Au53+ ions. J. Phys. B At. Mol. Phys. 2005, 38, 317. [Google Scholar] [CrossRef]
- Ciappina, M.F.; Cravero, W.R. CDW and CDW-EIS calculations for FDCSs in highly charged ion impact ionization of helium. J. Phys. B At. Mol. Phys. 2006, 39, 1091. [Google Scholar] [CrossRef]
- Dürr, M.; Najjari, B.; Schulz, M.; Dorn, A.; Moshammer, R.; Voitkiv, A.B.; Ullrich, J. Analysis of experimental data for ion-impact single ionization of helium with Monte Carlo event generators based on quantum theory. Phys. Rev. A 2007, 75, 062708. [Google Scholar] [CrossRef]
- McGovern, M.; Assafrão, D.; Mohallem, J.R.; Whelan, C.T.; Walters, H.R.J. Coincidence studies of He ionized by C6+, Au24+ and Au53+. Phys. Rev. A 2010, 81, 042704. [Google Scholar] [CrossRef]
- Frémont, F.; Belyaev, A.K. Excitation of hydrogen atoms in collisions with helium atoms: the role of electron-electron correlation. J. Phys. B At. Mol. Phys. 2017, 50, 045201. [Google Scholar] [CrossRef]
- Frémont, F. Quasiclassical treatment of the Auger effect in slow ion-atom collisions. Phys. Rev. A 2017, 96, 032712. [Google Scholar] [CrossRef]
- Kirschbaum, C.L.; Wilets, L. Classical many-body model for atomic collisions incorporating the Heisenberg and Pauli principles. Phys. Rev. A 1980, 21, 834. [Google Scholar] [CrossRef]
- Cohen, J.S. Quasiclassical effective Hamiltonian structure of atoms with Z = 1 to 38. Phys. Rev. A 1995, 51, 266. [Google Scholar] [CrossRef]
- Cohen, J.S. Quasiclassical-trajectory Monte Carlo methods for collisions with two-electron atoms. Phys. Rev. A 1996, 54, 573. [Google Scholar] [CrossRef]
- Cohen, J.S. Molecular effects on antiproton capture by H2 and the states of PP formed. Phys. Rev. A 1997, 56, 3583. [Google Scholar] [CrossRef]
- Abrines, R.; Percival, I. Classical theory of charge transfer and ionization of hydrogen atoms by protons. Proc. Phys. Soc. 1966, 88, 861. [Google Scholar] [CrossRef]
- Frémont, F. Electron capture and single ionization in H+ + Ar collisions: classical calculations. J. Phys. B At. Mol. Phys. 2016, 49, 065206. [Google Scholar] [CrossRef]
- Berg, H.; Ullrich, J.; Bernstein, E.; Unverzagt, M.; Spielberger, L.; Euler, J.; Schardt, D.; Jagutzki, O.; Schmidt-Bocking, H.; Mann, R.; et al. Absolute cross sections for helium single and double ionization in collisions with fast, highly charged projectiles. J. Phys. B At. Mol. Phys. 1992, 25, 3655. [Google Scholar] [CrossRef]
- Schiwietz, G.; Xiao, G.; Grande, P.L.; Schmoldt, A.; Grether, M.; Köhrbrück, R.; Spieler, A.; Stettner, U. Non Linear Effects In Ion Induced Electron Emission. Scanning Microsc. 1998, 12, 265. [Google Scholar]
- Moshammer, R.; Max Planck Institut für Kernphysik, Heidelberg, Germany; Schulz, M.; University of Missouri-Rolla, Physics Department and LAMOR, Rolla, MO 65409, USA. Personal communication, 2018.
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frémont, F. Transverse Momentum Transfer Distributions Following Single Ionization in 3.6 MeV/amu Au53+ + He Collisions: A 4-Body Classical Treatment. Atoms 2018, 6, 68. https://doi.org/10.3390/atoms6040068
Frémont F. Transverse Momentum Transfer Distributions Following Single Ionization in 3.6 MeV/amu Au53+ + He Collisions: A 4-Body Classical Treatment. Atoms. 2018; 6(4):68. https://doi.org/10.3390/atoms6040068
Chicago/Turabian StyleFrémont, François. 2018. "Transverse Momentum Transfer Distributions Following Single Ionization in 3.6 MeV/amu Au53+ + He Collisions: A 4-Body Classical Treatment" Atoms 6, no. 4: 68. https://doi.org/10.3390/atoms6040068
APA StyleFrémont, F. (2018). Transverse Momentum Transfer Distributions Following Single Ionization in 3.6 MeV/amu Au53+ + He Collisions: A 4-Body Classical Treatment. Atoms, 6(4), 68. https://doi.org/10.3390/atoms6040068




