Improving Quantitative Analysis of Lithium in Brines Using Laser-Induced Breakdown Spectroscopy with τ–Algorithm (τLIBS)
Abstract
1. Introduction
2. Theoretical Section
3. Materials and Methods
3.1. Brine Samples
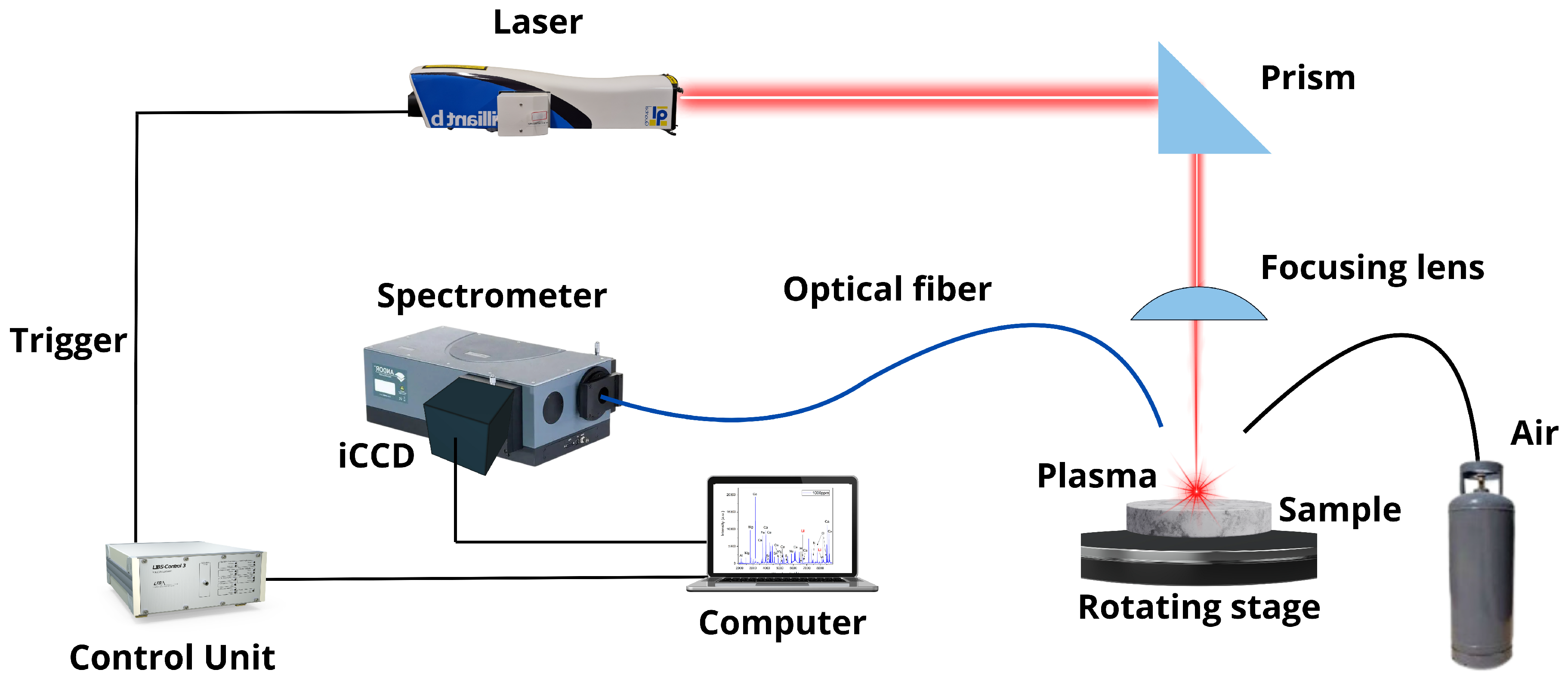
3.2. LIBS Setup
4. Results and Discussion
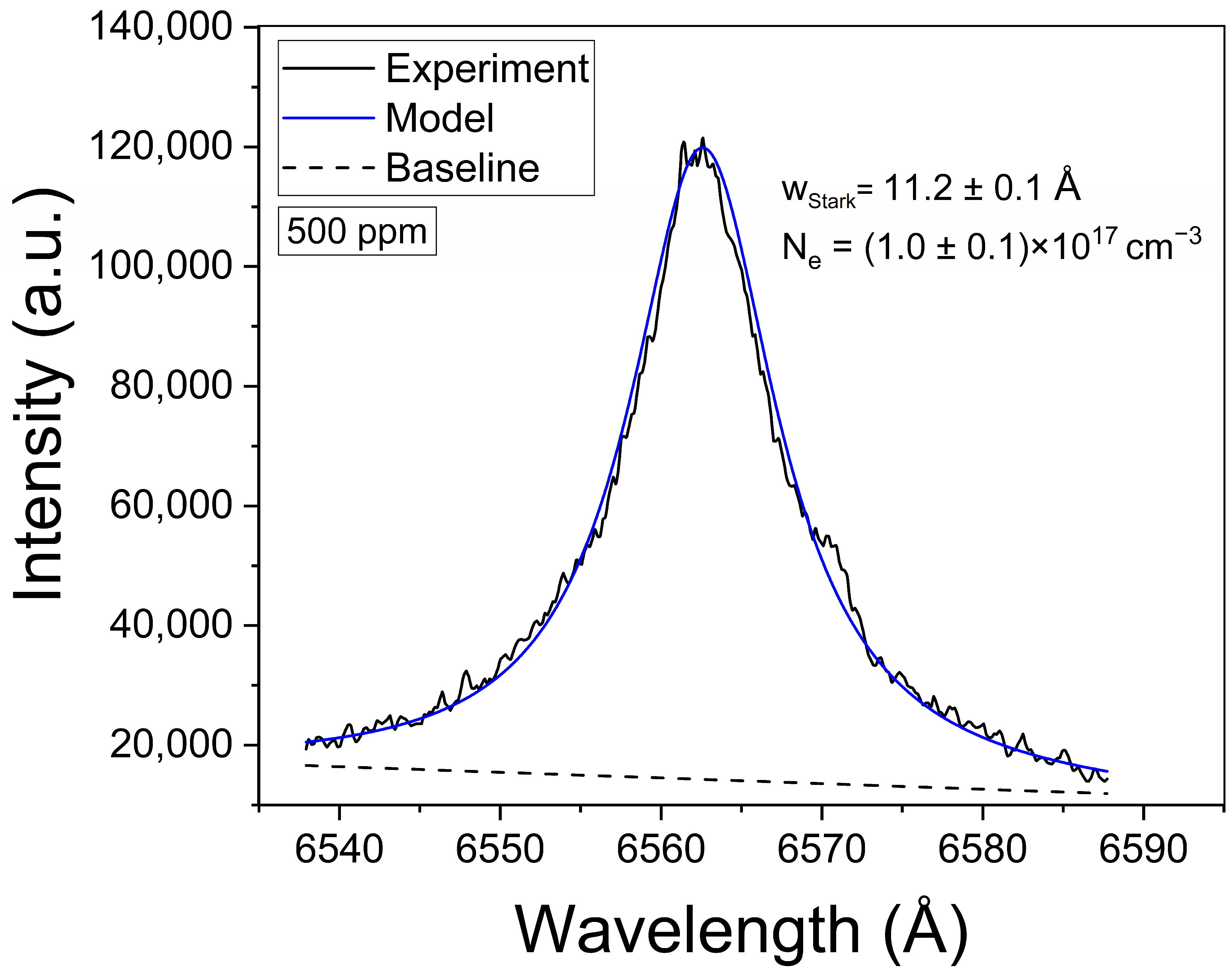
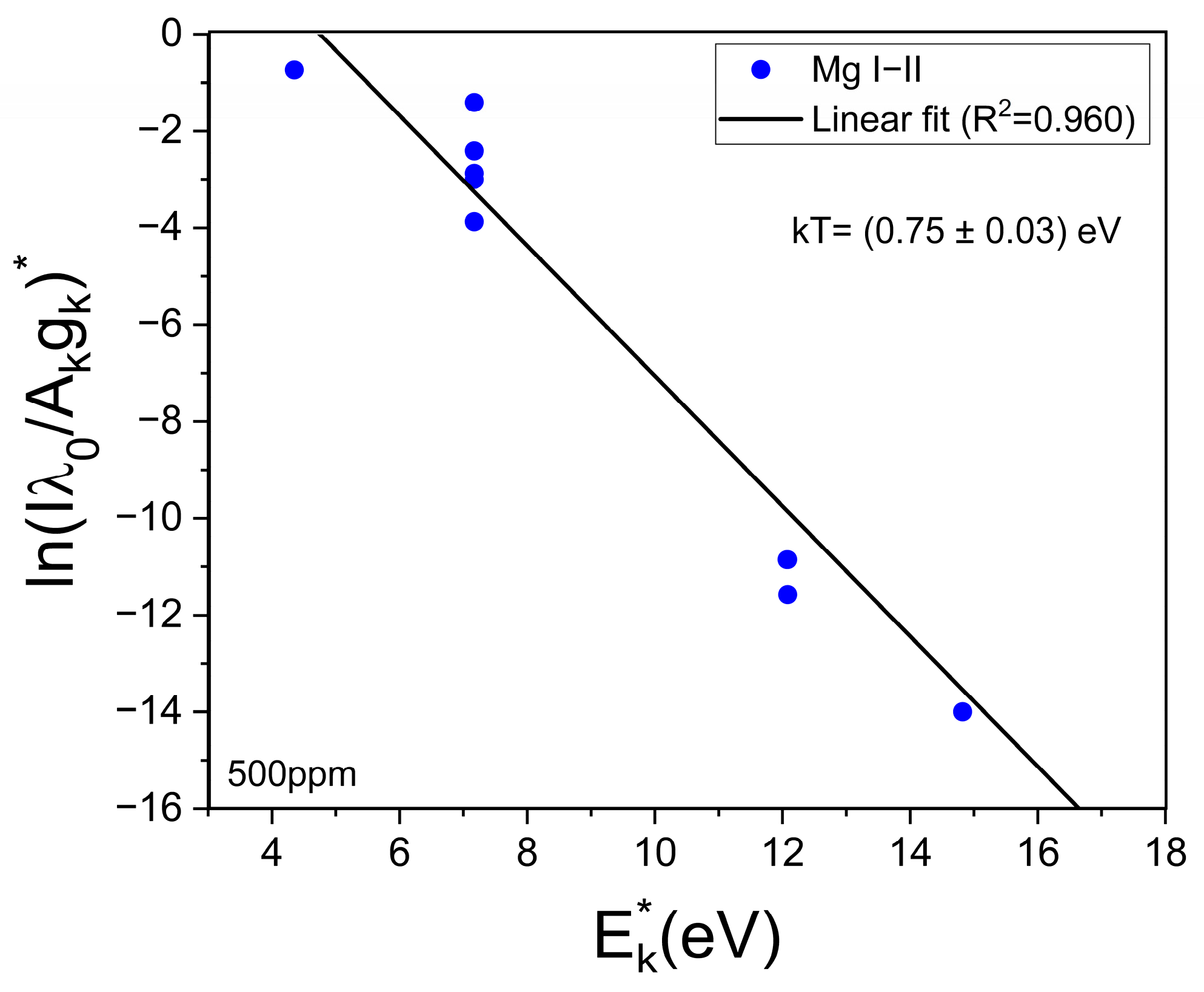
4.1. Plasma Characterization: Electron Density and Temperature
4.2. Plasma Analysis of Li Spectral Emission with τ–Algorithm
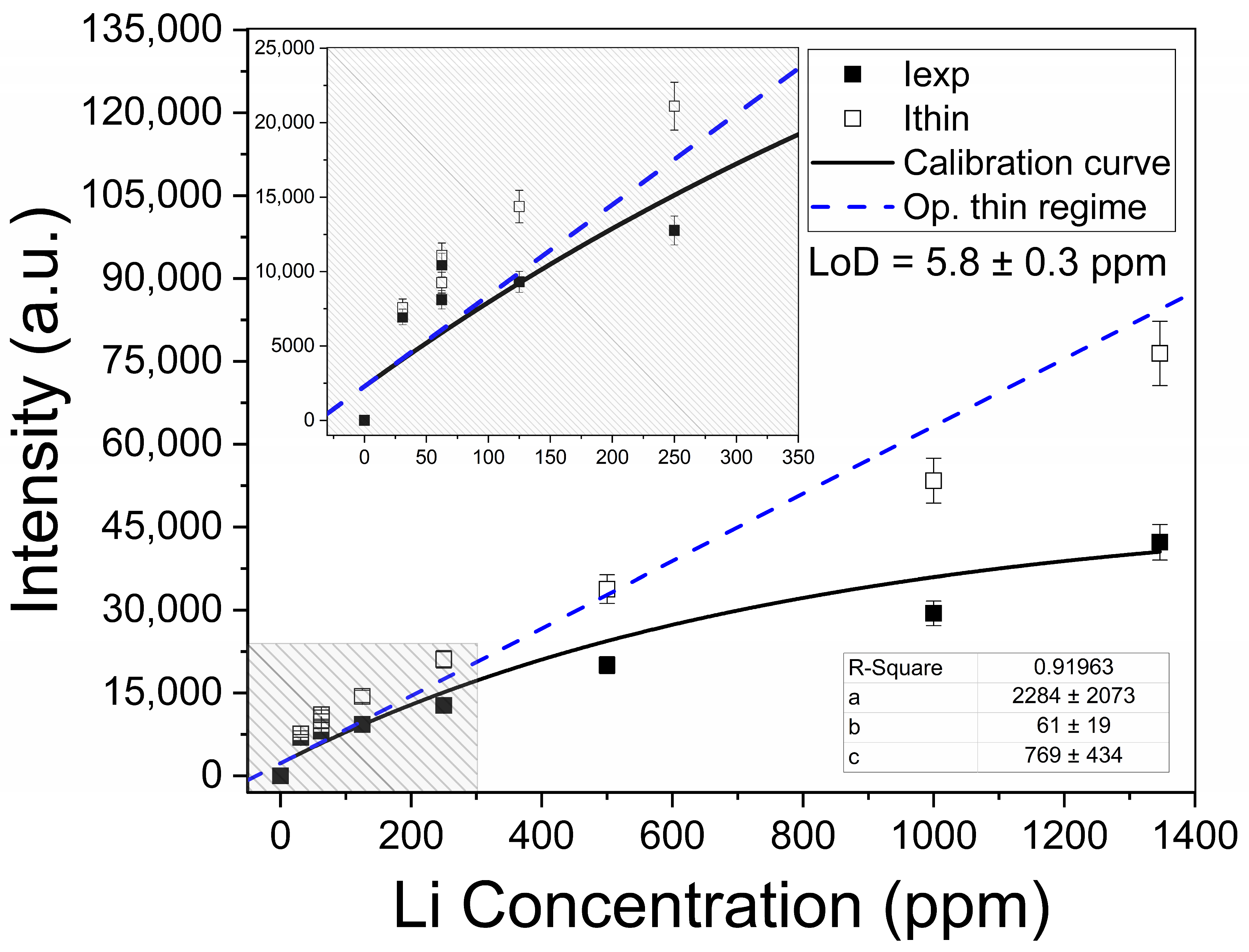
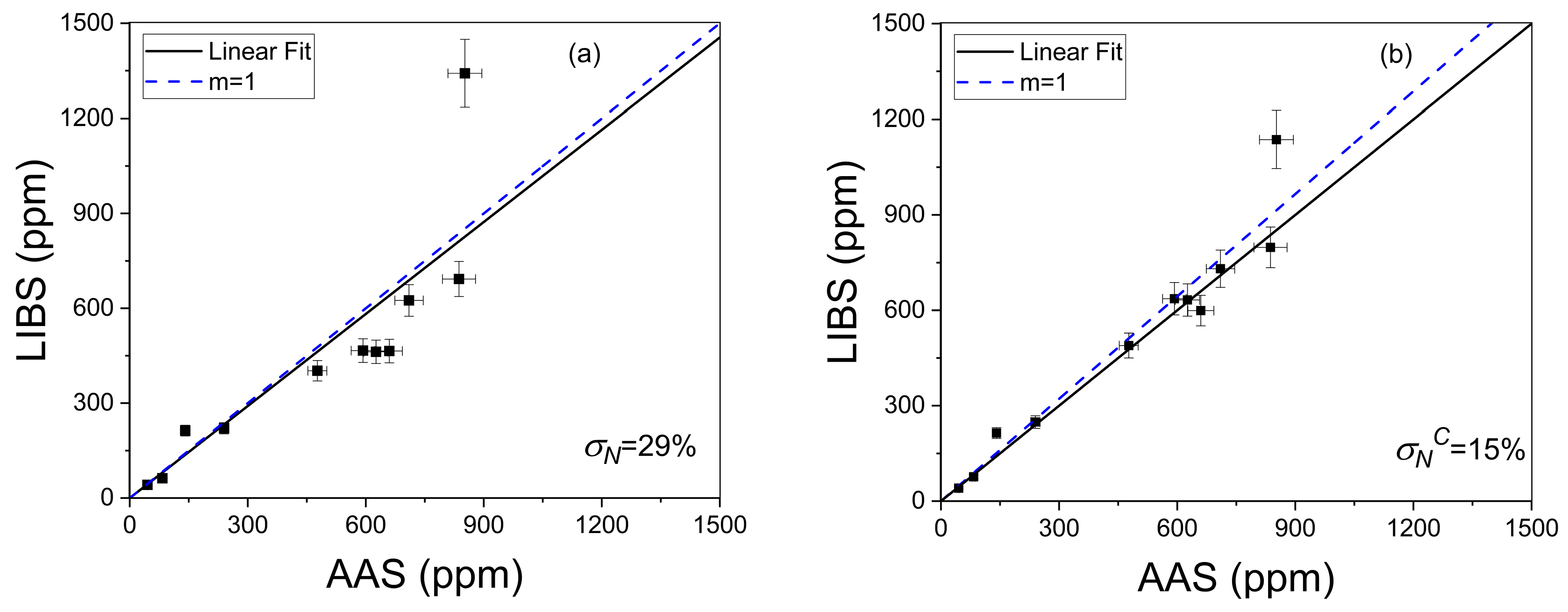
4.3. Quantitative Li Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Li | Sample | Itot (a.u.) | Ithin (a.u.) | τ0 (adim.) | SAl (%) | wStark (Å) |
|---|---|---|---|---|---|---|
| Calibration | 30.83 ppm | 6950 ± 530 | 7575 ± 580 | 1 ± 1 | 26 ± 2 | 0.39 ± 0.05 |
| 62.4 ppm | 8110 ± 620 | 9253 ± 700 | 2 ± 1 | 39 ± 3 | 0.35 ± 0.03 | |
| 62.5 ppm | 10,440 ± 790 | 11,073 ± 840 | 2 ± 1 | 44 ± 4 | 0.35 ± 0.03 | |
| 125 ppm | 9311 ± 700 | 14,365 ± 1000 | 4 ± 1 | 54 ± 4 | 0.35 ± 0.03 | |
| 250 ppm | 12,760 ± 970 | 21,110 ± 1600 | 7 ± 2 | 65 ± 5 | 0.35 ± 0.03 | |
| 500 ppm | 20,030 ± 1500 | 33,788 ± 2500 | 8 ± 2 | 69 ± 6 | 0.33 ± 0.03 | |
| 1000 ppm | 29,420 ± 2200 | 53,409 ± 4000 | 27 ± 5 | 84 ± 7 | 0.35 ± 0.03 | |
| 1346 ppm | 42,260 ± 3200 | 76,444 ± 5800 | 21 ± 4 | 82 ± 7 | 0.33 ± 0.03 | |
| Brines | # 1 | 4756 ± 360 | 4768 ± 370 | 1 ± 1 | 1 ± 1 | 0.35 ± 0.03 |
| # 2 | 5942 ± 450 | 6952 ± 530 | 1 ± 1 | 18 ± 1 | 0.40 ± 0.05 | |
| # 3 | 13,640 ± 1000 | 15,005 ± 1100 | 4 ± 1 | 54 ± 4 | 0.35 ± 0.03 | |
| # 4 | 13,990 ± 1000 | 17,451 ± 1300 | 3 ± 1 | 24 ± 2 | 0.39 ± 0.05 | |
| # 5 | 21,410 ± 1600 | 32,115 ± 2440 | 3 ± 1 | 50 ± 4 | 0.39 ± 0.05 | |
| # 6 | 23,630 ± 1800 | 41,109 ± 3100 | 11 ± 3 | 74 ± 6 | 0.35 ± 0.03 | |
| # 7 | 23,500 ± 1800 | 40,861 ± 3100 | 11 ± 3 | 74 ± 6 | 0.35 ± 0.03 | |
| # 8 | 23,580 ± 1800 | 38,824 ± 2900 | 7 ± 2 | 65 ± 5 | 0.39 ± 0.05 | |
| # 9 | 28,400 ± 2200 | 46,851 ± 3600 | 7 ± 2 | 65 ± 5 | 0.39 ± 0.05 | |
| # 10 | 30,160 ± 2300 | 50,958 ± 3900 | 9 ± 3 | 69 ± 5 | 0.39 ± 0.05 | |
| # 11 | 41,040 ± 3100 | 71,610 ± 5400 | 13 ± 3 | 74 ± 6 | 0.39 ± 0.05 |
References
- Miziolek, W.; Palleschi, V.; Schechter, I. Laser–Induced Breakdown Spectroscopy (LIBS) Fundamentals and Applications; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Winefordner, J.D.; Gornushkin, I.B.; Correll, T.; Gibb, E.; Smith, B.W.; Omenetto, N. Comparing several atomic spectrometric methods to the super stars: Special emphasis on laser-induced breakdown spectrometry, LIBS, a future super star. J. Anal. At. Spectrom. 2004, 19, 1061–1083. [Google Scholar] [CrossRef]
- Flexer, V.; Baspineiro, C.F.; Galli, C.I. Lithium recovery from brines: A vital raw material for green energies with a potential environmental impact in its mining and processing. Sci. Total Environ. 2018, 639, 1188–1204. [Google Scholar] [CrossRef]
- Kesler, S.E.; Gruber, P.W.; Medina, P.A.; Keoleian, G.A.; Everson, M.P.; Wallington, T.J. Global lithium resources: Relative importance of pegmatites, brine and other deposits. Ore Geol. Rev. 2012, 48, 55–69. [Google Scholar] [CrossRef]
- Steinmetz, R.L.L.; Salvi, S. Brine grades in Andean salars: When basin size matters—A review of the Lithium Triangle. Earth Sci. Rev. 2021, 217, 103615. [Google Scholar] [CrossRef]
- BP. Statistical Review of World Energy, 71st ed. 2022. Available online: https://www.bp.com/statisticalreview (accessed on 3 September 2024).
- Steinmetz, R.L.; Salvi, S.; García, M.G.; Arnold, Y.J.P.; Béziat, D.; Franco, G.; Constantini, O.; Córdoba, F.E.; Caffe, P.J. Northern Puna Plateau-scale survey of Li brine-type deposits in the Andes of NW Argentina. J. Geochem. Explor. 2018, 190, 26–38. [Google Scholar] [CrossRef]
- Alessia, A.; Alessandro, B.; Maria, V.G.; Carlos, V.A.; Francesca, B. Challenges for sustainable lithium supply: A critical review. J. Clean. Prod. 2021, 300, 126954. [Google Scholar] [CrossRef]
- Balaram, V.; Santosh, M.; Satyanarayanan, M.; Srinivas, N.; Gupta, H. Lithium: A review of applications, occurrence, exploration, extraction, recycling, analysis, and environmental impact. Geosci. Front. 2024, 15, 101868. [Google Scholar] [CrossRef]
- Tabelin, C.; Dallas, J.; Casanova, S.; Pelech, T.; Bournival, G.; Saydam, S.; Canbulat, I. Towards a low-carbon society: A review of lithium resource availability, challenges and innovations in mining, extraction and recycling, and future perspectives. Miner. Eng. 2021, 163, 106743. [Google Scholar] [CrossRef]
- Swain, B. Recovery and recycling of lithium: A review. Sep. Purif. Technol. 2017, 172, 388–403. [Google Scholar] [CrossRef]
- García, L.V.; Ho, Y.C.; Myo Thant, M.M.; Han, D.S.; Lim, J.W. Lithium in a Sustainable Circular Economy: A Comprehensive Review. Processes 2023, 11, 418. [Google Scholar] [CrossRef]
- Hahn, D.W.; Omenetto, N. Laser–induced breakdown spectroscopy (LIBS), part I: Review of basic diagnostics and plasma-particle interactions: Still-Challenging Issues within the Analytical Plasma Community. Appl. Spectrosc. 2010, 64, 335A–366A. [Google Scholar] [CrossRef]
- Ytsma, C.R.; Dyar, M.D. Accuracies of lithium, boron, carbon, and sulfur quantification in geological samples with laser-induced breakdown spectroscopy in Mars, Earth, and vacuum conditions. Spectrochim. Acta Part B 2019, 162, 105715. [Google Scholar] [CrossRef]
- Ferreira, M.F.S.; Capela, D.; Silva, N.A.; Gonçalves, F.; Lima, A.; Guimaraes, D.; Jorge, P.A.S. Comprehensive comparison of linear and non-linear methodologies for lithium quantification in geological samples using LIBS. Spectrochim. Acta Part B 2022, 195, 106504. [Google Scholar] [CrossRef]
- Galli, E.; Massa, M.; Zanoletti, A.; De Iuliis, S.; Bontempi, E.; Depero, L.E.; Palleschi, V.; Borgese, L. Determination of lithium concentration in black mass using laser-induced breakdown spectroscopy hand–held instrumentation. Sci. Rep. 2025, 15, 17483. [Google Scholar] [CrossRef] [PubMed]
- St-Onge, L.; Kwong, E.; Sabsabi, M.; Vadas, E.B. Rapid analysis of liquid formulations containing sodium chloride using laser-induced breakdown spectroscopy. J. Pharm. Biomed. Anal. 2004, 36, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Erbetta, N.; Puebla, G.; Day, D.; Jennings, M.; Loureiro, A.; Green, C.; Gallardo, L.; Quiroz, W. Direct determination of lithium in brine samples using handheld LIBS without sample treatment: Sample introduction by venturi system. Anal. Methods 2024, 16, 7311–7318. [Google Scholar] [CrossRef]
- Xing, P.; Dong, J.; Yu, P.; Zheng, H.; Liu, X.; Hu, S.; Zhu, Z. Quantitative analysis of lithium in brine by LIBS based on convolutional neural network. Anal. Chim. Acta. 2021, 1178, 338799. [Google Scholar] [CrossRef]
- Molina, J.M.; Sarchi, C.; Tesio, A.Y.; Costa-Vera, C.; Díaz Pace, D.M. Quantitative Analysis of Lithium in Natural Brines from the Lithium Triangle by Laser-Induced Breakdown Spectroscopy. Atoms 2025, 13, 56. [Google Scholar] [CrossRef]
- Pace, D.M.D.; Molina, J.M. τ-algorithm for gathering spectroscopic information by modeling emission line shapes: Application to laser–induced plasmas. J. Opt. Soc. Am. B 2023, 40, C1–C7. [Google Scholar] [CrossRef]
- Zwicker, H. Evaluation of Plasma Parameters in Optically Thick Plasmas. In Plasma Diagnostics; Lochte–Holtgreven, W., Ed.; North-Holland Publishing: Amsterdam, The Netherlands, 1968; pp. 214–248. [Google Scholar]
- Moon, H.Y.; Herrera, K.K.; Omenetto, N.; Smith, B.W.; Winefordner, J.D. On the usefulness of a duplicating mirror to evaluate self-absorption effects in laser induced breakdown spectroscopy. Spectrochim. Acta Part B 2009, 64, 702–713. [Google Scholar] [CrossRef]
- Pace, D.M.D.; D’Angelo, C.A.; Bertuccelli, D.; Bertuccelli, G. Analysis of heavy metals in liquids using LIBS by liquid-to-solid matrix conversion. Spectrochim. Acta Part B 2006, 61, 929–933. [Google Scholar] [CrossRef]
- American Public Health Association. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2023; pp. 16–17. [Google Scholar]
- Cowan, R.D.; Dieke, G.H. Self-absorption of Spectrum lines. Rev. Mod. Phys. 1948, 20, 418–455. [Google Scholar] [CrossRef]
- Tanra, I.; Pardede, M.; Karnadi, I.; Hedwig, R.; Suliyanti, M.M.; Lie, Z.S.; Ramli, M.; Abdulmadjid, S.N.; Khumaeni, A.; Kurniawan, D.P.; et al. In–Situ Lithium Analysis in MgLi Alloys Using Laser–Induced Breakdown Spectroscopy with a Compact Chamber. ChemPhysChem 2024, 25, e202300843. [Google Scholar] [CrossRef]
- Radziemski, L.J.; Loree, T.R.; Cremers, D.A.; Hoffman, N.M. Time resolved laser-induced breakdown spectrometry of aerosols. Anal. Chem. 1983, 55, 1246–1252. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardenoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- McWhirter, R.W.P.; Huddlestone, R.H.; Leonard, S.L. (Eds.) Plasma Diagnostic Techniques; Academic Press: New York, NY, USA, 1965; Chapter 5; pp. 201–264. [Google Scholar]
- NIST Physical Measurement Laboratory. Atomic Spectra Database, version 5.10; NIST: Gaithersburg, MD, USA, 2022. Available online: https://www.nist.gov/pml/atomic-spectra-database (accessed on 7 July 2025).
- Aguilera, J.A.; Aragón, C. Characterization of a laser-induced plasma by spatially resolved spectroscopy of neutral atom and ion emissions. Spectrochim. Acta Part B 2004, 59, 1861–1876. [Google Scholar] [CrossRef]
- Díaz Pace, D.M.; D’Angelo, C.A.; Bertuccelli, G. Calculation of Optical Thicknesses of Magnesium Emission Spectral Lines for Diagnostics of Laser-Induced Plasmas. Appl. Spectrosc. 2011, 65, 1202–1212. [Google Scholar] [CrossRef]
- Sabsabi, M.; Cielo, P. Quantitative analysis of aluminum alloys by laser induced breakdown spectroscopy and plasma characterization. Appl. Spectrosc. 1995, 49, 499–507. [Google Scholar] [CrossRef]
- Aguilera, J.A.; Aragón, C. CSigma graphs: A new approach for plasma characterization in laser–induced breakdown spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 90–102. [Google Scholar] [CrossRef]
- Urruchua, F.C.; Fernández, M.A.; Jaworski, M.; Mendoza Zelis, P.; Olivelli, M.S.; Montes, M.L. Yerba mate waste: Transformation to magnetic composites for the adsorption of chemically diverse pollutants. J. Environ. Chem. Eng. 2023, 11, 110824. [Google Scholar] [CrossRef]

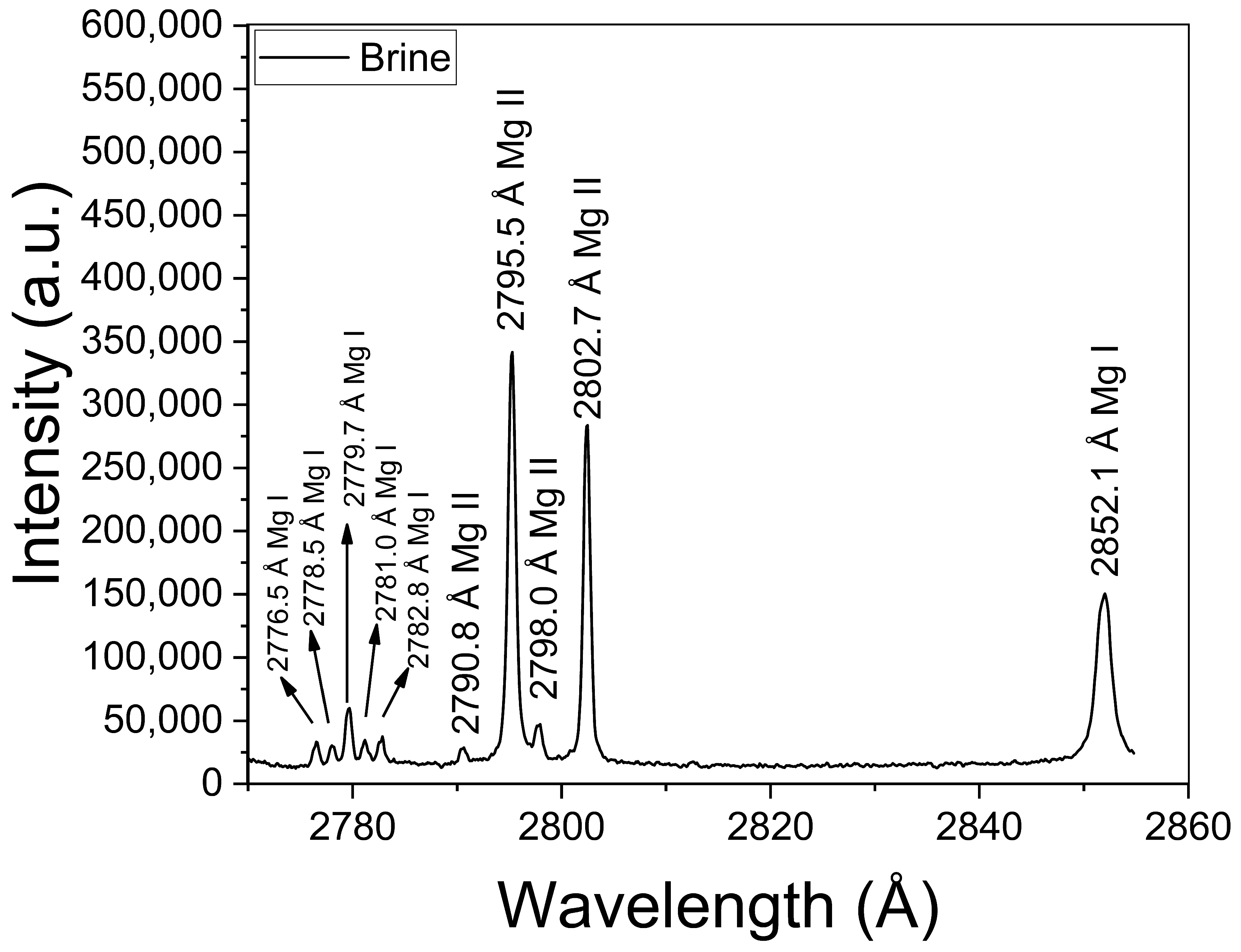


| Species | λ0 (Å) | Aki (108 s−1) | Ei (eV) | Ek (eV) | gi | gk |
|---|---|---|---|---|---|---|
| Mg I | 2776.5 | 1.32 | 2.712 | 7.175 | 3 | 5 |
| Mg I | 2778.5 | 1.82 | 2.709 | 7.170 | 1 | 3 |
| Mg I | 2779.7 | 1.36 | 2.712 | 7.170 | 3 | 3 |
| Mg I | 2781.0 | 5.43 | 2.717 | 7.173 | 5 | 3 |
| Mg I | 2782.8 | 2.14 | 2.717 | 7.170 | 5 | 3 |
| Mg I | 2852.1 | 4.91 | 0.000 | 4.345 | 1 | 3 |
| Mg II | 2790.8 | 4.01 | 4.422 | 8.864 | 2 | 4 |
| Mg II | 2795.5 | 2.60 | 0.000 | 4.434 | 2 | 4 |
| Mg II | 2798.0 | 4.79 | 4.434 | 8.863 | 4 | 6 |
| Mg II | 2802.7 | 2.57 | 0.000 | 4.422 | 2 | 2 |
| H I | 6563.0 | 0.44 | 10.199 | 12.087 | 8 | 18 |
| Li I | 6707.7 | 0.37 | 0.000 | 1.848 | 2 | 4 |
| Brine Samples | Li Concentration (ppm) | ||
|---|---|---|---|
| LIBS | AAS | ||
| Without SA Compensation | With SA Compensation | ||
| 1 | 42 ± 3 | 41 ± 3 | 45 ± 2 |
| 2 | 62 ± 5 | 77 ± 6 | 83 ± 4 |
| 3 | 213 ± 17 | 214 ± 18 | 141 ± 7 |
| 4 | 220 ± 18 | 248 ± 20 | 240 ± 12 |
| 5 | 402 ± 32 | 489 ± 39 | 477 ± 24 |
| 6 | 466 ± 37 | 636 ± 51 | 593 ± 30 |
| 7 | 462 ± 37 | 632 ± 51 | 626 ± 31 |
| 8 | 464 ± 38 | 599 ± 47 | 660 ± 33 |
| 9 | 625 ± 50 | 731 ± 58 | 710 ± 36 |
| 10 | 692 ± 55 | 798 ± 63 | 837 ± 42 |
| 11 | 1342 ± 107 | 1136 ± 91 | 852 ± 43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
M., J.M.; Aragón, C.; Aguilera, J.A.; Costa-Vera, C.; Díaz Pace, D.M. Improving Quantitative Analysis of Lithium in Brines Using Laser-Induced Breakdown Spectroscopy with τ–Algorithm (τLIBS). Atoms 2025, 13, 90. https://doi.org/10.3390/atoms13110090
M. JM, Aragón C, Aguilera JA, Costa-Vera C, Díaz Pace DM. Improving Quantitative Analysis of Lithium in Brines Using Laser-Induced Breakdown Spectroscopy with τ–Algorithm (τLIBS). Atoms. 2025; 13(11):90. https://doi.org/10.3390/atoms13110090
Chicago/Turabian StyleM., Juan Molina, Carlos Aragón, José A. Aguilera, César Costa-Vera, and Diego M. Díaz Pace. 2025. "Improving Quantitative Analysis of Lithium in Brines Using Laser-Induced Breakdown Spectroscopy with τ–Algorithm (τLIBS)" Atoms 13, no. 11: 90. https://doi.org/10.3390/atoms13110090
APA StyleM., J. M., Aragón, C., Aguilera, J. A., Costa-Vera, C., & Díaz Pace, D. M. (2025). Improving Quantitative Analysis of Lithium in Brines Using Laser-Induced Breakdown Spectroscopy with τ–Algorithm (τLIBS). Atoms, 13(11), 90. https://doi.org/10.3390/atoms13110090








