Computational and Spectroscopic Investigation of Diaminomethane Formation: The Simplest Geminal Diamine of Astrochemical Interest

Abstract

A high-level ab initio characterization and formation of diaminomethane (DAM), the simplest geminal diamine, is presented to support its spectroscopic detection and astrochemical relevance in the interstellar medium. The C_2v DAM conformer is identified as the global minimum, while C₁ DAM and C₂ DAM represent higher-energy local minima. The proposed reaction pathways are exothermic and proceed without activation barriers. Simulated infrared spectrum reproduces accurate key spectral signatures with several vibrational modes exhibiting strong IR intensities (>80 km mol⁻¹), particularly in the 800–3000 cm⁻¹ range and band shapes. Dipole moments and accurate rovibrational spectroscopic parameters, including rotational constants, anharmonic vibrational frequencies, quartic and sextic distortion constants, and nuclear quadrupole coupling constants are reported to assist with high-resolution spectroscopic identification. This study provides significant theoretical benchmarks for its formation and offers guidance for future laboratory spectroscopy and molecular searches in interstellar environments.

1. Introduction

A rising number of NH₃, NH₂, and NH-bearing species have been identified recently in the galactic core, increasing the likelihood of discovering different prebiotic complex organics in interstellar space [1]. Nitrogen-bearing complex organic molecules are particularly significant in terms of understanding the prebiotic chemistry of the interstellar medium (ISM) since they can be considered as an intermediary step in the production of biologically significant species such as nucleobases and amino acids [2].

In this context, nitrogen-rich species with geminal substitution patterns are especially intriguing, as they may represent key structural motifs in the progression toward biochemical complexity. Several such interstellar molecules featuring geminal substitution patterns have been identified in molecular clouds. Among these, acetone (CH₃)₂CO) has been observed towards hot cores such as Sgr B2(N) [3]. By contrast, aminoacetonitrile (NH₂CH₂CN) [4] and aminomethanol (NH₂CH₂OH), described as disubstituted methanes, are also key precursors in Strecker-type glycine formation, and have been detected in the same source. However, structurally simpler geminal diamines remain notably absent from the current interstellar inventory. Molecules such as diaminomethane ((NH₂)₂CH₂) represent such minimal geminal amine architectures. Among known N–C–N type interstellar molecules, viz. cyanamide (H₂N–C≡N) [5], carbodiimide (HN=C=NH) [6], and urea ((NH₂)₂CO [7], diaminomethane is the only fully saturated and symmetric diamine with such a backbone, where both –NH₂ groups are bonded to a central –CH₂– carbon.

Diaminomethane (hereafter referred to as DAM) is of particular astrochemical interest due to its bifunctional nature and compact geometry, allowing it to engage in both hydrogen bonding and radical recombination chemistry. Theoretical studies suggest that the structural simplicity of such species, coupled with their large dipole moments and active rotational spectra across the infrared to microwave range, makes them highly significant for detection via millimeter and submillimeter–wave radioastronomy in the interstellar medium [8,9,10,11]. Despite this astrochemical relevance, the conformational flexibility of DAM and its implications for detectability have not been fully addressed. An experimental study on DAM was performed by Marks et al. [12], in which they successfully synthesized DAM (CH₂(NH₂)₂) and characterized its spectroscopic properties. Their findings suggest that DAM could serve as a potential precursor to nucleobases in the interstellar medium [12]. Following this, a study addressing the detectability of DAM in the interstellar medium [13] has been reported, raising a question of further probability of finding more complex amines containing molecules in the space. Watrous et al. [13] provided the rotational constants for the C₁ and C₂ conformers, along with IR frequencies for the C_2v conformer for comparison with the experimental results obtained by Marks et al. [12]. While the conformational landscape of DAM has previously been investigated, including the identification of three minima on its potential energy surface, namely, a global minimum with C_2v symmetry (most stable), a higher-lying C₂ conformer above the minimum, and a higher-energy (less stable) C₁ conformer [12]. Previous high-level quantum chemical investigations, such as those by Watrous et al. [13], have restricted their analysis to the most stable C_2v form, largely in the context of benchmarking electronic structure methods. However, the astrochemical relevance and spectroscopic properties of the higher-energy conformers remain unexplored.

In this work, we address this gap by investigating the formation pathways of all three conformers under interstellar conditions. Specifically, we characterize the minimum energy geometries and harmonic vibrational spectra, compute rotational constants and dipole moments, and investigate formation pathways relevant to interstellar environments to support future observational identification. In particular, the formation of all three conformers of DAM is explored through radical–radical reaction mechanisms in the gas phase involving highly abundant and previously detected interstellar radicals. This choice is motivated by the well-established prevalence of such radicals (e.g., NH₃, NH₂, NH, CH₄, CH₂) in various astrophysical environments, which enhances the thermodynamic feasibility and kinetic accessibility of the proposed pathways. This comprehensive analysis establishes a molecular level framework for understanding the stability, detectability, and formation dynamics of DAM in astrochemical environments.

2. Methodology

2.1. Geometry Optimization and Vibrational Analysis

The molecular geometries of all relevant species including reactants, products were optimized using the B2PLYPD [14] functional in conjunction with the aug–cc–pVTZ basis set [15]. These methods were selected based on their ability to account for long-range dispersion interactions and their proven accuracy in astrochemical modeling. Vibrational frequency analyses at the same level of theory confirmed the nature of each optimized structure. Stationary points with no imaginary frequencies were confirmed as minima.

To improve the accuracy of the computed electronic energies, single-point energy calculations were performed at the CCSD [16,17,18] method in conjunction with aug–cc–pVTZ level using the B2PLYPD-optimized geometries. Additional calculations at the MP2/aug–cc–pVTZ [19,20,21,22,23] level were carried out to enable method comparison.

DFT-based quantum chemical computations provide a computationally efficient means of estimating energies and other chemical parameters with moderate accuracy. When modeling the interstellar formation of complex molecules, these reference approaches are frequently used [24,25,26,27,28,29,30,31,32,33,34,35,36]. Computational methods used in this study were mostly guided by benchmarking data from the literature, particularly those related to reactions involving radical species and nitrogen-containing functional groups [37,38,39]. The functional employed in our calculations provides a balanced description of energies and molecular properties, while higher-level coupled cluster methods were used where greater accuracy was required.

2.2. Reaction Energetics and Rate Constants

To assess the kinetic feasibility of the reaction mechanisms, potential energy surface (PES) scans were performed along relevant reaction coordinates to locate barrierless and exothermic pathways. The relative energies (ΔE) are computed as adiabatic differences between the energies plus corresponding ZPVEs of the optimized products and reactants.

Standard thermodynamic parameters including internal energy (ΔU), enthalpy (ΔH), and Gibbs free energy (ΔG) were computed at 298.150 K temperature and 1 atm using vibrational frequency data. Thermal corrections were included, and the net changes in these parameters for each reaction were calculated as follows:

$$Change in Internal energy (∆\mathrm{U})=⅀{∆\mathrm{U}}_{products}-⅀{∆\mathrm{U}}_{reactants}$$

$$Change in Enthalpy (∆\mathrm{H})=⅀{∆\mathrm{H}}_{products}-⅀{∆\mathrm{H}}_{reactants}$$

$$Change in Gibbs Free Energy (∆\mathrm{G})=⅀{∆\mathrm{G}}_{products}-⅀{∆\mathrm{G}}_{reactants}$$

For $∆\mathrm{U},∆\mathrm{G},∆\mathrm{H}<0,$ the reactions are exergonic and spontaneous.

Also, rate constants for the elementary steps were estimated using the Langevin capture theory [40], suitable for radical–radical interactions, as follows:

$$k=7.14\times {10}^{-10}{\alpha }^{1∕2}{\left(10∕\mu \right)}^{1∕2} {\mathrm{cm}}^3 {\mathrm{s}}^{-1}$$

where α is the polarizability (in ų) and μ is the reduced mass (in ¹²C amu). This approach, based on the Bates formalism, provides temperature-independent estimates suitable for interstellar conditions.

2.3. Vibro–Rotational and Nuclear Quadrupole Properties

Dipole moments and vibro–rotational constants including quartic and sextic distortion constants were computed at the ωB97XD/aug–cc–pVQZ level. A complete vibrational analysis including harmonic and anharmonic corrections was performed. Additionally, nuclear quadrupole coupling constants were calculated using the NMR module in Gaussian 16 at the same level of theory. Where available, these data were compared with experimental and theoretical values to ensure the reliability of predicted spectroscopic observables.

2.4. Spectroscopic Analysis: Infrared Spectroscopic Analysis

The infrared vibrational spectra of the C₁, C₂, and C_2v isomers of DAM were computed at the B2PLYPD/aug–cc–pVTZ level of theory. To simulate the IR spectra, a universal scaling factor of 0.9862 was applied to the computed harmonic frequencies to account for anharmonic effects and basis set deficiencies. The resulting spectra were convolved using a Gaussian line shape function with a full width at half maximum (FWHM) of 25 cm⁻¹, allowing for direct comparison with experimental or observational data.

The computational framework used in this work enabled a detailed exploration of the thermodynamic and kinetic aspects of the proposed reaction mechanisms. Four reaction pathways were identified as exothermic and barrierless, suggesting their significance in the formation of DAM under astrophysical conditions. Computational investigations were carried out using the Gaussian 16 program package [41].

3. Computational Result and Discussions

3.1. Reaction Mechanism and Potential Energy Profiles (PES)

The formation of DAM (CH₂(NH₂)₂) in the interstellar medium (ISM) can occur through different reaction pathways involving radicals, viz. NH, NH₂, CH₄, CH₃, CH₂, and CH₃NH₂ in the gas phase. The key reactants have all been detected in the ISM. These reactions are driven by the highly reactive nature of radicals and the low-temperature conditions typical of interstellar clouds, where activation barriers are minimized due to radical–radical recombination mechanisms [42].

Table 1 presents the total energies (in a.u. and kJ/mol) of the reactants and products at different computational levels (B2PLYPD and MP2) and same basis set. Additionally, the calculated rate constants at the temperature of 298.15 K for each reaction pathway are listed in Table 2, providing insights into the thermodynamic feasibility and kinetics of these reactions. The four exothermic and barrierless reaction routes are predicted for the formation of DAM. Figure 1 schematically represents the reaction mechanisms, illustrating the reactants and final products along each reaction route. The reaction pathways are color-coded: red for Reaction 1, green for Reaction 2, black for Reaction 3, and blue for Reaction 4.

Table 1. Total energies (a.u.) and relative energies in kJ/mol for the DAM at B2PLYPD/aug–cc–pVTZ and MP2/aug–cc–pVTZ level of DFT is listed.

	DAM (CH2(NH2)2)
	B2PLYPD		MP2
Reactants/Products	Total Energy	Relative Energy	Total Energy	Relative Energy
CH2	−39.092	−	−39.017	−
CH3	−39.783	−	−39.708	−
CH4	−40.443	−	−40.369	−
NH	−55.114	−	−55.030	−
NH2	−55.839	−	−55.757	−
CH3NH2	−95.749	−	−95.602	−
Reaction-1
CH4 + NH (R)	−95.557	−	−95.399	−
CH3NH2 (P)	−95.749	−503.190	−95.602	−533.462
CH3NH2 + NH (R)	−150.863	−	−150.633	−
C1 DAM (P)	−151.069	−541.436	−150.851	−573.572
Reaction-2
CH2 (1A1) + NH2 (R)	−94.931	−	−94.775	−
CH2NH2 (P)	−95.108	−465.123	−94.959	−484.363
CH2NH2 + NH2 (R)	−150.948	−	−150.716	−
C2v DAM (P)	−151.070	−321.495	−150.852	−356.144
Reaction-3
CH3NH2 + NH (R)	−150.863	−	−150.633	−
C1 DAM (P)	−151.069	−541.436	−150.851	−573.564
Reaction-4
CH3 + NH2 (R)	−95.622	−	−95.465	−
CH3NH2 (P)	−95.749	−333.460	−95.602	−360.114
CH3NH2 + NH (R)	−150.863	−	−150.633	−
C2 DAM (P)	−151.069	−541.441	−150.851	−572.107

Table 2. Calculated rate constants for DAM at B2PLYPD/aug−cc−pVTZ level of DFT is listed.

Reaction	Molecules	Rate Constants (cm3 s−1)
Reaction−1	CH4 + NH → CH3NH2	4.137 × 10−10
	CH3NH2 + NH → C1 DAM	4.262 × 10−10
Reaction−2	CH2 + NH2 → CH2NH2	4.321 × 10−10
	CH2NH2 + NH2 → C2v DAM	4.194 × 10−10
Reaction−3	CH3NH2 + NH → C1 DAM	4.262 × 10−10
Reaction−4	CH3 + NH2 → CH3NH2	4.137 × 10−10
	CH3NH2 + NH → C2 DAM	4.262 × 10−10

Figure 1. Schematic representation of reactants and products involved in the reaction pathways (Reaction 1–Red, Reaction 2–Green, Reaction 3–Black, Reaction 4–Blue). The same-colored arrows represent particular reaction routes. Color representations for atoms are gray–carbon, white–hydrogen, and blue–nitrogen.

Figure 2, Figure 3, Figure 4 and Figure 5 represent potential energy surface (PES) profiles for the formation of DAM via multiple radical-mediated reaction pathways under interstellar conditions. Each figure depicts graphs of a two–step process with energy variations along the reaction coordinate. The blue lines represent the first step (radical–radical recombination or hydrogen abstraction forming intermediates viz. CH₃NH₂ or CH₂NH₂), while the red lines represent the second step leading to different isomers of DAM (C₁, C₂, or C_2v).

3.2. Reaction Routes

• Reaction 1: From Methane (CH₄) and Imidogen (NH)

$$\mathbf{C}{\mathbf{H}}_{\mathbf{4}}+\mathbf{N}\mathbf{H}\to \mathbf{C}{\mathbf{H}}_{\mathbf{3}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}$$

$$\mathbf{C}{\mathbf{H}}_{\mathbf{3}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}+\mathbf{N}\mathbf{H}\to \mathbf{C}{\mathbf{H}}_{\mathbf{2}}(\mathbf{N}{\mathbf{H}}_{\mathbf{2}}{)}_{\mathbf{2}}$$

In the first pathway, CH₄ is a closed-shell, tetrahedral molecule and NH is a radical, highly reactive due to its singly occupied molecular orbital acting as initial reactants. Methane (CH₄) reacts with imidogen (NH) to form methylamine (CH₃NH₂). The reaction proceeds with energy −503.190 kJ/mol relative to reactants, indicating strong exoergicity and a rate constant of $4.137 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$. This occurs via hydrogen abstraction facilitated by the NH radical, which acts as a hydrogen acceptor, cleaving a C–H bond in CH₄ to form CH₃ radical and NH₂. Barrierless recombination occurs as the unpaired electrons pair to form the C–N bond. The PES (Figure 2) shows a steep energy well corresponding to the bond dissociation and abstraction process. The resulting CH₃NH₂ then undergoes a second reaction with another NH radical, where a hydrogen is abstracted from the methyl group, leading to the formation of C₁ DAM. This pathway is highly exothermic, with relative energy of −541.436 kJ/mol and a rate constant of $4.262 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$, and occurs without significant activation barriers, making it feasible under the low-temperature conditions of dense molecular clouds.

Figure 2. Schematic potential energy surface (PES) diagrams for the stepwise formation of C₁ DAM from methane (CH₄) and imidogen (NH). Relative energies (in kJ/mol) are computed at B2PLYPD/aug–cc–pVTZ.

• Reaction 2: From Methylene (CH₂) and Amidogen (NH₂)

$$\mathbf{C}{\mathbf{H}}_{\mathbf{2}}+\mathbf{N}{\mathbf{H}}_{\mathbf{2}}\to \mathbf{C}{\mathbf{H}}_{\mathbf{2}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}$$

$$\mathbf{C}{\mathbf{H}}_{\mathbf{2}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}+\mathbf{N}{\mathbf{H}}_{\mathbf{2}}\to \mathbf{C}{\mathbf{H}}_{\mathbf{2}}(\mathbf{N}{\mathbf{H}}_{\mathbf{2}}{)}_{\mathbf{2}}$$

In this reaction route, CH₂ and NH₂ are both open–shell radicals. Methylene (CH₂), a known reactive intermediate in the ISM, reacts directly with NH₂ via radical–radical recombination to form the CH₂NH₂ radical, forming a σ bond between carbon and nitrogen. Reactions of both CH₂ in its triplet (³B₁) and singlet (¹A₁) electronic states with the amino radical (NH₂) have been investigated, considering the possibility of spin-dependent reactivity. Although CH₂ (³B₁) is the electronic ground state of methylene in isolation, our results indicate that the CH₂NH₂ adduct formed via the singlet (¹A₁) pathway is more stable by ~191.7 kJ mol⁻¹ than that obtained through the triplet (³B₁) pathway. Thus, while both electronic states of CH₂ can, in principle, react with NH₂, the singlet channel is thermodynamically preferred.

It should be noted that in order for the triplet CH₂ (³B₁) to participate in the reaction, an intersystem crossing (³B₁ → ¹A₁) must first occur to conserve spin. This excitation introduces an energetic cost, effectively acting as a kinetic barrier to the triplet channel. In contrast, the reaction involving singlet CH₂ (¹A₁) with NH₂ proceeds without requiring spin inversion, leading to a barrierless and thermodynamically more favorable pathway. Consequently, while both reaction routes yield CH₂NH₂, the singlet pathway dominates under astrochemical conditions, whereas the triplet pathway may contribute only under circumstances where intersystem crossing is facilitated, such as on dust grains or via collisional processes.

PES (Figure 3) shows a direct plunge from reactants to a deep minimum corresponding to CH₂NH₂. This step releases −465.123 kJ/mol and has a rate constant of $4.321 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}.$ The radical then undergoes a secondary recombination with another NH₂ radical, yielding C_2v DAM with a relative energy of −321.495 kJ/mol and a rate constant of $4.194 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$. This step also lacks a transition state, with smooth energetic descent. C_2v DAM is the most stable isomer thermodynamically. This pathway demonstrates high reactivity of the CH₂ radical and the absence of activation barriers in radical–radical interactions, leading to the formation of C_2v DAM.

Figure 3. Schematic potential energy surface (PES) diagrams for the stepwise formation of C_2v DAM from methylene (CH₂) and amidogen (NH₂). Relative energies (in kJ/mol) are computed at B2PLYPD/aug–cc–pVTZ.

• Reaction 3: Direct Amination of Methylamine (CH₃NH₂)

$$\mathbf{C}{\mathbf{H}}_{\mathbf{3}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}+\mathbf{N}\mathbf{H}\to \mathbf{C}{\mathbf{H}}_{\mathbf{2}}(\mathbf{N}{\mathbf{H}}_{\mathbf{2}}{)}_{\mathbf{2}}$$

This is the most straightforward reaction, where methylamine (CH₃NH₂) directly reacts with an NH radical. Here, NH abstracts a hydrogen from the methyl group, forming the CH₂NH₂ radical, which then recombines with another NH₂ radical to produce C₁ DAM. The reaction is exothermic, with energy of −541.436 kJ/mol relative to the reactants and a rate constant of $4.262 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$. The entire PES (Figure 4) from CH₃NH₂ is one transition followed by a barrierless recombination. This pathway bypasses the need for complex intermediates, making it a potentially dominant formation mechanism in environments with high NH and CH₃NH₂ abundances.

Figure 4. Schematic potential energy surface (PES) diagrams for the formation of C₁ DAM from direct amination of methylamine (CH₃NH₂). Relative energies (in kJ/mol) are computed at B2PLYPD/aug–cc–pVTZ.

• Reaction 4: From Methyl (CH₃) and Amidogen (NH₂)

$$\mathbf{C}{\mathbf{H}}_{\mathbf{3}}+\mathbf{N}{\mathbf{H}}_{\mathbf{2}}\to \mathbf{C}{\mathbf{H}}_{\mathbf{3}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}$$

$$\mathbf{C}{\mathbf{H}}_{\mathbf{3}}+\mathbf{N}{\mathbf{H}}_{\mathbf{2}}\to \mathbf{C}{\mathbf{H}}_{\mathbf{3}}\mathbf{N}{\mathbf{H}}_{\mathbf{2}}$$

The fourth pathway involves the reaction of the methyl radical (CH₃) with NH₂, forming CH₃NH₂ through a direct radical combination. PES (Figure 5) reflects a steep descent to CH₃NH₂. This intermediate then reacts with NH through a mechanism analogous to Pathway 1, involving hydrogen abstraction and radical stabilization to ultimately form DAM (C₂ DAM). The CH₃ + NH₂ step has relative energy of −333.460 kJ/mol and a rate constant of $4.137 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$, while the conversion to C₂ DAM releases −541.441 kJ/mol, occurring at $4.262 \times {10}^{-10} {\mathrm{c}\mathrm{m}}^3{\mathrm{s}}^{-1}$. This highlights the role of NH as both a hydrogen abstractor and a stabilizing agent in the ISM.

Figure 5. Schematic potential energy surface (PES) diagrams for the stepwise formation of C₂ DAM from methyl (CH₃) and amidogen (NH₂). Relative energies (in kJ/mol) are computed at B2PLYPD/aug–cc–pVTZ.

All routes are energetically favorable. Across all four reactions, the PES profiles are characterized by strong exergonicity, making these pathways chemically viable under ISM conditions where thermal barriers cannot be overcome and relevant to the astrochemical origins of prebiotic molecules. The PES for each pathway is minimally activated and shaped by the radical character of the species involved. Rate constants are consistently high, supporting barrierless kinetics, and matching radical-driven ISM processes.

The computed total energies, reaction energies, and rate constants for the reactants, intermediates, and products show slight variations due to the difference in electron correlation treatment between these two levels of theory. The total energies of all species computed using the B2PLYPD functional are consistently lower (more negative) compared to those obtained from MP2. This suggests that B2PLYPD predicts a more stable electronic structure for these molecules than MP2. The total energy differences between the two functionals are ~572 kJ/mol, with B2PLYPD consistently computing lower energy (more stabilized) values relative to MP2. Given these observations, B2PLYPD appears to be the more reliable functional for modeling DAM formation under ISM conditions.

3.3. Conformers Energetics and Electronic Analysis

The computed dipole moments (μ), mean polarizabilities (α), and thermochemical functions; internal energy (ΔU), enthalpy (ΔH), and Gibbs free energy (ΔG) for the three conformers of DAM are summarized in Table 3. Calculations were performed using B2PLYPD/aug−cc−pVTZ and MP2/aug−cc−pVTZ levels of theory. The parameters reveal a strong energetic preference for the C₁ DAM and C₂ DAM. The results indicate that C_2v DAM is the most stable conformer, while C₁ DAM and C₂ DAM are nearly isoenergetic, with energy differences ≤ 3.6 kJ mol⁻¹. Such small energy separations suggest that under interstellar conditions, all three conformers may be populated, but C_2v DAM is expected to dominate, which is consistent with the barriers to interconversion and the hindered-rotor dynamics. At both levels of theory, the C_2v DAM conformer exhibits the highest dipole moment, with values of 1.760 D (B2PLYPD) and 1.835 D (MP2), suggesting a greater permanent charge separation. The lower symmetry C₁ DAM and C₂ DAM conformers exhibit slightly reduced dipole moments, with nearly identical values (~1.65 D at B2PLYPD and ~1.73–1.57 D at MP2), reflecting slight structural reorientations of the NH₂ groups. The polarizability values are nearly invariant across all conformers and computational levels, ranging between 5.241 and 5.336 ų, indicating minimal conformational influence on the overall electron cloud deformability.

Table 3. Dipole moment (µ) in debye (D), polarizability (α) in ų, relative energy (∆E), internal energy (∆U), enthalpy (∆H), and Gibbs free energy (∆G) relative to C_2v DAM in kJ/mol at MP2/aug–cc–pVTZ is listed.

Conformers	µ (D)	α (Å3)	∆E	∆U	∆H	∆G
C2v DAM	1.835	5.243	0.000	0.000	0.000	0.000
C1 DAM	1.733	5.241	2.087	2.255	2.253	1.901
C2 DAM	1.569	5.247	3.547	3.571	3.568	3.571

Table 4 details the dipole moment components (μ_a, μ_b, μ_c) along the principal rotational axes for all three conformers, computed at the MP2/aug−cc−pVTZ level, and compared with the literature values [12]. In the C_2v DAM, the dipole moment is strictly oriented along the b-axis (μ_b = −1.835 D), in agreement with its symmetric geometry and previous reports (μ = 1.72 D). The negligible components along μ_a and μ_c reflect its planarity and the presence of a mirror plane perpendicular to the dipole vector. The C₁ DAM conformer, being asymmetric and non-planar, exhibits significant dipole components along all three axes (μ_a = 1.279 D, μ_b = −0.180 D, μ_c = −1.157 D), resulting in a spatially distributed dipole (μ = 1.735 D). Such anisotropy in dipole orientation implies enhanced polar interactions and may affect its spectroscopic and condensed phase behavior. For the C₂ DAM, the dipole vector is predominantly aligned along the b-axis (μ_b = 1.569 D) with minor components along other axes, resembling the C_2v form in orientation but with a reduced magnitude, indicating some preservation of directional charge separation despite its lowered symmetry.

Table 4. Total dipole moment and their components (μ_a, μ_b, and μ_c) in debye (D) for C_2v, C₁, and C₂ DAM are computed at MP2/aug–cc–pVTZ level of theory and are listed.

Constant and Unit	C2v DAM		C1 DAM		C2 DAM
	Previous Work [12]	This Work	Previous Work [12]	This Work	Previous Work [12]	This Work
Dipole (D)	1.72	1.8353	1.22	1.7345	1.53	1.5687
μa (D)	–	−0.0006	–	1.2794	–	0.0011
μb (D)	–	−1.8353	–	−0.1798	–	1.5687
μc (D)	–	−0.0018	–	−1.1573	–	0.0007

3.4. Conformational Analysis

A comprehensive potential energy surface (PES) scan of C₁ DAM and C₂ DAM was performed with B2PLYPD in combination with the aug-cc-pVTZ basis set by systematically varying the dihedral coordinates defining the relative orientations of the amino groups with respect to the central methylene unit. This scan generated a discretized hypersurface that describes the conformational landscape of the molecule. Stationary points (minima and transition states) were located along the scan and were characterized by harmonic frequency analysis. Minima have no imaginary frequencies and transition states have a single imaginary frequency (frequency analyses were performed at the same level as the optimizations). The optimized geometries of the minima and transition states are shown in Figure 6, illustrating the torsional motion of the amino groups leading to conformational exchange.

Figure 6. Potential energy surface of C₁ DAM and C₂ DAM scan at the B2PLYPD/aug-cc-pVTZ level, depicting the optimized geometries of the conformers and transition states obtained along the scan. Relative energies are shown in kJ mol⁻¹.

The PES of C₁ DAM reveals one distinct minimum C₂ DAM separated by one transition state (TS1). The C₂ DAM scan produced multiple stationary points that we identify here using the labels provided; C₂ DAM as reference minimum; C₁ DAM as local minimum; C_2v DAM as global minimum; and TS1 and TS2 as transition states. C₂ DAM (reference minimum) is a relatively stable conformation representing a gauche–gauche arrangement of the amino groups. C₁ DAM (local minimum) is nearly isoenergetic with C₂ DAM (−1.3 kJ mol⁻¹ relative), likely corresponding to a different orientation of the NH₂ groups, such as a trans-gauche form. C_2v DAM (global minimum) is the most stable conformation (−3.3 kJ mol⁻¹ relative), exhibiting a near-planar arrangement stabilized by weak intramolecular N–H···N interactions. The transition states TS1 and TS2 in C₁ DAM and C₂ DAM respectively represent torsional barriers separating minima. In the C₁ DAM scan, TS1 (15.4 kJ mol⁻¹) connects C₁ DAM ↔ C₂ DAM, whereas in the C₂ DAM scan, TS1 (14.0 kJ mol⁻¹) connects C₂ DAM ↔ C₁ DAM, corresponding to the internal rotation of one amino group. TS2 (9.6 kJ mol⁻¹) connects C₂ DAM ↔ C_2v DAM, allowing direct relaxation into the global minimum geometry. The global minimum C_2v DAM is calculated to be ≈3.3 kJ mol⁻¹ more stable than the C₂ DAM reference and ≈2.0 kJ mol⁻¹ more stable than C₁ DAM.

These energy differences are small and the stabilization of C_2v DAM relative to other minima is consistent with intramolecular N–H···N interactions that reduce repulsion between lone pairs on the amino groups and permit a lower-energy conformation. The scan shows DAM exists in several nearly degenerate conformations, separated by small barriers of ~10–15 kJ mol⁻¹. In the interstellar medium, both thermal energy and tunneling are sufficient to ensure conformer exchange, shaping DAM’s observable spectra and its reactivity in astrochemical environments.

3.5. Rotational Spectroscopic Constants

The equilibrium and vibrationally corrected rotational constants (A, B, and C), along with quartic and sextic centrifugal distortion constants for C_2v, C₁, and C₂ DAM, were computed at ωB97XD/aug–cc–pVTZ level of theory. Also, nuclear quadrupole coupling constants including vibrational corrections are computed using NMR at the same level of theory. These data are summarized in Table 5. For comparison, the literature values for the equilibrium constants of the symmetric C_2v DAM conformer are also included. The calculated values are in good agreement with Marks et al.’s previous work [12].

Table 5. Rotational constants (A, B, and C) and quartic, sextic, and nuclear quadrupole coupling constants including vibrational corrections for C_2v, C₁, and C₂ DAM are computed at ωB97XD/aug–cc–pVTZ level of theory and are listed.

Constant and Unit	C2v DAM		C1 DAM	C2 DAM
	Previous Work [13]	This Work	This Work	This Work
Ae (MHz)	35,538.7	35,494.405	36,203.369	36,489.639
Be (MHz)	9156.0	9081.374	9278.307	9654.229
Ce (MHz)	8287.9	8230.010	8269.962	8384.761
A0 (MHz)	35,248.8	35,293.297	35,868.671	36,133.097
B0 (MHz)	9056.7	8978.241	9184.659	9562.709
C0 (MHz)	8191.6	8135.291	8183.081	8293.224
∆J (kHz)	8.039	7.645	8.168	8.184
∆K (kHz)	243.619	240.102	262.191	258.454
∆JK (kHz)	−26.568	−25.430	−31.827	−32.691
δj (kHz)	1.388	1.315	1.686	1.892
δk (Hz)	−909.344	−551.939	−635.356	−207.386
ϕJ (mHz)	12.081	10.980	13.653	11.706
ϕK (Hz)	6.815	6.609	6.783	6.414
ϕJK (mHz)	−11.778	−12.519	−37.659	−46.873
ϕKJ (Hz)	−1.987	−1.798	−1.649	−1.820
ϕj (mHz)	4.926	4.427	5.901	5.425
ϕjk (mHz)	31.208	30.259	16.849	29.790
ϕk (Hz)	−1.894	−1.232	0.542	0.151
χaa (MHz)	–	2.765	2.853	2.770
χbb–χcc (MHz)	–	6.571	6.475	6.309

The computed A_e, B_e, and C_e values exhibit conformer-specific trends, with the C₂ DAM conformer showing the largest A_e (36,489.639 MHz), indicative of a tighter rotational profile along the principal axis due to structural compaction or redistribution of mass. Correspondingly, vibrationally averaged rotational constants (A₀, B₀, C₀) reveal slight reductions across all conformers, reflecting zero-point vibrational effects. The C₁ DAM conformer exhibits intermediate values across both equilibrium and vibrationally averaged constants, which is consistent with its partially asymmetric geometry. The mean absolute percentage deviation for the equilibrium rotational constants (A_e: −0.12%, B_e: −0.82%, C_e: −0.70%) is approximately 0.55%, while that of the vibrationally corrected constants (A₀: +0.13%, B₀: −0.87%, C₀: −0.69%) is around 0.56%. This level of deviation falls well within the acceptable threshold for high-level DFT methods, consistent with the accuracy range (±0.1% to ±0.5%) deemed sufficient for spectroscopic applications [43]. Centrifugal distortion constants (Δ_J, Δ_K, Δ_JK, δ_j, δ_k) follow expected magnitudes for small polyatomic molecules. The quartic constants (Δ_J, Δ_K) and off-diagonal distortions such as Δ_JK show moderate variation between conformers, with the largest Δ_K observed for the C₂ DAM conformer (262.191 kHz), likely due to enhanced coupling of internal rotations and vibrational motions in its lower symmetry framework. The ϕ_JK parameter becomes significantly negative for both C₁ DAM and C₂ DAM (−37.659 and −46.873 mHz, respectively), suggesting stronger higher-order anharmonic interactions in these low-symmetry forms. Nuclear quadrupole coupling constants (χ_aa, χ_bb–χ_cc) are consistent across all three conformers, with χ_bb–χ_cc ~ 6.3–6.6 MHz, indicating that the electronic environment of the nitrogen nuclei remains relatively unaffected by conformational changes.

Rotational–vibrational coupling constants (α), which quantify the contribution of individual normal modes to changes in rotational constants upon vibrational excitation, are compiled in Table 6 for all 21 vibrational modes across the three conformers. The α-constants for each vibrational mode and rotational axis (A, B, C) provide detailed insight into the vibrational perturbations affecting molecular inertia. Among all modes, α₁–α₄, corresponding to low-frequency skeletal and NH₂ group motions, show consistently large values for all conformers, particularly at the a–axis (α₄ = 117.442 MHz for C₁ DAM), indicating their dominant influence on molecular rotation. In contrast, modes such as α₁₂–α₁₄ show divergent and often anomalously large contributions, reflecting strong anharmonic coupling or interactions between local and global vibrational motions. For instance, α₁₃ is extremely large for the C₂ DAM conformer (642.961 MHz), suggesting a mode highly coupled to internal geometry fluctuations. C_2v DAM, with its symmetric structure, shows more balanced α contributions across axes compared to C₁ DAM and C₂ DAM, where vibrational perturbations are more axis specific. This underlines the influence of molecular symmetry on rovibrational interaction anisotropy.

Table 6. The rotational–vibrational coupling constants (α) in MHz for C_2v, C₁, and C₂ DAM are computed at ωB97XD/aug–cc–pVTZ level of theory and are listed.

Constant	C2v DAM			C1 DAM			C2 DAM
	a	b	c	a	b	c	a	b	c
α1	98.103	−4.089	1.513	100.107	−3.055	1.054	71.456	6.086	4.710
α2	97.052	−4.088	1.424	100.342	−3.358	0.863	70.128	6.426	4.763
α3	102.426	0.809	1.833	105.738	1.188	1.494	88.820	4.584	3.979
α4	100.665	0.997	1.868	117.442	−3.594	1.135	91.174	3.723	3.840
α5	20.493	−1.570	−2.199	41.719	7.011	−3.932	11.438	−11.019	−6.779
α6	62.945	1.619	−2.532	59.878	6.961	−5.827	61.295	−5.311	−6.266
α7	61.871	4.000	−2.754	85.626	0.551	−5.366	−63.383	−1.459	−0.025
α8	84.069	1.179	−5.433	−51.289	0.313	0.853	−59.067	−2.457	−0.448
α9	49.722	23.665	−45.935	65.782	9.630	−48.853	98.710	−5.424	−56.359
α10	92.411	28.929	−28.766	48.767	−7.355	52.173	75.283	−3.441	64.002
α11	77.921	−42.699	57.333	42.339	19.402	−5.471	−15.426	7.896	−5.668
α12	−136.190	50.847	35.777	−60.432	−0.239	17.333	−519.439	−10.777	4.235
α13	6.905	36.435	27.775	145.079	22.541	−5.282	642.961	11.629	−9.659
α14	218.789	45.327	43.935	165.138	32.638	35.862	253.308	21.327	42.847
α15	2.310	6.504	−2.554	34.767	23.233	36.335	−52.095	38.328	29.175
α16	−46.715	20.627	23.389	−70.552	33.565	23.587	7.686	40.121	37.583
α17	−150.718	58.187	34.404	−111.143	42.326	26.074	28.695	9.111	7.985
α18	−170.765	33.679	15.740	21.301	20.134	17.278	40.267	13.332	17.118
α19	−261.895	1.650	17.409	−227.993	2.683	17.922	−207.490	7.609	22.434
α20	85.664	1.914	10.123	35.252	−1.508	5.416	−161.526	24.051	12.116
α21	7.144	10.285	7.0418	21.517	33.200	11.076	250.281	28.812	13.381

These parameters are essential for high-precision microwave spectroscopy, aiding in the identification of these conformers in laboratory conditions and their potential detection in the interstellar medium.

4. Spectroscopic Analysis

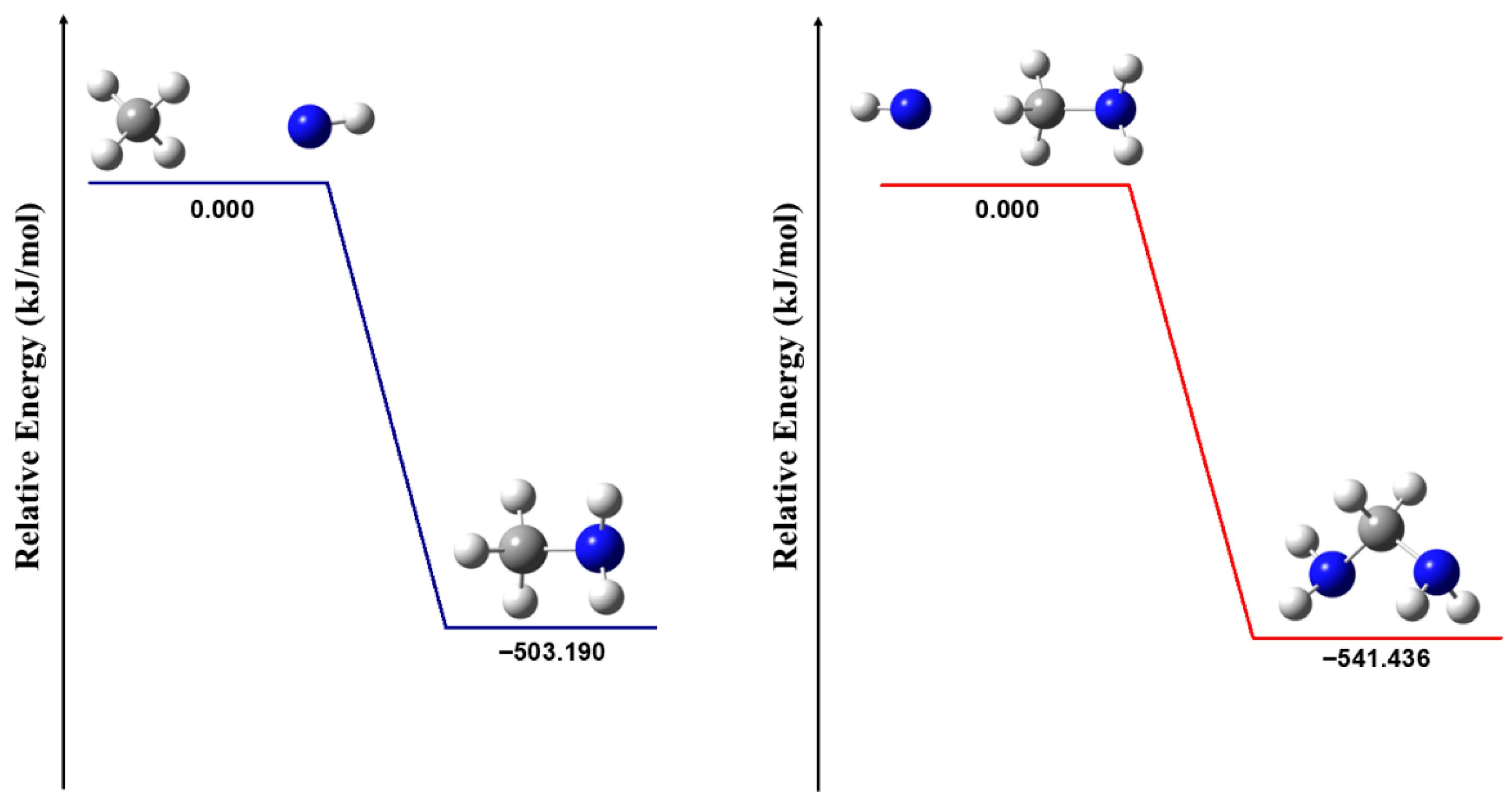
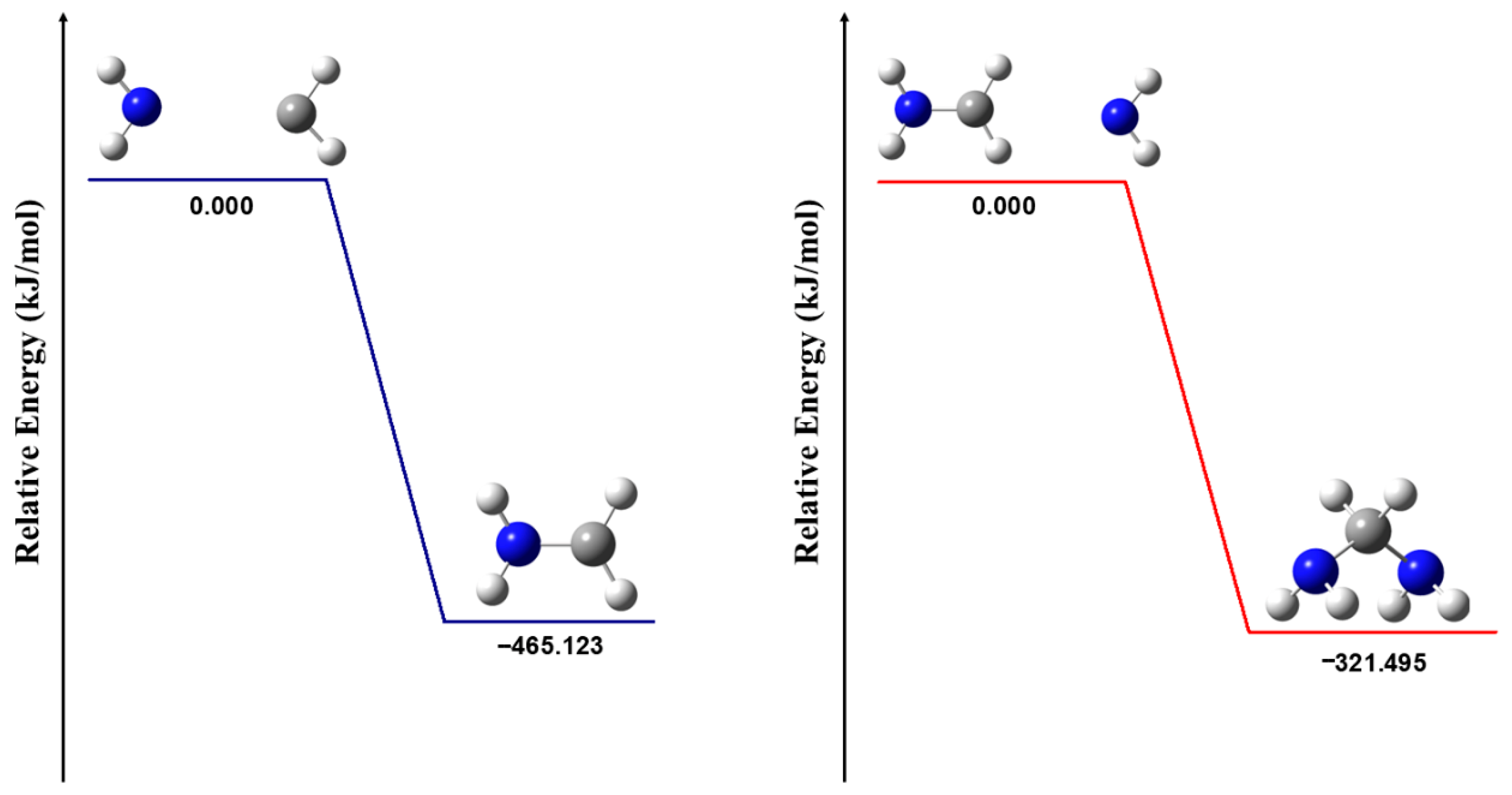
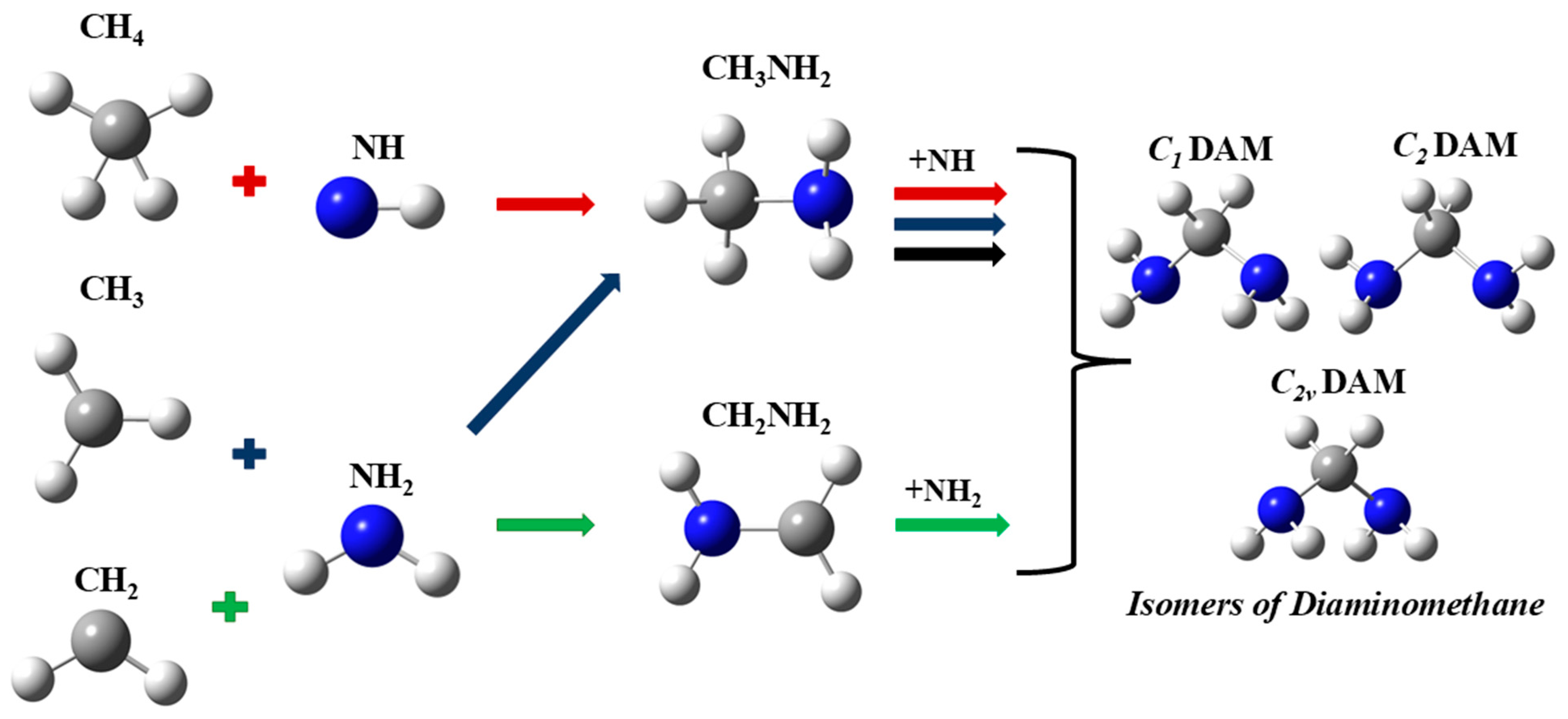
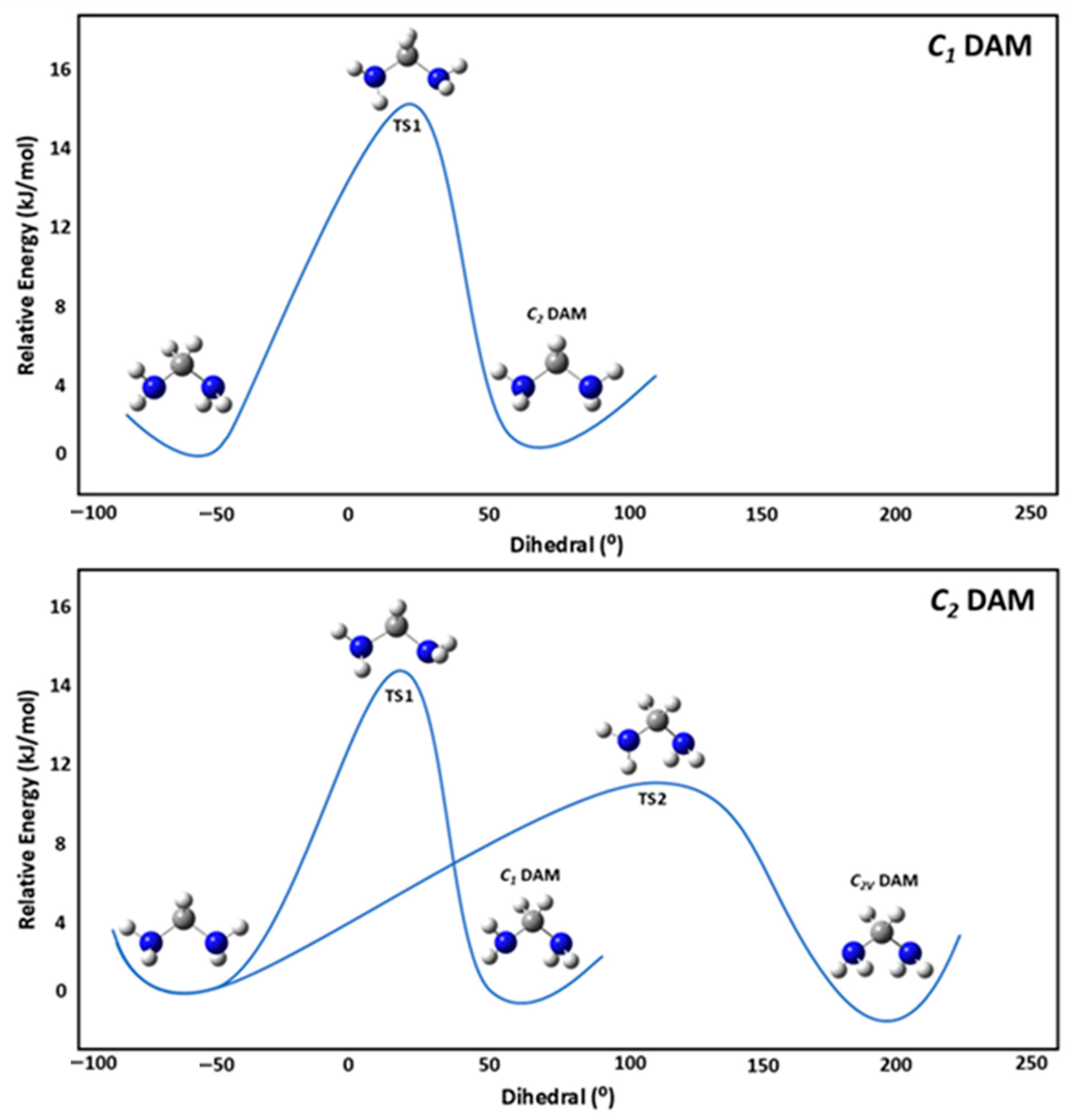
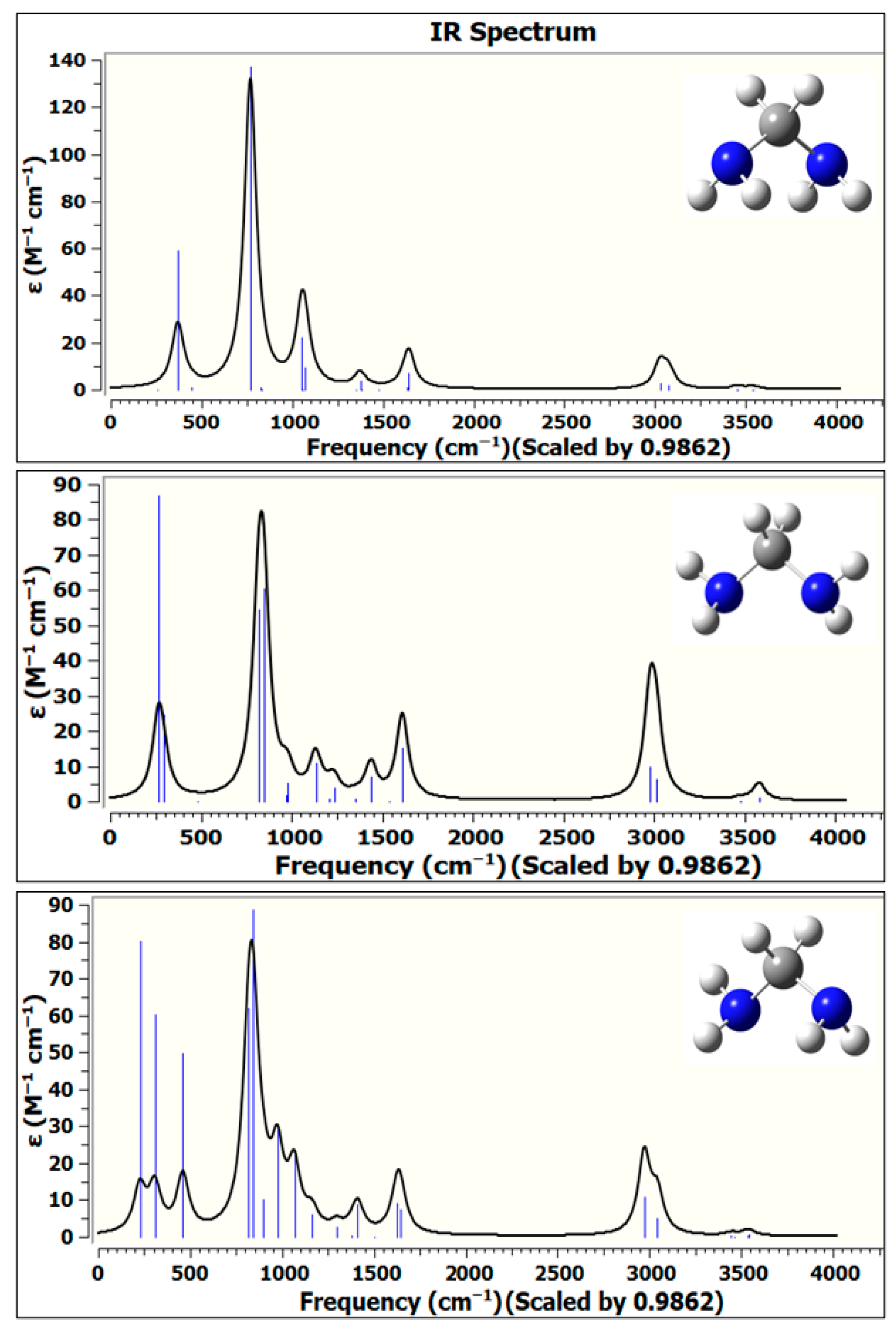
Infrared Spectral Analysis

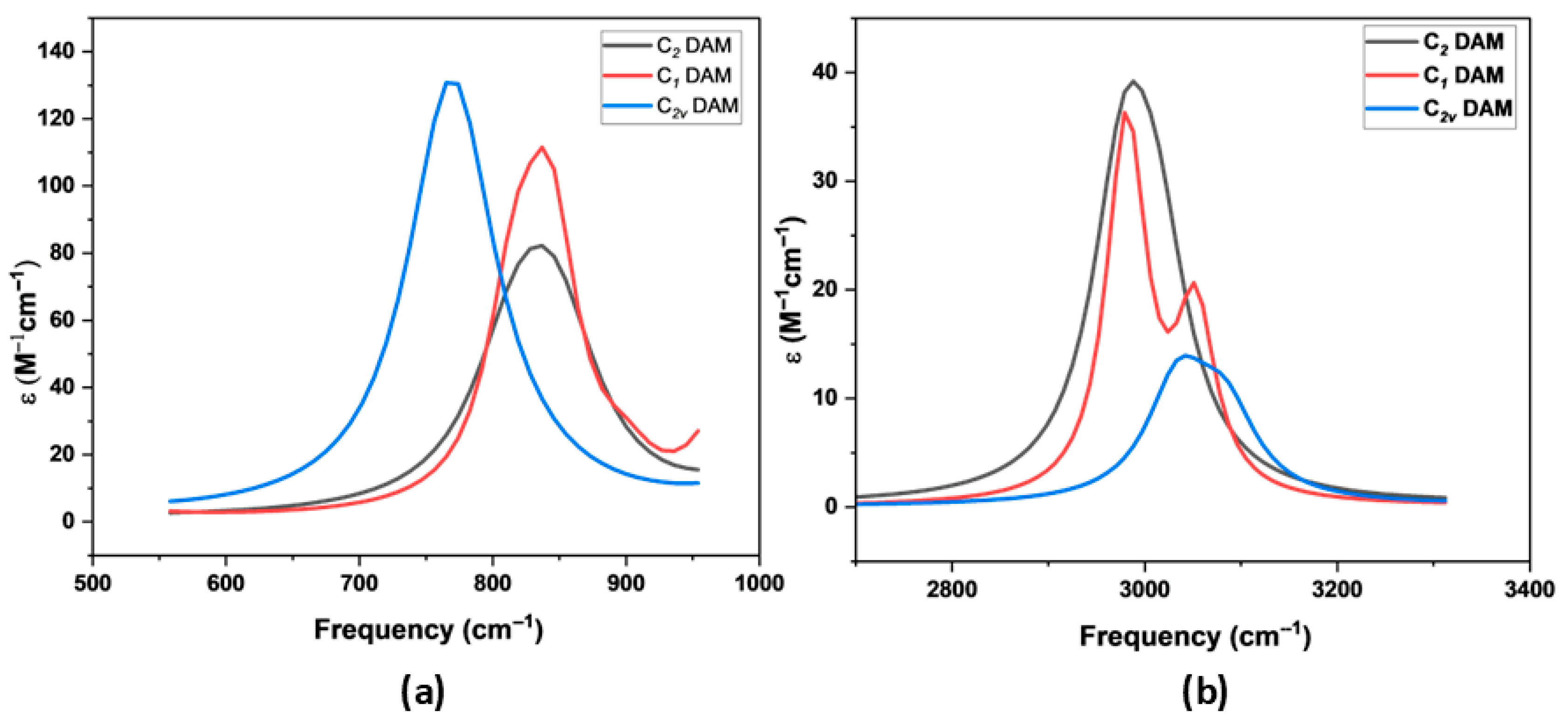
The infrared analysis of the spectrum for C₁ DAM, C₂ DAM, and C_2v DAM conformers of DAM were analyzed over the 0–4000 cm⁻¹ range, and provide detailed insights into its molecular vibrations, particularly involving its two amine groups and central methylene bridge (Figure 7). Detailed attention is given to two critical regions of the spectrum: 500–1000 cm⁻¹ and 2800–3400 cm⁻¹, where the most intense and diagnostic vibrational modes are observed. These zoomed-in views of both regions presented in Figure 8, reveal two major peaks: a high-intensity band from symmetric NH₂ rocking and another from anti-symmetric N–C stretching, both serving as key vibrational markers for distinguishing between the conformers. Table 7 presents the computed infrared vibrational frequencies and corresponding intensities and wavelengths for all three conformers. The data were computed using the B2PLYPD functional with the aug–cc–pVTZ basis set. Given the importance of accurately characterizing the vibrational modes of DAM, especially for spectroscopic identification and astrochemical applications, the infrared spectrum was generated with high precision. The spectral peaks were determined by Gaussian fitting of the computed IR absorption data, employing a full width at half maximum (FWHM) of 25 cm⁻¹.

Figure 7. Computed infrared spectrum of C₁ DAM, C₂ DAM, and C_2v DAM, as highlighted by different structures. Blue lines correspond to the vibration modes. The graph is broadened by 25 cm⁻¹ (FWHM).

Figure 8. Zoomed–in IR spectrum shows (a) high-intensity peaks at 847.3 cm⁻¹ (C₂ DAM), 842.7 cm⁻¹ (C₁ DAM), and 769.2 cm⁻¹ (C_2v DAM), attributed to symmetric NH₂ rocking and (b) intense peaks at 2978.4 cm⁻¹ (C₂ DAM), 2972.1 cm⁻¹ (C₁ DAM), and 3026.2 cm⁻¹ (C_2v DAM), which correspond to anti-symmetric CH stretching.

Table 7. Computed infrared (IR) frequencies (in cm⁻¹) and intensities (in km mol⁻¹), along with wavelength (λ in μ m) for C₁ DAM, C₂ DAM, and C_2v DAM are listed.

Vibrational Modes	C1 DAM			C2 DAM			C2v DAM
	Frequency	Intensity	λ	Frequency	Intensity	λ	Frequency	Intensity	λ
υ1	225.9	36	11.87	266.6	65	37.52	254.6	0	39.27
υ2	307.6	37	11.12	291.8	20	34.25	369.7	80	27.05
υ3	459.9	45	10.25	482.2	0	20.74	444.3	2	22.51
υ4	816.1	100	9.38	817.8	126	12.23	769.2	383	13.00
υ5	842.7	148	8.59	847.3	145	11.80	828.7	3	12.07
υ6	899.1	18	7.71	971.1	5	10.30	834.5	0	11.98
υ7	975.1	57	7.27	977.8	15	10.22	1053.6	85	9.49
υ8	1066.5	48	7.09	1132.7	34	8.83	1055.6	0	9.47
υ9	1163.4	14	6.66	1206.3	3	8.29	1072.7	37	9.32
υ10	1296.3	7	6.15	1234.3	14	8.10	1352.6	0	7.39
υ11	1375.6	1	6.08	1350.9	2	7.41	1374.5	18	7.28
υ12	1410.7	24	3.36	1437.9	28	6.96	1383.3	0	7.23
υ13	1501.1	0	3.29	1536.3	0	6.51	1478.7	0	6.76
υ14	1626.5	29	2.90	1611.3	68	6.21	1631.4	7	6.13
υ15	1645.3	24	2.89	1613.7	2	6.20	1642.4	43	6.09
υ16	2972.1	64	2.83	2978.4	82	3.36	3026.2	31	3.31
υ17	3043.6	31	2.82	3013.1	53	3.32	3074.5	22	3.25
υ18	3444.2	2	11.87	3474.4	2	2.88	3450.8	2	2.90
υ19	3459.1	1	11.12	3477.4	0	2.88	3454.8	3	2.89
υ20	3533.6	1	10.25	3578.1	6	2.80	3538.4	3	2.83
υ21	3542.8	4	9.38	3579.2	9	2.79	3543.2	1	2.82

A scaling factor of 0.9862 was applied to both the vibrational frequencies and the zero-point vibrational energies (ZPVEs). This scaling factor follows well-established computational protocols and is supported by the benchmarking results of Alecu et al. [44], who recommended a universal scaling factor ratio of λ_harm/λ_ZPVE = 1.014 ± 0.002. This corresponds to an experimental correction ratio of approximately 0.9862 for ZPVE, ensuring that the computed vibrational data more accurately reflect true molecular behavior. This correction is consistent with and further substantiated by our computational methodology [45].

The C_2v DAM spectrum displays diverse vibrational modes across the low and high wavenumber regions. At the low frequency region, the peak at 254.6 cm⁻¹ (39.26 μm) (very weak intensity) is assigned to rocking vibrations of hydrogen atoms on both NH₂ groups, specifically an anti-symmetric out-of-plane bending (OPB) mode. Moving up the spectrum, a significant absorption at 369.7 cm⁻¹ (27.05 µm) with high intensity (79 km mol⁻¹) corresponds to a twisting motion of H atoms on the NH₂ groups, accompanied by CH₂ rocking, indicative of a symmetric NH₂ out-of-plane bending. A moderate peak at 444.3 cm⁻¹ (1 km mol⁻¹, 22.50 µm) is associated with N–C–N wagging, which reflects the collective bending of the nitrogen atoms relative to the central carbon. At 769.2 cm⁻¹ (2.99 µm), a strong and highly intense band with an intensity of 383 km mol⁻¹ represents symmetric rocking of the NH₂ groups, a key diagnostic feature of primary amines. The next significant region is near 828.7 cm⁻¹ (12.07 µm), attributed to asymmetric N–C stretching, whereas 834.5 cm⁻¹ (11.98 µm) is a result of CH₂ rocking coupled with anti-symmetric twisting of the NH₂ groups. In the mid-IR region, 1053.6 cm⁻¹ (9.49 µm) shows a strong absorption (85 km mol⁻¹) from symmetric N–C stretching, a fundamental skeletal vibration, followed by a weak mode at 1055.6 cm⁻¹ that is linked to NH₂ and CH₂ twisting. Another notable skeletal vibration is the N–C–N symmetric stretching at 1072.7 cm⁻¹ (9.32 µm) with a moderate intensity of 36 km mol⁻¹, indicating structural stability along the backbone. Subsequent vibrations such as NH₂ twisting at 1352.6 cm⁻¹, CH₂ in-plane rocking at 1374.5 cm⁻¹, and a very weak symmetric H twist at 1383.3 cm⁻¹ further highlight internal rearrangements. The H–C–H rocking at 1478.7 cm⁻¹ and H–N–H anti-symmetric and symmetric bending modes at 1631.4 cm⁻¹ and 1642.4 cm⁻¹, respectively, demonstrate characteristic bending vibrations of the NH₂ groups. In the high-frequency region, CH₂ symmetric and asymmetric stretching modes appear at 3026.2 cm⁻¹ (λ ≈ 3.30 µm) and 3074.5 cm⁻¹ (λ ≈ 3.25 µm), showing moderate intensities. The NH₂ symmetric and asymmetric N–H stretches, often termed as amino stretches, are observed prominently in the 2800–3500 cm⁻¹ range, corresponding to wavelengths between 2.80 and 3.50 µm. Specifically, symmetric N–H stretches occur at 3450.8 cm⁻¹ and 3454.8 cm⁻¹, while asymmetric N–H stretches appear at 3538.4 cm⁻¹ and 3543.2 cm⁻¹, though with relatively lower intensities, which is typical for primary amines due to intermolecular hydrogen bonding and coupling effects.

To further validate our vibrational analysis, we compared the most important diagnostic IR modes of the C_2v DAM obtained in this work with those reported by Watrous et al. [13]. The agreement is very good across the spectral region. For the NH₂ stretching vibrations, our scaled harmonic frequencies predict an asymmetric stretch near 3490 cm⁻¹ and a symmetric stretch near 3380 cm⁻¹, while Watrous et al. [13] reported corresponding bands at 3482 and 3372 cm⁻¹, respectively (Δ < 10 cm⁻¹). The NH₂ scissoring mode is reproduced at 1615 cm⁻¹ in our work versus their value of 1625 cm⁻¹. Likewise, the CH₂ stretching region (2930–2985 cm⁻¹) differs by less than 15 cm⁻¹ from the previous values [13], and the NH₂ wagging/twisting modes in the 700–900 cm⁻¹ region are reproduced within 5–10 cm⁻¹. Such close agreement between the two independent computations confirms the robustness of our vibrational assignments and provides confidence that the predicted spectrum is reliable for astrochemical identification.

The C₂ DAM conformer exhibits prominent IR absorptions associated with various NH₂ group motions and CH₂/NC vibrations. The strongest IR active mode is the NH₂ anti-symmetric wagging at 847.3 cm⁻¹ with an intensity of 145 km mol⁻¹, indicating a significant dipole change along this vibrational coordinate. Another intense mode is the symmetric NH₂ rocking at 817.8 cm⁻¹ (126 km mol⁻¹), reinforcing the presence of strongly IR-active NH₂ group dynamics in this geometry. At higher wavenumbers, the C–H stretching vibrations are observed near 2978.4 cm⁻¹ (sym, intensity: 82 km mol⁻¹) and 3013.1 cm⁻¹ (anti-sym, 53 km mol⁻¹), which are typical for aliphatic CH groups. The NH₂ bending modes around 1611.3 cm⁻¹ (anti-sym, 68 km mol⁻¹) and 1613.7 cm⁻¹ (sym, 2 km mol⁻¹) further demonstrate significant out-of-plane deformation vibrations. A noteworthy feature is the N–C anti-symmetric stretch at 1132.7 cm⁻¹ with high intensity (34 km mol⁻¹), aiding potential identification. The CH₂ in-plane rocking and wagging/twisting modes between 1234 and 1438 cm⁻¹ show moderate intensities and suggest conformer-specific flexibility in methylene motion. The amino H stretching vibrations are found in the 3474–3579 cm⁻¹ region with relatively weak intensities (maximum 9 km mol⁻¹), consistent with free or weakly hydrogen-bonded NH₂ groups.

The C₁ DAM conformer, characterized by lower symmetry, shows slightly shifted but comparable vibrational modes with some distinctions in IR intensities, reflecting geometric variations. The NH₂ anti-symmetric wagging at 842.7 cm⁻¹ (148 km mol⁻¹) is the most intense peak, similar to C₂ DAM, but slightly red-shifted. The NH₂ rocking (816.1 cm⁻¹, 100 km mol⁻¹) and N–C anti-symmetric stretching (1066.5 cm⁻¹, 48 km mol⁻¹) also remain significant, underscoring the NH₂-related modes as dominant IR-active features in both conformers. Compared to C₂ DAM, the N–C symmetric stretch at 899.1 cm⁻¹ is weaker (18 km mol⁻¹) but still observable. The CH₂ wagging and rocking modes between 1296.3 and 1410.7 cm⁻¹ show slight shifts and moderate intensities, hinting at conformational flexibility. The C–H stretching region (2972–3043 cm⁻¹) shows strong absorptions with slightly lower intensity compared to C₂ DAM (2972.1 cm⁻¹, 64 km mol⁻¹). NH bending modes appear at 1626.5 cm⁻¹ (anti−sym, 29 km mol⁻¹) and 1645.3 cm⁻¹ (sym, 24 km mol⁻¹), indicating vibrational coupling differences due to asymmetric geometry. The amino hydrogen stretching modes between 3444 and 3542 cm⁻¹ are weak in intensity (all below 4 km mol⁻¹), similar to C₂ DAM, supporting the general IR inactivity of these high-frequency vibrations unless involved in strong interactions.

Compared to structurally analogous species such as methylamine (CH₃NH₂) and ethylenediamine (NH₂CH₂CH₂NH₂) [46], DAM conformers exhibit enhanced vibrational complexity due to their geminal diamine structure, leading to multiple coupled NH₂ modes. The dominance of NH₂ out-of-plane deformations in the IR spectrum of DAM parallels trends observed in other interstellar amines, reaffirming the diagnostic significance of these vibrations. Specifically, high dipole moment changes during NH₂ wagging and CH₂ bending motions are consistent with efficient IR excitation and radiative decay pathways, which can be exploited for remote sensing in the gas phase.

Given the high IR intensities of wagging, rocking, and bending modes associated with NH₂ and CH₂ groups, particularly in the 600–1200 cm⁻¹ region, all three conformers present spectroscopically observable fingerprints for gas-phase detection in laboratory simulations or astronomical environments. The presence of multiple vibrational modes with intensities exceeding 80 km mol⁻¹ indicates strong dipole moment changes during vibration, which significantly enhances its detectability in both astronomical observations and atmospheric studies.

5. Conclusions

In this study, we report a high-level quantum chemical investigation of all three conformers of diaminomethane, the simplest geminal diamine of astrochemical relevance. The formation of DAM via four radical–radical reaction routes was proposed, involving the most abundant and pre-detected interstellar precursors. All reactions were found to be barrierless and highly exothermic, with reaction energies ranging from −321.5 to −541.4 kJ mol⁻¹, and corresponding rate coefficients on the order of 4.2 × 10⁻¹⁰ cm³ s⁻¹, suggesting efficient formation in cold interstellar environments. Among them, C_2v DAM was found to be the PES global minimum, while C₁ DAM and C₂ DAM conformers represent energetically accessible local minima, with relative ΔG values of 1.901 and 3.571 kJ mol⁻¹, respectively, relative to C_2v DAM. Infrared spectral analysis revealed intense vibrational modes, notably NH₂ wagging and rocking around 842–847 cm⁻¹, with intensities of up to 148–383 km mol⁻¹, providing diagnostic features for astrophysical detection. The computed rotational constants (A, B, C) and dipole moments (1.76–1.83 D for C_2v DAM) further support the potential millimeter–submillimeter detectability of DAM conformers. Nuclear quadrupole coupling constants were also provided to aid high-resolution spectroscopic identification. These results provide key spectroscopic fingerprints and robust formation pathways that support future astronomical searches for DAM and similar saturated N–C–N bearing species. This work thus provides critical theoretical benchmarks for incorporating DAM into astrochemical networks and motivates its laboratory spectroscopic characterization and potential astronomical detection in nitrogen-rich star-forming regions.