Resonance States of Negative Hydrogen-like Ions in Quantum Plasmas
Abstract
1. Introduction
2. Theory
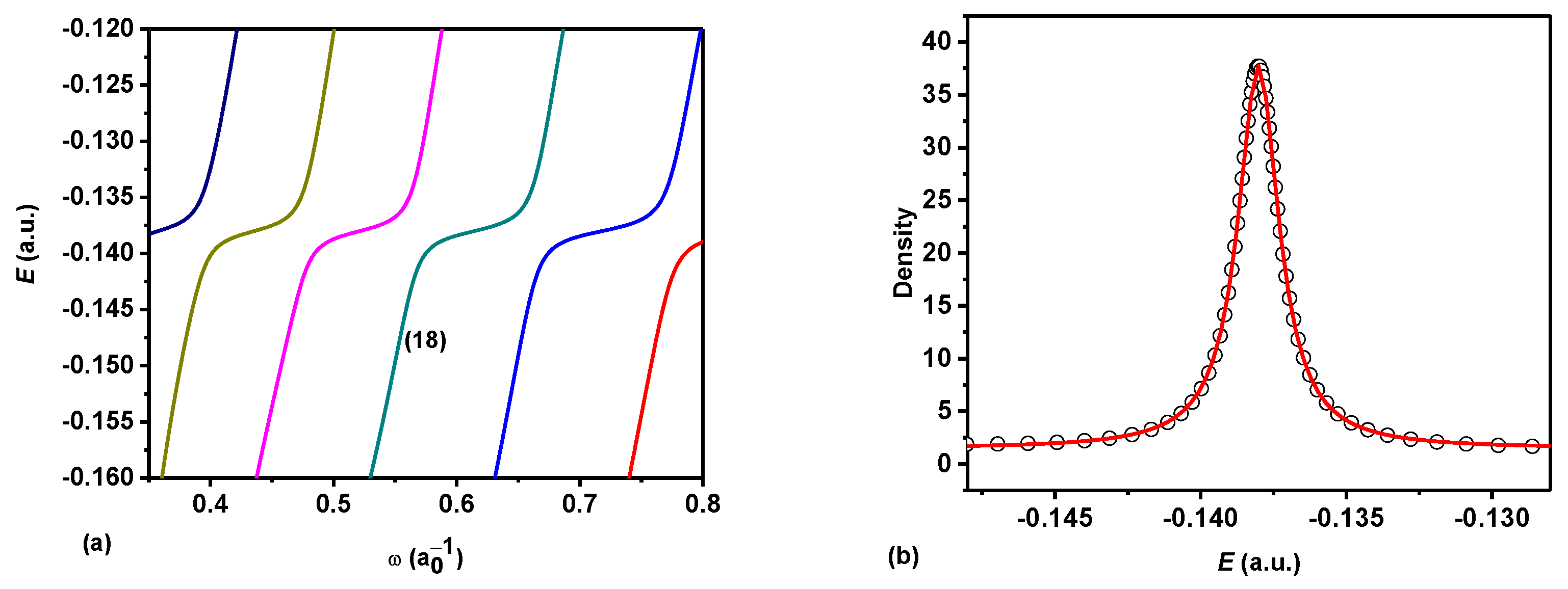
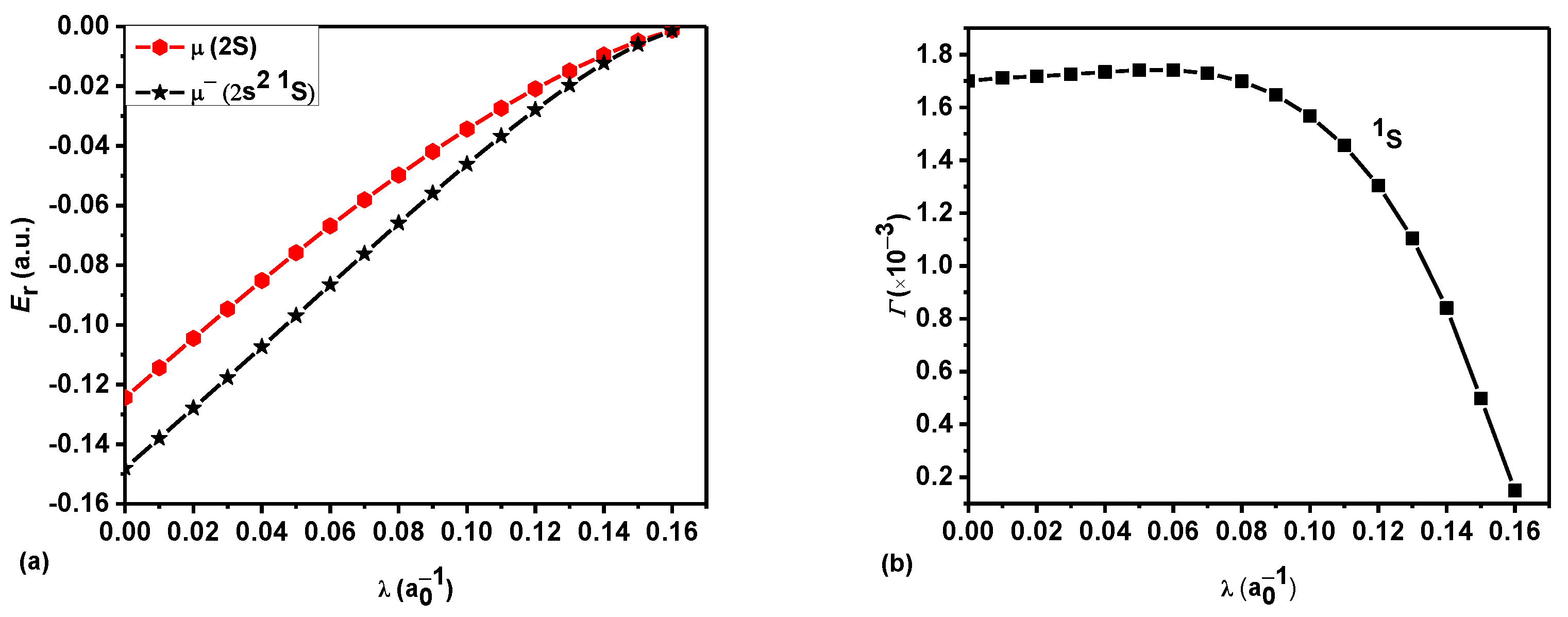
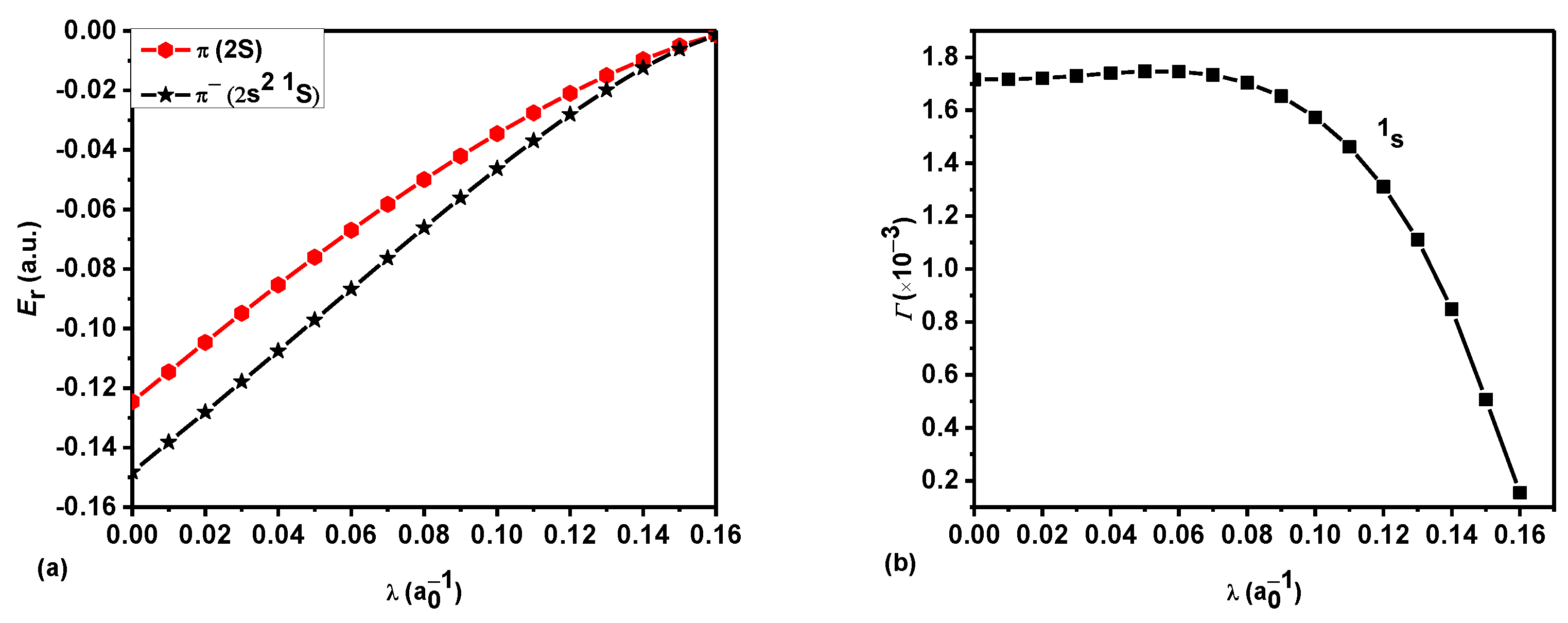
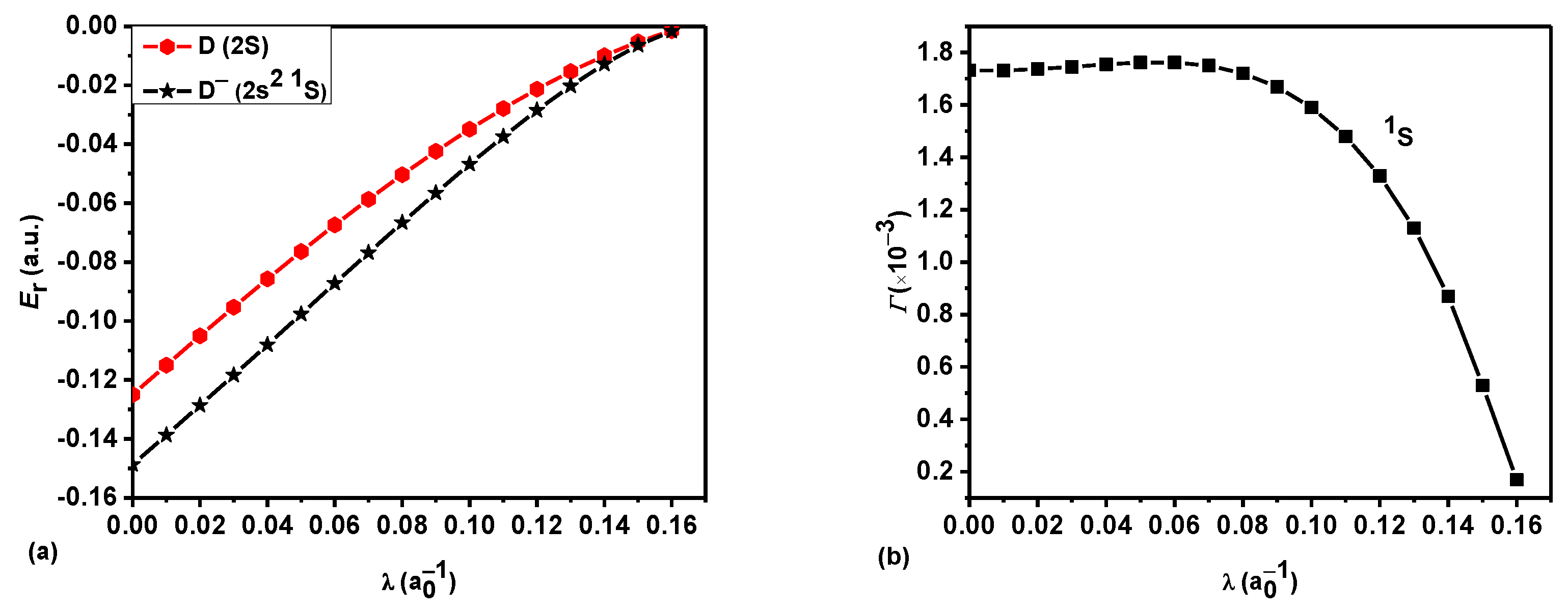
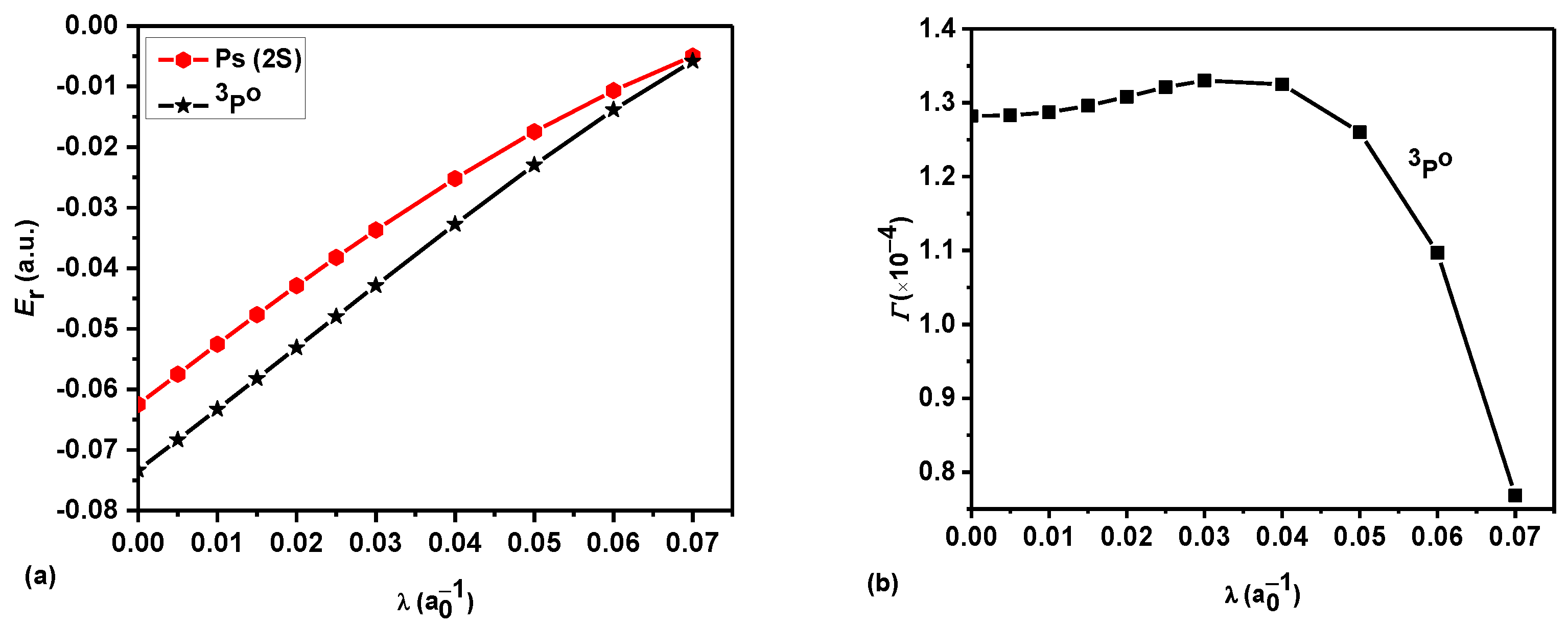
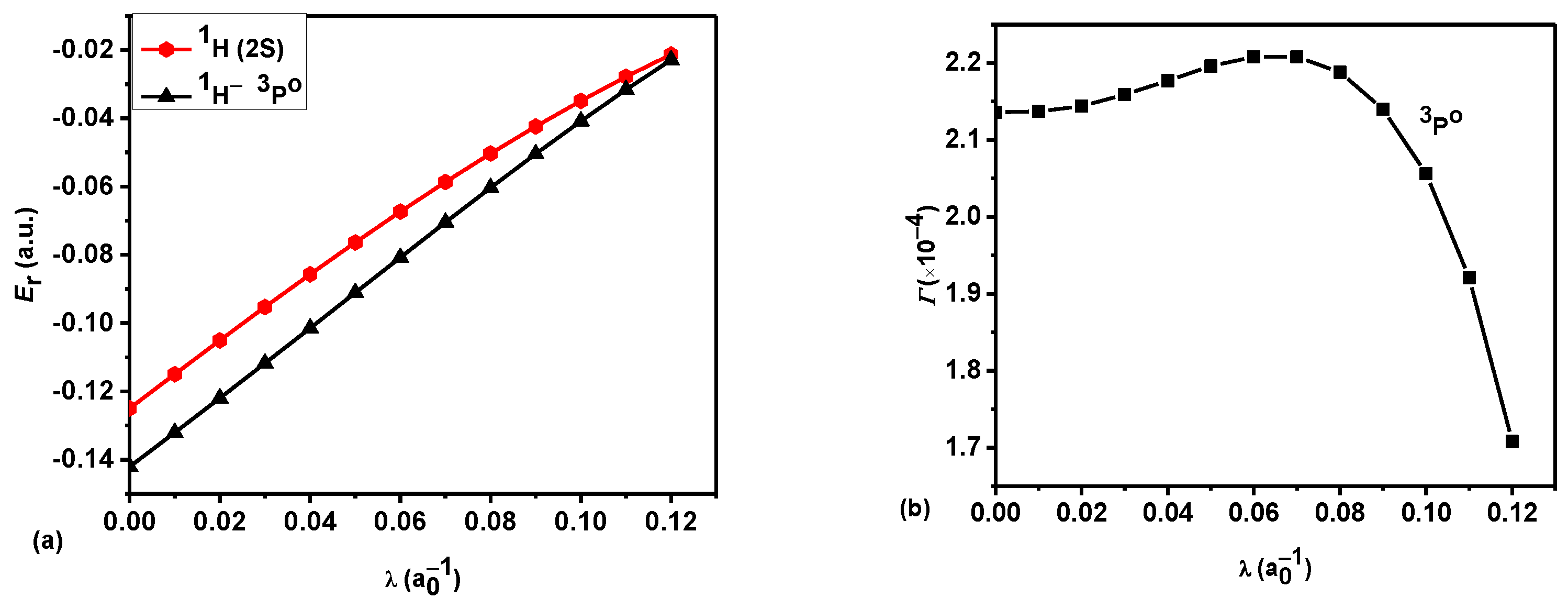
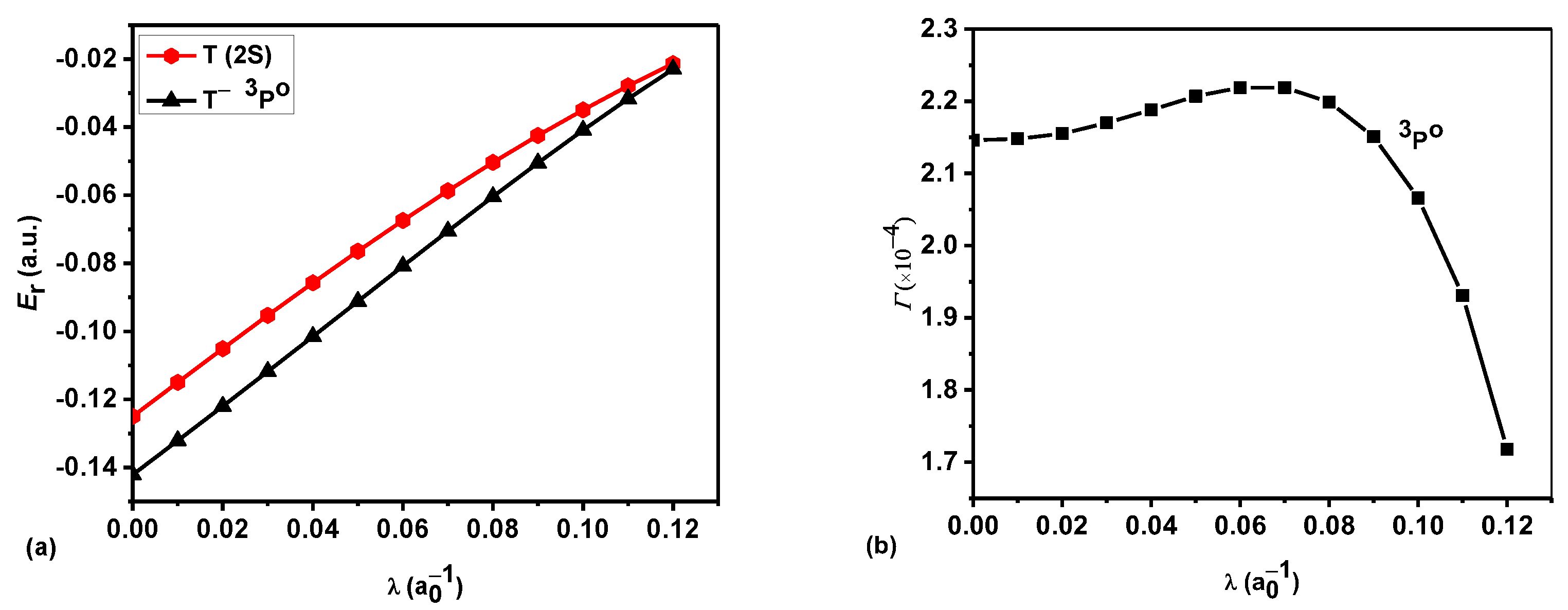
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wheeler, J.A. Polyelectrons. Ann. N. Y. Acad. Sci. 1946, 48, 219–238. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Observation of the positronium negative ion. Phys. Rev. Lett. 1981, 46, 717–720. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Measurement of the decay rate of the positronium negative ion. Phys. Rev. Lett. 1983, 50, 671–674. [Google Scholar] [CrossRef]
- Ho, Y.K. Autoionization states of the positronium negative ion. Phys. Rev. A 1979, 19, 2347–2352. [Google Scholar] [CrossRef]
- Ho, Y.K. Doubly excited resonances of positronium negative ions. Phys. Lett. A 1984, 102, 348–350. [Google Scholar] [CrossRef]
- Botero, J. Adiabatic study of the positronium negative ion. Phys. Rev. A 1987, 35, 36–50. [Google Scholar] [CrossRef]
- Ward, S.J.; Humberston, J.W.; McDowell, M.R.C. Elastic scattering of electrons (or positrons) from positronium and the photodetachment of the positronium negative ion. J. Phys. B At. Mol. Phys. 1987, 20, 127–149. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Ho, Y.K. Complex-coordinate calculation of 1,3P resonances in Ps using Hylleraas functions. Phys. Rev. A 1990, 42, 1119–1122. [Google Scholar] [CrossRef]
- Ho, Y.K.; Bhatia, A.K. 1,3Po resonance states in positronium ions. Phys. Rev. A 1991, 44, 2890–2894. [Google Scholar] [CrossRef]
- Rost, J.M.; Wintgen, D. Positronium negative ion: Molecule or Atom? Phys. Rev. Lett. 1992, 69, 2499–2502. [Google Scholar] [CrossRef]
- Ho, Y.K.; Bhatia, A.K. P-wave shape resonances in positronium ions. Phys. Rev. A 1993, 47, 1497–1499. [Google Scholar] [CrossRef]
- Ho, Y.K. Doubly excited states of positronium negative ions. Hyperfine Interact. 1994, 89, 401–406. [Google Scholar] [CrossRef]
- Igarashi, A.; Shimamura, I.; Toshima, N. Photodetachment cross sections of the positronium negative ion. New J. Phys. 2000, 2, 17. [Google Scholar] [CrossRef]
- Basu, A.; Ghosh, A.S. Feshbach resonances in electron-positronium continuum and the close-coupling model. Eur. Lett. 2002, 60, 46–52. [Google Scholar] [CrossRef]
- Li, T.; Shakeshaft, R. S-wave resonances of the negative positronium ion and stability of a system of two electrons and an arbitrary positive charge. Phys. Rev. A 2005, 71, 052505. [Google Scholar] [CrossRef]
- Basu, A.; Ghosh, A.S. Doubly excited resonant states of positronium negative ion. Phys. Rev. A 2006, 72, 062507. [Google Scholar] [CrossRef]
- Lin, C.H.; Ho, Y.K. Quantum Entanglement and Shannon Information Entropy for the doubly excited resonance state in positronium negative ion. Atoms 2015, 3, 422–432. [Google Scholar] [CrossRef]
- Kar, S.; Wanga, Y.; Ho, Y.K. Triplet P states in Ps− using correlated exponential wave functions. Chin. J. Phys. 2020, 68, 137–146. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Cross section for photoionization of the positronium negative ion at the lowest Feshbach resonance. Can. J. Phys. 2013, 91, 751–755. [Google Scholar] [CrossRef]
- Nagashima, Y. Experiments on positronium negative ions. Phys. Rep. 2014, 545, 95–123. [Google Scholar] [CrossRef]
- Mills, A.P., Jr. Possible experiments with high density positronium. AIP Conf. Proc. 2019, 2182, 030001. [Google Scholar]
- Orr, N.A.; Ploszajczak, M.; Marqués, F.M.; Carbonell, J. Recent Progress in Few-Body Physics: Proceedings of the 22nd International Conference on Few-Body Problems in Physics; Springer: Cham, Switzerland, 2020; Volume 238. [Google Scholar]
- Michishio, K.; Kanai, T.; Kuma, S.; Azuma, T.; Wada, K.; Mochizuki, I.; Hyodo, T.; Yagishita, A.; Nagashima1, Y. Observation of a shape resonance of the positronium negative ion. Nat. Commun. 2016, 7, 11060. [Google Scholar] [CrossRef] [PubMed]
- Nagashima, Y.; Sakai, T. First observation of positronium negative ions emitted from tungsten surfaces. New J. Phys. 2006, 8, 319. [Google Scholar] [CrossRef]
- Callaway, J. Energies and widths of the 1Po(1) and 1S(2) resonant states of H−. Phys. Lett. A 1978, 68, 315–316. [Google Scholar] [CrossRef]
- Wendoloski, J.J.; Reinhardt, W.P. Effects of an external electric field on 1Po resonances of H−. Phys. Rev. A 1978, 17, 195–200. [Google Scholar] [CrossRef]
- Pathakt, A.; Kingston, A.E.; Berrington, K.A. Resonances in H− associated with the n = 2, 3 and 4 hydrogenic thresholds. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 2939–2951. [Google Scholar] [CrossRef]
- Ho, Y.K.; Bhatia, A.K. Doubly excited shape resonances in H−. Phys. Rev. A 1993, 48, 3720–3724. [Google Scholar] [CrossRef]
- Tang, J.Z.; Wakabayashi, Y.; Matsuzawa, M.; Watanabe, S.; Shimamura, I. Critical study of photodetachment of H− at energies up to the n = 4 threshold. Phys. Rev. A 1994, 49, 1021–1028. [Google Scholar] [CrossRef]
- Lindroth, E. Photodetachment of H− and Li−. Phys. Rev. A 1995, 52, 2737–2749. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, C.D. Comparative studies of excitations and resonances in H−, Ps−, and e+ + H systems. Phys. Rev. Lett. 1995, 75, 2296–2299. [Google Scholar] [CrossRef]
- Chen, M.K. Doubly excited resonant states in H− below the n = 2 hydrogen threshold. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 1669–1676. [Google Scholar] [CrossRef]
- Gien, T.T. Feshbach resonances below the n = 2 H excitation threshold in electron–hydrogen scattering. J. Phys. B At. Mol. Opt. Phys. 1998, 31, L1001–L1008. [Google Scholar] [CrossRef]
- Kuan, W.H.; Jiang, T.F. Photodetachment of H−. Phys. Rev. A 1999, 60, 364–369. [Google Scholar] [CrossRef]
- Bürgersa, A.; Lindroth, E. Doubly excited states in the negative hydrogen ion. Eur. Phys. J. D 2000, 10, 327–340. [Google Scholar] [CrossRef]
- Jiao, L.G.; Ho, Y.K. Complete supermultiplet structures for the doubly excited intrashell resonances of H− associated with the H (N = 2, 3 and 4) thresholds. Phys. Rev. A 2014, 89, 052511. [Google Scholar] [CrossRef]
- Hamm, M.E.; Hamm, R.W.; Donahue, J.; Gram, P.A.M.; Pratt, J.C.; Yates, M.A.; Bolton, R.D.; Clark, D.A.; Bryant, H.C.; Frost, C.A.; et al. Observation of narrow resonances in the H photodetachment cross section near the n = 3 Threshold. Phys. Rev. Lett. 1979, 43, 1715–1718. [Google Scholar] [CrossRef]
- Halka, M.; Bryant, H.C.; Mackerrow, E.P.; Miller, W.; Mohagheghi, A.H.; Tang, C.Y.; Cohen, S.; Donahue, J.B.; Hsu, A.; Quick, C.R.; et al. Observation of the partial decay into H0 (n′ = 2) by excited H− near the n = 3 and 4 thresholds. Phys. Rev. A 1991, 44, 6127–6129. [Google Scholar] [CrossRef]
- Buckman, S.J.; Clark, C.W. Atomic negative-ion resonances. Rev. Mod. Phys. 1994, 66, 539. [Google Scholar] [CrossRef]
- Balling, P.; Andersen, H.H.; Brodie, C.A.; Pedersen, U.V.; Petrunin, V.V.; Raarup, M.K.; Steiner, P.; Andersen, T. High-resolution VUV spectroscopy of H− in the region near the H (n = 2) threshold. Phys. Rev. A 2000, 61, 022702. [Google Scholar] [CrossRef]
- Ross, T.; Baker, E.J.; Snow, T.P.; Destree, J.D.; Rachford, B.L.; Drosback, M.M.; Jensen, A.G. The search for H− in astrophysical environments. Astrophys. J. 2008, 684, 358–363. [Google Scholar] [CrossRef]
- Kuang, Y.; Arnold, K.-P.; Chmely, F.; Eckhause, M.; Hughes, V.W.; Kane, J.R.; Kettell, S.; Kim, D.-H.; Kumar, K.; Lu, D.C.; et al. First observation of the negative muonium ion produced by electron capture in a beam-foil experiment. Phys. Rev. A 1987, 35, 3172–3175. [Google Scholar] [CrossRef] [PubMed]
- Frolov, A.M. A discretisation of the Laplace transformation and an accurate method for the Coulomb three-body problem. Z. Phys. D At. Mol. Clust. 1986, 2, 61–65. [Google Scholar] [CrossRef]
- Petelenz, P.; Smith, V.H., Jr. Binding energies of the muonium and positronium negative ions. Phys. Rev. A 1987, 36, 5125–5126. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.K.; Drachman, R.J. Three-body Coulomb bound states. Phys. Rev. A 1987, 35, 4051–4054. [Google Scholar] [CrossRef] [PubMed]
- Frolov, A.M. Bound-state properties of negatively charged hydrogenlike ions. Phys. Rev. A 1998, 58, 4479–4483. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Ground state and resonance state of Ps− in plasmas with various Debye lengths. Phys. Rev. A 2005, 71, 052503. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Doubly excited 1,3Po resonance states of Ps− in weakly coupled plasmas. Phys. Rev. A 2006, 73, 032502. [Google Scholar] [CrossRef]
- Basu, A.; Ghosh, A.S. Electron–positronium scattering in Debye plasma environment. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 522–525. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Photodetachment of the positronium negative ion interacting with screened Coulomb (Yukawa) potentials. Few-Body Syst. 2008, 42, 73–81. [Google Scholar] [CrossRef]
- Ho, Y.K.; Kar, S. Complex-scaling calculations for doubly excited resonances in Ps− interacting with screened Coulomb (Yukawa) potentials. Few-Body Syst. 2012, 53, 437–443. [Google Scholar] [CrossRef]
- Ho, Y.K.; Kar, S. High-lying doubly excited resonances in Ps− interacting with screened Coulomb potentials. Chin. J. Phys. 2016, 54, 574–581. [Google Scholar] [CrossRef]
- Ho, Y.K. The combined screened Coulomb and varying charge effects on doubly excited resonance states in the positronium negative ion. JPS Conf. Proc. 2017, 18, 011027. [Google Scholar]
- Kar, S.; Ho, Y.K. Autoionizing 1Se resonance of H− in Debye plasma environments. Phys. Rev. E 2004, 70, 066411. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Ho, Y.K. Electron affinity of the hydrogen atom and a resonance state of the hydrogen negative ion embedded in Debye plasmas. New J. Phys. 2005, 7, 141. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Doubly-excited 1,3Po states of H− interacting with screened Coulomb (Yukawa) potentials. Few-Body Syst. 2006, 40, 13–20. [Google Scholar] [CrossRef]
- Shukla, P.K.; Eliasson, B. Screening and wake potentials of a test charge in quantum plasmas. Phys. Lett. A 2008, 372, 2897–2899. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Properties of the positronium negative ion interacting with exponential cosine-screened Coulomb potentials. Few-Body Syst. 2009, 46, 249–256. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Autoionization states of the positronium negative ion in exponential cosine-screened Coulomb potentials. Eur. Phys. J. D 2010, 56, 151–156. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Properties of hydrogen molecular ion with static screened Coulomb and exponential cosine screened Coulomb potentials. Int. J. Quantum Chem. 2011, 111, 4288–4295. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Ground states and doubly excited resonance states of H− embedded in dense quantum plasmas. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 175006. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. Excitons and the positronium negative ion: Comparison of spectroscopic properties. In Excitons; Pyshkin, S.L., Ed.; Intech: London, UK, 2018; pp. 69–90. [Google Scholar]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA recommended values of the fundamental physical constants: 2014. J. Phys. Chem. Ref. Data 2016, 45, 043102. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Saha, J.K.; Mukherjee, P.K.; Mukherjee, T.K. Three-body negative ions under Coulomb interaction. Phys. Scr. 2012, 85, 065305. [Google Scholar] [CrossRef]
- Frolov, A.M. Multibox strategy for constructing highly accurate bound-state wave functions for three-body systems. Phys. Rev. E 2001, 64, 036704. [Google Scholar] [CrossRef]
- Mandelshtam, V.A.; Ravuri, T.R.; Taylor, H.S. Calculation of the density of resonance states using the stabilization method. Phys. Rev. Lett. 1993, 70, 1932–1935. [Google Scholar] [CrossRef]
- Kar, S.; Ho, Y.K. S-wave resonances in e+ − He scattering below the Ps (n = 2) excitation threshold. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 3177–3186. [Google Scholar] [CrossRef]
- Ho, Y.K.; Bhatia, A.K.; Temkin, A. Precision calculation of the lowest 1S resonance in e-H scattering. Phys. Rev. A 1977, 15, 1423–1429. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Pesnell, W.D. A note on the opacity of the Sun’s atmosphere. Atoms 2020, 8, 37. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Photodetachment of H− in dense quantum plasmas. Phys. Rev. E 2010, 81, 016403. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Photodetachment of the positronium negative ions with exponential cosine-screened Coulomb potentials. Few-Body Syst. 2010, 47, 185–192. [Google Scholar] [CrossRef]
- Jung, A.D. Resonant Compton scattering in nonthermal astrophysical plasmas. Astrophys. J. 2009, 695, 917–920. [Google Scholar] [CrossRef]
- Li, H.W.; Kar, S. Plasma screening effects on resonant Compton scattering of photons by excited hydrogenic ions in Lorentzian plasmas. Eur. Phys. J. D 2012, 66, 304. [Google Scholar] [CrossRef]









| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | −0.0760300 −0.076030 a | −0.1480453 | −0.1482105 | −0.1486748 | −0.1487155 | −0.1487291 | −0.1487563 −0.14876 b |
| 0.01 | −0.0659912 −0.065992 a | −0.1380189 | −0.1381932 | −0.1386573 | −0.1386983 | −0.1387119 | −0.1387391 −0.13875 b |
| 0.02 | −0.0558114 −0.055812 a | −0.1279178 | −0.1280922 | −0.1285570 | −0.1285977 | −0.1286113 | −0.1286385 −0.12865 b |
| 0.03 | −0.0455464 | −0.1176989 | −0.1178735 | −0.1183388 | −0.1183796 | −0.1183932 | −0.1184205 |
| 0.04 | −0.0353743 | −0.1073700 | −0.1075448 | −0.1080105 | −0.1080513 | −0.1080649 | −0.1080922 |
| 0.05 | −0.0255309 −0.025531 a | −0.0969679 | −0.0971426 | −0.0976082 | −0.0976082 | −0.0976626 | −0.0976899 −0.09770 b |
| 0.06 | −0.0162967 | −0.0865485 | −0.0867227 | −0.0871872 | −0.0872279 | −0.0872414 | −0.0872686 |
| 0.07 | −0.0080506 | −0.0761792 | −0.0763524 | −0.0768141 | −0.0768545 | −0.0768680 | −0.0768951 |
| 0.08 | −0.0015421 | −0.0659352 | −0.0661066 | −0.0665635 | −0.0666035 | −0.0666168 | −0.0666436 |
| 0.09 | −0.0558972 | −0.0560658 | −0.0565152 | −0.0565546 | −0.0565677 | −0.0565941 | |
| 0.10 | −0.0461518 | −0.0463163 | −0.0467549 | −0.0467934 | −0.0468062 | −0.0468319 | |
| 0.11 | −0.0367941 | −0.0369530 | −0.0373767 | −0.0374139 | −0.0374263 | −0.0374512 | |
| 0.12 | −0.0279338 | −0.0280850 | −0.0284885 | −0.0285240 | −0.0285357 | −0.0285594 | |
| 0.13 | −0.0197075 | −0.0198483 | −0.0202241 | −0.0202571 | −0.0202681 | −0.0202902 | |
| 0.14 | −0.0123046 | −0.0124305 | −0.0127674 | −0.0127970 | −0.0128068 | −0.0128267 | |
| 0.15 | −0.0060262 | −0.0061298 | −0.0064081 | −0.0064327 | −0.0064408 | −0.0064573 | |
| 0.16 | −0.0013941 | −0.0014624 | −0.0016483 | −0.0016649 | −0.0016704 | −0.0016815 |
| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.01 | 4.303 4.30 a | 1.700 | 1.716 | 1.730 | 1.732 | 1.732 | 1.733 1.732 b |
| 0.01 | 4.321 4.32 a | 1.712 | 1.717 | 1.730 | 1.731 | 1.732 | 1.733 1.733 b |
| 0.02 | 4.400 4.41 a | 1.717 | 1.721 | 1.736 | 1.737 | 1.737 | 1.738 1.738 b |
| 0.03 | 4.516 | 1.725 | 1.730 | 1.744 | 1.745 | 1.745 | 1.746 |
| 0.04 | 4.599 | 1.734 | 1.740 | 1.753 | 1.755 | 1.755 | 1.756 |
| 0.05 | 4.549 4.54 a | 1.741 | 1.747 | 1.761 | 1.762 | 1.762 | 1.763 1.764 b |
| 0.06 | 4.231 | 1.741 | 1.746 | 1.760 | 1.762 | 1.762 | 1.763 |
| 0.07 | 3.422 | 1.729 | 1.734 | 1.748 | 1.750 | 1.750 | 1.751 |
| 0.08 | 1.662 | 1.699 | 1.704 | 1.719 | 1.720 | 1.721 | 1.722 |
| 0.09 | 1.647 | 1.653 | 1.668 | 1.669 | 1.669 | 1.700 | |
| 0.10 | 1.567 | 1.573 | 1.589 | 1.590 | 1.591 | 1.592 | |
| 0.11 | 1.456 | 1.462 | 1.478 | 1.479 | 1.480 | 1.481 | |
| 0.12 | 1.304 | 1.311 | 1.327 | 1.329 | 1.329 | 1.330 | |
| 0.13 | 1.104 | 1.111 | 1.128 | 1.130 | 1.131 | 1.130 | |
| 0.14 | 0.840 | 0.848 | 0.867 | 0.869 | 0.869 | 0.871 | |
| 0.15 | 0.498 | 0.506 | 0.527 | 0.529 | 0.530 | 0.531 | |
| 0.16 | 0.149 | 0.154 | 0.167 | 0.169 | 0.169 | 0.170 |
| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | −0.0733263 −0.07332659 a | −0.1414591 | −0.1416224 | −0.1420576 | −0.1420958 | −0.1421084 | −0.1421340 −0.142133 b |
| 0.01 | −0.0632875 | −0.1314427 | −0.1316061 | −0.1320414 | −0.1320795 | −0.1320922 | −0.1321177 |
| 0.02 | −0.0531113 | −0.1213487 | −0.1215121 | −0.1219477 | −0.1219859 | −0.1219986 | −0.1220242 |
| 0.03 | −0.0428660 | −0.111149 | −0.1113123 | −0.1117484 | −0.1117866 | −0.1117993 | −0.1118249 |
| 0.04 | −0.0327415 | −0.1008551 | −0.1010189 | −0.1014555 | −0.1014937 | −0.1015064 | −0.1015320 |
| 0.05 | −0.0229806 | −0.0905085 | −0.0906723 | −0.0911086 | −0.0911469 | −0.0911596 | −0.0911852 |
| 0.06 | −0.0138667 | −0.0801663 | −0.0803296 | −0.0807647 | −0.0808028 | −0.0808155 | −0.0808410 |
| 0.07 | −0.0058038 | −0.0698958 | −0.0700580 | −0.0704903 | −0.0705282 | −0.0705408 | −0.0705662 |
| 0.08 | −0.0597701 | −0.0599304 | −0.0603578 | −0.0603953 | −0.0604078 | −0.0604329 | |
| 0.09 | −0.0498661 | −0.0500237 | −0.0504437 | −0.0504805 | −0.0504928 | −0.0505174 | |
| 0.10 | −0.0402659 | −0.0404195 | −0.0408288 | −0.0408647 | −0.0408767 | −0.0409007 | |
| 0.11 | −0.0310604 | −0.0312083 | −0.0316030 | −0.0316376 | −0.0316491 | −0.0316723 | |
| 0.12 | −0.0223635 | −0.0225036 | −0.0228775 | −0.0229103 | −0.0229212 | −0.0229432 |
| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | 1.282 1.274 a | 2.009 | 2.043 | 2.136 | 2.144 | 2.146 | 2.152 2.14 b |
| 0.01 | 1.287 | 2.010 | 2.044 | 2.137 | 2.145 | 2.148 | 2.153 |
| 0.02 | 1.308 | 2.017 | 2.051 | 2.144 | 2.152 | 2.155 | 2.161 |
| 0.03 | 1.330 | 2.031 | 2.066 | 2.159 | 2.167 | 2.170 | 2.175 |
| 0.04 | 1.325 | 2.049 | 2.084 | 2.177 | 2.186 | 2.188 | 2.194 |
| 0.05 | 1.260 | 2.067 | 2.102 | 2.196 | 2.204 | 2.207 | 2.213 |
| 0.06 | 1.097 | 2.079 | 2.114 | 2.208 | 2.217 | 2.219 | 2.225 |
| 0.07 | 0.7683 | 2.079 | 2.114 | 2.208 | 2.216 | 2.219 | 2.225 |
| 0.08 | 2.060 | 2.095 | 2.188 | 2.196 | 2.199 | 2.204 | |
| 0.09 | 2.015 | 2.049 | 2.140 | 2.148 | 2.151 | 2.156 | |
| 0.10 | 1.935 | 1.967 | 2.056 | 2.063 | 2.066 | 2.071 | |
| 0.11 | 1.806 | 1.837 | 1.921 | 1.928 | 1.931 | 1.936 | |
| 0.12 | 1.601 | 1.629 | 1.708 | 1.715 | 1.718 | 1.723 |
| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | −0.06315584 | −0.1254399 | −0.1255875 | −0.1259808 | −0.1260153 | −0.1260268 | −0.1260498 |
| 0.01 | −0.05306434 | −0.1153986 | −0.1155463 | −0.1159398 | −0.1159743 | −0.1159858 | −0.1160089 |
| 0.02 | −0.04293079 | −0.1052296 | −0.1053774 | −0.1057712 | −0.1058057 | −0.1058172 | −0.1058402 |
| 0.03 | −0.09502556 | −0.09517295 | −0.09556560 | −0.09560001 | −0.09561146 | −0.09563447 |
| 1 | ∞ | ||||||
|---|---|---|---|---|---|---|---|
| 0.00 | 0.9132 | 1.452 | 1.443 | 1.421 | 1.419 | 1.418 | 1.417 |
| 0.01 | 1.297 | 1.534 | 1.525 | 1.500 | 1.497 | 1.497 | 1.495 |
| 0.02 | 2.902 | 2.095 | 2.081 | 2.043 | 2.039 | 2.038 | 2.036 |
| 0.03 | 3.418 | 3.397 | 3.343 | 3.338 | 3.336 | 3.333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Jiang, Z.; Kar, S. Resonance States of Negative Hydrogen-like Ions in Quantum Plasmas. Atoms 2023, 11, 69. https://doi.org/10.3390/atoms11040069
Yao S, Jiang Z, Kar S. Resonance States of Negative Hydrogen-like Ions in Quantum Plasmas. Atoms. 2023; 11(4):69. https://doi.org/10.3390/atoms11040069
Chicago/Turabian StyleYao, Suya, Zishi Jiang, and Sabyasachi Kar. 2023. "Resonance States of Negative Hydrogen-like Ions in Quantum Plasmas" Atoms 11, no. 4: 69. https://doi.org/10.3390/atoms11040069
APA StyleYao, S., Jiang, Z., & Kar, S. (2023). Resonance States of Negative Hydrogen-like Ions in Quantum Plasmas. Atoms, 11(4), 69. https://doi.org/10.3390/atoms11040069







