L-Shell Photoionization of Magnesium-like Ions with New Results for Cl5+
Abstract
1. Introduction
2. Experimental Details
3. Theoretical Details
3.1. R-Matrix Calculations
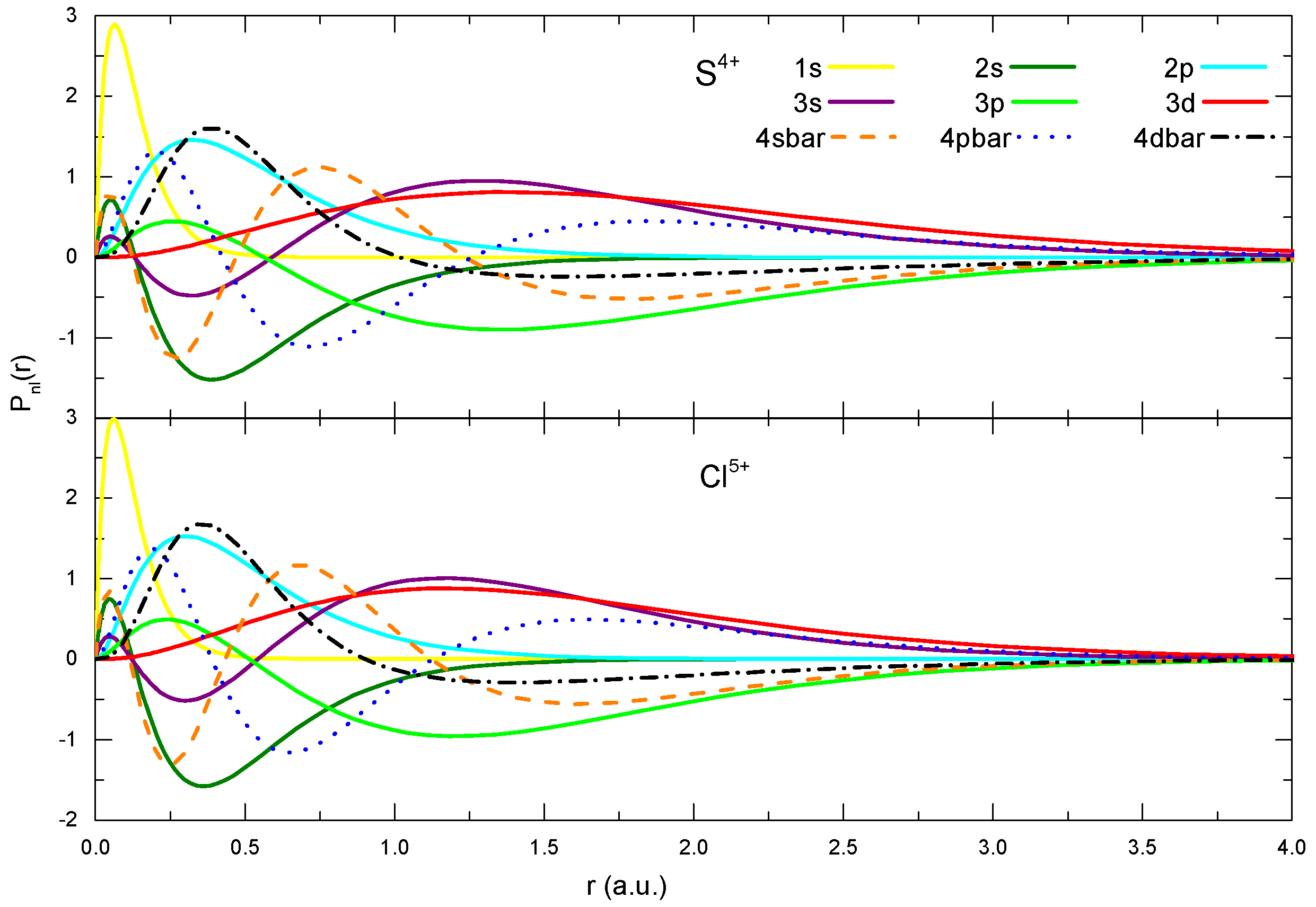
3.2. MCDF Calculations
4. Results
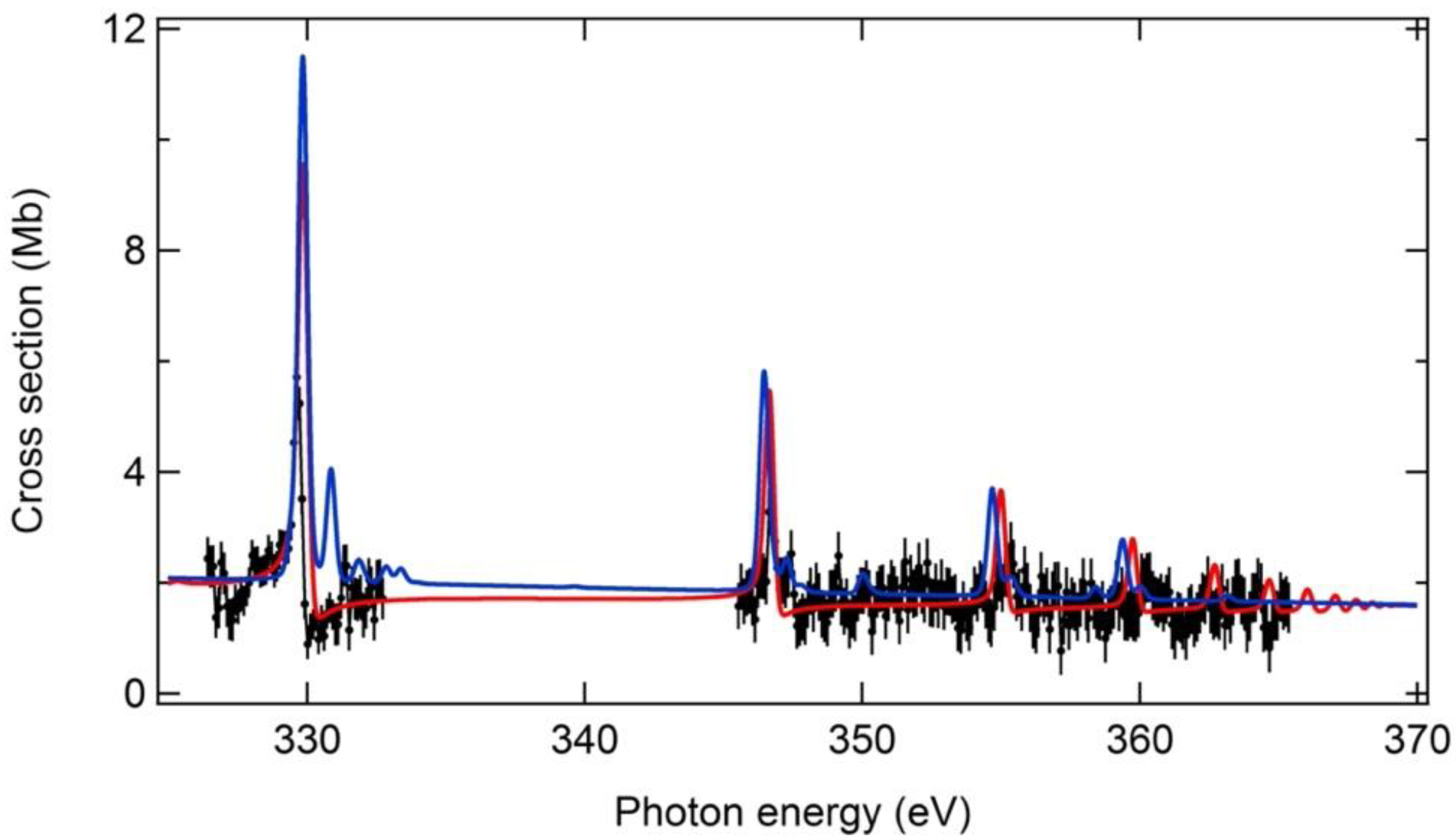
4.1. L-Shell Photoionization of Cl5+
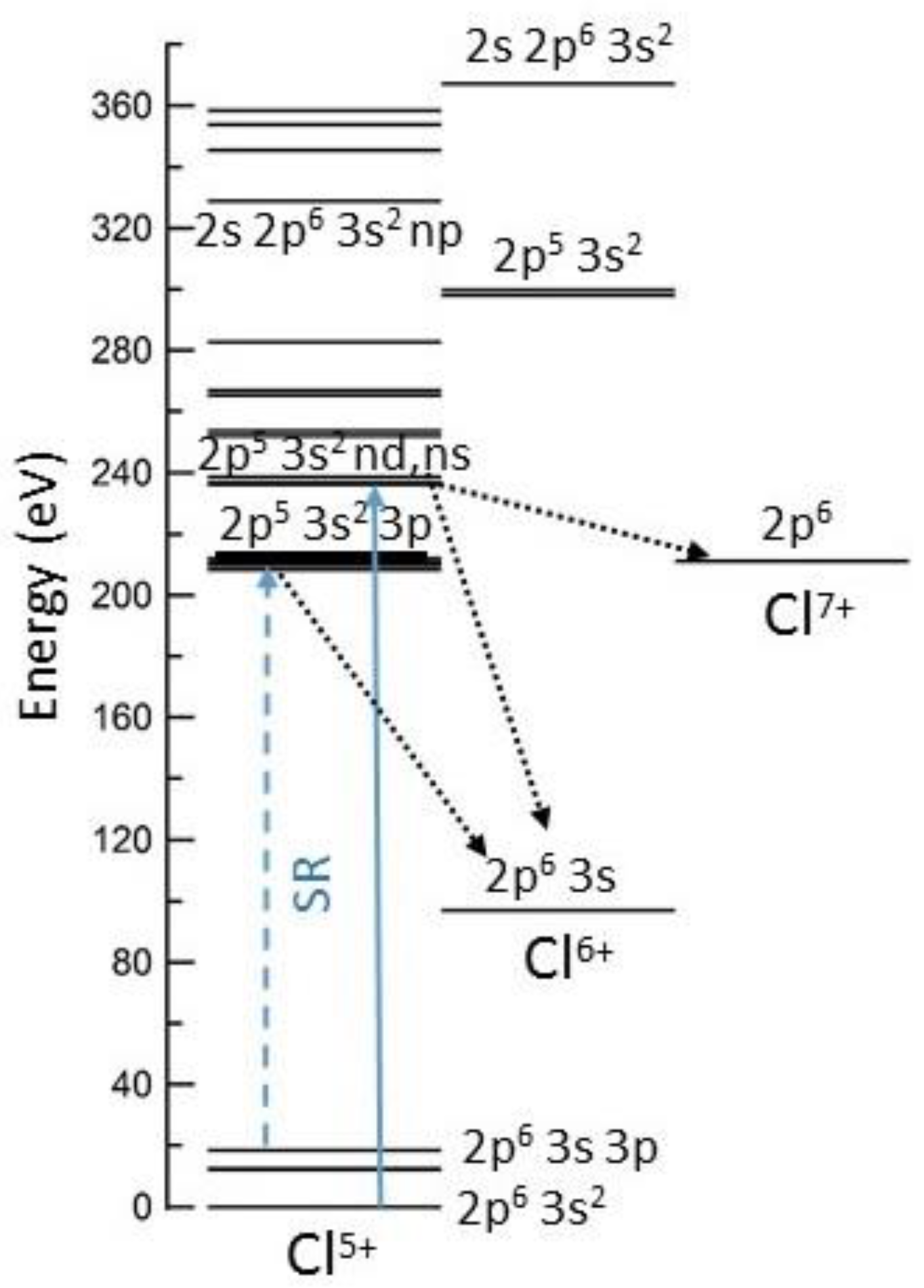
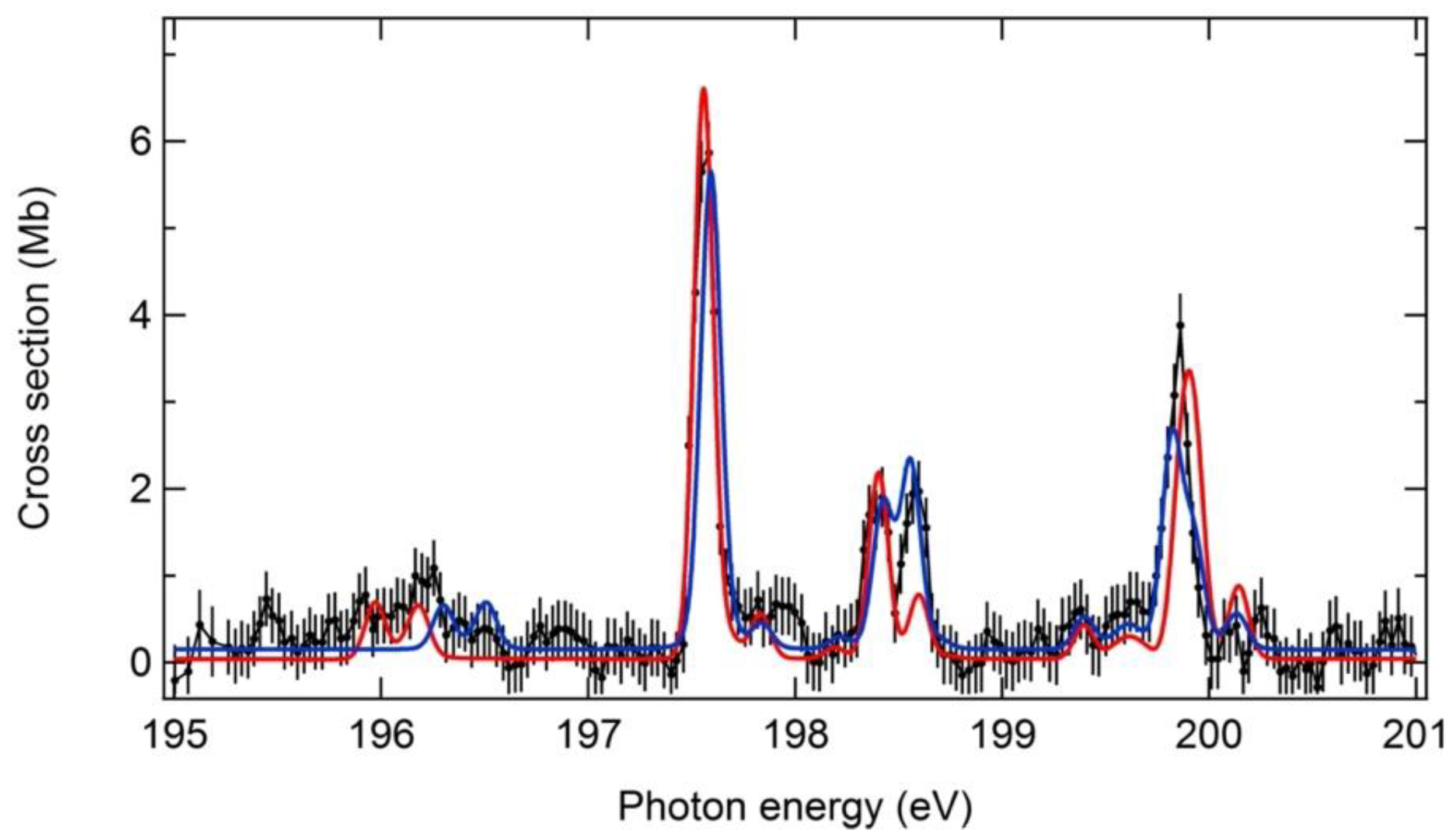
4.1.1. Metastable Resonance Region
4.1.2. 2p → 3d Excitation Region
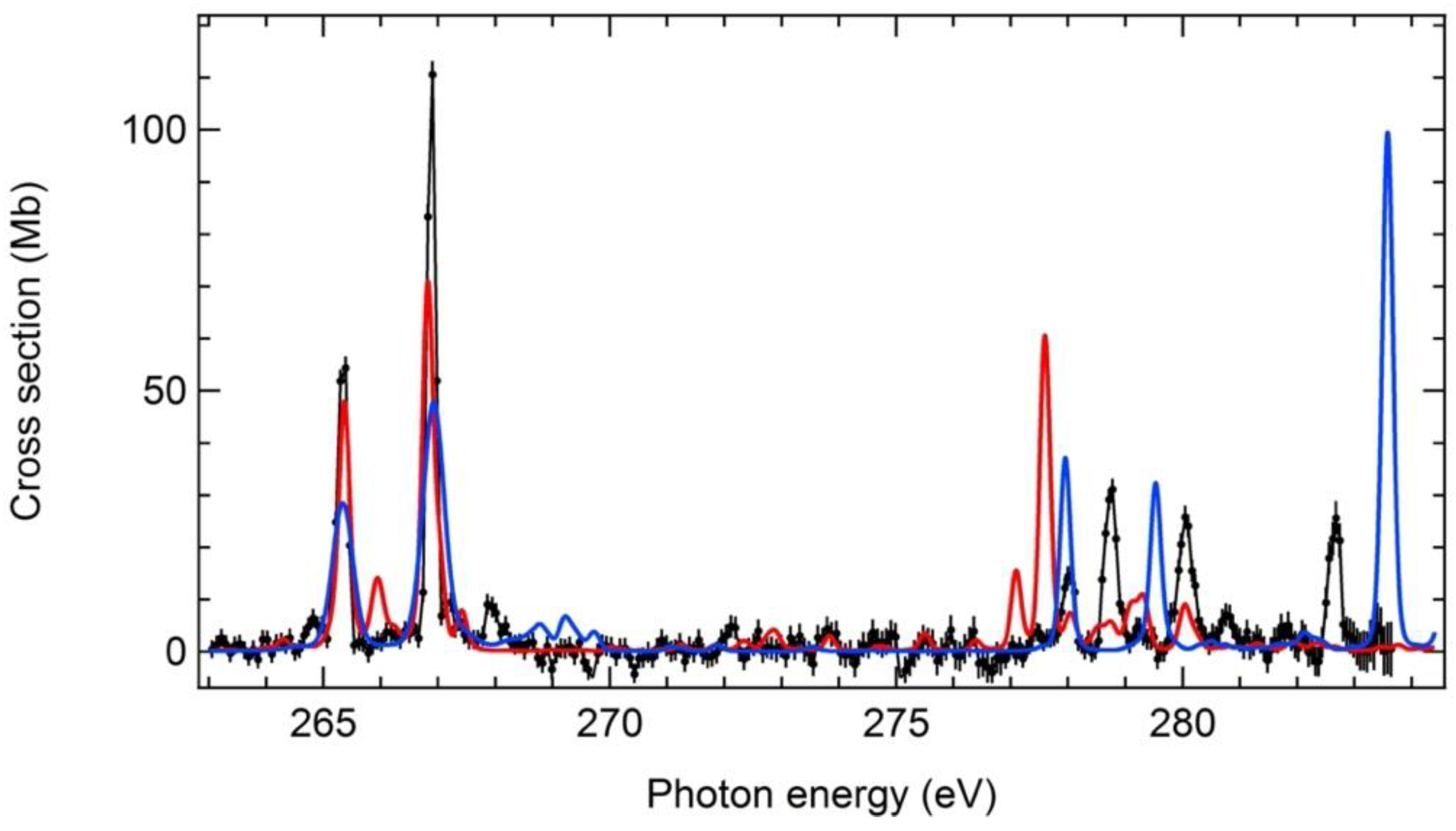
4.1.3. Region of 2p → nd Excitations
4.1.4. Region of 2s → np Excitations
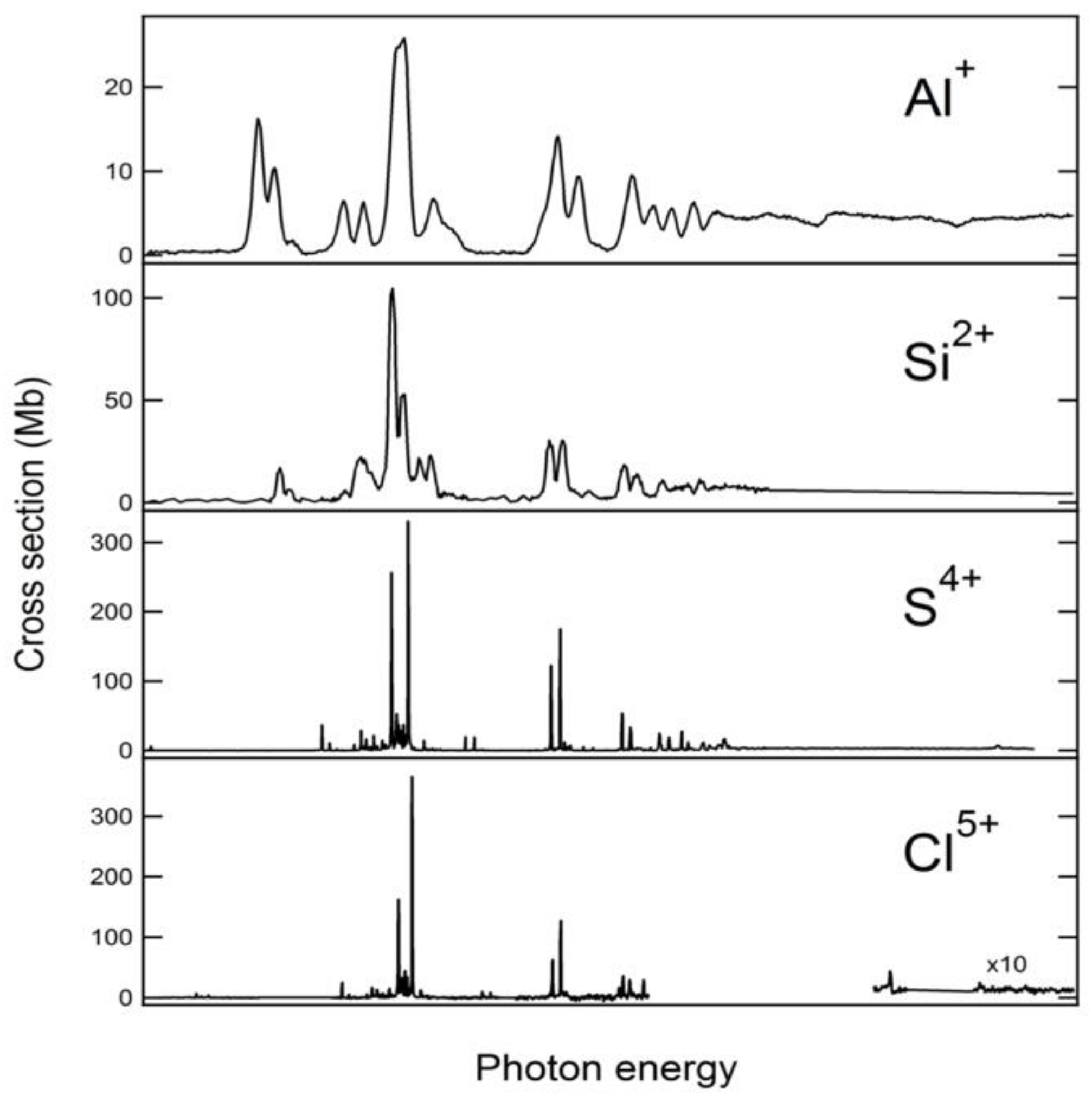
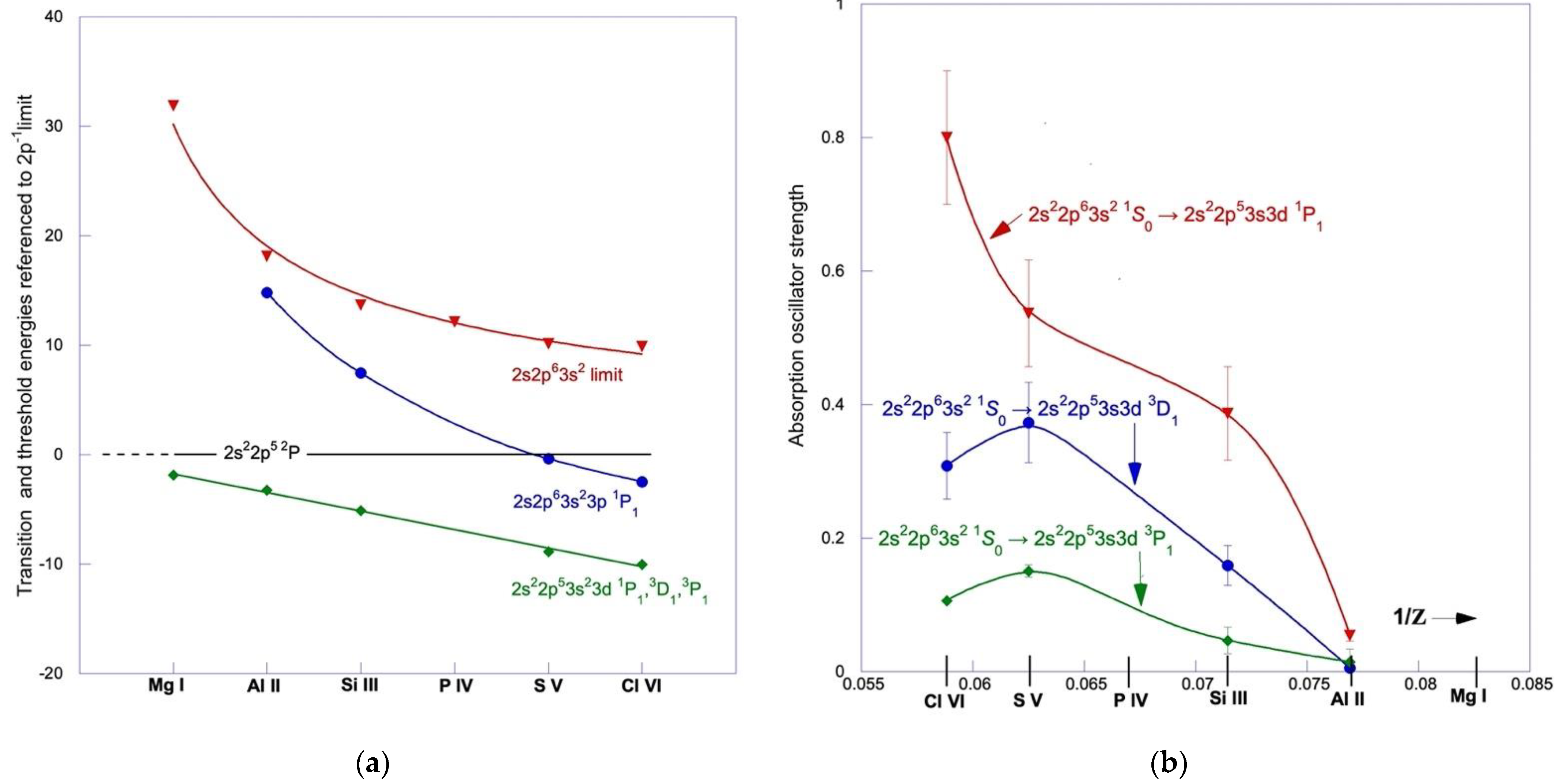
4.2. Evolution along the Mg-like Sequence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Esteva, J.M.; Mehlman, G. Autoionization Spectra of Magnesium (Mg I, Mg II and Mg III) in the 50- to 110-eV Energy Range. Astrophys. J. 1974, 193, 747–754. [Google Scholar] [CrossRef]
- Mehlman, G.; Weiss, A.W.; Esteva, J.M. Revised Classification of Mg II Levels between 59 and 63 EV. Astrophys. J. 1976, 209, 640–641. [Google Scholar] [CrossRef]
- Shorer, P.; Lin, C.D.; Johnson, W.R. Oscillator Strengths for the Magnesium Isoelectronic Sequence. Phys. Rev. A 1977, 16, 1109–1116. [Google Scholar] [CrossRef]
- Butler, K.; Mendoza, C.; Zeippen, C.J. Oscillator Strengths and Photoionization Cross-Sections for Positive Ions in the Magnesium Isoelectronic Sequence. Mon. Not. R. Astron. Soc. 1984, 209, 343–351. [Google Scholar] [CrossRef]
- Costello, J.T.; Evans, D.; Hopkins, R.B.; Kennedy, E.T.; Kiernan, L.; Mansfield, M.W.D.; Mosnier, J.-P.; Sayyad, M.H.; Sonntag, B.F. The 2p-Subshell Photoabsorption Spectrum of Al+ in a Laser-Produced Plasma. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 5055–5068. [Google Scholar] [CrossRef]
- Mosnier, J.P.; Costello, J.T.; Kennedy, E.T.; Kiernan, L.; Sayyad, M.H. Even-Parity Autoionizing States in the Extreme-Ultraviolet Photoabsorption Spectra of Mg, Al+, and Si2+. Phys. Rev. A 1994, 49, 755–761. [Google Scholar] [CrossRef]
- Sayyad, M.H.; Kennedy, E.T.; Kiernan, L.; Mosnier, J.-P.; Costello, J.T. 2p-Subshell Photoabsorption by Si2+ Ions in a Laser-Produced Plasma. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 1715–1722. [Google Scholar] [CrossRef]
- Fang, T.K.; Nam, B.I.; Kim, Y.S.; Chang, T.N. Resonant Structures of Overlapping Doubly Excited Autoionization Series in Photoionization of Mg-like Al+ and Si2+ Ions. Phys. Rev. A 1997, 55, 433–439. [Google Scholar] [CrossRef]
- West, J.B.; Andersen, T.; Brooks, R.L.; Folkmann, F.; Kjeldsen, H.; Knudsen, H. Photoionization of Singly and Doubly Charged Aluminum Ions in the Extreme Ultraviolet Region: Absolute Cross Sections and Resonance Structures. Phys. Rev. A 2001, 63, 052719. [Google Scholar] [CrossRef]
- Mosnier, J.-P.; Sayyad, M.H.; Kennedy, E.T.; Bizau, J.-M.; Cubaynes, D.; Wuilleumier, F.J.; Champeaux, J.-P.; Blancard, C.; Varma, R.H.; Banerjee, T.; et al. Absolute Photoionization Cross Sections and Resonance Structure of Doubly Ionized Silicon in the Region of the 2p−1 Threshold: Experiment and Theory. Phys. Rev. A 2003, 68, 052712. [Google Scholar] [CrossRef]
- Ho, H.C.; Johnson, W.R.; Blundell, S.A.; Safronova, M.S. Third-Order Many-Body Perturbation Theory Calculations for the Beryllium and Magnesium Isoelectronic Sequences. Phys. Rev. A 2006, 74, 022510. [Google Scholar] [CrossRef]
- Kim, D.-S.; Kim, Y.S. Theoretical Photoionization Spectra in the UV Photon Energy Range for a Mg-like Al+ Ion. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 165002. [Google Scholar] [CrossRef]
- Pradhan, G.B.; Jose, J.; Deshmukh, P.C.; Radojević, V.; Manson, S.T. Photoionization of Mg and Ar Isonuclear Sequences. Phys. Rev. A 2009, 80, 053416. [Google Scholar] [CrossRef]
- Kim, D.-S.; Kwon, D.-H. Theoretical Photoionization Spectra for Mg-Isoelectronic Cl 5+ and Ar 6+ Ions. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 105004. [Google Scholar] [CrossRef]
- Khatri, I.; Goyal, A.; Diouldé Ba, M.; Faye, M.; Sow, M.; Sakho, I.; Singh, A.K.; Mohan, M.; Wagué, A. Screening Constant by Unit Nuclear Charge Calculations of Resonance Energies and Widths of the 3pns 1,3P° and 3pnd 1P° Rydberg Series of Mg-like (Z = 13–26) Ions. Radiat. Phys. Chem. 2017, 130, 208–215. [Google Scholar] [CrossRef]
- Wehlitz, R.; Juranić, P.N. Relative Single- and Double-Photoionization Cross Sections of Mg around the 2p → nl Resonances. Phys. Rev. A 2009, 79, 013410. [Google Scholar] [CrossRef]
- Safronova, U.I.; Johnson, W.R.; Berry, H.G. Excitation Energies and Transition Rates in Magnesiumlike Ions. Phys. Rev. A 2000, 61, 052503. [Google Scholar] [CrossRef]
- Mosnier, J.-P.; Kennedy, E.T.; Cubaynes, D.; Bizau, J.-M.; Guilbaud, S.; Hasoglu, M.F.; Blancard, C.; Gorczyca, T.W. L-Shell Photoionization of Mg-like S4+ in Ground and Metastable States: Experiment and Theory. Phys. Rev. A 2022, 106, 033113. [Google Scholar] [CrossRef]
- Kallman, T.R.; Palmeri, P. Atomic Data for X-Ray Astrophysics. Rev. Mod. Phys. 2007, 79, 79–133. [Google Scholar] [CrossRef]
- Foster, A.R.; Smith, R.K.; Brickhouse, N.S.; Kallman, T.R.; Witthoeft, M.C. The Challenges of Plasma Modeling: Current Status and Future Plans. Space Sci. Rev. 2010, 157, 135–154. [Google Scholar] [CrossRef]
- Kallman, T.R. Modeling of Photoionized Plasmas. Space Sci. Rev. 2010, 157, 177–191. [Google Scholar] [CrossRef]
- Savin, D.W.; Brickhouse, N.S.; Cowan, J.J.; Drake, R.P.; Federman, S.R.; Ferland, G.J.; Frank, A.; Gudipati, M.S.; Haxton, W.C.; Herbst, E.; et al. The Impact of Recent Advances in Laboratory Astrophysics on Our Understanding of the Cosmos. Rep. Prog. Phys. 2012, 75, 036901. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, C.; Bautista, M.A.; Deprince, J.; García, J.A.; Gatuzz, E.; Gorczyca, T.W.; Kallman, T.R.; Palmeri, P.; Quinet, P.; Witthoeft, M.C. The XSTAR Atomic Database. Atoms 2021, 9, 12. [Google Scholar] [CrossRef]
- Nahar, S. Database NORAD-Atomic-Data for Atomic Processes in Plasma. Atoms 2020, 8, 68. [Google Scholar] [CrossRef]
- Kennedy, E.T.; Costello, J.T.; Mosnier, J.-P.; Cafolla, A.A.; Collins, M.; Kiernan, L.; Koeble, U.; Sayyad, M.H.; Shaw, M.; Sonntag, B.F.; et al. Extreme-Ultraviolet Studies with Laser-Produced Plasmas. Opt. Eng. 1994, 33, 3984–3992. [Google Scholar] [CrossRef]
- Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; El Eassan, N.; Al Shorman, M.M.; Bouisset, E.; Guigand, J.; Moustier, O.; Marié, A.; Nadal, E.; et al. A Merged-Beam Setup at SOLEIL Dedicated to Photoelectron–Photoion Coincidence Studies on Ionic Species. J. Electron. Spectrosc. Relat. Phenom. 2016, 210, 5–12. [Google Scholar] [CrossRef]
- Kjeldsen, H. Photoionization Cross Sections of Atomic Ions from Merged-Beam Experiments. J. Phys. B At. Mol. Opt. Phys. 2006, 39, R325–R377. [Google Scholar] [CrossRef]
- Phaneuf, R.A.; Kilcoyne, A.L.D.; Müller, A.; Schippers, S.; Aryal, N.; Baral, K.; Hellhund, J.; Aguilar, A.; Esteves-Macaluso, D.A.; Lomsadze, R. Cross-Section Measurements with Interacting Beams; American Institute of Physics: Gaithersburg, MD, USA, 2013; pp. 72–78. [Google Scholar] [CrossRef]
- Schippers, S.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Muller, A. Photoionization of ions with synchrotron radiation: From ions in space to atoms in cages. Contemp. Phys. 2016, 57, 215–229. [Google Scholar] [CrossRef]
- Schippers, S.; Buhr, T.; Borovik, A., Jr.; Holste, K.; Perry-Sassmannshausen, A.; Mertens, K.; Reinwardt, S.; Martins, M.; Klumpp, S.; Schubert, K.; et al. The Photon-Ion Merged-Beams Experiment PIPE at PETRAIII—The First Five Years. X-ray Spectrom. 2020, 49, 11–20. [Google Scholar] [CrossRef]
- Hudson, C.E.; West, J.B.; Bell, K.L.; Aguilar, A.; Phaneuf, R.A.; Folkmann, F.; Kjeldsen, H.; Bozek, J.; Schlachter, A.S.; Cisneros, C. A Theoretical and Experimental Study of the Photoionization of AlII. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2911–2932. [Google Scholar] [CrossRef]
- Simon, M.C.; Crespo López-Urrutia, J.R.; Beilmann, C.; Schwarz, M.; Harman, Z.; Epp, S.W.; Schmitt, B.L.; Baumann, T.M.; Behar, E.; Bernitt, S.; et al. Resonant and Near-Threshold Photoionization Cross Sections of Fe 14 +. Phys. Rev. Lett. 2010, 105, 183001. [Google Scholar] [CrossRef]
- Blake, G.A.; Anicich, V.G.; Huntress, W.T., Jr. Chemistry of Chlorine in Dense Interstellar Clouds. Astrophys. J. 1986, 300, 415. [Google Scholar] [CrossRef]
- Feldman, P.D.; Ake, T.B.; Berman, A.F.; Moos, H.W.; Sahnow, D.J.; Strobel, D.D.; Weaver, H.H. Detection of Chlorine Ions in the Far Ultraviolet Spectroscopic Explorer Spectrum of the IO Plasma Torus. Astrophys. J. 2001, 554, L123–L126. [Google Scholar] [CrossRef]
- Kounaves, S.P.; Carrier, B.L.; O’Neil, G.D.; Stroble, S.T.; Claire, M.W. Evidence of Martian Perchlorate, Chlorate, and Nitrate in Mars Meteorite EETA79001: Implications for Oxidants and Organics. Icarus 2014, 229, 206–213. [Google Scholar] [CrossRef]
- Neufeld, D.A.; Wiesemeyer, H.; Wolfire, M.J.; Jacob, A.M.; Buchbender, C.; Gerin, M.; Gupta, H.; Güsten, R.; Schilke, P. The Chemistry of Chlorine-Bearing Species in the Diffuse Interstellar Medium, and New SOFIA/GREAT*Observations of HCl+. Astrophys. J. 2021, 917, 104. [Google Scholar] [CrossRef]
- Maas, Z.G.; Pilachowski, C.A.; Hinkle, K. Chlorine Abundances in Cool Stars. Astron. J. 2016, 152, 196. [Google Scholar] [CrossRef]
- Wallström, S.H.J.; Muller, S.; Roueff, E.; Le Gal, R.; Black, J.H.; Gérin, M. Chlorine-Bearing Molecules in Molecular Absorbers at Intermediate Redshifts. Astron. Astrophys. 2019, 629, A128. [Google Scholar] [CrossRef]
- Ren, L.-M.; Wang, Y.-Y.; Li, D.-D.; Yuan, Z.-S.; Zhu, L.-F. Inner-Shell Excitations of 2 p Electrons of Argon Investigated by Fast Electron Impact with High Resolution. Chin. Phys. Lett. 2011, 28, 053401. [Google Scholar] [CrossRef]
- Thuillier, T.; Benitez, J.; Biri, S.; Rácz, R. X-ray Diagnostics of ECR Ion Sources—Techniques, Results, and Challenges. Rev. Sci. Instrum. 2022, 93, 021102. [Google Scholar] [CrossRef]
- Bieron, J.; Froese-Fischer, C.; Jonsson, P. Special Issue “The General Relativistic Atomic Structure Package—GRASP”. 2022. Available online: https://www.mdpi.com/journal/atoms/special_issues/the_grasp#info (accessed on 14 March 2023).
- Bruneau, J. Correlation and Relaxation Effects in Ns2-Nsnp Transitions. J. Phys. B At. Mol. Phys. 1984, 17, 3009. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge Invariance and Relativistic Radiative Transitions. J. Phys. B At. Mol. Phys. 1974, 7, 1458. [Google Scholar] [CrossRef]
- Savukov, I.M. Special Issue “Atomic Structure Calculations of Complex Atoms”. 2021. Available online: https://www.mdpi.com/journal/atoms/special_issues/AtomicStructureCalculations_ComplexAtoms (accessed on 14 March 2023).
- Schneider, B.I.; Hamilton, K.R.; Bartschat, K. Generalizations of the R-Matrix Method to the Treatment of the Interaction of Short-Pulse Electromagnetic Radiation with Atoms. Atoms 2022, 10, 26. [Google Scholar] [CrossRef]
- Sardar, S.; Xu, X.; Xu, L.-Q.; Zhu, L.-F. Relativistic R-Matrix Calculations for Photoionization Cross-Sections of C IV: Implications for Photorecombination of C V. Mon. Not. R. Astron. Soc. 2018, 474, 1752–1761. [Google Scholar] [CrossRef]
- Delahaye, F.; Ballance, C.P.; Smyth, R.T.; Badnell, N.R. Quantitative Comparison of Opacities Calculated Using the R -Matrix and Distorted-Wave Methods: Fe xvii. Mon. Not. R. Astron. Soc. 2021, 508, 421–432. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: New York, NY, USA, 2011. [Google Scholar]
- Berrington, K.A.; Eissner, W.B.; Norrington, P.H. RMATRX1: Belfast Atomic R-Matrix Codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; Version 5.10; NIST: Gaithersburg, MD, USA, 2022. [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Tachiev, G.; Irimia, A. Relativistic Energy Levels, Lifetimes, and Transition Probabilities for the Sodium-like to Argon-like Sequences. At. Data Nucl. Data Tables 2006, 92, 607–812. [Google Scholar] [CrossRef]
- Curtis, L.J. Bengt Edlén’s Handbuch Der Physik Article—26 Years Later. Phys. Scr. 1987, 35, 805–810. [Google Scholar] [CrossRef]
- Wiese, W. Regularities of Atomic Oscillator Strengths in Isoelectronic Sequences. In Beam-Foil Spectroscopy; Springer: Berlin/Heidelberg, Germany, 1976; pp. 145–178. [Google Scholar]
- Hasoğlu, M.F.; Nikolić, D.; Gorczyca, T.W.; Manson, S.T.; Chen, M.H.; Badnell, N.R. Nonmonotonic Behavior as a Function of Nuclear Charge of the K -Shell Auger and Radiative Rates and Fluorescence Yields along the 1s2s22p3 Isoelectronic Sequence. Phys. Rev. A 2008, 78, 032509. [Google Scholar] [CrossRef]
- Verner, D.A.; Yakovlev, D.G.; Band, I.M.; Trzhaskovskaya, M.B. Subshell Photoionization Cross Sections and Ionization Energies of Atoms and Ions from He to Zn. At. Data Nucl. Data Tables 1993, 55, 233–280. [Google Scholar] [CrossRef]
- Chakraborty, H.S.; Gray, A.; Costello, J.T.; Deshmukh, P.C.; Haque, G.N.; Kennedy, E.T.; Manson, S.T.; Mosnier, J.-P. Anomalous Behavior of the Near-Threshold Photoionization Cross Section of the Neon Isoelectronic Sequence: A Combined Experimental and Theoretical Study. Phys. Rev. Lett. 1999, 83, 2151–2154. [Google Scholar] [CrossRef]
- Brilly, J.; Kennedy, E.T.; Mosnier, J.P. The 2p-Subshell Absorption Spectrum of Al III. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 3685–3693. [Google Scholar] [CrossRef]




| Energy (eV)/Strength (Mb.eV) | |||
|---|---|---|---|
| Experimental * | R-Matrix | MCDF | Assignment |
| 195.66(4)/0.09(2) | 196.61/0.083 | 196.84/0.064 | 3P2-3S1 |
| 195.95(3)/0.15(3) | 196.83/0.074 | 197.05/0.064 | 3P0-3S1 |
| 197.29(2)/0.85(13) | 198.20/0.864 | 198.13/0.700 | 3P2-3D3 |
| 197.54(4)/0.09(2) | 198.47/0.118 | 198.38/0.036 | 3P1-3D2 |
| 198.12(3)/0.27(4) | 199.04/0.268 | 198.97/0.211 | 3P0-3D1 |
| 198.31(4)/0.28(5) | 199.24/0.076 | 199.10/0.273 | 3P2-3P2 |
| 199.09(4)/0.07(3) | 200.04/0.054 | 199.94/0.048 | 3P2-3D1 |
| 199.33(4)/0.09(2) | 200.18/0.013 | 200.08/0.012 | 3P1-3D1 |
| 199.49(4)/0.11(2) | 200.25/0.028 | 200.15/0.024 | 3P0-3D1 |
| 199.59(2)/0.47(8) | 200.51/0.478 | 200.36/0.306 | 3P2-3D2 |
| 200.57/0.252 | 200.47/0.156 | 3P2-3P1 | |
| 199.97(5)/0.05(2) | 200.79/0.067 | 200.68/0.50 | 3P0-3P1 |
| Energy (eV)/Strength (Mb eV)/Auger Width (meV) * Experimental ** | Energy (eV)/Strength (Mb eV)/Auger Width (meV) * R-matrix | Energy (eV)/Strength (Mb eV)/Auger Width (meV) * MCDF | Assignment (MCDF) |
|---|---|---|---|
| 225.28(3)/4.0(7)/x | 226.77/3.94/x | 224.78/5.06/x | |
| 226.56(7)/0.7(4)/x | 228.08/0.63/x | 225.93/6.57/x | |
| 230.03(7)/0.9(4)/x | 231.91/1.07/x | ||
| 231.01(3)/2.9(6)/x | 232.88/2.75/x | 231.25/1.32/x | |
| 231.93(4)/2.2(5)/x | 233.80/2.12/x | ||
| 232.49(7)/0.8(4)/x | |||
| 233.05(5)/1.2(4)/x | 235.18/0.19/x | ||
| 233.64(10)/0.5(4)/x | |||
| 234.26(4)/2.4(5)/x | 234.48/2.83/x | ||
| 234.73(6)/1.0(4) /x | |||
| 235.98(2)/26(4)/51(4) | 237.81/29/37 | 236.01/39.8/45 | |
| 236.35(3)/1.1(4)/x | |||
| 236.54(3)/1.5(4)/x | |||
| 236.71(3)/9(2)/158(65) | 238.69/20.3/134 | 236.97/28/92 | |
| 237.27(3)/2.2(3)/x | |||
| 237.34(3)/4.7(8)/x | 237.73/5.5/x | *** | |
| 237.49(4)/0.5(4)/x | |||
| 237.66(3)/4.8(8)/x | 238.16/2.7/x | *** | |
| 238.01(3)/2.3(5)/x | 238.45/1.72/ x | *** | |
| 238.61(2)/78(12)/46(2) | 240.58/58.1/69 | 239.46/42.6/86 | |
| 240.26(4)/2.0(5)/x | 240/2.24/x | *** | |
| 240.47(7)/9(4)/x | |||
| 251.98(2)/1.5(2)/x | 255.97/1.9/ 87 | 251.10/1.0/x | |
| 253.55(2)/1.4(2)/x | 257.51/1.8/87 | 252.71/0.8/x | |
| 265.33(3)/13(2)/x | 269.73/12.2/59 | 264.36/14.0/x | |
| 266.88(3)/21(3)/x | 271.18/17.9/53 | 265.96/21.8/x | |
| 278.01(3)/4.1(7)/x | |||
| 278.75/8.5(1.3)/x | 276.98/9.09/x | ||
| 280.05(3)/8.4(1.3)/x | 278.56/7.57/x | ||
| 282.66(3)/6.5(1.0)/x | 282.60/21.9/x | ||
| 329.6(1)/x/x | 336.88/x/x | 328.85/4.27/x | |
| 346.7(1)/x/x | 353.38/x/x | 345.47/1.77/x | |
| 355.3(1)/x/x | 362.03/x/x | 353.69/0.88/x | |
| 360.4(1)/x/x | 366.67/x/x | 358.38/0.49/x |
| Atom/Ion | 2p Limit | ||||
|---|---|---|---|---|---|
| Mg I | 55.492(1) | 55.677(1) | 55.838(1) | 57.658(2) e | x |
| 4.6(9) | 5.0(1) | 8.2(4) | |||
| x | x | x | |||
| Al II | 84.99(2) | 85.36(2) | 85.57(2) | 91.75(15) c | 121.5(5) |
| x | x | x | |||
| 5.6 b | 0.54 b | 1.5 b | |||
| Si III | 117.6(1) | 118.1(1) | 118.8(1) | 133.5(1) c | 155.7(4) |
| x | x | x | |||
| 37(7) b | 17(3) b | 5(1) b | |||
| P IV (present work) a | 154.4 | 153.9 | 154.7 | 180.5 | 193.6 |
| x x | x x | x x | |||
| S V | 194.88 51 46(7) b | 192.74 47 32(5) b | 193.42 149 13(2) b | 237.35 c | 235.4 |
| Cl VI (present work) | 238.61(2) 46(2) 68(10) b | 235.98(2) 51(4) 26(4) b | 236.71(3) 158(65) 9(2) b | 299.6 d | 282.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosnier, J.-P.; Kennedy, E.T.; Bizau, J.-M.; Cubaynes, D.; Guilbaud, S.; Blancard, C.; Hasoğlu, M.F.; Gorczyca, T.W. L-Shell Photoionization of Magnesium-like Ions with New Results for Cl5+. Atoms 2023, 11, 66. https://doi.org/10.3390/atoms11040066
Mosnier J-P, Kennedy ET, Bizau J-M, Cubaynes D, Guilbaud S, Blancard C, Hasoğlu MF, Gorczyca TW. L-Shell Photoionization of Magnesium-like Ions with New Results for Cl5+. Atoms. 2023; 11(4):66. https://doi.org/10.3390/atoms11040066
Chicago/Turabian StyleMosnier, Jean-Paul, Eugene T. Kennedy, Jean-Marc Bizau, Denis Cubaynes, Ségolène Guilbaud, Christophe Blancard, M. Fatih Hasoğlu, and Thomas W. Gorczyca. 2023. "L-Shell Photoionization of Magnesium-like Ions with New Results for Cl5+" Atoms 11, no. 4: 66. https://doi.org/10.3390/atoms11040066
APA StyleMosnier, J.-P., Kennedy, E. T., Bizau, J.-M., Cubaynes, D., Guilbaud, S., Blancard, C., Hasoğlu, M. F., & Gorczyca, T. W. (2023). L-Shell Photoionization of Magnesium-like Ions with New Results for Cl5+. Atoms, 11(4), 66. https://doi.org/10.3390/atoms11040066









