Photoionization Study of Neutral Chlorine Atom

Abstract

Photoionization of neutral chlorine atom is investigated in this paper in the framework of the screening constant per unit nuclear charge (SCUNC) method. Resonance energies, quantum defects and effective charges of the 3s²3p⁴ (³P_2,1,0)ns and 3s²3p⁴ (³P_1,0)nd Rydberg series originating from both the ²P⁰_3/2 ground state and the ²P⁰_1/2 excited state of chlorine atom are reported. The present study believed to be the first theoretical investigation is compared with the recent experimental measurements (Yang et al., Astrophys. J. 810:132, 2015). Good agreements are obtained between theory and experiments. New SCUNC data are tabulated as useful references for interpreting astrophysical spectra from neutral atomic chlorine.

1. Introduction

Photoionization is a fundamental tool for probing our understanding of atomic structure and spectra. Knowledge of the latter is important for many derived processes and studies. Examples include understanding photon–plasma interactions, determining the abundance of chemical elements in astronomical objects [1], and modeling and diagnosing astrophysical and laboratory plasmas [2,3], to name but a few. One of the most important elements to study is chlorine which has been detected in numerous astrophysical objects, such as the planetary nebula NGC2818 [4], Jupiter’s moon Io [5] and others. In addition, chlorine is used in many different applications in our daily lives, and more than that, it can be used to determine the physical conditions and chemical evolution of astronomical objects. However, as a chemical element existing both on Earth and in space, it is important to study its properties to facilitate its identification in astrophysical and laboratory plasmas, as well as its modeling for different applications. However, to date, determining its abundance remains a challenge and has been the subject of several studies over the last decade [6]. Experimental and theoretical studies were the subject of active researches as far as chlorine element is concerned. In the past, the R-matrix approach was used in the calculation of photoionization cross sections of Cl and Br [7,8]. In addition, the first absolute photoionization cross-section measurements for atomic chlorine were made from the1Sionization threshold at 16.4 eV to 75 [9].On the other hand, investigations were carried out in the calculations of oscillator strengths for ultraviolet resonances in Cl⁺ and Cl²⁺ [7,10], in the photoionization cross section measurements of chlorine Cl⁺ cation [8,11], in the experimental and theoretical photoionization of Cl²⁺ [9,12] and in the L-shell photoionization of magnesium-like ions with new results for Cl⁵⁺ [10,13]. In addition, theoretical investigations were carried out for Cl⁺ in the framework of the dirac-coulomb R-matrix method [11,14] and for Cl⁵⁺ using the clean-channel R-matrix approach [15]. In the recent past, photoionization on Cl⁺ was performed with the framework of the screening constant per unit nuclear charge (SCUNC) method [16] and of the relativistic Breit-Pauli R-matrix method (BPRM) [3]. Despite major efforts to understand the properties of neutral chlorine and its ions, atomic data on neutral chlorine are still scarce in the literature. The scarcity of theoretical calculations for Cl is due to its open-shell structure, which makes it a difficult atom for theorists, but also to some extent to its high reactivity [17]. In the recent past, vacuum ultraviolet photoion (VUV-PI) and VUV photoion pulsed field ionization (VUV-PFI-PI) measurements of the resonance energies in Cl were taken and the dominant series due to the 3p → ns and 3p → nd resonances were identified [18] to perfect and extend the earlier measurements [19] to more excited states n = 61. However, in the experiment carried out by Yang et al. [18], we note a number of shortcomings. The resonance energies measured for certain series of resonances are uncertain, and for all the series considered by these authors in their experiments, the quantum defects derived from experimental measurements of resonance energies are imprecise, and their variation in all directions is considered unsatisfactory. The goal of the present study is to report accurate resonance energies and quantum defects belonging to the identified 3p → ns and 3p → nd resonances in Cl [18]. For this purpose, we apply the SCUNC formalism [16,20,21]. Section 2 gives a brief overview of the calculation methodology. In Section 3, we present and discuss the results obtained, andwe draw conclusions in Section 4.

2. Theory

For a given (^2S+1L_J)nl—Rydberg series, the general expression for the resonance energies E_n is given by (in Rydberg) [16,20,21]

$$E_n=E_{\infty }-\frac{Z^2}{n^2}{\left[1-\beta (nl;s;\mu ,\nu ;{}^{2S+1}L_J;Z)\right]}^{{}^2}$$

(1)

In Equation (1), ν and µ (µ > ν) denote the principal quantum numbers of the (^2S+1L_J)nl Rydberg series used in the empirical determination of the f_k—screening constants, s represents the spin of the nl-electron (s = 1/2), E_∞ is the energy value of the series limit and Z stands for the atomic number. The β-parameters are screening constants by unit nuclear charge expanded in inverse powers of Z and given by the following equation:

$$\beta \left(Z,{}^{2S+1}L_J,n,s,\mu ,\nu \right)={\displaystyle \sum _{k=1}^q{f}_k{\left(\frac{1}{Z}\right)}^k}$$

(2)

where $f_k=f_k({}^{2S+1}L_J,n,s,\mu ,\nu )$ are screening constants to be evaluated empirically. In Equation (2), q stands for the number of terms in the expansion of the β–parameter. The resonance energy (E_n) is in the following form:

$$E_n=E_{\infty }-\frac{Z^2}{n^2}\left\{1-\frac{f_1{(}^{2S+1}{L}_J^{\pi })}{Z(n-1)}-\frac{f_2{(}^{2S+1}{L}_J^{\pi })}{Z}\right.{\left.\pm {\displaystyle \sum _{k=1}^q{\displaystyle \sum _{k^{\prime }=1}^{q^{\prime }}{f}_1^{k^{\prime }}F(n,\mu ,\nu ,s)\times {\left(\frac{1}{Z}\right)}^k}}\right\}}^2.$$

(3)

In Equation (3), $f_1{(}^{2S+1}{L}_J^{\pi })$ and $f_2{(}^{2S+1}{L}_J^{\pi })$ are screening constants to be evaluated. $\pm {\displaystyle \sum _{k=1}^q{\displaystyle \sum _{k^{\prime }=1}^{q^{\prime }}{f}_1^{k^{\prime }}F(n,\mu ,\nu ,s)\times {\left(\frac{1}{Z}\right)}^k}}$ is a corrective term introduced to stabilize the resonance energies with increasing the principal quantum number n.

In general, resonance energies are analyzed from the standard quantum-defect expansion formula

$$E_n=E_{\infty }-\frac{R{Z}_{core}^2}{{(n-\delta )}^2}.$$

(4)

In Equation (4), E_∞ denotes the converging limit, R is the Rydberg constant, here, R = R_Cl = 109,735.6176 cm⁻¹ represents the Rydberg constant for the Cl atom, which is obtained from the relation R_Cl = R_∞/(1 + m_e/M), where R_∞ = 109,737.3157 cm⁻¹, M is the mass of Cl⁺, and m_e is the rest mass of the electron; Z_core represents the electric charge of the core ion and δ means the quantum defect. In addition, theoretical and measured energy positions can be analyzed by calculating the Z*-effective charge in the framework of the SCUNC-procedure.

$$E_n=E_{\infty }-\frac{Z^{\ast 2}}{n^2}R.$$

(5)

Furthermore, comparing Equations (3) and (5), the effective charge is in the following form:

$$Z^{\ast }=Z\left\{1-\frac{f_1{(}^{2S+1}{L}_J^{\pi })}{Z(n-1)}-\frac{f_2{(}^{2S+1}{L}_J^{\pi })}{Z}\right.\left.\pm {\displaystyle \sum _{k=1}^q{\displaystyle \sum _{k^{\prime }=1}^{q^{\prime }}{f}_1^{k^{\prime }}F(n,\mu ,\nu ,s)\times {\left(\frac{1}{Z}\right)}^k}}\right\}.$$

(6)

In addition, the f₂-parameter in Equation (3) is theoretically determined from Equation (6) with the following conditions:

$$\underset{n\to \infty }{\lim }{Z}^{\ast }=Z\left(1-\frac{f_2{(}^{2S+1}{L}^{\pi })}{Z}\right)=Z_{core}.$$

(7)

So, we then get the following form:

$$f_2\left({}^{2S+1}{L}_J^{\pi }\right)=Z-Z_{core}$$

(8)

For a photoionization process from an atomic X^p+, we obtain the following form:

γ + X^p+ → X^p+1 + e⁻

(9)

where γ is the absorbed photon. Using (9), we find Z_core = p +1. For the neutral chlorine atom (Cl) considered in this work, Equation (9) becomes γ + Cl → Cl⁺ + e⁻, therefore Z_core = 1 and $f_2\left({}^{2S+1}{L}_J^{\pi }\right)=\left(17-1\right)=16.0$. The remaining $f_1\left({}^{2S+1}{L}_J^{\pi }\right)$-parameter is evaluated empirically using experimental data [18] for a given (^2S+1L_J)nl level with ν = 0 in Equation (3). The results obtained are indicated in the caption of the corresponding table. The details of the calculation are clearly explained in our previous original papers [16,20,21].

In addition, using Equations (4) and (5), we get

$$\frac{Z^{2\ast }}{n^2}=\frac{Z_{core}^2}{{(n-\delta )}^2}$$

which means

$$Z^{\ast }=\frac{Z_{core}}{\left(1-\frac{\delta }{n}\right)}.$$

(10)

Equation (10) indicates clearly that each Rydberg series must satisfy the following SCUNC conditions:

$$\left\{\begin{array}{l}{Z}^{\ast }\ge Z_{core}if\delta \ge 0\\ Z^{\ast }\le Z_{core}if\delta \le 0\\ \underset{n\to \infty }{\lim Z^{\ast }}=Z_{core}\end{array}\right..$$

(11)

The resonance energies, quantum defects and effective charges of the 3s²3p⁴ (³P_2,1,0)ns and 3s²3p⁴ (³P_1,0)nd Rydberg series of Cl studied in the present work are listed in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, and comparisons are done with previous experimental measurements [18,19]. From (4) we obtain the following form for the quantum defect:

$$\delta =n-Z_{core}\sqrt{\frac{R}{\left(E_{\infty }-E_n\right)}}.$$

(12)

Table 1. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₂)ns (⁴P_5/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18]. Here, f₁ (³P₂; ⁴P_5/2; ²P⁰_3/2) = −2.2115 ± 0.0078 with μ = 23.

ns	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P2)ns (4P5/2)
	SCUNC	Experimental Data	SCUNC	Experimental Data	SCUNC
	En (cm−1)	En (cm−1) a	δ	δ a	Z*
23	104,339.78	104,339.78	2.101	2.108	1.101
24	104,362.21	104,361.03	2.100	2.157	1.096
25	104,381.78	104,380.42	2.099	2.173	1.092
26	104,398.94	104,397.54	2.098	2.185	1.088
27	104,414.07	104,413.48	2.097	2.139	1.085
28	104,427.49	104,426.07	2.096	2.207	1.082
29	104,439.43	104,438.29	2.094	2.195	1.079
30	104,450.12	104,448.99	2.093	2.204	1.076
31	104,459.71	104,458.49	2.091	2.225	1.074
32	104,468.36	104,467.04	2.090	2.250	1.071
33	104,476.18	104,476.51	2.088	2.043	1.069
34	104,483.28	104,483.55	2.086	2.045	1.067
35	104,489.74	104,490.51	2.084	1.958	1.065
36	104,495.63	104,495.51	2.083	2.104	1.063
37	104,501.02	104,500.80	2.081	2.124	1.061
38	104,505.97	104,505.65	2.079	2.147	1.060
39	104,510.53	104,510.02	2.077	2.193	1.058
40	104,514.72	104,514.27	2.076	2.187	1.057
41	104,518.60	104,518.21	2.074	2.178	1.055
42	104,522.19	104,522.23	2.072	2.060	1.054
43	104,525.51	104,525.23	2.071	2.159	1.053
44	104,528.61	104,528.27	2.069	2.182	1.051
45	104,531.49	104,531.11	2.067	2.202	1.050
46	104,534.17	104,533.69	2.066	2.250	1.049
47	104,536.68	104,536.29	2.064	2.222	1.048
48	104,539.02	104,538.66	2.062	2.220	1.047
49	104,541.21	104,540.83	2.061	2.241	1.046
50	104,543.27	104,542.87	2.059	2.261	1.045
51	104,545.21	104,544.89	2.058	2.227	1.044
52	104,547.03	104,546.65	2.056	2.269	1.043
53	104,548.74	104,548.45	2.055	2.228	1.043
54	104,550.35	104,550.06	2.053	2.240	1.042
55	104,551.88	104,551.57	2.052	2.259	1.041
56	104,553.32	104,552.97	2.050	2.297	1.040
57	104,554.68	104,554.38	2.049	2.274	1.039
58	104,555.97	104,555.67	2.048	2.284	1.039
59	104,557.19	104,556.95	2.046	2.247	1.038
60	104,558.35	104,558.08	2.045	2.282	1.037
61	104,559.45	104,559.14	2.044	2.330	1.037
62	104,560.49		2.042		1.036
63	104,561.49		2.041		1.036
64	104,562.44		2.040		1.035
65	104,563.34		2.039		1.035
66	104,564.20		2.038		1.034
67	104,565.02		2.036		1.034
68	104,565.80		2.035		1.033
69	104,566.55		2.034		1.033
70	104,567.27		2.033		1.032
71	104,567.95		2.032		1.032
72	104,568.61		2.031		1.031
73	104,569.23		2.030		1.031
74	104,569.83		2.029		1.030
75	104,570.41		2.028		1.030
76	104,570.97		2.027		1.029
77	104,571.50		2.026		1.029
78	104,572.01		2.025		1.029
79	104,572.50		2.024		1.028
80	104,572.97		2.023		1.028
⁞	…	…	…		…
∞	104,591.02	104,591.02			1.000

^a Ref. [18].

Table 2. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18,19]. Here, f₁ (³P₁; ²D_5/2; ²P⁰_3/2) = −0.3042 ± 0.0015 with μ = 13.

nd	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P1)nd (2D5/2)
	SCUNC	Experimental Data		SCUNC	Experimental Data		SCUNC
	En (cm−1)	En (cm−1) a	En (cm−1) b	δ	δ a	δ b	Z*
13	104,604.35	104,604.35	104,606.8	0.321	0.321	0.299	1.025
14	104,700.63	104,703.87	104,705.2	0.320	0.282	0.266	1.023
15	104,777.89	104,777.92	104,780.9	0.319	0.318	0.275	1.022
16	104,840.81	104,842.25	104,845.1	0.318	0.292	0.242	1.020
17	104,892.75	104,892.28	104,892.2	0.317	0.327	0.328	1.019
18	104,936.11	104,937.67	104,939.4	0.316	0.276	0.232	1.018
19	104,972.69	104,973.23	104,973.9	0.315	0.299	0.279	1.017
20	105,003.84	105,003.28		0.314	0.334		1.016
21	105,030.57	105,031.67		0.314	0.269		1.015
22	105,053.69	105,053.38		0.313	0.327		1.014
23	105,073.81	105,073.38		0.313	0.336		1.014
24	105,091.44	105,092.21		0.312	0.266		1.013
25	105,106.97	105,107.15		0.312	0.299		1.013
26	105,120.72	105,120.57		0.311	0.323		1.012
27	105,132.95	105,132.67		0.311	0.335		1.012
28	105,143.88	105,144.51		0.311	0.250		1.011
29	105,153.69	105,153.87		0.310	0.291		1.011
30	105,162.52	105,162.61		0.310	0.300		1.010
31	105,170.51	105,170.49		0.310	0.312		1.010
32	105,177.74	105,177.63		0.309	0.326		1.010
33	105,184.33	105,184.86		0.309	0.224		1.010
34	105,190.34	105,191.94		0.309	0.026		1.009
35	105,195.83	105,196.08		0.308	0.261		1.009
36	105,200.87	105,201.08		0.308	0.264		1.009
37	105,205.50	105,205.61		0.308	0.285		1.008
38	105,209.77	105,209.96		0.308	0.261		1.008
39	105,213.71	105,213.83		0.308	0.276		1.008
40	105,217.36	105,217.38		0.307	0.301		1.008
41	105,220.74	105,220.77		0.307	0.298		1.008
42	105,223.88	105,224.01		0.307	0.265		1.007
43	105,226.81	105,226.91		0.307	0.270		1.007
44	105,229.53	105,229.49		0.307	0.322		1.007
45	105,232.07	105,232.39		0.306	0.177		1.007
46	105,234.45	105,234.81		0.306	0.150		1.007
47	105,236.68	105,236.91		0.306	0.199		1.007
48	105,238.77	105,238.85		0.306	0.266		1.006
49	105,240.73	105,240.69		0.306	0.327		1.006
50	105,242.57	105,242.59		0.306	0.297		1.006
51	105,244.31	105,244.41		0.306	0.247		1.006
52	105,245.95	105,245.89		0.305	0.341		1.006
53	105,247.49	105,247.41		0.305	0.359		1.006
54	105,248.95			0.305			1.006
55	105,250.33			0.305			1.006
56	105,251.63			0.305			1.006
57	105,252.87			0.305			1.005
58	105,254.04			0.305			1.005
59	105,255.16			0.305			1.005
60	105,256.22			0.305			1.005
61	105,257.22			0.304			1.005
62	105,258.18			0.304			1.005
63	105,259.09			0.304			1.005
64	105,259.96			0.304			1.005
65	105,260.79			0.304			1.005
66	105,261.58			0.304			1.005
67	105,262.34			0.304			1.005
68	105,263.06			0.304			1.005
69	105,263.76			0.304			1.004
70	105,264.42			0.304			1.004
⁞	…			…			…
∞	105,287.01	105,287.01

^a Ref. [18]. ^b Ref. [19].

Table 3. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₁)ns (²P_3/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18,19]. Here, f₁ (³P₁; ²P_3/2; ²P⁰_3/2) = −2.2052 ± 0.0016 with μ = 14.

ns	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P1)ns (2P3/2)
	SCUNC	Experimental Data		SCUNC	Experimental Data		SCUNC
	En (cm−1)	En (cm−1) a	En (cm−1) b	δ	δ a	δ b	Z*
14	104,521.08	104,521.08	104,520.0	2.030	2.030	2.039	1.170
15	104,634.67	104,636.11	104,630.8	2.030	2.016	2.068	1.158
16	104,724.79	104,720.65	104,716.7	2.029	2.080	2.129	1.147
17	104,797.47	104,794.65	104,790.1	2.028	2.071	2.139	1.138
18	104,856.94	104,854.28	104,854.3	2.026	2.075	2.075	1.130
19	104,906.20	104,907.24		2.025	2.001		1.123
20	104,947.46	104,945.08		2.023	2.085		1.116
21	104,982.37	104,980.03		2.021	2.093		1.110
22	105,012.15	105,009.19		2.019	2.125		1.105
23	105,037.78	105,036.02		2.017	2.090		1.100
24	105,059.98	105,058.38		2.015	2.091		1.096
25	105,079.34	105,079.18		2.013	2.021		1.092
26	105,096.32	105,095.29		2.011	2.075		1.088
27	105,111.31	105,109.68		2.009	2.123		1.085
28	105,124.59	105,123.33		2.007	2.107		1.082
29	105,136.42	105,135.24		2.005	2.110		1.079
30	105,147.00	-		2.004	-		1.076
31	105,156.51	105,155.48		2.002	2.115		1.074
32	105,165.08	105,163.91		2.000	2.142		1.071
33	105,172.83	105,171.71		1.999	2.148		1.069
34	105,179.86	105,179.08		1.997	2.112		1.067
35	105,186.27			1.996			1.065
36	105,192.11			1.994			1.063
37	105,197.47			1.993			1.061
38	105,202.38			1.992			1.060
39	105,206.89			1.990			1.058
40	105,211.06			1.989			1.057
41	105,214.91			1.988			1.055
42	105,218.47			1.987			1.054
43	105,221.78			1.985			1.053
44	105,224.85			1.984			1.051
45	105,227.71			1.983			1.050
46	105,230.37			1.982			1.049
47	105,232.86			1.981			1.048
48	105,235.19			1.980			1.047
49	105,237.38			1.979			1.046
50	105,239.42			1.978			1.045
51	105,241.35			1.977			1.044
52	105,243.16			1.977			1.043
53	105,244.86			1.976			1.042
54	105,246.47			1.975			1.042
55	105,247.98			1.974			1.041
56	105,249.42			1.973			1.040
57	105,250.77			1.972			1.039
58	105,252.05			1.972			1.039
59	105,253.27			1.971			1.038
60	105,254.42			1.970			1.037
61	105,255.52			1.970			1.037
62	105,256.56			1.969			1.036
63	105,257.55			1.968			1.036
64	105,258.49			1.968			1.035
65	105,259.39			1.966			1.034
66	105,260.25			1.966			1.034
67	105,261.06			1.966			1.033
68	105,261.84			1.965			1.033
69	105,262.59			1.965			1.032
70	105,263.30			1.965			1.032
⁞
∞	105,287.01	105,287.01

^a Ref. [18]. ^b Ref. [19].

Table 4. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18]. Here, f₁ (³P₁; ²D_5/2; ²P⁰_3/2) = −0.0881 ± 0.0016 with μ = 13.

nd	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P1)nd (2D5/2)
	SCUNC	Experimental Data	SCUNC	Experimental Data	SCUNC
	En (cm−1)	En (cm−1) a	δ	δ a	Z*
13	104,628.11	104,628.11	0.095	0.095	1.007
14	104,719.51	104,709.09	0.094	0.220	1.007
15	104,793.13	104,788.03	0.094	0.170	1.006
16	104,853.30	104,845.55	0.094	0.234	1.006
17	104,903.10	104,903.72	0.093	0.079	1.006
18	104,944.79	104,939.93	0.093	0.219	1.005
19	104,980.05	104,973.23	0.093	0.299	1.005
20	105,010.12	105,006.44	0.092	0.223	1.005
21	105,035.97	105,031.67	0.092	0.269	1.004
22	105,058.37	105,054.03	0.092	0.297	1.004
23	105,077.90	105,077.62	0.092	0.107	1.004
24	105,095.03		0.092		1.004
25	105,110.14		0.092		1.004
26	105,123.53		0.092		1.004
27	105,135.46		0.091		1.003
28	105,146.12		0.091		1.003
29	105,155.70		0.091		1.003
30	105,164.34		0.091		1.003
31	105,172.15		0.091		1.003
32	105,179.23		0.091		1.003
33	105,185.69		0.091		1.003
34	105,191.57		0.091		1.003
35	105,196.96		0.091		1.003
36	105,201.91		0.091		1.003
37	105,206.46		0.091		1.002
38	105,210.65		0.091		1.002
39	105,214.53		0.091		1.002
40	105,218.11		0.090		1.002
41	105,221.44		0.090		1.002
42	105,224.53		0.090		1.002
43	105,227.41		0.090		1.002
44	105,230.09		0.090		1.002
45	105,232.60		0.090		1.002
46	105,234.95		0.090		1.002
47	105,237.14		0.090		1.002
48	105,239.20		0.090		1.002
49	105,241.14		0.090		1.002
50	105,242.96		0.090		1.002
51	105,244.67		0.090		1.002
52	105,246.29		0.090		1.002
53	105,247.81		0.090		1.002
54	105,249.25		0.090		1.002
55	105,250.61		0.090		1.002
56	105,251.91		0.090		1.002
57	105,253.13		0.090		1.002
58	105,254.29		0.090		1.002
59	105,255.39		0.090		1.002
60	105,256.44		0.090		1.001
61	105,257.43		0.090		1.001
62	105,258.38		0.090		1.001
63	105,259.28		0.090		1.001
64	105,260.14		0.090		1.001
65	105,260.97		0.090		1.001
66	105,261.75		0.090		1.001
67	105,262.50		0.090		1.001
68	105,263.22		0.090		1.001
69	105,263.90		0.090		1.001
70	105,264.56		0.090		1.001
⁞
∞	105,287.01	105,287.01

^a Ref. [18].

Table 5. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18,19]. Here, f₁ (³P₀;²P_1/2; ²P⁰_3/2) = −2.3766 ± 0.0273 with μ = 10.

ns	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P0)ns (2P1/2)
	SCUNC	Experimental Data		SCUNC	Experimental Data		SCUNC
	En (cm−1)	En (cm−1) a	En (cm−1) b	δ	δ a	δ b	Z*
10	103,834.02	103,834.01	103,831.8	2.089	2.089	2.094	1.264
11	104,205.62	104,204.13	104,203.7	2.089	2.093	2.094	1.238
12	104,470.57	-		2.088	-		1.216
13	104,666.06	104,665.63		2.087	2.089		1.198
14	104,814.39	104,813.74		2.086	2.090		1.183
15	104,929.59	104,928.56		2.085	2.093		1.170
16	105,020.83	105,019.83		2.084	2.094		1.158
17	105,094.33	-		2.083	-		1.149
18	105,154.40	-		2.082	-		1.140
19	105,204.12	105,203.12		2.081	2.099		1.132
20	105,245.75	-		2.080	-		1.125
21	105,280.94	105,281.56		2.080	2.055		1.119
22	105,310.97			2.079			1.113
23	105,336.79			2.078			1.108
24	105,359.15			2.077			1.103
25	105,378.65			2.077			1.099
26	105,395.75			2.076			1.095
27	105,410.83			2.076			1.091
28	105,424.20			2.075			1.088
29	105,436.11			2.075			1.085
30	105,446.76			2.074			1.082
31	105,456.33			2.074			1.079
32	105,464.95			2.074			1.077
33	105,472.75			2.073			1.074
34	105,479.83			2.073			1.072
35	105,486.27			2.073			1.070
36	105,492.15			2.072			1.068
37	105,497.53			2.072			1.066
38	105,502.47			2.072			1.064
39	105,507.01			2.072			1.063
40	105,511.20			2.071			1.061
41	105,515.07			2.071			1.059
42	105,518.65			2.071			1.058
43	105,521.97			2.071			1.057
44	105,525.06			2.071			1.055
45	105,527.94			2.070			1.054
46	105,530.62			2.070			1.053
47	105,533.12			2.070			1.052
48	105,535.46			2.070			1.051
49	105,537.66			2.070			1.050
50	105,539.71			2.070			1.049
51	105,541.65			2.069			1.048
52	105,543.46			2.069			1.047
53	105,545.18			2.069			1.046
54	105,546.79			2.069			1.045
55	105,548.31			2.069			1.044
56	105,549.75			2.069			1.043
57	105,551.11			2.069			1.042
58	105,552.40			2.069			1.042
59	105,553.62			2.068			1.041
60	105,554.78			2.068			1.040
61	105,555.88			2.068			1.040
62	105,556.93			2.068			1.039
63	105,557.92			2.068			1.038
64	105,558.87			2.068			1.038
65	105,559.77			2.068			1.037
66	105,560.63			2.068			1.037
67	105,561.45			2.068			1.036
68	105,562.24			2.068			1.035
69	105,562.99			2.068			1.035
70	105,563.70			2.068			1.034
⁞	…			…			…
∞	105,587.48	105,587.48

^a Ref. [18].; ^b Ref. [19].

Table 6. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18,19]. Here, f₁ (³P₀;²P_3/2; ²P⁰_3/2) = −0.2916 ± 0.0028 with μ = 16.

nd	Chlorine Initial State: 3s23p5 2P03/2
	Rydberg Series 3s23p4 (3P0)nd (2P3/2)
	SCUNC	Experimental Data		SCUNC	Experimental Data		SCUNC
	En (cm−1)	En (cm−1) a	En (cm−1) b	δ	δ a	δ b	Z*
16	105,142.00	105,142.00	105,148.0	0.305	0.302	0.195	1.019
17	105,193.81	105,194.50		0.304	0.286		1.018
18	105,237.08	105,237.77		0.303	0.282		1.017
19	105,273.59	105,274.04		0.302	0.284		1.016
20	105,304.67	105,305.21		0.302	0.277		1.015
21	105,331.35	105,331.58		0.301	0.285		1.015
22	105,354.43	105,354.70		0.301	0.280		1.014
23	105,374.52	105,374.94		0.300	0.269		1.013
24	105,392.12	105,392.28		0.299	0.280		1.013
25	105,407.63	105,407.79		0.299	0.276		1.012
26	105,421.36	105,421.57		0.299	0.269		1.012
27	105,433.57	105,433.69		0.298	0.273		1.011
28	105,444.49	105,444.61		0.298	0.269		1.011
29	105,454.28	105,454.48		0.297	0.257		1.010
30	105,463.10	105,463.45		0.297	0.235		1.010
31	105,471.07	105,471.25		0.297	0.251		1.010
32	105,478.30			0.296			1.009
33	105,484.88			0.296			1.009
34	105,490.88			0.296			1.009
35	105,496.37			0.296			1.009
36	105,501.40			0.295			1.008
37	105,506.03			0.295			1.008
38	105,510.29			0.295			1.008
39	105,514.23			0.295			1.008
40	105,517.87			0.295			1.007
41	105,521.25			0.294			1.007
42	105,524.39			0.294			1.007
43	105,527.31			0.294			1.007
44	105,530.03			0.294			1.007
45	105,532.58			0.294			1.007
46	105,534.95			0.294			1.006
47	105,537.18			0.293			1.006
48	105,539.26			0.293			1.006
49	105,541.22			0.293			1.006
50	105,543.07			0.293			1.006
51	105,544.80			0.293			1.006
52	105,546.44			0.293			1.006
53	105,547.98			0.293			1.006
54	105,549.44			0.293			1.006
55	105,550.81			0.292			1.005
56	105,552.12			0.292			1.005
57	105,553.36			0.292			1.005
58	105,554.53			0.292			1.005
59	105,555.64			0.292			1.005
60	105,556.70			0.292			1.005
61	105,557.70			0.292			1.005
62	105,558.66			0.292			1.005
63	105,559.57			0.292			1.005
64	105,560.44			0.292			1.005
65	105,561.27			0.291			1.005
66	105,562.06			0.291			1.004
67	105,562.82			0.291			1.004
68	105,563.54			0.291			1.004
69	105,564.24			0.291			1.004
70	105,564.90			0.291			1.004
⁞
∞	105,587.48	105,587.48

^a Ref. [18]. ^b Ref. [19].

Table 7. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_1/2 → 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18]. Here, f₁ (³P₀; ²P_3/2; ²P⁰_1/2) = −0.2711 ± 0.0040 with μ= 18.

nd	Chlorine Initial State: 3s23p5 2P01/2
	Rydberg Series 3s23p4 (3P0)nd (2P3/2)
	SCUNC	Experimental Data	SCUNC	Experimental Data	SCUNC
	En (cm−1)	En (cm−1) a	δ	δ a	Z*
18	104,355.55	104,355.55	0.283	0.282	1.016
19	104,391.93	104,391.13	0.282	0.305	1.015
20	104,422.91	104,422.71	0.281	0.288	1.014
21	104,449.51	104,449.01	0.281	0.300	1.014
22	104,472.52	104,472.08	0.280	0.300	1.013
23	104,492.55	104,492.02	0.280	0.308	1.012
24	104,510.11	104,509.52	0.279	0.314	1.012
25	104,525.57	-	0.279	-	1.011
26	104,539.27	-	0.278	-	1.011
27	104,551.45	104,551.11	0.278	0.307	1.010
28	104,562.34	104,562.22	0.278	0.289	1.010
29	104,572.12	104,572.18	0.277	0.269	1.010
30	104,580.92	104,581.29	0.277	0.231	1.009
31	104,588.87	104,589.20	0.277	0.232	1.009
32	104,596.09		0.277		1.009
33	104,602.65		0.276		1.008
34	104,608.64		0.276		1.008
35	104,614.12		0.276		1.008
36	104,619.15		0.276		1.008
37	104,623.77		0.275		1.008
38	104,628.02		0.275		1.007
39	104,631.95		0.275		1.007
40	104,635.59		0.275		1.007
41	104,638.97		0.275		1.007
42	104,642.10		0.275		1.007
43	104,645.02		0.274		1.006
44	104,647.74		0.274		1.006
45	104,650.27		0.274		1.006
46	104,652.65		0.274		1.006
47	104,654.87		0.274		1.006
48	104,656.95		0.274		1.006
49	104,658.91		0.274		1.006
50	104,660.75		0.273		1.006
51	104,662.48		0.273		1.005
52	104,664.12		0.273		1.005
53	104,665.66		0.273		1.005
54	104,667.11		0.273		1.005
55	104,668.49		0.273		1.005
56	104,669.79		0.273		1.005
57	104,671.03		0.273		1.005
58	104,672.20		0.273		1.005
59	104,673.31		0.272		1.005
60	104,674.37		0.272		1.005
61	104,675.37		0.272		1.005
62	104,676.33		0.272		1.004
63	104,677.24		0.272		1.004
64	104,678.11		0.272		1.004
65	104,678.94		0.272		1.004
66	104,679.73		0.272		1.004
67	104,680.49		0.272		1.004
68	104,681.21		0.272		1.004
69	104,681.90		0.272		1.004
70	104,682.56		0.272		1.004
⁞	…		…		…
∞	104,705.13	104,705.13

^a Ref. [18].

Table 8. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_1/2 → 3s²3p⁴ (³P₁)ns (²P_3/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18]. Here, f₁ (³P₁;²P_3/2; ²P⁰_1/2) = −2.3230 ± 0.0100 with μ = 25.

ns	Chlorine Initial State: 3s23p5 2P01/2
	Rydberg Series 3s23p4 (3P1)ns (2P3/2)
	SCUNC	Experimental Data	SCUNC	Experimental Data	SCUNC
	En (cm−1)	En (cm−1) a	δ	δ a	Z*
25	104,193.41	104,193.41	2.206	2.209	1.097
26	104,210.79	104,210.83	2.206	2.206	1.093
27	104,226.11	104,225.45	2.206	2.254	1.089
28	104,239.68	104,238.49	2.206	2.301	1.086
29	104,251.77	104,245.29	2.206	2.759	1.083
30	104,262.58	104,263.32	2.205	2.135	1.080
31	104,272.28	104,272.34	2.204	2.201	1.077
32	104,281.02	104,280.49	2.203	2.271	1.075
33	104,288.93	104,288.40	2.202	2.276	1.073
34	104,296.10	104,295.65	2.201	2.271	1.070
35	104,302.62	104,302.52	2.200	2.221	1.068
36	104,308.57	104,309.47	2.199	2.045	1.066
37	104,314.02	104,314.25	2.197	2.159	1.065
38	104,319.02	104,318.65	2.196	2.279	1.063
39	104,323.61	104,323.57	2.194	2.211	1.061
40	104,327.85	104,327.56	2.193	2.271	1.060
41	104,331.76	104,331.42	2.191	2.289	1.058
42	104,335.38	104,335.11	2.190	2.276	1.057
43	104,338.74	104,338.65	2.188	2.224	1.055
44	104,341.85	104,341.48	2.187	2.321	1.054
45	104,344.76	104,344.34	2.185	2.344	1.053
46	104,347.46	-	2.184	-	1.052
47	104,349.99	-	2.182	-	1.051
48	104,352.35	-	2.181	-	1.049
49	104,354.56	104,354.87	2.179	2.049	1.048
50	104,356.64	104,356.60	2.178	2.211	1.047
51	104,358.59	104,358.53	2.176	2.221	1.046
52	104,360.42		2.175		1.046
53	104,362.14		2.173		1.045
54	104,363.77		2.172		1.044
55	104,365.30		2.170		1.043
56	104,366.75		2.169		1.042
57	104,368.12		2.167		1.041
58	104,369.42		2.166		1.041
59	104,370.65		2.165		1.040
60	104,371.82		2.163		1.039
61	104,372.92		2.162		1.039
62	104,373.97		2.160		1.038
63	104,374.97		2.159		1.037
64	104,375.93		2.158		1.037
65	104,376.83		2.156		1.036
66	104,377.70		2.155		1.036
67	104,378.52		2.154		1.035
68	104,379.31		2.152		1.035
69	104,380.06		2.151		1.034
70	104,380.78		2.150		1.034
⁞	…		…		…
∞	104,404.62	104,404.62			1.000

^a Ref. [18].

Table 9. Resonance energies (E_n), quantum defect (δ) and effective charge (Z*) for the 3s²3p^{5 2}P⁰_1/2 → 3s²3p⁴ (³P₂)ns (⁴P_3/2) Rydberg series in Cl I. The present SCUNC- calculations are compared with experiments [18]. Here, f₁ (³P₂; ⁴P_3/2; ²P⁰_1/2) = −2.3603 ± 0.0128 with μ = 27.

ns	Chlorine Initial State: 3s23p5 2P01/2
	Rydberg Series 3s23p4 (3P2)ns (4P3/2)
	SCUNC	Experimental Data	SCUNC	Experimental Data	SCUNC
	En (cm−1)	En (cm−1) a	δ	δ a	Z*
27	103,529.65	103,529.65	2.247	2.247	1.091
28	103,543.29	103,542.03	2.247	2.345	1.087
29	103,555.42	103,553.29	2.247	2.432	1.084
30	103,566.28	103,564.01	2.247	2.465	1.081
31	103,576.02	103,575.44	2.247	2.309	1.079
32	103,584.79	103,583.78	2.246	2.367	1.076
33	103,592.73	103,594.21	2.246	2.048	1.074
34	103,599.93	103,600.99	2.245	2.089	1.072
35	103,606.48	103,607.12	2.244	2.140	1.069
36	103,612.45	103,612.94	2.243	2.157	1.067
37	103,617.92	103,618.14	2.242	2.199	1.066
38	103,622.93	103,623.11	2.241	2.204	1.064
39	103,627.54	103,627.60	2.240	2.227	1.062
40	103,631.79	103,631.81	2.238	2.234	1.061
41	103,635.72	103,634.41	2.237	2.580	1.059
42	103,639.35	103,639.85	2.236	2.092	1.058
43	103,642.72	103,642.77	2.234	2.218	1.056
44	103,645.85	103,645.66	2.233	2.294	1.055
45	103,648.76	103,648.54	2.231	2.309	1.054
46	103,651.47	103,651.21	2.230	2.329	1.052
47	103,654.00	103,653.63	2.229	2.381	1.051
48	103,656.37	103,656.01	2.227	2.385	1.050
49	103,658.59	103,658.36	2.226	2.334	1.049
50	103,660.67	103,660.33	2.224	2.394	1.048
51	103,662.63	103,662.35	2.223	2.369	1.047
52	103,664.46	103,664.03	2.221	2.464	1.046
53	103,666.19		2.220		1.045
54	103,667.82		2.218		1.045
55	103,669.36		2.217		1.044
56	103,670.82		2.215		1.043
57	103,672.19		2.214		1.042
58	103,673.49		2.213		1.041
59	103,674.72		2.211		1.041
60	103,675.89		2.210		1.040
61	103,677.00		2.208		1.039
62	103,678.06		2.207		1.039
63	103,679.06		2.206		1.038
64	103,680.01		2.204		1.037
65	103,680.92		2.203		1.037
66	103,681.79		2.201		1.036
67	103,682.62		2.200		1.036
68	103,683.41		2.199		1.035
69	103,684.16		2.198		1.035
70	103,684.88		2.196		1.034
⁞
∞	103,708.75	103,708.75

^a Ref. [18].

3. Results and Discussion

Let us first determine the sign of the quantum defect (δ) using the SCUNC analysis conditions (11), considering the lowest resonance corresponding to the first entry of the Rydberg series under study. For example, for the 3s²3p⁴ (³P₂)ns (⁴P_5/2) Rydberg series originating from the 3s²3p⁵ (²P⁰_3/2) ground state of Cl (Table 1), the lowest Resonance corresponds to n_low = 23. From Table 1, we deduce f₁ (³P₂; ⁴P_5/2; ${}^{2}P_{3/2}^0$) = −2.2115. From Equation (6), we derive the expression for the effective nuclear charge $Z_{\max }^{\ast }$ as follows:

$$Z_{\max }^{\ast }=Z\left\{1-\frac{f_1}{Z(n_{low}-1)}-\frac{16.0}{Z}\right\}=17\left\{1+\frac{2.2115}{17(23-1)}-\frac{16.0}{17}\right\}=1.101.$$

(13)

As Z_core = 1.000, $Z_{\max }^{\ast }$ = 1.101 > Z_core. Then, the quantum defect is positive. So, for all the series analyzed in this work, positive quantum defects are allowed according to the according to the SCUNC analysis conditions (11). This is verified for all the data quoted in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. Table 1 presents Resonance energies, quantum defects and effective charges of the 3s²3p⁴ (³P₂)ns (⁴P_5/2) Rydberg series originating from the 3s²3p^{5 2}P⁰_3/2 ground stateCl and converging to the ³P₂ series limit in Cl⁺. For this Rydberg Resonance, only the VUV-PI and VUV-PFI-PI measurements [18] are available in the literature to our knowledge. Comparison of resonance energies shows excellent agreement between theoretical data (SCUNC) and (VUV-PI and VUV-PFI-PI) measurements [18] up to n = 61, as well highlightedin Figure 1. In contrast, for quantum defects, the present SCUNC calculations provide good quantum defect behavior that is virtually constant or decreases slightly with increasing principal quantum number n up to n = 80, while experimental quantum defects vary anomalously in all directions, as shown in Figure 2. Table 2 lists resonance energies, quantum defects and effective chargesof the 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg resonance series from the 3s²3p^{5 2}P⁰_3/2 ground state of atomic chlorine. As shown in Figure 3, there is an excellent agreement between the SCUNC resonance energies and the quoted measurements [18,19]. But if the SCUNC quantum defect is constant or decreases slightly with increasing principal quantum number n, the measured quantum defect varies considerably [18,19], as shown in Figure 4. It is well known that quantum defects must be constant or decrease with increasing n. Especially when n→∞, we obtain a hydrogen-like system for which the quantum defect is zero. Table 3 and Table 4 present the resonance energies, quantum defects and effective charges of the 3s²3p⁴ (³P₁)ns (²P_3/2) and of the 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg originating from the 3s²3p^{5 2}P⁰_3/2 ground state of Cl and converging to the ³P₁ series limit in Cl⁺. Once again, the SCUNC results agree excellently with all the experimental resonance energies up to n = 34 (Table 3) and up to n = 23 (Table 4). These good agreements allow us to consider as accurate the extrapolated SCUNC data up to n = 70. Comparisons of quantum defects indicate irregular behavior of the experimental values in contrast with the SCUNC quantum defect varying correctly up to n = 70. Table 5 and Table 6 list resonance energies, quantum defects and effective charges calculated for the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₀)ns (²P_1/2) and the 3s²3p^{5 2}P⁰_3/2 → 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg resonance series. For the 3s²3p⁴ (³P₀)ns (²P_1/2) series, experimental data are presented in Table 5 up to n = 21 with missing energy positions for n = 12, 17 18, 20. SCUNC data associated with a nearly constant quantum defect at around 2.08 are provided for the missing experimental resonance energies [18,19]. In addition, the good behavior of the SCUNC quantum defect is observed up to n = 70 allowing us to consider the extrapolated news resonance energies as correct. Table 6 indicates resonance parameters of the 3s²3p⁴ (³P₀)nd (²P_3/2) series. Here again, very good consistency is obtained between the theoretical and the experimental resonance energies up to n = 31 as shown in Figure 5. New resonance energies associated with an almost constant quantum defect are tabulated for high-lying states n = 32–70 (see Figure 6). Table 7, Table 8 and Table 9 compare resonance energies and quantum defects, respectively of the 3s²3p⁴ (³P₀)nd (²P_3/2), 3s²3p⁴ (³P₁)ns (²P_3/2) and 3s²3p⁴ (³P₂)ns (⁴P_3/2) Rydberg series. Comparison shows reasonably good agreement between resonance energies for all the considered series as highlighted in Figure 7 and Figure 8. For the 3s²3p⁴ (³P₀)nd (²P_3/2) series presented in Table 7, the absent experimental resonance energies for n = 25 and 26 [18] and that for the 3s²3p⁴ (³P₁)ns (²P_3/2) series quoted in Table 8 for n = 46, 47 and 48 were calculated via the present formalism. As far as quantum defects are concerned, for the above series, the SCUNC data remain again virtually constant up to n = 70 in contrast with the measured [18] as shown in Figure 9 and Figure 10. For all the series investigated in this work, the effective nuclear charge decreases the monotony toward the value of the electric charge of the core ion Z_core = 1.0.

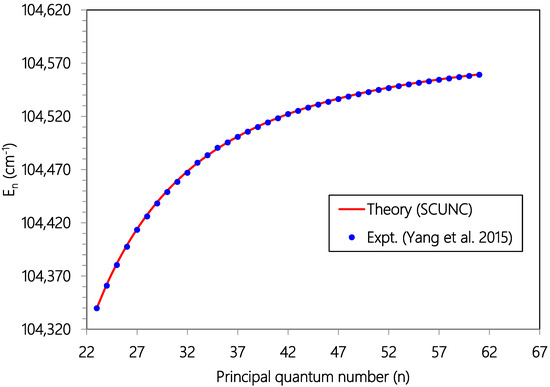
Figure 1. Plot of Resonance energies (E_n, cm⁻¹) versus principal quantum number (n) for the 3s²3p⁴ (³P_2,1)ns (⁴P_5/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles, Ref. [18] and theoretical estimates (solid red line, SCUNC).

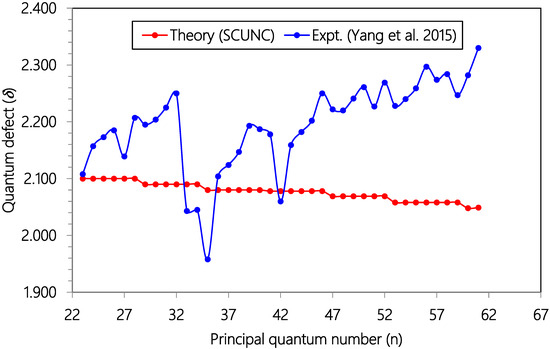
Figure 2. Plot of quantum defects (δ) versus principal quantum number (n) for the 3s²3p⁴ (³P_2,1)ns (⁴P_5/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles, Ref. [18]) and theoretical estimates (solid red circles, SCUNC).

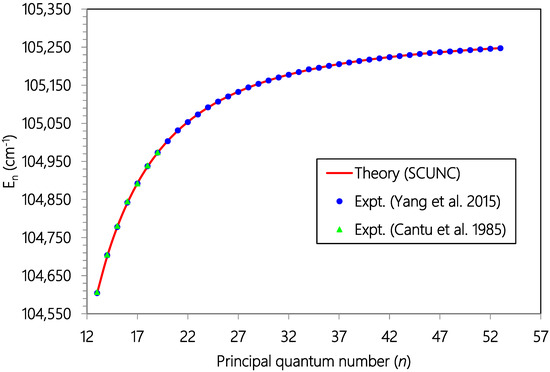
Figure 3. Plot of resonance energies (E_n, cm⁻¹) versus principal quantum number (n) for the 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles Ref. [18] and solid green triangles Ref. [19]) and theoretical estimates (solid red line, SCUNC).

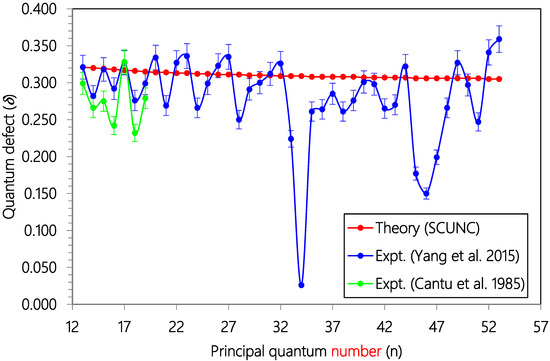
Figure 4. Plot of quantum defects (δ) versus principal quantum number (n) for the 3s²3p⁴ (³P₁)nd (²D_5/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles Ref. [18] and solid green circles Ref. [19]) and theoretical estimates (solid red circles, SCUNC).

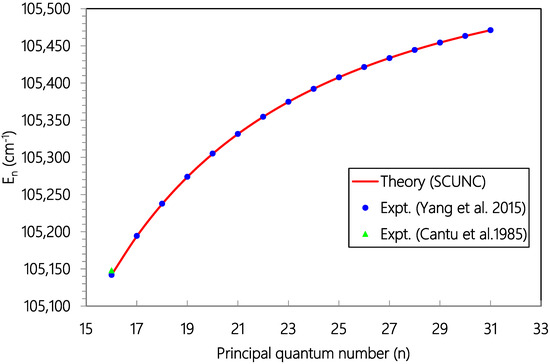
Figure 5. Plot of resonance energies (E_n, cm⁻¹) versus principal quantum number (n) for the 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles Ref. [18] and solid green triangles Ref. [19]) and theoretical estimates (solid red line, SCUNC).

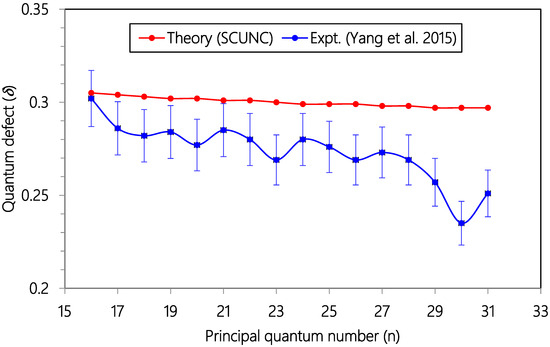
Figure 6. Plot of quantum defects (δ) versus principal quantum number (n) for the 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_3/2) ground state. Experimental data (solid blue circles Ref. [18]) and theoretical estimates (solid red circles, SCUNC).

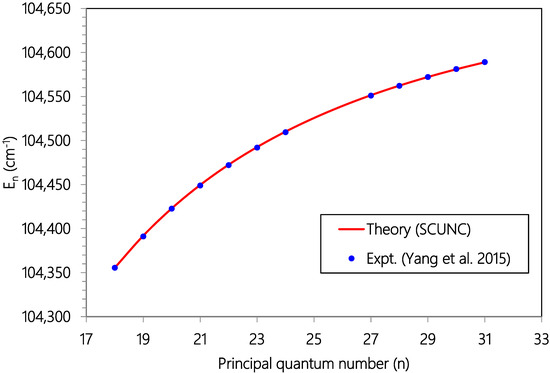
Figure 7. Plot of resonance energies (E_n, cm⁻¹) versus principal quantum number (n) for the 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_1/2) excited state. Experimental data (solid blue circles Ref. [18]) and theoretical estimates (solid red line, SCUNC).

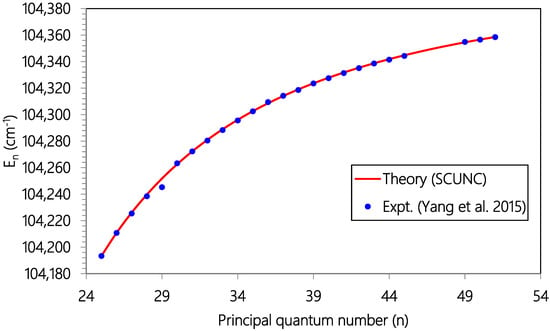
Figure 8. Plot of resonance energies (E_n, cm⁻¹) versus principal quantum number (n) for the 3s²3p⁴ (³P₁)ns (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_1/2) excited state. Experimental data (solid blue circles Ref. [18]) and theoretical estimates (solid red line, SCUNC).

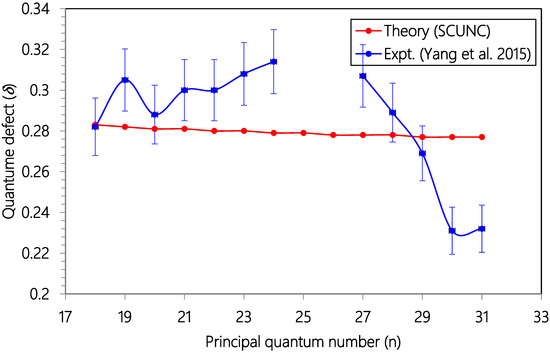
Figure 9. Plot of quantum defects (δ) versus principal quantum number (n) for the 3s²3p⁴ (³P₀)nd (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_1/2) excited state. Experimental data (solid blue circles Ref. [18]) and theoretical estimates (solid red circles, SCUNC).

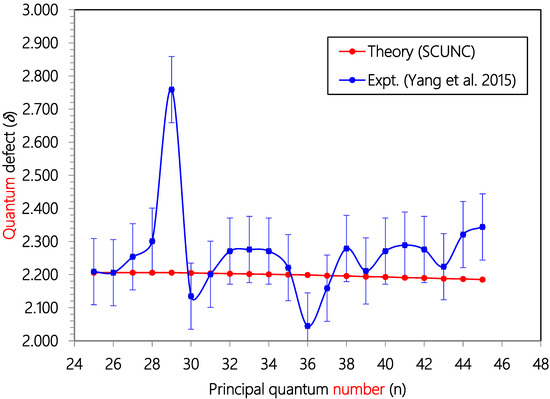
Figure 10. Plot of quantum defects (δ) versus principal quantum number (n) for the 3s²3p⁴ (³P₁)ns (²P_3/2) Rydberg series of resonances originating from the Cl (²P⁰_1/2) excited state. Experimental data (solid blue circles Ref. [18]) and theoretical estimates (solid red circles, SCUNC).

4. Summary and Conclusions

In this paper, the first calculations of resonance energies, quantum defects and effective charges of several Rydberg series resulting from the ejection of 3p electrons from the ²P⁰_3/2 ground state and ²P⁰_1/2 excited state of the neutral chlorine atom was carried out. Overall, very good agreements were obtained between the present SCUNC calculations and the available experimental data for resonance energies. In addition, for all the resonance energies associated with an experimental quantum defect that varied in all directions, an almost constant SCUNC quantum defect was tabulated up to n = 70. The new SCUNC data quoted in the listed tables may be of great interest for the physical community focusing their studies on the photoionization of atomic chlorine.