Abstract
The ionization data of a neutral molecule are crucial to model the energy deposition and dissociative ionization process. We study theoretically the electron impact ionization process and report on the dissociative ionization cross sections of the tungsten hexafluoride cations invoking the modified-binary-encounter-Bethe model. In this model, the binary-encounter-Bethe model is modified by applying the transformation to the binding energies of the molecular orbitals and then normalizing the partial ionization cross sections of the cations using the branching ratios. The normalization is performed at a particular energy and ensures that the branching ratios of different fragments are summed to unity. The model yielded satisfactory results for both the singly and doubly ionized ions. The approach validates the results of Basner et al. The advantages and limitations of this model are also discussed. This work corroborates the importance of mass spectrometry data in the proper understanding of the ionization process.
1. Introduction
Electron ionization is an important technique in mass spectrometry (MS) for the characterization of the cations formed due to dissociative ionization [1]. In low-pressure non-thermal plasmas, the electron impact ionization is a dominant process for the formation of ions and radicals at energies beyond ionization threshold. This formation occurs via dissociative ionization of the molecules. The ions, free electrons, neutral and excited atoms, and molecules, present in plasma modify the structural properties and expedite the surface reactions at low activation energies, thus enhancing the plasma processing rates [2]. The positively charged ions stimulate the plasma polymerization [3,4], influencing the rate of combustion [5,6], and play an important role in plasma etching [7]. The total and partial ionization cross sections due to electron impact are, therefore, needed to understand the electron ionization processes and to develop plasma models [8,9,10].
Unfortunately, the ab initio methods have proved successful in computing the partial ionization cross sections only for the lightest molecules [11]. This is due to the inherent nature of the close-coupling (CC) scheme adopted to compute the cross sections. In these methods, the accurate representation of the scattering states requires a large number of target states, a large basis set and accurate representation of continuum states of incident and ejected electron. This makes the ab initio calculations intractable for simple and complex targets even with the latest computing systems. A need is therefore to have methods that can provide reliable estimates of ionization cross section data quickly and in the least expensive way. The modified-binary-encounter-Bethe (m-BEB) model is a variant of the binary-encounter-Bethe (BEB) model [12] and has shown promising results for electron impact partial ionization cross sections for both simple and complex systems [13,14,15,16,17,18,19,20]. In all these systems, the singly ionized (SI) positive ions dominated the ionization process and hence the model was tested only for the SI ions. The tungsten hexafluoride () is one such target where the ionization process is dominated by SI ions, but the doubly ionized (DI) ions contribute significantly to total ionization cross sections (TICS) [21]. Thus, this target is ideally suited to test the performance of the m-BEB model. gas is preferred over and because of its higher deposition rates [22]. It slows down the flame chemistry of the mixture and thus reduces the flame temperature [23]. is primarily used in the semiconductor industry to deposit tungsten metal through a chemical vapor deposition process [24,25] on conducting and insulating substrates [26,27]. It is used as a precursor in the synthesis of high-purity tungsten oxide nanoparticles [23], two-dimensional deposition of at low temperatures [28,29]. The two-dimensional transition metal dichalcogenides are considered as potential low dissipative semiconductor materials for nanoelectronic devices.
Although is an essential plasma-enriched material processing molecule, the partial ionization cross section data is not extensively available. Only Basner et al. have performed experimental measurements of partial and total ionization cross sections for this molecule [21]. The theoretical calculations involve the calculations of the total ionization cross sections using semi-empirical models [30,31] and have not been applied to compute the cross section data for doubly ionized ions.
Thus, in view of the limitations of the CC approaches and the fact that partial ionization cross section data is required for simple and complex molecules in different fields where the ionization process is of importance [32,33,34,35,36], the m-BEB model offers a solution to the computing problem. This model is extremely simple, reliable, and independent of the processes involved in the formation of the ions. Moreover, it does not suffer from any bottleneck due to a lack of available data. In this work, the partial ionization cross sections of the fragments of generated are reported using the m-BEB model for SI and DI ions. The study of electron impact ionization of has provided useful insights for a better understanding and interpretation of the BEB and m-BEB model results. Several aspects of the m-BEB model, such as the role of electron ionization mass spectrometry (EIMS) data and the normalization of cross section data are also discussed.
2. Methodology
The BEB and Modified-BEB Models
In the BEB model [12], the total electron impact ionization cross section is the sum of the cross sections of individual molecular orbitals, i.e.,
where i denotes the particular molecular orbital, = / and are the reduced orbital kinetic energy and incident energies, respectively. . The notations E, R, and refer to the incident energy of the incident electron, Rydberg constant, and Bohr’s radius, respectively. and are the magnitudes of the binding energy and orbital kinetic energy; and is the occupancy number of the ith molecular orbital. The ionization cross sections are zero if energy of the incident electron is less than the first ionization threshold.
The advantages of this model are plenty. The TICS are expressed in a simple analytical form. The input parameters such as , , and appearing in Equation (1) are easily obtained using quantum chemical software for any basis set and at a desired level of theory. The impact of basis sets on input parameters is minimal. This means that even a moderate-quality basis set will yield TICS comparable to a bigger and superior basis set. The model, in spite of having limitations [37], has received huge attention due to its simplicity and effectiveness in estimating TICS [38]. One of the drawbacks of this model is that it cannot be applied to computing the partial ionization cross sections (PICS) of ions created during the electron impact dissociative ionization process. The two working groups of Tennyson et al. and Baluja et al. have amended the BEB model differently to estimate the PICS [13,14,15,18,19,20]. The form used in this work was proposed by Baluja and co-workers. It involves two-way modification of the BEB model vis-à-vis (a) scaling of molecular binding energies of orbitals and (b) normalizing the cross sections. The latter modification results in the branching ratios (BR) which have the same values as those provided by the mass spectrometry data. The details of the m-BEB model, including the limitations, are discussed in another paper which the readers can refer to [13]. The normalized PICS in the m-BEB model are given by:
where the sum is over all the molecular orbitals i. In Equation (2), , , , . is the normalization factor for jth cation.
3. Computational Details
The input parameters to compute PICS were obtained at the optimized ground state geometry of using the quantum chemistry software Gaussian [39] at the Hartree–Fock (HF) level using effective core potentials (ECP) [30,40]. The LANL2DZ ECP-type basis set was used to obtain the input values of B, U, and N for different molecular orbitals. It is a shape-consistent basis set from the Los Alamos group of double zeta quality based on scalar relativistic all-electron calculations. Its pseudo-valence orbitals preserve the shape of all electron valence orbital [40]. We can use other basis sets as well to obtain input values. The BEB results are, however, insensitive to basis sets. The summation in Equations (1) and (2) runs over 34 molecular orbitals. The precise threshold behavior of the theoretical cross sections was obtained by using the experimental values of appearance energies (AE) of cations and ionization energy of the molecule. The ionization energy and mass spectrometry data are referenced from NIST Chemistry Webbook database [41]. The theoretical TICS were obtained using the BEB model. Being a complicated molecule, and considering the fact that the availability of experimental ionization scattering data is very limited, it would be appropriate to discuss the BEB results first for their logical interpretation.
4. Results and Discussion
During the electron impact ionization process, a target molecule undergoes ionization as well as dissociative ionization depending upon the energy of the projectile electron. The dissociative ionization occurs only if the energy of the electron is greater than the ionization threshold of the target molecule. The absolute partial ionization cross sections from threshold to 900 eV were measured by Basner et al. using the time-of-flight (TOF) spectrometer in the linear model [21]. The mass spectrometry data were recorded in linear and reflection modes, but the values were not reported. The PICS were reported for 12 cations, which include both the SI and DI cations. These results had an uncertainty of 15%. The ionization cross section results reveal that at 70 eV, the major contribution to TICS comes from SI ions only. The parent ion does not exist and the dissociative ionization process dominates the ionization process. The dominant ion shows peak cross sections at around 120 eV. Its contribution at 70 eV is around 56%, but it is reduced to 43% at 120 eV. The TICS of exhibit a peak in cross sections at 160 eV. This shift in peak is attributed to the sizeable contribution of DI coming at higher energies. All DI ions have their magnitudes lower than the most dominating ion SI by one order. These features make the TICS of different from all our earlier studies in which the TICS were purely dominated by SI and there was no visible impact of DI over the entire energy range studied [13,14,15,16,17,18]. While the BEB model is valid for SI ions, it would be interesting to compare the results obtained from the BEB model with the experimental results of Basner et al. [21] who have reported SI, DI, TICS over a broad energy range.
The TICS computed using the BEB approach are shown in Figure 1. The figure also shows the TICS of SI, DI ions their sum, and the experimentally measured TICS as reported by Basner et al. [21]. Several interesting observations are made on the basis of the results and their comparison. The sum of experimentally measured SI and DI ions is a little underestimated as compared to the TICS reported by Basner et al. [21]. This is baffling. This variation may be due to the normalization procedure adopted or to the fact that the complete contribution of ion current was not taken into account. The BEB-TICS are overestimated compared with the experimental SI, but are in close agreement with the experimentally measured TICS and the sum of SI and DI ions. It is reiterated that the BEB model provides the estimates of SI ions and hence, comparison has to be made only with SI results and not TICS. This is because the TICS may have a contribution from DI ions as well, such as the itself. The BEB results still lie within the acceptable uncertainties which are usually between 15 and 20% [38]. In fact, the agreement between the BEB results and of Basner et al. [21] is much better than for Probst et al. [31]. Thus, while comparing, one has to analyze the results carefully. For the sake of clarity, we have not displayed the results of Probst et al. [31] and earlier results of Huo et al. [30] in Figure 1.
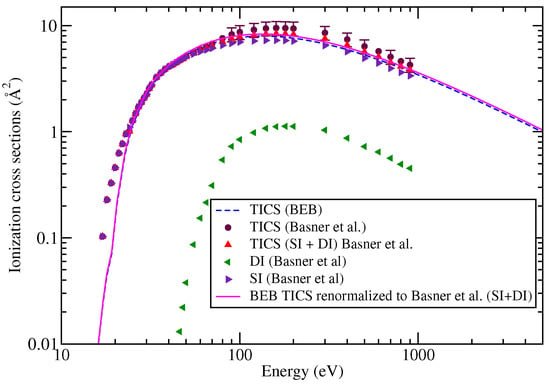
Figure 1.
Total ionization cross sections of : dashed curve, BEB; circles, Basner et al. [21]; triangles, sum of SI and DI ions from Basner et al. [21]; left triangles, summed PICS of DI cations from Basner et al. [21]; right triangles, summed PICS of SI cations from Basner et al. [21]; line curve, renormalized BEB results.
The contribution of SI and DI ions at 70 eV as reported by Basner et al. [21] is supported by the EIMS data available at NIST Chem-Webbook [41]. At this energy, the total contribution of SI ions to TICS is around 98%, whereas it is reduced to 76% at 140 eV. The DI contribution increases to 24% at 140 eV. The EIMS provides an important clue for the TICS at a particular energy. Since the EIMS data are not available at 140 eV, this comparison cannot be made with the experimental measurements of Basner et al. [21]. A piece of fine information can be extracted on the fragmentation yields of the cations from the NIST EIMS data [41]. The NIST data includes the relative cation abundances of the isotopes also, which are missing from the work of Basner et al. [21]. The element tungsten has five naturally occurring isotopes. The lowest isotope has an integral mass of 180 Da and the heaviest has an integral mass of 187 Da. The other isotopes correspond to integral masses 182 Da, 183 Da, and 184 Da. Of the five isotopes, the most abundant isotope is 184 Da. The three dominating peaks in EIMS data of correspond to m/z = 279, 281, and 277. These three isotopes contribute about 19.7%, 18.4%, and 17% to the TICS at 70 eV. Together, all the isotopes of have a contribution of about 65% to TICS at the same energy. This crucial information is missing in the work of Basner et al. [21] as they have reported the PICS only in linear mode using a TOF spectrometer. One can still compare the contribution of the fragments from the cross section data of Basner et al. [21] and NIST Chem-Webbook [41]. The two are in agreement, provided we ignore the isotopic forms and consider them as a single entity, or if we renormalize the fragmentation yield data by considering the cations common to both EIMS data and Basner et al. This is shown in Table 1. The NIST Chem-Webbook [41] does not report an ion.

Table 1.
Branching ratios (BR) of various cations of produced by electron impact dissociation at 70 eV.
To compute SI and DI PICS, we renormalized the BEB results to the TICS of Basner et al. [21] obtained from the sum of SI and DI ions. This is discussed later. This permitted us to apply the m-BEB to test its validity for the SI and DI ions. This practice has been followed in the past as well [13,14,17] and it helps to rule out the variations in PICS arising from TICS. The BR for all cations were obtained from the cross section data of Basner et al. [21] at an energy of 140 eV as the peak value of TICS occurs near this value. These values are listed in Table 2. The EIMS data could not be used as they were recorded at 70 eV energy, where the contribution of DI is negligible.

Table 2.
Branching ratios and Normalization constant () of various cations of produced by electron impact dissociation at 140 eV. These are obtained using the cross section data of Basner et al. [21].
The PICS of various cations, doubly and singly ionized, generated due to dissociative ionization, computed using the m-BEB approach, are presented in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. It is observed that the results are very good for the SI ions such as , after 40 eV. This is the most dominating ion in the ionization process. The experimental results show a shift in the peak in cross section for ions and to lower energy values around 55 eV from 120 eV. The rise in these cross sections is very sharp, while the high energy behavior is similar to . The m-BEB results for these ions are in fair agreement with the experimental data after 50 eV, but they are unable to reproduce the experimental peaks. The same is true for , and ions. The theoretical results are very good for the ion at all energies. The results show substantial deviations in the case of the ion although the quantitative agreement can be noticed. The use of experimental values of AE provides better results near the threshold region.
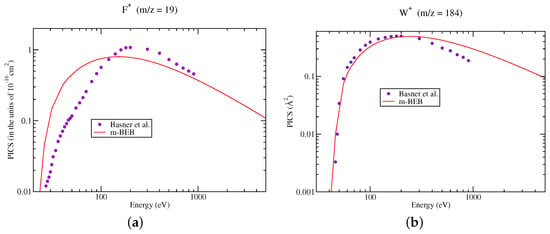
Figure 2.
Partial ionization cross sections of SI cations of : (a) m/z = 19, (b) m/z = 184. Line curve, m-BEB results after renormalizing BEB TICS to the sum of SI and DI PICS of Basner et al. [21]; Circles, the sum of SI and DI PICS of Basner et al. [21].
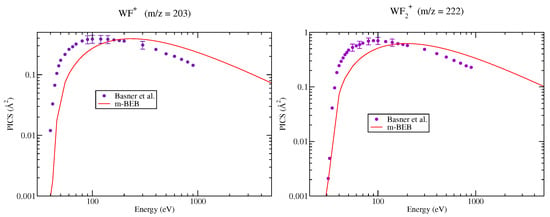
Figure 3.
Partial ionization cross sections of SI cations of for different m/z values. Line curve, m-BEB results; Circles, SI PICS of Basner et al. [21].
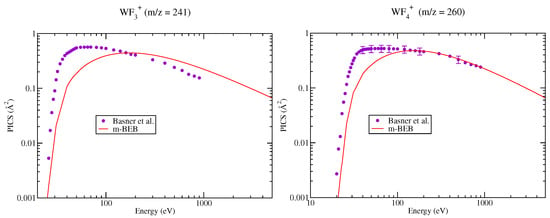
Figure 4.
Partial ionization cross sections of SI cations of for different m/z values. Line curve, m-BEB results; Circles, SI PICS of Basner et al. [21].
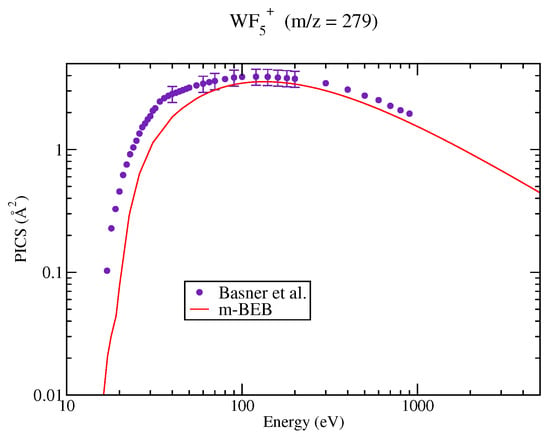
Figure 5.
Partial ionization cross sections of SI cations of for different m/z values. Line curve, m-BEB results; Circles, SI PICS of Basner et al. [21].
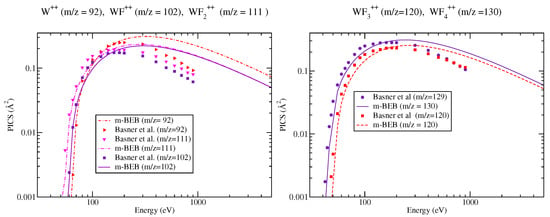
Figure 6.
Partial ionization cross sections of DI cations of for different m/z values. Line curves, m-BEB results; Symbols, DI PICS of Basner et al. [21].
The PICS due to DI ions are displayed in Figure 6. The DI shows a sharp fall in PICS with an increase in incident energy. However, in the region between the threshold and 200 eV, the m-BEB results show excellent agreement with the corresponding experimental results. A similar positive trend was also observed in the case of hexamethyldisiloxane [15]. However, the number of ions was smaller and the dissociative ionization process could not be discussed in detail. However, present work and earlier work indicate that even the DI can be reproduced satisfactorily using the m-BEB model. This is encouraging as there are not many methods available to compute the PICS of DI.
The visible disagreement between theory and experiment is observed in case of ionization cross sections from Figure 2a. The modeling of partial ionization cross sections requires multiplication of theoretical cross sections by a normalization factor (refer to Equation (2)). This simply scales down the cross section data without shifting the peak position in m-BEB model. This cation (, m/z = 19) shows the peak value of the ionization cross section at 200 eV, whereas the TICS of shows the peak occurring around 140 eV. This means that the peaks of cation and TICS occur at different energies. Since the scaling does not shift the peak position in the cross section curve, this leads to appreciable disagreement between the experimental and theoretical data sets. It is reiterated that this work emphasizes the importance of EIMS data in obtaining the PICS. This data is determined at a single electron energy of around 70 eV. This makes EIMS data less useful in tungsten hexafluoride. At 70 eV, the doubly ionized ions just start appearing and also it does not correspond to maximum value of its relative cation abundance data in few cases. We need EIMS data at different electron energies in order to correctly reproduce the experimental peaks. However, this proposition is not practical. Thus, we are bound to see this type of disagreement whenever cations and TICS show peaks in a cross section curve at different energies.
The shift in peak has to be understood as each ion has its distinct energy profile. The fact that PICSs show a deviation simply means that the BR exhibits energy dependence. This feature has also been discussed in earlier work [15,16]. The present work suggests that the m-BEB model is dependent upon the cross section results as the BR were computed using this data. This appears to be a serious limitation to this work. However, the model can be made independent of experimental cross sections data, provided that EIMS data are available at higher energies. Computing BR from EIMS data would have provided results that would be in agreement with the experimental data only at 70 eV. Since the TICS show a maximum value at 140 eV, the PICS computed from the m-BEB model using the BR calculated at 70 eV would have shown significant variation in the results. Thus, it is imperative to have EIMS data at an energy value where the TICS show the maximum. Otherwise, the m-BEB results would not be very attractive.
The m-BEB PICS, as shown in Figure 3, Figure 4a, and Figure 6, overestimate the measurements at high energies. The cations that are formed by indirect processes or by multiple pathways have shown a sharper fall in the experimentally determined PICS (present and even in earlier studies) and are usually lower in magnitude than the m-BEB model results at higher energies. It appears that there are some other factors which are playing a role in the physical process, which cannot be modeled very accurately within the BEB model framework using the m-BEB model.
The most attractive part of the work is that with limited resources and without going into details about the chemical processes involved, one can estimate the PICS of any ion easily. The inputs required to compute these results do not create any bottleneck as these are easily available. This is in contrast to the Jain–Khare semi-empirical model [42,43] where differential oscillator strengths happen to be the key input quantity. This quantity is not easy to obtain and thus limits the wider applicability of their model. The ab initio calculations of electron-impact ionization cross sections is a difficult proposition because they couple two continuum electrons with the ion. The CC-based approach models are intractable for both simple and complex molecules and may also suffer from computational issues [11]. Under such circumstances, the proposed model would be very useful in supplementing the cross section data. The utility of this model increases manifold in case the species undergoing ionization are very reactive, toxic or difficult to handle in laboratories for some different reason. has both characteristics [44,45,46].
The EIMS data are very useful for the study of the dissociative ionization process as they provide the correct contribution of each ion as well as the number of fragments participating in the ionization process at a particular energy. The crux of the problem is that once the fractional yields or the branching ratios of fragmented cations are known, and are then multiplied by the theoretical TICS, the absolute partial cross sections can be obtained. This also explains the need to have a good representation of the total ionization cross section as a function of incident energy. A better representation of TICS (in agreement with experimental data) would provide good estimates of the PICS of the cations. The partial ionization cross sections are dependent on intramolecular processes that follow the stripping of an electron off of a molecule. However, in the m-BEB model, we are not concerned with this process involved in the creation of ions. The BR can be obtained from the cross section data or the EIMS data [20]. Using the EIMS makes the model predict the PICS of a cation.
Basner et al. [21] reported SI, DI, and TICS. Their experimental TICS is somewhat higher than the sum of SI and DI PICS. We have preferred to normalize the BEB TICS to the sum of SI and DI ions. This is because the branching ratios would add over to give unity. We could have also used their TICS data. Then, the comparison would have required a uniform scaling of SI and DI ions to match their sum to experimental TICS. Hence, the errors arising in present calculations can be treated as systematic only.
It is equally important to discuss the effect of the lack of core electrons in some of the terms utilized for the Equation (1) (e.g., the orbital kinetic energy). The valence electron when it is in the core region is difficult to ionize due to the strong attractive potential from the nucleus, as well as the shielding by the core electrons. The ionization is more likely to happen if the electron is away from the nucleus. At this distance, it is expected to move slower on an average. The electrons of a heavy atom are represented by an ECP-type basis set. As a consequence of using the ECP basis set, the valence electron is allowed much less penetration into the core region. This is reflected in the values of valence electron kinetic energies (an input parameter in computing TICS and PICS) obtained using relativistic ECP. These values are significantly smaller than the non-relativistic all-electron approach. This, in turn, leads to the larger BEB cross sections from the ECP method obtained using any non-scalar relativistic effect approach. The fact that the inner shell orbitals are removed using ECP has very little effect on the BEB cross section at low energies as the core orbitals do not contribute significantly. It is only the high energy tail of the cross section which may be underestimated.
5. Conclusions
The m-BEB model is based on the BEB model and it attempts to model the scattering of bound electrons with unbound electrons of known energy. The PICS is determined by using the bound state properties of the target. The general shape of the cross sections wherever is similar to experimental results, and it helps to predict the PICS accurately. The m-BEB model shows the best results where the fragmentation of the molecular ion is fast and the energy barrier is small. The results may not appear attractive for lighter ions in terms of reproducing the peaks where the indirect process may be contributing to the ionization process. However, the proposed semi-empirical approach can provide good estimates with reasonable accuracy and correct orders of magnitude of all ions when we consider the fact that there is no clean ab inito theory to estimate PICS to date. The DI results show a remarkably good trend in the cross sections. The theoretical calculations reported in this paper are the first of their kind and are the only available work conducted on computing PICS of cations of . The computation of branching ratios in the m-BEB model can be performed either from the experimental cross section or from EIMS data. This quantity is actually energy-dependent, but in the computation of PICS, it is calculated at a particular energy. This has undoubtedly simplified the calculations. Yet, by adjusting the threshold for each ion, we have mitigated the damage from the approximation of energy-independent branching ratios. These scattering data can be generated in an effortless manner for a complicated molecule such as . The results would help experimentalists to assess the consistency of their experimental outcomes. This study has proved that mass spectrometry data is an effective tool for studying the ionization phenomena.
Author Contributions
Conceptualization, supervision, methodology, K.L.B. and A.B.; calculations, M.L. and K.G.; writing the original draft, K.G. and M.L.; review and editing, A.B.; K.L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Can be obtained from the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEB | Binary-Encounter-Bethe |
| m-BEB | modified Binary-Encounter-Bethe |
| SI | Singly Ionized |
| DI | Doubly Ionized |
| EIMS | Electron Ionization Mass Spectrometry |
| HF | Hartree-Fock |
| CC | Close Coupling |
| TICS | Total Ionization Cross Sections |
| PICS | Partial Ionization Cross Sections |
| eV | electron volt |
| AE | Appearance Energy |
| BR | Branching Ratios |
| Da | Dalton |
| TOF | Time-of-Flight |
References
- Watson, J.T.; Sparkman, O.D. Introduction to Mass Spectrometry: Instrumentation, Applications, and Strategies for Data Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing, 2nd ed.; Wiley-Interscience; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Inagaki, N. Plasma Surface Modification and Plasma Polymerization, 1st ed.; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Economou, D.J. Hybrid simulation of low temperature plasmas: A brief tutorial. Plasma Process Polym. 2017, 14, 1600152. [Google Scholar] [CrossRef]
- Prager, J.; Riedel, U.; Warnatz, J. Modeling ion chemistry and charged species diffusion in lean methane–oxygen flames. Proc. Combust. Inst. 2007, 31, 1129–1137. [Google Scholar] [CrossRef]
- Chen, B.; Wang, H.; Wang, Z.; Han, J.; Alquaity, A.B.; Wang, H.; Hansen, N.; Sarathy, S.M. Ion chemistry in premixed rich methane flames. Combust. Flame 2019, 202, 208–218. [Google Scholar] [CrossRef]
- Donnelly, V.M.; Kornblit, A. Plasma etching: Yesterday, today, and tomorrow. J. Vac. Sci. Technol. Vacuum Surf. Film. 2013, 31, 050825. [Google Scholar] [CrossRef]
- Carbone, E.; Graef, W.; Hagelaar, G.; Boer, D.; Hopkins, M.M.; Stephens, J.C.; Yee, B.T.; Pancheshnyi, S.; van Dijk, J.; Pitchford, L. Data needs for modeling low-temperature non-equilibrium plasmas: The LXCat project, history, perspectives and a tutorial. Atoms 2021, 9, 16. [Google Scholar] [CrossRef]
- Mohr, S.; Tudorovskaya, M.; Hanicinec, M.; Tennyson, J. Targeted Cross-Section Calculations for Plasma Simulations. Atoms 2021, 9, 85. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron– and positron–molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [PubMed]
- Luthra, M.; Goswami, K.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV. Atoms 2022, 10, 74. [Google Scholar] [CrossRef]
- Bharadvaja, A.; Bassi, M.; Arora, A.K.; Baluja, K.L. Electron interactions with tetramethylsilane from the ionization threshold up to 5000 eV. Plasma Sources Sci. Technol. 2021, 30, 095012. [Google Scholar] [CrossRef]
- Arora, A.K.; Gupta, K.K.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. A binary-encounter-Bethe approach to compute electron-impact partial ionization cross sections of plasma relevant molecules such as hexamethyldisiloxane and silane. Plasma Sources Sci. Technol. 2022, 31, 015008. [Google Scholar] [CrossRef]
- Goswami, K.; Luthra, M.; Bharadvaja, A.; Arora, A.K.; Baluja, K.L. Electron impact partial ionization cross sections of 1-butanol. Eur. Phys. D 2022, 76, 97. [Google Scholar] [CrossRef]
- Goswami, K.; Luthra, M.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Electron-impact cross sections of acetylene up to 5 keV. Eur. Phys. J. D 2022, 76, 94. [Google Scholar] [CrossRef]
- Goswami, K.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Electron impact partial ionization cross sections of methyl alcohol up to 5 keV using the mass spectrometry data. Eur. Phys. D 2021, 75, 1–8. [Google Scholar] [CrossRef]
- Graves, V.; Cooper, B.; Tennyson, J. Calculated electron impact ionisation fragmentation patterns. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 235203. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Tennyson, J.; Huang, S.; Kushner, M.J. Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 2017, 26, 065010. [Google Scholar] [CrossRef]
- Basner, R.; Schmidt, M.; Becker, K. Measurements of absolute total and partial cross sections for the electron ionization of tungsten hexafluoride (WF6). Int. J. Mass Spectrom. 2004, 233, 25–31. [Google Scholar] [CrossRef]
- Choy, K.L. Chemical vapour deposition of coatings. Prog. Mater. Sci. 2003, 48, 57–170. [Google Scholar] [CrossRef]
- Gupta, A.; Ifeacho, P.; Schulz, C.; Wiggers, H. Synthesis of tailored WO3 and WOx (2.9 < x < 3) nanoparticles by adjusting the combustion conditions in a H2/O2/Ar premixed flame reactor. Proc. Combust. Inst. 2011, 33, 1883–1890. [Google Scholar] [CrossRef]
- Matsui, S.; Mori, K. New selective deposition technology by electron–beam induced surface reaction. J. Vac. Sci. 1986, 4, 299–304. [Google Scholar] [CrossRef]
- Kirss, R.U.; Lamartine, M. Chemical vapor deposition of tungsten oxide. Appl. Organomet. Chem. 1998, 12, 155–160. [Google Scholar] [CrossRef]
- Dushik, V.V.; Rozhanskii, N.V.; Zalavutdinov, R.K. IR Study of the Transformation of WF6 on a W Substrate. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2019, 13, 919–924. [Google Scholar] [CrossRef]
- Hulkko, J.G.; Boo, K.; Qiu, R.; Backe, O.; Boman, M.; Halvarsson, M.; Lindahl, E. Kinetics of the low-pressure chemical vapor deposited tungsten nitride process using tungsten hexafluoride and ammonia precursors. J. Vac. Sci. Technol. A 2021, 39, 063403. [Google Scholar] [CrossRef]
- Groven, B.; Heyne, M.; Mehta, A.N.; Bender, H.; Nuytten, T.; Meersschaut, J.; Conard, T.; Verdonck, P.; Van Elshocht, S.; Vandervorst, W.; et al. Plasma-Enhanced Atomic Layer Deposition of Two-Dimensional WS2 from WF6, H2 Plasma, and H2S. Chem. Mater. 2017, 29, 2927. [Google Scholar] [CrossRef]
- Delabie, A.; Caymax, M.; Groven, B.; Heyne, M.; Haesevoets, K.; Meersschaut, J.; Nuytten, T.; Bender, H.; Conard, T.; Verdonck, P.; et al. Low Temperature Deposition of 2D WS2 Layers WF6, H2S Precursors: Impact of Reducing Agents. Chem. Commun. 2015, 51, 15692–15695. [Google Scholar] [CrossRef]
- Huo, W.M.; Kim, Y.-K. Use of relativistic effective core potentials in the calculation of total electron-impact ionization cross-sections. Chem. Phys. Lett. 2000, 319, 576. [Google Scholar] [CrossRef]
- Probst, M.; Deutsch, H.; Becker, K.; Mark, T.D. Calculations of absolute electron-impact ionization cross sections for molecules of technological relevance using the DM formalism. Int. J. Mass Spectrom. 2001, 206, 13–25. [Google Scholar] [CrossRef]
- Pitchford, L.C.; McKoy, B.V.; Chutjian, A.; Trajmar, S. Swarm Studies and Inelastic Electron–Molecule Collisions. In Proceedings of the Meeting of the Fourth International Swarm Seminar and the Inelastic Electron-Molecule Collisions Symposium 1985; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Janev, R.K.; Reiter, D. Collision processes of CHy and hydrocarbons with plasma electrons and protons. Phys. Plasmas 2002, 9, 4071. [Google Scholar] [CrossRef]
- Clark, R.E.H.; Reiter, D.H. Nuclear Fusion Research: Understanding Plasma-Surface Interactions; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Mark, T.D.; Dunn, G.H. (Eds.) Electron Impact Ionization; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Christophorou, L.G.; Olthoff, J.K. Fundamental Electron Interactions with Plasma Processing Gases; Springer: Boston, MA, USA, 2004. [Google Scholar]
- Kim, Y.K. Total ionization cross sections of molecules by electron impact. In Gaseous Dielectrics X; Christophorou, L.C., Olthoff, J.K., Vassiliou, P., Eds.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Tanaka, H.; Brunger, M.J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A.R.P. Scaled plane-wave Born cross sections for atoms and molecules. Rev. Mod. Phys. 2016, 88, 025004. [Google Scholar] [CrossRef]
- GAUSSIAN 03; Gaussian, Inc.: Wallingford, UK, 2003.
- Graves, V.; Cooper, B.; Tennyson, J. The efficient calculation of electron impact ionization cross sections with effective core potentials. J. Chem. Phys. 2021, 154, 114104. [Google Scholar] [CrossRef] [PubMed]
- NIST Chemistry WebBook. NIST Standard Reference Database Number 69. Available online: https://webbook.nist.gov/chemistry/ (accessed on 31 July 2022).
- Kumar, Y.; Kumar, M. Theoretical partial ionization cross sections by electron impact for production of cations from CH3OH, CO2 and NH3. Chem. Phys. Lett. 2020, 740, 137071. [Google Scholar] [CrossRef]
- Pal, S.; Kumar, J.; Mark, T.D. Differential, partial and total electron impact ionization cross sections for SF6. J. Chem. Phys. 2004, 120, 4658. [Google Scholar] [CrossRef] [PubMed]
- Hurly, J.J. Thermo physical Properties of Gaseous Tungsten Hexafluoride from Speed-of-Sound Measurements. Int. J. Thermophys. 2000, 21, 185. [Google Scholar] [CrossRef]
- Jung, H.; Hwang , J.; Chun, H.; Han, B. Elucidation of hydrolysis reaction mechanism of tungsten hexafluoride (WF6) using first-principles calculations. J. Ind. Eng. Chem. 2019, 70, 19. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Li, Y.; Kabbaj, N. Research status of replacement gases for SF6 in power industry. AIP Adv. 2020, 10, 050702. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).