Abstract
This article reports on the scattering of unpolarized and spin polarized electrons and positrons from NiCuPd, and Pt, covering light to heavy precious metal targets. To cover the wide energy domain of 1 eV MeV, Dirac partial-wave phase-shift analysis is employed, using a complex optical potential for MeV and a potential derived from the nuclear charge distribution for MeV. Results are presented for the differential and integral cross-sections, including elastic, momentum transfer, and viscosity cross-sections. In addition, the inelastic, ionization, and total (elastic + inelastic) cross-section results are provided, together with mean free path estimates. Moreover, the polarization correlations , and U, which are sensitive to phase-dependent interference effects, are considered. Scaling laws with respect to collision energy, scattering angle, and nuclear charge number at ultrahigh energies are derived using the equivalence between elastic scattering and tip bremsstrahlung emission. In addition, a systematic analysis of the critical minima in the differential cross-section and the corresponding total polarization points in the Sherman function S is carried out. A comparison with existing experimental data and other theoretical findings is made in order to test the merit of the present approach in explaining details of the measurements.
1. Introduction
Much of our knowledge on the interaction between elementary and composite particles, and on the structures of isolated atoms, molecules, and bulk matter is derived from the analysis of experimental data on scattering processes in conjunction with respective theoretical predictions. Electron-impact collisional data, for instance, are required in such diverse fields of science and technology [1,2,3] as plasma physics, radiation dosimetry, atmospheric modeling, surface electron spectroscopy, semiconductor etching, and many more. Positron scattering data are used in medicine and material science as well as in high-energy physics and astrophysics. To name only a few areas, the positron emission technology (PET [4]) has been applied in the diagnosis of cancer and brain function disorders. By comparing electron and positron scattering, it is possible to assess radiative corrections [5]. Fundamentally, this leads to more detailed understanding of electronic or nuclear charge densities and the related interaction potentials, thanks to the sign difference between the charge of the two probing particles.
In our present investigation, we consider electron and positron scattering from the naturally abundant precious metal atoms Ni, Pd, and Pt, which share the same column in the periodic table and have similar electronic configurations. Included is the study of Cu, adjacent to nickel, which has already been touched upon in an earlier paper [6]. The one-by-one increase in the electron shells allows the influence of the shell-structured electron density distribution on the measured scattering observables to be studied.
In this study, we investigate the angular and energy dependence of the differential cross-section (DCS) for the elastic scattering of unpolarized projectiles. In addition, we investigate the Sherman function, S [7,8], which is more sensitive to details of the collision process and which determines the degree of vertical polarization after the scattering process. Equivalently, S is responsible for the left–right cross-section asymmetry if the beam particles are spin polarized perpendicular to the scattering plane. If, on the other hand, they are polarized in the scattering plane, the cross-section change using polarized projectiles is characterized by the parameters T and U. The measurement of T and U, however, requires the additional determination of the spin polarization of the scattered lepton. The accuracy of this experimental determination can be assessed using the sum rule, [7].
Particular weight is placed on the critical minima (CM) of the DCS, as in this proximity the Sherman function is close to its maxumum value, |S| ≈ 1. This knowledge of CM analysis can be used for the production of polarized beams of electrons or positrons, and has fundamental as well as practical relevance.
In addition to the differential cross-section, the integrated cross-sections are determined both for elastic (IECS) and inelastic (INCS) scattering. These cross-sections are inversely related to the mean free path for low-energy electrons in solids. The knowledge of is important for both quantitative surface analysis by Auger-electron and X-ray–photoelectron spectroscopy [9], and is needed to calculate the transport of signal electrons in solids as well [10]. In addition, the momentum transfer and the viscosity cross-sections are calculated. This knowledge, in combination with the DCS, is required to determine multiple scattering in solid matter, particularly at collision energies above 200 eV.
Our theoretical investigations, which are compared with the existing experimental data on the precious metal targets, are based on the optical potential model (OPM). This model reduces the many-body problem to the use of an effective local monopole potential [11], which is subsequently considered in phase-shift analysis for potential scattering [12]. This model has been applied successfully for wider collision energies, above several tens of eV, as reviewed in [13]. For very low impact energies, investigators use more sophisticated theories, such as four-state close coupling [14], convergent close coupling, coupled-channel optical theories [15], and the B-spline R-matrix method [16]. However, these theories are far too involved to extend their region of applicability beyond 50–100 eV. By comparing the present results down to 1 eV with these advanced theoretical and experimental findings, it is possible to judge the validity of more computationally simple theories such as OPM.
When extending the range of the considered collision energies to about 300 MeV, nuclear structure phenomena become accessible. Scaling laws have been discovered in this high-energy region, which in the forward hemisphere hold for the DCS, and in the case of heavier atoms, for the spin asymmetry as well.
The paper is organized as follows. Section 2 comprises an overview of the theory, and Section 3 describes the role of the different constituents of the optical potential for the elastic scattering cross-section. Section 4 deals with the angular and energy distribution of the DCS, including an investigation of the critical minima, as well as the Sherman function and the high-energy scaling laws for electron impact. Positron impact and the polarization parameters T and U are considered in Section 5. Integrated cross sections and mean free paths are studied in Section 6. Finally, the conclusions are drawn in Section 7. Atomic units () are used unless indicated otherwise.
2. Theory
For estimation of the observables in elastic lepton–atom scattering, phase shift analysis is employed. This implies that the interaction between the collision partners is approximated by a local potential V, which at impact energies below 1 MeV is an optical potential, , with
where is the electrostatic potential, composed of the nuclear contribution, , and that of the electron cloud, . Here, is the potential of a point-like nucleus, while is derived from the electronic charge distribution , which is provided either by the numerical Dirac–Fock density [17] or in a parametric form fitted to a Hartree–Fock charge distribution [18]. The prefactor is for electrons and for positrons. The exchange potential, , accounts for the indistinguishability between the impinging electron and the target electrons, and is absent for positron scattering. is a correlation-polarization potential which is caused by the polarizability of the electron cloud due to the incident particle. The last term, , is an imaginary absorption potential which considers the depletion of the elastic channel by means of target excitation or positronium formation. All these potential constituents are provided in the local density approximation, and their target dependence results almost exclusively from . Potential details and corresponding references can be found in [13,19].
For energies above 1 MeV, only contributes to the potential, and is provided by . When MeV, the finite nuclear size has to be taken into account; is derived from the charge distribution, , of the target nucleus. For the precious metals considered here, is provided in terms of a Fourier–Bessel expansion [20] fitted to the experimental elastic cross-section data. High-energy recoil effects due to the finite target mass are considered by replacing with the average , where is the recoil-reduced kinetic energy of the scattered lepton.
With this local potential V and total energy (respectively, above 1 MeV), the Dirac equation can be solved for the partial-wave expanded leptonic scattering state. To this end, we used the Fortran code RADIAL [21]. The corresponding phase shifts of each partial wave enter into a weighted sum of Legendre polynomials and associated Legendre functions of the scattering angle. This sum provides the direct (A) and the spin-flip (B) scattering amplitudes [12,13]. From these scattering amplitudes, the differential cross-section (DCS), averaged and summed, respectively, over the leptonic polarization degrees of freedom, can be calculated:
For fully screened target atoms, (2) serves to calculate the integrated elastic cross-section ) as well as the weighted angular distributions defining the momentum transfer () and the viscosity cross-sections, which are required in the context of multiple scattering phenomena involving the transport of projectiles through matter. These are obtained from
where is the scattering angle.
Accounting for the polarizations and of the lepton in its initial and final scattering state, respectively, the DCS can be expressed in terms of the three polarization correlations , and U [7]:
with and from (2). The momenta of the impinging and scattered lepton, and , respectively, define the -scattering plane (see Figure 1), while its normal is in the direction of . Thus, the parameter S is accessible for leptons polarized perpendicular to the scattering plane, and is the only polarization correlation which exists even for an unpolarized beam. For leptons in an outgoing helicity eigenstate (i.e., when is aligned with such that ), T and U can be measured for beam particles polarized in the scattering plane, and all three polarization correlations can be expressed in terms of the scattering amplitudes A and B [7,8,22]:
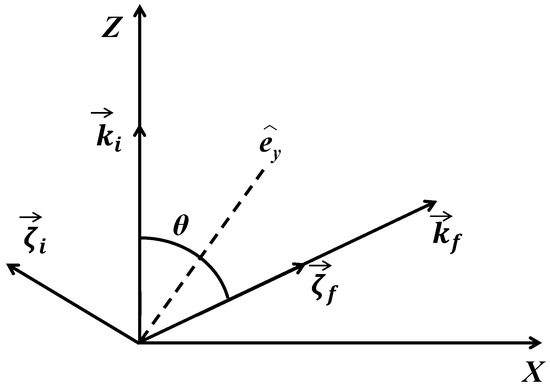
Figure 1.
Coordinate system showing the scattering plane spanned by the lepton momenta and , the spin polarization vectors and , and the scattering angle .
It follows that S and U depend on the phases of A and B, and are therefore more sensitive to the details of the theoretical models than the differential cross-section or T.
The way of evaluating the phase-shift sums leading to A and B depends on the collision energy. Due to the fact that the necessary number of partial waves increases with , a direct summation is only feasible for 1 MeV; however, this requires 25,000 for proper convergence at the highest energies. At MeV, an -fold convergence acceleration has to be applied [23], which strongly reduces the convergence at the foremost scattering angles. For , an appropriate choice is , as it means that is sufficient. Using , we can get down to for the DCS and for S, with 20,000.
Turning to inelastic scattering processes, which exist due to the presence of the absorption potential, they are accessible by means of the total cross-section, . This cross-section accounts for elastic plus inelastic scattering, and is related to the imaginary part of the direct scattering amplitude in the forward direction via the optical theorem [12]:
The inelastic cross-section, , is therefore provided by
with the elastic cross-section from (3). It can be split into an excitation part and an ionization part,
where refers to the excitation cross section of a given bound configuration n.
Above the ionization threshold I, the ionization cross-section provides the dominant contribution to It can tentatively be obtained from a parametrization of the ratio according to the following empirical formula [24,25]:
where refers to the reduced impact energy with respect to the ionization threshold. Here, and C are energy-dependent fit parameters satisfying these three conditions on R:
where is the impact energy at which attains its maximum. From the general experimental observations, is in the range 0.7−0.8 [25]. In cases where experimental ionization cross-sections are not available, the midpoint value of the above range will serve the same purpose. Here, we take for Cu and 0.8 for the other elements, which provides the best overall fit to the experimental data.
Inelastic processes such as nuclear excitation can be disregarded in the high-energy region, as high-resolution spectrometers allow the elastic peak to be distinguished from nearby nuclear excitations. At MeV, radiative corrections and higher-order scattering processes come into play. While the radiative corrections induce a global lowering of the DCS, the virtual nuclear excitations tend to fill the DCS minima which exist at large momentum transfers. At MeV, such dispersion effects change the differential cross-section by less than 10%, as exemplified for the C nucleus [26]. More crucial is the omission of magnetic scattering for the Cu nucleus, which in contrast to the other nuclei investigated has a nonzero spin of . At backward angles, particularly near , the magnetic scattering may well dominate the DCS for MeV [13,27,28]. Unfortunately, we are not aware of any calculated or measured ground-state magnetization distribution or magnetic form factors for the Cu nucleus, a necessary ingredient for the calculation of magnetic scattering.
3. Potential Constituents and Their Influence on the DCS
At low-to-intermediate collision energies, when the projectile cannot reach out to the periphery of the nucleus, the potentials determining the scattering observables depend nearly exclusively on the charge distributions of the atomic target electrons surrounding a point-like nucleus. However, at relativistic energies, when the projectile approaches and finally penetrates the nucleus, the role of the electronic charge distribution is taken over by the charge distribution in the nucleus. This basic dependence on the charge distributions determines all the components of the lepton–atom interaction and induces differences between the four target species concerning cross-sections or spin asymmetry parameters.
The atomic structures of Ni, Pd, and Pt differ in that every consecutive element has one more filled inner shell, while their similarities involve the presence of two -electrons in the outermost shell and eight electrons in the d-subshell of the adjacent shell. For example, Pt has filled -shells, filled - and -subshells, and a partially filled -subshell. Cu, adjacent to Ni, has nine electrons in the -subshell.
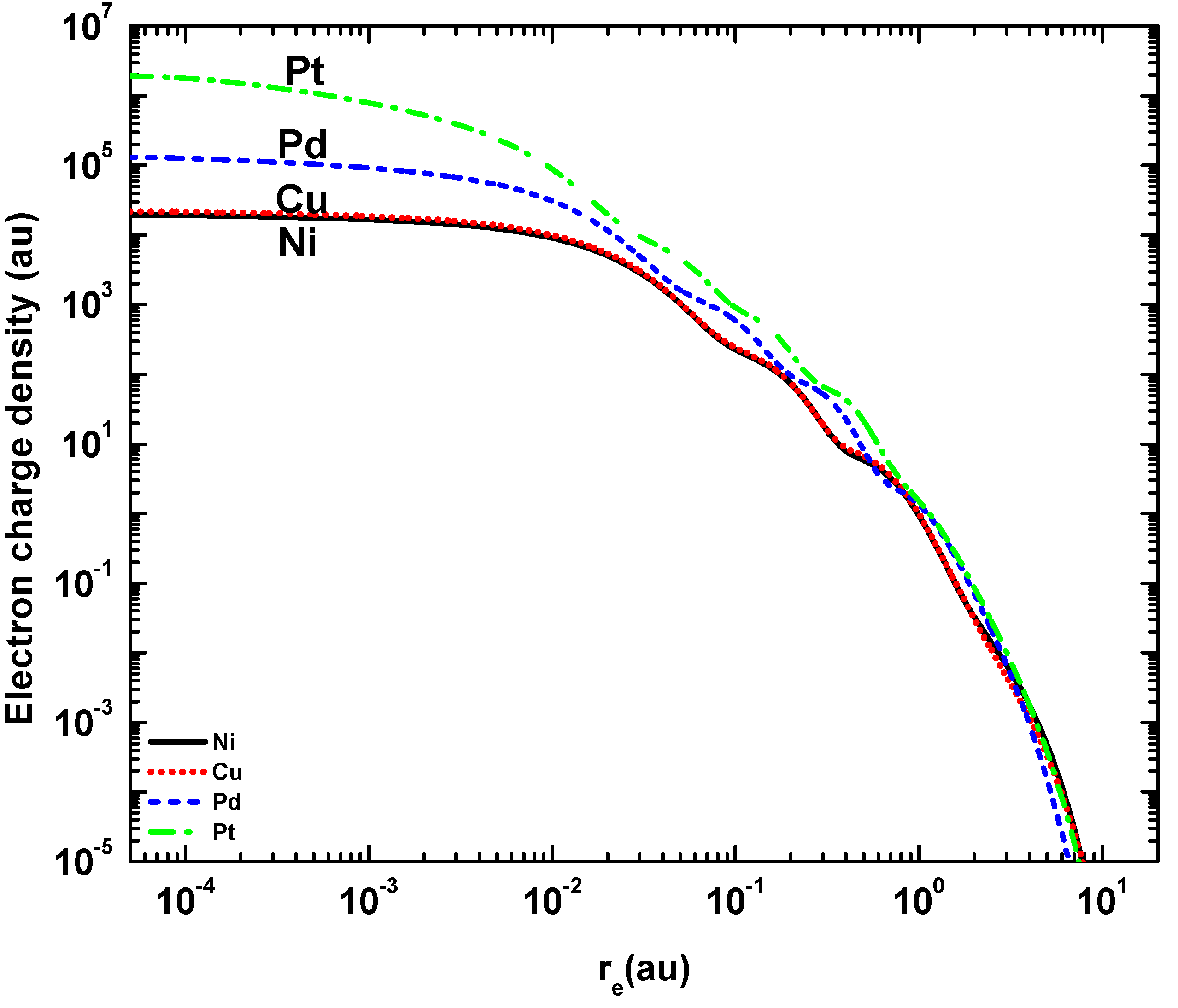
Figure 2 compares the electron density distributions of the target atoms, which are obtained from the purely quantum mechanical Dirac–Fock (DF) calculation. As the electron density is plotted versus the distance from the nucleus, the curves show the locations of the electronic shells of the targets by means of humps. The radius of the outermost electronic shell can be estimated by the Bohr radius, = 1 a.u. and the location of the nth electronic shell is predicted near [29]. For example, according to the semi-classical theory of Bohr [30], the locations of the K, L, M and N electronic shells for the heaviest atom Pt (with = 78) are at a.u., 0.05 a.u., 0.12 a.u. and 0.21 a.u., respectively, which correlate approximately with the humps in the associated densities, as depicted in Figure 2. However, there are two more humps present in , the positions of which are underpredicted by the above formula. This is due to fact that there are only sixteen and two electrons in the O and P shells, respectively. For Ni, the three pronounced humps correspond to the K (0.036 a.u.), L (0.14 a.u.), and M (0.32 a.u.) shell electrons, which are more loosely bound and thus at a larger distance than those belonging to Pt. The extension of is much alike for the four targets considered here.
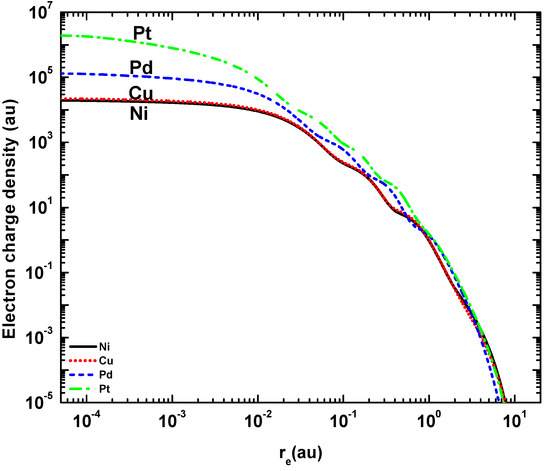
Figure 2.
Electron charge density () for Ni (—, black), Cu, red), Pd (−-−-, blue), and Pt, green) as a function of the distance from the nucleus.
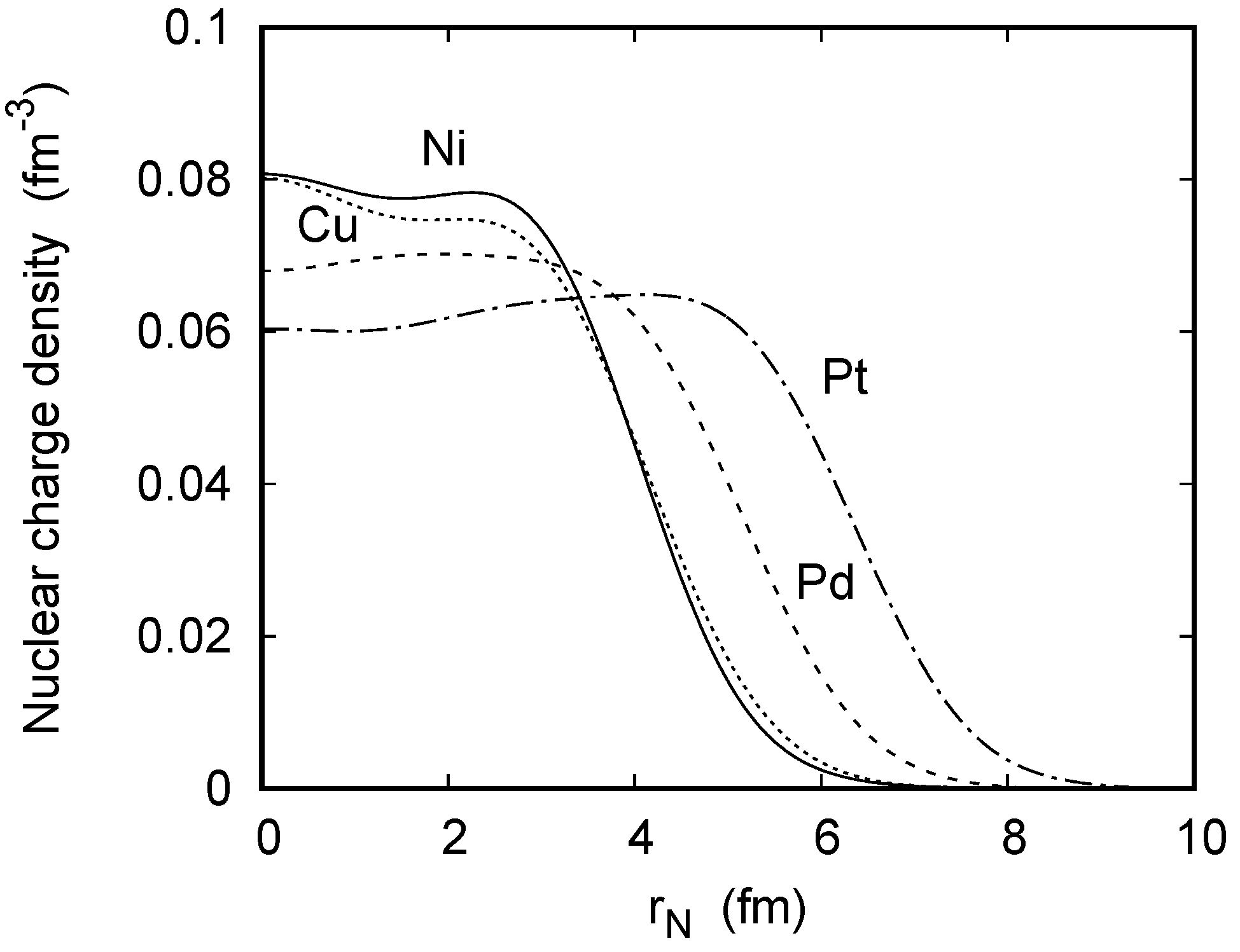
Figure 3 displays the respective nuclear charge densities. Clearly, the heavier the target nucleus, the larger their extensions. In contrast to the densities resulting from nuclear structure calculations (see, e.g., [13,31]), the shell structure at small distances is washed out due to the fit of the Fourier–Bessel expansions to experimental elastic electron scattering data, which is used here. Nevertheless, the pronounced minimum for Ni relates to a magic number of protons (), whereas Cu has an additional loosely bound proton which widens the charge distribution [32]. Pd and Pt are elements with open-shell nuclei, showing only very shallow minima.
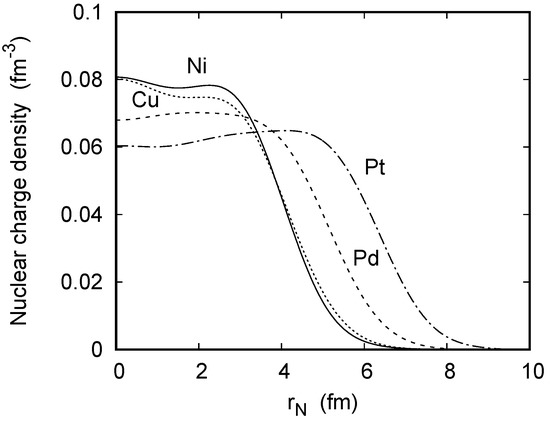
Figure 3.
Nuclear charge density () for Ni (—), Cu, Pd, and Pt as a function of the nuclear coordinate, .
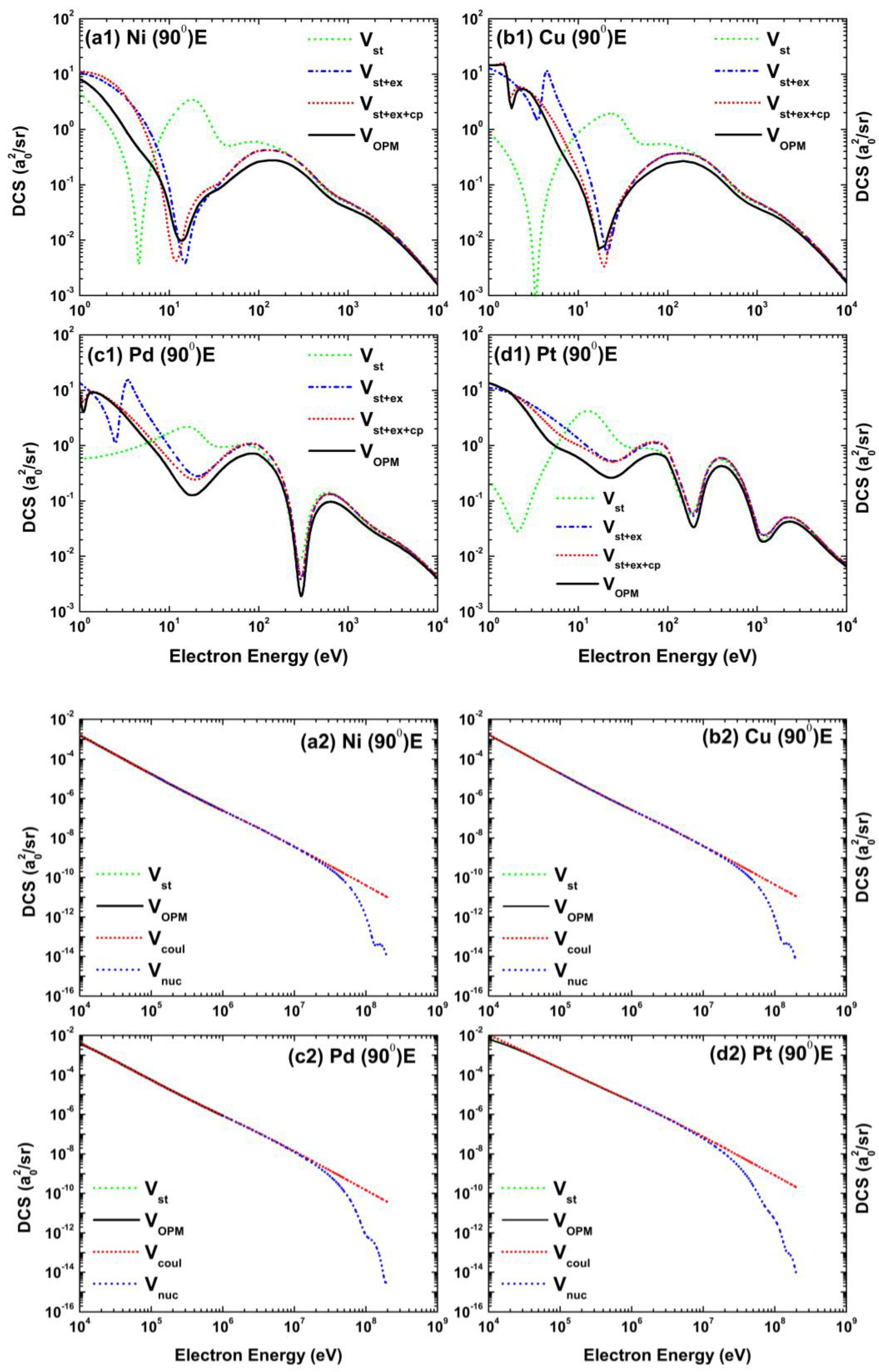
Figure 4 and Figure 5 display the influence of the potential constituents on the differential cross section when proceeding from to by successively adding , and . It is well known that when the collision energy is sufficiently high, the static potential is the main contributor to the DCS in the OPM approach. This fact is clearly demonstrated in the energy-dependent DCS depicted in Figure 4. As shown in the top part of this figure, the effects of , , and are substantial at 100 eV. It is evident that the inclusion of leads to a noticeable modification of the structures. For the lighter atoms, the prominent minimum is essentially shifted to higher energies, while the DCS for the heaviest atom is severely altered and changed by two orders of magnitude. A significant contribution of the correlation–polarization potential is only observed at 20 eV, where tends to diminish the contribution of . Beyond 100 eV, and are the basic contributors. Starting from the ionization threshold, the absorption potential remains important up to 5 keV by reducing the value of the DCS.
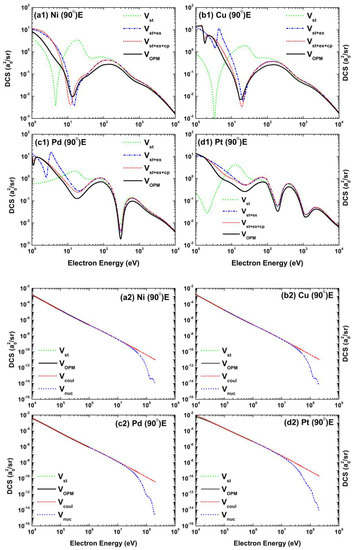
Figure 4.
Energy dependence (top: 1–10 eV, bottom: – eV) of the differential cross-sections for electron scattering from (a1,a2) Ni, (b1,b2) Cu, (c1,c2) Pd, and (d1,d2) Pt at a fixed scattering angle . Shown in the top panels are the results from , green), , blue), , red), and (—, black). The bottom panels show the results from , green), (—, black), , red), and , blue).
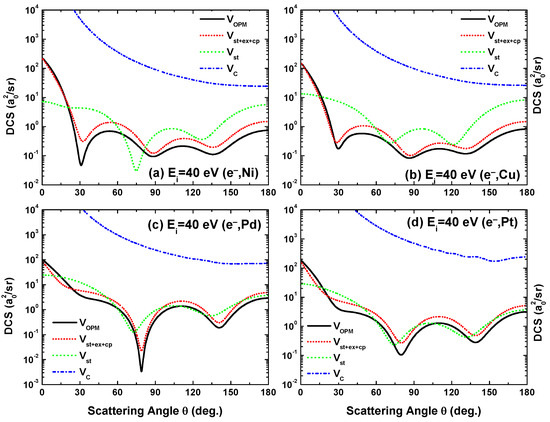
Figure 5.
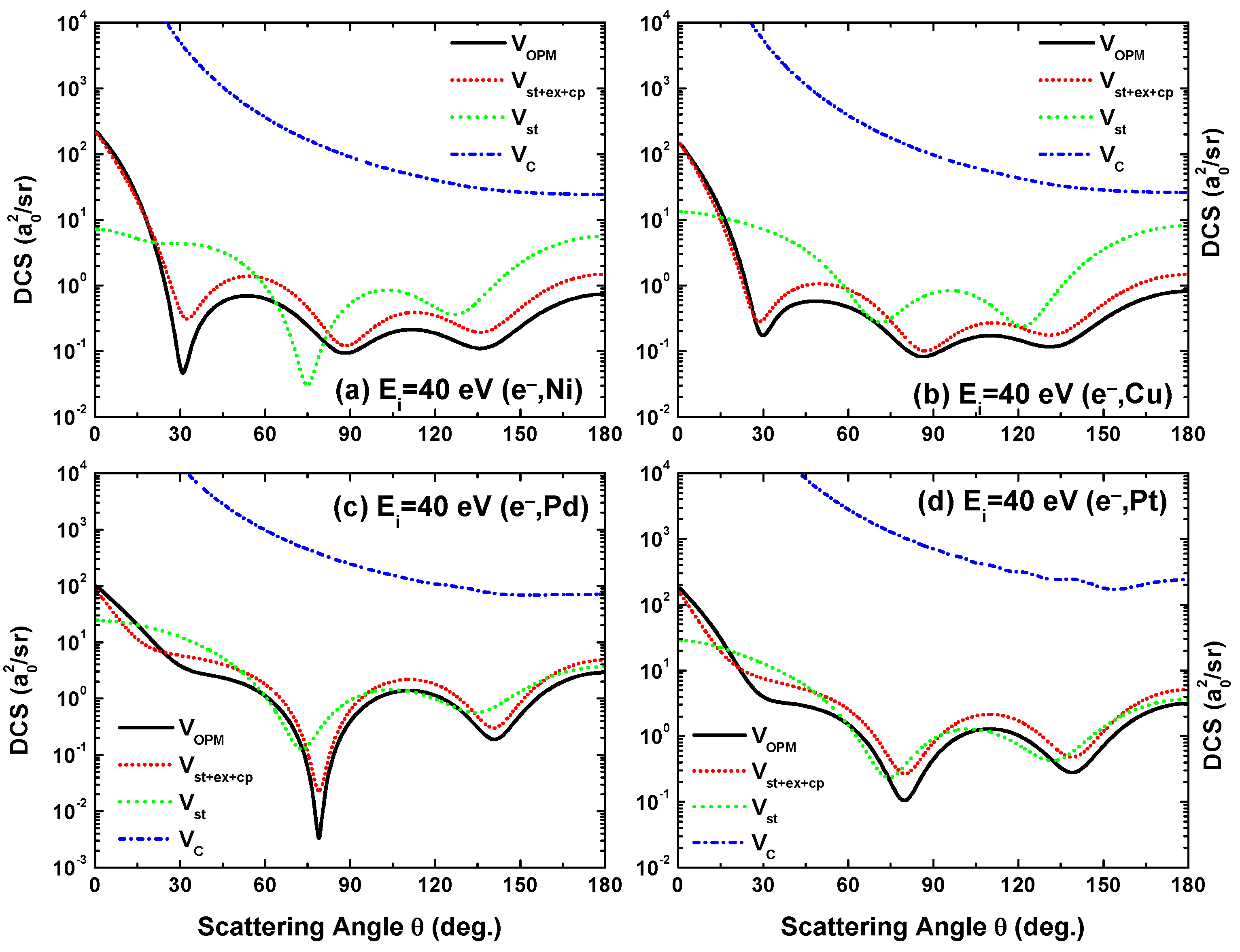
Angular dependence of the differential cross sections for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a fixed energy = 40 eV. Shown are the results from , green); , red); and (—, black), along with the results for the Coulomb field, , blue).
The bottom part of Figure 4 shows the dependence of the DCS on the choice of potentials at energies from 10 keV to 200 MeV. While the pure Coulomb field overestimates below 100 keV, particularly for the heaviest atom, V is well approximated by in the energy region 0.5−5 MeV. However, the Coulomb field strongly overestimates the DCS at the higher energies.
Figure 5 depicts the effects of the potential constituents on the angular dependence of the DCS for 40 eV electrons colliding with the four considered metal targets. At this low energy, the figure reveals a significant difference between the DCS results due to and . This influence is even stronger in the forward hemisphere, and affects the lighter targets quite considerably. For those, the inclusion of and produces more structures in the DCS angular distribution. The absorption potential, , reduces the DCS by a factor of two on average. All these effects, however, gradually decrease with increasing of the target. Figure 5 includes the DCS results from the Coulomb field , for which the DCS diverges at zero angle. At this low energy, the difference between the DCS resulting from and is huge. This reveals the significant screening effect of the nuclear charge by the electron cloud.
4. Results
4.1. Angle-Dependent DCS
Figure 6, Figure 7 and Figure 8 display our OPM results of the DCS for electron scattering from the studied four metal targets at impact energies = 40, 100, 500 and 10,000 eV. It is evident that Ramsauer–Townsend structures [33,34] appear in the DCS, caused by the interference effects of the projectile electrons scattering from the individual electrons of the atom. As expected, the interference structures disappear at higher energies (well above 1 keV), when the collision becomes so energetic that the projectile–atom interaction occurs inside the K-shell.
For e-Ni scattering, Jablonski et al. [35] reported DCS calculations using Dirac–Fock (DF) and Hartree–Fock (HF) density functions. Both of their results for 100 eV impact energy are included in Figure 7a. As seen in this figure, the present results agree well with the DF ones from [35], except for a slight deviation at low scattering angles ().
The OPM-predicted DCS for e-Cu scattering are compared with the measurements of Madison et al. [36] at 40 eV in Figure 6b and 100 eV in Figure 7b, and with those of Trajmar et al. [37] at 100 eV in Figure 7b. Included are the fully relativistic B-spline R-matrix results of Zatsarinny and Bartschat [16], the convergent close-coupling (CCC) results of Zhou et al. [15] at 40 eV in Figure 6b, the HF calculations of Czyzewski et al. [38], and the three-state close-coupling results of Msezane and Henry [14] at 100 eV in Figure 7b. The comparison shows that the OPM calculations produce a fair agreement with both data sets [36,37] at 100 eV. However, the OPM and the other theoretical predictions [15,16] overestimate the data of [36] at 40 eV beyond , albeit all these theories show the same oscillatory features as the experimental data. Additional data are required in order to clarify these discrepancies.
A notable feature is the dependence of the interference structures on the target species and their shell structure as regards the number and location of the DCS minima in the angular distribution. For the alkali atoms studied in [13], this number increases with the number of target shells for all energies between 40 eV and 500 eV; the metal atoms, however, do not show this feature for eV. At 40 and 100 eV (Figure 6 and Figure 7) three minima are found irrespective of the target, except for Pt at 100 eV, for which there are only two minima. At the lowest energy (40 eV), their locations exhibit target independence. At 500 eV, on the other hand (Figure 8a), the number of minima is one, one, two, and three (plus a shallow one) for the Ni, Cu, Pd and Pt targets, respectively. The onset of the first oscillation decreases with , as evident from the appearance of the first minimum at , and for Ni, Cu, Pd, and Pt, respectively. At yet higher energies, the structures gradually fade out (Figure 8b).
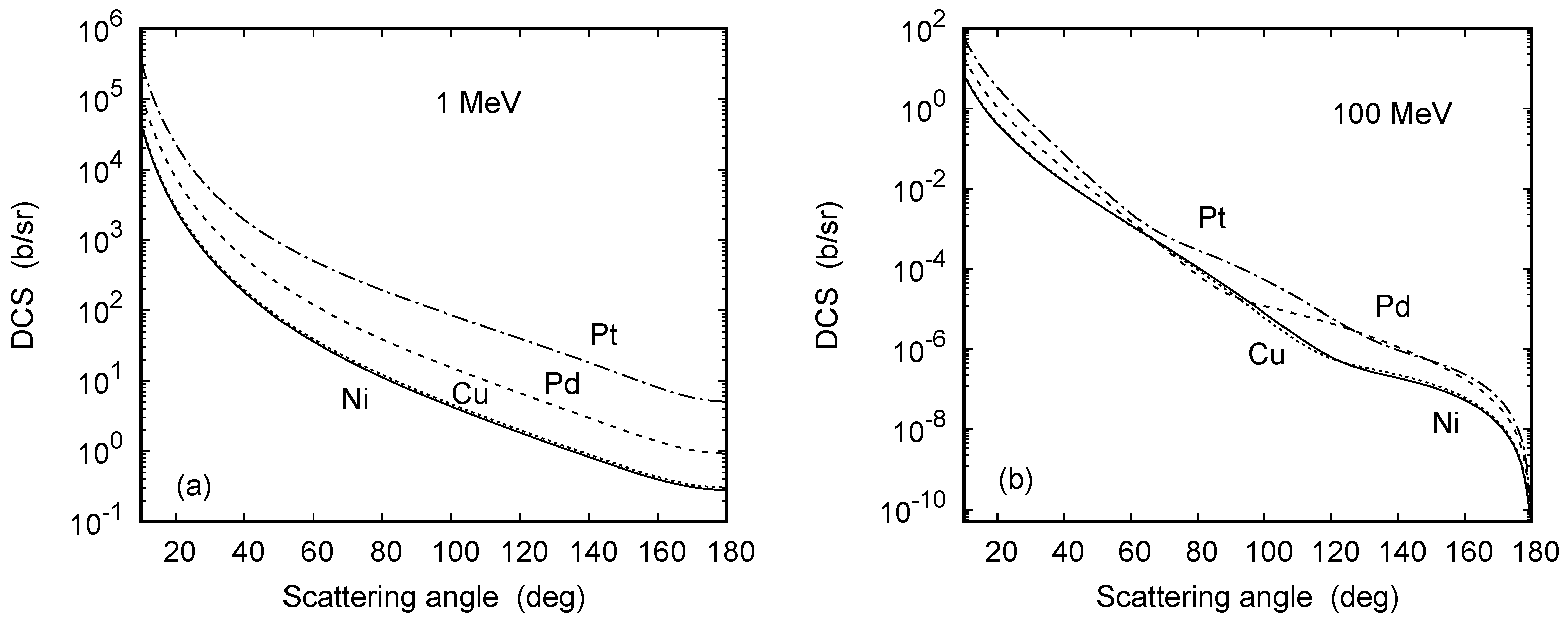
Our calculated high-energy DCS is presented in Figure 9 at energies of 1 MeV and 100 MeV. While the angular dependence at 1 MeV is monotonous for all targets, as is characteristic for the Coulomb field, structures reappear at 100 MeV. These regular oscillations are due to the diffraction effects resulting from the projectiles scattering from the individual protons of the target nucleus. The high-energy structures roughly follow a pattern, where is the nuclear radius, is the momentum transfer, and is a spherical Bessel function [27]. As in Figure 8a, the onset of the structures occurs at smaller angles with increasing .
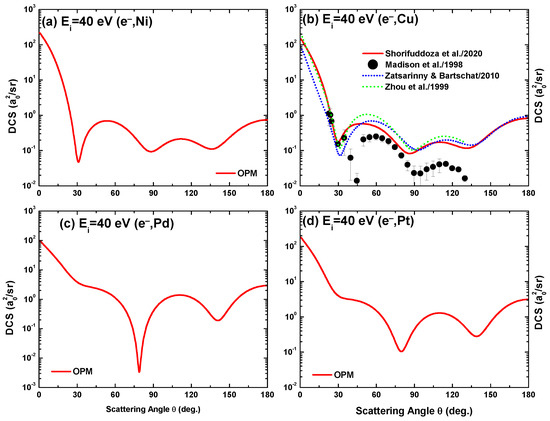
Figure 6.
Angular dependence of the differential cross-sections for 40 eV electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: Madison el al. [36]. Theory: OPM (—), Zatsarinny and Bartschat [16] and Zhou et al. [15].
Figure 6.
Angular dependence of the differential cross-sections for 40 eV electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: Madison el al. [36]. Theory: OPM (—), Zatsarinny and Bartschat [16] and Zhou et al. [15].
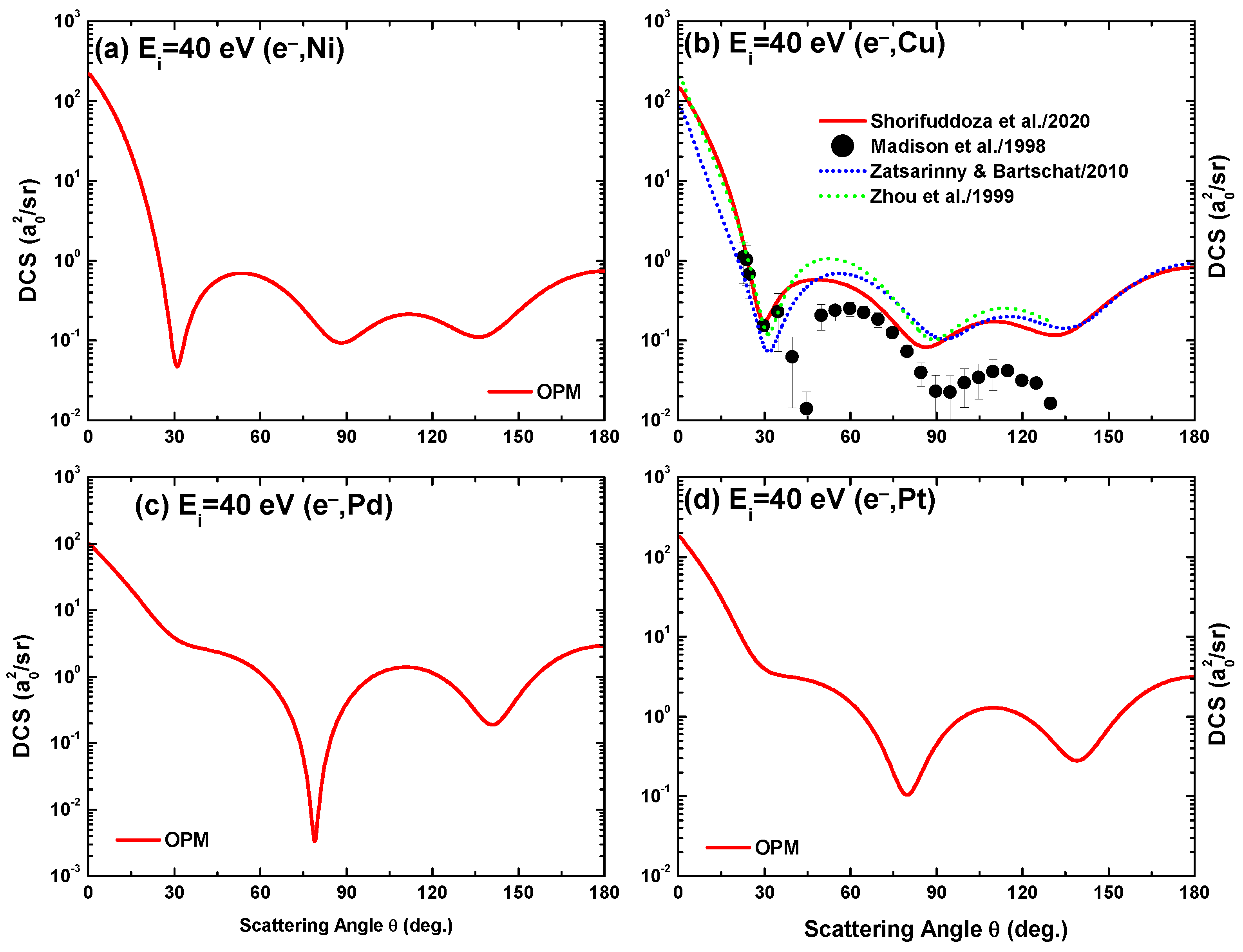
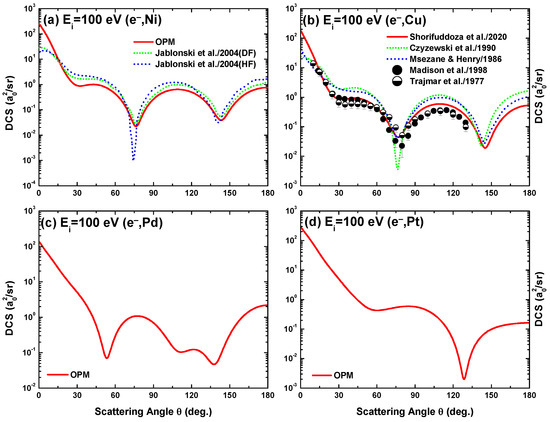
Figure 7.
Angular dependence of the differential cross-sections for 100 eV electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: Madison el al. [36] and Trajmar et al. [37]. Theory: Present OPM (—), Jablonski et al. [35], Czyzewski et al. [38], and Msezane and Henry [14].
Figure 7.
Angular dependence of the differential cross-sections for 100 eV electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: Madison el al. [36] and Trajmar et al. [37]. Theory: Present OPM (—), Jablonski et al. [35], Czyzewski et al. [38], and Msezane and Henry [14].
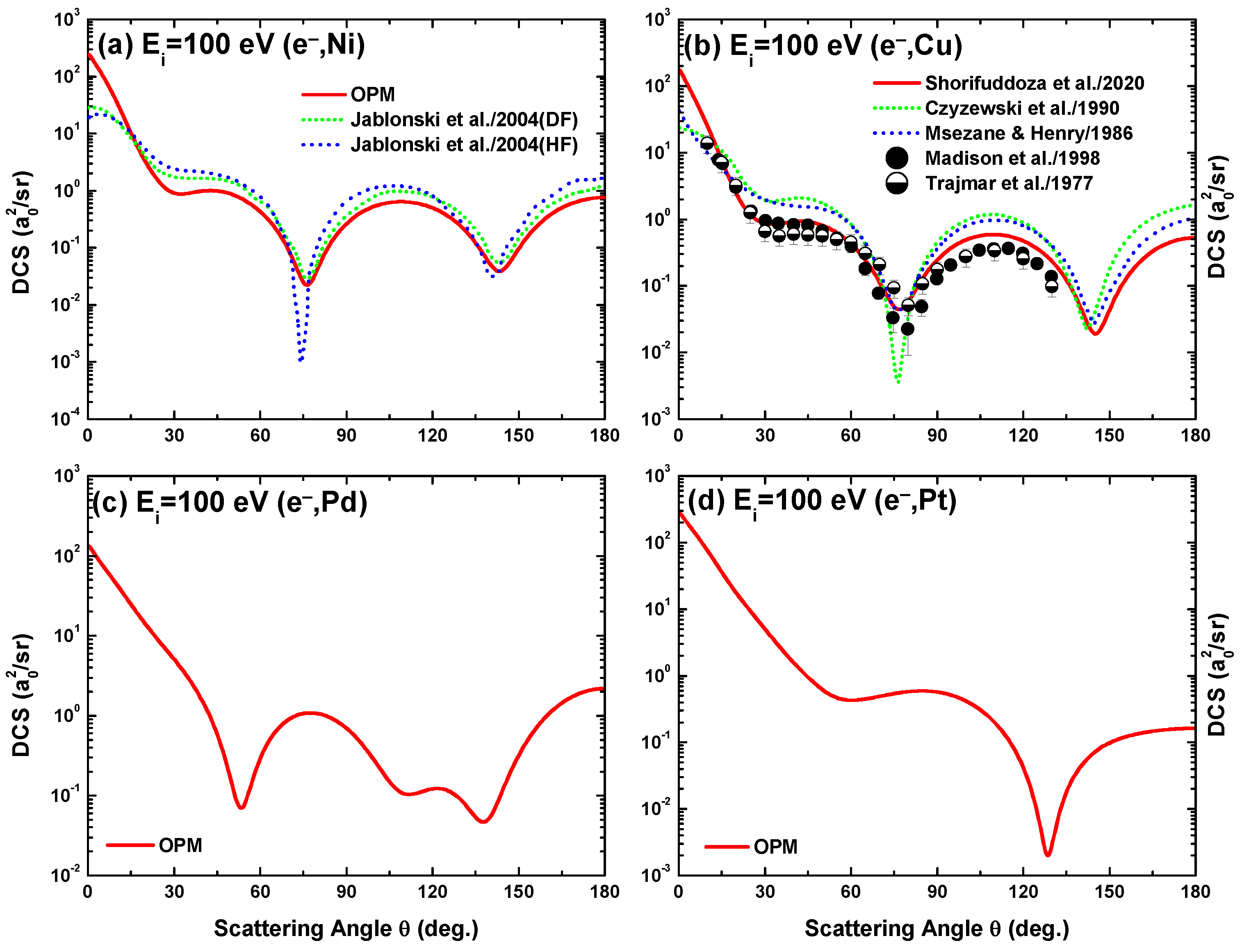
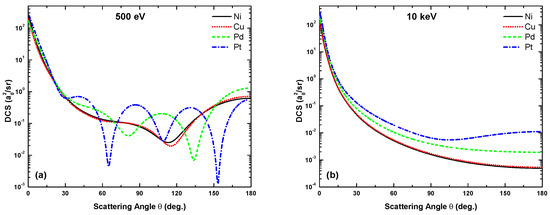
Figure 8.
Angular dependence of the differential cross-sections due to the OPM approach for electron scattering from Ni, Cu, Pd, and Pt at impact energies of (a) 500 eV and (b) 10 keV.
Figure 8.
Angular dependence of the differential cross-sections due to the OPM approach for electron scattering from Ni, Cu, Pd, and Pt at impact energies of (a) 500 eV and (b) 10 keV.
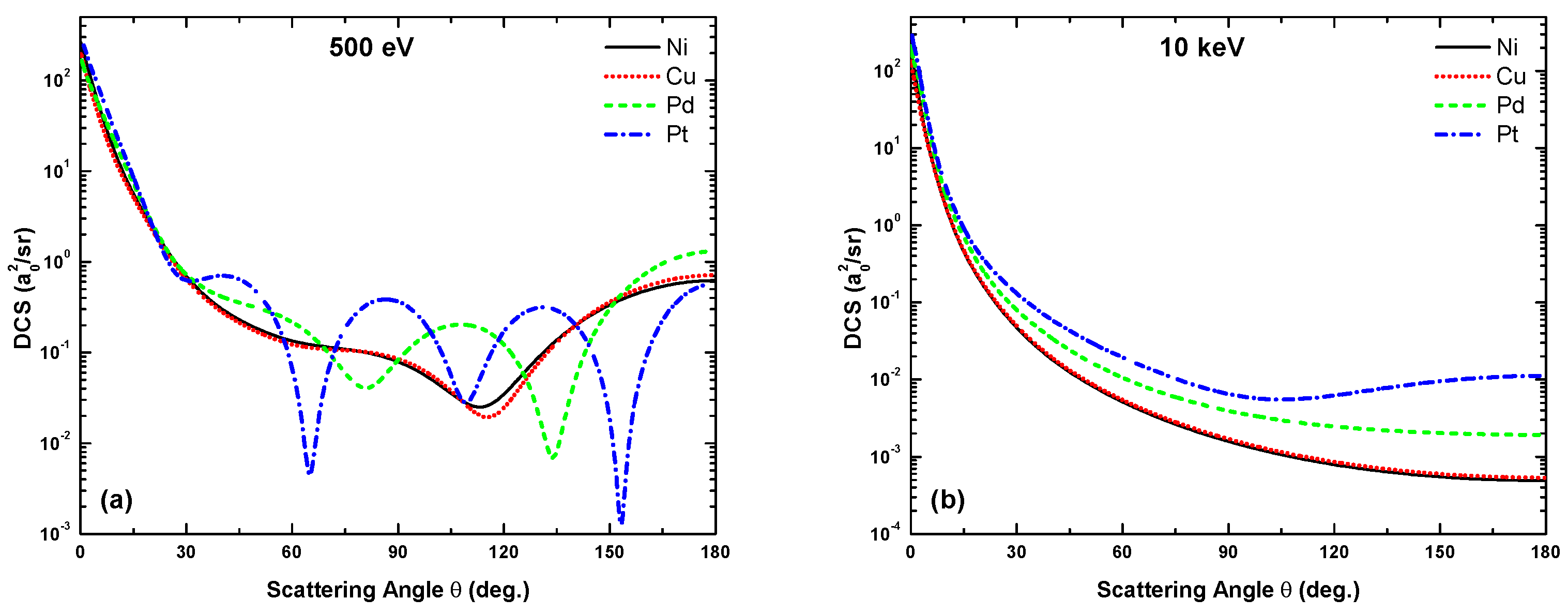
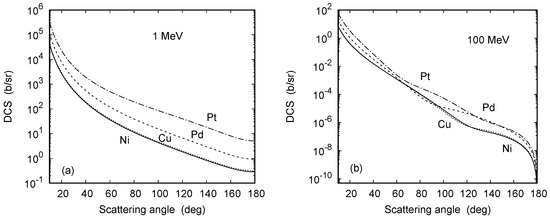
Figure 9.
Angular dependence of the differential cross-sections for electron scattering from Ni (—), Cu), Pd, and Pt at impact energies of (a) 1 MeV and (b) 100 MeV.
Figure 9.
Angular dependence of the differential cross-sections for electron scattering from Ni (—), Cu), Pd, and Pt at impact energies of (a) 1 MeV and (b) 100 MeV.
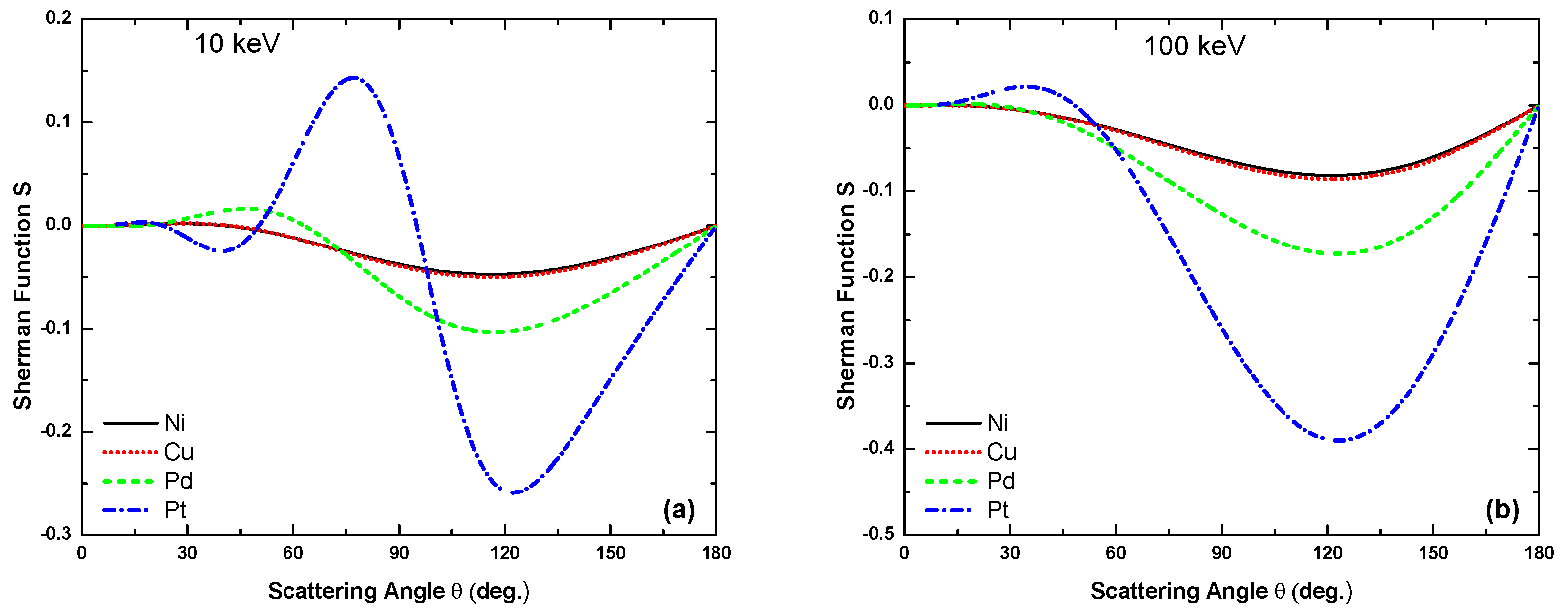
4.2. Angle-Dependent Sherman Function
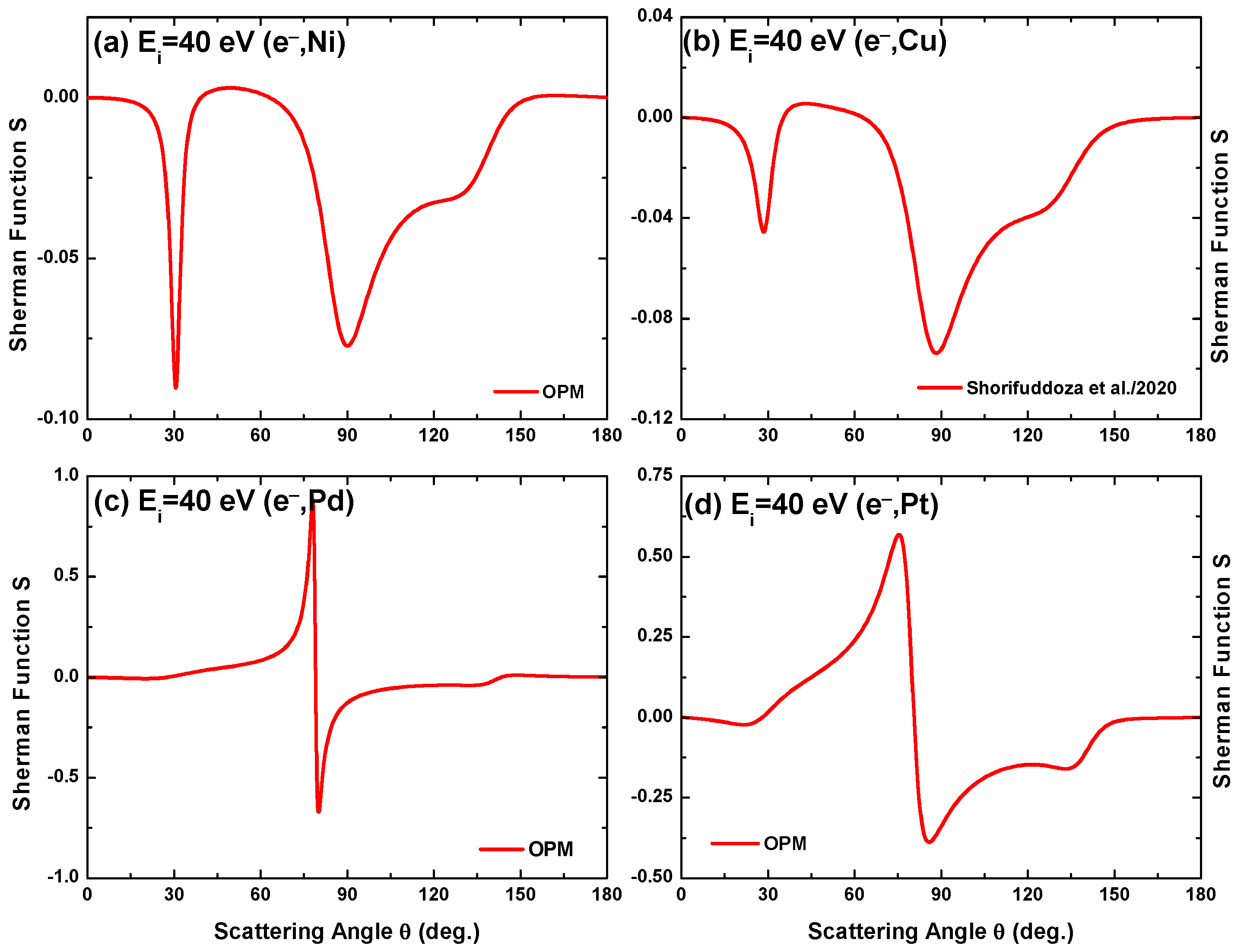
Our OPM results of the Sherman function for electron scattering from Ni, Cu, Pd, and Pt at impact energies = 40 eV, 100 eV, 500 eV, 1 keV, 10 keV, and 100 keV are displayed in Figure 10, Figure 11, Figure 12 and Figure 13. Included are calculations by Fink and Ingram [39] for the Cu target at 100, 500, and 1000 eV for comparison with our findings. As seen in Figure 11b, apart from minor differences near the extrema our OPM results agree well with the relativistic calculation of [39]. The same is true for the two higher energies [6]. It is worth mentioning that although the present OPM and the work of [39] are based on Dirac’s relativistic dynamics, the latter did not include the exchange, polarization, and absorption potentials in their calculation. Furthermore, they used the Hartree–Fock–Slater (HFS) atomic potential in their calculation. As such, the differences between these two calculations can reveal the sensitiveness of the Sherman function, primarily by the potential adaptation.
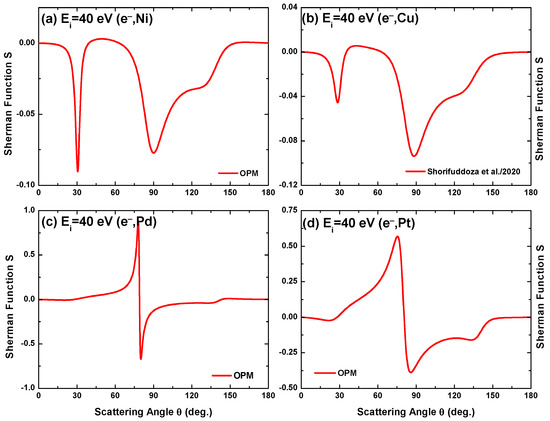
Figure 10.
Angular variation of the Sherman function predicted by the OPM approach for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at impact energy = 40 eV.
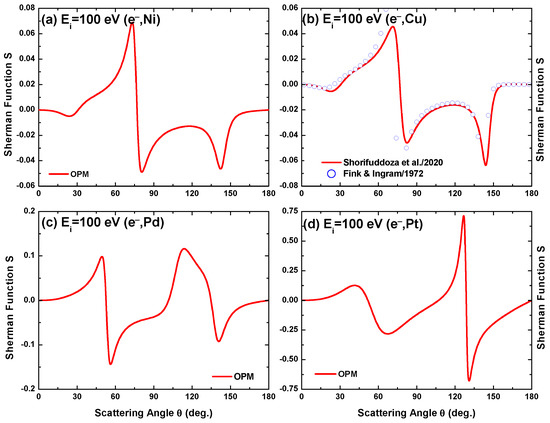
Figure 11.
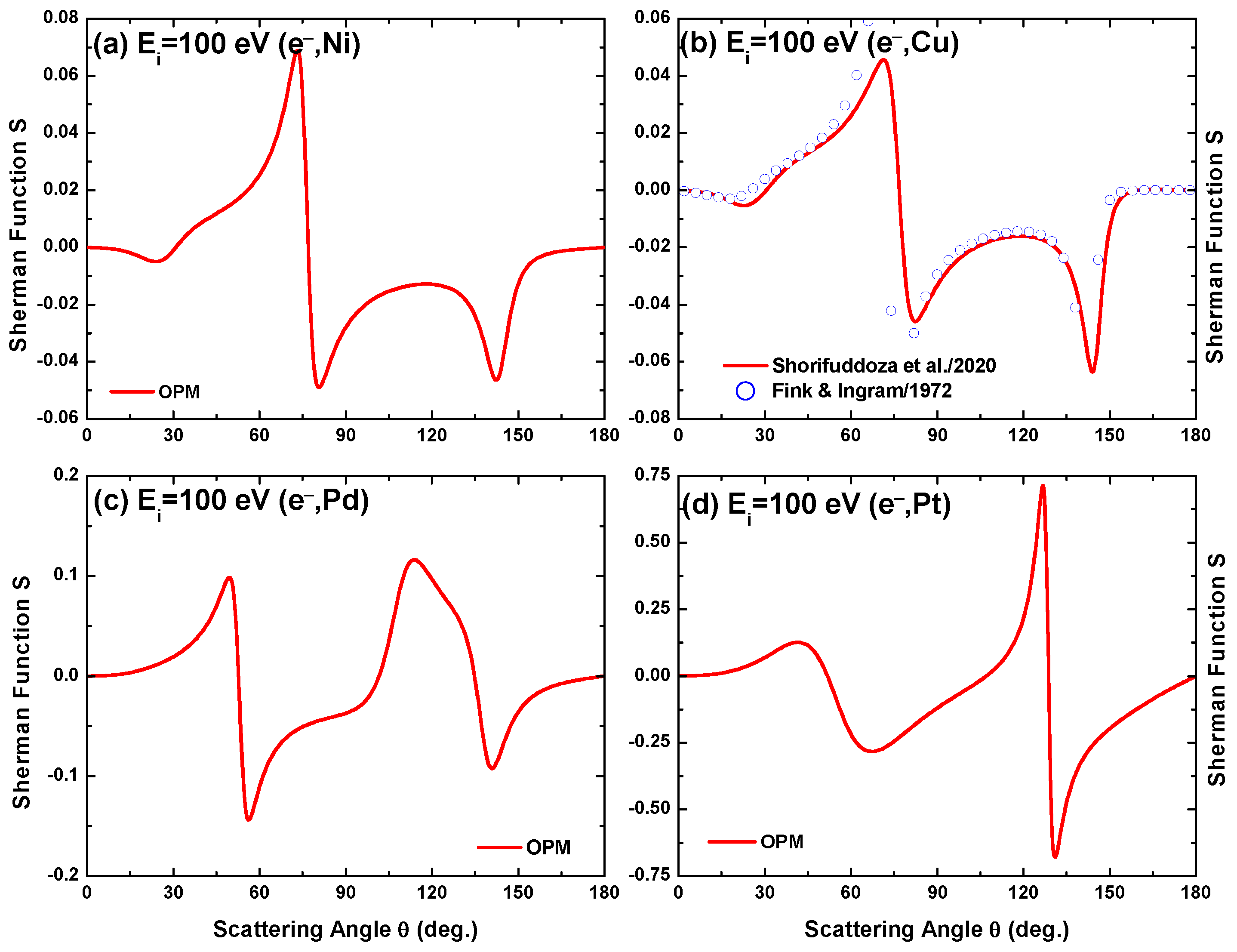
Angular variation of the Sherman function for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at impact energy = 100 eV as computed by the present OPM (—) and by Fink and Ingram [39].
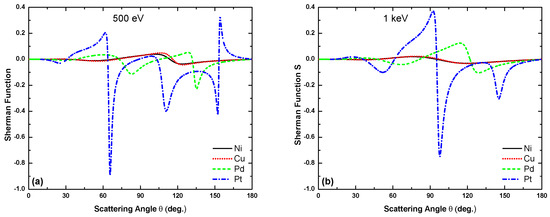
Figure 12.
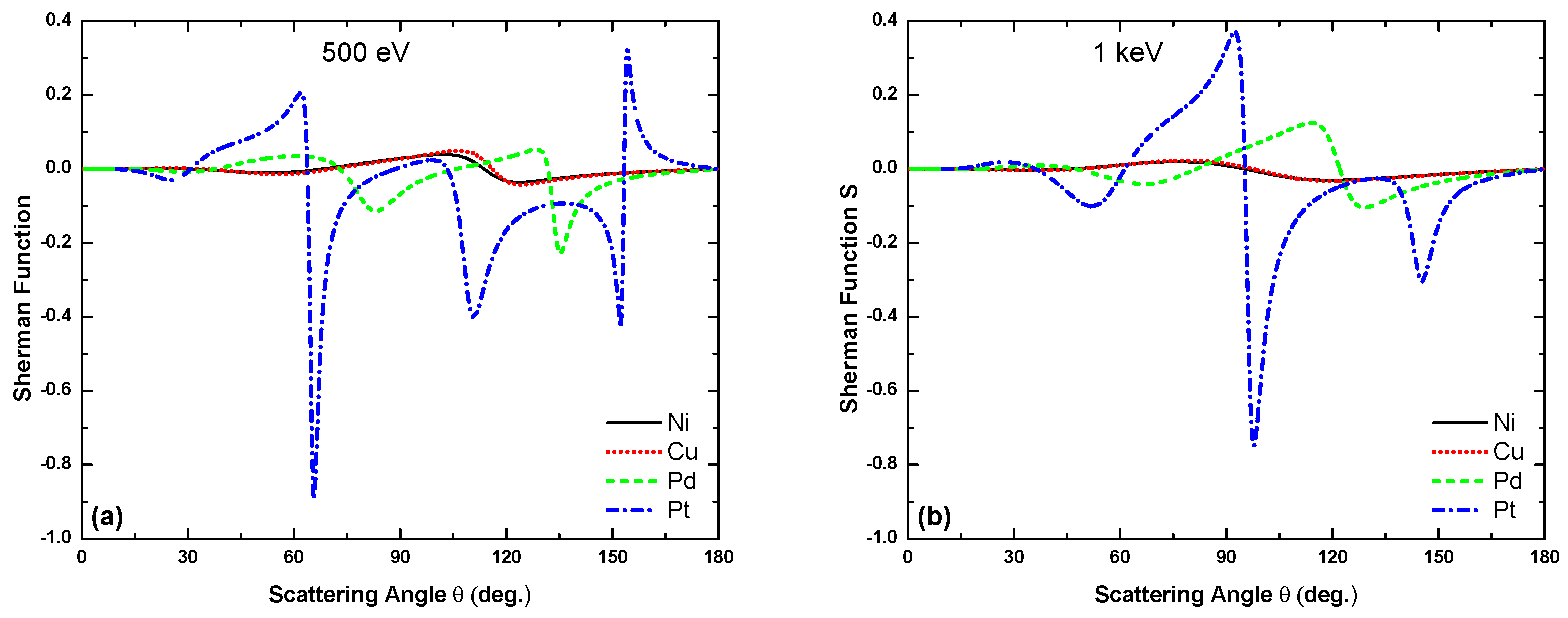
Angular variation of the Sherman function predicted by the OPM approach for electron scattering from Ni, Cu, Pd, and Pt at impact energies of (a) 500 eV and (b) 1 keV.
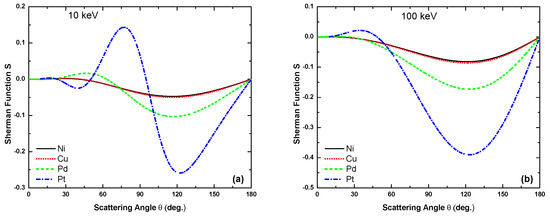
Figure 13.
Angular variation of the Sherman function due to the present OPM approach for electron scattering from Ni, Cu, Pd, and Pt at impact energies of 10 keV (a) and 100 keV (b).
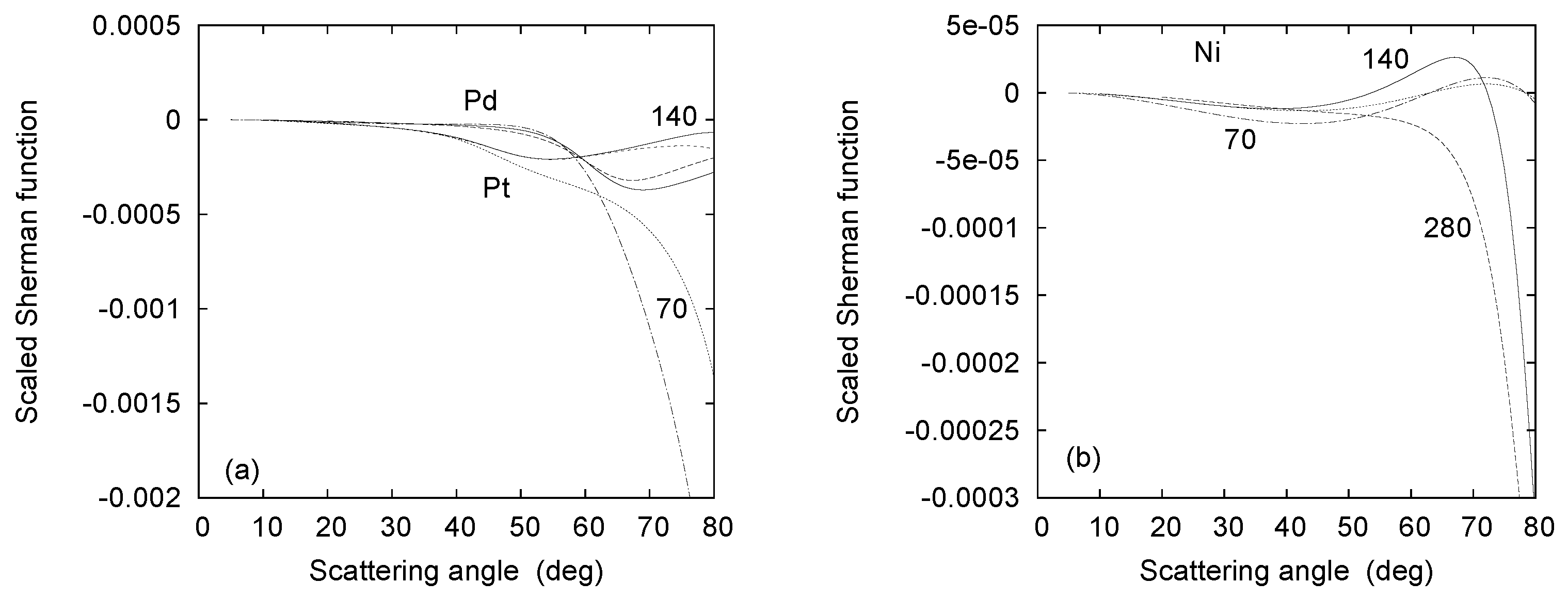
It is evident from Figure 10, Figure 11, Figure 12 and Figure 13 that, as expected, the minima in relate to the minima in the DCS. However, the structures in are much more pronounced because of the greater sensitivity of to the variation of the potential, leading to a variation of the phases of the scattered waves, as compared to the DCS. It can be seen that between 500 eV and 10 keV the number of minima becomes larger when proceeding to heavier metal atoms. Moreover, for eV, the magnitude of the Sherman function increases strongly with the size of the target atoms. For example, at 500 eV the maxima of vary from 0.05 for Ni to 0.88 for Pt.
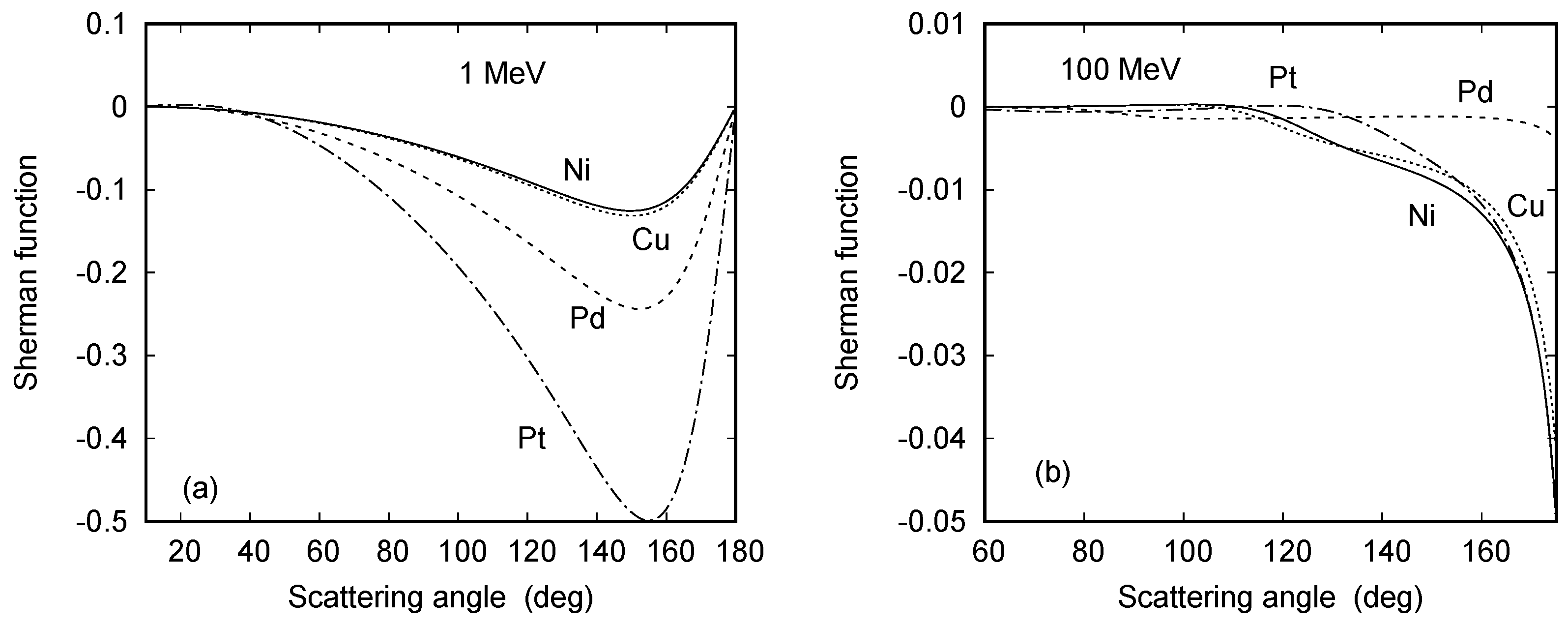
When considering the Sherman function at yet higher energies of 1 MeV and 100 MeV (Figure 14), the following additional systematics are noted. At keV the dominant structures are sharp, corresponding to deep minima in the DCS, while the extrema in S become increasingly broader at keV, and the relation to the cross section minima gradually disappears. In addition, the pronounced maximum in the forward hemisphere completely disappears near 1 MeV; at 100 MeV, the minimum shifts from (at 10 keV) to near , beyond which S increases sharply to zero at . At this ultrahigh energy, the structures reappear in concord with the oscillatory behavior of the DCS.
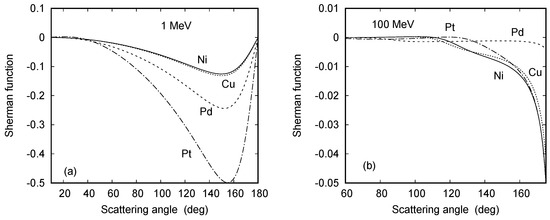
Figure 14.
Angular variation of the Sherman function S for electron scattering from Ni (—), Cu, Pd, and Pt at impact energies of (a) 1 MeV and (b) 100 MeV.
4.3. Energy-Dependent DCS and Sherman Function
Figure 15 and Figure 16 show the energy dependent DCS of the electrons scattering from the four metal atoms over the energy range of 1 eV GeV at scattering angles and . Note that the results for Cu up to 2 keV are taken from Shorifuddoza et al. [6]. As seen in Figure 15 and Figure 16, the DCS as calculated separately for two different energy regions, namely, low-to-intermediate and high energies, merges smoothly in the energy region 0.1–1 MeV. This bridging of these two calculations is due to the fact that the potentials used in this energy region are well represented by the Coulomb field, , of a point nucleus. The lower limit of the matching region shifts towards a slightly higher energy as the atomic number of the target material increases, as can be seen at the bottom of Figure 4.
The interference structures are clearly visible at both scattering angles for 1 keV. These low-energy structures gradually fade out as the impact energy approaches the M-subshell binding energies of the targets. Because of the dominant Coulomb field of the nucleus, the DCS then decreases monotonously with energies up to about 50 MeV. The structures reappear at ultra-relativistic energies in a similar way as in the angular distribution (Figure 9b) due to their q-dependence via .
Figure 15 and Figure 16 include other theoretical calculations in the low-to-intermediate energy region [39,40], as well as experimental data from Madison et al. [36] and Trajmar et al. [37] at the lower energies and from Ficenec et al. [41], Antonov et al. [42], Shevchenko et al. [43], and van der Laan [44] at ultrahigh energies. Our calculations agree well with these experimental and theoretical results.
The variation of the Sherman function S with energy computed with our theory at a fixed scattering angle of is displayed in Figure 17 for electron impact scattering from the four metal atoms. As in the angular distribution of S (Figure 10, Figure 11 and Figure 12), the structures in the low-to-intermediate energy region correspond to the minima in the DCS and are again much more pronounced than those in the DCS. It can be seen that the structures extend towards higher energies and that the number of oscillations grows larger as the target size increases. This is related to the successively larger number of electronic shells encountered as increases. The present results can be compared with the theoretical predictions of Fink and Ingram [39]; although these are only available for Cu, there is good agreement between the present OPM results and those of Fink and Ingram [39].
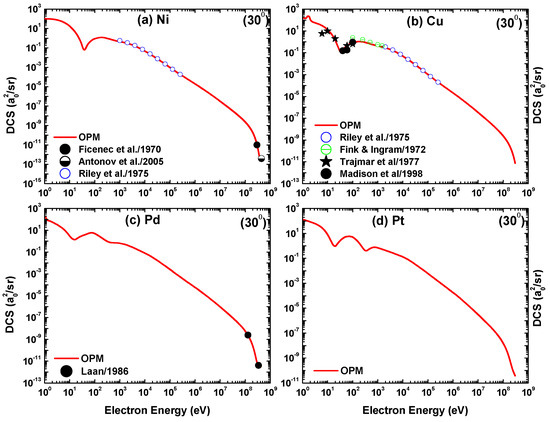
Figure 15.
Energy dependence of the differential cross-sections for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of . Experiment: Madison el al. [36], Trajmar et al. [37], Ficenec et al. [41], Antonov et al. [42], and van der Laan [44]. Theory: Present OPM (—), Riley et al. [40], and Fink and Ingram [39].
Figure 15.
Energy dependence of the differential cross-sections for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of . Experiment: Madison el al. [36], Trajmar et al. [37], Ficenec et al. [41], Antonov et al. [42], and van der Laan [44]. Theory: Present OPM (—), Riley et al. [40], and Fink and Ingram [39].
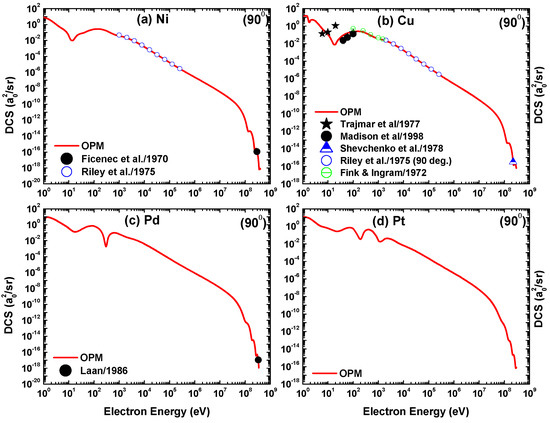
Figure 16.
Energy dependence of the differential cross-sections for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of . Experiment: Madison el al. [36], Trajmar et al. [37], Ficenec et al. [41], van der Laan [44], and Shevchenko [43]. Theory: Present OPM (—), Riley et al. [40], and Fink and Ingram [39].
Figure 16.
Energy dependence of the differential cross-sections for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of . Experiment: Madison el al. [36], Trajmar et al. [37], Ficenec et al. [41], van der Laan [44], and Shevchenko [43]. Theory: Present OPM (—), Riley et al. [40], and Fink and Ingram [39].
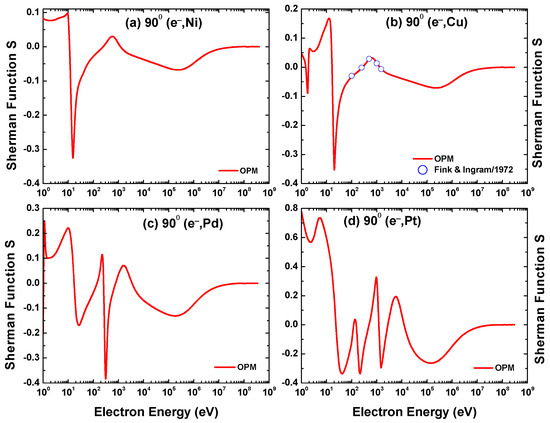
Figure 17.
Energy-dependent Sherman function S for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of , in comparison with the calculations of Fink and Ingram [39] for Cu.
Figure 17.
Energy-dependent Sherman function S for electron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle of , in comparison with the calculations of Fink and Ingram [39] for Cu.
4.4. Critical Minima and Total Polarization Points
This section provides a detailed analysis of the positions of the critical minima (CM) in the DCS for the studied metal targets. In addition, the points with maximum spin polarization (MSP) which lie in the vicinity of these CM are determined. An MSP point with spin polarization greater than 50% is considered as a total polarization point [45]. In judging between theories, the CM have the advantage over the DCS distributions, as the former require cross-sections only at a few energies and angles. The determination of the CM in the present study is based on three criteria [46]: (i) the spin-flip scattering amplitude becomes larger in magnitude than the direct scattering amplitude ; (ii) the DCS reaches its minimum value, which is several orders of magnitude smaller than those at nearby energies and angles; and (iii) the scattered electron undergoes total polarization in the vicinity of the CM.
It is worth mentioning that there is no CM in the high-energy regime [19]. Our present investigations of CM are therefore confined to the low-to-intermediate energy region.
In the DCS distribution for e-Ni scattering, by simultaneously varying the energy and angle, we were able to obtain a total of seven deep minima (DM). Table 1 presents their critical energies , critical angles , and scattering amplitudes A and B. Among these seven DM only two, at ( = 29.5 eV; 34.5°) and ( = 74.5 eV; 146.5°), do not satisfy criterion (i), as for these points. In the vicinity of these seven DM, we have determined the MSP points at which reaches the extremal values of both signs. Table 2 shows the fourteen corresponding MSP points for which the extremum of S, termed , varies from 0.53 to 0.98 and 0.69 to 1.00, respectively, in the positive and negative excursions. All of these MSP points can therefore be considered as total polarization points.

Table 1.
The energy and angular positions and the values of direct and spin-flip scattering amplitudes of the deep minima (DM) in the DCS for elastic e-Ni scattering.

Table 2.
Maximum spin polarization points, along with their positions and deviations in energy and angle from their respective critical minima positions, for e-Ni elastic scattering.
Table 2 records the energy width and angular width of the obtained MSP points. The energy width, , is defined as the energy difference between the energy position of the CM point and the energy position of the MSP point. Similarly, denotes the respective difference in the angular position. When summed, these energy and angular widths determine the width of the DCS valley at a CM position. For example, in the case of the CM at ( = 15.5 eV; 54.5°), the corresponding spin polarization, = +0.98 at ( = 15.6 eV; 53.0°) with ( = 0.1 eV and 1.5°) and = −0.99 at ( = 15.45 eV; 55.5°) with ( = 0.05 eV and 1.0°), yields the widths of the DCS valley as 0.1 + 0.05 = 0.15 eV along the energy axis and 1.5° + 1.0° = 2.5° along the angular axis.
For e-Cu scattering, Table 3 displays and of the eight existing DM. As seen in this table, all DM points are qualified as CM, as they have spin-flip scattering amplitudes greater than their direct counterparts. It can be observed that the CM with the highest critical energy occurs at ( = 337.4 eV; 122.5°) and the one with the highest critical angle occurs at ( = 86.0 eV; 145.0°). In the neighborhood of the eight deep minima, we obtain the sixteen MSP points listed in Table 4. The polarization is found to vary between and , respectively, in the positive and negative excursions. All of these MSP points therefore qualify as total polarization points.

Table 3.
The energy and angular positions and the values of direct and spin-flip scattering amplitudes of the deep minima (DM) in the DCS for elastic e-Cu scattering [6].

Table 4.
Maximum spin polarization points, along with their positions and deviations in energy () and angle () from the respective critical minimum positions, for e-Cu scattering [6].
For e-Pd elastic scattering, there are nine DM in total. The energy and angular positions of these DM are listed in Table 5. Among the nine DM, only the one at ( eV; = 51.40°) fails to satisfy criterion (i) for a CM. For the qualified eight CM points, the highest critical energy and angle are seen at ( = 638.90 eV; 129.4°) and ( = 196.20 eV; 151.0°), respectively. We searched for MSP points at which the polarization reaches the extremal values of both signs. The energy and angle positions of seventeen such MSP points are tabulated in Table 6. The magnitude of the spin polarization of these MSP points, except at ( eV; 52.5°), varies from +82% to +100% and −53% to −100%, respectively, in the positive and negative excursions. Note that the MSP point at ( eV; 52.5°) with corresponds to the DM at ( eV; 51.40°), which is not a CM.

Table 5.
The energy and angular positions and the values of direct and spin-flip scattering amplitudes of the deep minima (DM) in the DCS for elastic e-Pd scattering.

Table 6.
Maximum spin polarization points with their positions and deviations in energy () and angle () from the respective critical minimum positions for e-Pd scattering.
For e-Pt scattering, there are thirteen DM in total. Table 7 records the position () and magnitude of the scattering amplitudes of these DM. Of the thirteen, the two DM at ( eV; ) and ( eV; 36.0°) do not qualify to be a CM, as they fail to satisfy the criterion of . The CM with the highest critical energy appears at ( = 1594.10 eV; 136.5°), and the one with the highest critical angle appears at ( = 526.09 eV; 153.0°). In the vicinity of the eleven qualified CM and the two DM at 27.26 eV and 230.68 eV, we traced a total of twenty-five MSP points, which are presented in Table 8. As seen in this table, a large polarization of 87% 100% is achieved in twenty-three MSP points, which are therefore considered as total polarization points. As the values (−0.40 and −0.26) of the remaining two MSP points at ( eV; 85.0°) and ( eV; 39.0°) are less than 50%, they are not total polarization points.

Table 7.
The energy and angular positions and the values of direct and spin-flip scattering amplitudes of the deep minima (DM) in the DCS for elastic e-Pt scattering.

Table 8.
Maximum spin polarization points with their positions and deviations in energy () and angle () from the respective critical minimum positions for e-Pt scattering.
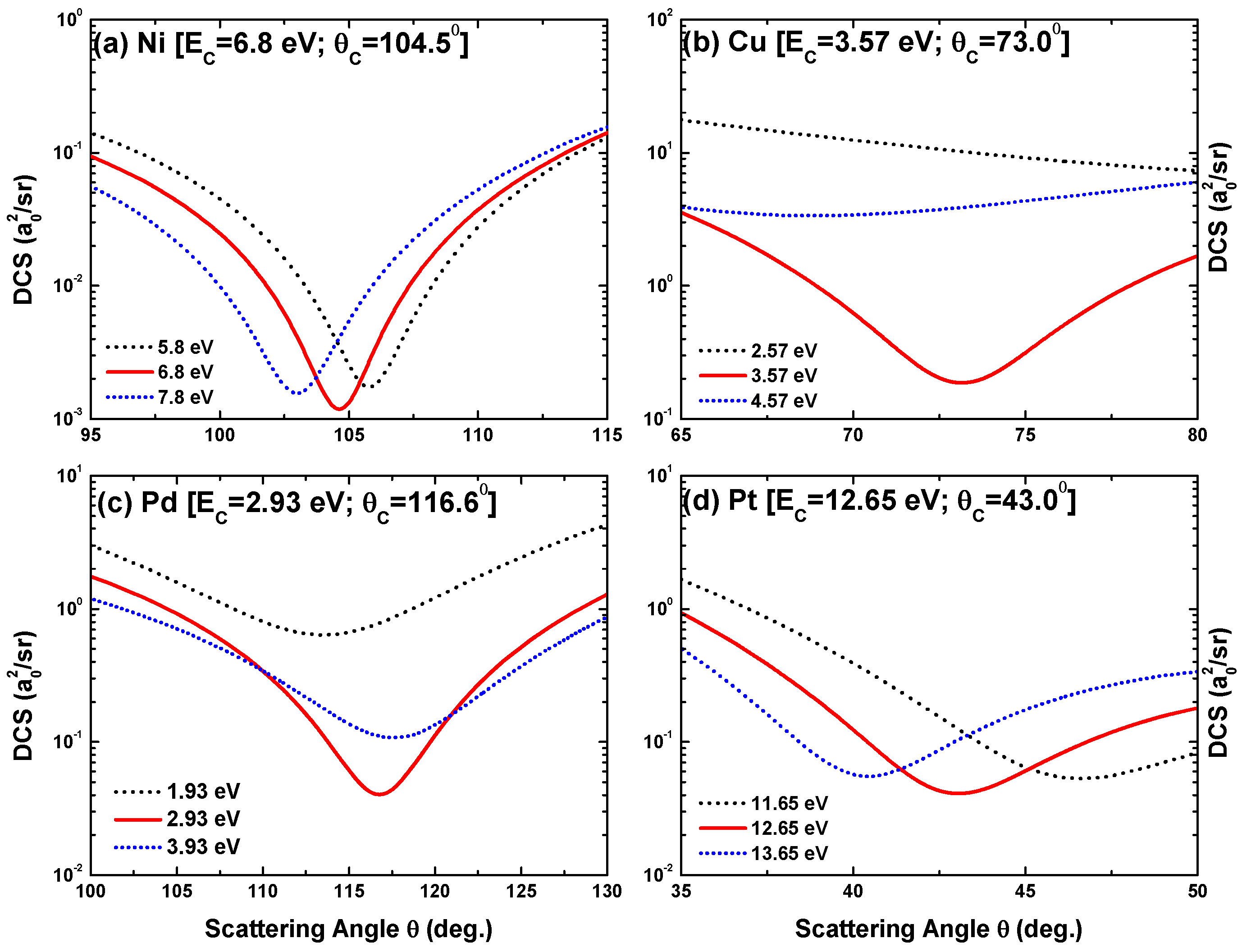
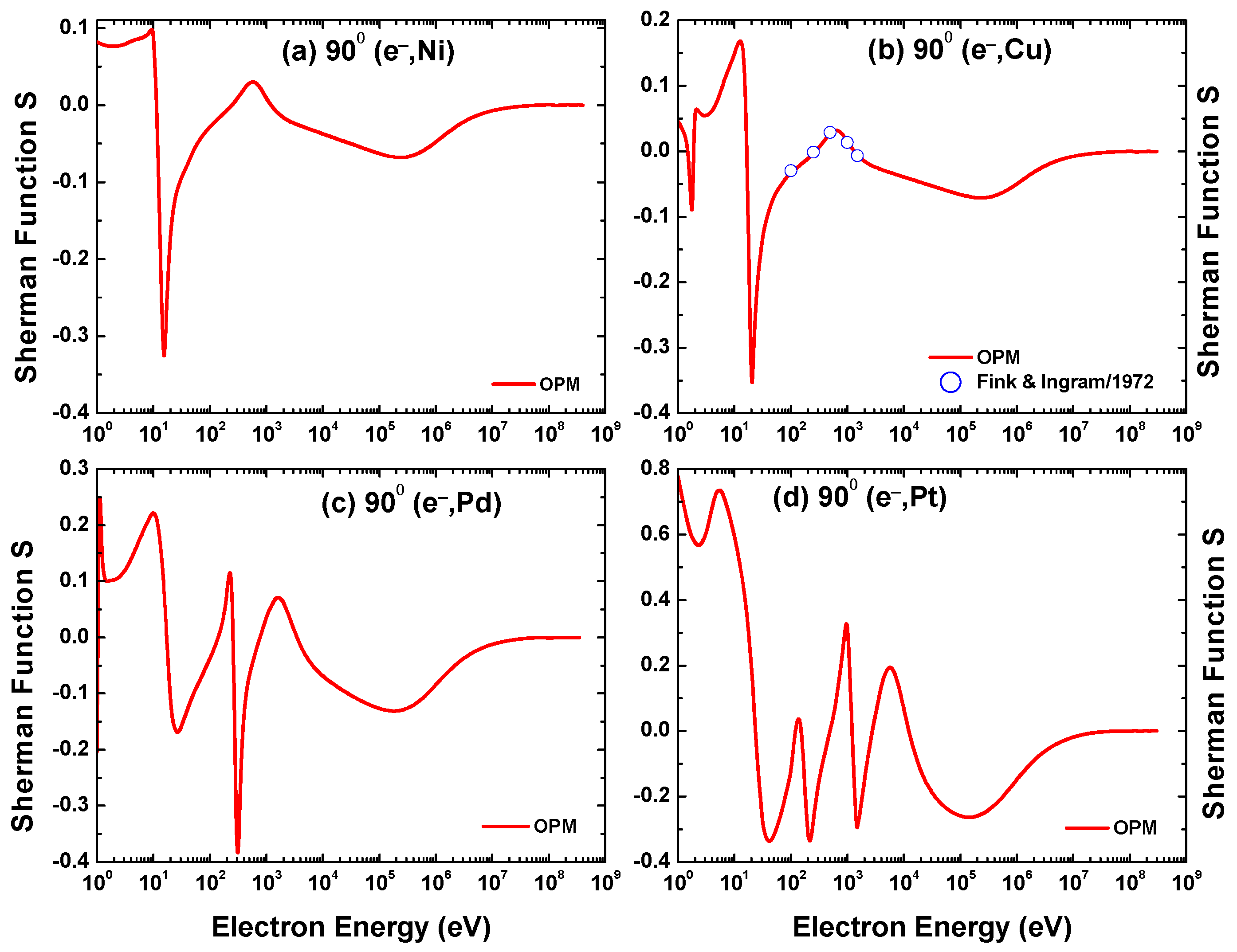
In order to check criterion (ii) of a CM for each target, the DCS at some critical energy along with two different energies in the vicinity of that critical energy are depicted in Figure 18. These results demonstrate that the DCS value attains its lowest value at exactly the critical energy of each CM. The DCS is higher if the energy is higher or lower by 1 eV. For example, in Figure 18a for Ni and with the CM at ( 104.5°), the DCS value is the lowest at exactly 6.8 eV as compared to those at 5.8 eV and 7.8 eV. We observe similar behavior for the targets Cu, Pd, and Pt, respectively, in Figure 18b–d. These results demonstrate the efficacy of the present electron–atom optical potential method for accurately determining the CM positions.
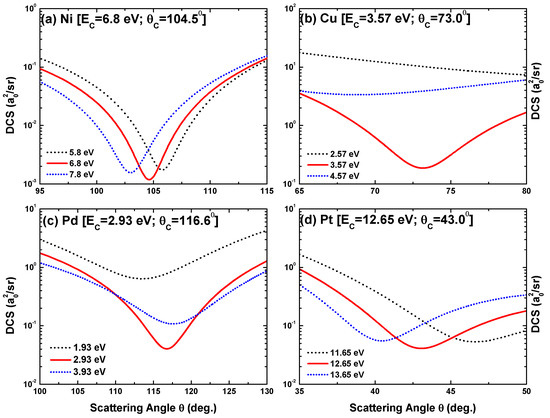
Figure 18.
Angular dependence of the DCS for three incident energies in the vicinity of the critical minima: (a) ( 104.5°) for Ni, (b) ( 73.0°) for Cu, (c) ( 116.6°) for Pd, and (d) ( 43.0°) for Pt.
To investigate the dependence on the electronic shell structure of those critical or deep minima which lead to high polarization in their vicinity, in Table 9 we compile our present results along with those of [13] for alkali atoms, for which details of the atomic electron density distribution are available. In this table, we provide the number n of inner shells (starting from the L-shell) for nine elements, as well as the number of deep DCS minima inducing a spin polarization in both positive and negative excursions. Yb is included in this list in order to guarantee an average increase of of not larger than ten from element to element.

Table 9.
Compilation of the features of the metal atoms, alkali atoms [13], and Yb [19], providing the charge , number n of shells (without K-shell and outermost shell), and number of the deep DCS minima for which the corresponding spin asymmetry .
It can be seen that, in general, increases with the number of inner shells. While the deep minima are located in a similar angular region () irrespective of , they are found up to a collision energy which increases with , approximately like . In addition, is closer to unity in heavier atoms. The reason for this is that a larger number of electron scattering centers allows for more numerous and more pronounced interference structures. An exception to the general trend described above is Cs, which has an extraordinarily high number. This can be attributed to the larger extension of its electron distribution , which for au is au [13], whereas for Pt it is au (Figure 2). Hence, for Cs the projectile needs a lower energy to reach the electron cloud, leading to the possibility of a larger number of structures when is increased. In fact, the smallest is 2 eV for Cs, while it is 13 eV for Pt.
It is instructive to compare the results for the metal atoms with the earlier results for alkali atoms [13] as concerns the effect of the electronic charge density. For the alkali atoms, the extension and magnitude of increases with , leading to an earlier structure onset for all eV. In contrast, as shown in Figure 2, the extension of for the metal atoms is similar for all , and only below au does a higher value of correspond to a larger . As a consequence, the onset and number of oscillations is effectively independent of below 100 eV. A strict decrease of the onset with in combination with an increase in the number of oscillations with the number of target shells is only observed for the metal atoms at much higher energies.
4.5. High-Energy Scaling Laws
- (a)
- Differential cross section
Profiting from the equivalence of elastic scattering and tip bremsstrahlung emission for collision energies high enough that the electron mass m can be neglected [47], and guided by the existence of scaling laws in bremstrahlung [48], the following scaling law for the elastic scattering DCS is postulated for small scattering angles (i.e., such that ):
provided . Here, the scaling relies on the facts that for high collision energies the momentum transfer which governs the scattering cross section is constant if the product is constant and that the cross section increases with energy.
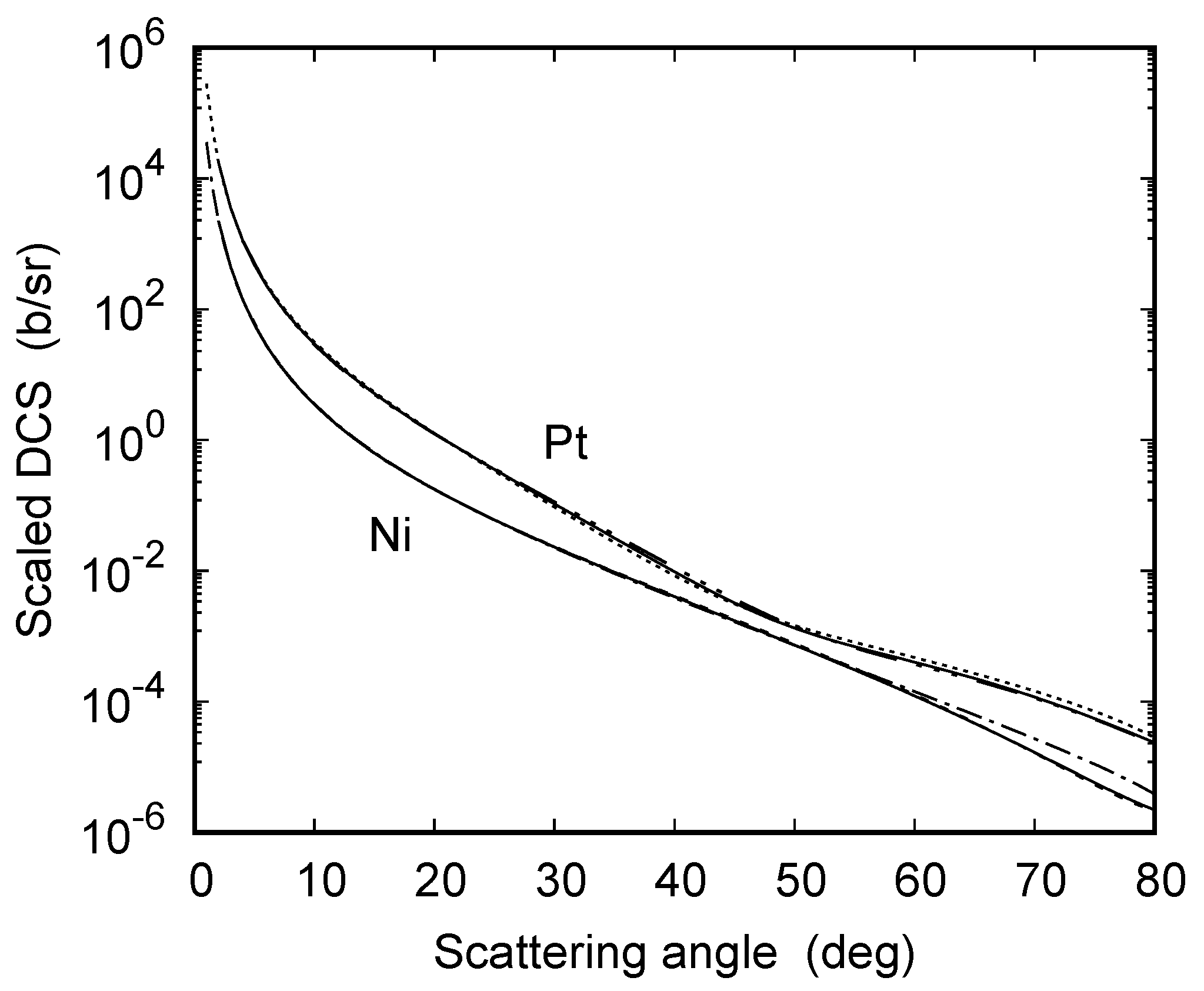
Figure 19 shows the cross section for MeV and 280 MeV, scaled to 140 MeV, for the targets Ni and Pt. It can be seen that for Ni the scaling holds approximately for , while for the heavier Pd and Pt targets the deviations start beyond . We note that 70 MeV is too low for the scaling to hold at the higher angles considered, particularly as concerns the lighter nuclei.
Figure 19.
Differential cross section for 140 MeV electron impact (—) on Ni (lower line) and Pt (upper line) as function of the scattering angle . Included are the results at 70 MeV impact for Ni and Pt (scaled to 140 MeV) as well as the scaled results at 280 MeV impact for Ni and Pt according to (15), with = 140 MeV.
It turns out that the scaling property can be derived from the first-order Born approximation,
where is the charge form factor derived from the nuclear charge density, , and is the Mott cross-section [49],
For small angles where , the momentum transfer is , such that is constant if is scaled according to . Moreover, in this case the Mott cross-section behaves as
increasing quadratically with . These Born-based considerations explain why the scaling is better satisfied for the lighter targets.
- (b)
- Sherman function
Again motivated by the existence of scaling for the spin asymmetry in tip bremsstrahlung emission [48], the following scaling property of the Sherman function for collision energies above 50 MeV is conjectured:
which implies the same angular scaling, but with reversed scaling of the magnitude of S as the DCS appears in the denominator of S (see (7) with (2)).
Figure 20a shows the result of this scaling for Pt and Pd, which holds for an angle of up to if MeV, the deviations below being less for the heavier platinum. Unfortunately, the Born approximation is unable to explain the scaling behavior, which may be related to the fact that S vanishes in the first-order Born expression. From the second-order Born expression for S [7,47] we can derive the behavior , in contradiction to the -dependence of (19).
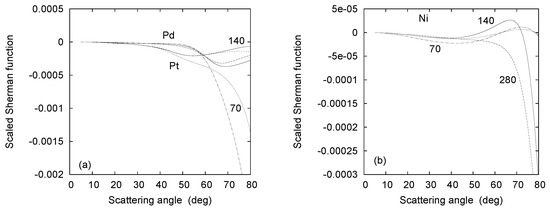
Figure 20.
Sherman function from 140 MeV electron impact (—) on (a) Pd (upper line near ) and Pt (lower line near ) and (b) Ni as function of the scattering angle . Included in (a) are the scaled results (to 140 MeV, according to (19)) for 70 MeV impact on Pd and Pt and for 280 MeV impact on Pd and Pt (short-dashed line). Included in (b) are the scaled results according to (19) for 70 MeV and 280 MeV impact. The scaled results for 70 MeV impact according to Born scaling of the magnitude of are included as well.
An attempt to determine the S-scaling for the lightest target, Ni, for which the Born approximation should be reasonable, is provided in Figure 20b. If performed according to (19), there are considerable deviations in the scaled results from the 70 MeV and 280 MeV impacts when scaled to 140 MeV, even at the smallest angles. Coinciding results (up to ) are found if, for the 70 MeV case, the scaling prefactor (0.0727) is derived from the behavior, in contrast to the result (0.125) obtained from scaling. This finding indicates that the scaling property for S, which is valid at sufficiently small scattering angles, is dependent on .
5. Positron Scattering and In-Plane Spin Asymmetries
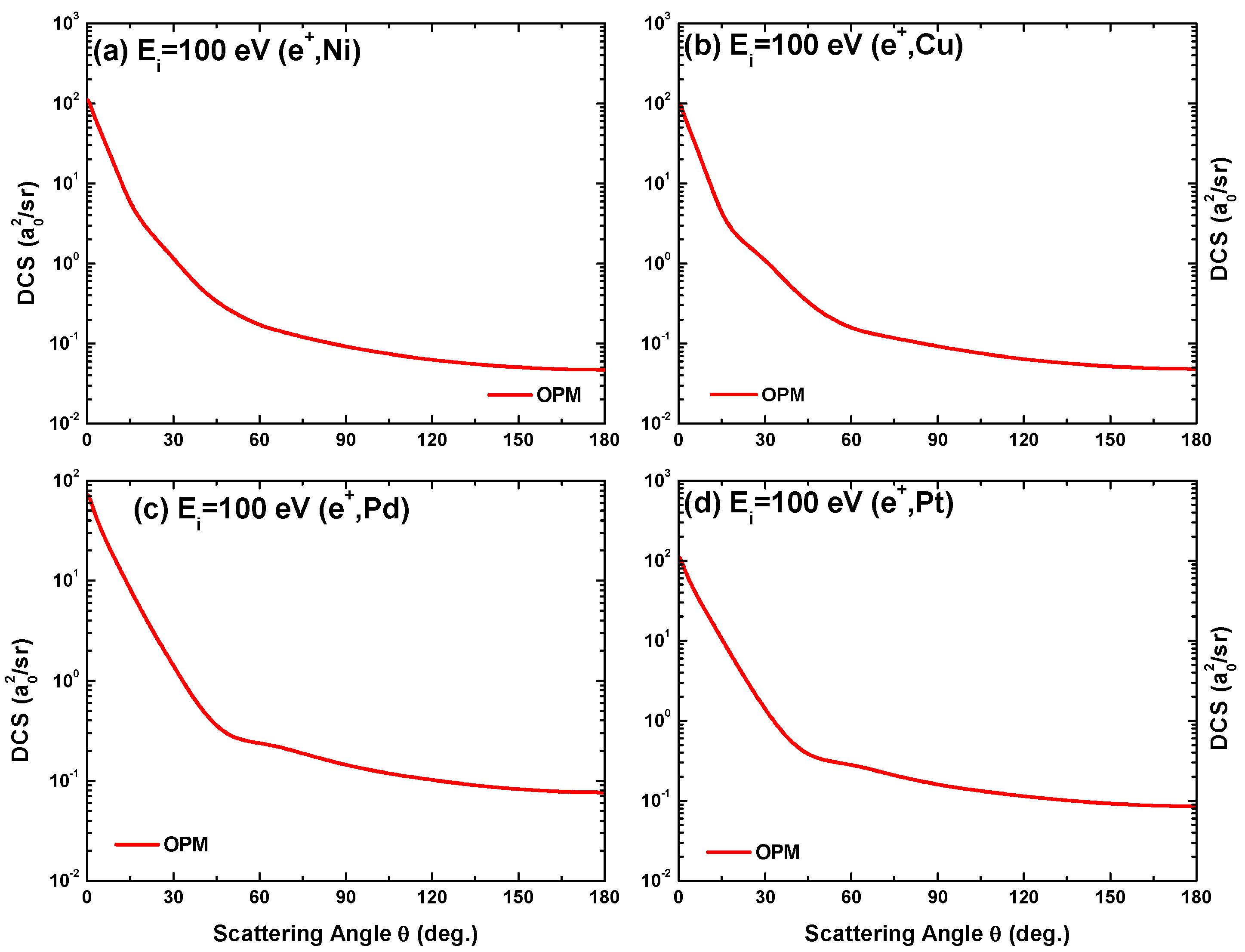
5.1. Angle-Dependent DCS
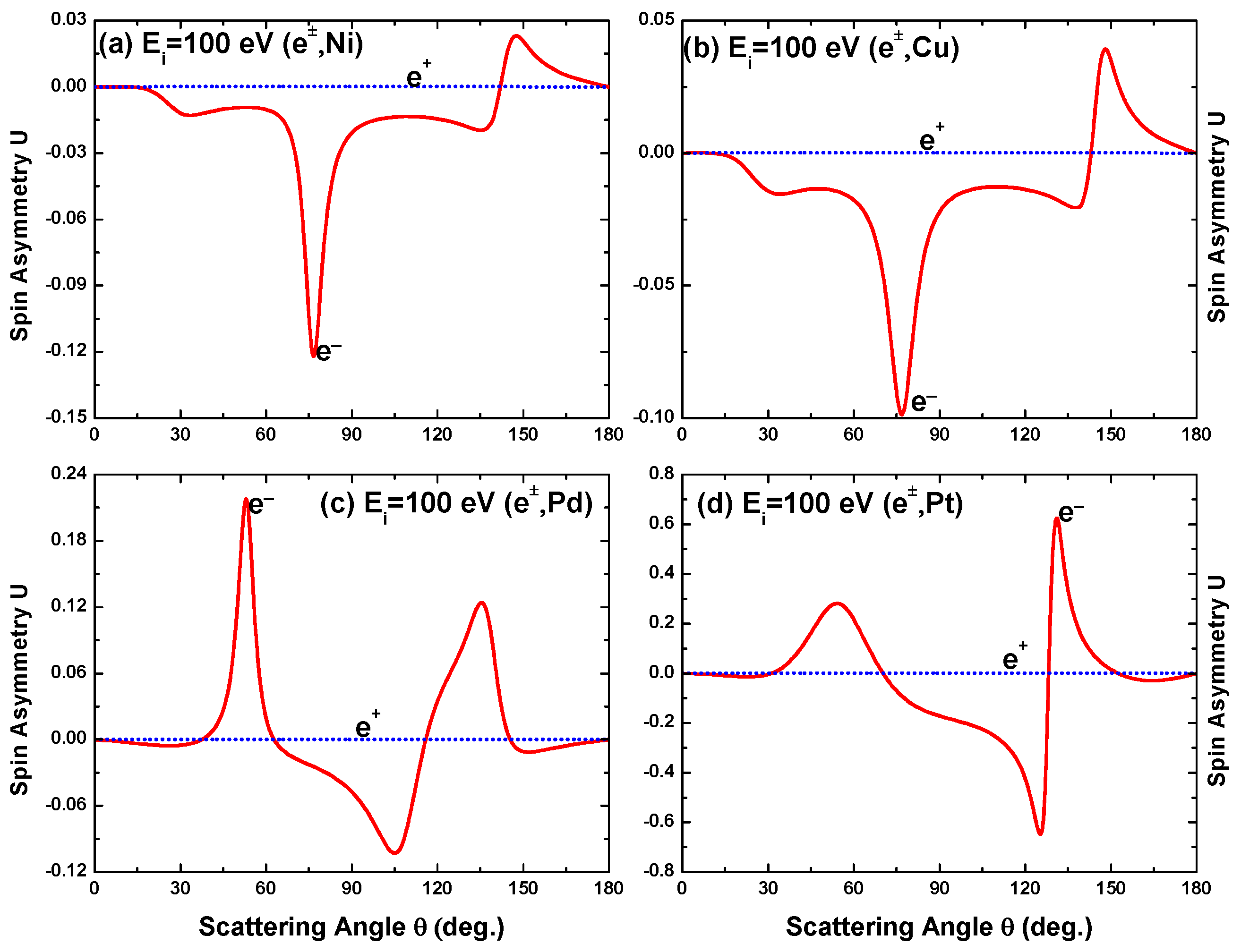
The differential cross sections predicted by our OPM theory for positron scattering from the four metal atoms at impact energies of 100 eV and 500 eV are shown in Figure 21 and Figure 22. It can be seen that, in contrast to electron scattering, the DCS for positron scattering decreases monotonously with increasing scattering angle. In particular, the structures in the DCS seen for electron impacts are either absent or much weaker for positron scattering. This is due to the absence of exchange between the positron and the target electrons and to the differences between electrons and positrons in terms of polarization interaction (see Figure 4, top). Moreover, while electrons are repelled, positrons can trespass the electronic shells without being significantly deflected by the target electrons. The basic origin of the structures, namely, diffraction, is thus suppressed.
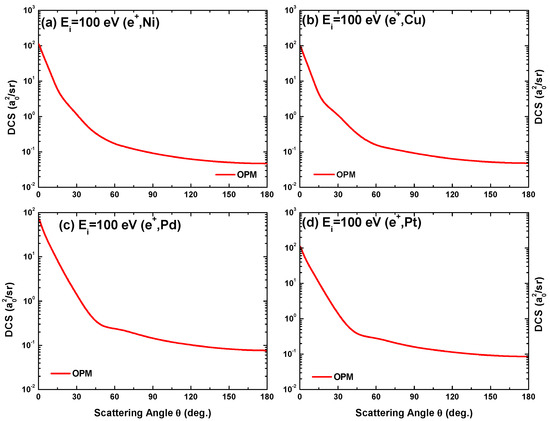
Figure 21.
Angular dependence of the differential cross-sections calculated using our OPM approach for 100 eV positron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt.
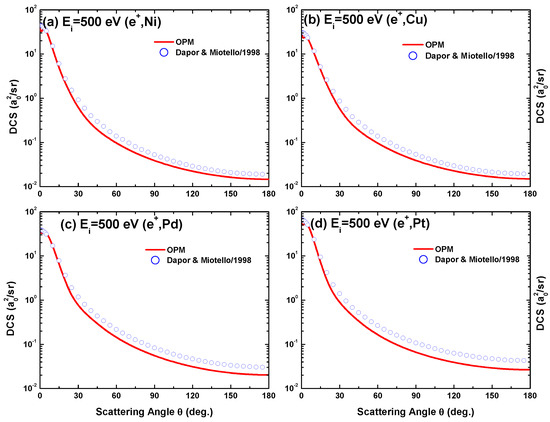
Figure 22.
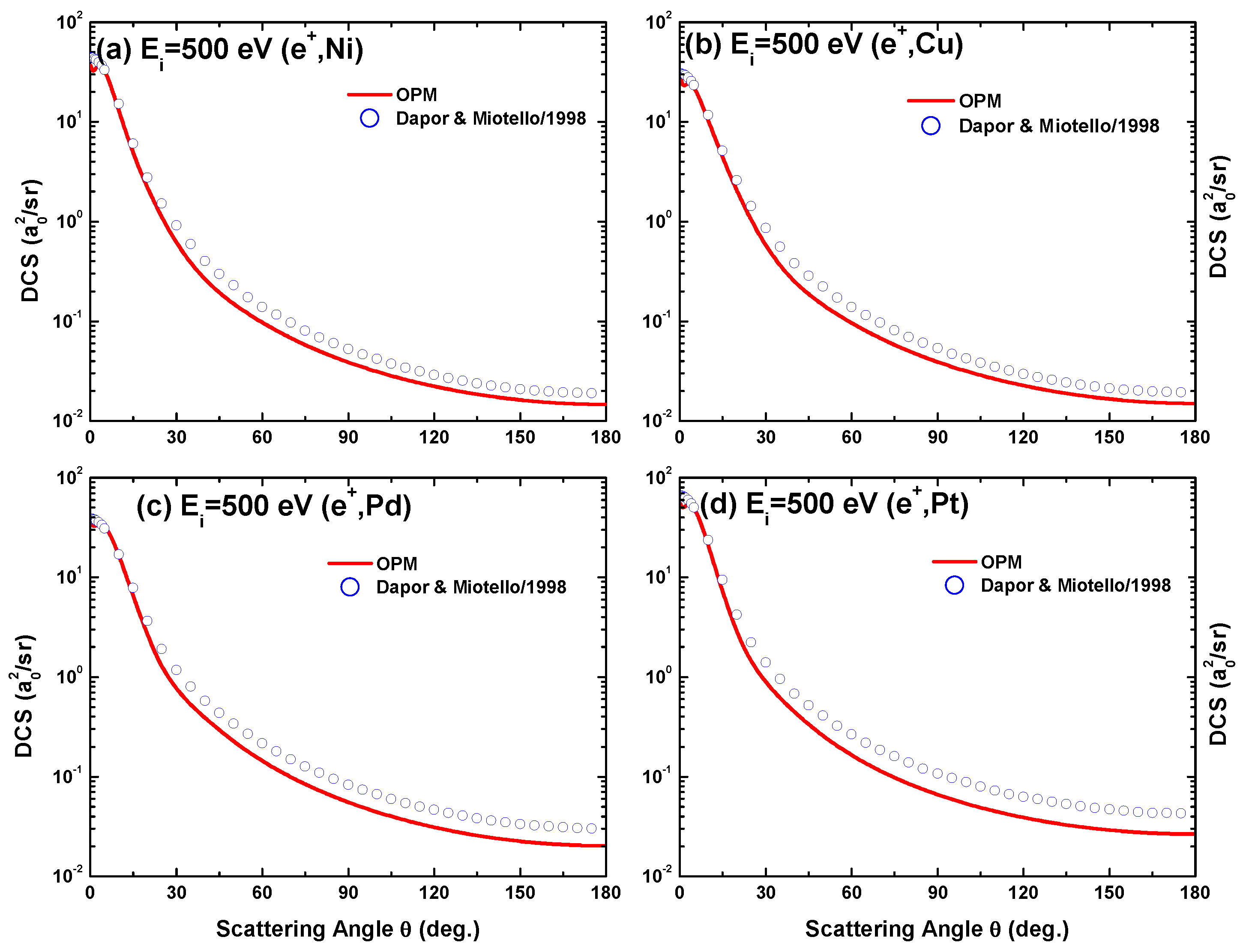
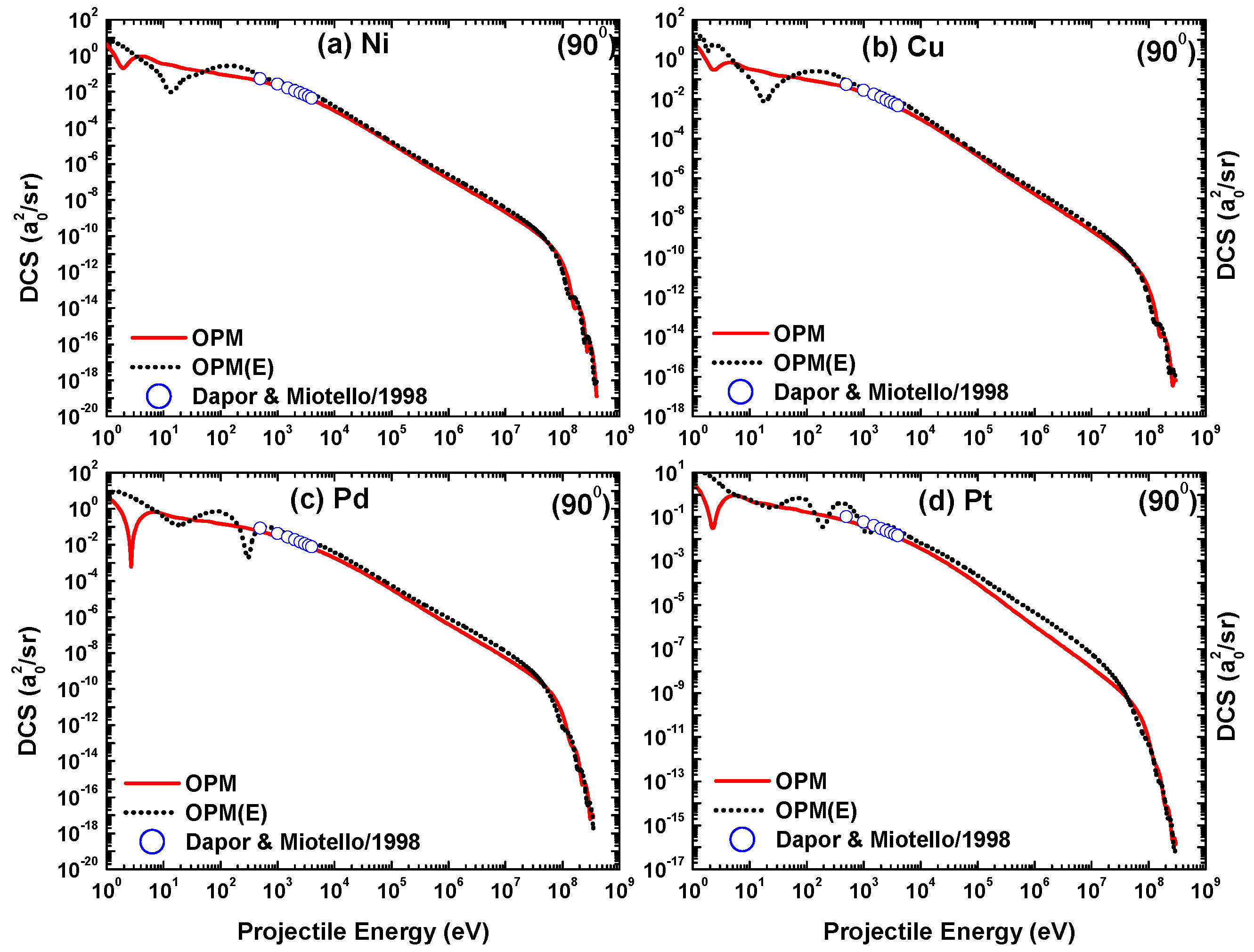
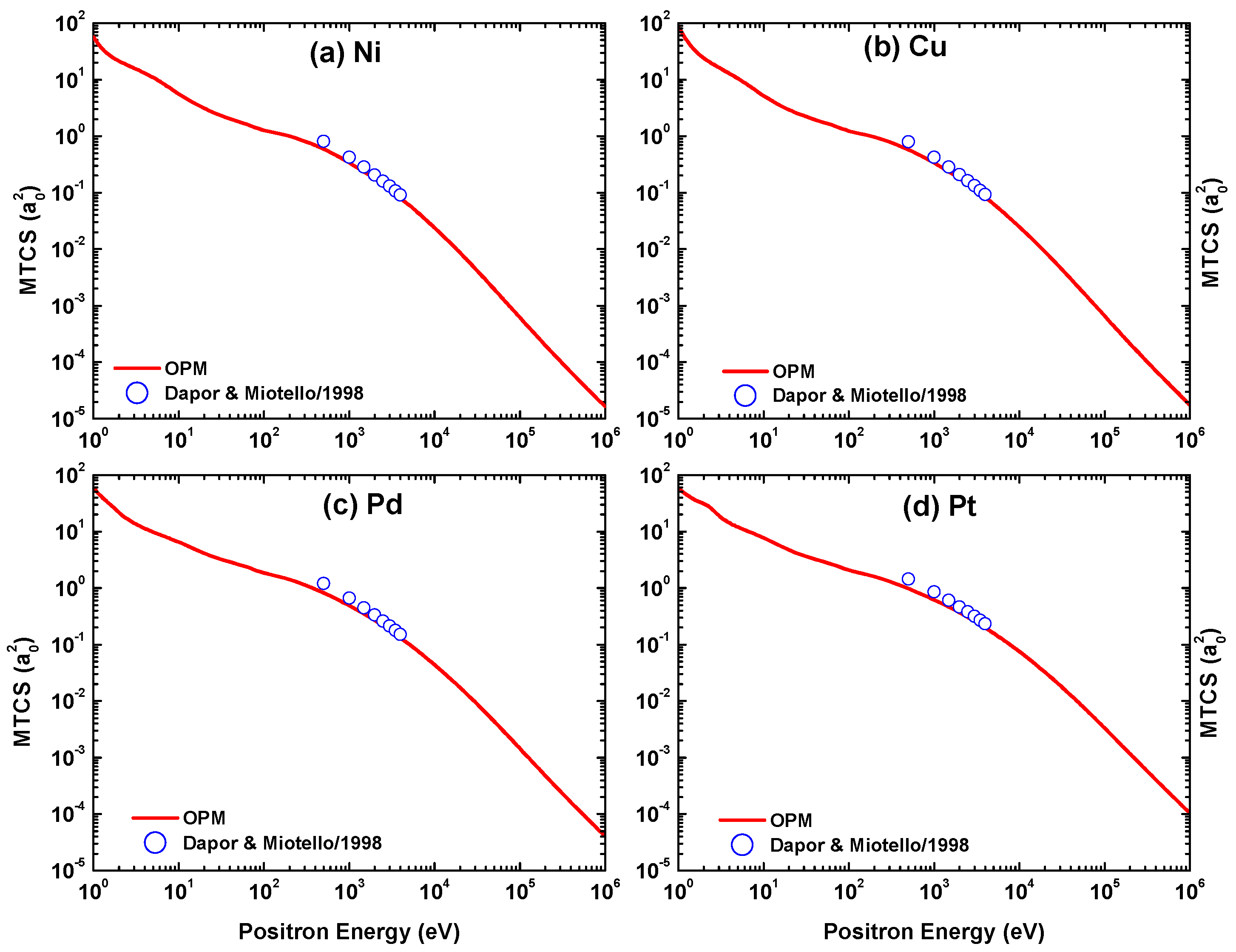
Angular dependence of the differential cross-sections for 500 eV positron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt calculated from our OPM approach in comparison with the results of Dapor and Miotello [50].
Figure 22 includes the theoretical results based on the Dirac–Hartree–Fock–Slater (DHFS) potential of Dapor and Miotello [50]. Our OPM results agree well with those of Dapor and Miotello. However, the structures in the near-forward direction are not reproduced by their calculations. This result shows that the exchange component of the OPM plays an important role in producing interference structures in the DCS.
5.2. Energy-Dependent DCS
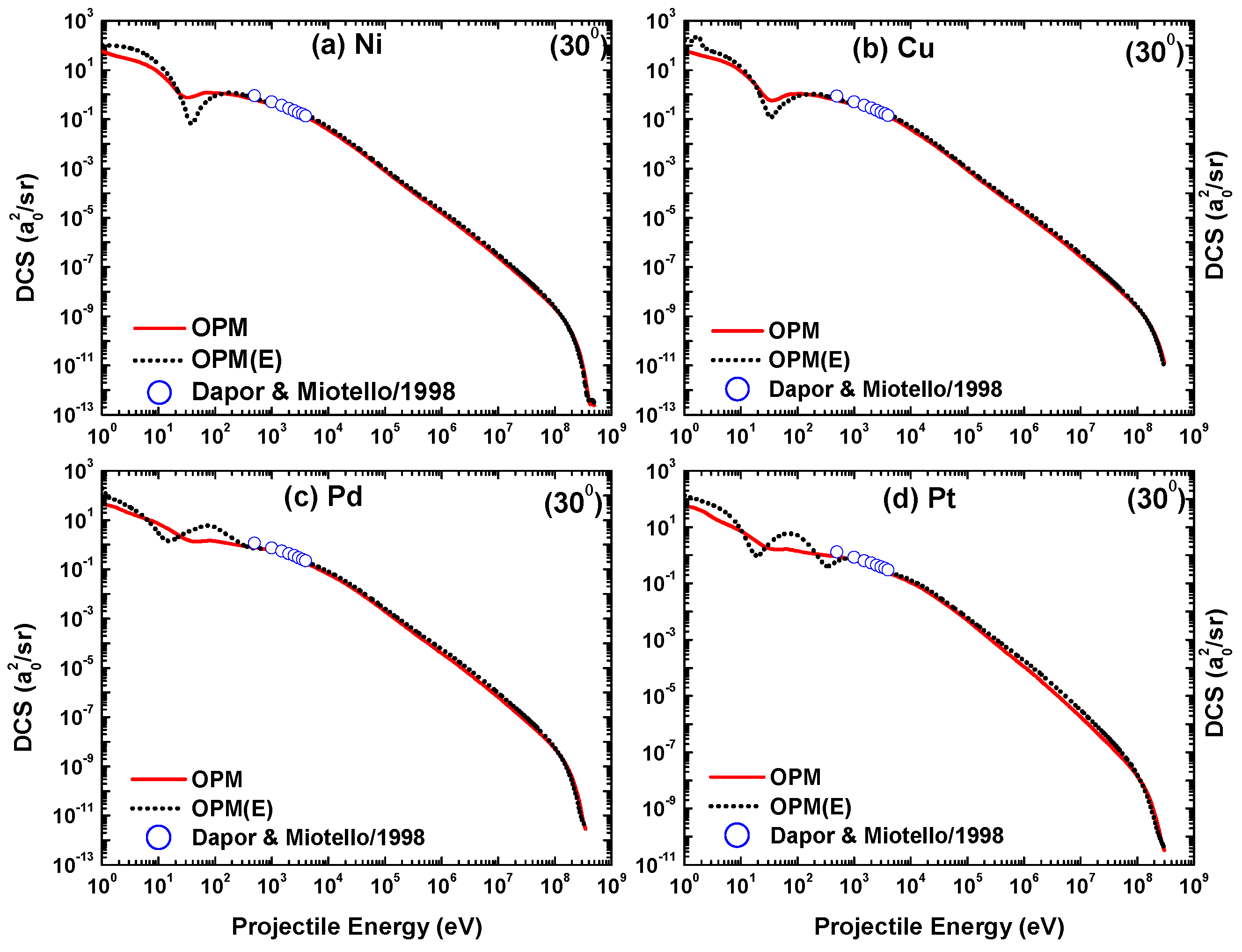
The energy-dependent DCS computed in the 1 eV 0.3 GeV region for positron scattering from the four metal targets is displayed in Figure 23 at and in Figure 24 at . Included are the theoretical results from Dapor and Miotello [50], available for the energy region from 500 eV to 4000 eV. It can be observed from these figures that only one DCS minimum appears in the low-energy (≤30 eV) region. This minimum can be traced back to the influence of the correlation-polarization potential [13]. At , the DCS minima become less pronounced with increasing target size. This situation is basically opposite for the angle of .
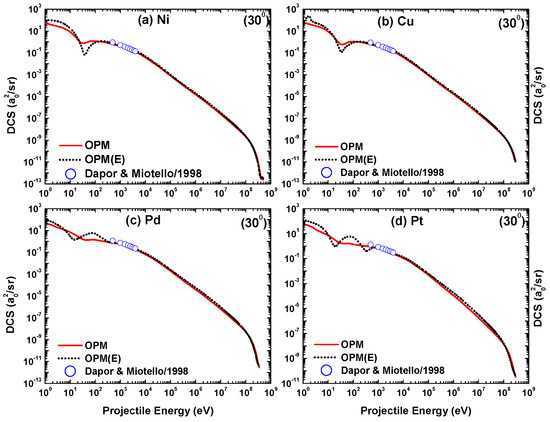
Figure 23.
Energy-dependent differential cross-sections for positron scattering (—) from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle . The calculations of Dapor and Miotello [50] are shown as well. The electron scattering results () from Figure 15 are included here for comparison.
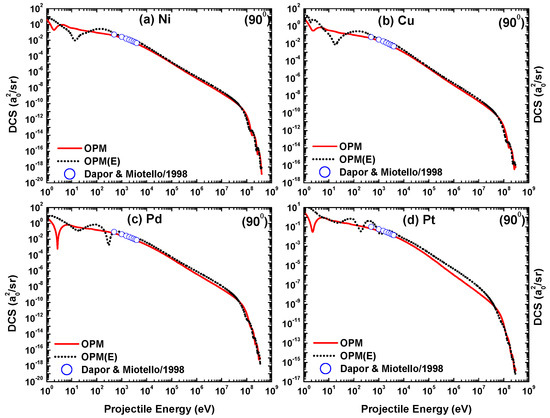
Figure 24.
Energy dependent differential cross-sections for positron (—) scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle . The calculations of Dapor and Miotello [50] are shown as well. The electron scattering results () from Figure 16 are included for comparison.
When compared with the electron impact results, it can be clearly seen that, in the low-energy region, the diffraction structures caused by the interference of projectile electrons scattered from the individual target electrons are suppressed. In the Coulombic region (between 10 keV and 50 MeV), the DCS for both lepton species decreases smoothly, with somewhat lower positron cross sections because of the repulsion between projectile and nucleus. At ultrarelativistic energies, the DCS for electrons and positrons exhibits similar oscillations, which start at a slightly higher energy for positrons due to their larger distance from the nucleus at fixed collision energies.
5.3. Sherman Function
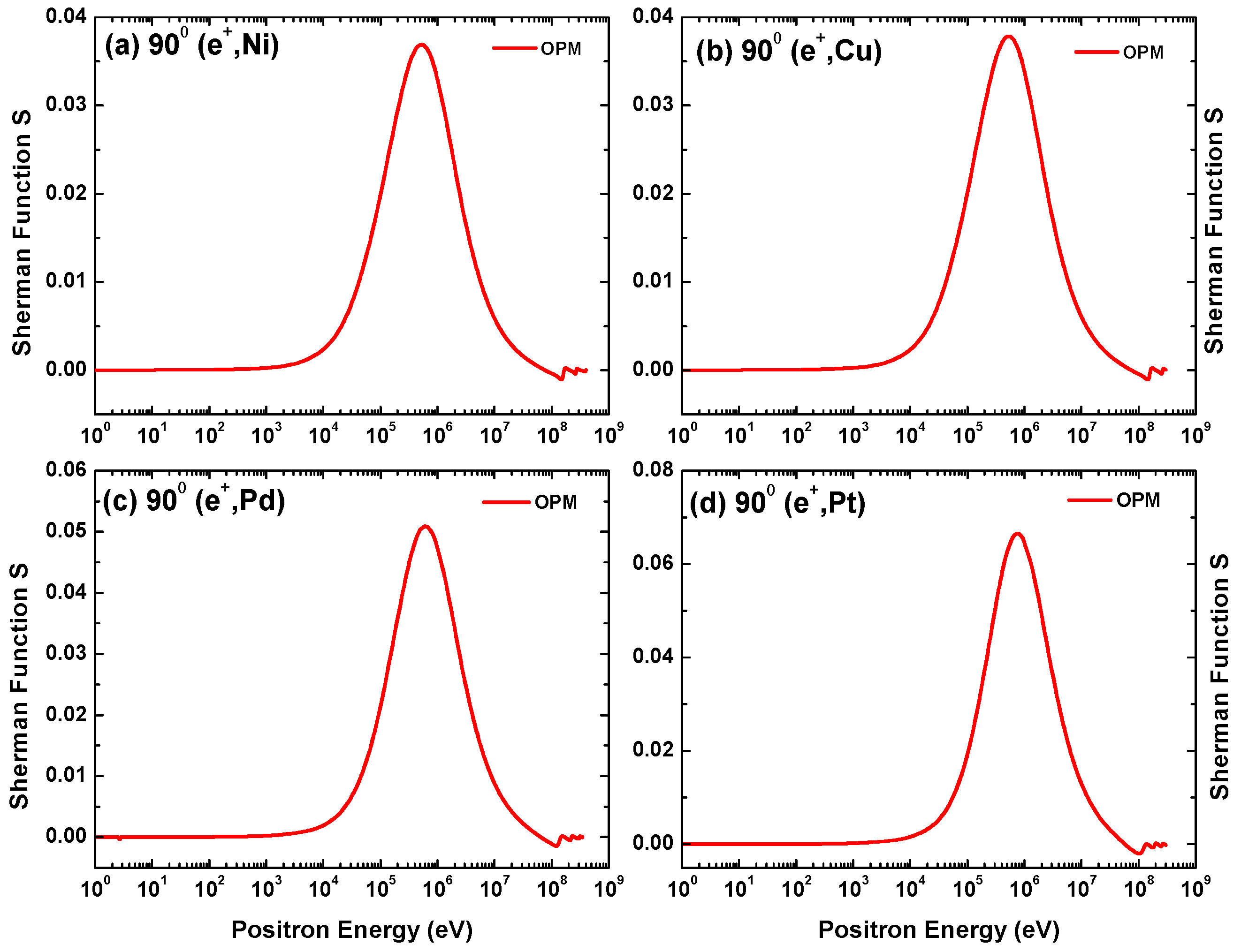
The present results of the Sherman function S for positron scattering from the four metal targets is shown in Figure 25. A fixed scattering angle of and energies from 1 eV to 0.3 GeV were chosen. As is evident in this figure, S for positron scattering is very small compared to its electron counterpart. This strong suppression of the spin asymmetry without showing any significant structure persists up to a few keV. A degree of reduction is to be expected, as at a given energy and angle the positrons experience a repulsive interaction with the target nucleus, preventing them from reaching as close to the nucleus as the electrons. A detailed explanation of the properties of the positronic Sherman function is provided in [13]. At higher energies, reaches a maximum which, while only slightly smaller than that for electron impact, appears at a somewhat higher energy (around 1 MeV) and with an opposite sign. It can be seen that diffraction structures in S, in concord with the DCS, appear at 100 MeV and then persist.
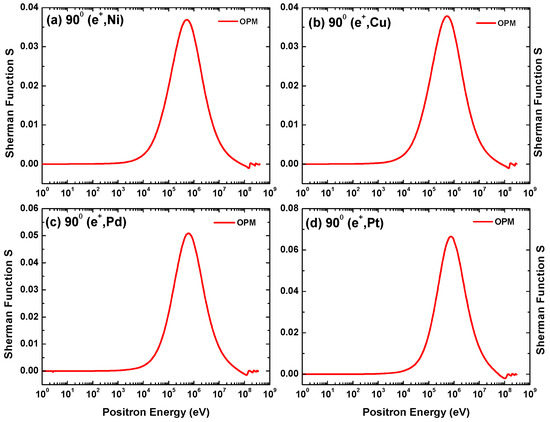
Figure 25.
Energy-dependent Sherman function S for positron scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a scattering angle .
Concerning critical minima for positrons, our previous studies [19] have indicated that they are absent even in the low-energy region. In fact, as the positron spin asymmetry is tiny at small energies (see Figure 25), such investigations are of no relevance from an experimental point of view. Therefore, we have omitted the search for critical minima in the case of positron impacts.
5.4. In-Plane Spin Polarization for Electrons and Positrons
- (a)
- Angular and energy dependence of U and T
Combined with the DCS and the Sherman function, the spin asymmetry parameters U and T provide a complete characterization of the scattering process for a given impact energy and scattering angle in the case of unpolarized targets.
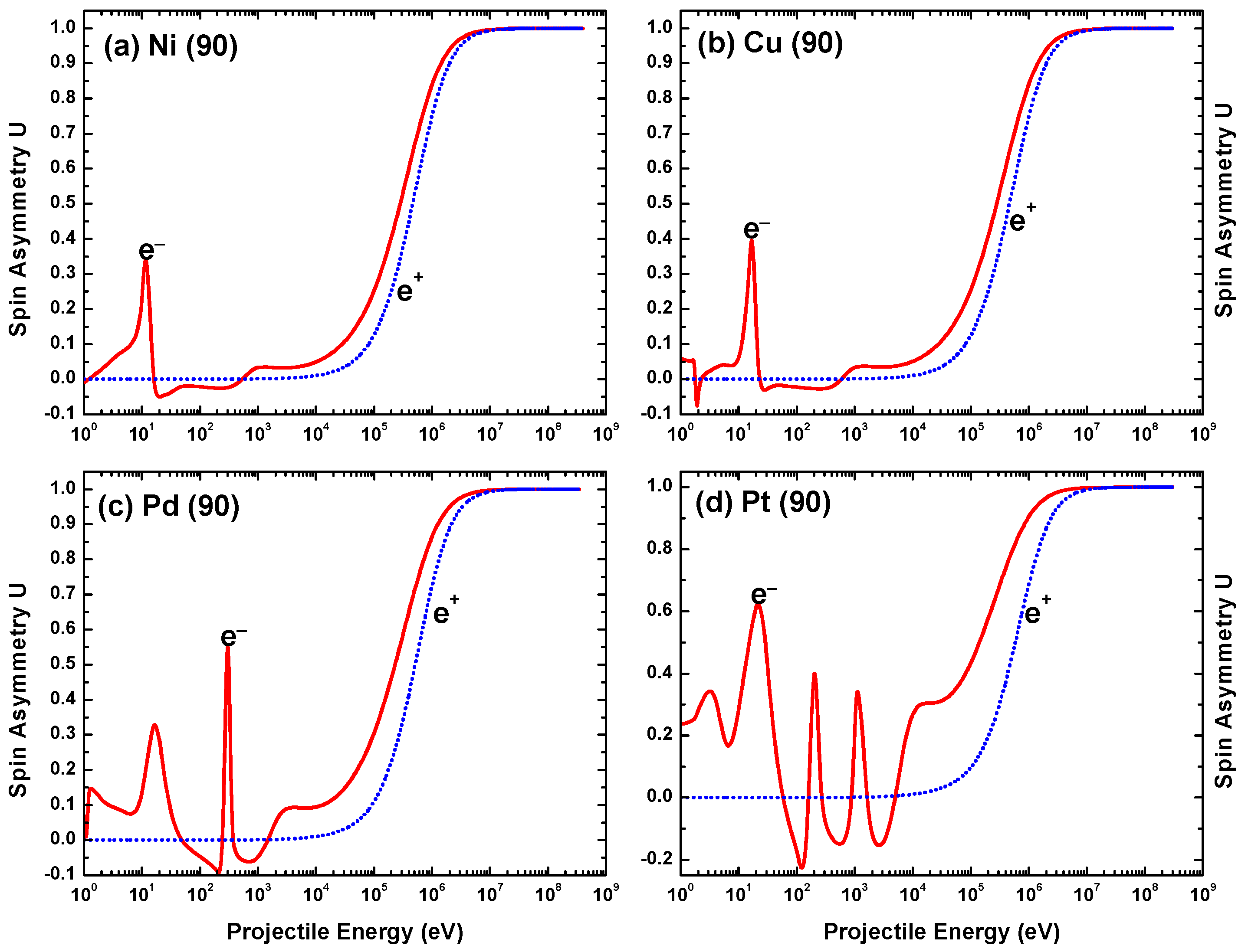
The energy variation of U for both electron and positron impacts on the four metal targets, calculated at , is displayed in Figure 26. For electron impact scattering: (i) U exhibits pronounced oscillations in the low-to-intermediate energy region; and (ii) as for S, the number of oscillations increases as the atomic number of the target material increases. For the positron projectiles, on the other hand, U shows no oscillation and keeps its near-zero value until an impact energy of about 10 keV. Beyond this energy, U exhibits a similar variation with energy for both projectiles, approaching unity at around 100 MeV.
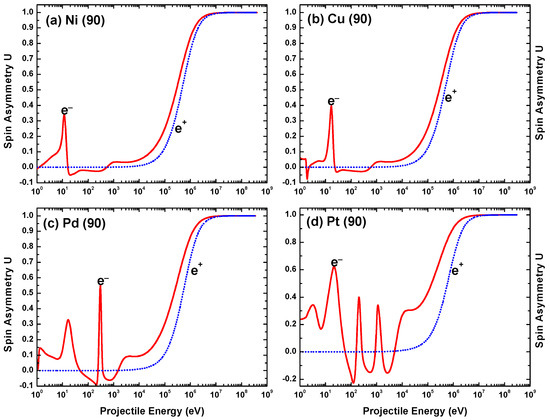
Figure 26.
Energy variation of the spin asymmetry parameter U for both electron (—) and positron () impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at scattering angle .
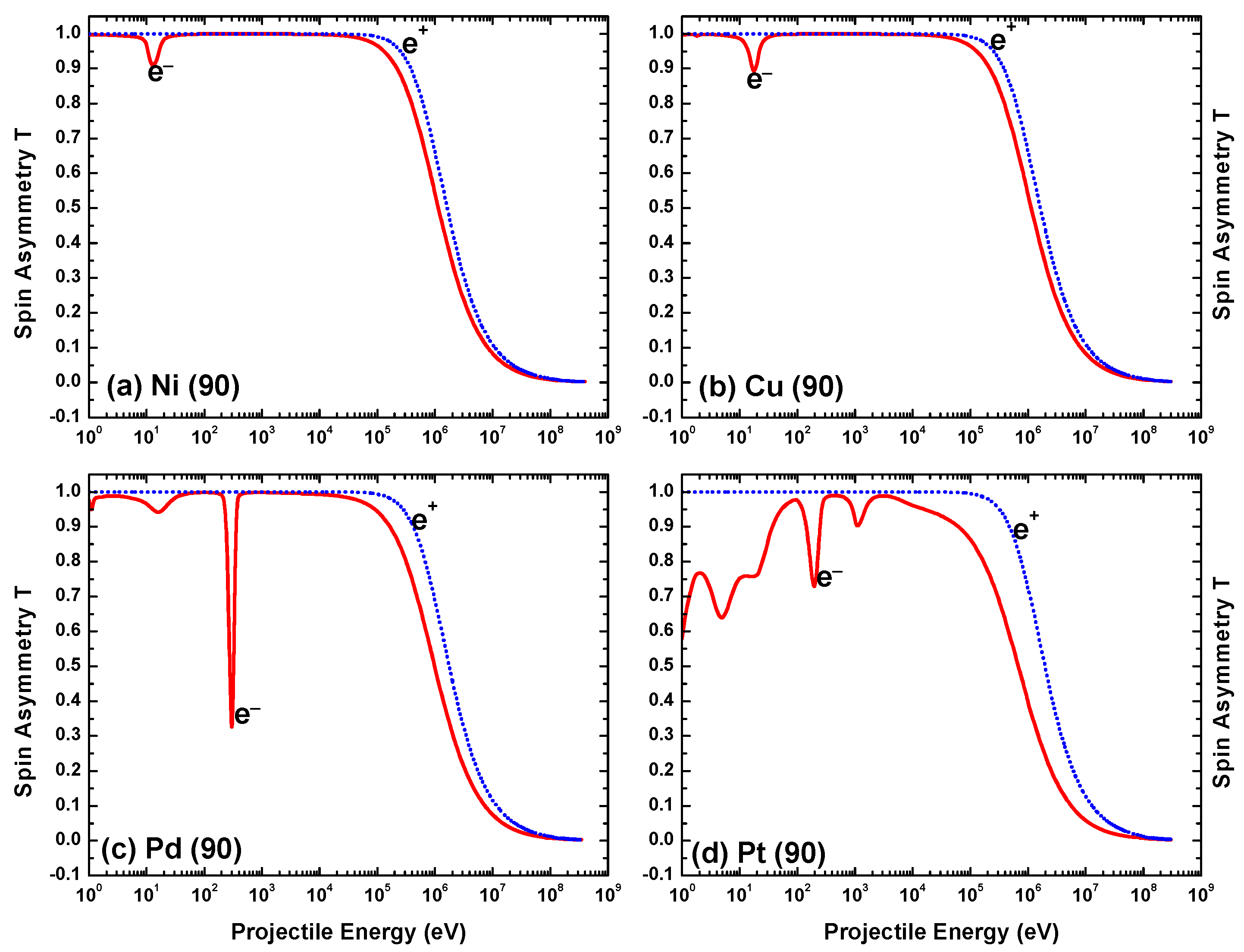
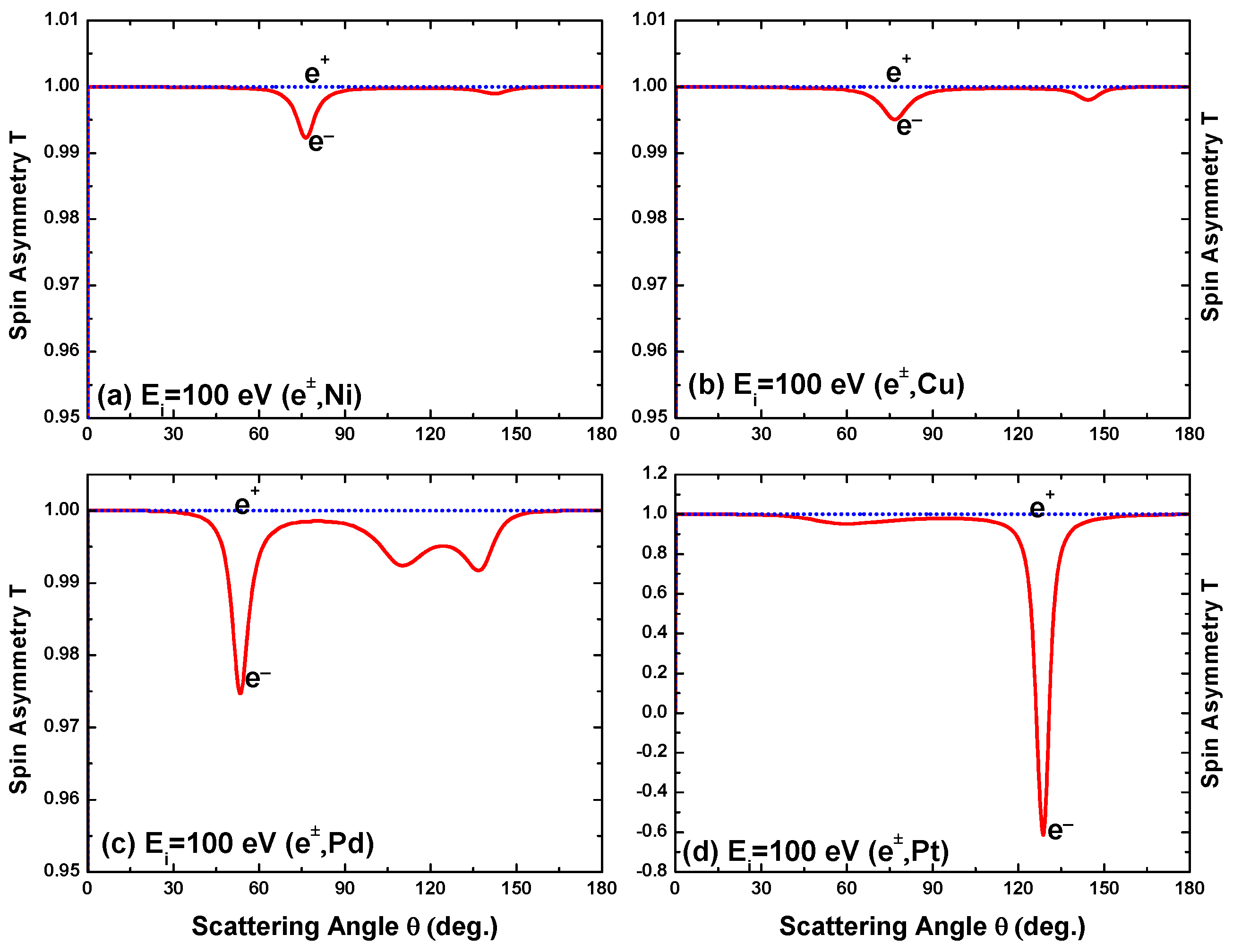
Figure 27 depicts the energy variation of the spin asymmetry, T, for both electron and positron impact scattering. Due to the sum rule, , for the lighter targets T is mostly close to unity in the low-energy regime where S and U are small. As is the case for U and S, structures appear in T at lower energies in the case of electron scattering, and the number of oscillations increases with the size of the target. For both projectiles, the high-energy behavior of T is opposite to that of U. While U increases with projectile energy, T decreases with increasing energy. Asymptotically, U tends to 1 while T tends to 0. This is, however, specific for the scattering angle of . Again, the energy dependence for electrons and positrons is similar in the energy region above 0.1 MeV, although in this case the difference increases with .
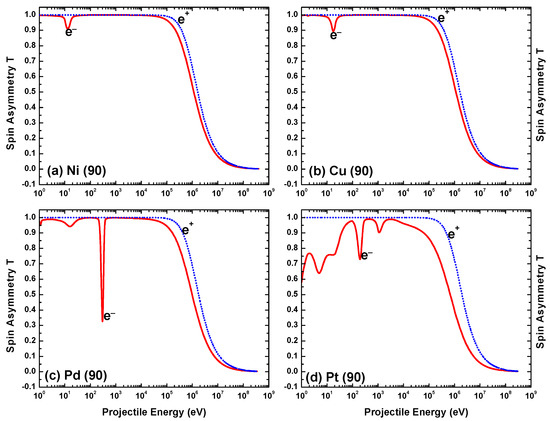
Figure 27.
Energy variation of the spin asymmetry parameter T for both electron and positron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at scattering angle .
The angular dependence of U and T for a collision energy of 100 eV is displayed in Figure 28 and Figure 29. For positron impacts, and irrespective of angle and target, while it can be seen that for electron impacts the deviation of T from this limiting value is considerably smaller than that of U (except for the heaviest atom), confirming the greater sensitivity of U to the details of the theoretical model. In fact, for the heavier atoms the location and size of the structures of U are quite similar to those in S at the same energy (Figure 11), pointing to a similar susceptibility of both U and S to the extremum structure of the DCS.
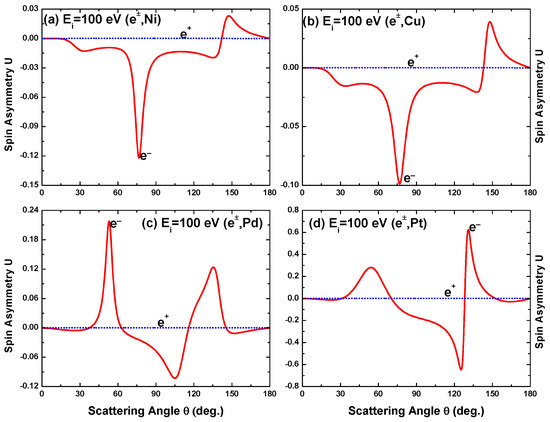
Figure 28.
Angular variation of the spin asymmetry parameter U for e scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a collision energy of 100 eV. (—, red), electrons; (, blue), positrons.
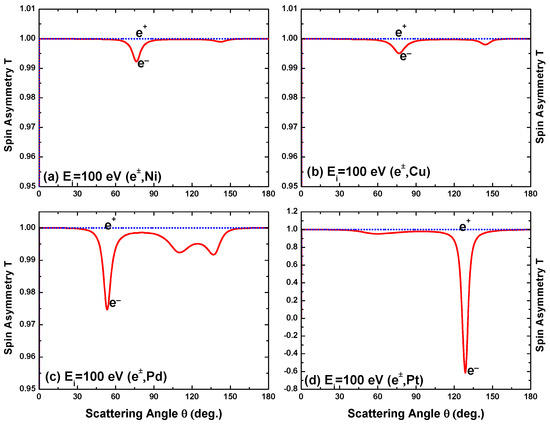
Figure 29.
Angular variation of the spin asymmetry parameter T for e impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt at a collision energy of 100 eV. (—, red), electrons; (, blue), positrons.
- (b)
- High-energy scaling of U and T
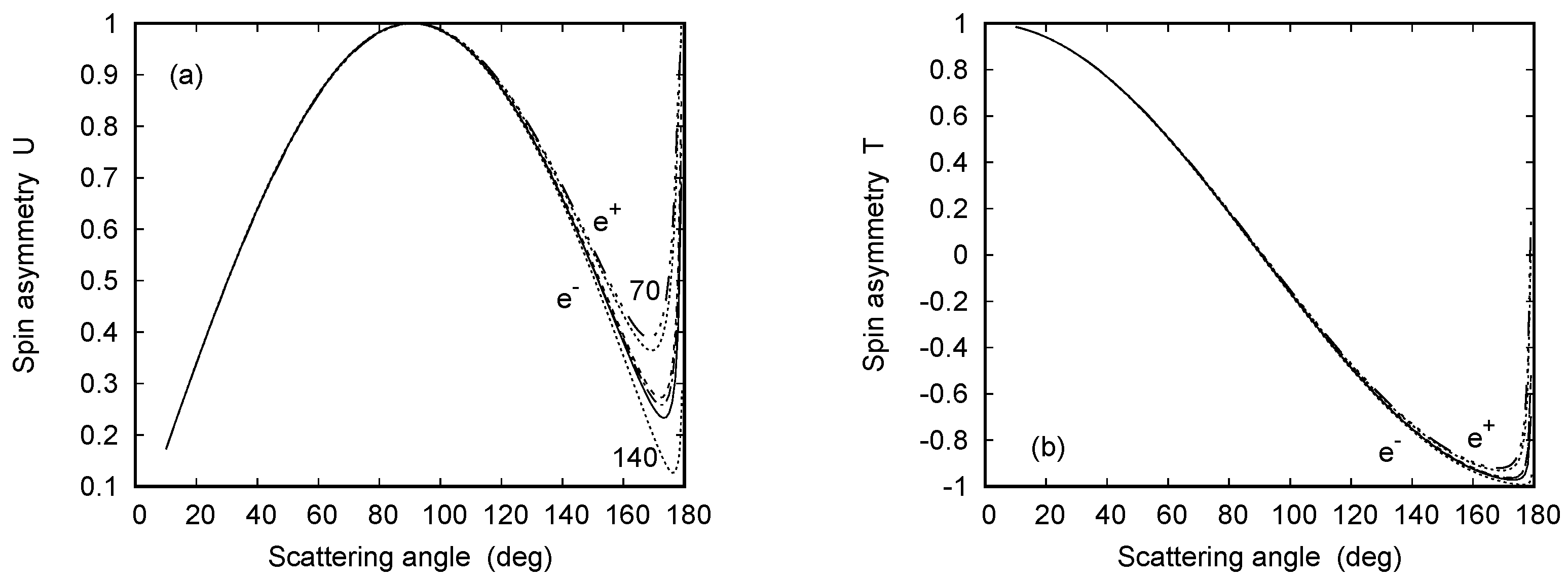
As with the DCS, the two polarization correlations T and U scale for . Moreover, they are effectively independent of and for angles below . This is shown in Figure 30, which depicts their angular distribution for the three target atoms Ni, Pd, and Pt resulting from electron and positron scattering.
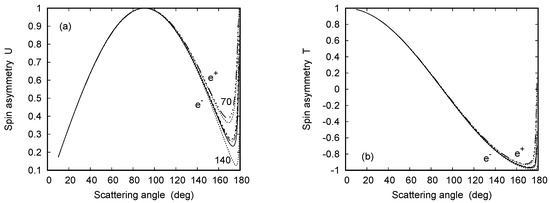
Figure 30.
(a) Spin asymmetry U and (b) spin asymmetry T as functions of the scattering angle . Shown are results for 70 MeV electron scattering from Ni, Pd, and Pt (—), as well as for 70 MeV positron scattering from Ni, upper line) and Pt. Included are results for 140 MeV electron scattering from Pt, lower line).
In contrast to the Sherman function, U and T do not vanish in the first-order Born approximation. Therefore, similar to the DCS, the Born approximation for U and T is employed to derive the scaling property, which postulates a weak dependence on energy and independence, as follows [7]:
where and . Because these expressions are independent of , they are valid for positrons as well. For and , they reduce to
independent of . The Born limit (21) reproduces the asymptotic behaviour of U and T from Figure 26 and Figure 27. Moreover, it follows from Figure 30 that the behaviour (21) is to a high degree valid in the forward hemisphere, and the validity regime extends to larger angles as increases. We note that this basic -independence does not hold for the equivalent spin asymmetry parameters R and L, which are linear combinations of T and U [7].
6. Integrated Cross-Sections and Mean Free Paths
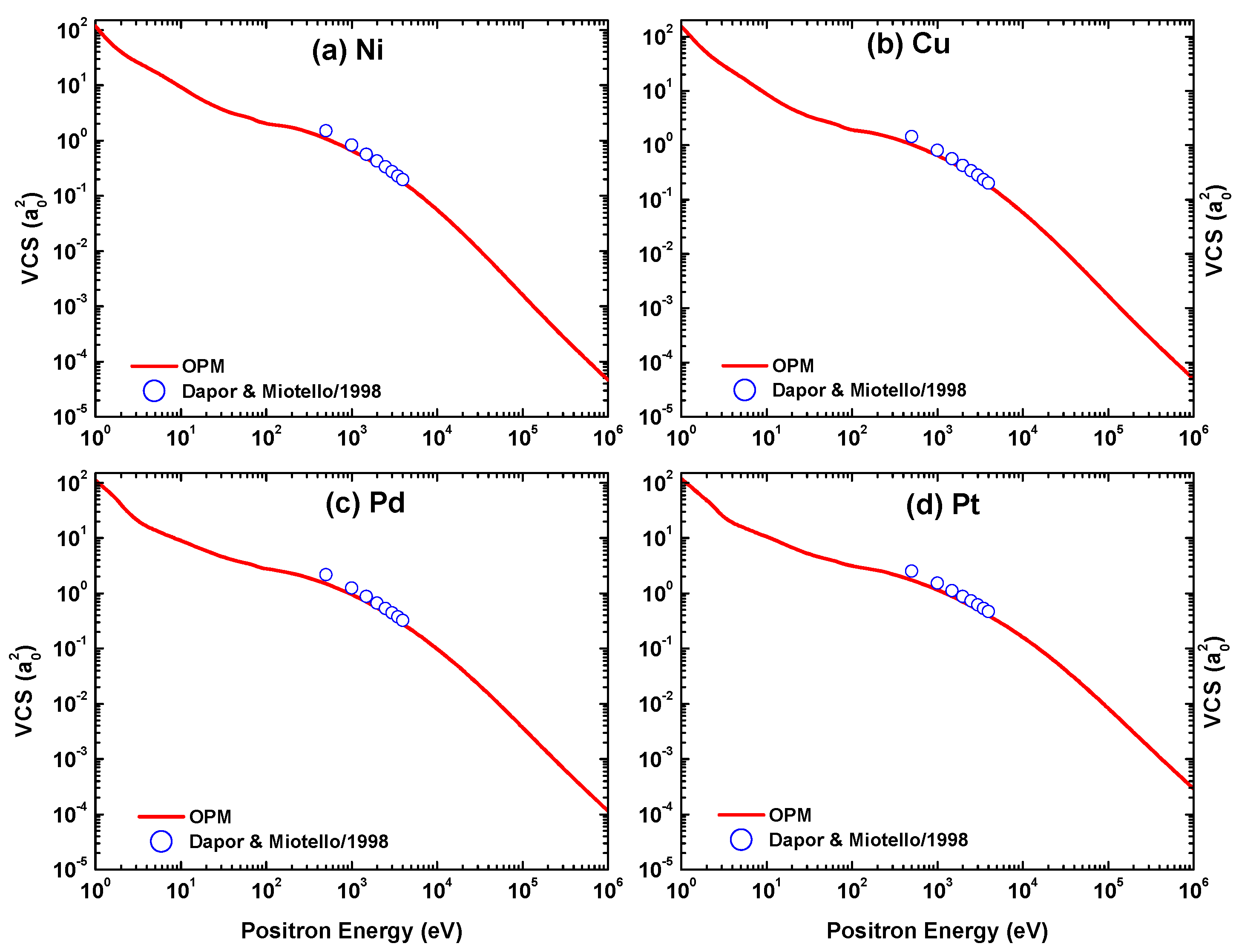
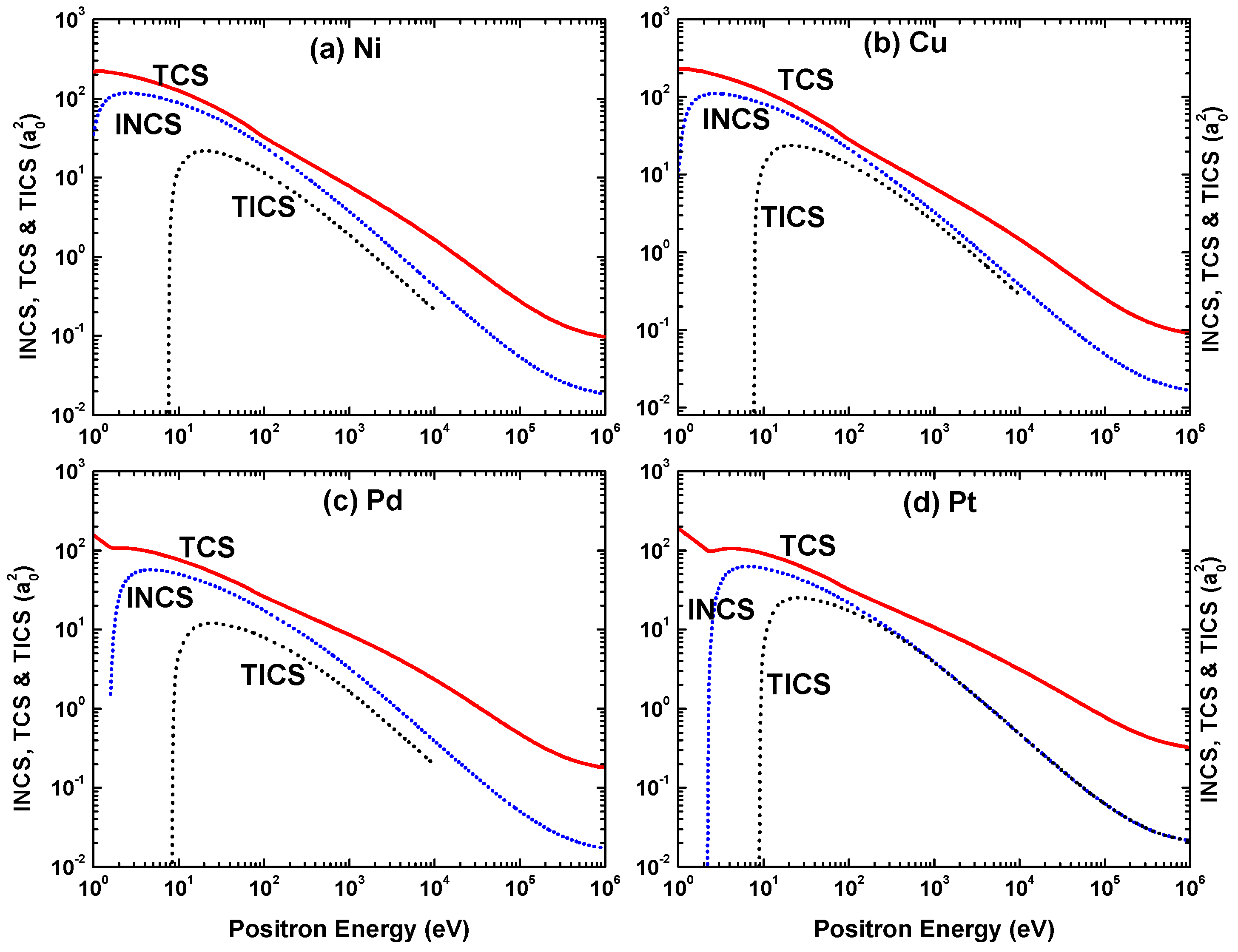
This section furnishes further scattering observables: the integrated elastic cross-section (IECS) and inelastic cross-section (INCS), the momentum-transfer cross-section (MTCS), the viscosity cross-section (VCS), the total cross-section (TCS), and the total ionization cross-section (TICS), as defined in (3)–(5) and (10)–(12), for scattering of both lepton species from the four metal targets. These quantities have paramount importance in dense media and solid-state physics. For example, the IECS provides an estimate of the mean free path between two elastic collisions, and the VCS is used as an input in Monte Carlo simulations of electron transport in solids. In the following subsections, we first present the above scattering characteristics for electron scattering, then discuss the results due to positron impacts.
6.1. Integrated Cross-Sections for Electron Scattering
For the incident electron energies eV, the present OPM calculations of the IECS, MTCS, VCS, INCS, and TCS for the four metal targets are shown in Figure 31, Figure 32, Figure 33 and Figure 34. For the Cu target, our IECS and MTCS results can be compared with the experimental data of Trajmar et al. [37]. The comparison shows that the present OPM predictions of IECS and MTCS roughly reproduce the energy dependence of the experimental cross-sections [37], with the exceptions of overestimation of the IECS near 6 eV and 60 eV (Figure 31b) and underprediction of the MTCS around 20 eV (Figure 32b).
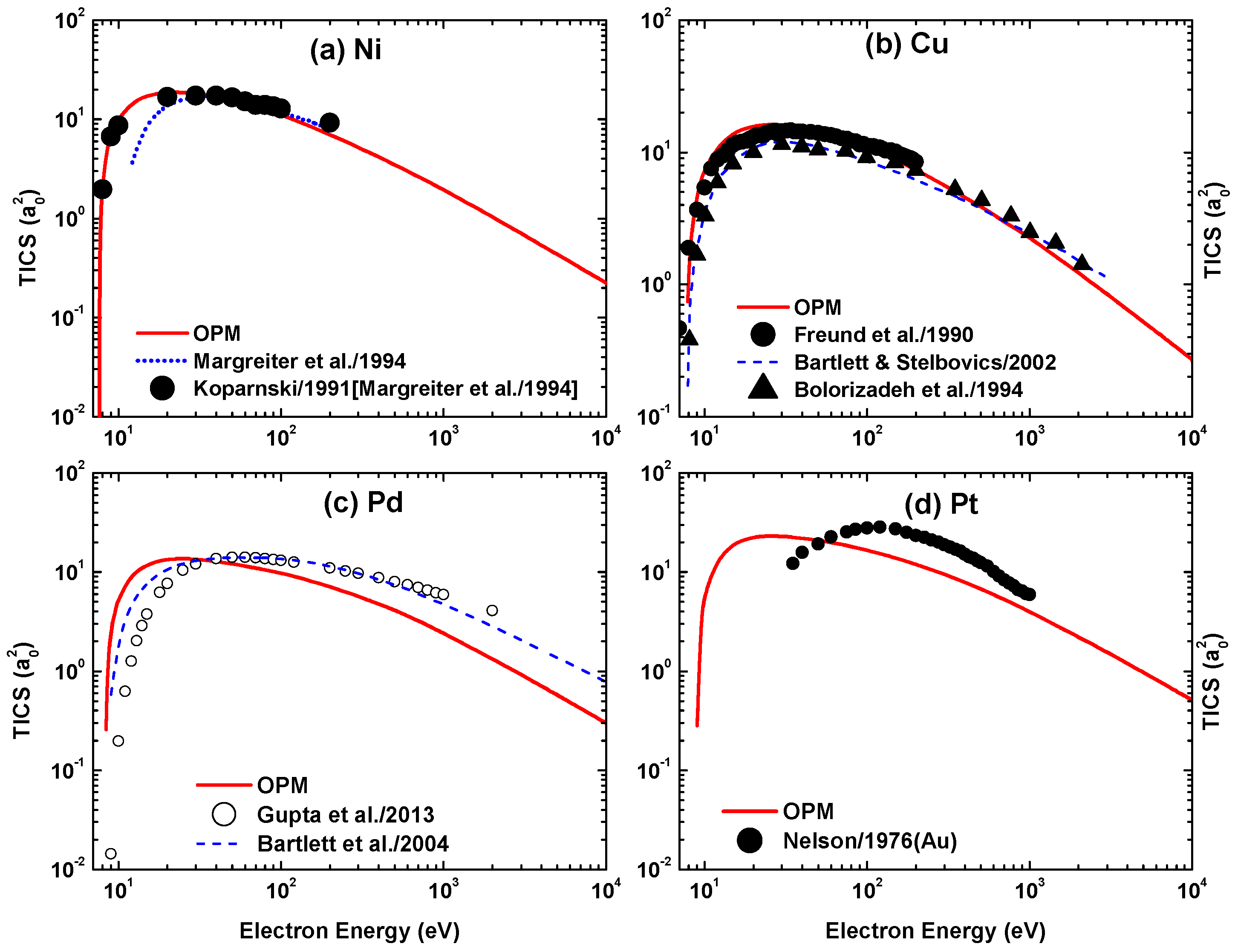
Figure 35 shows our TICS results for electron scattering from the four metal targets in the energy range eV. Included are calculations with the semiclassical approach (DM formalism) of Margreiter et al. [51] for Ni at 10–200 eV, the Hartree–Fock–Slater approach of Bartlett and Stelbovics [52] for Cu at 3 keV, and the SCOP of Gupta et al. [53] and Roothaan–Hartree–Fock–Slater method of Bartlett et al. [54] for Pd at 10 keV. The theoretical results are compared with the data from Koparnski reported in [51], Freund et al. [55], Bolorizadeh et al. [56], and Nelson [57]. In Figure 35a, it can be seen that the present TICS results for Ni are in excellent agreement with the data of Koparnski, whereas the calculations of Margreiter et al. [51] underestimate them significantly in the energy domain of 10–40 eV. For the Cu target (Figure 35b), both our predictions and those of [52] show good agreement with the experimental results [55,56]. For the heavier targets, however, there are serious discrepancies with the experimental data. In particular, the present calculations for Pt, as shown in Figure 35d, differ from the data [57] in the peak position. These measurements were actually carried out for the neighboring Au target; however, judging from the similar TICS energy distributions for the two adjacent atoms Ni and Cu, the Pt atom seems to be well represented by Au. In the case of Pd (Figure 35c), our calculated position of the TICS maximum is lower in energy than the theoretical predictions of Gupta et al. [53] and Bartlett et al. [54].
From a physical point of view, it is indeed to be expected that the peak of the ionization cross-section moves to a higher collision energy with . In fact, ionization will be maximal if the energy of the impinging electron matches the binding energy of the electron shell from which the electrons are predominantly ejected. For Ni and Cu, this is the M-shell, for Pd it is the M- and N-shells, and for Pt it is the N- and O-shells. On average, these shells are more tightly bound as increases. The deficiency of our theoretical model seems to originate from the rather crude estimates in (13) and (14) used to calculate .
Figure 31, Figure 32, Figure 33 and Figure 34 include the Dirac–Hartree–Fock calculations of Mayol and Salvat [58] of IECS, MTCS, and VCS for all four metal targets available at = – eV, the relativistic static approximation results of Riley et al. [40] of IECS and MTCS for Ni and Cu targets at = 1–300 keV and of Zatsarinny and Bartschat [16] of IECS and MTCS for Cu at = 1–100 eV, and the calculations based on the spherical complex optical potential (SCOP) of Gupta et al. [53] of TCS for Pd at 2000 eV. As seen in these figures, the present calculations yield good overall agreement with the other calculations at energies near and above 100 eV. However, at lower energies there are discrepancies with the results from Zatsarinny and Bartschat [16] and Gupta et al. [53]. In particular, these theories do not yield the structures which appear in our IECS results near 2 eV for Cu and in our TCS results for Pd around 10 eV. The deviation of our results from those of [16] is ascribed to their use of the B-spline R-matrix model, which is more accurate at very low energies.
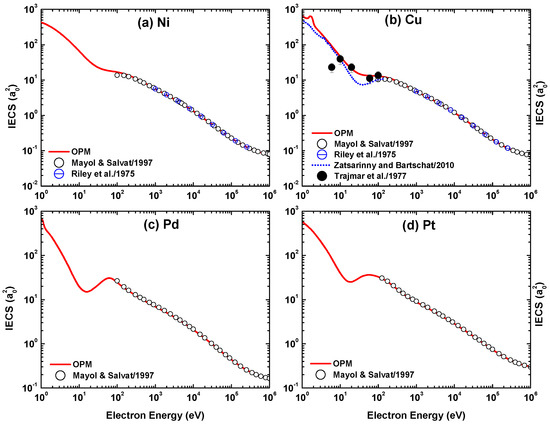
Figure 31.
Energy dependence of the integrated elastic cross-section (IECS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Trajmar et al. [37]. Theory: (—) present OPM approach, (◯) Mayol and Salvat [58], (⊖) Riley et al. [40], and (···) Zatsarinny and Bartschat [16].
Figure 31.
Energy dependence of the integrated elastic cross-section (IECS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Trajmar et al. [37]. Theory: (—) present OPM approach, (◯) Mayol and Salvat [58], (⊖) Riley et al. [40], and (···) Zatsarinny and Bartschat [16].
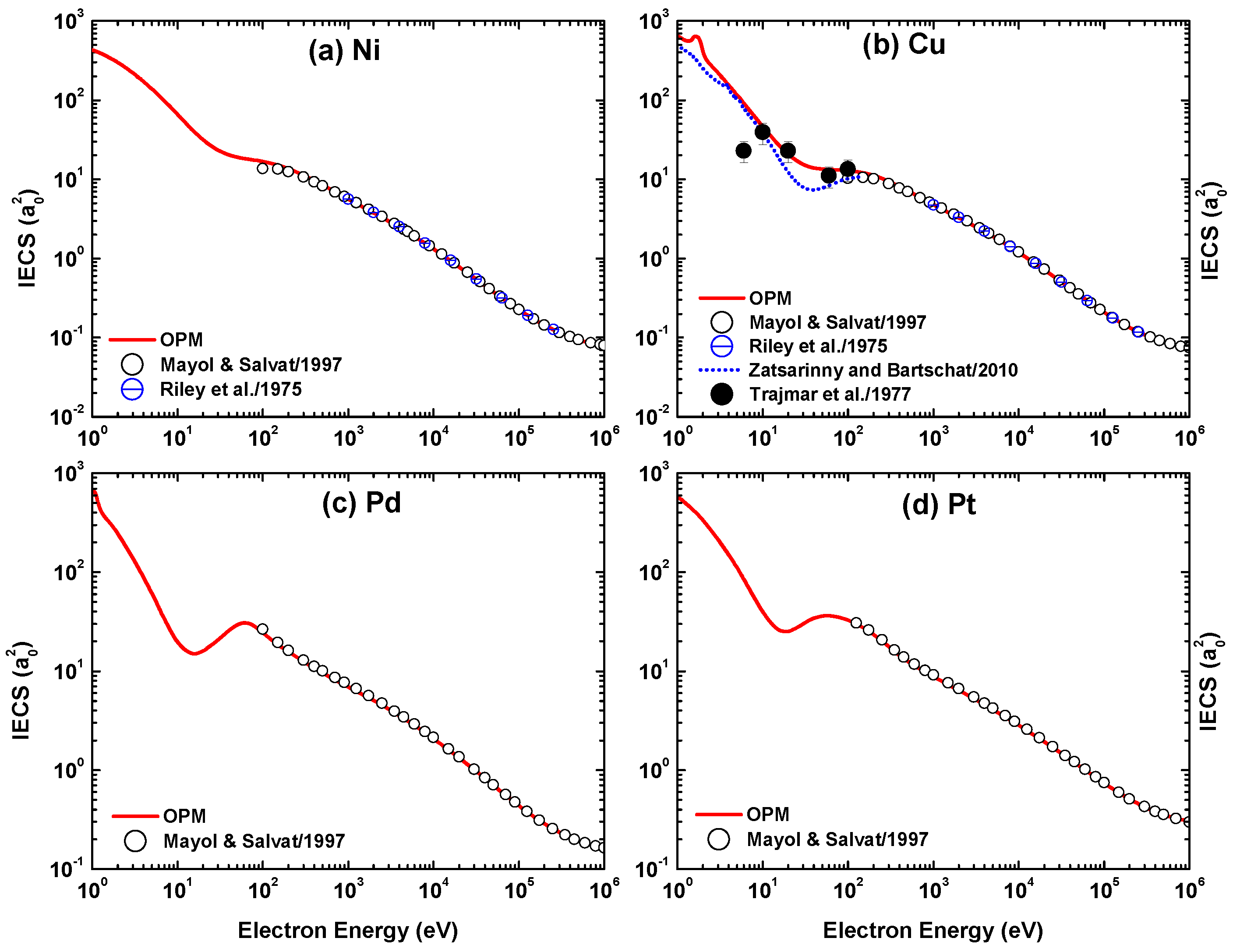
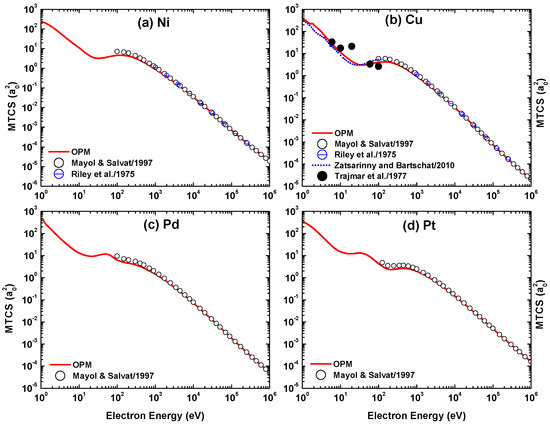
Figure 32.
Energy dependence of the momentum-transfer cross-section (MTCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Trajmar et al. [37]. Theory: (—) present OPM approach, (◯) Mayol and Salvat [58], (⊖) Riley et al. [40], and (···) Zatsarinny and Bartschat [16].
Figure 32.
Energy dependence of the momentum-transfer cross-section (MTCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Trajmar et al. [37]. Theory: (—) present OPM approach, (◯) Mayol and Salvat [58], (⊖) Riley et al. [40], and (···) Zatsarinny and Bartschat [16].
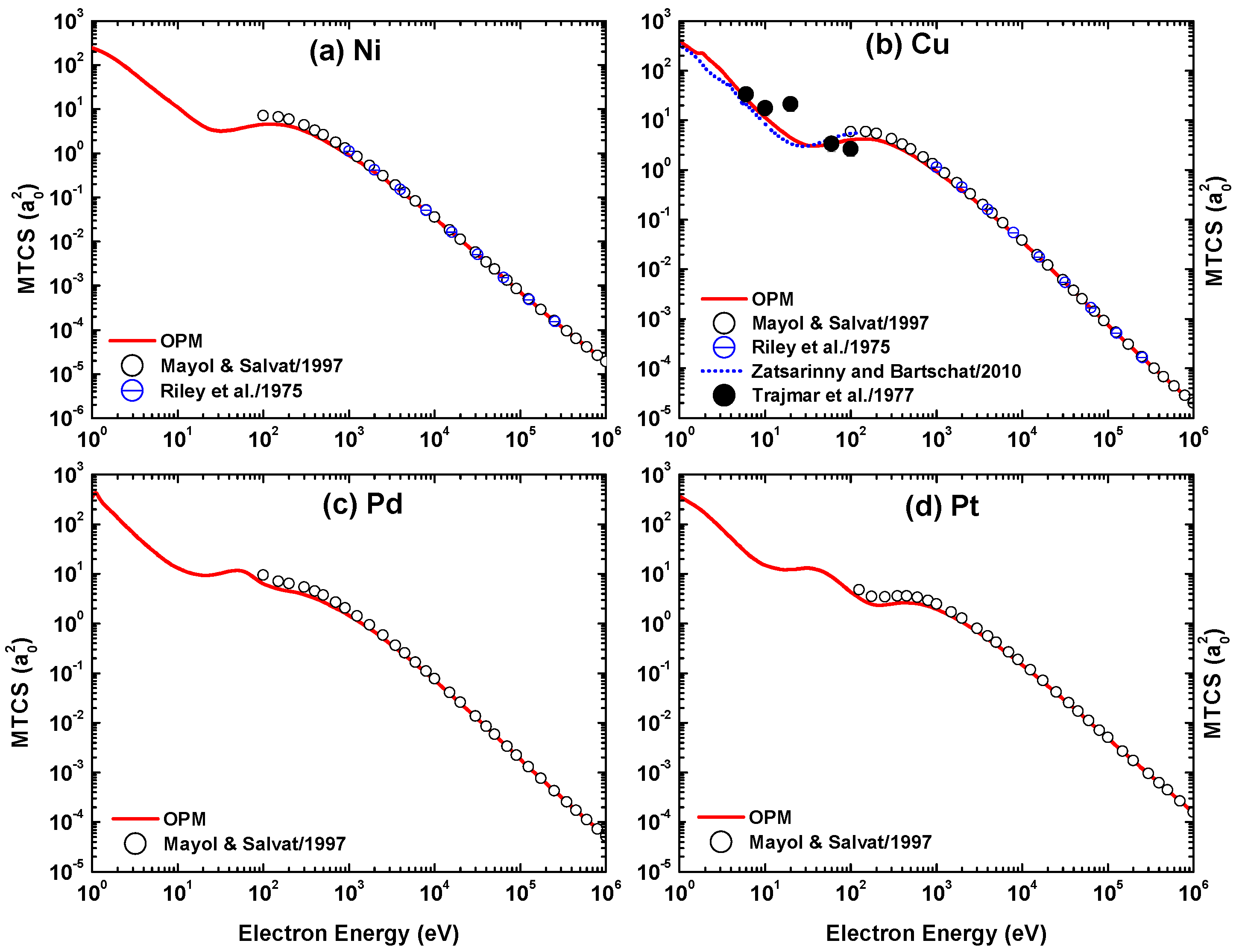
Figure 33.
The present OPM calculations of the viscosity cross-section (VCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt in comparison with the Dirac–Hartree–Fock (DHF) calculations of Mayol and Salvat [58].
Figure 33.
The present OPM calculations of the viscosity cross-section (VCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt in comparison with the Dirac–Hartree–Fock (DHF) calculations of Mayol and Salvat [58].
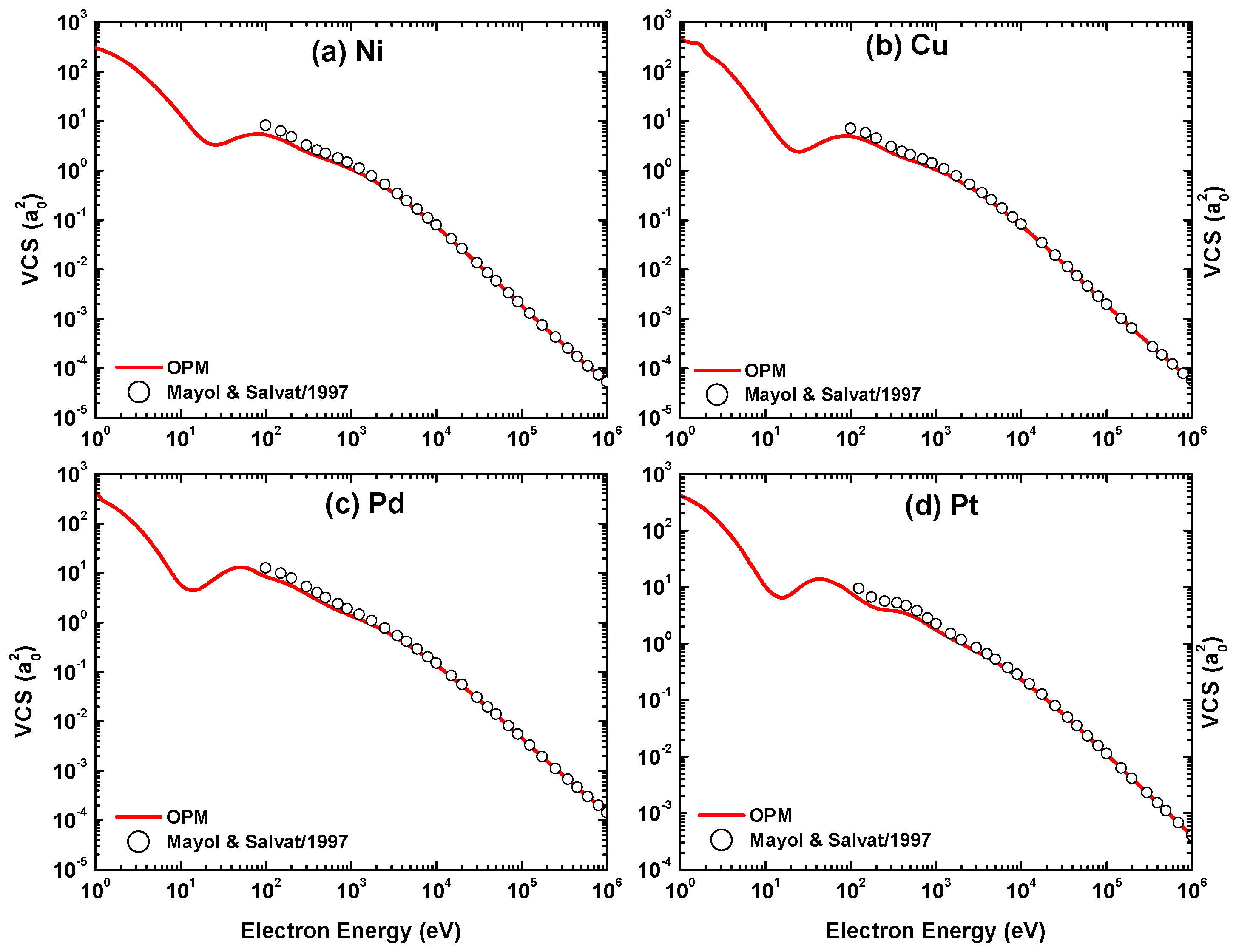
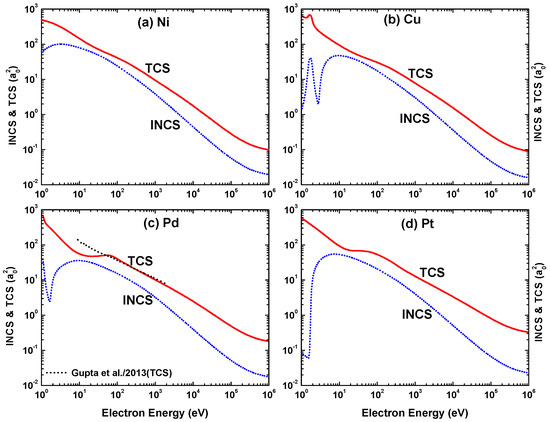
Figure 34.
Energy dependence of the integrated inelastic cross-section (INCS) and total cross section (TCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Theory: (—) present OPM approach and () Gupta et al. [53].
Figure 34.
Energy dependence of the integrated inelastic cross-section (INCS) and total cross section (TCS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Theory: (—) present OPM approach and () Gupta et al. [53].
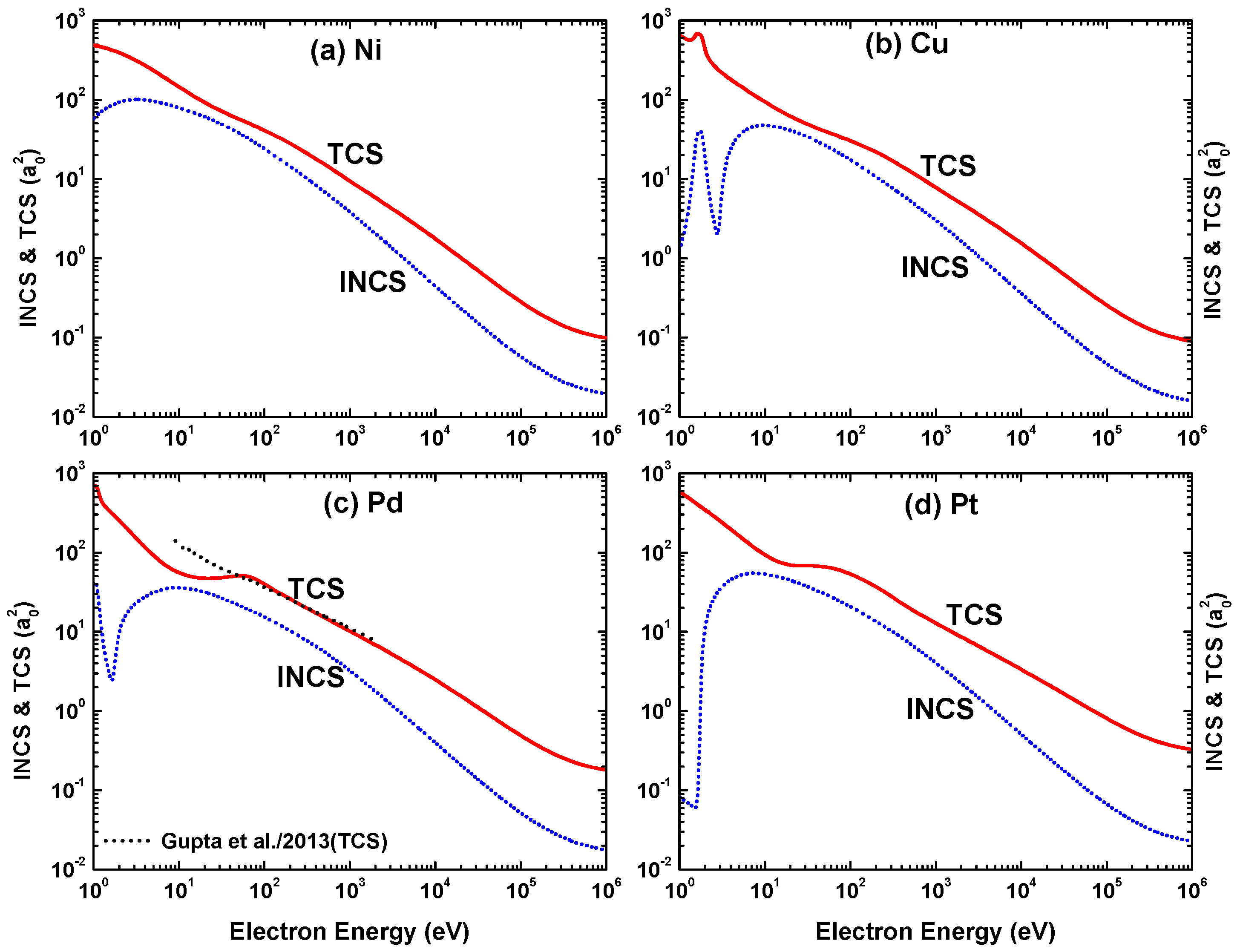
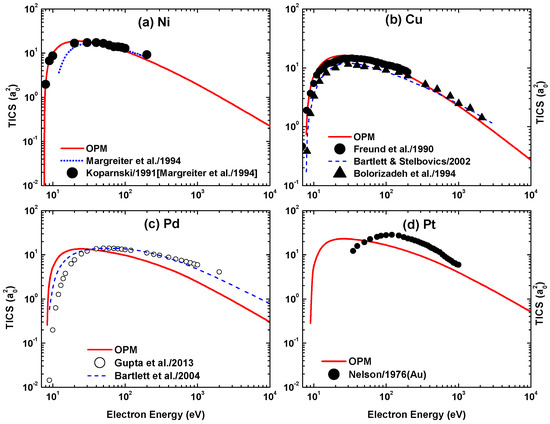
Figure 35.
Energy dependence of the total ionization cross-section (TICS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Koparnski reported in [51] for Ni, Freund et al. [55] and (▴) Bolorizadeh et al. [56] for Cu, and Nelson [57] for Au. Theory: (—) present OPM approach, () Margreiter et al. [51], () Bartlett and Stelbovics [52] and Bartlett et al. [54], and (∘) Gupta et al. [53].
Figure 35.
Energy dependence of the total ionization cross-section (TICS) for electron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt. Experiment: (•) Koparnski reported in [51] for Ni, Freund et al. [55] and (▴) Bolorizadeh et al. [56] for Cu, and Nelson [57] for Au. Theory: (—) present OPM approach, () Margreiter et al. [51], () Bartlett and Stelbovics [52] and Bartlett et al. [54], and (∘) Gupta et al. [53].
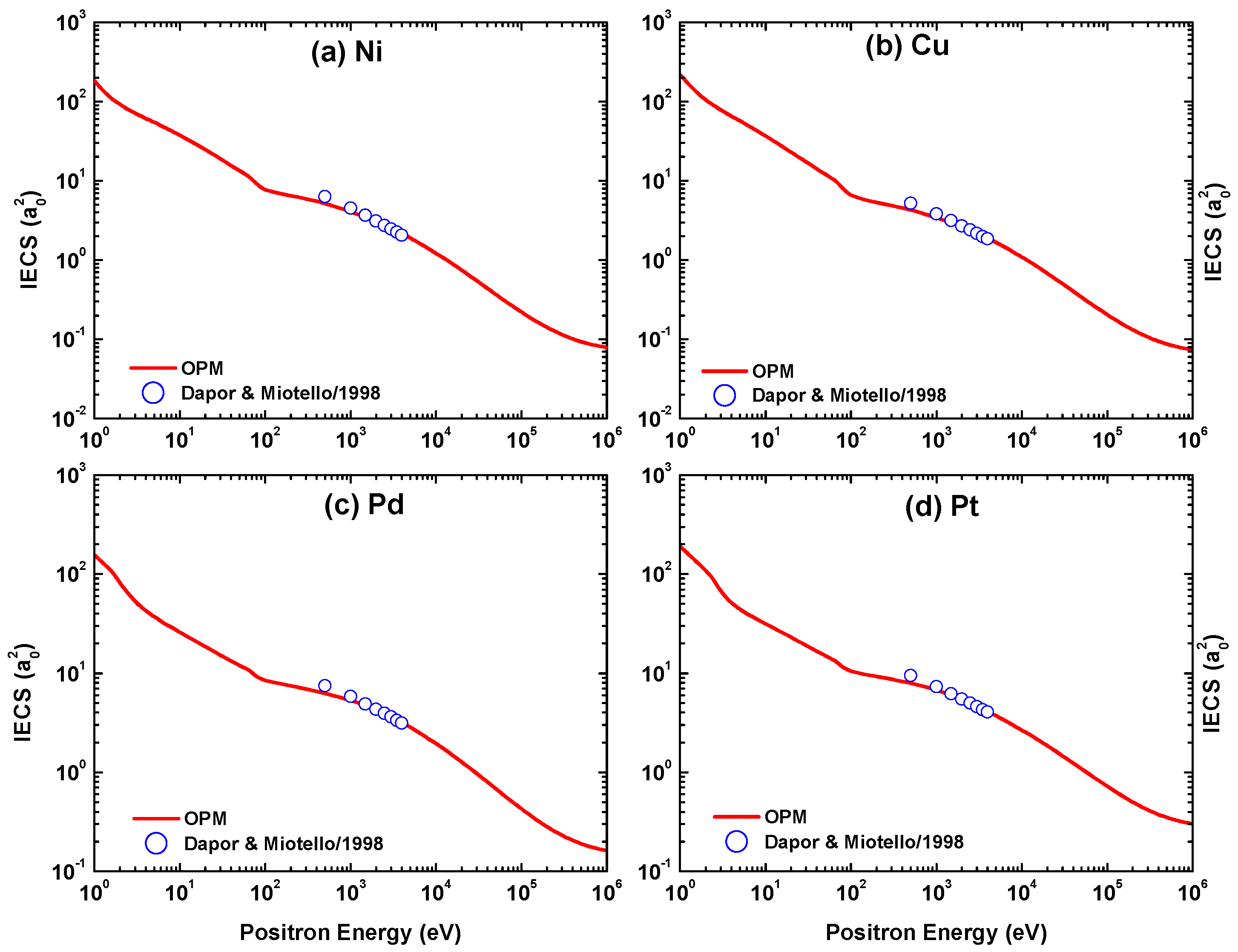
6.2. Integrated Cross-Sections for Positron Scattering
In Figure 36, Figure 37, Figure 38 and Figure 39 we display our OPM calculations of the IECS, MTCS, VCS, INCS, TCS, and TICS for positron scattering from the four metal targets in the energy range of 1– eV. The energy variations of IECS, MTCS, and VCS for positron scattering are significantly different in shape from their electron counterparts. In the energy domain 100 eV, the IECS, MTCS, and VCS for the electron projectile show a maxima and minima pattern which is absent in the case of positron projectiles. These features may be due to the deviation of electron and positron impact interactions. In this context, it is worth mentioning that for positrons the static potential is repulsive and the exchange potential is absent. Moreover, it is well established that the positron–atom interaction is weaker in comparison with its electron counterpart.
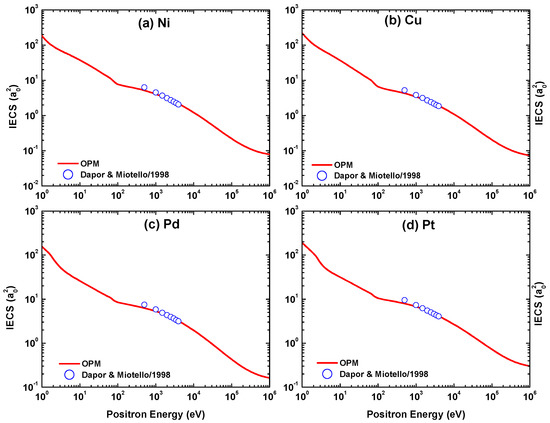
Figure 36.
The present OPM calculations of the IECS for positron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt in comparison with the results of Dapor and Miotello [50].
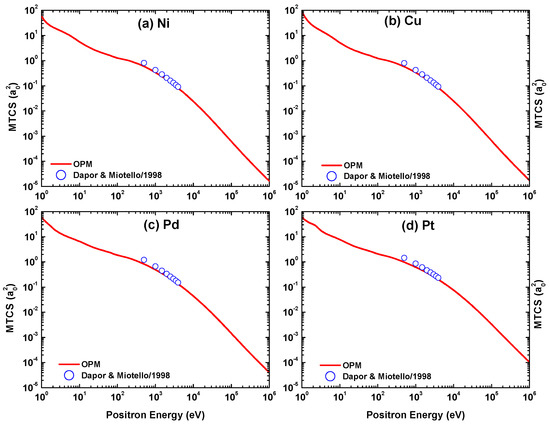
Figure 37.
The present OPM calculations of the MTCS for positron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt in comparison with the results of Dapor and Miotello [50].
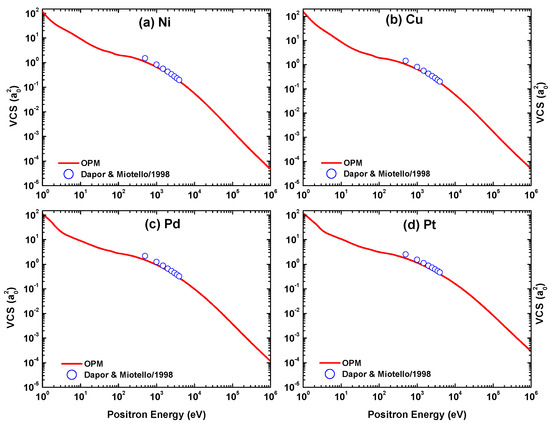
Figure 38.
The present OPM calculations of the VCS for positron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt in comparison with the results from Dapor and Miotello [50].
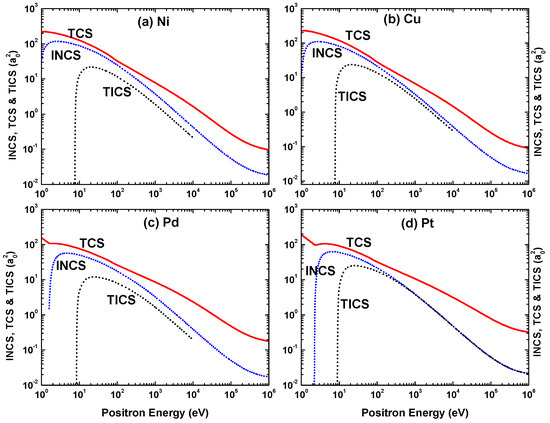
Figure 39.
The present OPM calculations of the INCS, TCS, and TICS for positron impact scattering from (a) Ni, (b) Cu, (c) Pd, and (d) Pt.
We include in the figures the theoretical predictions of IECS, MTCS, and VCS by Dapor and Miotello [50] for the energy domain = 300–3000 eV. It is evident from this comparison that the two theories agree well throughout the compared energy range. In contrast to electron scattering, the maximum of the inelastic cross section for positron impact shifts to a larger energy when the target is heavier. However, the predicted peak position of the TICS is again approximately independent of .
6.3. Mean Free Paths
In dense media, multiple collisions take place. The penetration of a particle through matter and its energy loss depends on the frequency of such collisions. This is related to the mean free path , which is the average distance the particle covers between two successive collisions. In a simplified model, is inversely proportional to the collisional cross section , and is defined by [19,59]
where is the atomic mass number, is the Avogadro number, and is the density of atoms in the target.
We can distinguish the mean free paths (MFPs) and related to elastic and inelastic collisions and define the MFP between arbitrary collisions ().
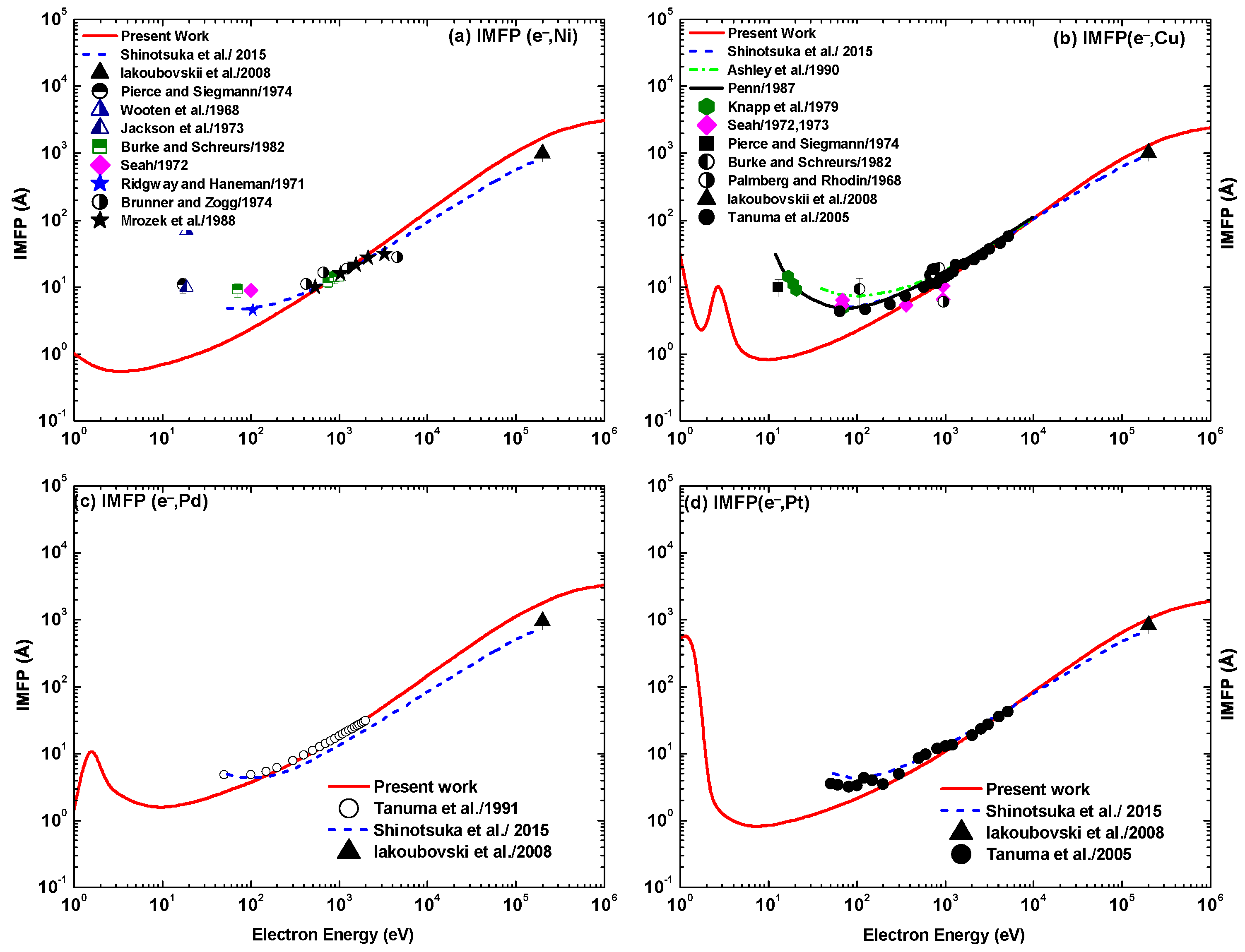
Figure 40 shows the present results of the inelastic mean free path (IMFP) for 1– eV electrons colliding with the four metal targets. As prescribed in (22), using a cross section evaluated within the OPM, the IMFP exhibits for all elements a monotonous increase beyond 100 eV, while at the lower energies structures are present. This relates to the corresponding behaviour of the cross-section (see Figure 34), as increases as becomes smaller. In comparison with the available experimental data [60,61,62,63,64,65,66,67,68,69,70,71], our electron impact IMFP results are in satisfactory agreement with the measurements for collision energies above 200 eV. Additional comparisons are made with calculations using the Penn algorithm by Shinotsuka et al. [72], the model dielectric function of Penn [73], the optical data model of Ashley [74], and the TPP-2 formula of Tanuma et al. [75]. While their results are close to ours at the higher energies, they are able to reproduce the experimental increase of with decreasing at the lower energies.
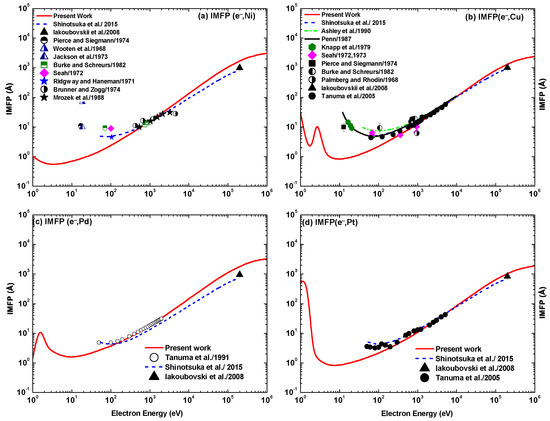
Figure 40.
Inelastic mean free path (IMFP) in for electrons colliding with (a) Ni, (b) Cu, (c) Pd, and (d) Pt as a function of collision energy, . Shown are the present results (—, red) and the theoretical results from Shinotsuka et al. (, blue [72]), Ashley green [74]), and Penn (in (b): upper full line, black [73]). Included are the experimental data from Iakoubovskii et al. [60], Pierce and Siegmann [61], Wooten et al. [62], Jackson et al. [63], Burke and Schreurs [64], Seah [66], Ridgway and Haneman [65], Brunner and Zogg [67], Mrozek et al. [68], Knapp et al. [69], Palmberg and Rhodin [70], and Tanuma et al. [71].
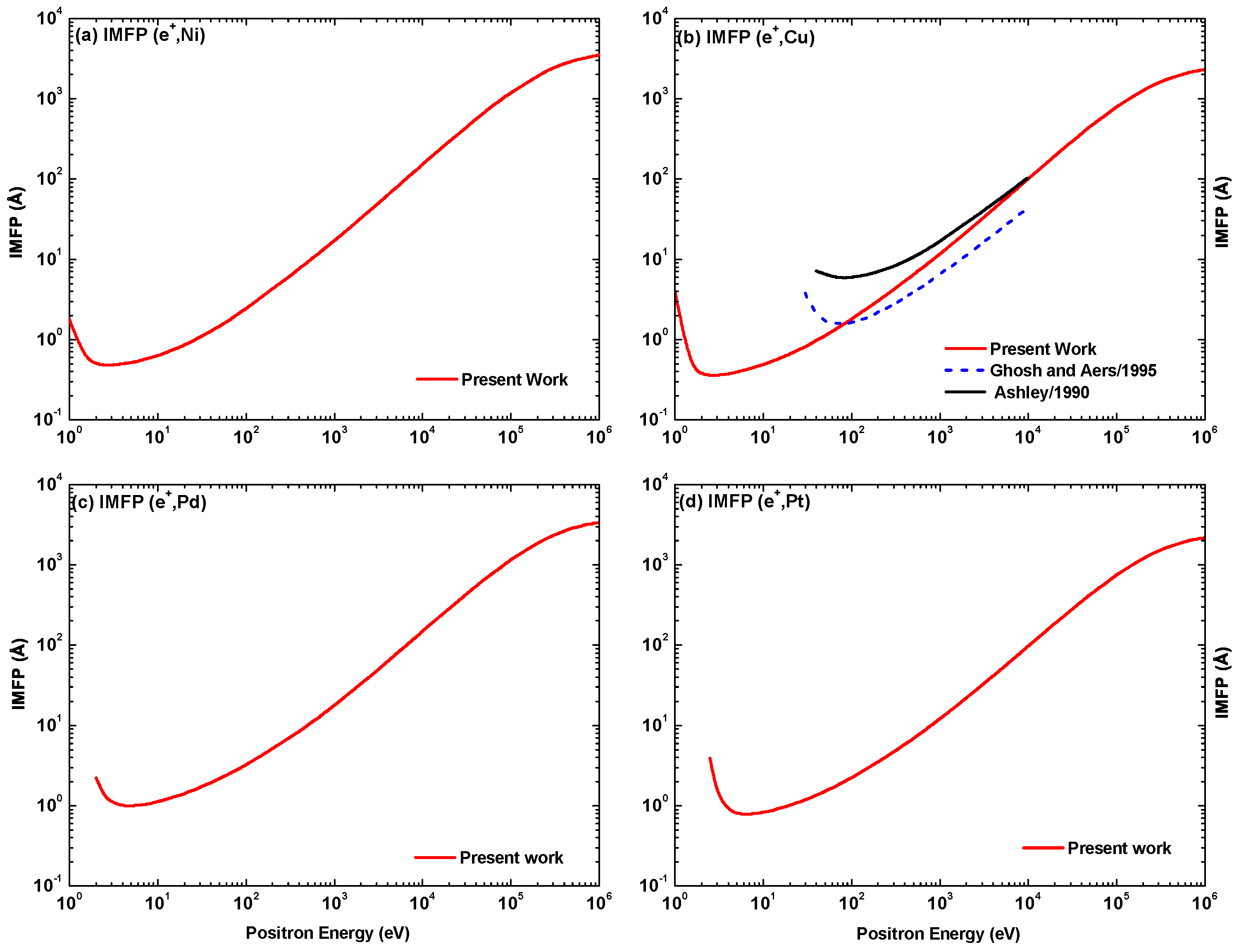
Figure 41 shows our IMFP results for positrons inelastically scattered from the four target species in comparison with the predictions from the optical data model of Ashley [74] and the BNL Monte Carlo scheme of Ghosh and Aers [76]. It is evident that the positron impact IMFP shows a similar pattern as its electron counterpart beyond 100 eV. At lower energies the energy dependence is rather smooth, without any significant structure. It can be seen that for positron projectiles the differences in the IMFP between the target species are rather small, apart from a shift in the minimum. The comparison shows that our calculations are in substantial disagreement with those of [74,76], also above 200 eV. Further experimental and theoretical investigations are needed in order to clarify these discrepancies.
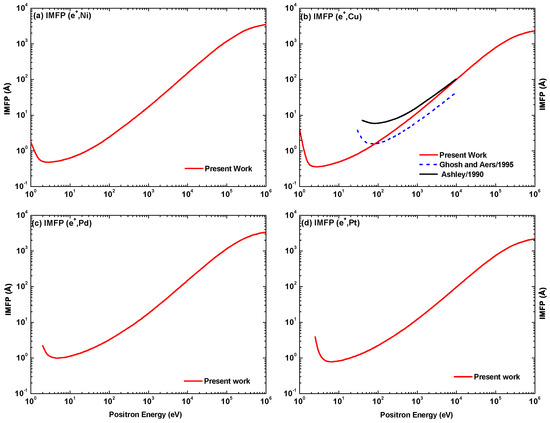
Figure 41.
Inelastic mean free path (IMFP) in for positrons colliding with (a) Ni, (b) Cu, (c) Pd, and (d) Pt as function of collision energy, . Shown are the present results (—, red) and the theoretical results from Ashley (—, upper line in (b), black [74]) and Ghosh and Aers (, blue [76]).
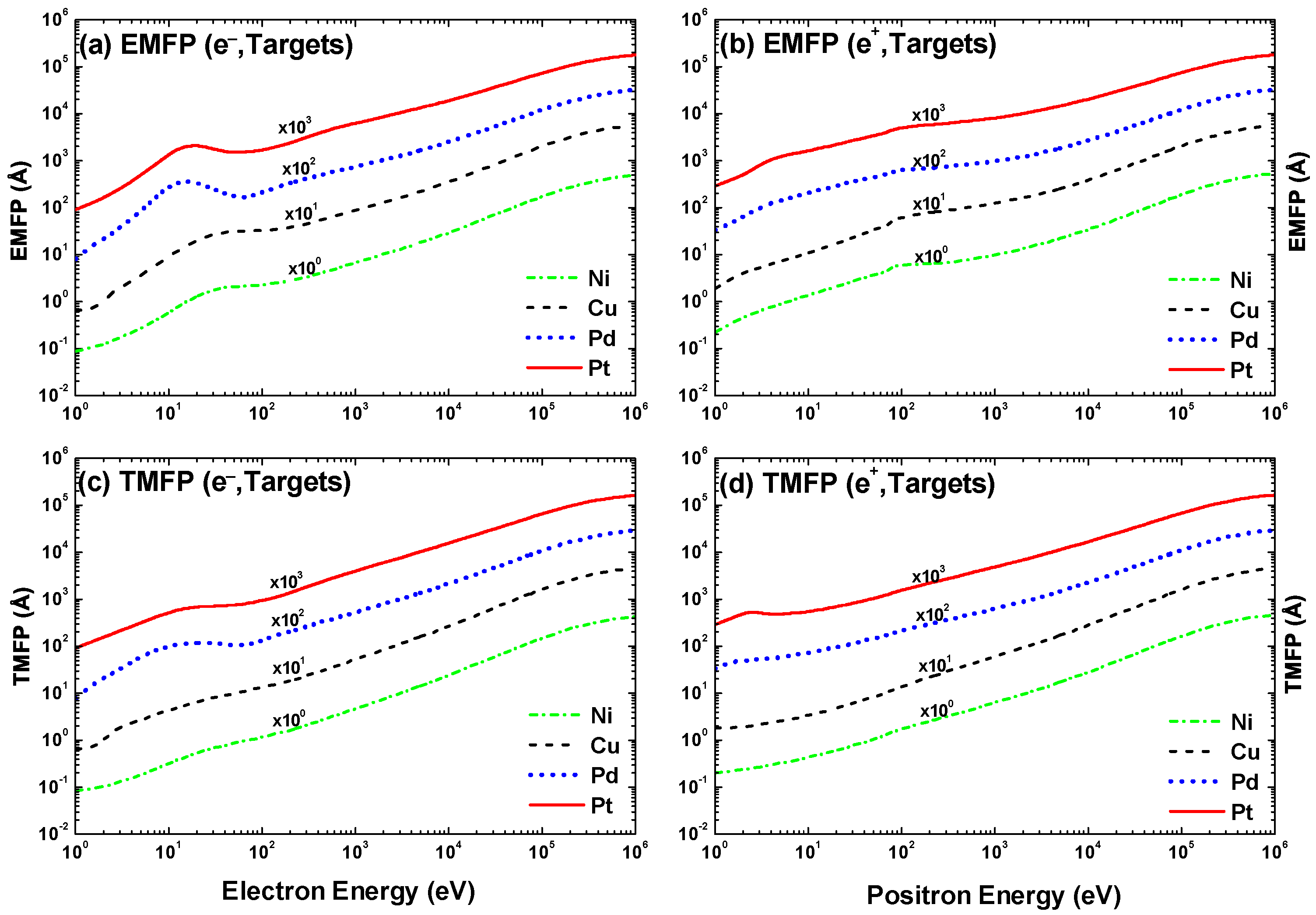
The (EMFP) and (TMFP) for both electron and positron impacts on the four targets are displayed in Figure 42. It can be seen that the results for both electrons and positrons are very alike beyond 100 MeV in both magnitude and shape. This is true for both and . Around 20 eV, for electrons shows a peak structure which becomes more pronounced with increasing and is related to the minimum of the elastic cross-section (Figure 31). For positron impacts, and increase almost monotonously with energy.
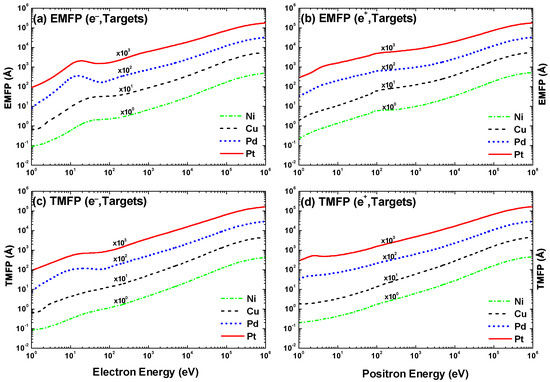
Figure 42.
(a,b) Elastic mean free path (EMFP) and (c,d) total mean free path (TMFP) in for (a,c) electrons and (b,d) positrons colliding with Ni (, green), Cu (, black), Pd (, blue), and Pt (—, red) as function of collision energy .
7. Conclusions
Based on the relativistic phase-shift theory’s embodying an optical potential, we have presented relevant observables for lepton–metal atom scattering, including the elastic differential and total cross-sections, spin asymmetries, inelastic cross-sections, and mean free paths. Comparisons with experimental data and with results from different theoretical models provide generally good agreement for collision energies near and beyond 100 eV.
In conjunction with previous investigations on the alkali atoms, our main result for the lower collision energies is the strong dependence of the differential cross-sections on the shell structure and on the extension of the electronic density distribution, . For electron impacts, diffraction structures can be clearly identified, with their onset occurring at lower energies as is more extended. For positron impacts no comparable structures are found, which points to a screening effect of the target electrons rather than their active contribution to the scattering process. In the ultrarelativistic regime, it is the nuclear charge distribution which governs the DCS, and both lepton species induce similar diffraction patterns.
For the spin asymmetries , and T, large electron–positron differences are found at the lower collision energies. For electron impacts, their diffraction structure corresponds to that in the DCS and leads to a large polarization, with the number of total polarization points of S increasing with the number of shells. For positrons, on the other hand, the spin asymmetries remain close to their asymptotic values of zero (S and U) or one (T), again pointing to ineffective positron–electron cloud scattering.
In the relativistic collision energy regime above 100 MeV, scaling laws were discovered for the differential cross-section and for the spin asymmetries. We found that the DCS increases with for sufficiently small scattering angles if the product is simultaneously kept fixed. For the Sherman function, scaling with at fixed holds for the heavier atoms below . The parameters U and T tend to their Born limits below , which are independent of and of the target species.
From the action of the absorption potential, we determined an estimate of the inelastic and ionization cross-section. We found that for the lightest atoms, Cu and Ni, the agreement with experimental cross-section data and other theoretical results is satisfactory, while a more accurate model is needed for correctly describing the inelastic mean free path at low energies.
Our work justifies the importance of the charge density distribution, upon which the description of the scattering observables presented herein relies, in conjunction with the fact that the collision dynamics, as treated in our work, lead to overall agreement with both experimental results and other theories. Thus, the present procedure provides the possibility of quickly generating accurate elastic cross-sections and spin asymmetries in the energy regime extending from 100 eV to 300 MeV. These raw data are required for computer simulations of multiple scattering processes occurring in many fields of science and technology.
Author Contributions
D.H.J.-A.: conceptualization, software, investigation, analysis, and writing (High energy domain); review and editing; A.K.F.H.: investigation and analysis (Intermediate energy domain); M.M.H.: writing original draft preparation (Intermediate energy domain), review and editing; M.M.B.: investigation, analysis (MFP part), editing and data curation; A.K.B.: visualization and review; B.C.S.: review, resources and editing; M.A.U.: conceptualization, software (Intermediate energy domain), review, and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gargioni, E.; Grosswendt, B. Electron Scattering From Argon: Data Evaluation and Consistency. Rev. Mod. Phys. 2008, 80, 451. [Google Scholar] [CrossRef]
- Horowitz, C. Parity violation in astrophysics. Eur. Phys. J. A 2005, 24, 167–170. [Google Scholar] [CrossRef]
- Ichimura, S.; Shimizu, R. Backscattering correction for quantitative Auger analysis: I. Monte Carlo calculations of backscattering factors for standard materials. Surf. Sci. 1981, 112, 386. [Google Scholar] [CrossRef]
- Mitroy, J.; Bromley, M.W.J.; Ryzhikh, G.G. Positron and positronium binding to atoms. J. Phys. B At. Mol. Opt. Phys. 2002, 35, R81. [Google Scholar] [CrossRef]
- Breton, V.; Bricault, P.; Cardman, L.S.; Frois, B.; Goutte, D.; Isabelle, D.B.; Linzey, A.J.; Masson, G.; Maximon, L.C.; Offermann, E.A.J.M.; et al. High-accuracy comparison of electron and positron scattering from nuclei. Phys. Rev. Lett 1991, 66, 572–575. [Google Scholar] [CrossRef] [PubMed]
- Shorifuddoza, M.; Das, P.K.; Kabir, R.; Haque, A.F.; Uddin, M.A. Angular distributions and critical minima in the elastic scattering of electrons by atomic copper. Int. J. Quantum Chem. 2021, 121, e26460. [Google Scholar] [CrossRef]
- Motz, J.W.; Olsen, H.; Koch, H.W. Electron scattering without atomic or nuclear excitation. Rev. Mod. Phys. 1964, 36, 881–928. [Google Scholar] [CrossRef]
- Kessler, J. Electron spin polarization by low-energy scattering from unpolarized targets. Rev. Mod. Phys. 1969, 41, 3–25. [Google Scholar] [CrossRef]
- Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths for 31 materials. Surf. Interface Anal. 1988, 11, 577–589. [Google Scholar] [CrossRef]
- Powell, C.J.; Jablonski, A. Progress in quantitative surface analysis by X-ray photoelectron spectroscopy: Current status and perspectives. J. Electron. Spectrosc. Relat. Phenom. 2010, 178, 331–346. [Google Scholar] [CrossRef]
- McCarthy, I.E.; Noble, C.J.; Phillips, B.A.; Turnbull, A.D. Optical model for electron scattering from inert gases. Phys. Rev. A 1977, 15, 2173. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics; Elsevier: Oxford, UK, 1982; Volume 4. [Google Scholar]
- Saha, B.C.; Jakubassa-Amundsen, D.H.; Basak, A.K.; Haque, A.K.F.; Haque, M.M.; Khandker, M.H.; Uddin, M.A. Elastic scattering of electrons and positrons from alkali atoms. Adv. Quantum Chem. in press. [CrossRef]
- Msezane, A.Z.; Henry, R.J.W. Electron-impact excitation of atomic copper. Phys. Rev. A 1986, 33, 1631–1635. [Google Scholar] [CrossRef]
- Zhou, Y.; Bray, I.; McCarthy, I. Model calculations of electron scattering from copper. J. Phys. B 1999, 32, 1033–1039. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. Electron collisions with copper atoms: Elastic scattering and electron-impact excitation of the (3d10 4s)2S→(3d104p)2P resonance transition. Phys. Rev. A 2010, 82, 062703. [Google Scholar] [CrossRef]
- Desclaux, J.P. A multiconfiguration relativistic Dirac-Fock program. Comput. Phys. Commun. 1975, 9, 31–45. [Google Scholar] [CrossRef]
- Koga, T. Analytical Hartree-Fock electron densities for atoms He through Lr. Theor. Chim. Acta 1997, 95, 113–130. [Google Scholar]
- Shorifuddoza, M.; Patoary, M.A.R.; Jakubassa-Amundsen, D.H.; Haque, A.K.F.; Uddin, M.A. Scattering of e± from ytterbium atoms. Eur. Phys. J. D 2019, 73, 164. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.W.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495–530. [Google Scholar] [CrossRef]
- Salvat, F.; Fernández-Varea, J.M.; Williamson, W., Jr. Accurate numerical solution of the radial Schrödinger and Dirac wave equations. Comput. Phys. Commun. 1995, 90, 151–168. [Google Scholar] [CrossRef]
- Haque, A.K.F.; Haque, M.M.; Bhattacharjee, P.P.; Uddin, M.A.; Patoary, M.A.R.; Hossain, M.I.; Basak, A.K.; Mahbub, M.S.; Maaza, M.; Saha, B.C. Relativistic calculations for spin-polarization of elastic electron-mercury scattering. J. Phys. Commun. 2017, 1, 035014. [Google Scholar] [CrossRef]
- Yennie, D.R.; Ravenhall, D.G.; Wilson, R.N. Phase-shift calculation of high-energy electron scattering. Phys. Rev. 1954, 95, 500. [Google Scholar] [CrossRef]
- Joshipura, K.N.; Limbachiya, C.G. Theoretical total ionization cross-sections for electron impact on atomic and molecular halogens. Int. J. Mass Spectrom. 2002, 216, 239–247. [Google Scholar] [CrossRef]
- Joshipura, K.N.; Vinodkumar, M.; Antony, B.K.; Mason, N.J. Theoretical total ionization cross-sections of CHx, CFx, SiHx, SiFx () and CCl4 targets by electron impact. Eur. Phys. J. D 2003, 23, 81–90. [Google Scholar] [CrossRef]
- Guèye, P.; Kabir, A.A.; Giuliani, P.; Glister, J.; Lee, B.W.; Gilman, R.; Higinbotham, D.W.; Piasetzky, E.; Ron, G.; Sarty, A.J.; et al. Dispersive corrections in elastic electron-nucleus scattering: An investigation in the intermediate energy regime and their impact on the nuclear matter. Eur. Phys. J. A 2020, 56, 126. [Google Scholar] [CrossRef]
- Überall, H. Electron Scattering from Complex Nuclei; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Donnelly, T.W.; Sick, I. Elastic magnetic electron scattering from nuclei. Rev. Mod. Phys. 1984, 56, 461–566. [Google Scholar] [CrossRef]
- Beiser, B.A. Concepts of Modern Physics, 2nd ed.; McGraw-Hill Co.: New York, NY, USA, 1973. [Google Scholar]
- Bohr, N. XXXVII. On the constitution of atoms and molecules. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1913, 26, 476–502. [Google Scholar] [CrossRef]
- Sandor, R.K.J.; Blok, H.P.; Garg, U.; Harakeh, M.N.; De Jager, C.W.; Ponomarev, V.Y.; Vdovin, A.I.; De Vries, H. Interplay between single-particle and collective degrees of freedom in the excitation of the low-lying states in 142Nd. Nucl. Phys. A 1991, 535, 669–700. [Google Scholar] [CrossRef]
- Segre, E. Nuclei and Particles: An Introduction to Nuclear and Subnuclear Physics; WA Benjamin: New York, NY, USA, 1974; p. 246. [Google Scholar]
- Ramsauer, C. Über den Wirkungsquerschnitt der Gasmoleküle gegenüber langsamen Elektronen. i. fortsetzung. Ann. Phys. 1921, 66, 546–558. [Google Scholar] [CrossRef]
- Townsend, J.S.; Bailey, V.A. LXX. The motion of electrons in argon. Philos. Mag. 1922, 43, 593–600. [Google Scholar] [CrossRef]
- Jablonski, A.; Salvat, F.; Powell, C.J. Comparison of electron elastic-scattering cross sections calculated from two commonly used atomic potentials. J. Phys. Chem. Ref. Data 2004, 33, 409–451. [Google Scholar] [CrossRef]
- Madison, D.H.; McEachran, R.P.; Ismail, M.; Teubner, P.J.O. Elastic scattering of electrons from copper at intermediate energies. J. Phys. B 1998, 31, 1127. [Google Scholar] [CrossRef]
- Trajmar, S.; Williams, W.; Srivastava, S.K. Electron-impact cross sections for Cu atoms. J. Phys. B 1977, 10, 3323. [Google Scholar] [CrossRef]
- Czyźewski, Z.; MacCallum, D.O.; Romig, A.; Joy, D.C. Calculations of Mott scattering cross section. J. Appl. Phys. 1990, 68, 3066–3072. [Google Scholar] [CrossRef]
- Fink, M.; Ingram, J. Theoretical electron scattering amplitudes and spin polarizations: Electron energies 100 to 1500 eV Part II. Be, N, O, Al, Cl, V, Co, Cu, As, Nb, Ag, Sn, Sb, I, and Ta targets. At. Data Nucl. Data Tables 1972, 4, 129–207. [Google Scholar] [CrossRef]
- Riley, M.E.; MacCallum, C.J.; Biggs, F. Theoretical electron-atom elastic scattering cross sections: Selected elements, 1 keV to 256 keV. At. Data Nucl. Data Tables 1975, 15, 443–476. [Google Scholar] [CrossRef]
- Ficenec, J.R.; Trower, W.P.; Heisenberg, J.; Sick, I. Elastic electron-nickel scattering. Phys. Lett. B 1970, 32, 460–462. [Google Scholar] [CrossRef]
- Antonov, A.N.; Kadrev, D.N.; Gaidarov, M.K.; de Guerra, E.M.; Sarriguren, P.; Udias, J.M.; Lukyanov, V.K.; Zemlyanaya, E.V.; Krumova, G.Z. Charge and matter distributions and form factors of light, medium, and heavy neutron-rich nuclei. Phys. Rev. C 2005, 72, 044307. [Google Scholar] [CrossRef]
- Shevchenko, N.G.; Polishchuk, V.N.; Kasatkin, Y.A.; Khomich, A.A.; Buki, A.Y.; Mazanko, B.V.; Shula, G.V. Charge-density distribution in the nuclei CR-50, CR-52, CR-53, CR-54 AND FE-54, FE-56. Sov. J. Nucl. Phys. 1978, 28, 139–142. [Google Scholar]
- van der Laan, J.B. Electron Scattering Off Palladium Isotopes. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1986. [Google Scholar]
- Walker, D.W. Relativistic effects in low energy electron scattering from atoms. Adv. Phys. 1971, 20, 257–323. [Google Scholar] [CrossRef]
- Kelemen, V.I.; Remeta, E.Y. Critical minima and spin polarization in the elastic electron scattering by the mercury atoms. J. Phys. B 2012, 45, 185202. [Google Scholar] [CrossRef]
- Jakubassa-Amundsen, D.H. Equivalence of a tip bremsstrahlung quantum and an elastically scattered electron at ultrahigh energies. Phys. Rev. A 2012, 85, 042714. [Google Scholar] [CrossRef]
- Jakubassa-Amundsen, D.H. An asymptotic DSM theory for high-energy near-tip bremsstrahlung. J. Phys. G 2020, 47, 075102, The angular scaling in (4.1) and (4.7) therein should be reversed. [Google Scholar] [CrossRef]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Mechanics; Mc Graw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Dapor, M.; Miotello, A. Differential, total, and transport cross sections for elastic scattering of low energy positrons by neutral atoms (Z = 1–92, E = 500–4000 eV). At. Data Nucl. Data Tables 1998, 69, 1–100. [Google Scholar] [CrossRef]
- Margreiter, D.; Deutsch, H.; Märk, T.D. A semiclassical approach to the calculation of electron impact ionization cross-sections of atoms: From hydrogen to uranium. Int. J. Mass Spectrom. Ion Process. 1994, 139, 127–139. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Stelbovics, A.T. Calculation of electron-impact total-ionization cross sections. Phys. Rev. A 2002, 66, 012707. [Google Scholar] [CrossRef]
- Gupta, D.; Naghma, R.; Antony, B. Electron impact total and ionization cross sections for Sr, Y, Ru, Pd, and Ag atoms. Can. J. Phys. 2013, 91, 744–750. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Stelbovics, A.T. Electron-impact ionization cross sections for elements Z= 1 to Z= 54. At. Data Nucl. Data Tables 2004, 86, 235–265. [Google Scholar] [CrossRef]
- Freund, R.S.; Wetzel, R.C.; Shul, R.J.; Hayes, T.R. Cross-section measurements for electron-impact ionization of atoms. Phys. Rev. 1990, 41, 3575. [Google Scholar] [CrossRef]
- Bolorizadeh, M.A.; Patton, C.J.; Shah, M.B.; Gilbody, H.B. Multiple ionization of copper by electron impact. J. Phys. B 1994, 27, 175. [Google Scholar] [CrossRef]
- Nelson, A.N. Technical Report AFML-TR-75-198; Massachusetts Inst of Tech.: Cambridge, MA, USA, 1975. [Google Scholar]
- Mayol, R.; Salvat, F. Total and transport cross sections for elastic scattering of electrons by atoms. At. Data Nucl. Data Tables 1997, 65, 55–154. [Google Scholar] [CrossRef]
- Liljequist, D. A simple calculation of inelastic mean free path and stopping power for 50 eV–50 keV electrons in solids. J. Phys. D 1983, 16, 1567. [Google Scholar] [CrossRef]
- Iakoubovskii, K.; Mitsuishi, K.; Nakayama, Y.; Furuya, K. Mean free path of inelastic electron scattering in elemental solids and oxides using transmission electron microscopy: Atomic number dependent oscillatory behavior. Phys. Rev. B 2008, 77, 104102. [Google Scholar] [CrossRef]
- Pierce, D.T.; Siegmann, H.C. Attenuation Length of Hot Electrons in Ferromagnetic Ni. AIP Conf. Proc. 1974, 18, 1393. [Google Scholar]
- Wooten, F.; Breen, W.M.; Stuart, R.N. Hot-electron scattering and the rigid-band model in ferromagnetic Ni and Ni-Al alloys. Phys. Rev. 1968, 165, 703–706. [Google Scholar] [CrossRef]
- Jackson, D.C.; Gallon, T.E.; Chambers, A. A model for the Auger electron spectroscopy of systems exhibiting layer growth, and its application to the deposition of silver on nickel. Surf. Sci. 1973, 36, 381–394. [Google Scholar] [CrossRef]
- Burke, M.A.; Schreurs, J.J. The inelastic mean free paths of auger electrons in thin films of copper and nickel. Surf. Interface Anal. 1982, 4, 42–46. [Google Scholar] [CrossRef]
- Ridgway, J.W.; Haneman, D. Auger spectra and LEED patterns from vacuum cleaved silicon crystals with calibrated deposits of iron. Surf. Sci. 1971, 24, 451–458. [Google Scholar] [CrossRef]
- Seah, M.P. Quantitative Auger electron spectroscopy and electron ranges. Surf. Sci. 1972, 32, 703–728. [Google Scholar] [CrossRef]
- Brunner, J.; Zogg, H. Angular dependence of X-ray photoelectrons. J. Electron Spectrosc. Relat. Phenom. 1974, 5, 911–920. [Google Scholar] [CrossRef]
- Mrozek, P.; Jablonski, A.; Sulyok, A. The inelastic mean free path of electrons in the ordered Al48Ni52 alloy. Surf. Interface Anal. 1988, 11, 499–501. [Google Scholar] [CrossRef]
- Knapp, J.A.; Himpsel, F.J.; Eastman, D.E. Experimental energy band dispersions and lifetimes for valence and conduction bands of copper using angle-resolved photoemission. Phys. Rev. B 1979, 19, 4952. [Google Scholar] [CrossRef]
- Palmberg, P.W.; Rhodin, T.N. Auger electron spectroscopy of fcc metal surfaces. J. Appl. Phys. 1968, 39, 2425–2432. [Google Scholar] [CrossRef]
- Tanuma, S.; Shiratori, T.; Kimura, T.; Goto, K.; Ichimura, S.; Powell, C.J. Experimental determination of electron inelastic mean free paths in 13 elemental solids in the 50 to 5000 eV energy range by elastic-peak electron spectroscopy. Surf. Interface Anal. 2005, 37, 833–845. [Google Scholar] [CrossRef]
- Shinotsuka, H.; Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths. X. Data for 41 elemental solids over the 50 eV to 200 keV range with the relativistic full Penn algorithm. Surf. Interface Anal. 2015, 47, 871–888. [Google Scholar] [CrossRef]
- Penn, D.R. Electron mean-free-path calculations using a model dielectric function. Phys. Rev. B 1987, 35, 482–486. [Google Scholar] [CrossRef]
- Ashley, J.C. Energy loss rate and inelastic mean free path of low-energy electrons and positrons in condensed matter. J. Electron Spectrosc. Relat. Phenom. 1990, 50, 323–334. [Google Scholar] [CrossRef]
- Tanuma, S.; Powell, C.J.; Penn, D.R. Calculations of electron inelastic mean free paths. III. Data for 15 inorganic compounds over the 50–2000 eV range. Surf. Interface Anal. 1991, 17, 927–939. [Google Scholar] [CrossRef]
- Ghosh, V.J.; Aers, G.C. Positron stopping in elemental systems: Monte Carlo calculations and scaling properties. Phys. Rev. B 1995, 51, 45–59. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).