Nonlinear Dynamics in Isotropic and Anisotropic Magneto-Optical Traps
Abstract
:1. Introduction
2. Model and Time-Dependent Variational Method
3. Results
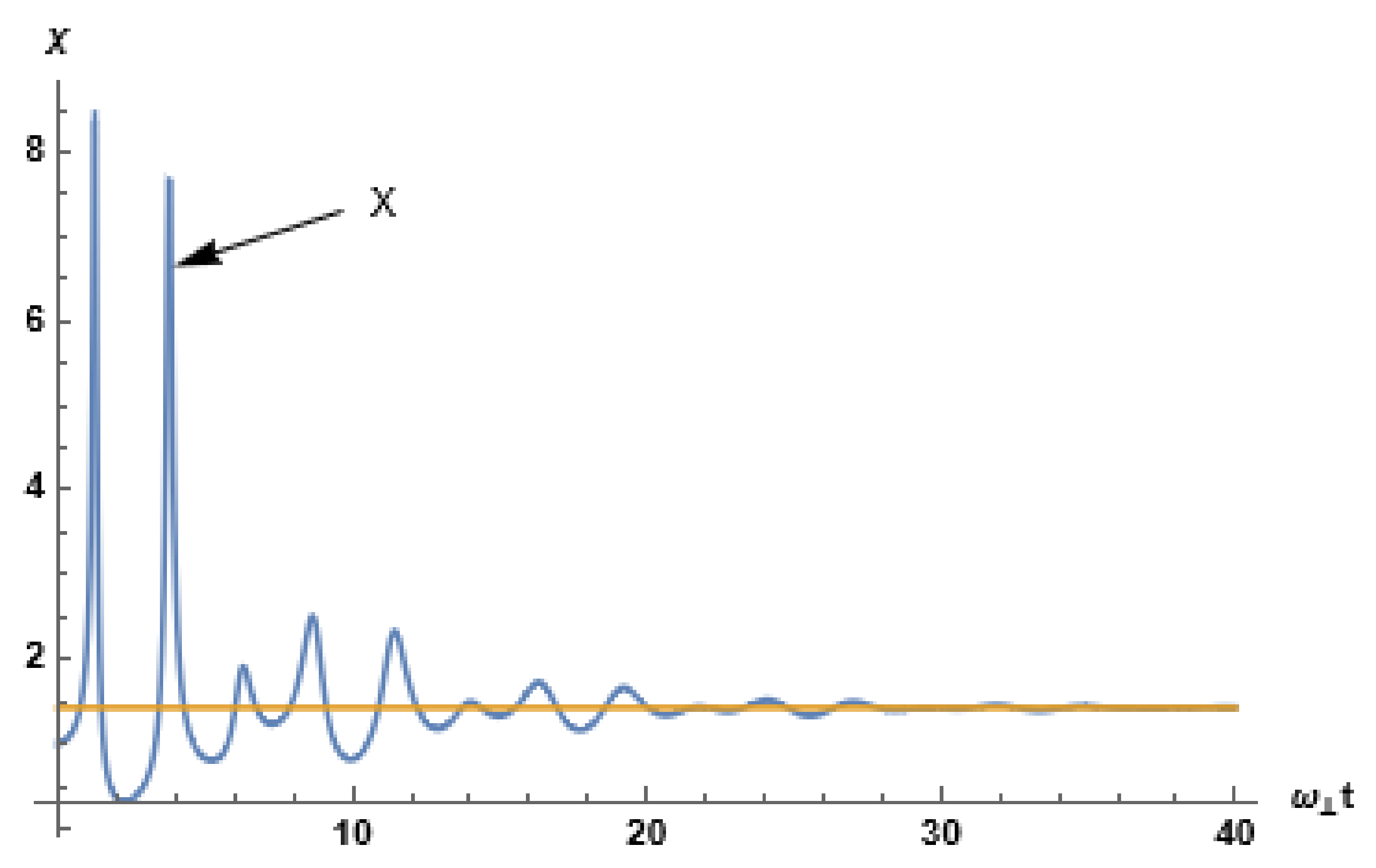
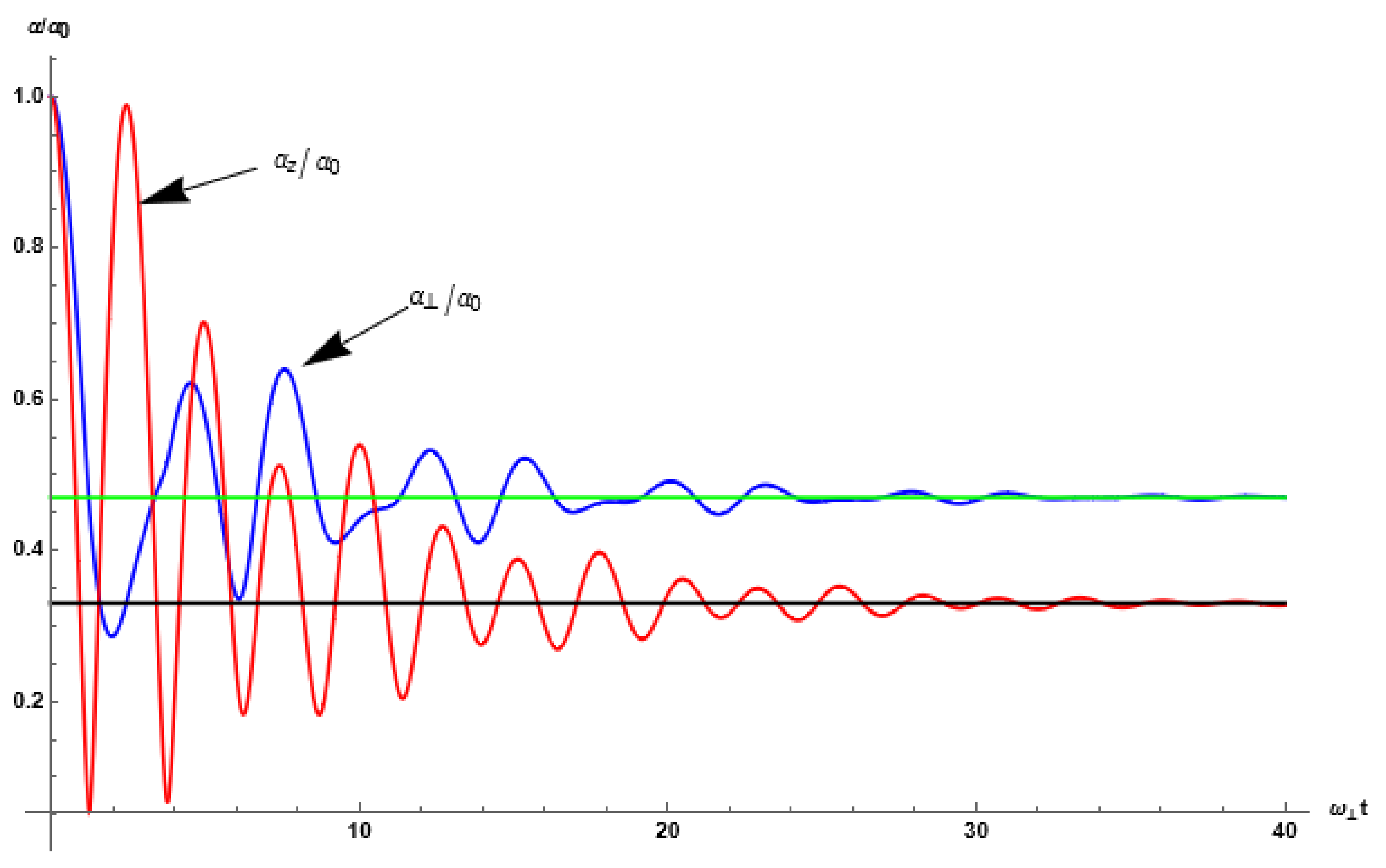
3.1. Anisotropic MOT
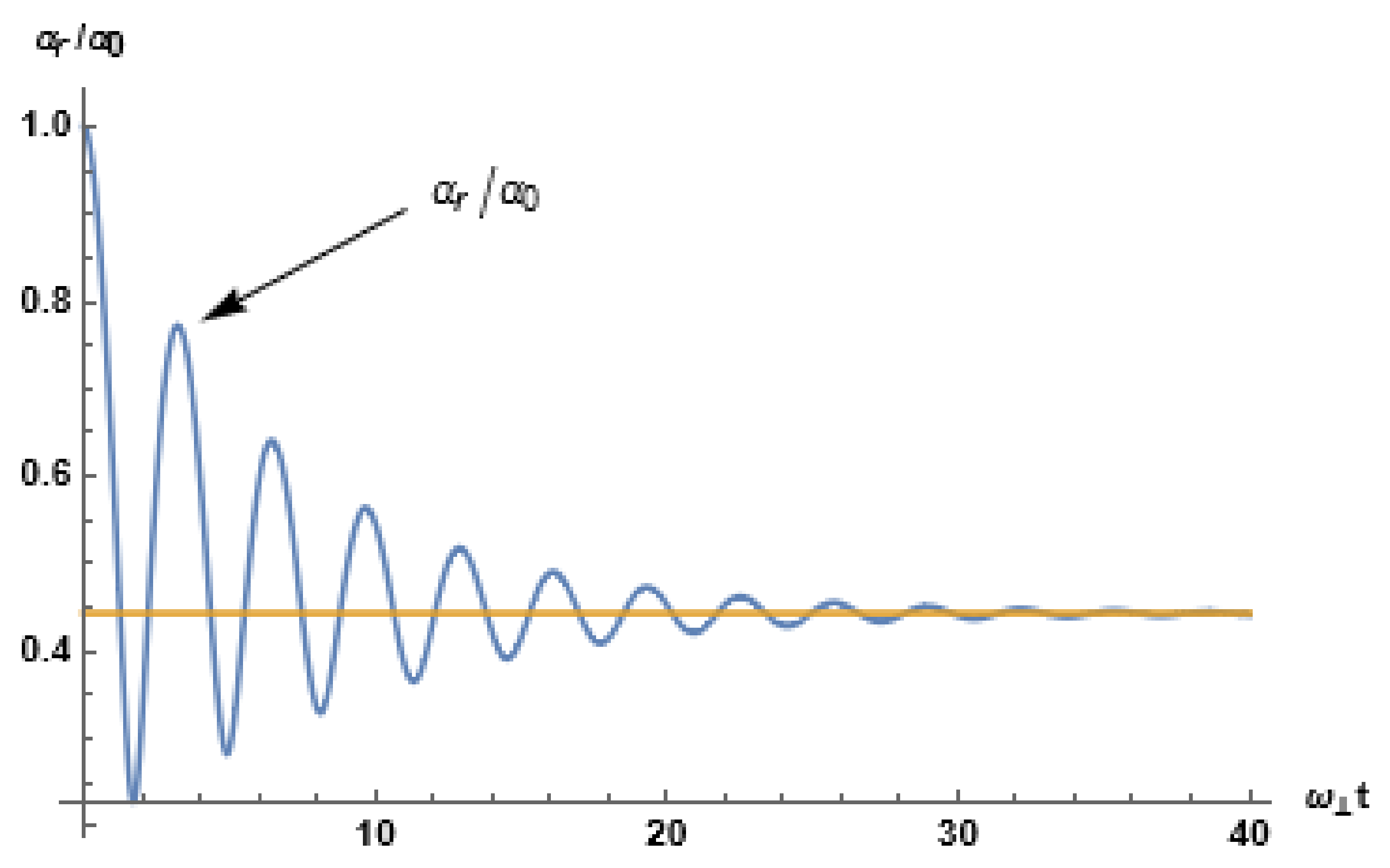
3.2. Isotropic MOT
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Labeyrie, G.; Michaud, F.; Kaiser, R. Self-Sustained Oscillations in a Large Magneto-Optical Trap. Phys. Rev. Lett. 2006, 96, 023003. [Google Scholar] [CrossRef] [PubMed]
- Di Stefano, A.; Fauquembergue, M.; Verkerk, P.; Hennequin, D. Giant Oscillations in a Magneto-Optical Trap. Phys. Rev. A 2003, 67, 033404. [Google Scholar] [CrossRef]
- Townsend, C.G.; Edwards, N.H.; Cooper, C.J.; Zetie, K.P.; Foot, C.J.; Steane, A.M.; Szriftgiser, P.; Perrin, H.; Dalibard, J. Phase-Space Density in the Magneto-Optical Trap. Phys. Rev. A 1995, 52, 1423. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198. [Google Scholar] [CrossRef] [PubMed]
- Guidoni, L.; Verkerk, P. Optical Lattices: Cold Atoms Ordered by Light. J. Opt. B Quantum Semiclass. Opt. 1999, 1, R23. [Google Scholar] [CrossRef]
- Bloch, I. Ultracold Quantum Gases in Optical Lattices. Nat. Phys. 2005, 1, 23. [Google Scholar] [CrossRef]
- Stellmer, S.; Pasquiou, B.; Grimm, R.; Schreck, F. Laser Cooling to Quantum Degeneracy. Phys. Rev. Lett. 2013, 110, 263003. [Google Scholar] [CrossRef] [PubMed]
- Labeyrie, G.; Tesio, E.; Gomes, P.M.; Oppo, G.L.; Firth, W.J.; Robb, G.R.M.; Arnold, A.S.; Kaiser, R.; Ackemann, T. Optomechanical Self-Structuring in a Cold Atomic Gas. Nat. Photonics 2014, 8, 321. [Google Scholar] [CrossRef]
- Manfredi, G.; Hervieux, P.-A. Adiabatic Cooling of Trapped Non-Neutral Plasmas. Phys. Rev. Lett. 2012, 109, 255005. [Google Scholar] [CrossRef] [PubMed]
- Cox, J.P. Theory of Stellar Pulsation; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Terças, H.; Mendonça, J.T.; Kaiser, R. Driven Collective Instabilities in Magneto-Optical Traps: A Fluid-Dynamical Approach. Europhys. Lett. 2010, 89, 53001. [Google Scholar] [CrossRef]
- Terças, H.; Kaiser, R.; Mendonça, J.T.; Loureiro, J. Collective Oscillations in Ultracold Atomic Gas. Phys. Rev. A 2008, 78, 013408. [Google Scholar]
- Terças, H.; Mendonça, J.T. Polytropic Equilibrium and Normal Modes in Cold Atomic Traps. Phys. Rev. A 2013, 88, 023412. [Google Scholar] [CrossRef]
- Soares, L.G.F.; Haas, F. Nonlinear Oscillations of Ultra-Cold Atomic Clouds in a Magneto-Optical Trap. Phys. Scr. 2019, 94, 125214. [Google Scholar] [CrossRef]
- Soares, L.G.F.; Haas, F. Dynamics and Stability of Axially Symmetric Atomic Clouds in Magneto-Optical Trap. Acta Phys. Pol. A 2021, 139, 6. [Google Scholar] [CrossRef]
- Sesko, D.W.; Walker, T.G.; Wieman, C.E. Behavior of Neutral Atoms in a Spontaneous Force Trap. J. Opt. Soc. Am. B 1991, 8, 946. [Google Scholar] [CrossRef]
- Walker, T.; Sesko, D.; Wieman, C. Collective Behavior of Optically Trapped Neutral Atoms. Phys. Rev. Lett. 1990, 64, 408. [Google Scholar] [CrossRef]
- Steane, A.M.; Chowdhury, M.; Foot, C.J. Radiation force in the magneto-optical trap. J. Opt. Soc. Am. B 1992, 9, 2142. [Google Scholar] [CrossRef]
- De Oliveira, R.S.; Raposo, E.P.; Vianna, S.S. Numerical Study of Magneto-Optical Traps through a Hierarchical Tree Method. Phys. Rev. A 2004, 70, 023402. [Google Scholar] [CrossRef]
- Fioretti, A.; Molisch, A.F.; Müller, J.H.; Verkerk, P.; Allegrini, M. Observation of Radiation Trapping in a Dense Cs Magneto-Optical Trap. Opt. Commun. 1998, 149, 415. [Google Scholar] [CrossRef]
- Arnold, A.S.; Manson, P.J. Atomic Density and Temperature Distributions in Magneto-Optical Traps. J. Opt. Soc. Am. B 2000, 17, 497. [Google Scholar] [CrossRef]
- Gajda, M.; Mostowski, J. Three-Dimensional Theory of the Magneto-Optical Trap: Doppler Cooling in the Low-Intensity Limit. Phys. Rev. A 1994, 49, 4864. [Google Scholar] [CrossRef] [PubMed]
- Haas, F. Variational Method for the Three-Dimensional Many-Electron Dynamics of Semiconductor Quantum Wells. AIP Conf. Proc. 2012, 1421, 100. [Google Scholar]
- Hurst, J.; Lévêque-Simon, K.; Hervieux, P.A.; Manfredi, G.; Haas, F. High-Harmonic Generation in a Quantum Electron Gas Trapped in a Nonparabolic and Anisotropic Well. Phys. Rev. A 2016, 93, 205402. [Google Scholar] [CrossRef]
- Manfredi, G.; Hervieux, P.A.; Haas, F. Nonlinear Dynamics of Electron–Positron Clusters. New J. Phys. 2012, 14, 075012. [Google Scholar] [CrossRef]
- Haas, F.; Eliasson, B. Time-Dependent Variational Approach for Bose–Einstein Condensates with Nonlocal Interaction. J. Phys. B 2018, 51, 175302. [Google Scholar] [CrossRef]
- Adhikari, S.K. Finite-Well Potential in the 3D Nonlinear Schrödinger Equation: Application to Bose-Einstein Condensation. Eur. Phys. J. D 2007, 42, 279. [Google Scholar] [CrossRef]
- Ghosh, T.K. Vortex Formation in a Slowly Rotating Bose-Einstein Condensate Confined in a Harmonic-plus-Gaussian Laser Trap. Eur. Phys. J. D 2004, 31, 101. [Google Scholar] [CrossRef]
- Salasnich, L. Time-Dependent Variational Approach to Bose–Einstein Condensation. Int. J. Mod. Phys. B 2000, 14, 1. [Google Scholar] [CrossRef]
- Salasnich, L. Generalized Nonpolynomial Schrödinger Equations for Matter Waves under Anisotropic Transverse Confinement. J. Phys. A 2009, 42, 335205. [Google Scholar] [CrossRef]
- Perez-Garcia, V.M.; Michinel, H.; Cirac, J.I.; Lewenstein, M.; Zoller, P. Dynamics of Bose-Einstein Condensates: Variational Solutions of the Gross-Pitaevskii Equations. Phys. Rev. A 1997, 56, 1424. [Google Scholar] [CrossRef]
- Perez-Garcia, V.M.; Michinel, H.; Cirac, J.I.; Lewenstein, M.; Zoller, P. Low Energy Excitations of a Bose-Einstein Condensate: A Time-Dependent Variational Analysis. Phys. Rev. Lett. 1996, 77, 5320. [Google Scholar] [CrossRef] [PubMed]
- Anwara, M.; Faisal, M.; Ahmed, M. An Experimental Investigation of the Trap-Dynamics of a Cesium Magneto-Optical Trap at High Laser Intensities. Eur. Phys. J. D 2013, 67, 270. [Google Scholar] [CrossRef]
- Gattobigio, G.L.; Michaud, F.; Labeyrie, G.; Pohl, T.; Kaiser, R. Long Range Interactions between Neutral Atoms. AIP Conf. Proc. 2006, 862, 211. [Google Scholar]
- Chanelière, T.; He, L.; Kaiser, R.; Wilkowski, D. Three Dimensional Cooling and Trapping with a Narrow Line. Eur. Phys. J. D 2006, 46, 507. [Google Scholar] [CrossRef]
- Gaudesius, M.; Zhang, Y.-C.; Pohl, T.; Kaiser, R.; Labeyrie, G. Three-Dimensional Simulations of Spatiotemporal Instabilities in a Magneto-Optical Trap. Phys. Rev. A 2022, 105, 013112. [Google Scholar] [CrossRef]
- Gaudesius, M.; Kaiser, R.; Labeyrie, G.; Zhang, Y.-C.; Pohl, T. Instability Threshold in a Large Balanced Magneto-Optical Trap. Phys. Rev. A 2020, 101, 053626. [Google Scholar] [CrossRef]
- Boudot, R.; McGilligan, J.P.; Moore, K.R.; Maurice, V.; Martinez, G.D.; Hansen, A.; de Clercq, E.; Kitching, J. Enhanced Observation Time of Magneto-Optical Traps using Micro-Machined Non-Evaporable Getter Pumps. Sci. Rep. 2020, 10, 16590. [Google Scholar] [CrossRef]
- Pérez-Ríos, J.; Sanz, A.S. How does a Magnetic Trap Work? Am. J. Phys. 2013, 81, 836. [Google Scholar] [CrossRef]
- Devlin, J.A.; Tarbutt, M.R. Laser Cooling and Magneto-Optical Trapping of Molecules Analyzed using Optical Bloch Equations and the Fokker-Planck-Kramers Equation. Phys. Rev. A 2018, 98, 063415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, F.; Soares, L.G.F. Nonlinear Dynamics in Isotropic and Anisotropic Magneto-Optical Traps. Atoms 2022, 10, 83. https://doi.org/10.3390/atoms10030083
Haas F, Soares LGF. Nonlinear Dynamics in Isotropic and Anisotropic Magneto-Optical Traps. Atoms. 2022; 10(3):83. https://doi.org/10.3390/atoms10030083
Chicago/Turabian StyleHaas, Fernando, and Luiz Gustavo Ferreira Soares. 2022. "Nonlinear Dynamics in Isotropic and Anisotropic Magneto-Optical Traps" Atoms 10, no. 3: 83. https://doi.org/10.3390/atoms10030083
APA StyleHaas, F., & Soares, L. G. F. (2022). Nonlinear Dynamics in Isotropic and Anisotropic Magneto-Optical Traps. Atoms, 10(3), 83. https://doi.org/10.3390/atoms10030083