Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival
Abstract
:1. Introduction
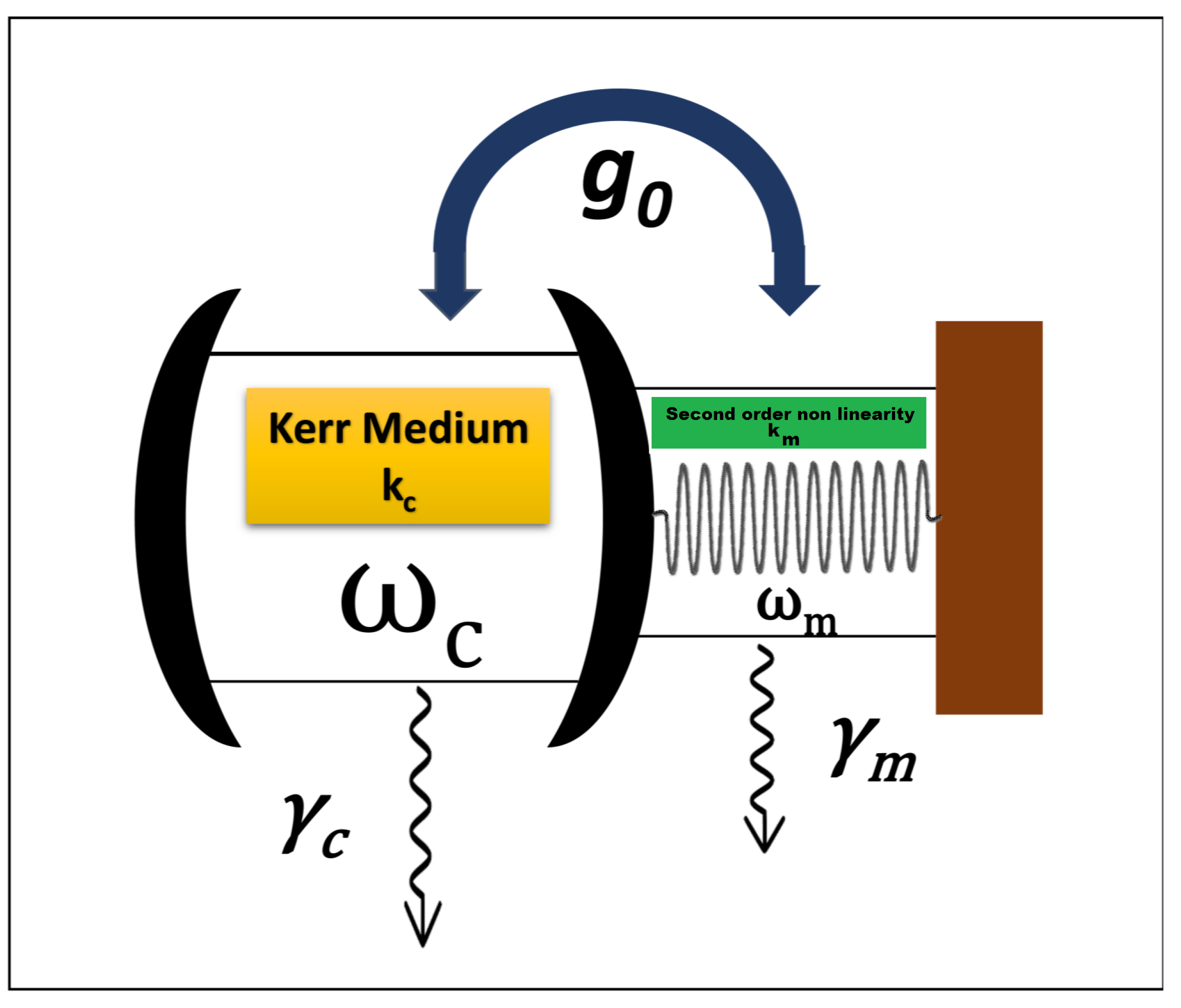
2. Quantum Memory Model
2.1. Hamiltonian for Quantum Information Dynamics
2.2. Master Equation and Phase Space Representation of Quantum States
2.3. Details of Numerical Simulations
3. Results and Discussion
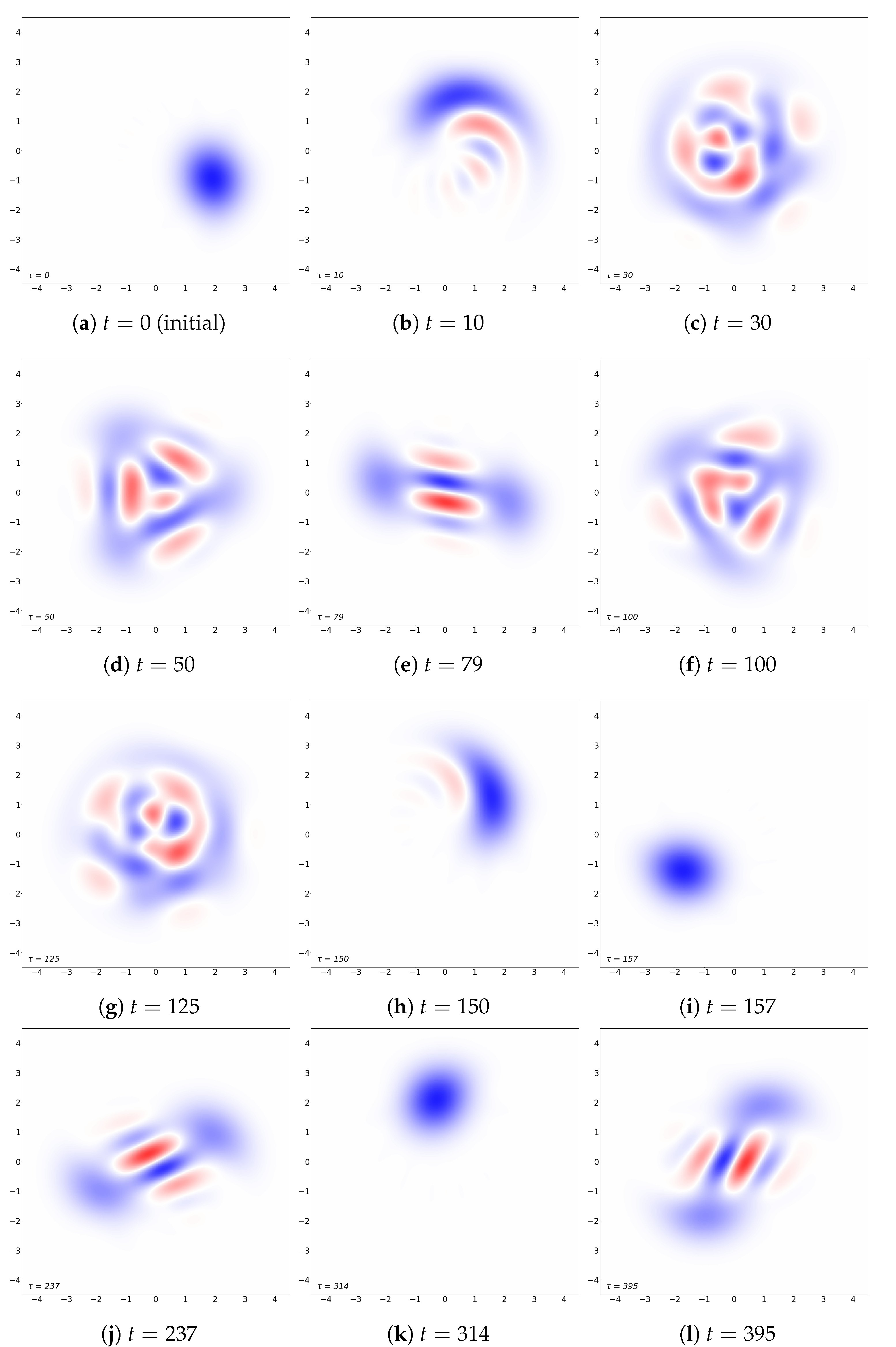
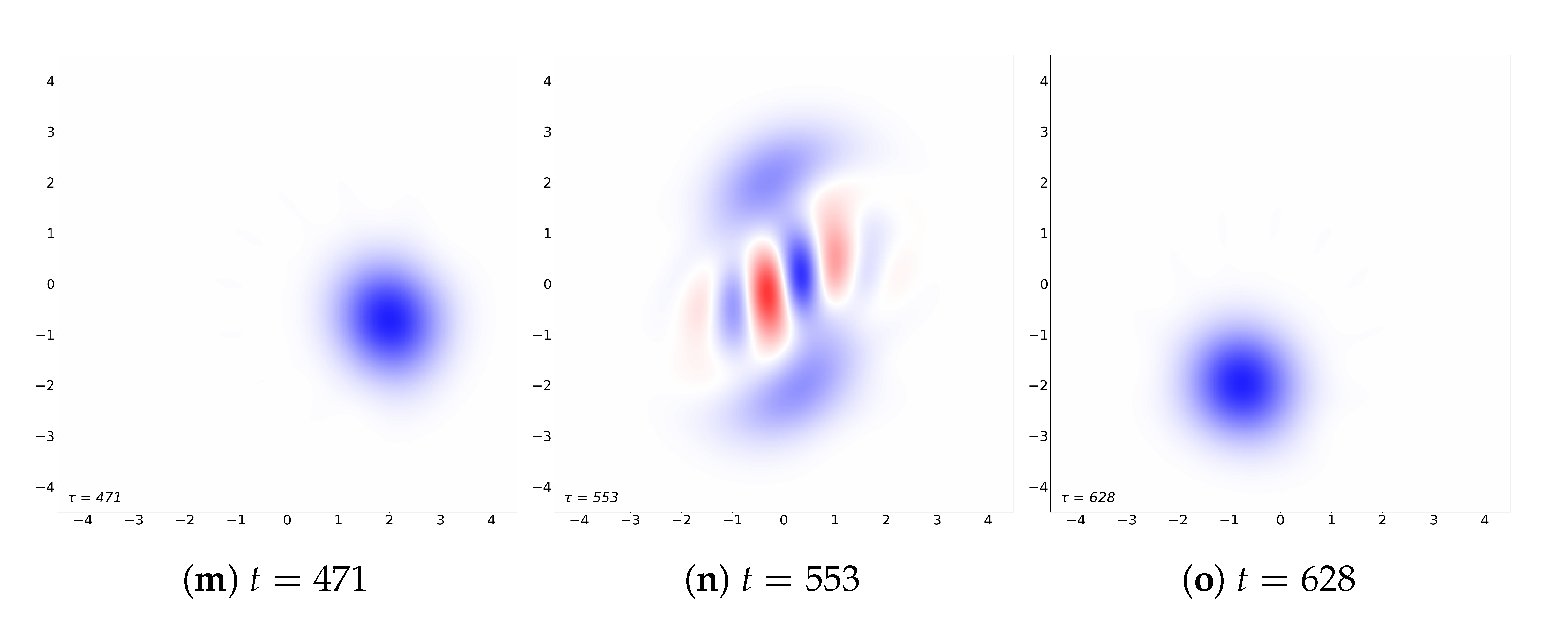
3.1. Visualization of the Time Evolution through Wigner Representation
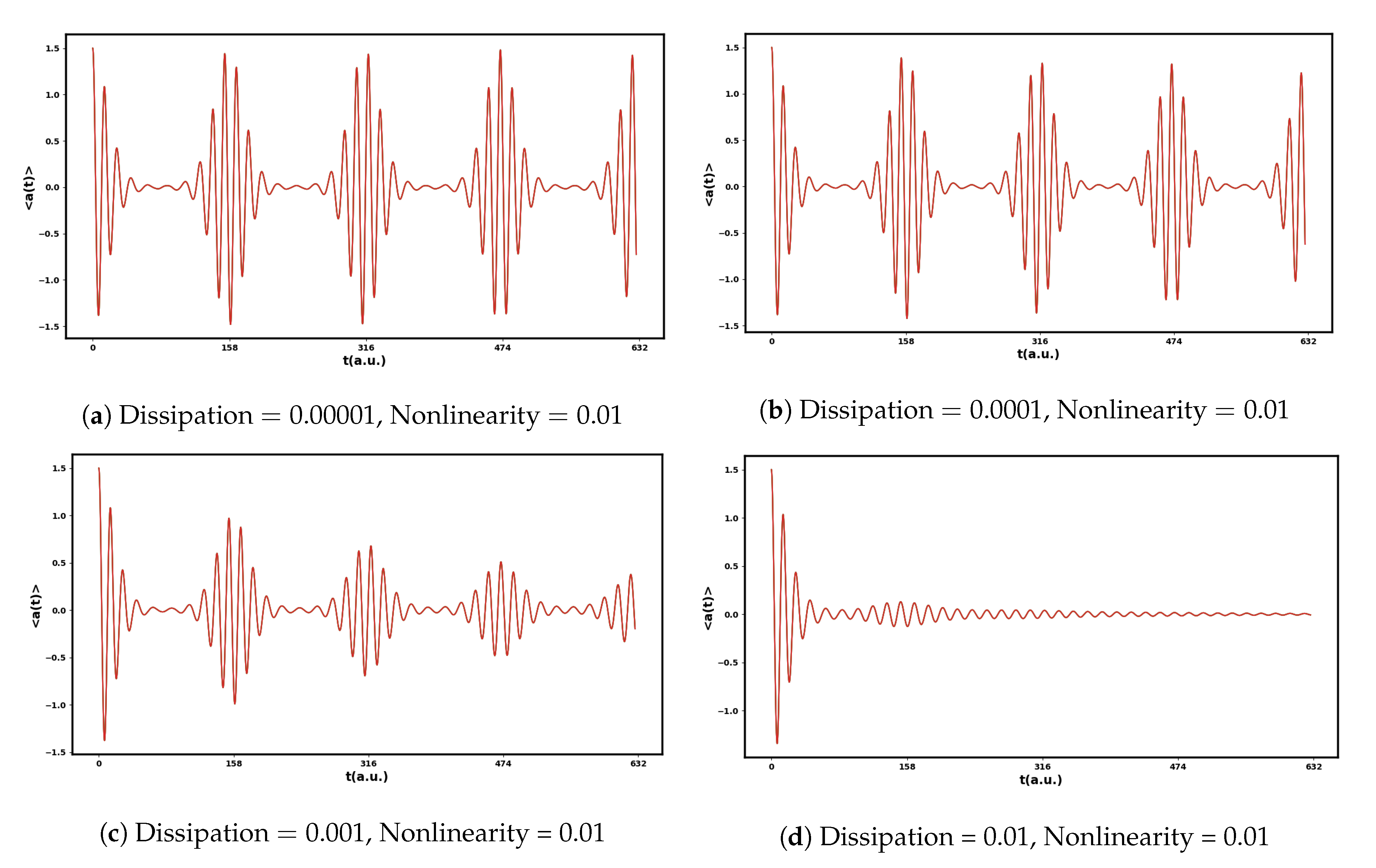
3.2. Evolution of the Expectation Value of the Amplitude
3.2.1. The Effect of Environment
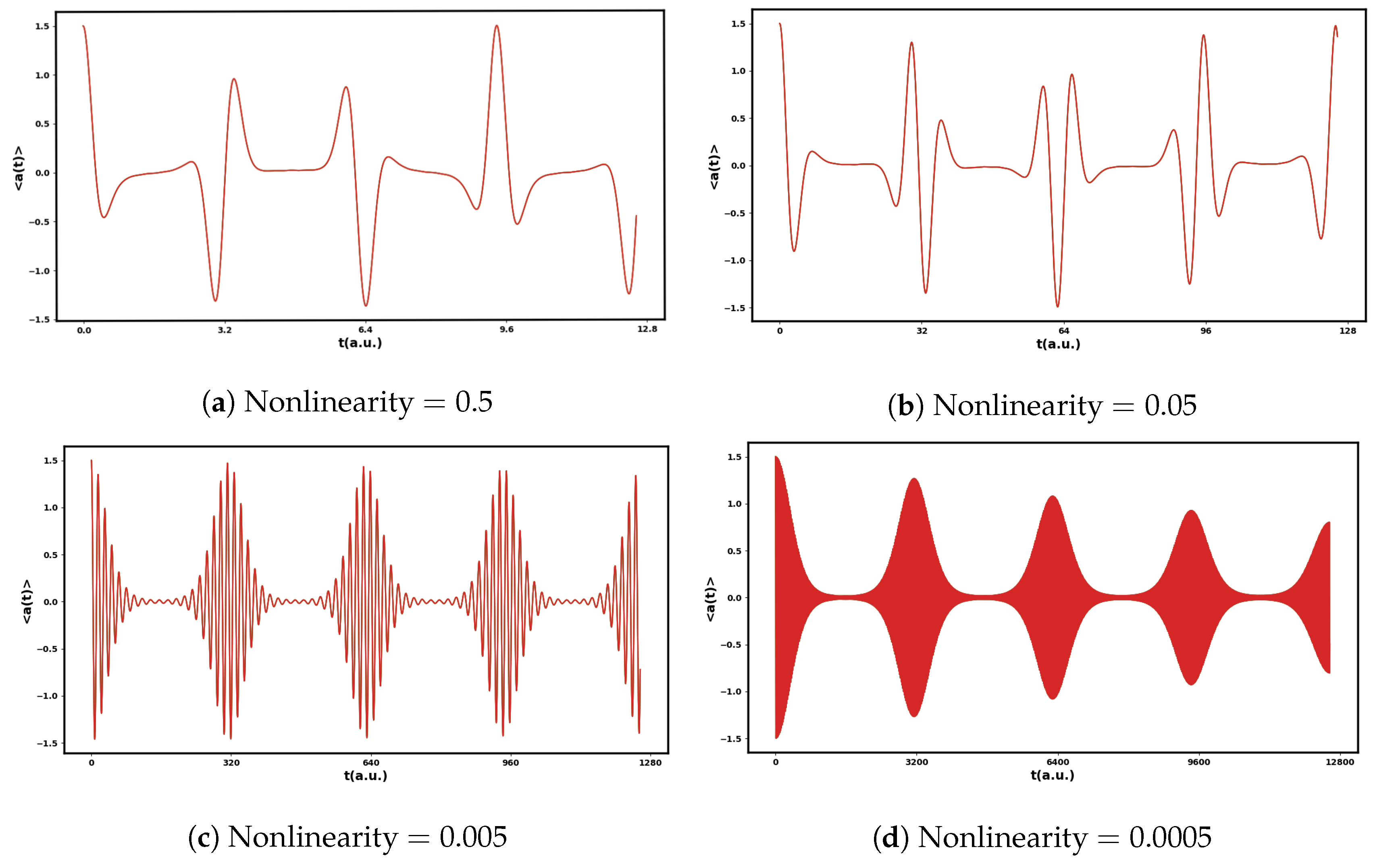
3.2.2. The Effect of Nonlinearity in System
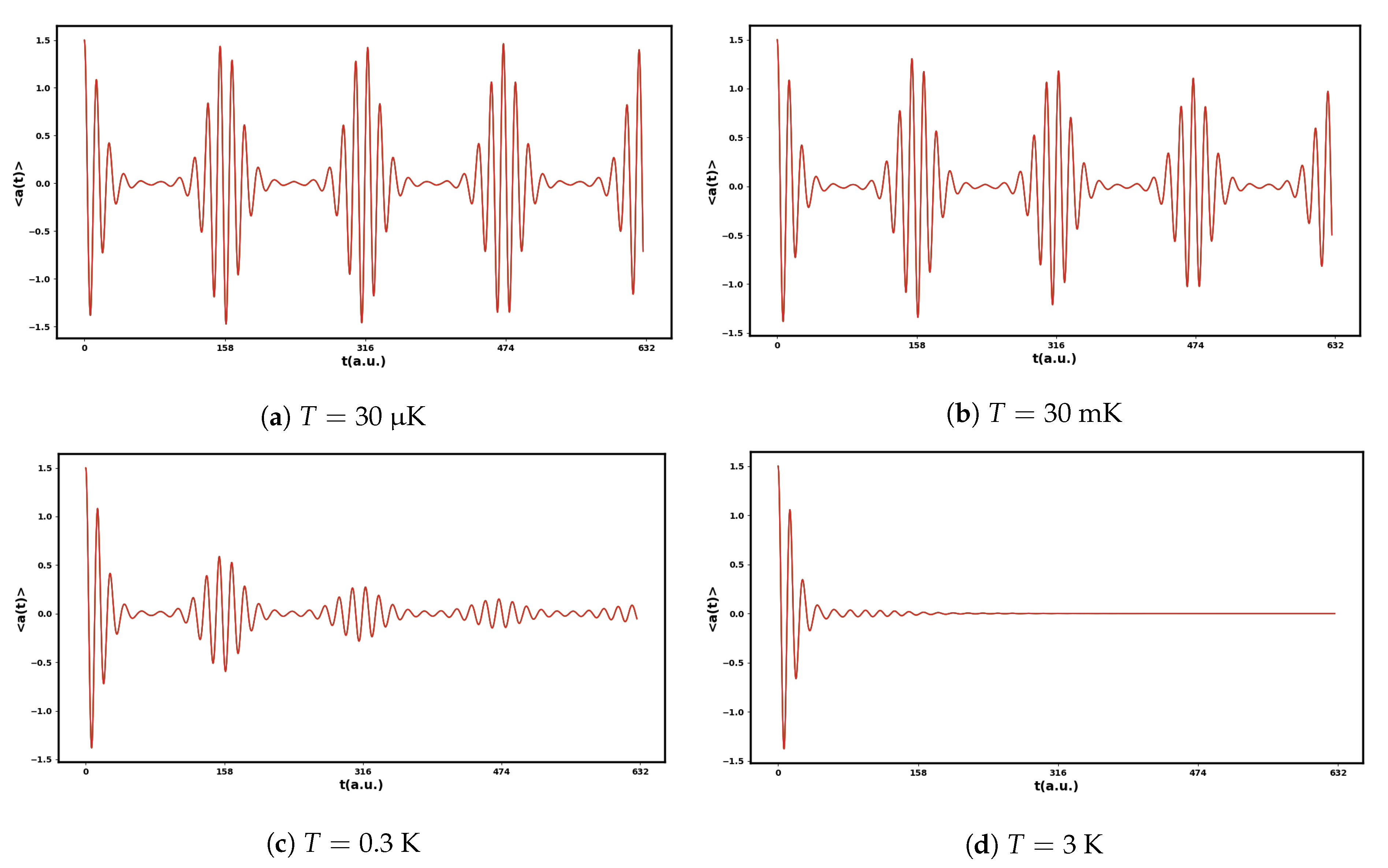
3.2.3. The Effect of Bath Temperature
3.2.4. The Effect of Initial Amplitude of Coherent State
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lvovsky, A.; Sanders, B.; Tittel, W. Optical quantum memory. Nat. Photonics 2009, 3, 706–714. [Google Scholar] [CrossRef]
- Bussières, F.; Sangouard, N.; Afzelius, M.; de Riedmatten, H.; Simon, C.; Tittel, W. Prospective applications of optical quantum memories. J. Mod Opt. 2013, 60, 1519–1537. [Google Scholar] [CrossRef]
- Lobino, M.; Kupchak, C.; Figueroa, E.; Lvovsky, A.I. Memory for Light as a Quantum Process. Phys. Rev. Lett. 2009, 102, 203601. [Google Scholar] [CrossRef]
- Bimbard, E.; Boddeda, R.; Vitrant, N.; Grankin, A.; Parigi, V.; Stanojevic, J.; Ourjoumtsev, A.; Grangier, P. Homodyne Tomography of a Single Photon Retrieved on Demand from a Cavity-Enhanced Cold Atom Memory. Phys. Rev. Lett. 2014, 112, 033601. [Google Scholar] [CrossRef]
- Cao, M.; Hoffet, F.; Qiu, S.; Sheremet, A.S.; Laurat, J. Efficient reversible entanglement transfer between light and quantum memories. Optica 2020, 7, 1440–1444. [Google Scholar] [CrossRef]
- Hétet, G.; Peng, A.; Johnsson, M.T.; Hope, J.J.; Lam, P.K. Characterization of electromagnetically-induced-transparency-based continuous-variable quantum memories. Phys. Rev. A 2008, 77, 012323. [Google Scholar] [CrossRef]
- Afzelius, M.; Simon, C.; de Riedmatten, H.; Gisin, N. Multimode quantum memory based on atomic frequency combs. Phys. Rev. A 2009, 79, 052329. [Google Scholar] [CrossRef]
- Nunn, J.; Reim, K.; Lee, K.C.; Lorenz, V.O.; Sussman, B.J.; Walmsley, I.A.; Jaksch, D. Multimode Memories in Atomic Ensembles. Phys. Rev. Lett. 2008, 101, 260502. [Google Scholar] [CrossRef]
- Vivoli, V.C.; Sangouard, N.; Afzelius, M.; Gisin, N. High-bandwidth quantum memory protocol for storing single photons in rare-earth doped crystals. New J. Phys. 2013, 15, 095012. [Google Scholar] [CrossRef]
- Teh, R.Y.; Kiesewetter, S.; Reid, M.D.; Drummond, P.D. Simulation of an optomechanical quantum memory in the nonlinear regime. Phys. Rev. A 2017, 96, 013854. [Google Scholar] [CrossRef]
- Teh, R.Y.; Kiesewetter, S.; Drummond, P.D.; Reid, M.D. Creation, storage, and retrieval of an optomechanical cat state. Phys. Rev. A 2018, 98, 063814. [Google Scholar] [CrossRef]
- Braasch, W.F.; Friedman, O.D.; Rimberg, A.J.; Blencowe, M.P. Wigner current for open quantum systems. Phys. Rev. A 2019, 100, 012124. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sarma, A.K. Enhancing quantum correlations in an optomechanical system via cross-Kerr nonlinearity. J. Opt. Soc. Am. B 2017, 34, 1503–1510. [Google Scholar] [CrossRef]
- He, Q.Y.; Reid, M.D.; Giacobino, E.; Cviklinski, J.; Drummond, P.D. Dynamical oscillator-cavity model for quantum memories. Phys. Rev. A 2009, 79, 022310. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
- Sangouard, N.; Simon, C.; De Riedmatten, H.; Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 2011, 83, 33. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. [Google Scholar] [CrossRef]
- Zaiser, S.; Rendler, T.; Jakobi, I.; Wolf, T.; Lee, S.Y.; Wagner, S.; Bergholm, V.; Schulte-Herbrüggen, T.; Neumann, P.; Wrachtrup, J. Enhancing quantum sensing sensitivity by a quantum memory. Nat. Commun. 2016, 7, 12279. [Google Scholar] [CrossRef]
- Palomaki, T.; Harlow, J.; Teufel, J.; Simmonds, R.; Lehnert, K.W. Coherent state transfer between itinerant microwave fields and a mechanical oscillator. Nature 2013, 495, 210–214. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.; Mayer, K.; Teufel, J.; Burkhart, L.; Pfaff, W.; Reagor, M.; Sletten, L.; Ma, X.; Schoelkopf, R.; Knill, E.; et al. Faithful conversion of propagating quantum information to mechanical motion. Nat. Phys. 2017, 13, 1163–1167. [Google Scholar] [CrossRef]
- Wang, Y.D.; Clerk, A.A. Using Interference for High Fidelity Quantum State Transfer in Optomechanics. Phys. Rev. Lett. 2012, 108, 153603. [Google Scholar] [CrossRef] [PubMed]
- Kirchmair, G.; Vlastakis, B.; Leghtas, Z.; Nigg, S.E.; Paik, H.; Ginossar, E.; Mirrahimi, M.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 2013, 495, 205–209. [Google Scholar] [CrossRef]
- Rohith, M.; Sudheesh, C. Visualizing revivals and fractional revivals in a Kerr medium using an optical tomogram. Phys. Rev. A 2015, 92, 053828. [Google Scholar] [CrossRef]
- Wigner, E.P. On the quantum correction for thermodynamic equilibrium. In Part I: Physical Chemistry. Part II: Solid State Physics; Springer: Berlin/Heidelberg, Germany, 1997; pp. 110–120. [Google Scholar]
- Hillery, M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Jeong, H.; Ralph, T.C. Schrodinger Cat States for Quantum Information Processing. In Quantum Information with Continuous Variables of Atoms and Light; Imperial College Press: London, UK, 2007; pp. 159–179. [Google Scholar] [CrossRef]
- Curtright, T.L.; Fairlie, D.B.; Zachos, C.K. A Concise Treatise on Quantum Mechanics in Phase Space; World Scientific: Singapore, 2014. [Google Scholar] [CrossRef]
- Katz, I.; Lifshitz, R.; Retzker, A.; Straub, R. Classical to quantum transition of a driven nonlinear nanomechanical resonator. New J. Phys. 2008, 10, 125023. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Cahill, K.E.; Glauber, R.J. Ordered Expansions in Boson Amplitude Operators. Phys. Rev. 1969, 177, 1857–1881. [Google Scholar] [CrossRef]
- Kaur, M.; Arora, B.; Arvind. Effect of dissipative environment on collapses and revivals of a non-linear quantum oscillator. Eur. Phys. J. D 2018, 72, 136. [Google Scholar] [CrossRef]
- Case, W.B. Wigner functions and Weyl transforms for pedestrians. Am. J. Phys. 2008, 76, 937–946. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaur, T.; Kaur, M.; Arvind; Arora, B. Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival. Atoms 2022, 10, 81. https://doi.org/10.3390/atoms10030081
Kaur T, Kaur M, Arvind, Arora B. Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival. Atoms. 2022; 10(3):81. https://doi.org/10.3390/atoms10030081
Chicago/Turabian StyleKaur, Tavshabad, Maninder Kaur, Arvind, and Bindiya Arora. 2022. "Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival" Atoms 10, no. 3: 81. https://doi.org/10.3390/atoms10030081
APA StyleKaur, T., Kaur, M., Arvind, & Arora, B. (2022). Generating Sustained Coherence in a Quantum Memory for Retrieval at Times of Quantum Revival. Atoms, 10(3), 81. https://doi.org/10.3390/atoms10030081






