Cross Sections for Electron Scattering from Atomic Tin

Abstract

The relativistic convergent close-coupling method is applied to calculate cross sections for electron scattering from atomic tin. We present integrated and momentum-transfer cross sections for elastic scattering from the ground and the first four excited states of tin for projectile energies ranging from 0.1 to 500 eV. Integrated and selected differential cross sections are presented for excitation to the $5p^2$, $5p6s$, $5p5d$ and $5p6p$ manifolds from the ground state. The total ionisation cross sections are calculated from the ground and the first four excited states, accounting for the direct ionisation of the $5p$ valence shell and the closed $5s$ shell and the indirect contributions from the excitation–autoionisation. The presented results are compared with previous theoretical predictions and an experiment where available. For the total ionisation cross sections, we find good agreement with the experiment and other theories, while for excitation cross sections, the agreement is mixed.

1. Introduction

Tin is a heavy atom with two p-electrons above a cadmium-like core. It has a sufficiently large atomic number for relativistic effects to be important, such as the fine-structure splitting of low-lying energy levels. Accurate data for electron scattering on neutral tin is of great interest for fusion research. The erosion of vessel walls in future tokamak fusion reactors such as ITER is an issue, especially for the graphite divertor tiles which are estimated to erode at rates up to 16 nm/s [1]. A proposed method of monitoring this erosion is to embed a marker such as tin into the wall tiles which will enter the core after some amount of erosion to the tiles, producing an observable spectral signature which can be used to identify and locate the damage. Accurate and comprehensive collision data for electron scattering on neutral and all ion stages of tin will enable the modelling of plasma containing tin and the identification of tin spectral signatures across the different regions of the fusion plasma.

Data presented by this work will also be useful to the nano-lithography industry, particularly in relevance to extreme ultraviolet (EUV) lithography [2]. Highly charged ions of tin are needed to generate the hundreds of watts of EUV radiation required for lithographic processes. These ions are produced through the irradiation of a droplet of molten tin with a laser, resulting in a hot and dense plasma [3]. However, the exact origins of EUV light from this plasma are not well-understood and plasma models have been produced to investigate this phenomenon [4]. Comprehensive datasets for electron interaction with various charge states of tin are required for the accurate modelling of such plasma. Here, we consider the interaction with neutral tin while the study of scattering from tin ions is planned for the future.

The collision data available for electron scattering on atomic tin is limited to a few theoretical works and one experimental study. The electron impact excitation of tin was first studied theoretically by Srivastava et al. [5], in 2002, using the relativistic distorted-wave (RDW) method. They used the multi-configuration Dirac–Fock (MCDF) program [6] for the calculation of the target wave functions. Differential cross sections (DCSs) and spin-polarisation parameters were presented for the Group IV elements of C, Si, Ge and Sn at incident electron energies of 25 and 40 eV. These cross sections and spin-polarisation parameters were calculated for excitations from the ground $5p^2$ ${}^3{P}_0$ state to the ${}^3{P}_1$, ${}^3{P}_2$ and ${}^1{D}_2$ states. As there were no previous calculations or experimental data to compare with for tin, good agreement found by Srivastava et al. [5] using the same methodology for lead [7] gave some indications on the reliability of the produced results.

Sharma et al. [8] studied the electron-impact excitation of the 5$p^2$ ground state to the entire 5p6s manifold in the tin atom. The target states were calculated using the GRASP2k program [9]. The first few low-lying energy levels were presented together with oscillator strengths for dipole-allowed transitions. Comparisons with the recommended values from NIST [10] alongside the Breit–Pauli configuration-interaction (CI) calculations performed by Oliver and Hibbert [11] were also provided. Good agreement was found for both the energy levels and oscillator strengths. Sharma et al. [8] presented DCSs for excitations from the ground $5p^2$ ${}^3{P}_0$ state to all states in the $5s6s$ manifold at 20, 50, 80 and 100 eV. Alongside these, integrated cross sections (ICS) were also presented for all 20 possible transitions from all states in the ground $5p^2$ configuration to the $5p6s$ manifold in the incident electron energy range of 5–100 eV. To estimate the accuracy of their results, Sharma et al. [8] repeated the calculations using the flexible atomic code (FAC) [12]. It was found that the RDW and FAC results were in good agreement over the entire projectile energy range. As there were no other calculations to compare with, the reliability of these results was attributed to the good agreement found in the structure model.

The only experimental results available for e-Sn scattering were published in 1990 by Freund et al. [13] as a part of the single-ionisation cross-sectional measurements for many atoms. These target atoms were prepared by neutralising any charged atoms in the beams by means of a charge transfer. This leads to open-shell atoms forming in meta-stable states alongside the ground state. The uncertainties associated with these measurements were set to be at 10%. They found poor agreement with the theoretical predictions at the time for many of the group 14 elements, including tin. There were no alternative measurements for tin and the agreement Freund et al. [13] found for the other neutral atoms they presented results for was quite variable. Theoretical calculations for the electron-impact total ionisation cross sections for tin (alongside many other elements) were first attempted by McGuire [14], using the generalised oscillator-strength formulation of the Born approximation. A similar work was then published by Bartlett and Stelbovics, in 2002 [15], in which they presented the electron-impact total ionisation cross sections for many atoms, including tin. This included cross sections from not only the valence $5p$ shell but also the closed $5s$ and $4d$ shells. These results were calculated using a non-relativistic analytical Born approximation. They found good agreement with the available data at the time even with the use of a non-relativistic approach. Kim and Stone [16] theoretically modelled the total ionisation cross sections for Sn alongside Ge, Si and Pb. They performed atomic structure calculations using a Dirac–Fock wave function code. The binary-encounter Bethe approximation (BEB) was used for the direct ionisation and scaled plane-wave Born approximation for excitations to autoionising levels. It was found that for open-shell targets such as Sn, direct ionisation from low-lying meta-stable levels and the inclusion of excitation–autoionisation was important. These calculations were performed for the ground and first four excited (meta-stable) states. They found good agreement with the experimental results published by Freund et al. [13].

Here, we present a cross-section dataset for electron scattering on neutral tin in the ground and low-lying excited states. Large-scale close-coupling calculations were performed using the relativistic convergent close-coupling (RCCC) method [17,18,19]. The cross sections were obtained for elastic scattering, various excitation channels and ionisation. The excitation cross sections were calculated for transitions to levels in the $5p^2$, $5p6s$, $5p5d$ and $5p6p$ manifolds. The estimates for the total scattering and total inelastic-scattering cross sections are presented. We compare with the available theoretical results and experiment.

2. RCCC Method

2.1. Target Structure

Atomic tin can be well-described by a model of two active electrons above an inert Dirac–Fock cadmium-like core. The standard two-electron configuration interaction technique [18,20] with the j-j coupling scheme is used to produce the target spectrum. Although this spectrum is dominantly one-electron excitations from the open p-orbital, there are some states corresponding to the excitations from the $5s$ shell that are not modelled by the present approach. The structure calculations are performed in a number of steps. The core [Kr]$4d^{10}$$5s^2$ orbitals are obtained using the GRASP package [21]. A Dirac (L-spinor) basis [22] was used to diagonalise the quasi one-electron Dirac–Fock Hamiltonian for Sn⁺ to produce one-electron orbitals for the s_1/2 to g_9/2 symmetries. The j-dependant fall-off radii for the one-electron polarisation potentials were chosen to best represent the experimental spectrum of Sn, and the static dipole polarisability of Sn²⁺ was taken as 17.75 $a_0^3$ [23] (where $a_0=0.529\times {10}^{-10}$ m denotes the Bohr radius).

The set of two-electron configurations is chosen to best model both bound and continuum spectrum of the tin atom. It contains configurations of the form ($5p_{1/2},n{l}_j$) and ($5p_{3/2},n{l}_j$) with 20 one-electron orbitals included for each j and parity. A total of 180 one-electron orbitals were used, all taken from the Sn⁺ diagonalisation. A second set of configurations of the form ($n{l}_j,n^{\prime }{l}_{j^{\prime }}^{\prime }$) with orbitals restricted to $6s_{1/2}$, $7s_{1/2}$, $5p_{1/2,3/2}$, $6p_{1/2,3/2}$, $5d_{3/2,5/2}$, $6d_{3/2,5/2}$ is included to account more accurately for electron–electron correlations. A total of 1088 of target states with total electronic angular momentum spanning from J = 0 to J = 6 of both positive and negative parity are produced. This includes both bound and continuum pseudo-states. Smaller models were produced which only included different subsets of the total number of states generated. The first model includes all states up to the entire $5p5d$ manifold, comprising a total of 33 bound states. The second model included all 75 bound target states. Three more models were produced, each of which included continuum pseudo-states with energies up to 2, 5 and 10 eV with 152, 237 and 399 states, respectively.

The optical oscillator strength (OOS) (in length form) for the $5p^2$ ${}^3{P}_0$ → $5p6s$ ${}^3{P}_1^{\circ }$ transition was fitted to the value recommended by NIST, $f=0.200$ [10]. This was performed by including a two-electron polarisation potential (described in [24]), with its fall-off radius set to $r_c^{diel}$ = 4.2. The value of the OOS given by the present calculation is 0.211.

Table 1. First 20 excitation energies (eV) for the tin spectrum compared with NIST [10] and Sharma et al. [8].

State	RCCC	NIST	Sharma
$5p^2$  ${}^3{P}_1$	0.210	0.210	0.199
$5p^2$  ${}^3{P}_2$	0.440	0.425	0.423
$5p^2$  ${}^1{D}_2$	1.159	1.068	1.026
$5p^2$  ${}^1{S}_0$	2.345	2.127	2.153
$5p6s$  ${}^3{P}_0^{\circ }$	4.293	4.294	4.234
$5p6s$  ${}^3{P}_1^{\circ }$	4.324	4.328	4.303
$5p6s$  ${}^3{P}_2^{\circ }$	4.814	4.788	4.757
$5p6s$  ${}^1{P}_1^{\circ }$	4.881	4.866	5.003
$5p6p$  ${}^3{D}_1$	5.275	5.248	-
$5p6p$  ${}^3{P}_1$	5.411	5.376	-
$5p6p$  ${}^3{D}_2$	5.415	5.383	-
$5p5d$  ${}^3{F}_2^{\circ }$	5.416	5.414	-
$5p6p$  ${}^3{P}_0$	5.474	5.429	-
$5p5d$  ${}^3{F}_3^{\circ }$	5.546	5.525	-
$5p5d$  ${}^3{D}_2^{\circ }$	5.581	5.472	-
$5p5d$  ${}^3{D}_1^{\circ }$	5.675	5.517	-
$5p6p$  ${}^1{P}_1$	5.835	5.777	-
$5p6p$  ${}^3{D}_3$	5.877	5.827	-
$5p6p$  ${}^3{P}_2$	5.917	5.855	-
$5p5d$  ${}^3{F}_4^{\circ }$	5.946	5.963	-
ionisation limit ($5p^2$)	7.344	7.344	-

shows our first 20 calculated energy levels with comparison with other available data, and

Table 2. Oscillator strengths (in length form and atomic units) for the ground state of tin. RCCC values are compared with NIST [10], Oliver and Hibbert [11] and Sharma et al. [8].

Transition	RCCC	NIST	Oliver	Sharma
$5p^2$${}^3{P}_0$ → $5p6s$ ${}^3{P}_1^{\circ }$	0.211	0.200	0.205	0.202
$5p^2$${}^3{P}_0$ → $5p6s$ ${}^1{P}_1^{\circ }$	0.077	0.061	0.060	0.063
$5p^2$${}^3{P}_0$ → $5p5d$ ${}^3{D}_1^{\circ }$	0.553	0.360	0.388	-

shows comparison of a select few OOS values.

Thierfelder et al. [25] determined the static dipole polarisability for tin both experimentally and theoretically. The experimental value was found to be 42.4 ± 11 $a_0^3$, with the large uncertainty in this value being attributed to difficulty in maintaining the intensity of the tin atom beam. Their theoretical calculation was conducted using all-electron relativistic coupled-cluster theory, which produced a value of 52.9 $a_0^3$. It was found that this theoretical value was in good agreement with previous literature at the time [26]. In the present methodology, the calculated static dipole polarisability of the ground state of tin changed, depending on which RCCC model was used. The smallest 33-state model gave a minimum static dipole polarisability of 26.24 $a_0^3$, which increased with the number of states and converged to a maximum value of 37.94 $a_0^3$ when all 1088 states were included. Our maximum value is systematically lower than those of experiment and accurate theoretical calculations. The reason for this is the structure model adopted in the RCCC calculations that does not allow excitations of the core electrons.

2.2. Scattering Calculations

Once the target states have been calculated, the next step involves producing a set of coupled relativistic Lippmann–Schwinger equations. We only provide a brief introduction to the relativistic convergent close-coupling method here, as it has already been extensively covered in literature [17,18,19].

Expanding the total scattering wave function in the set of target pseudo-states leads to a set of coupled relativistic Lippmann–Schwinger equations for the partial-wave T-matrix for each total angular momentum J and parity $\mathsf{\Pi }$. These equations have the following form,

$$\begin{array}{c}\hfill {\displaystyle T_{fi}^{\mathsf{\Pi }J}(k_f{\kappa }_f,k_i{\kappa }_i)=V_{fi}^{\mathsf{\Pi }J}(k_f{\kappa }_f,k_i{\kappa }_i)+\sum _n\sum _{\kappa }{\displaystyle ⨋}\mathrm{d}k\frac{V_{fn}^{\mathsf{\Pi }J}(k_f{\kappa }_f,k\kappa )T_{ni}^{\mathsf{\Pi }J}(k\kappa ,k_i{\kappa }_i)}{E-{ϵ}_n^N-{ϵ}_k+i0}.}\end{array}$$

(1)

Here, i and f refer to the initial and final states of the projectile and target. k and $\kappa$ refer to the momenta and state of the projectile. $V_{fn}^{\mathsf{\Pi }J}$ refers to the partial-wave V-matrix for each target symmetry. Equation (1) is solved numerically, using a parallelised implementation that invokes a hybrid OpenMP-MPI scheme [17,27]. The T-matrix is then used to calculate scattering amplitudes, cross sections and other collision data for transitions of interest.

Close-coupling calculations have been conducted using several models with an increasing number of states from 33 to 399. We denote these models RCCC(33), RCCC(75), RCCC(152), RCCC(237) and RCCC(399), where the number of states included in the close-coupling calculations are given in parentheses. These models were used to test for convergence and then combined to produce smooth results for the elastic, excitation and total cross sections presented in this work. Calculations were typically performed for partial waves with up to total electronic angular momentum $J=41/2$ for both parities, with calculations at some projectile energies requiring a greater number of partial waves for convergence. An analytical Born subtraction technique is used to speed up the partial-wave convergence. Calculations of ionisation cross sections required the use of larger models, which are discussed in Section 3.7.

3. Results

We first present our results for the elastic scattering, including a discussion about the resonance behaviour. Secondly, we provide a comparison with the previous literature for excitation ICS and DCS to the $5p^2$ manifold as well as the $5p6s$ manifold from the ground ${}^3{P}_0$ state. Following this, we provide our estimates for the integrated cross sections to the $5p5d$ and $5p6p$ manifolds from the ${}^3{P}_0$ ground state. As most of the cross sections are small for transitions to these manifolds, we provide summed results only. We provide a discussion on the convergence of our RCCC models when appropriate. Finally, we present the total cross sections (TCS) and total ionisation cross sections (TICS) from the ground state and low-lying excited states, alongside a comparison with the experiment and previous theoretical results.

3.1. Elastic Scattering

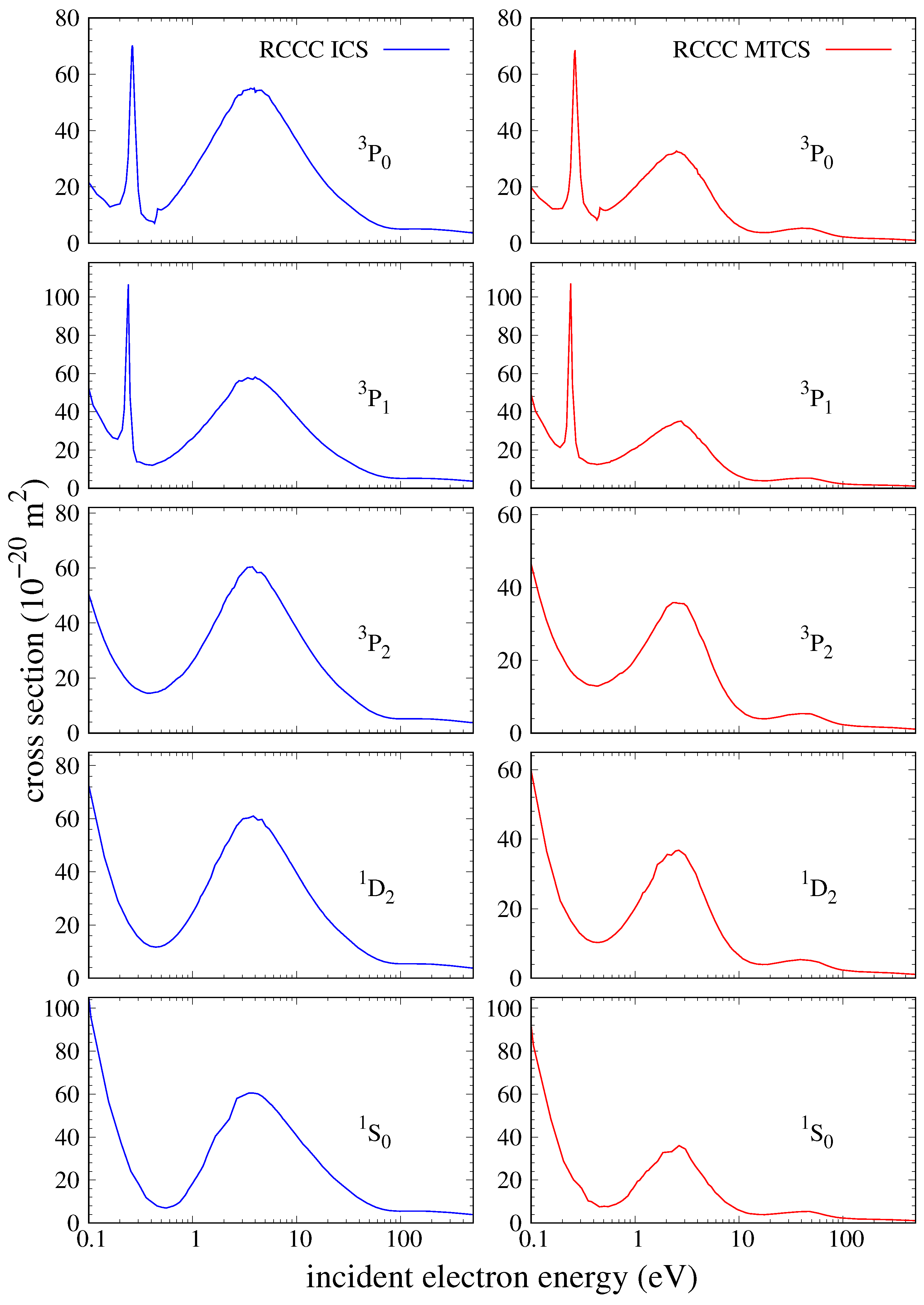
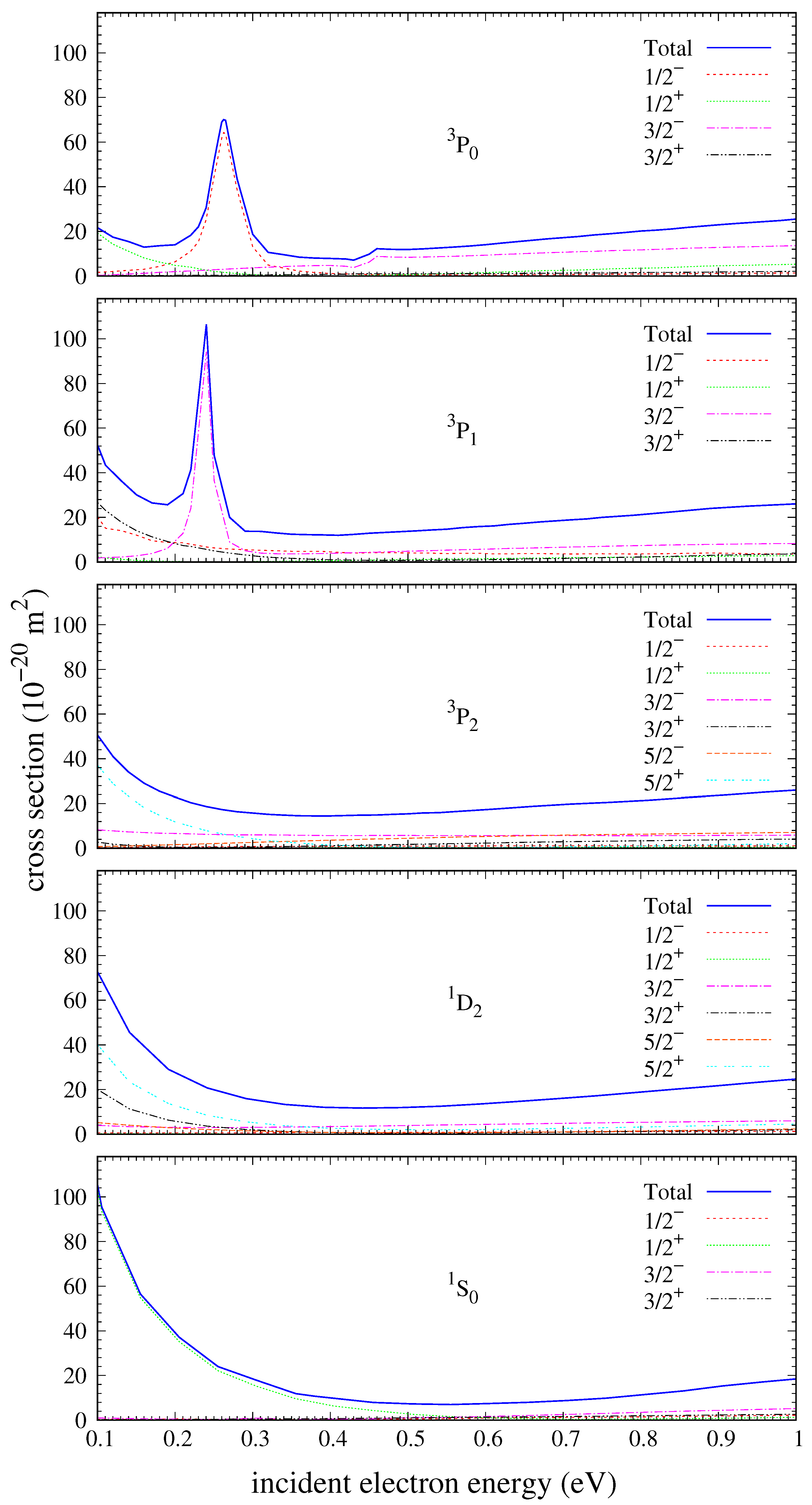
In Figure 1, we present our elastic scattering integrated and momentum-transfer cross sections for the ground and first four excited states of neutral tin. There is no previous experimental or theoretical data to compare with. The elastic ICS for scattering on the ground ${}^3{P}_0$ state displays strong resonance behaviour, with a sharp peak arising at low energy (≈0.2 eV). The partial-wave decomposition for the elastic-scattering cross section is presented in Figure 2 which shows the resonance is in the $J=0.5$ and $\mathsf{\Pi }=-1$ partial wave. Given that the initial target state in this case has $J_T=0$ and ${\mathsf{\Pi }}_T=+1$, the projectile electron must have $J_P=0.5$ and ${\mathsf{\Pi }}_P=-1$. The projectile, therefore, is in a p-wave. The existence of this resonance indicates a short-lived bound state formed between the projectile electron and the tin atom with the formation of Sn⁻. This p-wave resonance is visible again for elastic scattering on the first excited state (with term ${}^3{P}_1$), for which it appears in the $J=1.5$ and $\mathsf{\Pi }=-1$ partial wave. The locations and magnitudes of these resonances changed marginally with the increasing static dipole polarisability within our models, and as models with larger numbers of states were unstable in this low-energy regime, the RCCC(33) model was utilised.

The resonance behaviour at about 0.2 eV is only present for elastic scattering from the ground and first excited states with the second, third and fourth excited states having smooth behaviour in that region. The cross section for the ground state has a small structure at about 0.4 eV. The partial-wave decomposition of this cross section, given in Figure 2, shows that this behaviour comes from the $J=1.5$ and $\mathsf{\Pi }=-1$ partial wave. The projectile is in a p-wave, with $J_P=1.5$ and ${\mathsf{\Pi }}_P=-1$. All the elastic-scattering cross sections for the $5p^2$ manifold have a wide resonance which peaks at about 4 eV. The cross sections become relatively small from about 80 eV onwards. The momentum-transfer cross sections follow the same trends, except that they have smaller peaks and fall off much faster, becoming relatively small by 10 eV. At projectile energies of about 40–50 eV, the momentum-transfer cross sections also have a relatively small second peak.

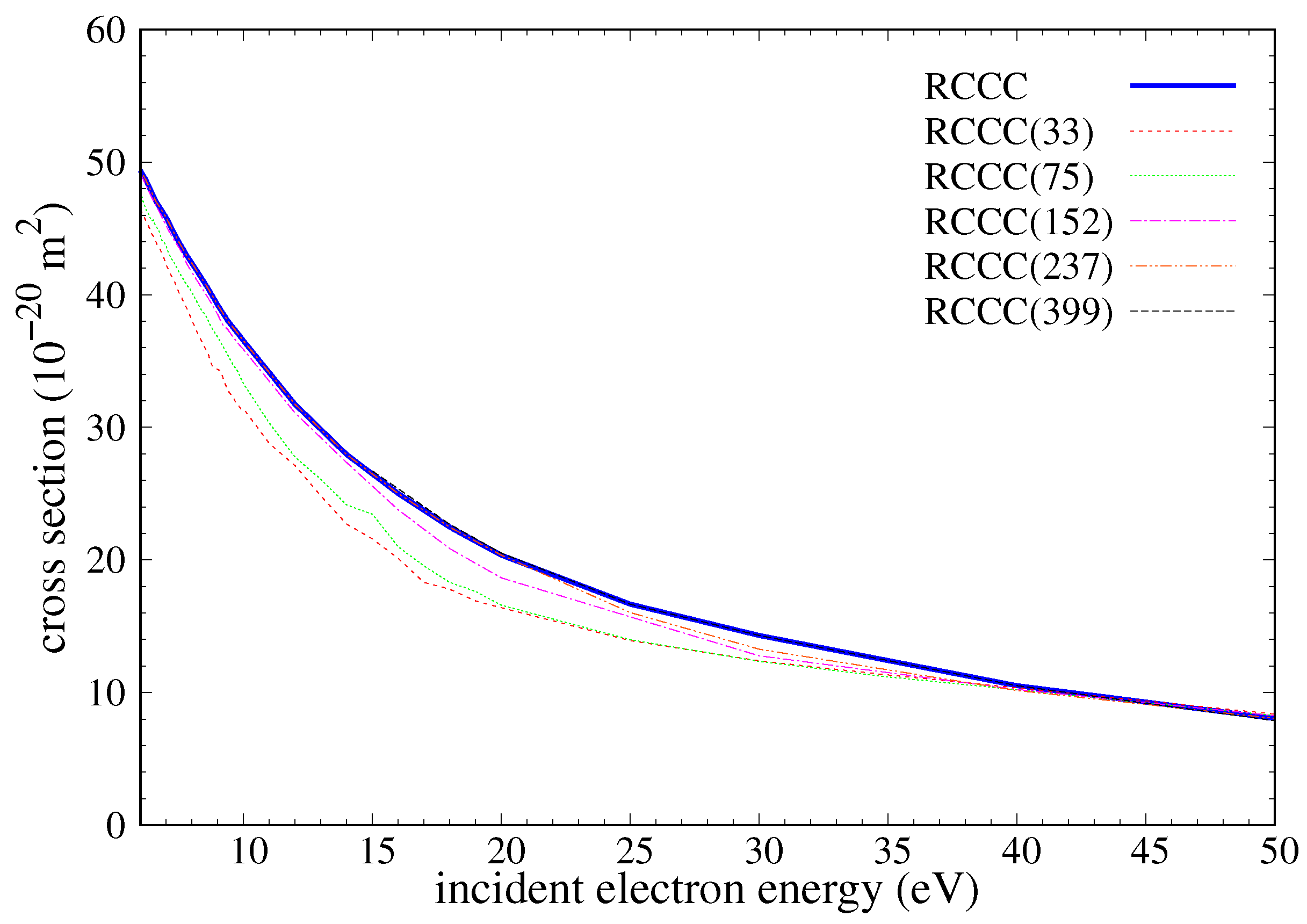
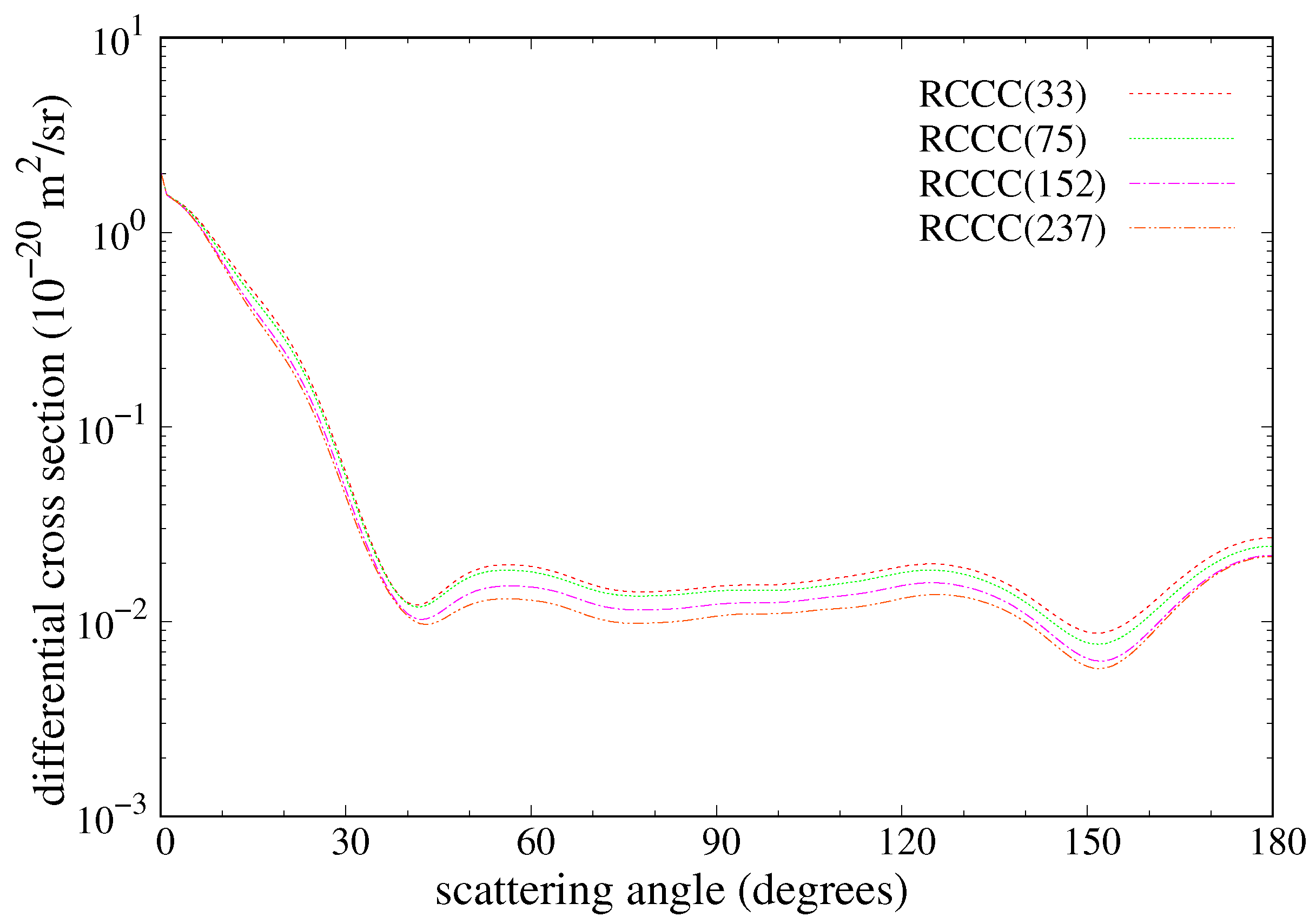
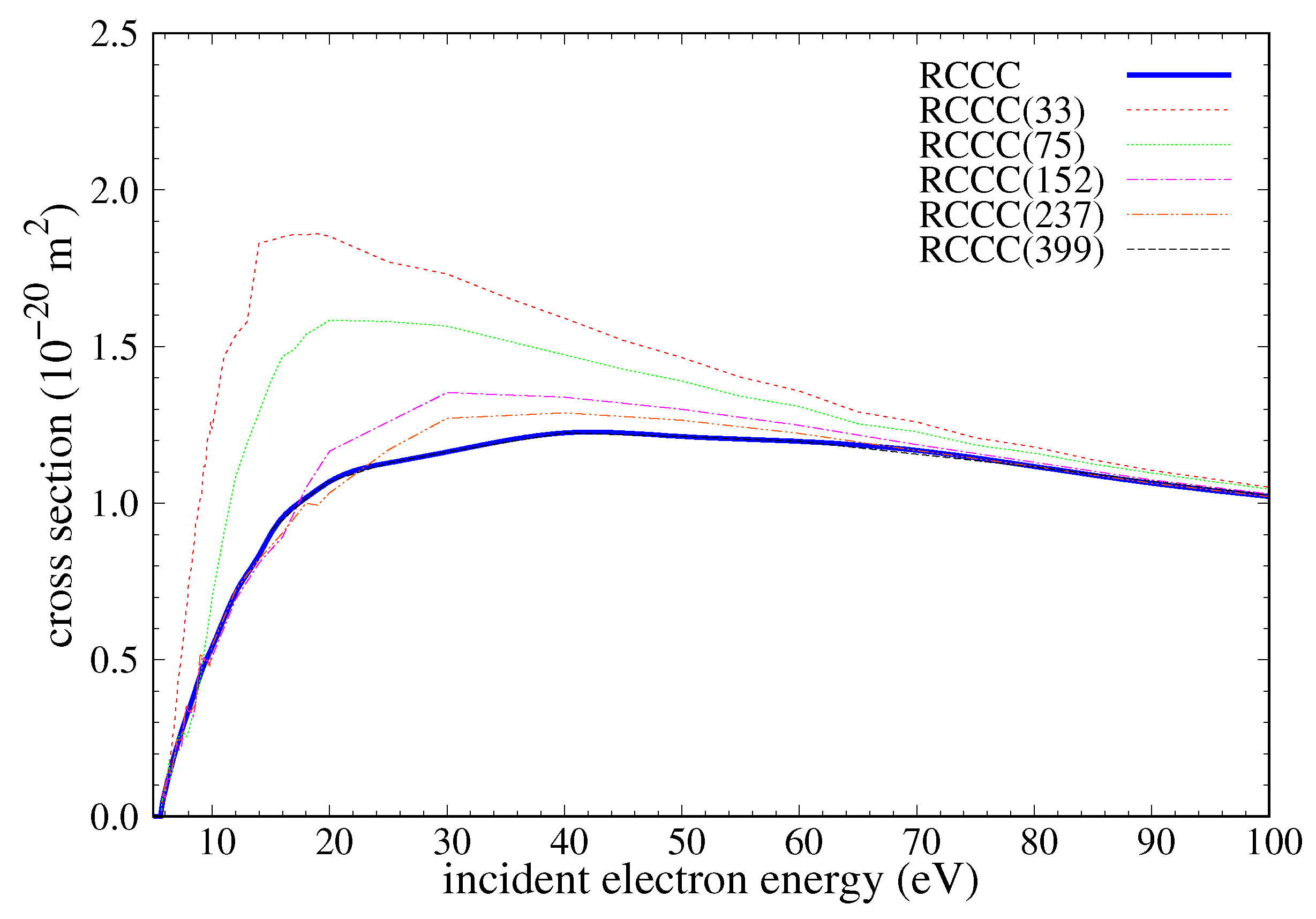
Figure 3 demonstrates the convergence of the RCCC elastic-scattering cross section with the number of states included in the close-coupling expansion. There is good agreement between the two largest models (RCCC(237) and RCCC(399)) over the energy range, and all the models converge at high energy. The combined cross section refers to the final result produced by taking the appropriate RCCC models in different parts of the energy range. The low energy results shown in Figure 1 and Figure 2 are obtained from the smaller RCCC(33) and RCCC(75) models. The intermediate-to-high-energy regions are better represented by the RCCC(237) and RCCC(399) models. The larger models were only run at energies above 4 eV due to their significant computational cost. All the models suffer from the numerical instabilities related to the non-uniqueness of the solutions of the T-matrix equations [20], though the smaller models are effected less. In order to minimise the effects of numerical instability on our cross sections, we ran our calculations several times with differing numerical parameters and averaged the results to produce sufficiently smooth estimates.

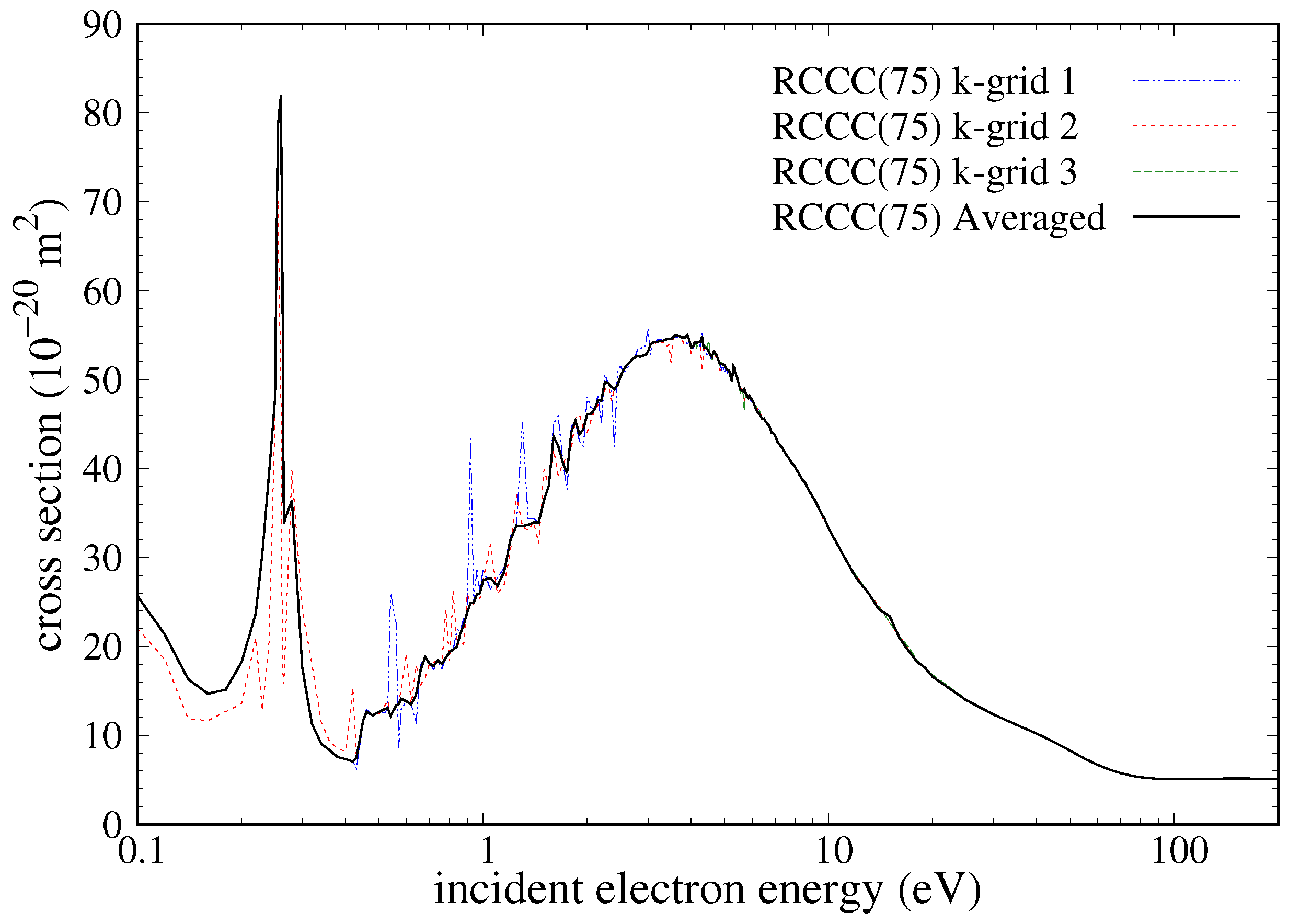
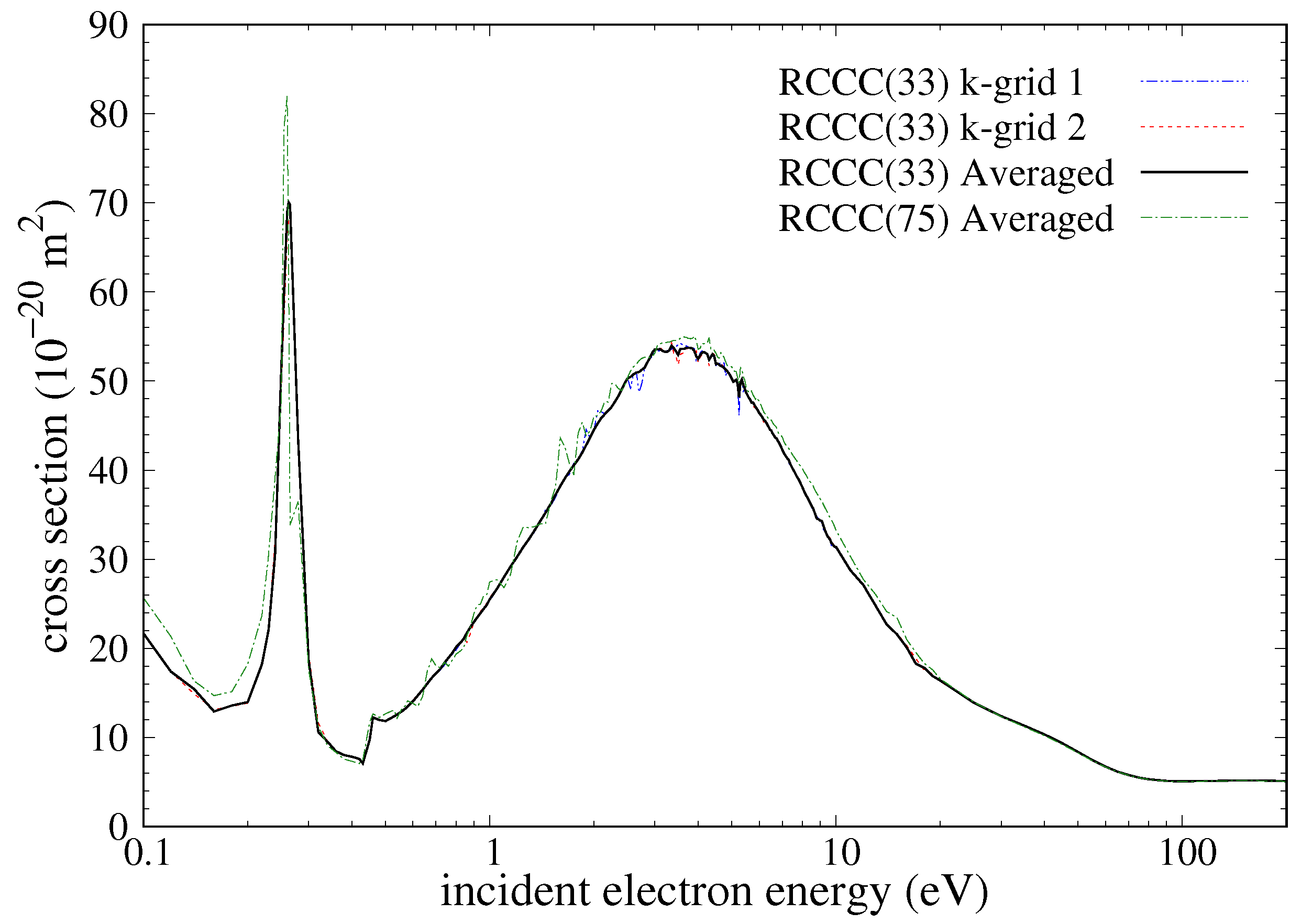
The averaging procedure applied takes in two or more cross sections for the same scattering process which have been calculated using varying numerical parameters and produces a smooth result. The procedure calculates the gradient between adjacent points in the cross section and chooses the next point from either of the input calculations based on which minimises the change in the gradient. Figure 4 illustrates the impact of the used averaging technique on the elastic-scattering cross section for the ground state calculated using the RCCC(75) model. A total of three slightly different momentum-space integration grids (k-grids) were used, with one of them only being used to calculate for projectile energies greater than 4 eV. For the cross section below 4 eV, the RCCC(33) model was used as it is stable and sufficiently converged to the averaged RCCC(75) results as shown in Figure 5. As the RCCC(33) model was sufficiently smooth over most of the projectile energy domain, it was only calculated using two different k-grids which were then averaged using the described technique. Above 4 eV, the RCCC(75) averaged results provide a sufficiently smooth cross section which when combined with the larger RCCC models in the intermediate-to-high-energy range produced the final presented cross section.

3.2. Excitation to the $5p^2$ Manifold

In this section, we present our estimates for the cross sections for excitations to the low-lying levels of the ground $5p^2$ configuration of tin. A comparison with other theoretical results for the corresponding differential cross sections (DCS) at select energies is also given. There are no experimental results to compare with.

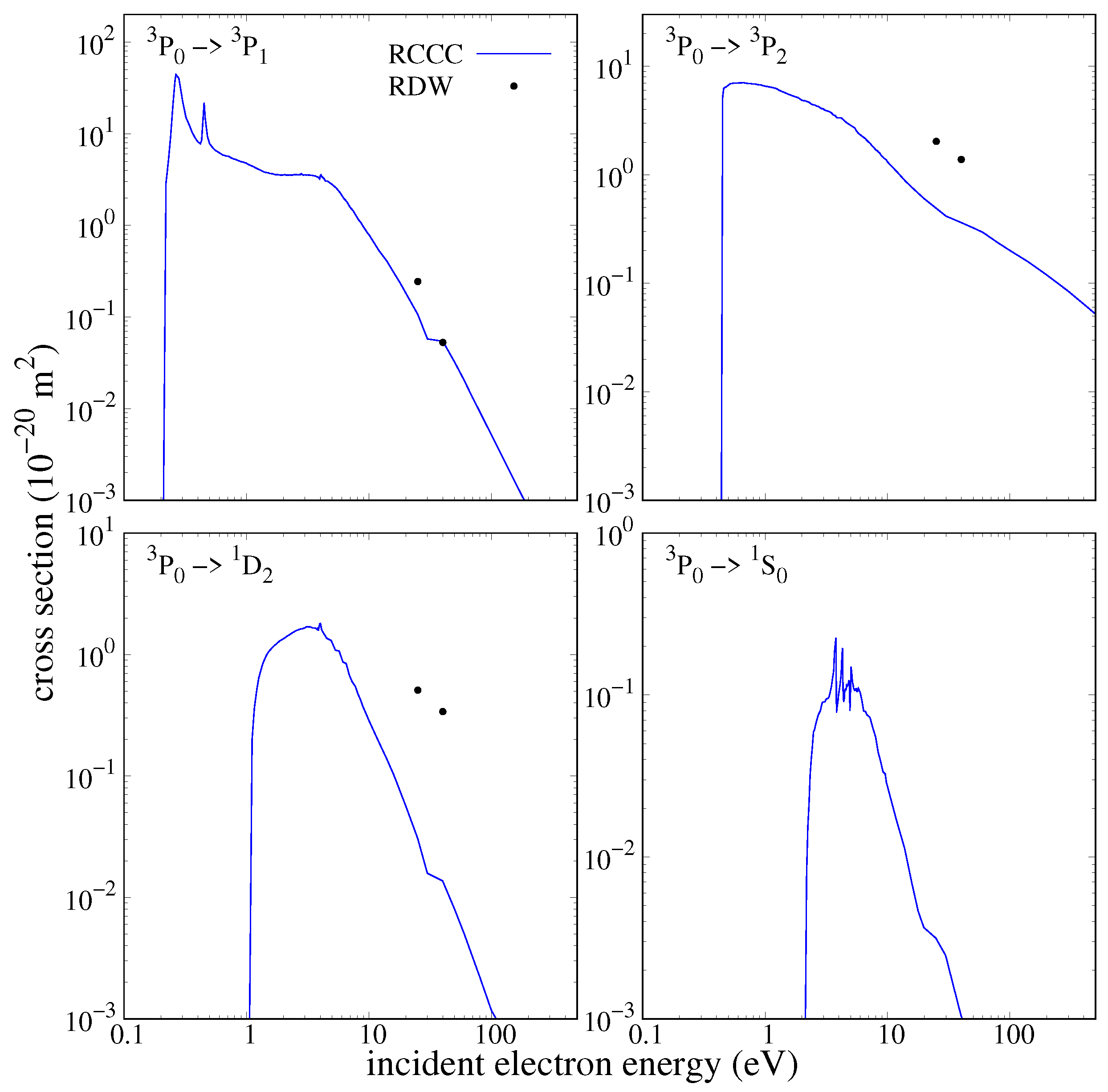
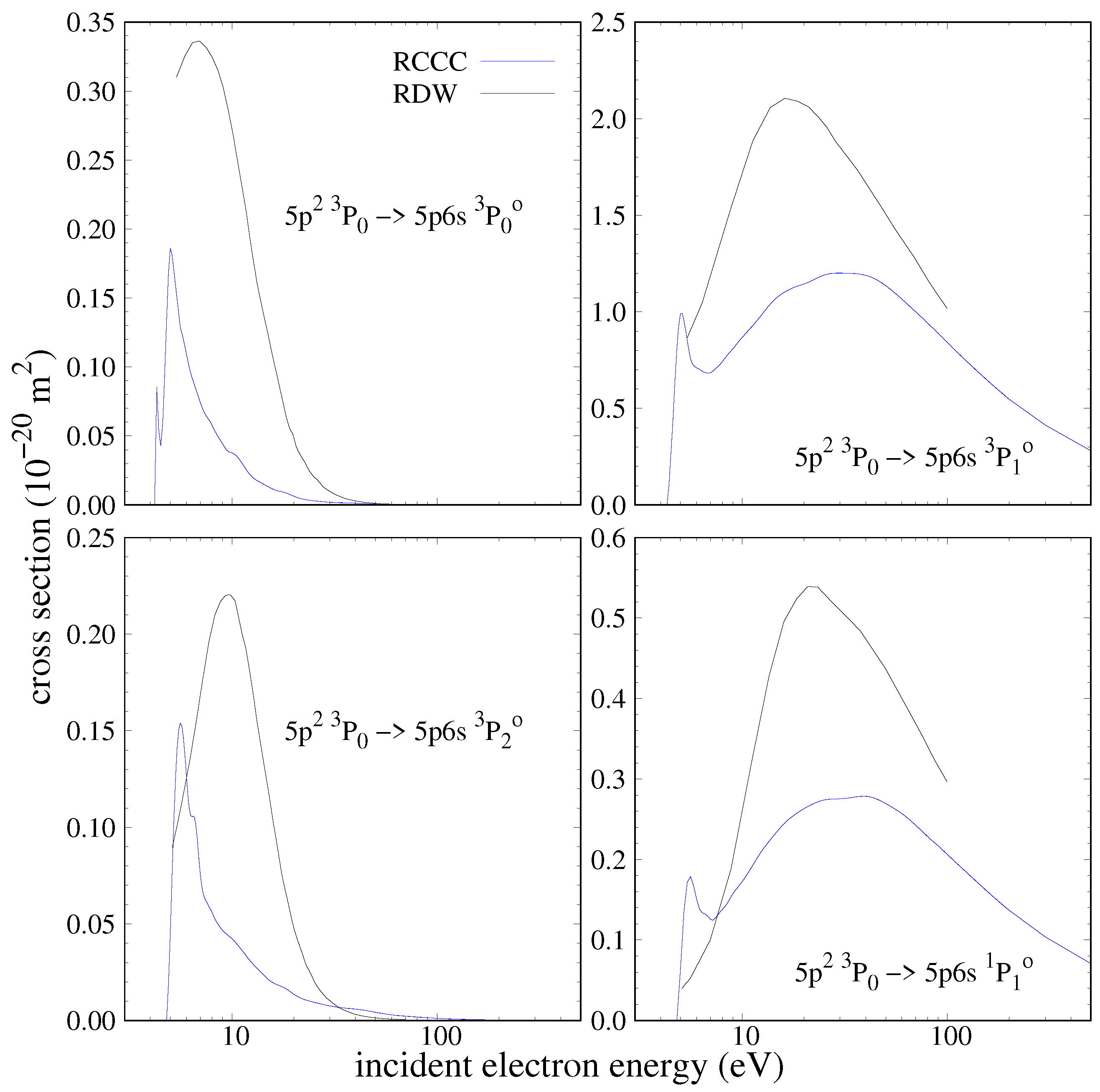
Figure 6 shows the ICS for excitation to the low-lying levels from the ${}^3{P}_0$ state. These are dipole-prohibited transitions by parity and some by spin. The cross sections at low energy are quite large but then drop off quickly with increasing projectile energy. The transition to the first excited ${}^3{P}_1$ state has a sharp double peak and a small plateau before an exponential decline with increasing energy. The transitions to the second ${}^3{P}_2$ and third ${}^1{D}_2$ excited states have a similar sharp rise at the threshold and a fast decline with no significant resonances. The excitation cross section for the ${}^1{S}_0$ state displays some resonance behaviour at its peak and is much smaller in magnitude than the other transitions. A comparison with the ICS calculated by Srivastava et al. [5] using the RDW model for excitation to the first three excited states is also provided. Only DCSs were available at projectile energies of 25 and 40 eV; therefore, we numerically integrated the DCS in order to compare the RDW results with the RCCC ICS. Good agreement with the RDW results is found only at 40 eV for the ${}^3{P}_1$ ICS, and it is worse at 25 eV where the RDW is larger than the RCCC. For the remaining transitions, agreement is bad as the RDW cross sections are much larger than the RCCC ones at both projectile energies. For the ${}^1{D}_2$ transition, the agreement is the worst as the RDW cross sections seem to show a shallower decline with increasing projectile energy compared to the RCCC.

A comparison between our DCS and those of Srivastava et al. [5] for excitation to the first three excited levels are presented in Figure 7. These are given for projectile energies of 25 and 40 eV. Our results were taken from the RCCC(237) model. There is good agreement between the RCCC and RDW results only for the transition to ${}^3{P}_1$ at 40 eV, but not at 25 eV. At the latter energy, the troughs and peaks of the two results are slightly misaligned which is likely due to the first-order nature of the RDW calculations losing accuracy at lower energies. For ${}^3{P}_2$, the shapes are very similar but there is significant disagreement in absolute values. For ${}^1{D}_2$, the two calculations show strong disagreement in both shape and absolute value. The predictions by Srivastava et al. [5] for the ${}^1{D}_2$ forward-scattering DCS are about two orders of magnitude larger than the RCCC for both considered energies. For the same transition, the backwards scattering behaviour is also quite different between the two calculations. The difference in the structure models and also the fact that the RDW is a high-energy approximation are reasons for this disagreement.

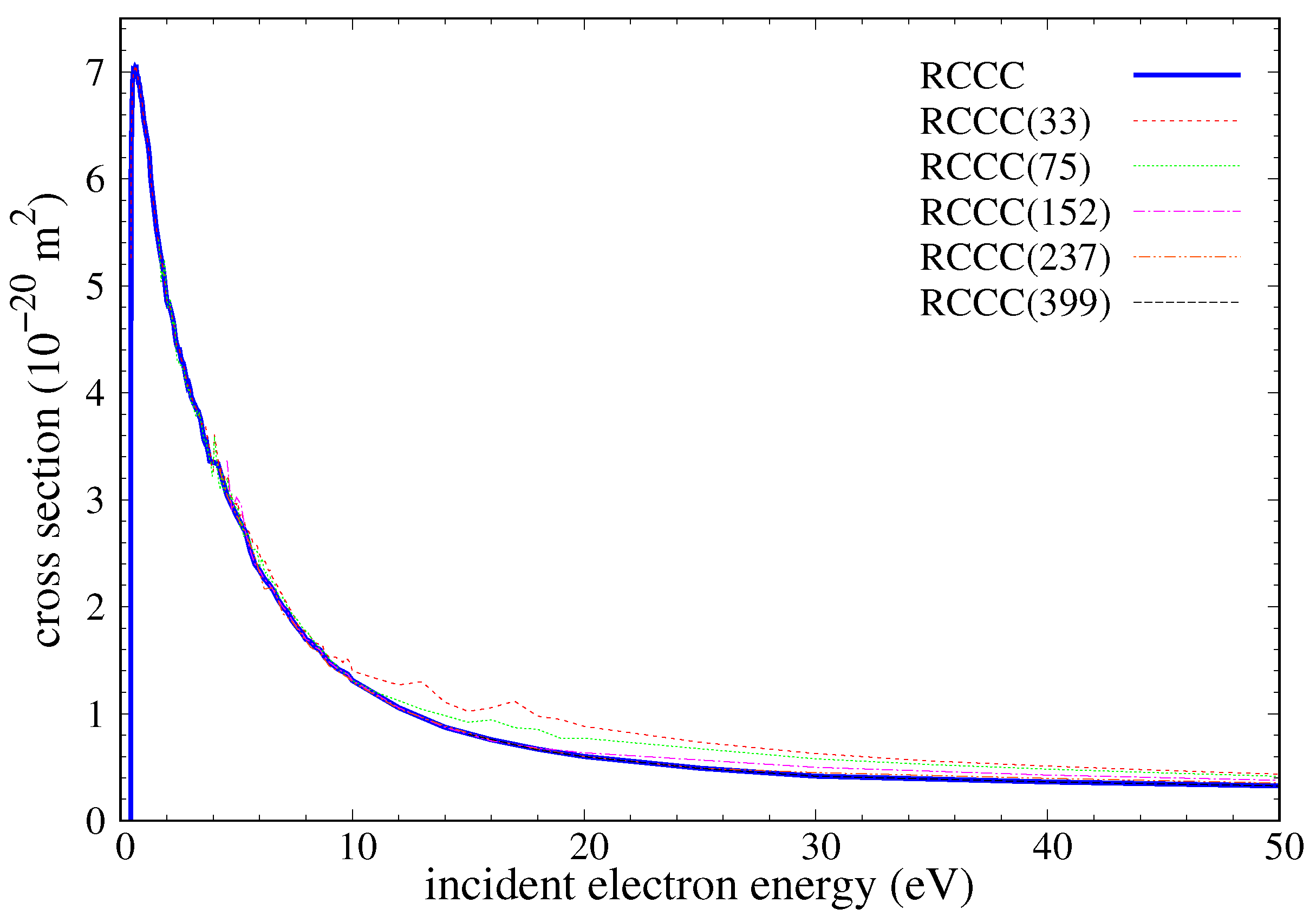
The convergence of the integrated excitation cross sections is illustrated in Figure 8 for ${}^3{P}_2$ excitation where the RCCC results are presented for models with increasing numbers of states. In the intermediate energy range, this transition is strongly affected by inter-channel coupling with smaller models significantly overestimating the cross section. To obtain the estimate of this transition, we have used the RCCC(33) and RCCC(75) models at low energies (below 4 eV) and RCCC(237) and RCCC(399) at larger energies. The convergence for the DCS is demonstrated in Figure 9 for the transition from ${}^3{P}_0$ to ${}^3{P}_2$ at 40 eV. RCCC(237) was the largest model considered for these differential cross sections, which is sufficiently large. The convergence for the other transitions shows similar behaviour.

3.3. Excitation to the $5p6s$ Manifold

The $5p6s$ manifold includes four states with symmetries ${}^3{P}_0^{\circ }$, ${}^3{P}_1^{\circ }$, ${}^3{P}_2^{\circ }$ and ${}^1{P}_1^{\circ }$. Out of the four transitions from the ground state to this manifold, two are dipole-allowed and have large cross sections. The latter transitions are particularly important in determining the dynamics of plasma containing tin. Cross sections for transitions to this manifold from the ground state were studied theoretically by Sharma et al. [8] using the RDW approach. They presented differential and integrated cross sections with which we compare the RCCC results.

In Figure 10, we compare the RCCC ICS with the results of Sharma et al. [8]. They found that their RDW results agreed well with those calculated using the flexible atomic code (FAC) [12]. However, when comparing with the RCCC results, the agreement is poor, especially in the low-to-intermediate-energy range. Even looking at the dipole-allowed transitions $5p^2$ ${}^3{P}_0$ → $5p6s$ ${}^3{P}_1^{\circ }$ and $5p^2$ ${}^3{P}_0$ → $5p6s$ ${}^1{P}_1^{\circ }$ (the latter is an exchange transition in non-relativistic formulation), the agreement in the intermediate-energy range is poor with the RDW-predicted peaks being substantially larger than those of the RCCC. Agreement for all transitions in the high-energy range is reasonable but imperfect. The RCCC cross sections for the dipole-allowed transitions are smaller at 100 eV compared to the RDW.

The OOS value from Sharma et al. [8] for the transition to $5p6s$ ${}^3{P}_1^{\circ }$ is 0.202, whereas in the present calculation, we obtain a value of 0.211 as given in Table 2. For the second dipole-allowed transition to ${}^1{P}_1^{\circ }$, Sharma et al. [8] produced an OOS value of 0.063, whereas the present calculations yield 0.077. Our OOS values are systematically slightly higher than those of Sharma et al. [8], NIST [10] and Oliver and Hibbert [11]. In order to account for this difference, we scaled our cross sections using the ratio of the present OOS values and those of Oliver and Hibbert [11] for the dipole-allowed transitions (given in Table 2). This reduces our cross sections and ensures the RCCC results go to the correct high-energy limit. However, it further amplifies the difference with the RDW results. Apparently, at 100 eV, the high-energy limit is still not reached.

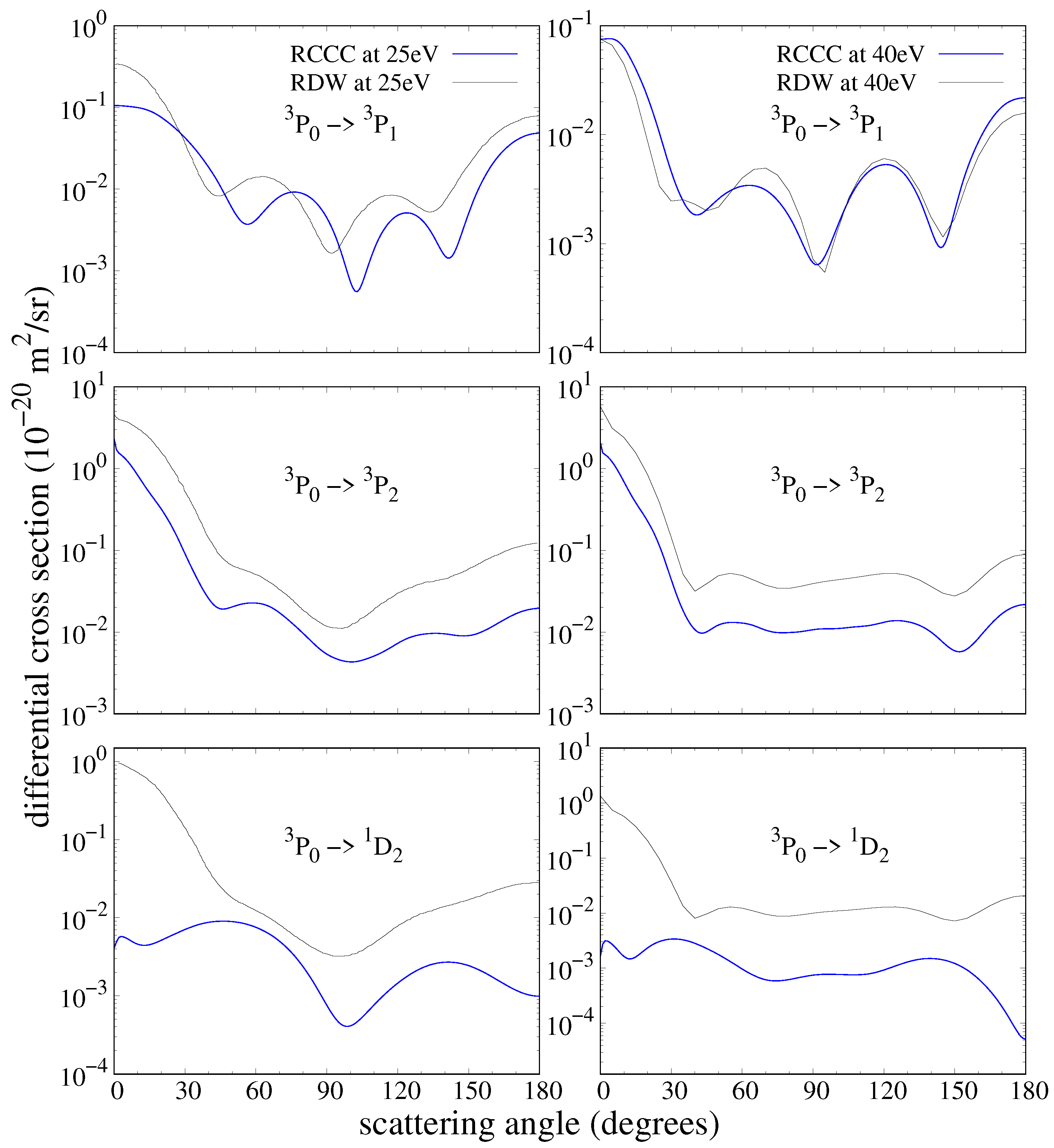
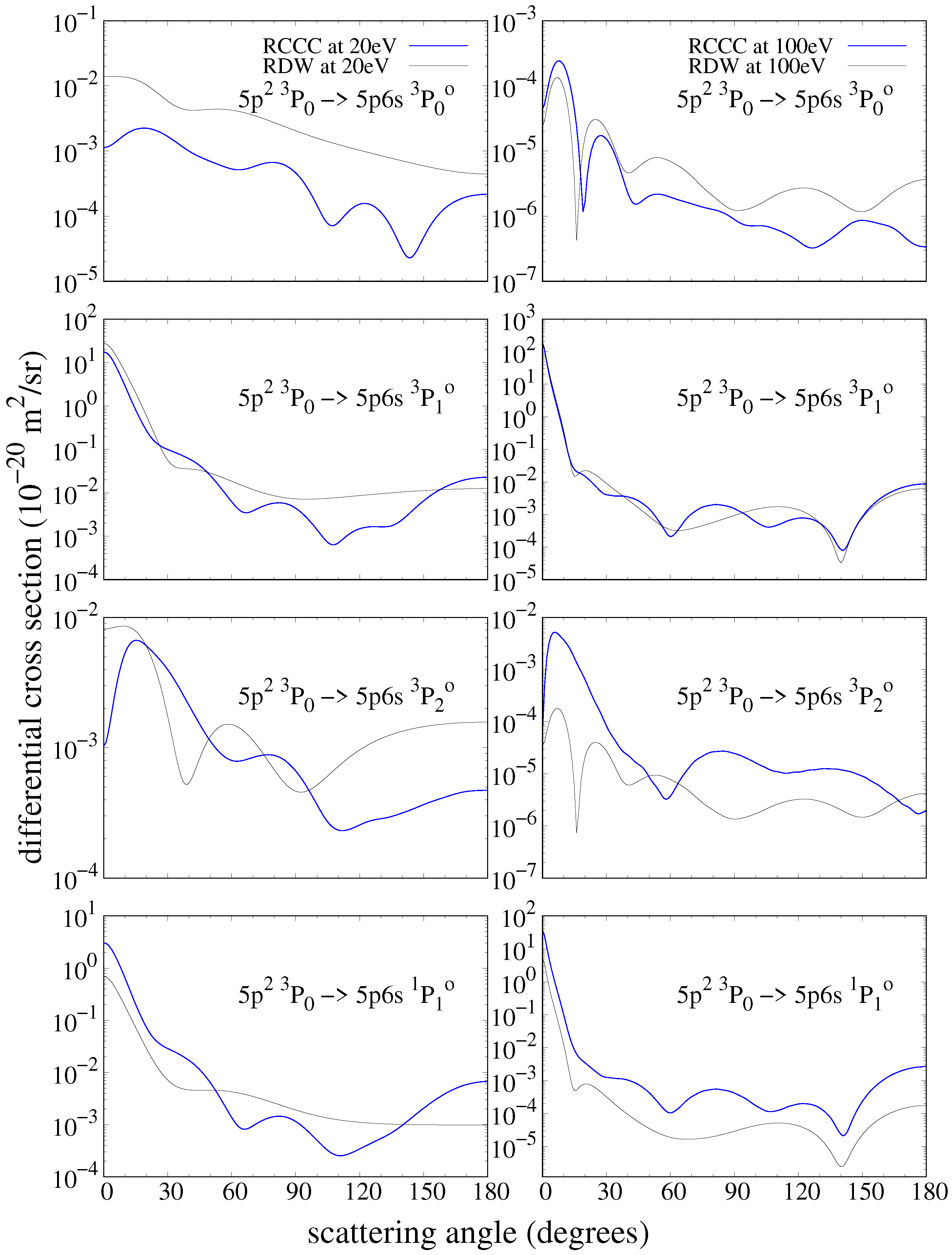
The differential cross sections for the transitions to the $5p6s$ manifold from the ${}^3{P}_0$ ground state are presented in Figure 11 at projectile energies of 20 and 100 eV. A comparison with corresponding RDW results by Sharma et al. [8] is also given. The agreement between the RCCC and RDW is good for some transitions and worse for others, and the overall agreement at 100 eV is better for all the transitions compared at 20 eV. The dipole-allowed transition to the ${}^3{P}_1^{\circ }$ state has the best agreement at both given energies; however, it is not perfect. There is disagreement between the RCCC and RDW for forward and backwards scattering at both 20 and 100 eV, but it is not as great as the discrepancies in the fine-structure DCS presented in Figure 7. The discrepancy is particularly pronounced for the transition to the ${}^3{P}_2^{\circ }$ state, for which the dominant peaks and troughs are mismatched.

Figure 12 shows the convergence with the number of states for the ${}^3{P}_1^{\circ }$ state ICS. This transition is dipole-allowed and has the largest cross section out of all the results presented for this manifold. RCCC(33) was used in the low-energy regime to capture the resonance behaviour, after which the results were smoothly matched to the larger RCCC(399) model to ensure the convergence at intermediate and high energies. Smoothing once again was applied to these results to minimise the effects of the numerical instabilities.

The convergence in the DCS is presented in Figure 13. The results for 100 eV are calculated for partial waves up to $J=101/2$ compared to the $J=41/2$ required for all other calculations due to the cross sections being particularly small at some scattering angles. RCCC(237) was the largest model we used for these calculations.

3.4. Excitation to the $5p5d$ Manifold

The $5p5d$ manifold has a total of 12 states for which excitation-integrated cross sections from the ground state were calculated. As most of these were small, we present only one level-to-level result for the transition to the $5p5d$ ${}^3{D}_1$ state, which was relatively large, and also a sum over the entire manifold.

Figure 14 presents the cross section for the dipole-allowed transition $5p^2$ ${}^3{P}_0$ → $5p5d$ ${}^3{D}_1^{\circ }$. The presently calculated OOS value for this transition was 0.553, whereas a more accurate calculation by Oliver and Hibbert [11] yielded a value of 0.388. As our OOS value was too high, we scaled our cross section using the ratio of the RCCC value and the one calculated by Oliver and Hibbert [11]. This leads to a decrease in the magnitude of the RCCC result. Same as for the $5p6s$ manifold, this ensured that at high energy, the RCCC cross section goes to the correct high-energy limit.

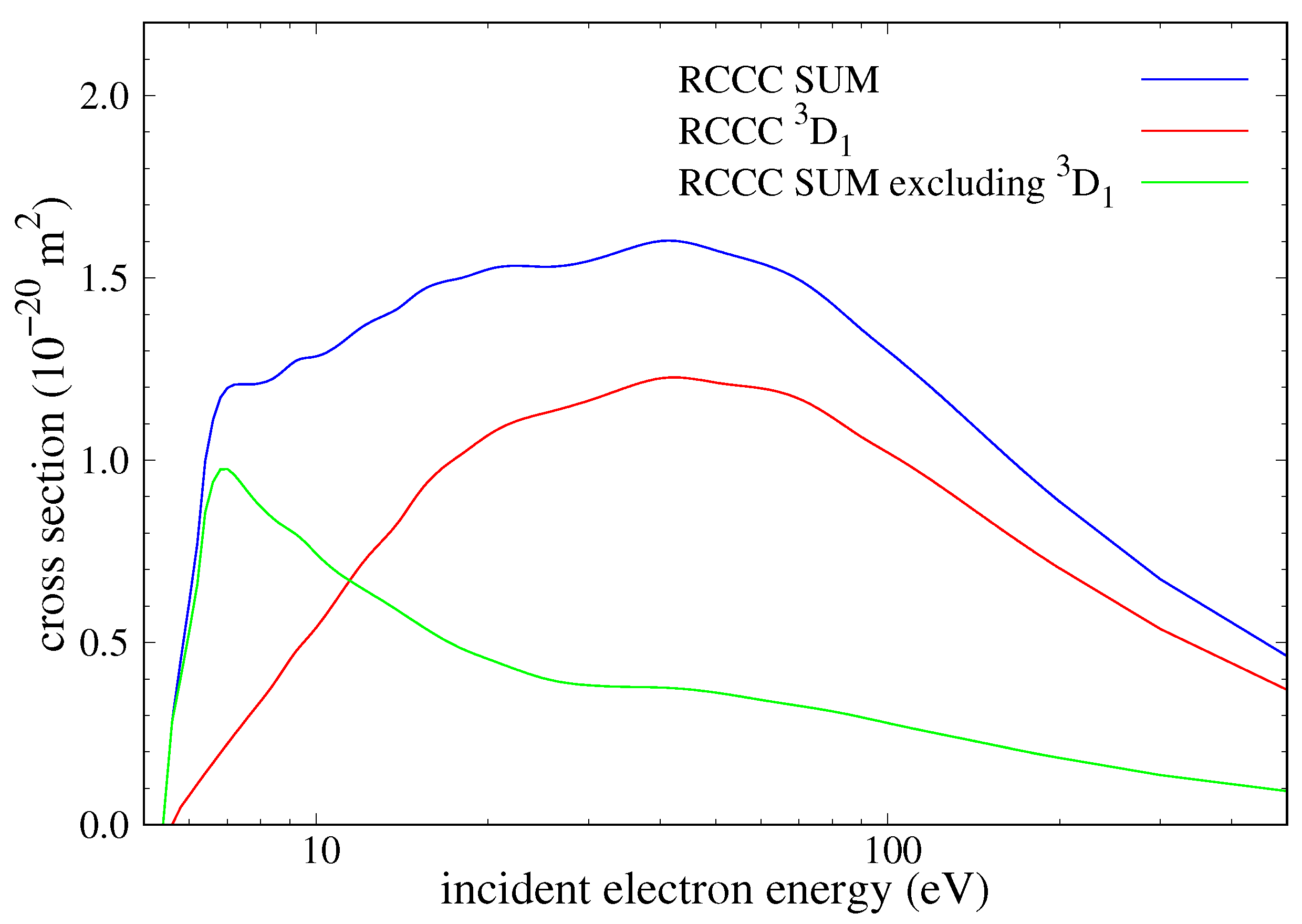
The summed cross section over the entire $5p5d$ manifold is also presented in Figure 14, in which it can be seen that the peak is not that much larger than that of the $5p5d$ ${}^3{D}_1^{\circ }$ result. The shape of the excitation onset however is different, as the summed cross section has a sharper rise compared to that of the dipole-allowed transition. This behaviour originates from the many dipole-prohibited cross sections in this manifold as they all have fast onsets after which they exponentially drop off with increasing projectile energy. This can be more clearly seen in the summed contributions to the cross section from all the transitions except the one to ${}^3{D}_1$ which is also illustrated in Figure 14. This partial sum, however, does not show an exponential decline with increasing energy as there are two dipole-allowed transitions which are included. The cross sections associated with these two transitions are relatively small but do not drop off quickly with increasing projectile energy.

The convergence for the transition to the $5p5d$ ${}^3{D}_1^{\circ }$ state is shown in Figure 15. The coupling-to-ionisation continuum is important for this dipole-allowed transition, more than it was for the $5p^2$ ${}^3{P}_0$ → $5p6s$ ${}^3{P}_1^{\circ }$ transition. The cross section is reduced by about 25% at the peak for the $5p5d$ ${}^3{D}_1^{\circ }$ transition when comparing the RCCC(75) result (which has only bound pseudo-states) with the fully converged RCCC(399) result. In comparison, the $5p6s$ ${}^3{P}_1^{\circ }$ cross section decreased at the peak by about 10%.

3.5. Excitation to the $5p6p$ Manifold

All the transitions to the $5p6p$ manifold from the $5p^2$ ${}^3{P}_0$ ground state are dipole prohibited by at-least parity; hence, the integrated excitation cross sections for level-to-level calculations are small. Therefore, in Figure 16, we only present a sum over the cross sections for transitions to the 10 states in the $5p6p$ manifold. This cross section shows a fast rise at the threshold typical for dipole-prohibited transitions followed by a steep decline at larger energies. There are no other results, theoretical or experimental, to compare with.

3.6. Total Cross Sections

In Figure 17, we present the RCCC total and total inelastic cross sections for the ${}^3{P}_0$ ground state. Both the total and total inelastic cross sections share the same features at low energy, with sharp structures appearing where the first two excited states lie.

Between 0.2 and 0.3 eV, the large structure in the total cross section (TCS) is produced by the sum of the p-wave resonance from the elastic scattering (Figure 1) and the onset for excitation to the first excited state (Figure 6). The latter can clearly be seen in the total inelastic cross section (inelastic-TCS) as well. The onset for excitation to the second excited state can also be seen as large structures in both the TCS and inelastic TCS at a projectile energy roughly between 0.4 and 0.5 eV. The wide peak at 4 eV in the TCS is due to the peak in the elastic scattering at that energy. At an energy of about 35 eV, there is a small peak in the inelastic TCS which is due to the contributions from the ionisation channels.

3.7. Total Ionisation Cross Sections

The total single-ionisation cross sections for tin were measured by Freund et al. [13], in 1990, with no new experimental data available since then. Bartlett and Stelbovics [15] calculated electron-impact ionisation cross sections for tin using a non-relativistic analytic Born approximation for the valence $5p$ and closed $5s$ and $4d$ sub-shells. Kim and Stone [16] studied TICS theoretically, using the binary-encounter Bethe (BEB) method, with which they calculated the direct ionisation out of the $5p$ and $5s$ sub-shells. They also calculated the excitation–autoionisation (EA) cross sections using a scaled plane-wave Born approximation as it was found that the contribution was significant for large open-shell atoms such as tin. Kim and Stone [16] presented these results for all five fine-structure levels in the $5p^2$ ground configuration. In this study, we only consider single ionisation out of the $5p$ and $5s$ orbitals as well as contributions from the EA. Same as Kim and Stone [16], we ignore the contributions to the TICS from the core orbitals below the $5s$ shell as the binding energies are large and the cross sections are small.

The direct ionisation out of the $5p$ shell is the dominant contributor to the TICS from the threshold (7.344 eV) to 14 eV projectile energy. The EA onset is at about 8 eV, but its contribution near the threshold is small compared to the DI out of the $5p$ shell. At larger energies, the $5s$ electrons and EA also start contributing. The ionisation threshold for the $5s$ electrons from our RCCC calculation is 13.691 eV, and Kim and Stone [16] found this value to be 13.689 eV, indicating that the agreement between the two structure calculations is good. To obtain the TICS, we first determined our best estimate for direct ionisation from the $5p$ shell using RCCC. This was then summed with direct ionisation from the $5s$ sub-shell also estimated using RCCC and with the scaled Born EA cross sections presented by Kim and Stone [16].

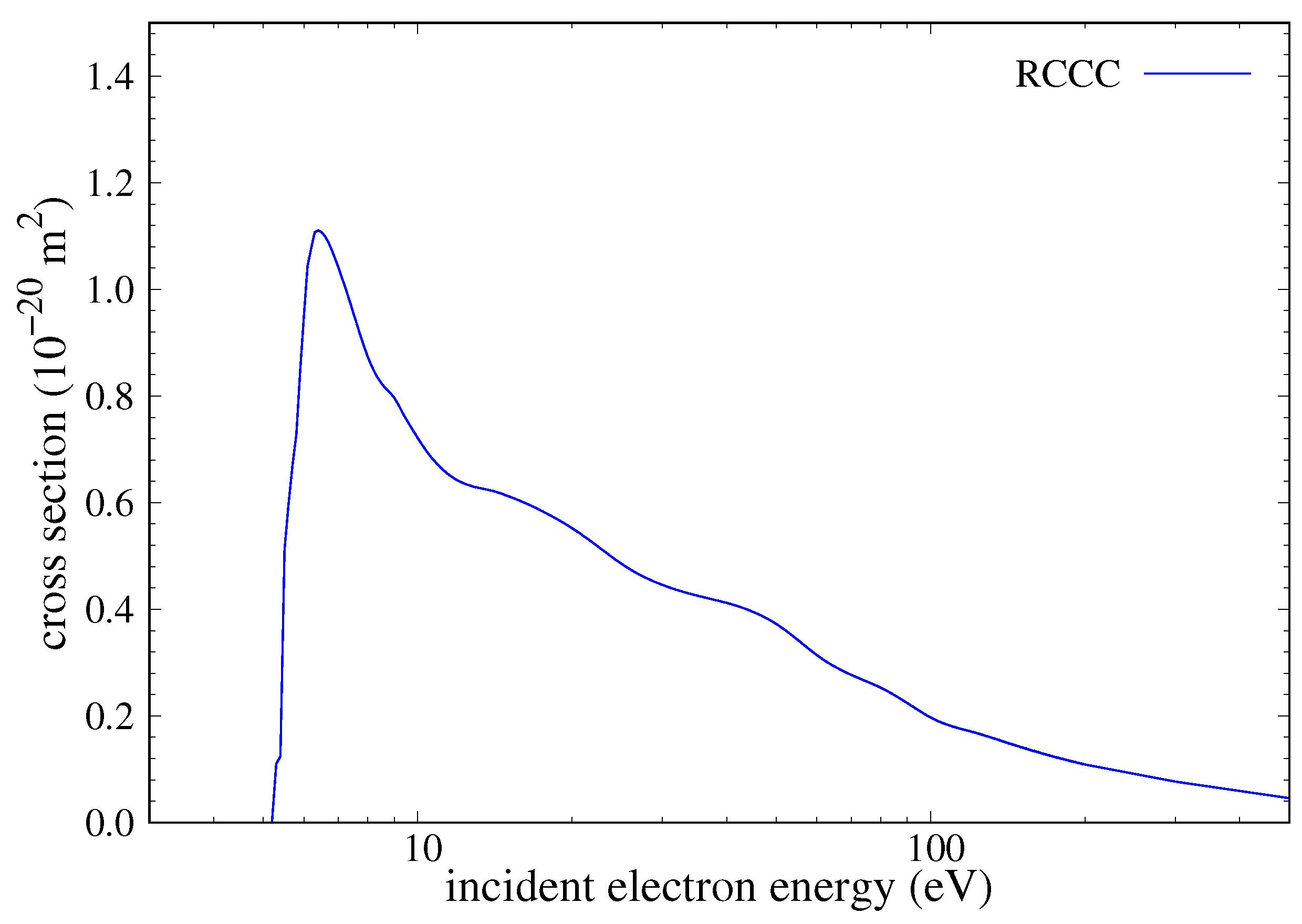
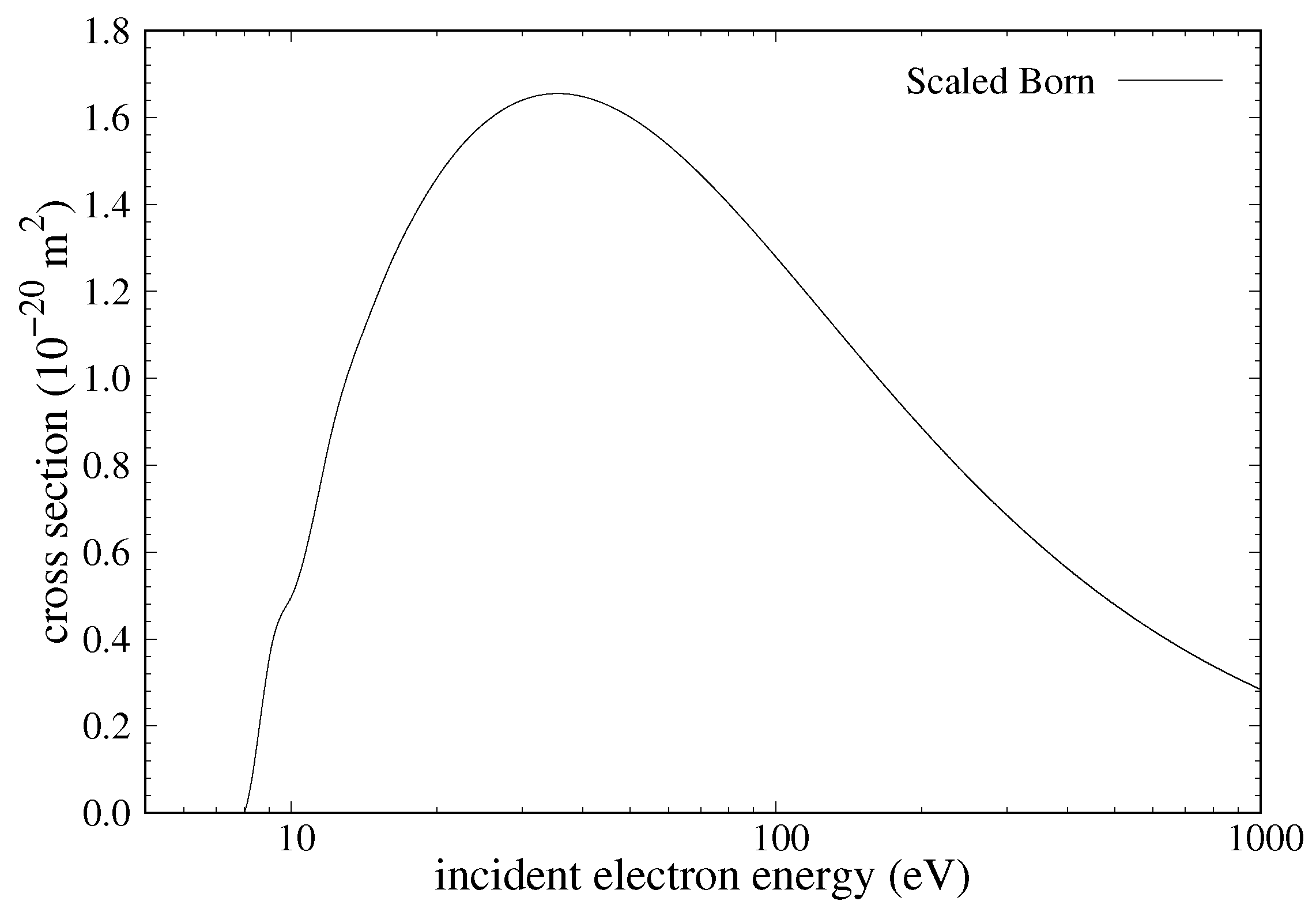
The direct ionisation out of the $5p$ shell requires a large number of states in the close-coupling method, as for scattering from a p-orbital, the ejected electron can have larger orbital angular momentum compared to a more common case of scattering from an s-orbital. The RCCC(237) model was sufficient to describe this cross section up to incident electron energies of 12 eV as it has target pseudo-states with maximum angular momentum $J=6$ and energies up to 5 eV. The RCCC(399) model has the same maximum angular momentum but a larger number of pseudo-states which have energies up to 10 eV. This allows to obtain a reliable estimate for projectile energies up to about 18 eV. Finally, an RCCC(482) model was produced which again has the same maximum angular momentum but now with an even larger number of pseudo-states with energies up to 15 eV. Combining the RCCC(152), RCCC(399) and RCCC(482) calculations at appropriate energy intervals, we have produced the RCCC estimate for ionisation out of the $5p$ orbital which we denote RCCC(482) from this point onwards. For the complete convergence of the TICS at high energies, pseudo-states with even larger angular momentum and energies are required. A model was then built to include target pseudo-states with total angular momentum up to $J=11$ which spanned up to 1000 eV into the continuum, denoted by RCCC(3388). This large model could not be used for the full RCCC calculations as it would be computationally too expensive, so instead, we performed first-order Born calculations. The Born-TICS for this model is fully converged and provides an accurate estimate for ionisation at high energies. The RCCC(3388) Born results were then used to extrapolate the RCCC(482) cross sections in order to account for the excluded pseudo-states and larger required angular momentum.

Figure 18 shows the extrapolation procedure we used on our RCCC DI cross sections for the $5p$ ${}^3{P}_0$ ground state. This extrapolation procedure relies on using the ratio of the RCCC(3388) Born calculations and the RCCC(482) results to scale the cross section. The scaling ensures that the cross sections go to the converged Born results (RCCC(3388)) at high energy whilst maintaining the original RCCC(482) results at low energy. The low-energy limit we chose to begin the scaling at was about 12 eV, as it is the energy at which the first-order Born-TICS for RCCC(482) and RCCC(3388) begin diverging from one another. The high-energy limit at which the cross section becomes the RCCC(3388) Born result was chosen to be 250 eV. The scaling procedure connects these two extremes using a smooth linear transition from no scaling at low energy to full scaling at high energy. This means the scaled cross section has a slightly larger peak than the original close-coupling result which now accounts for larger orbital angular momentum pseudo-states which did not exist in the original RCCC(482) calculations. We denote our extrapolated result using RCCC from this point onwards.

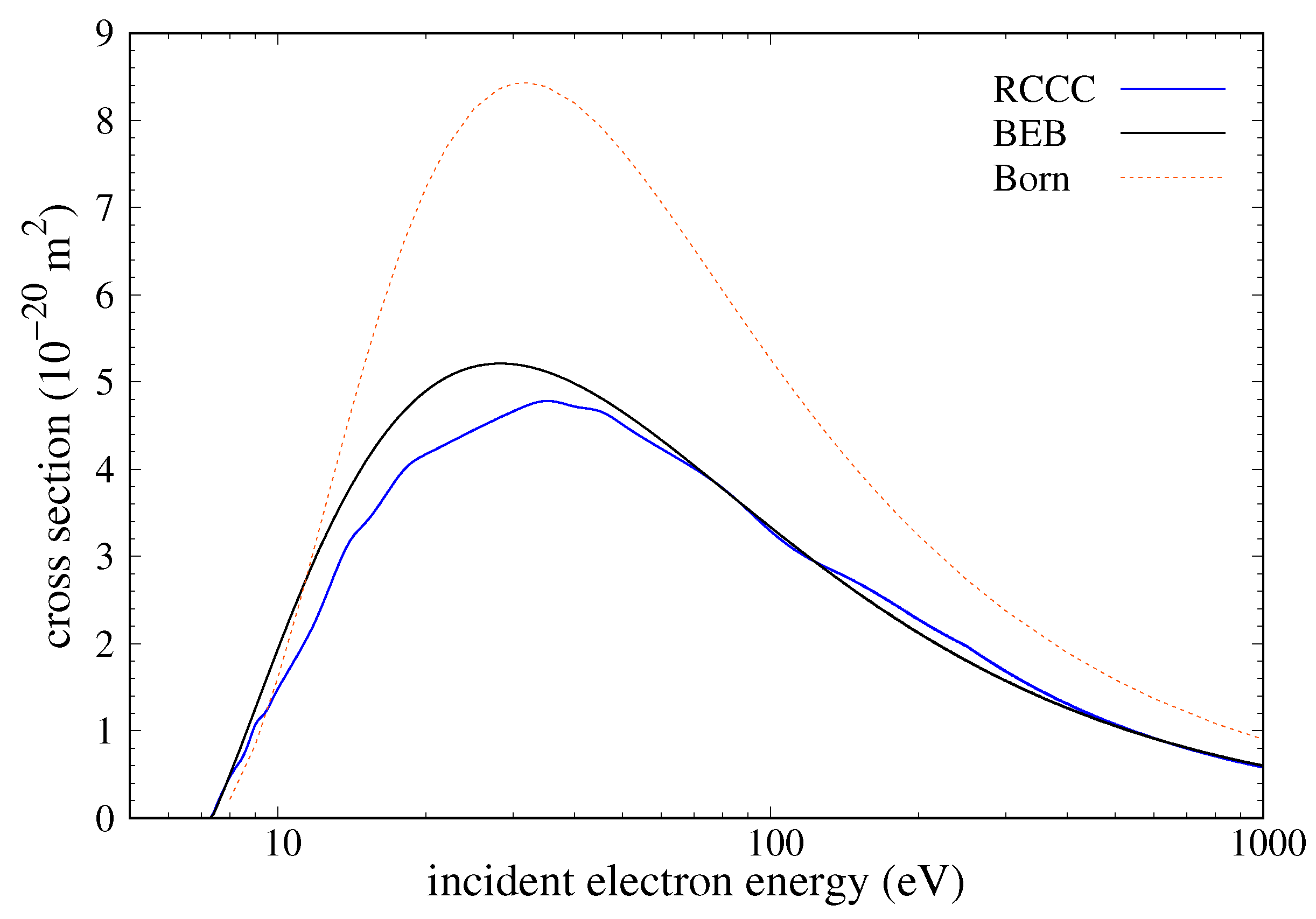
Figure 19 shows our RCCC DI result from the $5p^2$ ${}^3{P}_0$ ground state compared with the BEB result of Kim and Stone [16] and the first-order results of Bartlett and Stelbovics [15]. In the low-to-intermediate-energy regime, our RCCC results are systematically lower than those of Kim and Stone [16]. At higher energies, the agreement between the RCCC and BEB is very good with both results going to the same high-energy limit. Comparing both the RCCC and BEB to the Born approximation by Bartlett and Stelbovics [15], both rise slightly faster near the threshold but are then systematically smaller over the entire projectile energy domain. The peak of the first-order Born approximation result [15] is about 60% larger than that of the other two. The calculations by Bartlett and Stelbovics [15] presented in Figure 19 are similar to our first-order Born results given in Figure 18. The results of [15] also tend to a slightly larger cross section in the high-energy limit, which could be due to the BEB and RCCC results accounting for the relativistic nature of the target, while the first-order Born calculations do not.

The RCCC method allows for an estimate of direct single ionisation out of the $5s$ shell by treating the $5p^2$ electrons as inert. The leading configuration for the ${}^3{P}_0$ ground state of tin is $5s^{2}5p_{1/2}^2$ with a mixing coefficient of 0.890 as calculated by Sharma et al. [8] using the GRASP2k program [9]. The RCCC calculations produce a mixing coefficient of 0.884 which is in agreement with the value given by Sharma et al. [8]. By fixing the two p electrons in the $5p_{1/2}^2$ configuration, a closed shell is formed and one-electron excitations from the active $5s^2$ shell can be calculated. The presently calculated ionisation threshold for the $5s$ electrons is 13.691 eV. Scattering calculations were performed using several models, similar to what was conducted for the DI of the $5p$ shell. These models have a maximum angular momentum of $J=5$, continuum pseudo-states with energies up to 2, 5, 20 and 60 eV, which are comprised of a total of 59, 85, 161 and 263 states, respectively. The RCCC results calculated using these models were combined to produce a convergent cross section for ionisation out of the $5s$ shell (denoted by RCCC(263)). Same as the $5p$ case, the RCCC(263) DI cross section for the $5s$ shell was extrapolated to account for missing larger angular momentum and high-energy continuum pseudo-states. This was performed using a Born cross section produced using a large model with 1019 target pseudo-states which have energies up to 975 eV and a maximum angular momentum of $J=9$. This Born cross section is fully converged and provides an accurate estimate for the DI out of the $5s$ shell at high projectile energies.

Figure 20 presents the RCCC DI result from the $5s$ shell plotted alongside the BEB results of Kim and Stone [16] and the Born results of Bartlett and Stelbovics [15]. The agreement from the threshold to before the peak is good between the BEB and RCCC, but then, the RCCC result becomes larger at the peak compared to the BEB. After the peak, however, the RCCC result drops off faster and becomes smaller than the BEB in the high projectile energy region. The Born result of Bartlett and Stelbovics [15] is similar to both the BEB and RCCC results near the threshold but then becomes larger than the BEB at the peak. The RCCC and the Bartlett and Stelbovics [15] Born results have a similar magnitude at the peak but display disagreement in the sharpness and position of the peak. The RCCC peak is shifted towards higher energy compared to the Born result, similar to the position of the BEB peak. At the high energy limit, the BEB cross section is the largest followed by the RCCC which is slightly larger than the Born result of Bartlett and Stelbovics [15].

As stated by Kim and Stone [16], the major autoionisation channels involve one electron excitations from the ground configuration to ones of the form $5s^{1}5p^3$. However, the RCCC formulation does not include electron configurations of this type. Therefore, we decided to use the EA cross sections which were published by Kim and Stone [16]. When calculating EA cross sections, Kim and Stone [16] assumed that EA occurs with 100% probability with radiative decay not being allowed. Figure 21 presents their EA cross section for the ${}^3{P}_0$ ground state. EA cross sections for the first four excited states were also available from [16] which we used alongside our RCCC results to produce TICSs from each of these meta-stable states.

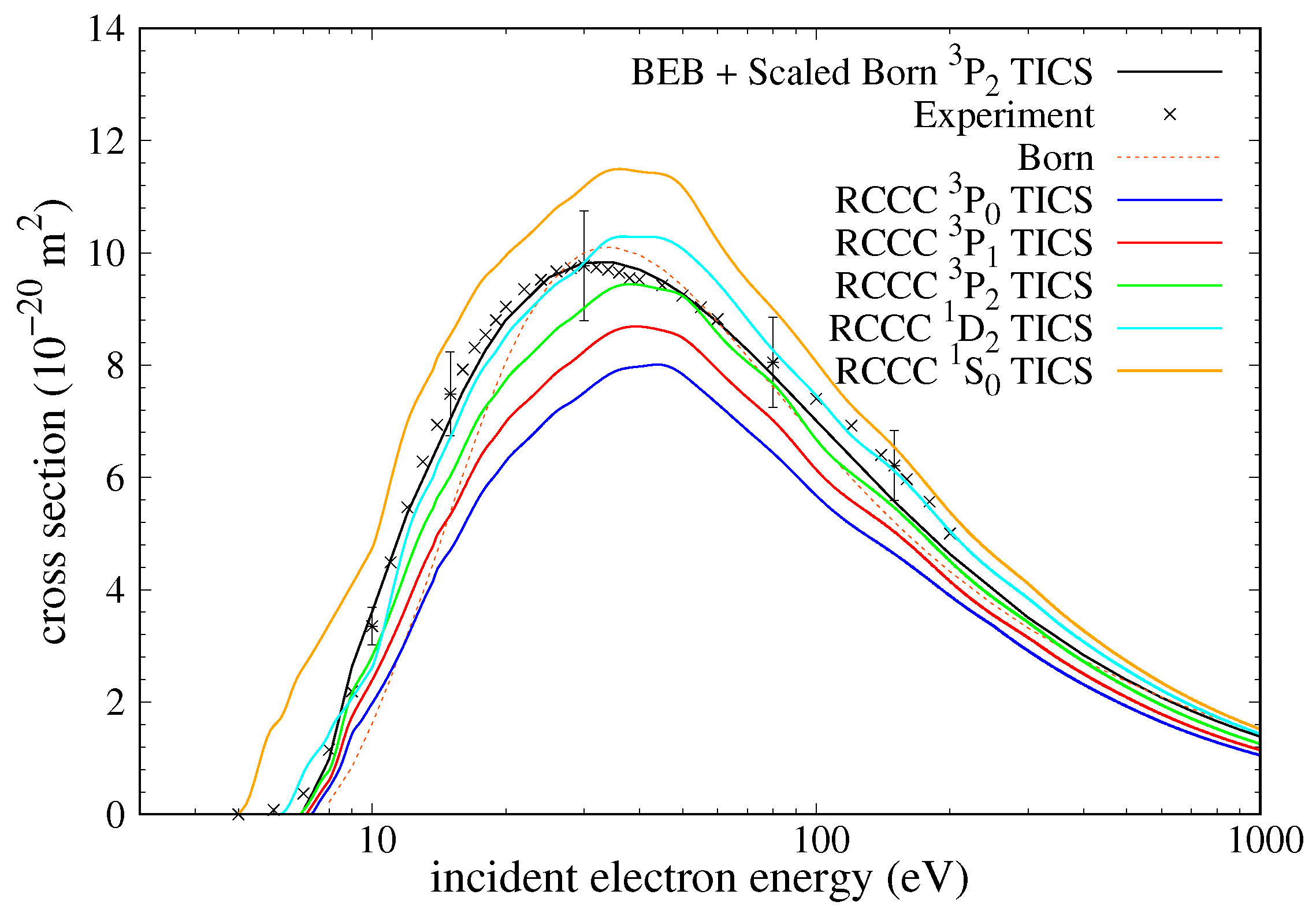
In Figure 22, we present the summed total single-ionisation cross section (denoted as TICS) for the ground state and the first four excited states (fine-structure levels) of tin. We show a comparison with the TICS presented by Kim and Stone [16] and Bartlett and Stelbovics [15] and experimental results published by Freund et al. [13]. The BEB [16] results are presented for ionisation out of the ${}^3{P}_2$ state as it provides the best fit to the experimental data out of all their results. Looking at the experimental data, it is clear from a comparison with the theoretical results that the tin atoms used in the experiment were mostly in meta-stable states, as the ionisation threshold is noticeably displaced before that of the ground state. The relative percentages of each meta-stable state present in the experimental atom beam is unknown, but in their study, Kim and Stone [16] suggested that 90% of the atoms were in the ${}^3{P}_2$ and 10% in the ${}^1{D}_2$ levels. Based on the current RCCC results, we believe that there may also be some fraction of the atoms in the ${}^1{S}_0$ meta-stable state. This is because the RCCC cross sections are rising towards the peak slower compared to the experimental results, with the cross sections from the ${}^1{S}_0$ state being the only ones larger than the experimental results before the peak. The RCCC calculation which fits closest to the experiment is the TICS from the ${}^1{D}_2$ meta-stable state. However, it still underestimates the experiment slightly from the threshold to 20 eV projectile energy after which it overestimates the experimental cross section. Bartlett and Stelbovics [15] found reasonable agreement with the experiment; however, their results underestimated the cross section before and after the peak, only briefly overestimating at the vertex. This may be due to the non-relativistic Born calculations not being able to distinguish between fine-structure levels. The predicted position of the peak from the RCCC results is shifted higher in energy compared to that of the experiment by about 5–15 eV (depending on the target state). A similar trend was observed in a study for lead (which has a similar electronic structure as tin) in which experimental results published by Freund et al. in the same publication as the one for tin [13] were compared with the RCCC results [28]. This misalignment of the peaks is also noticed when comparing the RCCC with the BEB [16] results, which is something that was not seen in the lead study. The energy dependence of the TICS between the BEB and RCCC is slightly different up until the peak, but then agreement is good towards the high-energy limit.

4. Summary and Conclusions

We applied the RCCC method to calculate cross sections for various transitions in electron scattering on atomic tin. This included integrated and momentum-transfer cross sections for elastic scattering on not only the ground state but also the first four excited states that form the $5p^2$ manifold. We also studied excitation to the $5p^2$ and $5p6s$ manifolds from the ground state for which integrated and differential cross sections are provided alongside a comparison with Srivastava et al. [5] and Sharma et al. [8]. Reasonable agreement is found for large cross sections at high energy, such as the dipole-allowed transition from the ground state to $5p6s$ ${}^3{P}_1$, whilst agreement for other transitions is rather variable. Agreement across all transitions is better at high than at low energies. This is consistent with the RDW method being a first-order technique which is more accurate at high energies. We also presented summed angle-integrated cross sections for excitation to the $5p5d$ and $5p6p$ manifolds for which there are no other results to compare with. The total cross section and total inelastic cross section for scattering on the ground state have been provided. Our estimations for the electron-impact total ionisation cross sections have been provided for scattering on the ground and the first four excited states. These were constructed by summing the RCCC DI calculations for the $5p$ and $5s$ sub-shells and the excitation–autoionisation results presented by Kim and Stone [16]. A comparison was provided with measurements presented by Freund et al. [13], the BEB results of Kim and Stone [16] and the first-order Born calculations performed by Bartlett and Stelbovics [15], all for which agreement was found to be good. Similar to Kim and Stone [16], we conclude that the experimental results of Freund et al. [13] are likely to have tin atoms in a mixture of meta-stable states, with which our calculations for ionisation out of the $5p^2$ ${}^1{D}_2$ state seemed to agree the best. We hope that the presented cross section dataset will be useful for various modelling applications in fusion plasma physics, nano-lithography and other fields.