An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering
Abstract
:1. Introduction
2. Theoretical Details
3. Results
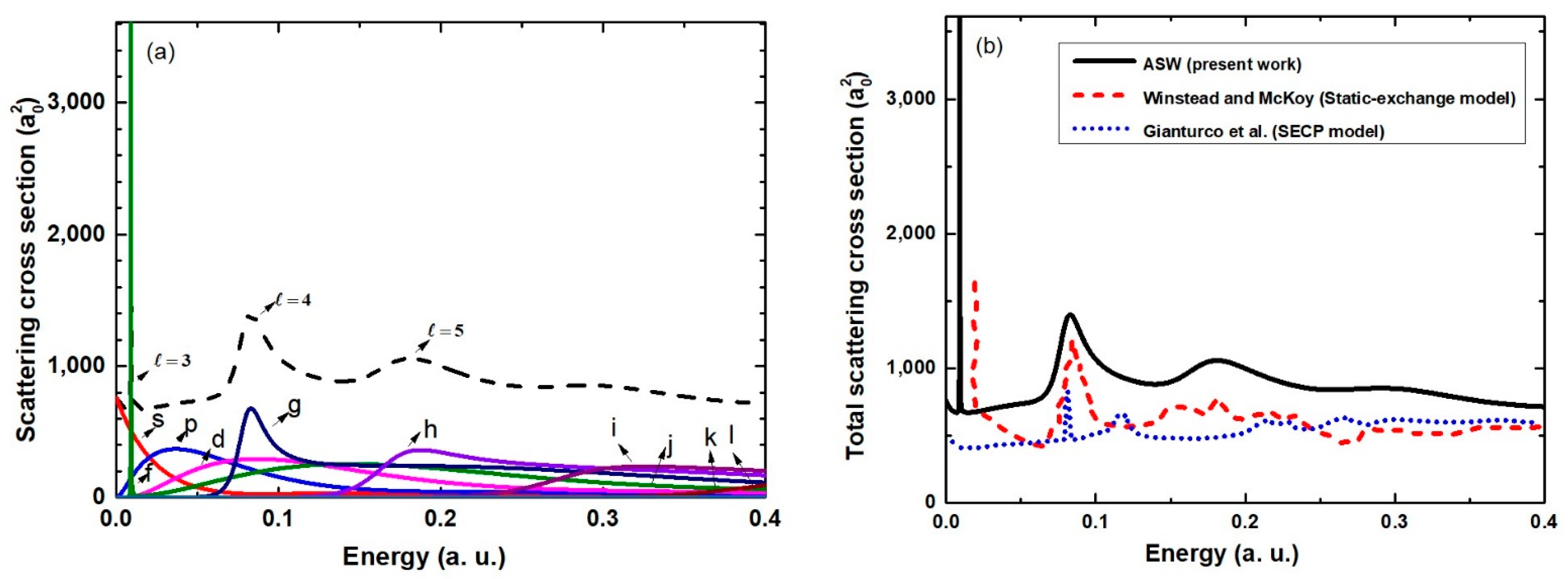
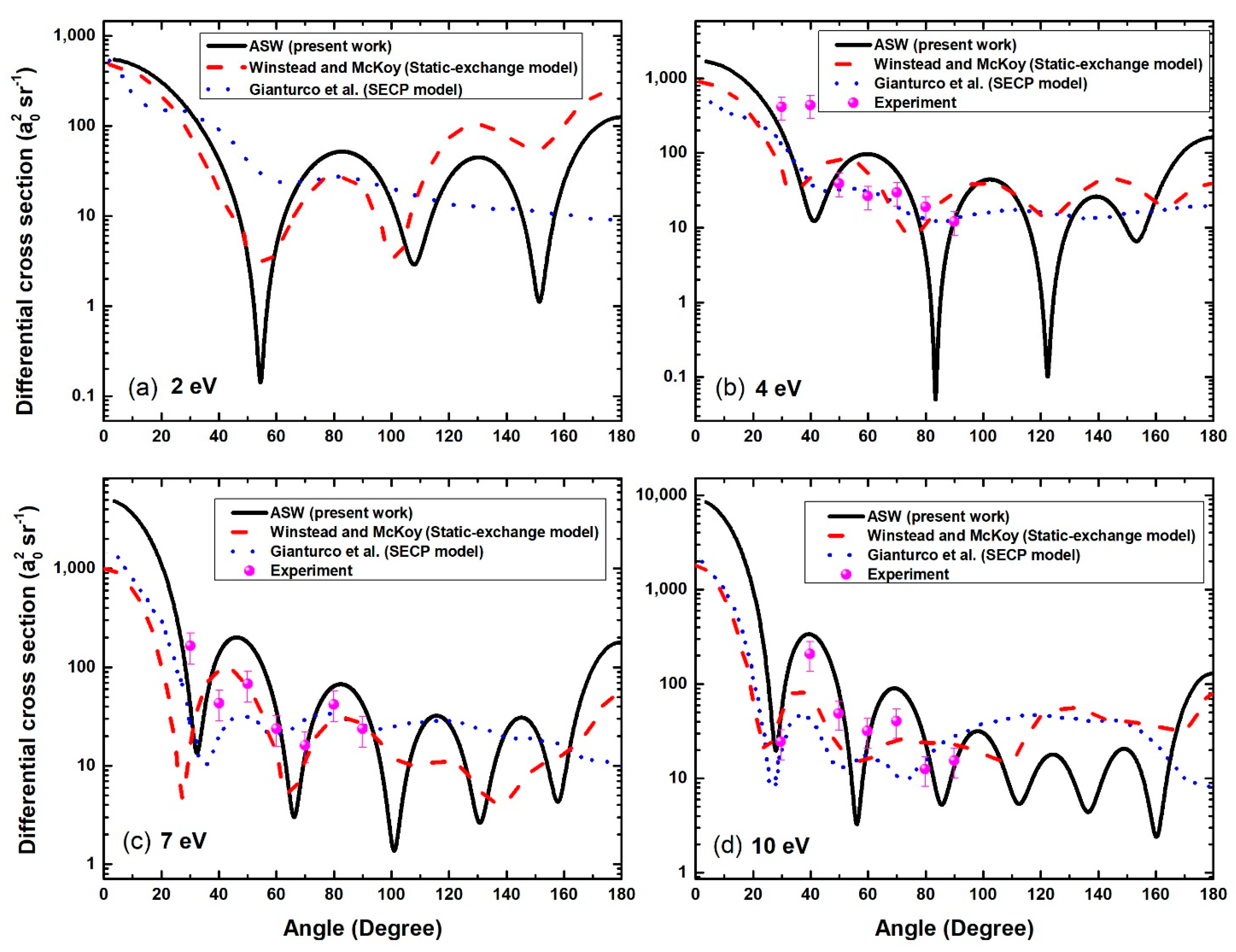
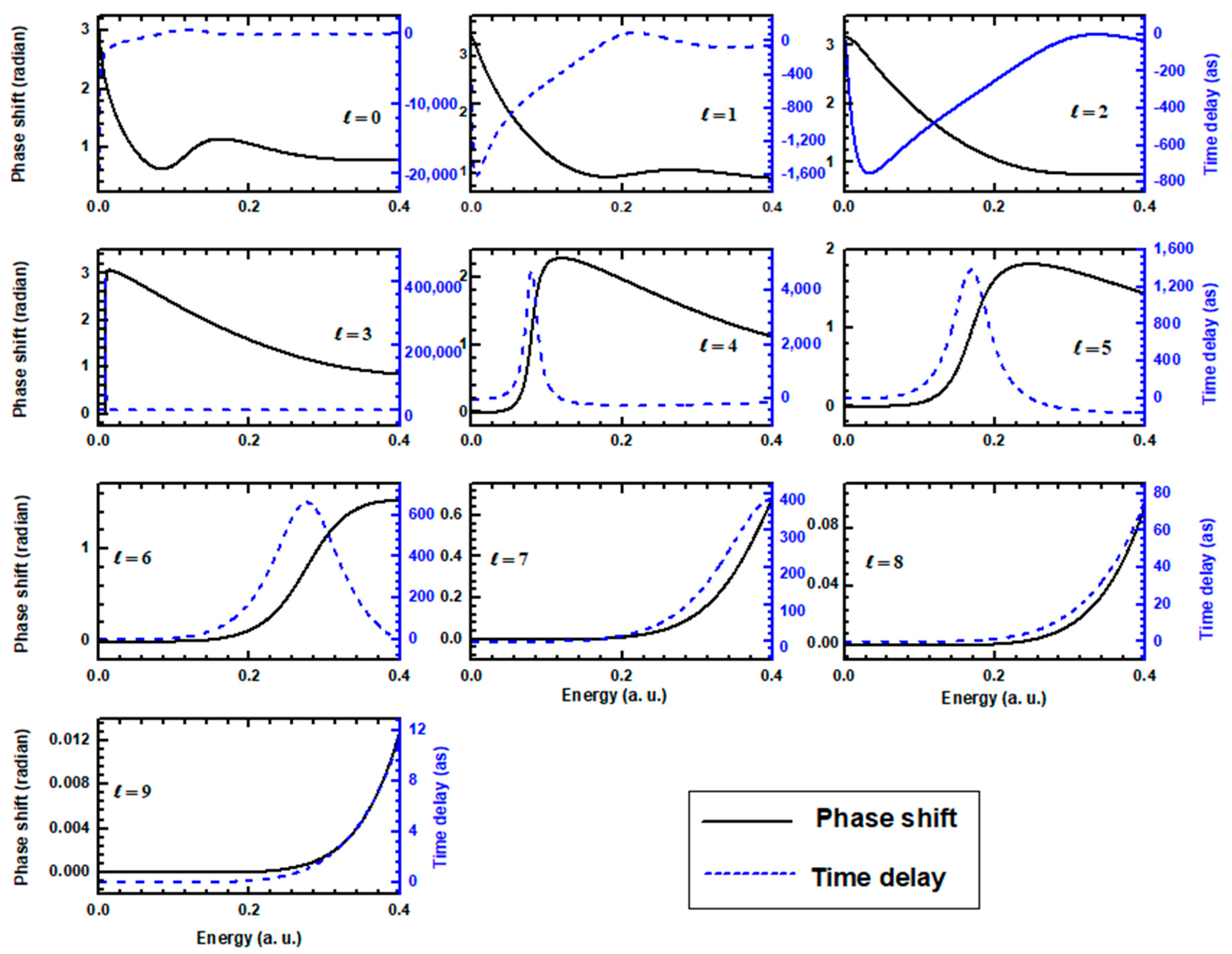
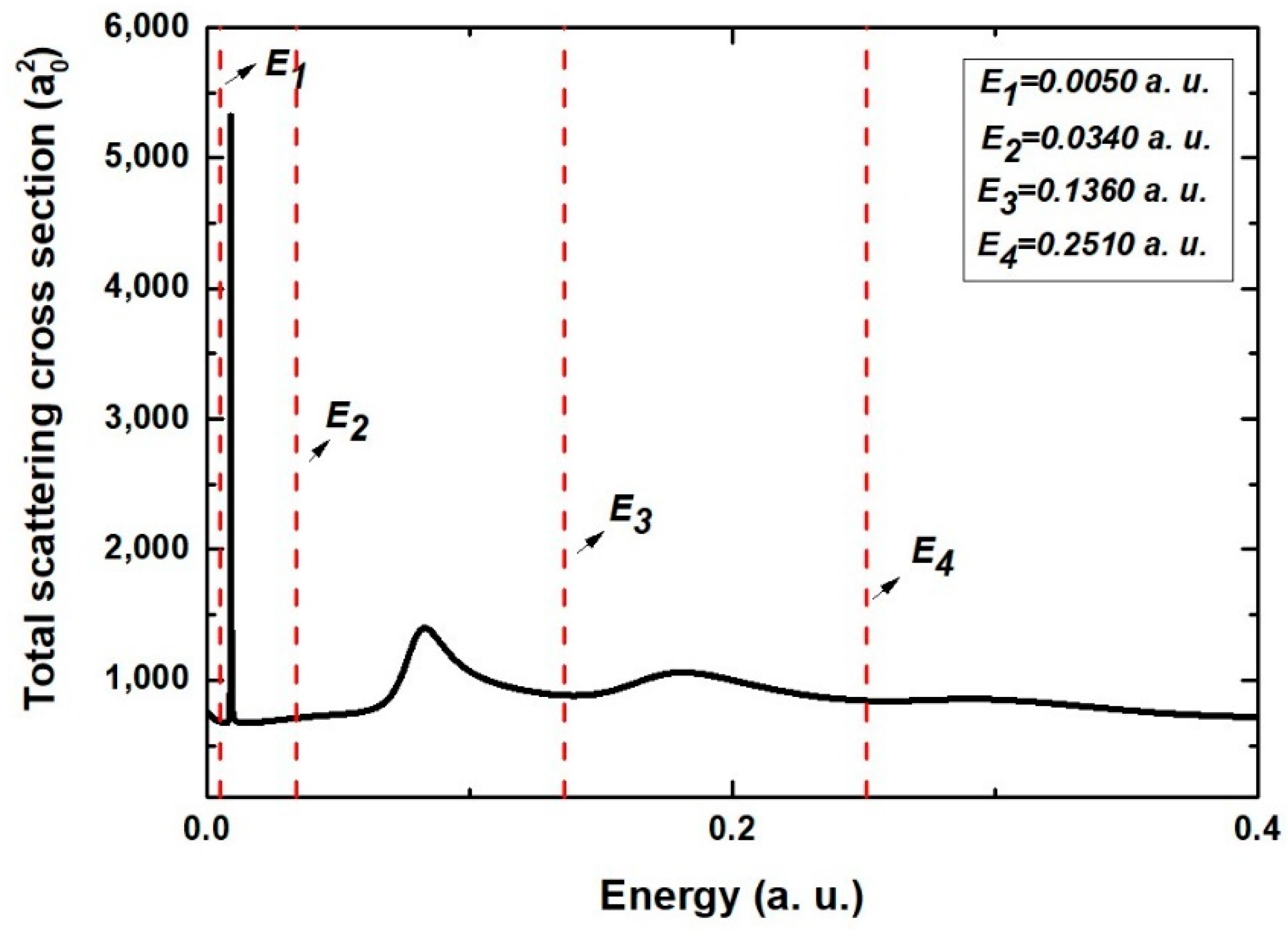
3.1. TCS, PCS, and EWS Time Delays
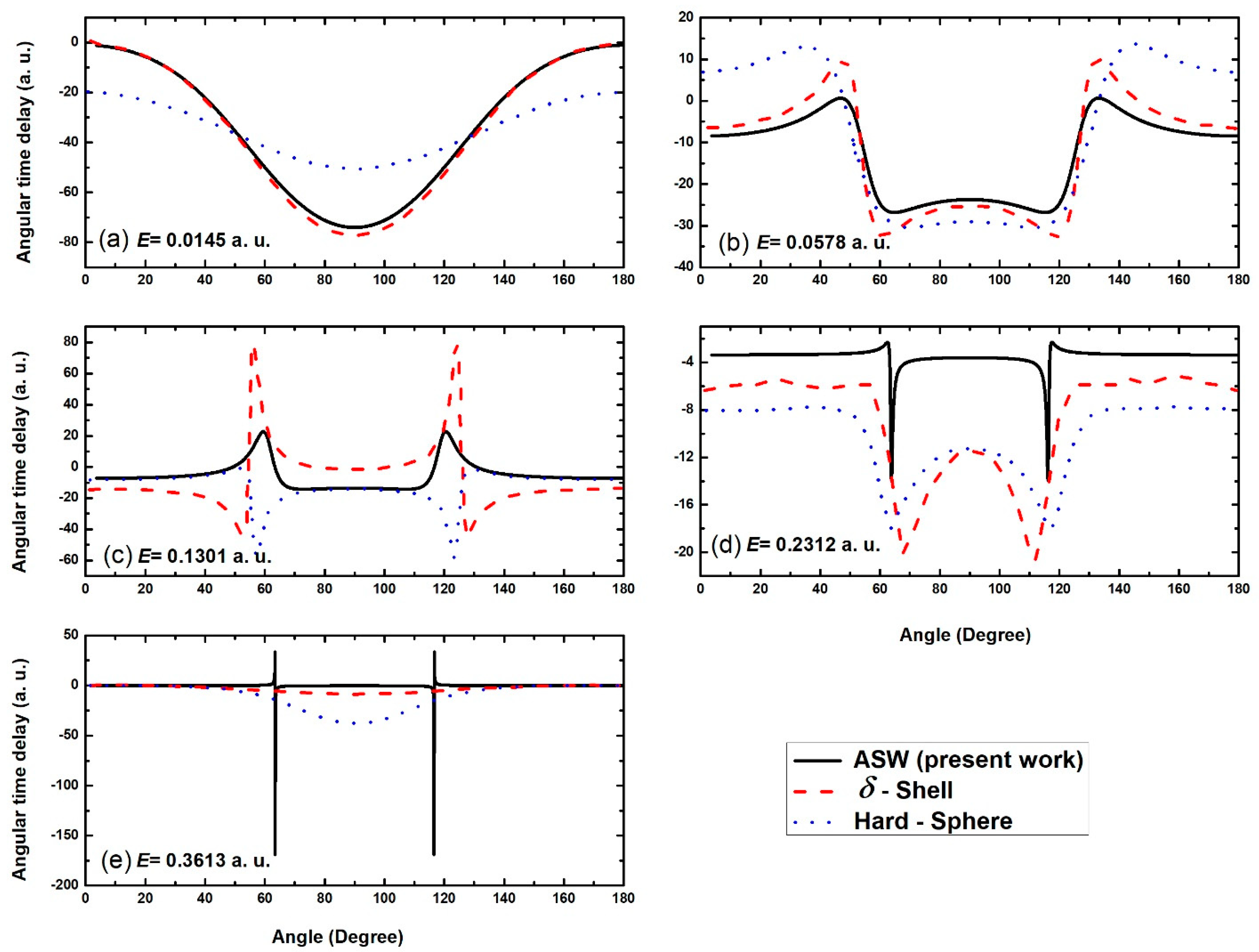
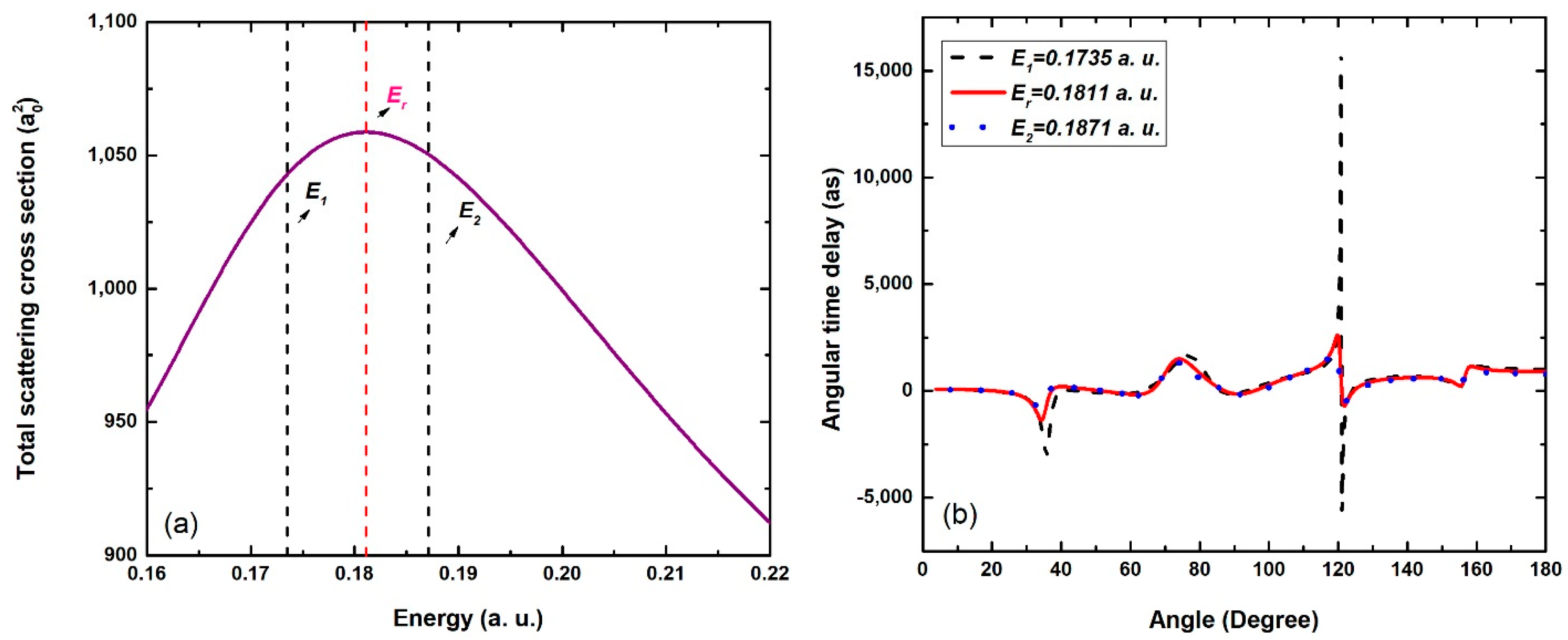
3.2. Resonant Angular Time Delay
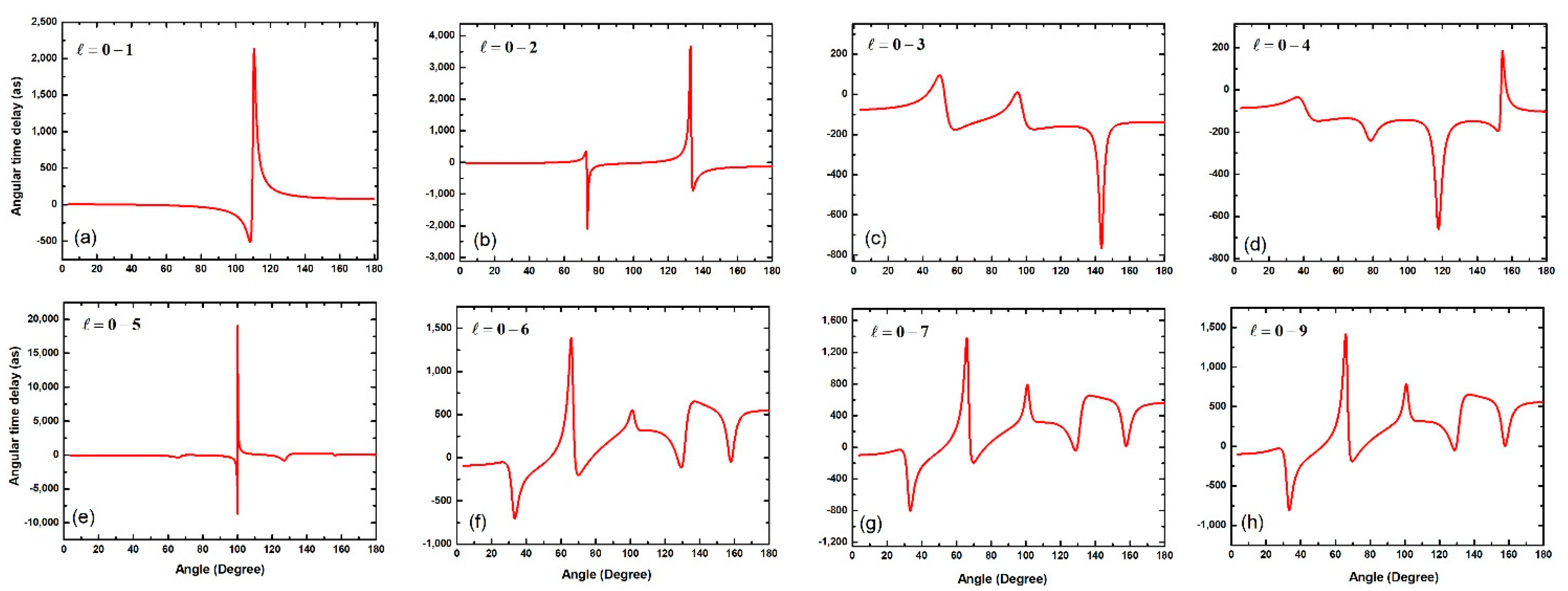
3.3. Angular Time Delay, , at Far-Off Resonant Energies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rutherford, E. The scattering of α and β particles by matter and the structure of the atom. Mag. J. Sci. 1911, 21, 669–688. [Google Scholar] [CrossRef]
- Bohr, N. On the constitution of atoms and molecules. Philos. Mag. 1913, 26, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Gearhart, C.A. The Franck-Hertz experiments, 1911–1914 experimentalists in search of a theory. Phys. Perspect. 2014, 16, 293–343. [Google Scholar] [CrossRef]
- Davisson, C.; Germer, L.H. The Diffraction of Electrons by a Crystal of Nickel. Phys. Rev. 1927, 30, 705–741. [Google Scholar] [CrossRef] [Green Version]
- Massey, H.S.W. Scattering of fast electrons and nuclear magnetic moments. Proc. R. Soc. A 1930, 127, 666–670. [Google Scholar]
- Mott, N.F. The scattering of electrons by atoms. Proc. R. Soc. Lond. A 1930, 127, 658–665. [Google Scholar]
- Mason, N.J.; Gingell, J.M.; Jones, N.C.; Kaminski, L. Experimental studies on electron scattering from atoms and molecules: The state of the art. Philos. Trans. R. Soc. A 1999, 357, 1175–1200. [Google Scholar] [CrossRef]
- Bain, R.A.; Bardsley, J.N. Shape resonances in atom-atom collisions. I. Radiative association. J. Phys. B At. Mol. Phys. 1972, 5, 277–285. [Google Scholar] [CrossRef]
- Bianconi, A. On the possibility of new high Tc superconductors by producing metal heterostructure as in the cuprate perovskites. Commun. Solid State 1994, 89, 933–936. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, A.; Congiu-Castellano, A.; Durham, P.J.; Hasnain, S.S.; Phillips, S. The CO bond angle of carboxymyoglobin determined by angular-resolved XANES spectroscopy. Nature 1985, 318, 685–687. [Google Scholar] [CrossRef]
- Bianconi, A.; Petersen, H.; Brown, F.C.; Bachrach, R.Z. K-shell photoabsorption spectra of N2 and N2O using synchrotron radiation. Phys. Rev. A 1978, 17, 1907–1911. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.C.; Qi, R.; Liu, X.-P.; Wang, X.-Q.; Wang, Y.-X.; Wu, Y.-P.; Chen, H.-Z.; Zhang, P.; Zhai, H.; Chen, Y.-A.; et al. Degenerate Bose gases near a d-wave shape resonance. Nat. Phys. 2019, 15, 570–576. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Chai, Y.; Guo, T.; Jin, C.; Haufler, R.E.; Chibante, L.P.F.; Fure, J.; Wang, L.; Alford, J.M.; Smalley, R.E. Fullerenes with metals inside. J. Phys. Chem. 1991, 95, 7564–7568. [Google Scholar] [CrossRef]
- Cerón, M.R.; Echegoyen, L. Recent progress in the synthesis of regio-isomerically pure bis-adducts of empty and endohedral fullerenes. J. Phys. Org. Chem. 2016, 29, 613–619. [Google Scholar] [CrossRef]
- Tanaka, H.; Hoshino, M.; Brunger, M.J. Elastic and inelastic scattering of low-energy electrons from gas-phase C60: Elastic scattering angular distributions and coexisting solid-state features revisited. Eur. Phys. J. D 2021, 75, 293. [Google Scholar] [CrossRef]
- Müller, A.; Kilcoyne, A.L.D.; Schippers, S.; Phaneuf, R.A. Experimental studies on photoabsorption by endohedral fullerene ions with a focus on Xe@C60+ confinement resonances. Phys. Scr. 2021, 96, 064004. [Google Scholar] [CrossRef]
- Obaid, R.; Xiong, H.; Augustin, S.; Schnorr, K.; Ablikim, U.; Battistoni, A.; Wolf, T.J.A.; Bilodeau, R.C.; Osipov, T.; Gokhberg, K.; et al. Intermolecular Coulombic Decay in Endohedral Fullerene at the 4d→4f Resonance. Phys. Rev. Lett. 2020, 124, 113002. [Google Scholar] [CrossRef]
- Miller, A.; Halstead, M.; Besley, E.; Stace, A.J. Designing stable binary endohedral fullerene lattices. Phys. Chem. Chem. Phys. 2022, 24, 10044–10052. [Google Scholar] [CrossRef]
- Shu, C.-Y.; Ma, X.-Y.; Zhang, J.-F.; Corwin, F.D.; Sim, J.H.; Zhang, E.-Y.; Dorn, H.C.; Gibson, H.W.; Fatouros, P.P.; Wang, C.-R.; et al. Conjugation of a water-soluble gadolinium endohedral fulleride with an antibody as a magnetic resonance imaging contrast agent. Bioconjug. Chem. 2008, 19, 651–655. [Google Scholar] [CrossRef]
- Hartman, K.B.; Wilson, L.J.; Rosenblum, M.G. Detecting and treating cancer with nanotechnology. Mol. Diagn. Ther. 2008, 12, 1–14. [Google Scholar] [CrossRef]
- Harneit, W.; Boehme, C.; Schaefer, S.; Huebener, K.; Fostiropoulos, K.; Lips, K. Room temperature electrical detection of spin coherence in C60. Phys. Rev. Lett. 2007, 98, 216601. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.W.; Hwang, H.J. Nanoscale carbon nanotube motor schematics and simulations for micro-electro-mechanical machines. Nanotechnology 2004, 15, 1633–1638. [Google Scholar] [CrossRef]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; Van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 2009, 8, 208–212. [Google Scholar] [CrossRef]
- Hedley, G.; Ward, A.J.; Alekseev, A.; Howells, C.; Martins, E.; Serrano, L.A.; Cooke, G.; Ruseckas, A.; Samuel, I. Determining the optimum morphology in high-performance polymer-fullerene organic photovoltaic cells. Nat. Commun. 2013, 4, 2867. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Kim, Y.H.; Dillon, A.C.; Heben, M.J.; Zhang, S.B. Hydrogen storage in novel organometallic buckyballs. Phys. Rev. Lett. 2005, 94, 155504. [Google Scholar] [CrossRef] [Green Version]
- Zadik, R.H.; Takabayashi, Y.; Klupp, G.; Colman, R.H.; Ganin, A.Y.; Potočnik, A.; Jeglič, P.; Arčon, D.; Matus, P.; Kamarás, K.; et al. Optimised unconventional superconductivity in a molecular Jahn-Teller metal. Sci. Adv. 2015, 1, e1500059. [Google Scholar] [CrossRef] [Green Version]
- Böhme, D.K. Multiply-charged ions and interstellar chemistry. Phys. Chem. Chem. Phys. 2011, 13, 18253–18263. [Google Scholar] [CrossRef]
- Campbell, E.K.; Holz, M.; Gerlich, D.; Maier, J.P. Laboratory confirmation of C60+ as the carrier of two diffuse interstellar bands. Nature 2015, 523, 322–323. [Google Scholar] [CrossRef]
- Cami, J.; Bernard-Salas, J.; Peeters, E.; Malek, S.E. Detection of C60 and C70 in a young planetary nebula. Science 2010, 329, 1180–1182. [Google Scholar] [CrossRef] [Green Version]
- Cordiner, M.A.; Linnartz, H.; Cox, N.L.J.; Cami, J.; Najarro, F.; Proffitt, C.R.; Lallement, R.; Ehrenfreund, P.; Foing, B.H.; Gull, T.R. Confirming Interstellar C60+ Using the Hubble Space Telescope. Astrophys. J. 2019, 875, 2. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, L.R.; Lohmann, B.; Winstead, C.; McKoy, V. Elastic scattering of intermediate-energy electrons from C60 molecules. Phys. Rev. A At. Mol. Opt. Phys. 2010, 82, 062716. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, K.A.; Giblin, D.E.; Gross, M.L. High-Energy Collisions of Fullerene Radical Cations with Target Gases: Capture of the Target Gas and Charge Stripping of C60.+, C70.+, and C84.+. J. Am. Chem. Soc. 1992, 114, 3743–3756. [Google Scholar] [CrossRef]
- Eisenbud, L.E. The Formal Properties of Nuclear Collisions. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1948. [Google Scholar]
- Wigner, E.P. Lower limit for the energy derivative of the scattering phase shift. Phys. Rev. 1955, 98, 145–147. [Google Scholar] [CrossRef]
- Smith, F.T. Lifetime matrix in collision theory. Phys. Rev. 1960, 118, 349–356. [Google Scholar] [CrossRef]
- Neppl, S.; Ernstorfer, R.; Bothschafter, E.M.; Cavalieri, A.L.; Menzel, D.; Barth, J.V.; Krausz, F.; Kienberger, R.; Feulner, P. Attosecond time-resolved photoemission from core and valence states of magnesium. Phys. Rev. Lett. 2012, 109, 22–26. [Google Scholar] [CrossRef] [Green Version]
- Cavalieri, A.L.; Müller, N.; Uphues, T.; Yakovlev, V.; Baltuška, A.; Horvath, B.; Schmidt, B.; Blümel, L.; Holzwarth, R.; Hendel, S.; et al. Attosecond spectroscopy in condensed matter. Nature 2007, 449, 1029–1032. [Google Scholar] [CrossRef]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Wang, H.; Chini, M.; Chen, S.; Zhang, C.H.; He, F.; Cheng, Y.; Wu, Y.; Thumm, U.; Chang, Z. Attosecond time-resolved auto ionisation of argon. Phys. Rev. Lett. 2010, 105, 3–6. [Google Scholar] [CrossRef]
- Klünder, K.; Dahlström, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guenot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A.; et al. Probing single-photon ionisation on the attosecond time scale. Phys. Rev. Lett. 2011, 106, 143002. [Google Scholar] [CrossRef] [PubMed]
- Dahlström, J.M.; L’Huillier, A.; Maquet, A. Introduction to attosecond delays in photoionization. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 183001. [Google Scholar] [CrossRef]
- Dixit, G.; Chakraborty, H.S.; Madjet, M.E.A. Time delay in the recoiling valence photoemission of Ar endohedrally confined in C60. Phys. Rev. Lett. 2013, 111, 203003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amusia, M.Y.; Chernysheva, L.V. Time Delay of Photoionization by Endohedrals. JETP Lett. 2020, 112, 219–224. [Google Scholar] [CrossRef]
- Kumar, A.; Varma, H.R.; Deshmukh, P.C.; Manson, S.T.; Dolmatov, V.; Kheifets, A. Wigner photoemission time delay from endohedral anions. Phys. Rev. A 2016, 94, 043401. [Google Scholar] [CrossRef] [Green Version]
- Deshmukh, P.C.; Banerjee, S. Time delay in atomic and molecular collisions and photoionisation/photodetachment. Int. Rev. Phys. Chem. 2020, 40, 127–153. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Banerjee, S.; Mandal, A.; Manson, S.T. Eisenbud–Wigner–Smith time delay in atom–laser. Eur. Phys. J. Spec. Top. 2021, 230, 4151–4164. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics Non-Relativistic Theory, 2nd ed.; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Amusia, M.Y.; Baltenkov, A.S.; Woiciechowski, I. Time Delay in Electron Collision with a Spherical Target as a Function of the Scattering Angle. Atoms 2021, 9, 105. [Google Scholar] [CrossRef]
- de Carvalhoa, C.A.; Nussenzveig, H.M. Time delay. Phys. Rep. 2002, 364, 83–174. [Google Scholar] [CrossRef]
- Froissart, M.; Goldberger, M.L.; Watson, K.M. Spatial separation of events in S-matrix theory. Phys. Rev. 1963, 131, 2820–2826. [Google Scholar] [CrossRef] [Green Version]
- Holzmeier, F.; Joseph, J.; Houver, J.C.; Lebech, M.; Dowek, D.; Lucchese, R.R. Influence of shape resonances on the angular dependence of molecular photoionisation delays. Nat. Commun. 2021, 12, 7343. [Google Scholar] [CrossRef] [PubMed]
- Cirelli, C.; Marante, C.; Heuser, S.; Petersson, L.; Galan, A.J.; Argenti, L.; Zhong, S.; Busto, D.; Isinger, M.; Nandi, S.; et al. Anisotropic photoemission time delays close to a Fano resonance. Nat. Commun. 2018, 9, 955. [Google Scholar] [CrossRef] [PubMed]
- Busto, D.; Vinbladh, J.; Zhong, S.; Isinger, M.; Nandi, S.; Maclot, S.; Johnsson, P.; Gisselbrecht, M.; L’Huillier, A.; Lindroth, E.; et al. Fano’s Propensity Rule in Angle-Resolved Attosecond Pump-Probe Photoionization. Phys. Rev. Lett. 2019, 123, 133201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heuser, S.; Galan, A.J.; Cirelli, C.; Marante, C.; Sabbar, M.; Boge, R.; Lucchini, M.; Gallmann, L.; Ivanov, I.; Kheifets, A.; et al. Angular dependence of photoemission time delay in helium. Phys. Rev. A 2016, 94, 063409. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, I.A. Time delay in strong-field photoionisation of a hydrogen atom. Phys. Rev. A-At. Mol. Opt. Phys. 2011, 83, 023421. [Google Scholar] [CrossRef]
- Ivanov, I.A.; Kheifets, A.S. Angle-dependent time delay in two-color XUV+IR photoemission of He and Ne. Phys. Rev. A 2017, 96, 013408. [Google Scholar] [CrossRef]
- Bray, A.W.; Naseem, F.; Kheifets, A.S. Simulation of angular-resolved RABBITT measurements in noble-gas atoms. Phys. Rev. A 2018, 97, 063404. [Google Scholar] [CrossRef] [Green Version]
- Amusia, M.Y.; Baltenkov, A.S. Time delay in electron-C60 elastic scattering in a dirac bubble potential model. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 015101. [Google Scholar] [CrossRef] [Green Version]
- Trabert, D.; Brennecke, S.; Fehre, K.; Anders, N.; Geyer, A.; Grundmann, S.; Schöffler, M.S.; Schmidt, L.P.H.; Jahnke, T.; Dörner, R.; et al. Angular dependence of the Wigner time delay upon tunnel ionisation of H2. Nat. Commun. 2021, 12, 1697. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Baltenkov, A.S.; Connerade, J.P.; Manson, S.T. Structure and photoionisation of confined atoms. Radiat. Phys. Chem. 2004, 70, 417–433. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Lucchese, R.R.; Sanna, N. Computed elastic cross sections and angular distributions of low-energy electron scattering from gas phase C60 fullerene. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 2181–2193. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V. Elastic electron scattering by fullerene C60. Phys. Rev. A-At. Mol. Opt. Phys. 2006, 73, 012711. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181–1186. [Google Scholar] [CrossRef] [Green Version]
- Dolmatov, V.K.; Cooper, M.B.; Hunter, M.E. Electron elastic scattering off endohedral fullerenes A@C60: The initial insight. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 115002. [Google Scholar] [CrossRef] [Green Version]
- Dubey, K.A.; Jose, J. Elastic electron scattering from Ar@C60 z+: Dirac partial-wave analysis. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 115204. [Google Scholar] [CrossRef]
- Wei, J.; Li, B.; Chen, X. Elastic electron scattering from A@ Cn (A = Ca, Mg, n = 60, 20). J. Phys. B At. Mol. Opt. Phys. 2020, 53, 205202. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Manson, S.T. A Unique situation for an endohedral metallofullerene. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 395–403. [Google Scholar] [CrossRef]
- Amusia, M.; Baltenkov, A.; Krakov, B. Photodetachment of negative C60 ions. Phys. Rev. A 1975, 12, 475–479. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 015003. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Thuppilakkadan, A.; Varma, H.R.; Jose, J. Photoionization dynamics of endohedrally confined atomic H and Ar: A contrasting study between compact versus diffused model potential. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 145001. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; King, J.L.; Oglesby, J.C. Diffuse versus square-well confining potentials in modelling A@C60 atoms. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 105102. [Google Scholar] [CrossRef]
- Thijssen, J.M. Computational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Joachain, C.J. Quantum Collision Theory; North-Holland: Amsterdam, The Netherlands; North-Holland Publishing Company: NewYork, NY, USA, 1975. [Google Scholar]
- Sarswat, S.; Aiswarya, R.; Jose, J. Shannon entropy of resonant scattered state in the e–C60 elastic collision. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 055003. [Google Scholar] [CrossRef]
- Dubey, K.A.; Jose, J. Effect of charge transfer on elastic scattering of electron from Ar@C60: Dirac partial wave calculation. Eur. Phys. J. Plus 2021, 136, 713. [Google Scholar] [CrossRef]
- Wigner, E.P. On the Behavior of Cross Sections Near Thresholds. Phys. Rev. 1948, 73, 1002–1009. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
R., A.; Jose, J. An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering. Atoms 2022, 10, 77. https://doi.org/10.3390/atoms10030077
R. A, Jose J. An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering. Atoms. 2022; 10(3):77. https://doi.org/10.3390/atoms10030077
Chicago/Turabian StyleR., Aiswarya, and Jobin Jose. 2022. "An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering" Atoms 10, no. 3: 77. https://doi.org/10.3390/atoms10030077
APA StyleR., A., & Jose, J. (2022). An Investigation of the Resonant and Non-Resonant Angular Time Delay of e-C60 Elastic Scattering. Atoms, 10(3), 77. https://doi.org/10.3390/atoms10030077





