The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization
Abstract
:1. Introduction
2. Methodology
2.1. The BED Model
2.2. The BEB Model
2.3. Average Secondary Electron Energy
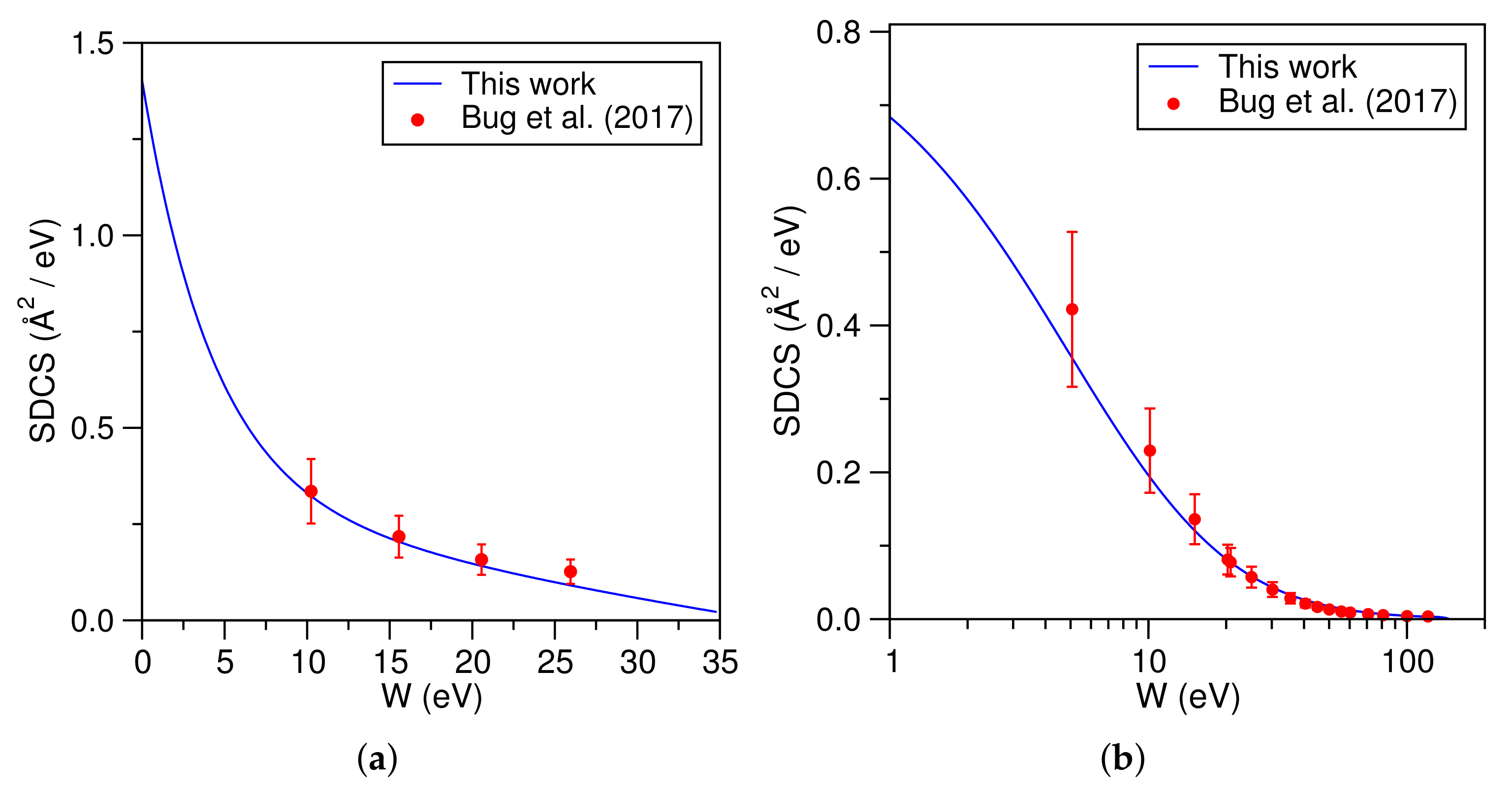
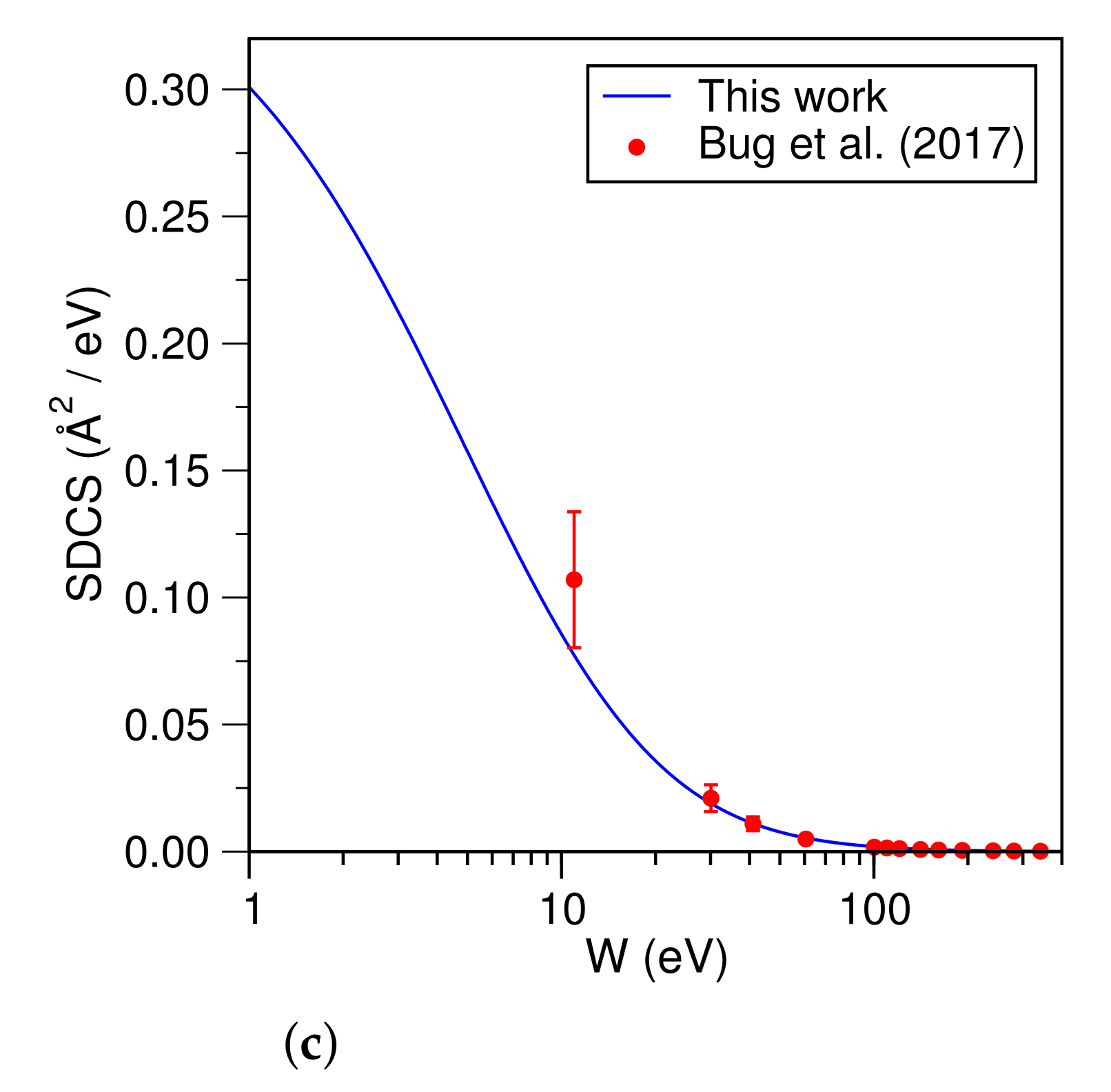
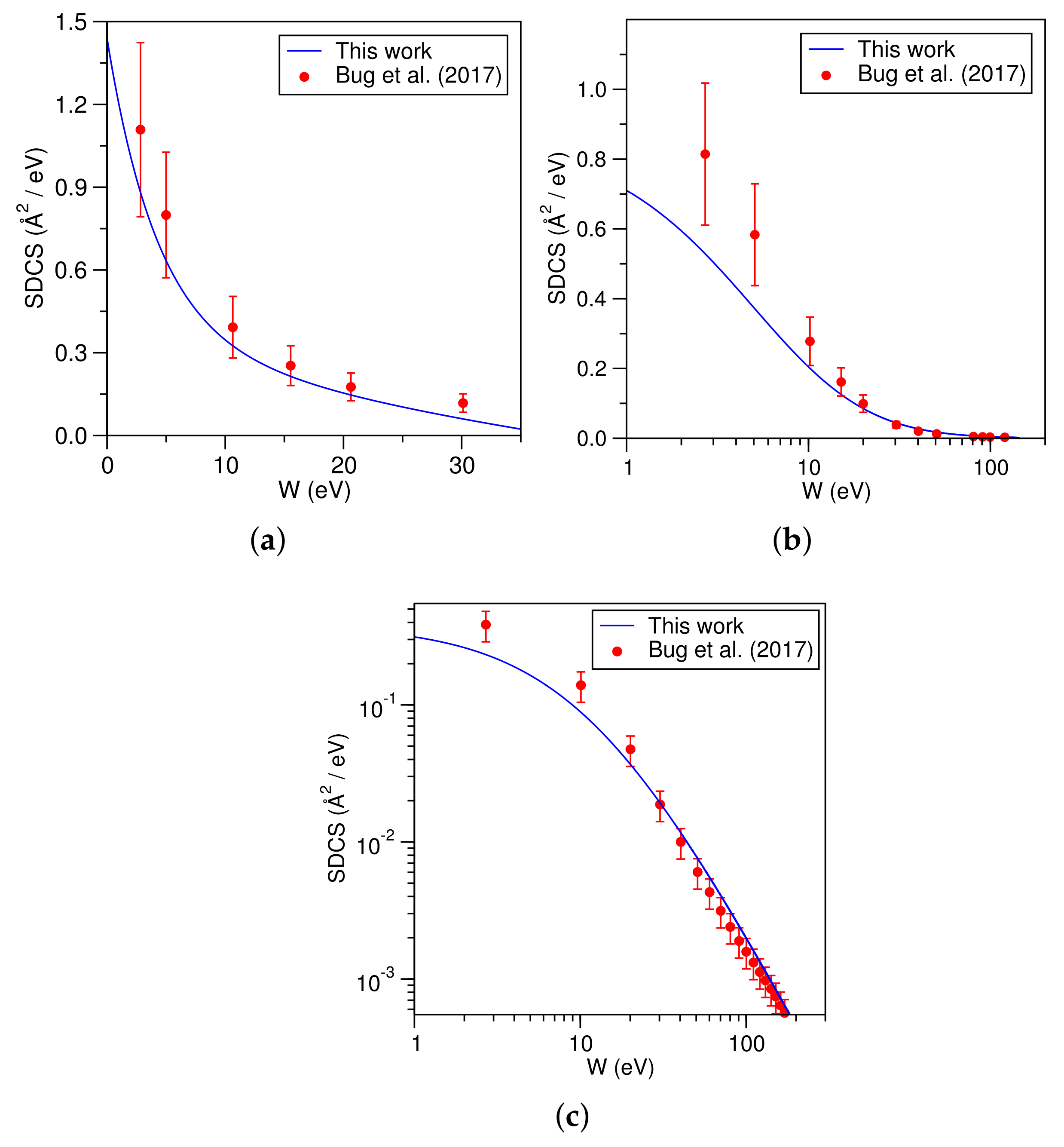
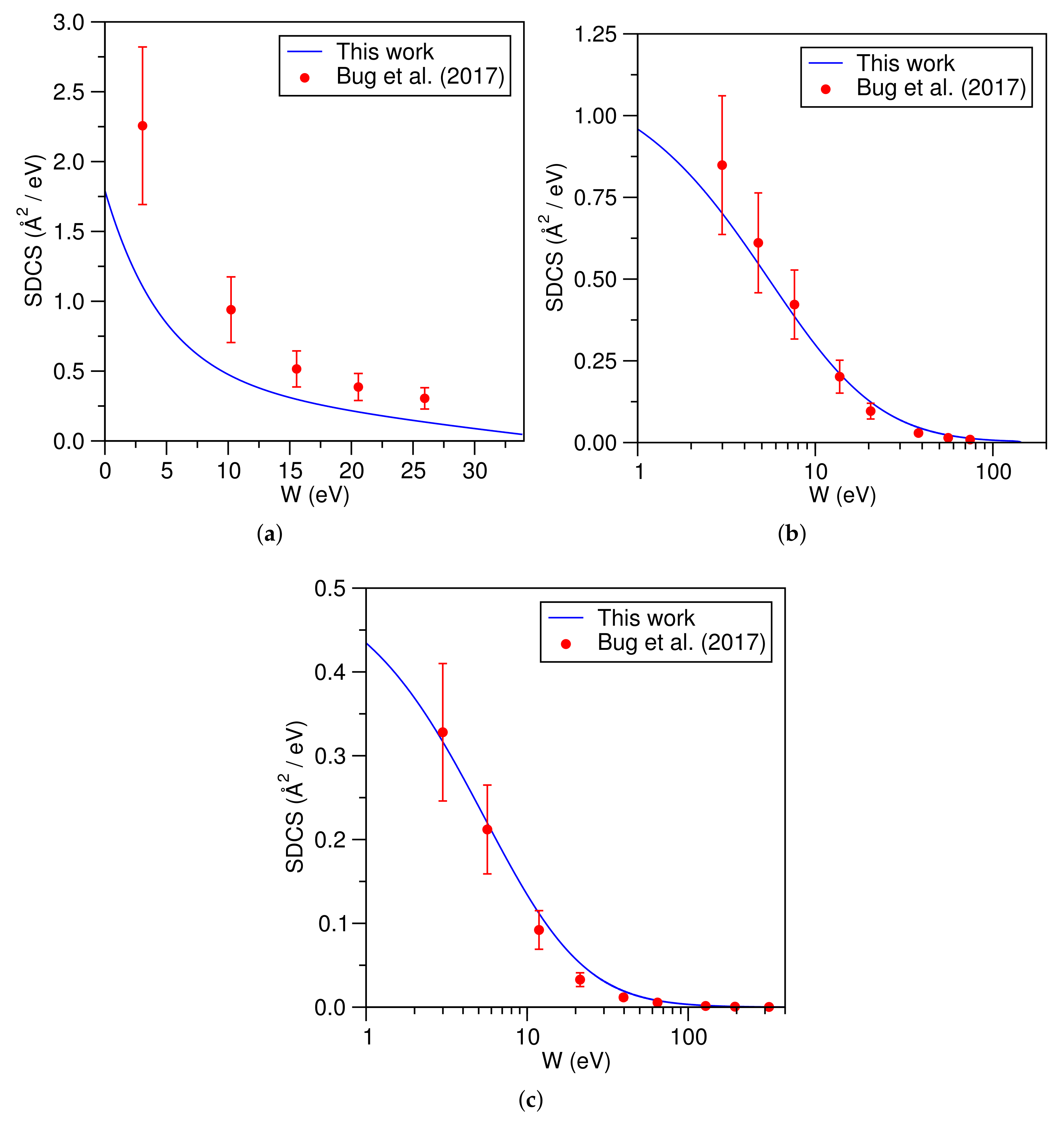
3. Computational Details and Results
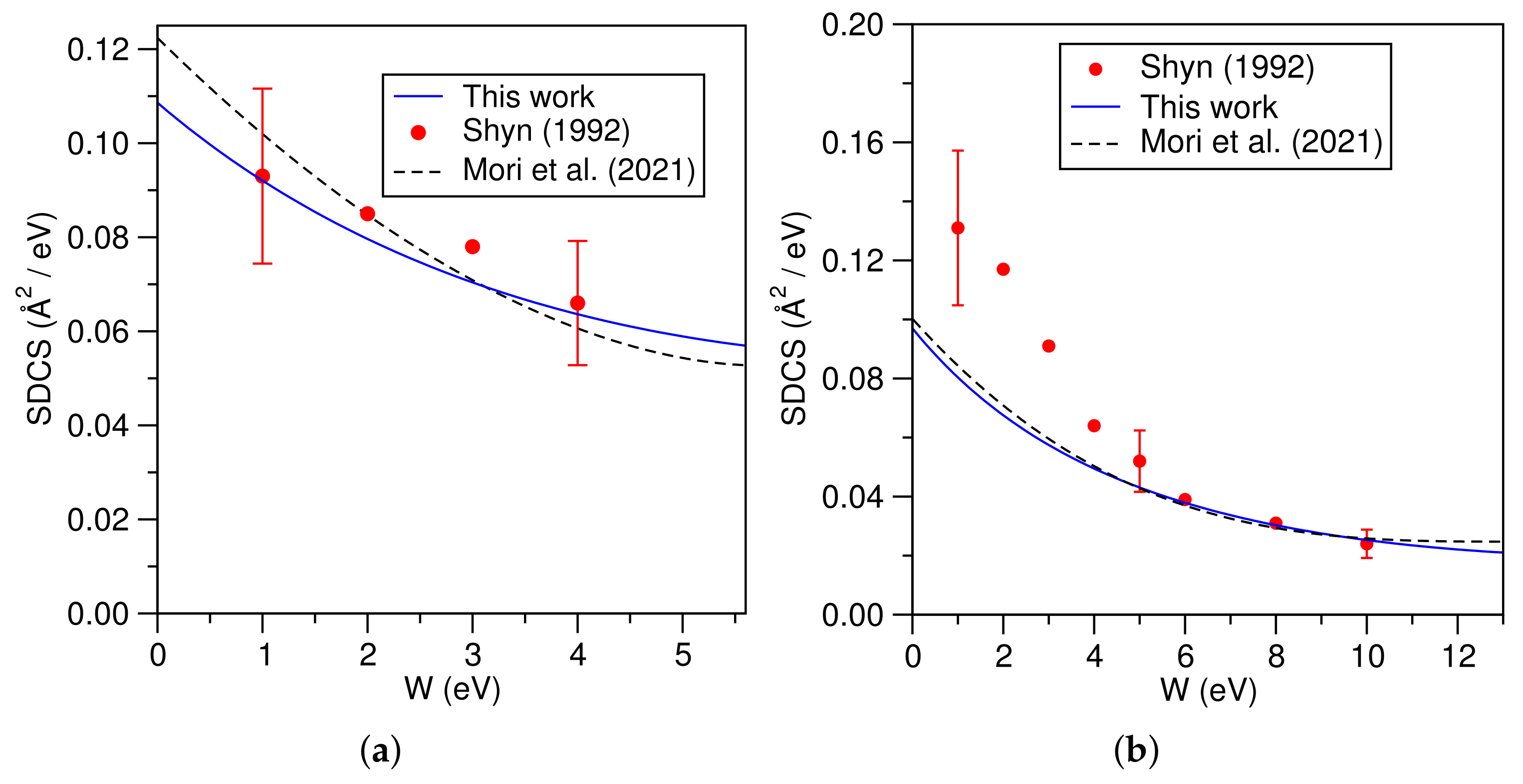
3.1. Hydrogen Atom (H)
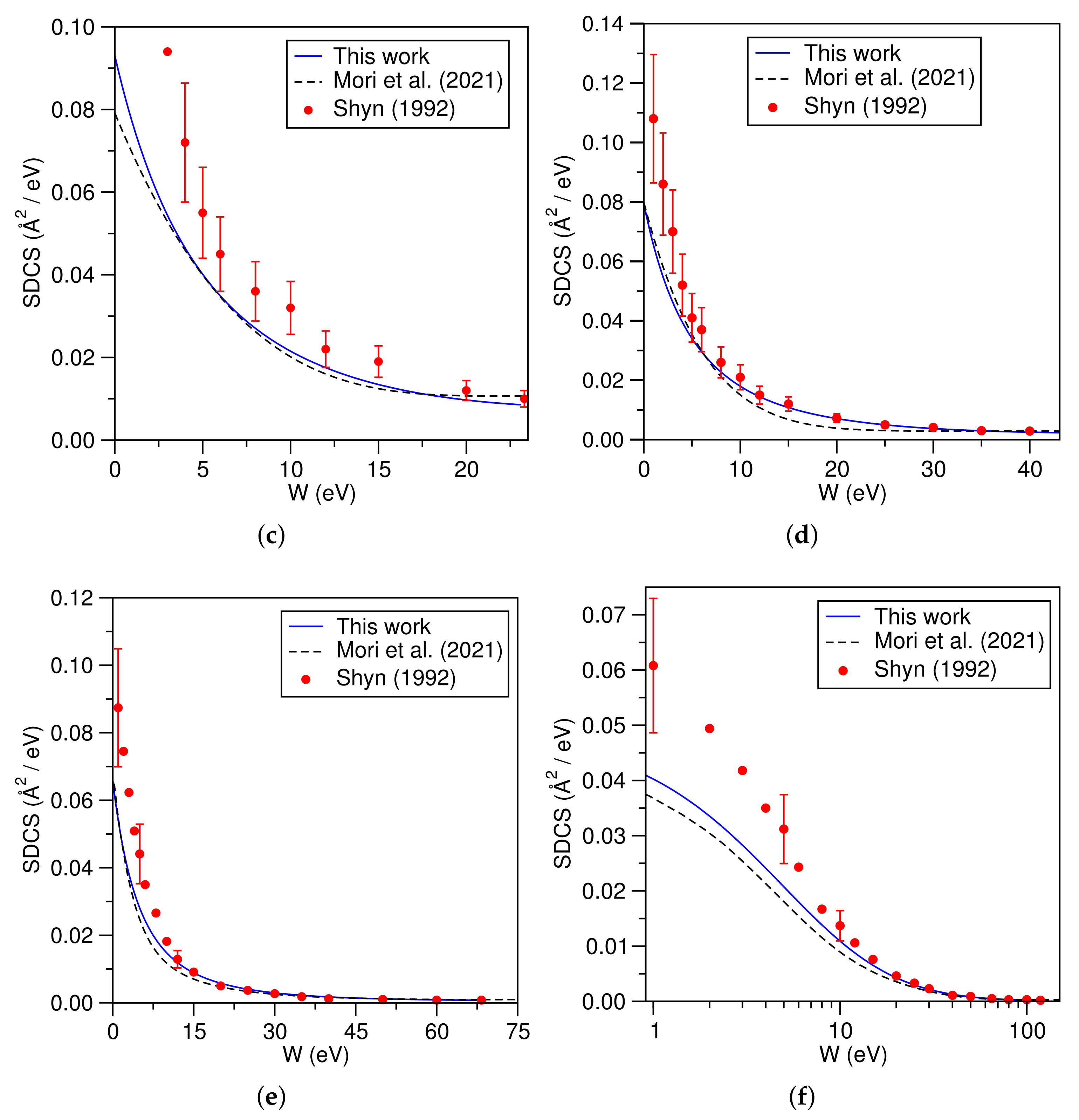
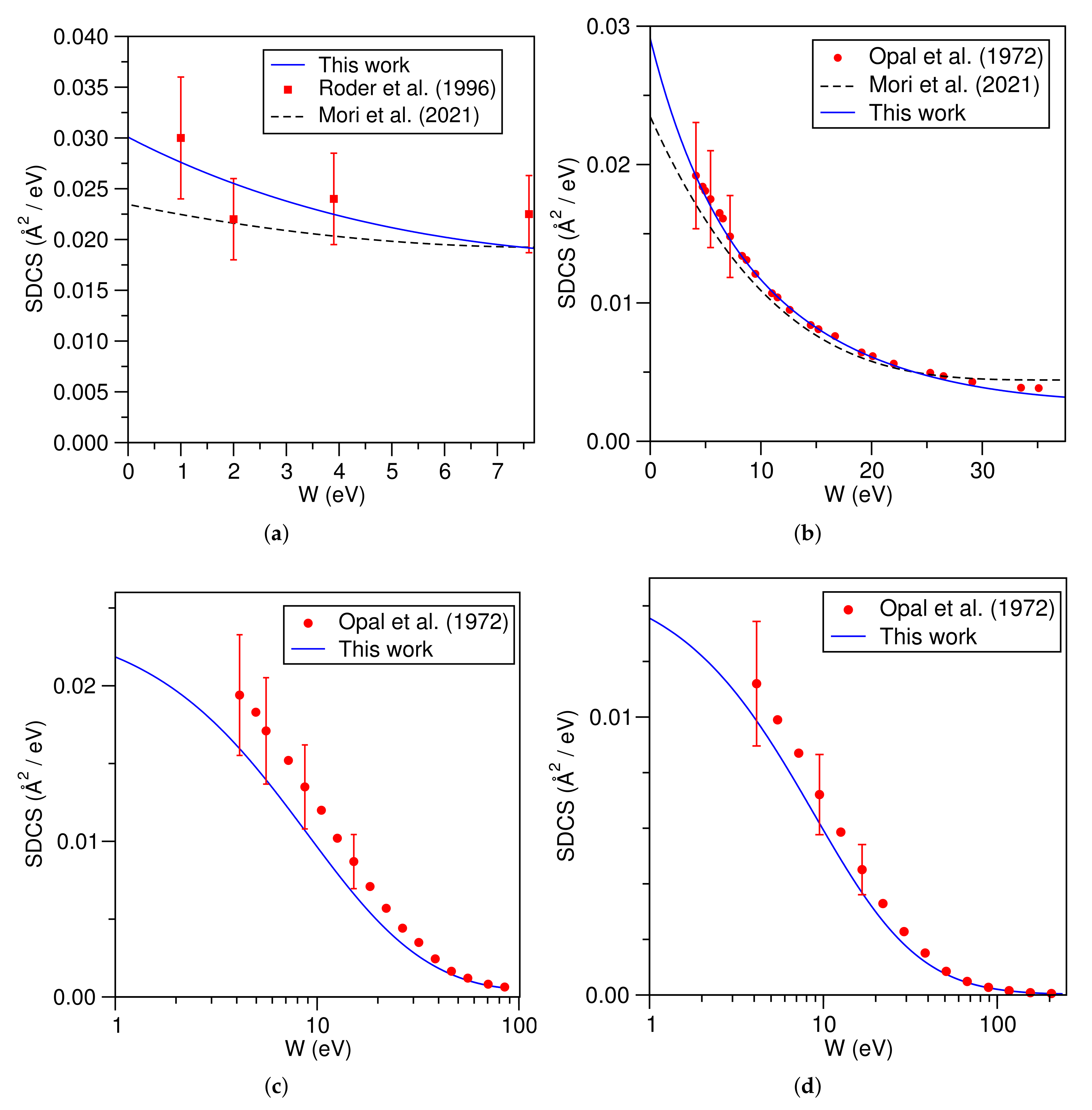
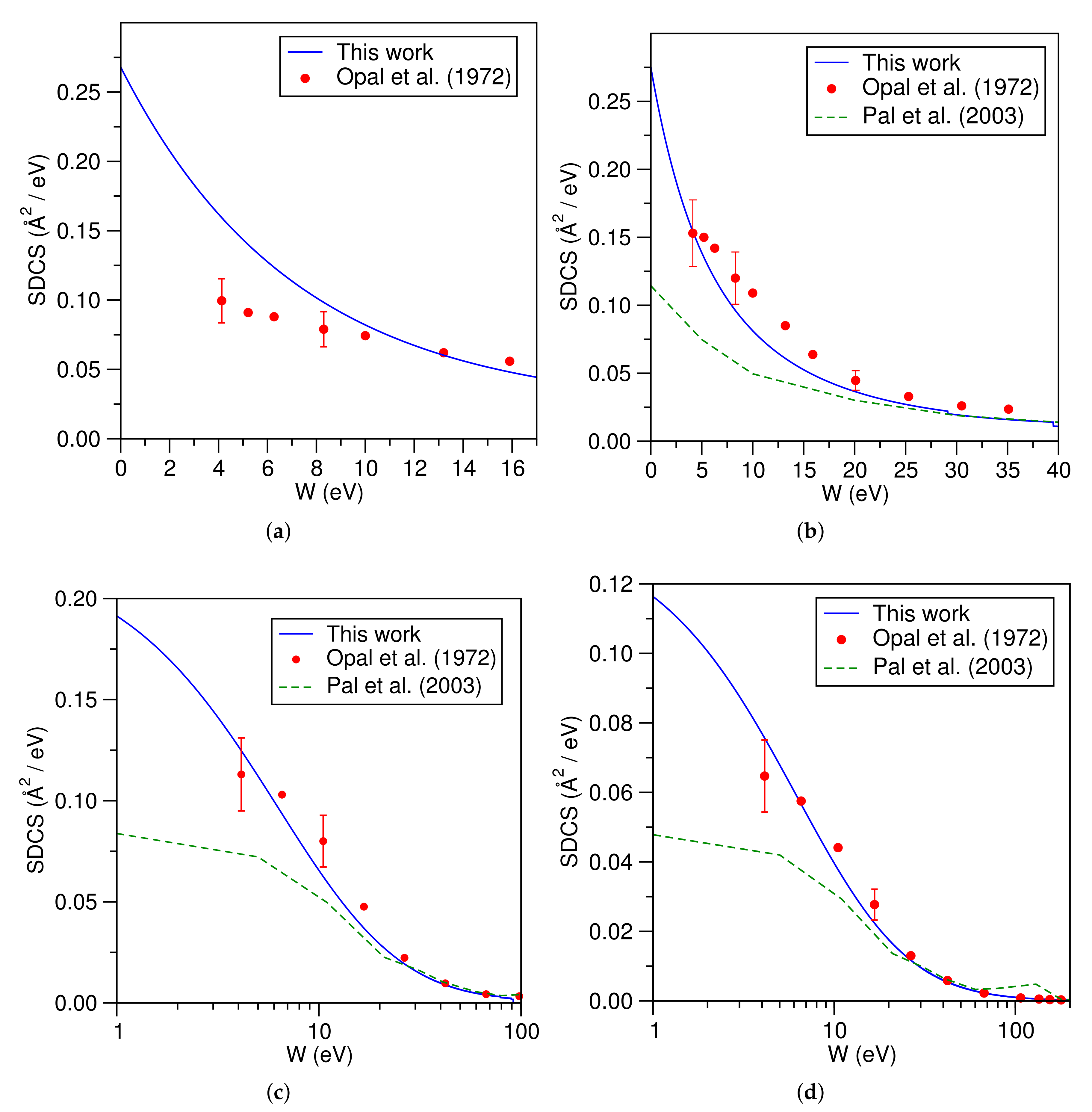
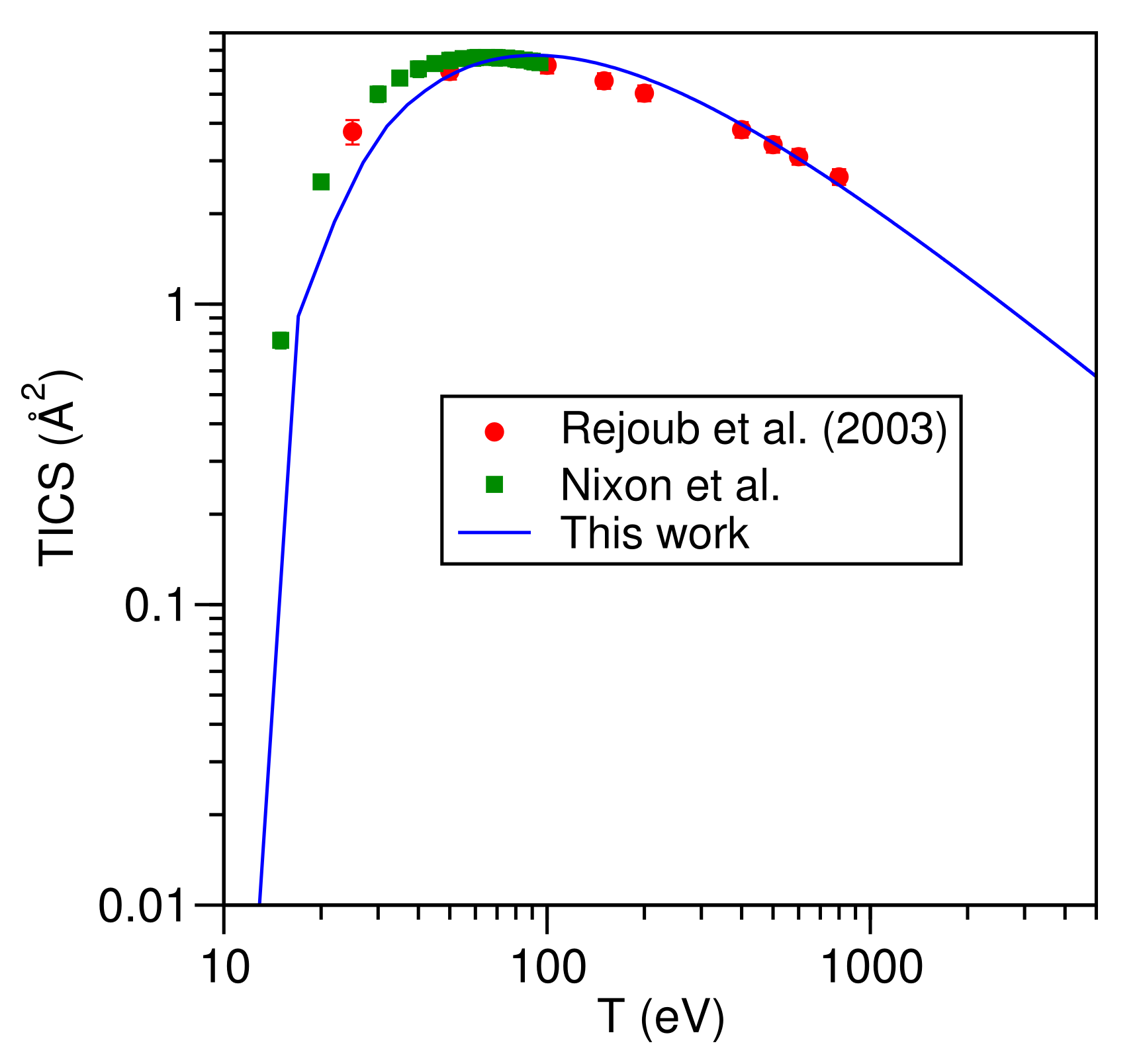
3.2. Helium Atom (He)
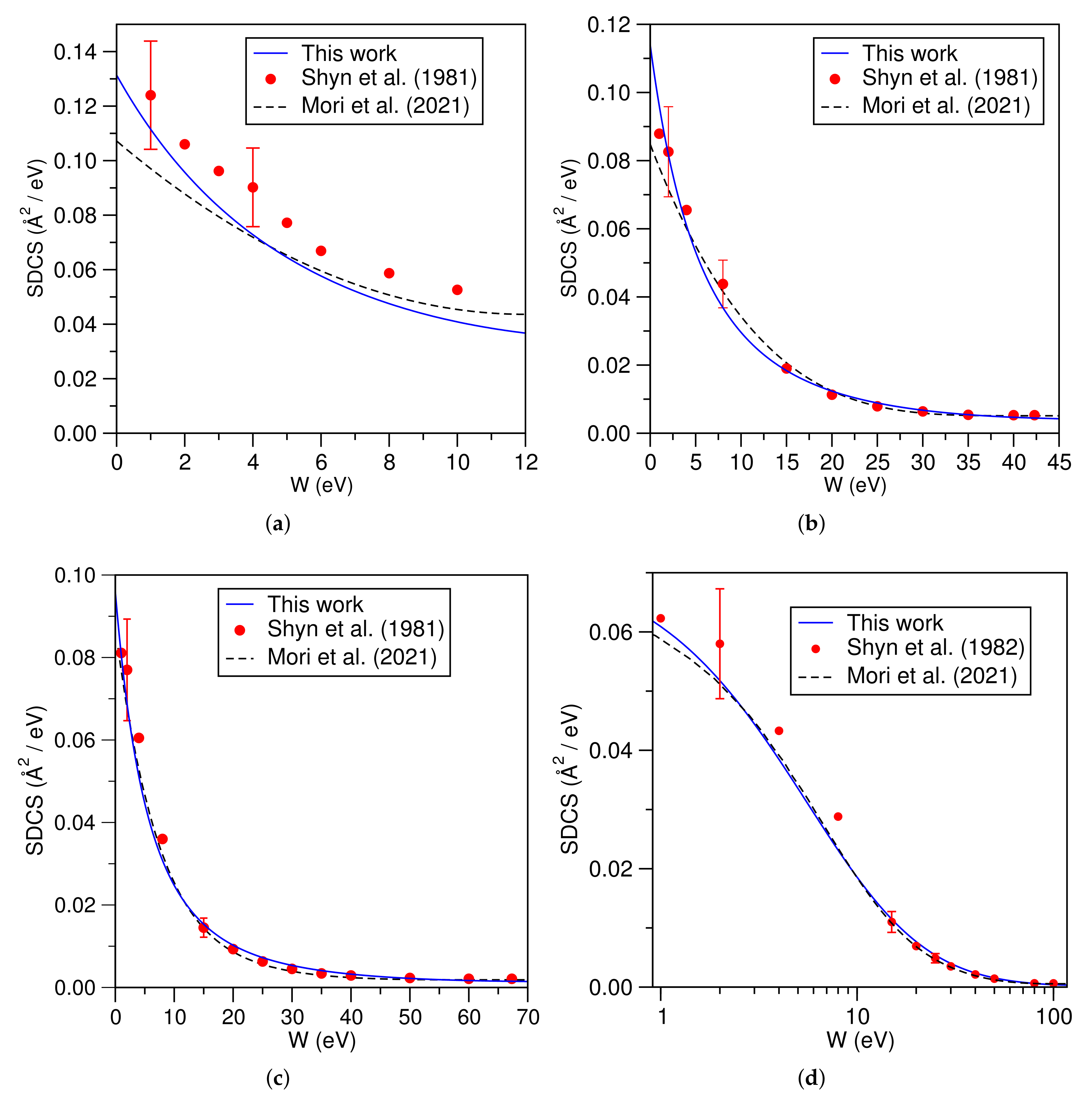
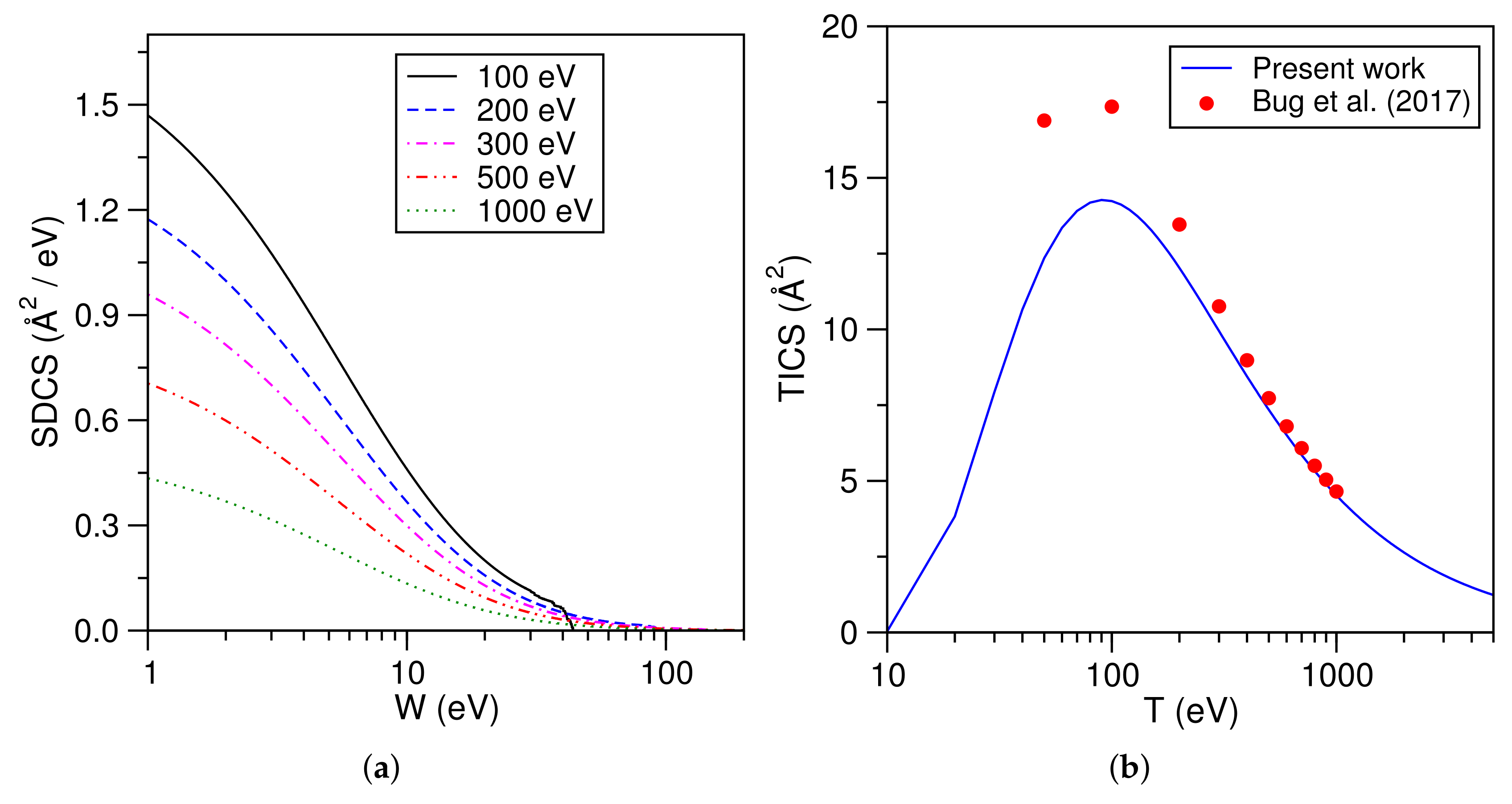
3.3. Molecular Hydrogen (H)
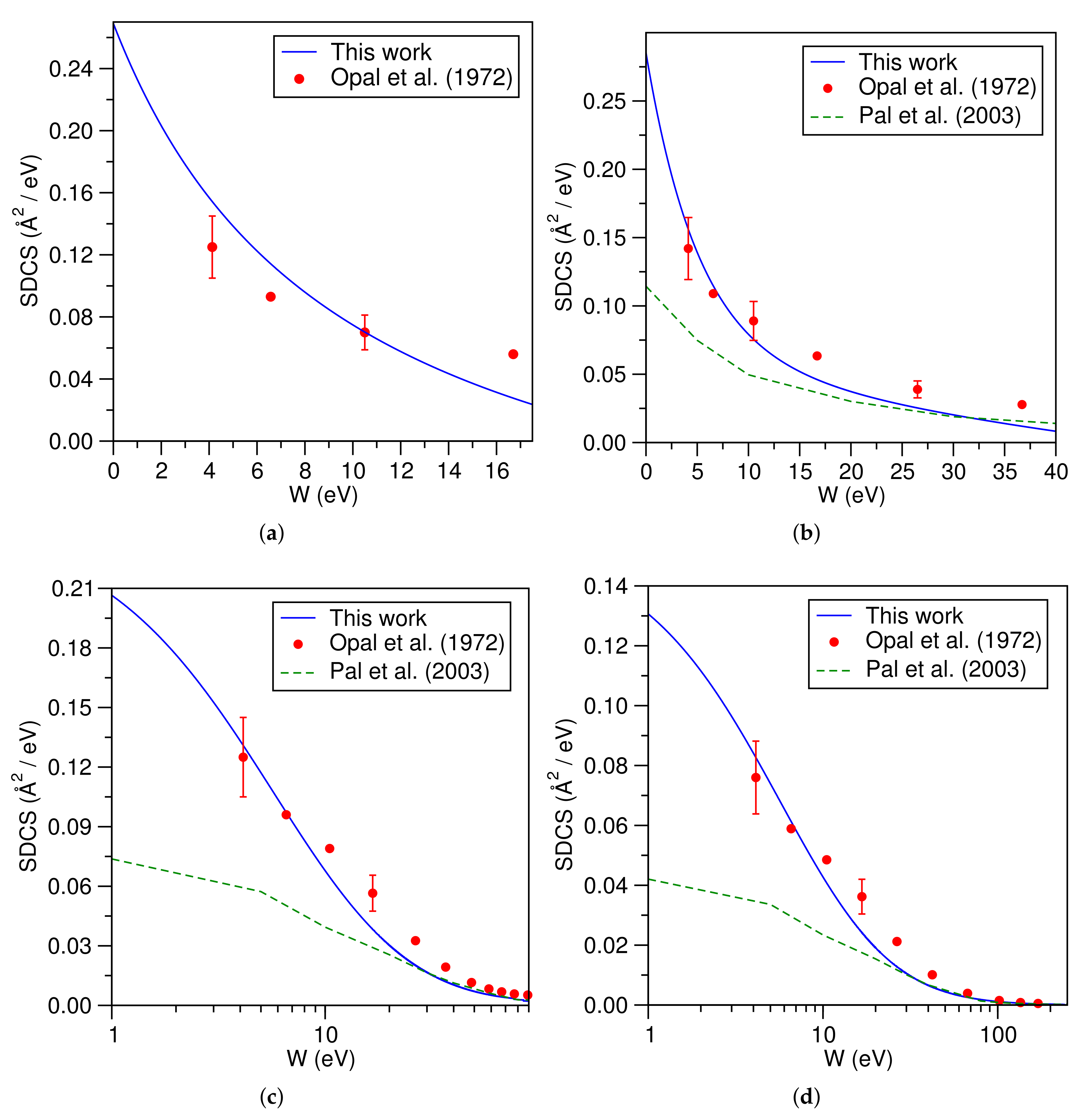
3.4. Molecular Nitrogen (N)
3.5. Molecular Oxygen (O)
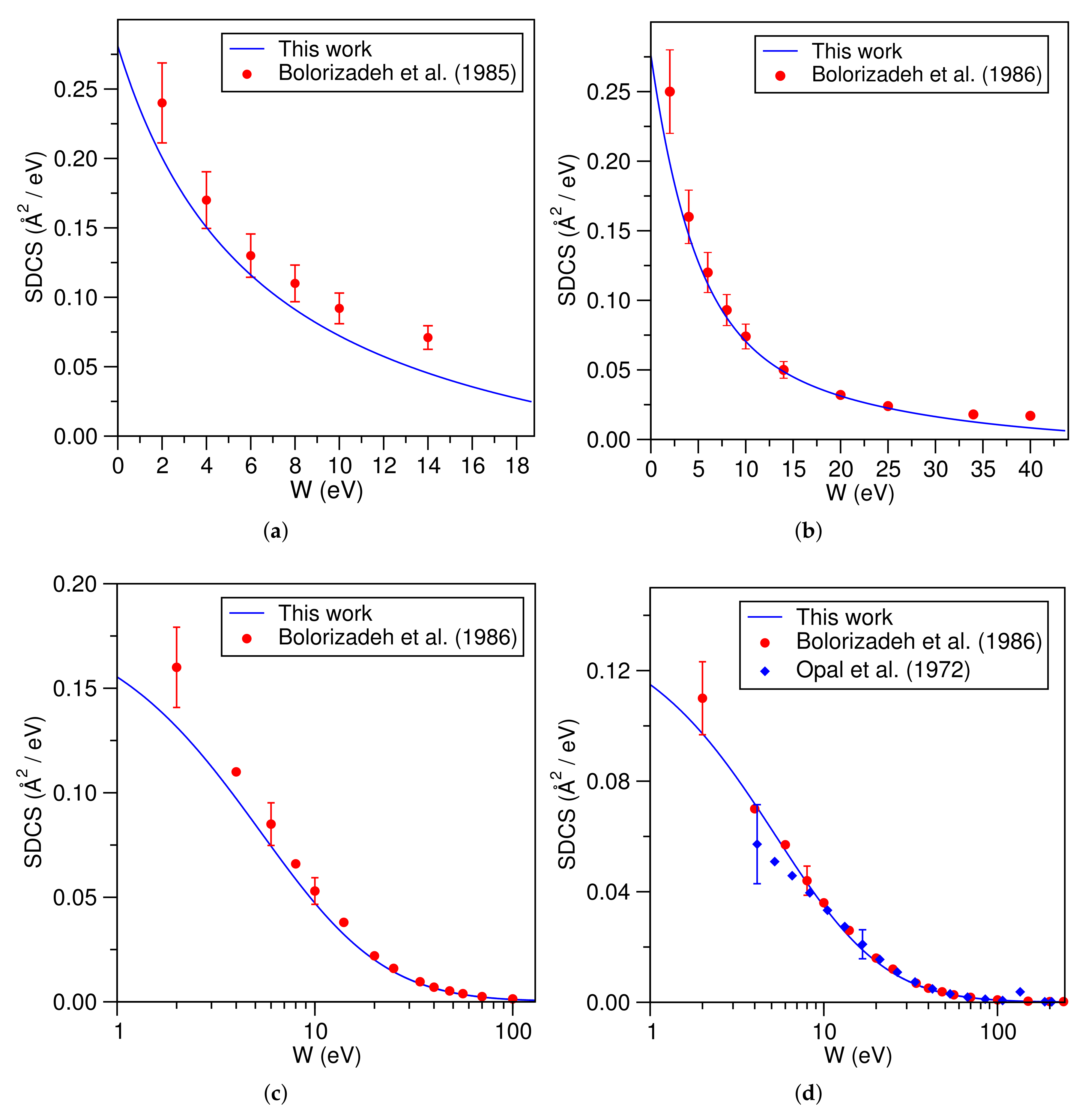
3.6. Water (HO)
3.7. Acetylene (CH)
3.8. Ethanol (CHOH)
3.9. DNA Constituents
3.9.1. Pyrimidine (CHN)
3.9.2. THF (CHO)
3.9.3. TMP (CHOP)
3.9.4. Purine (CHN)
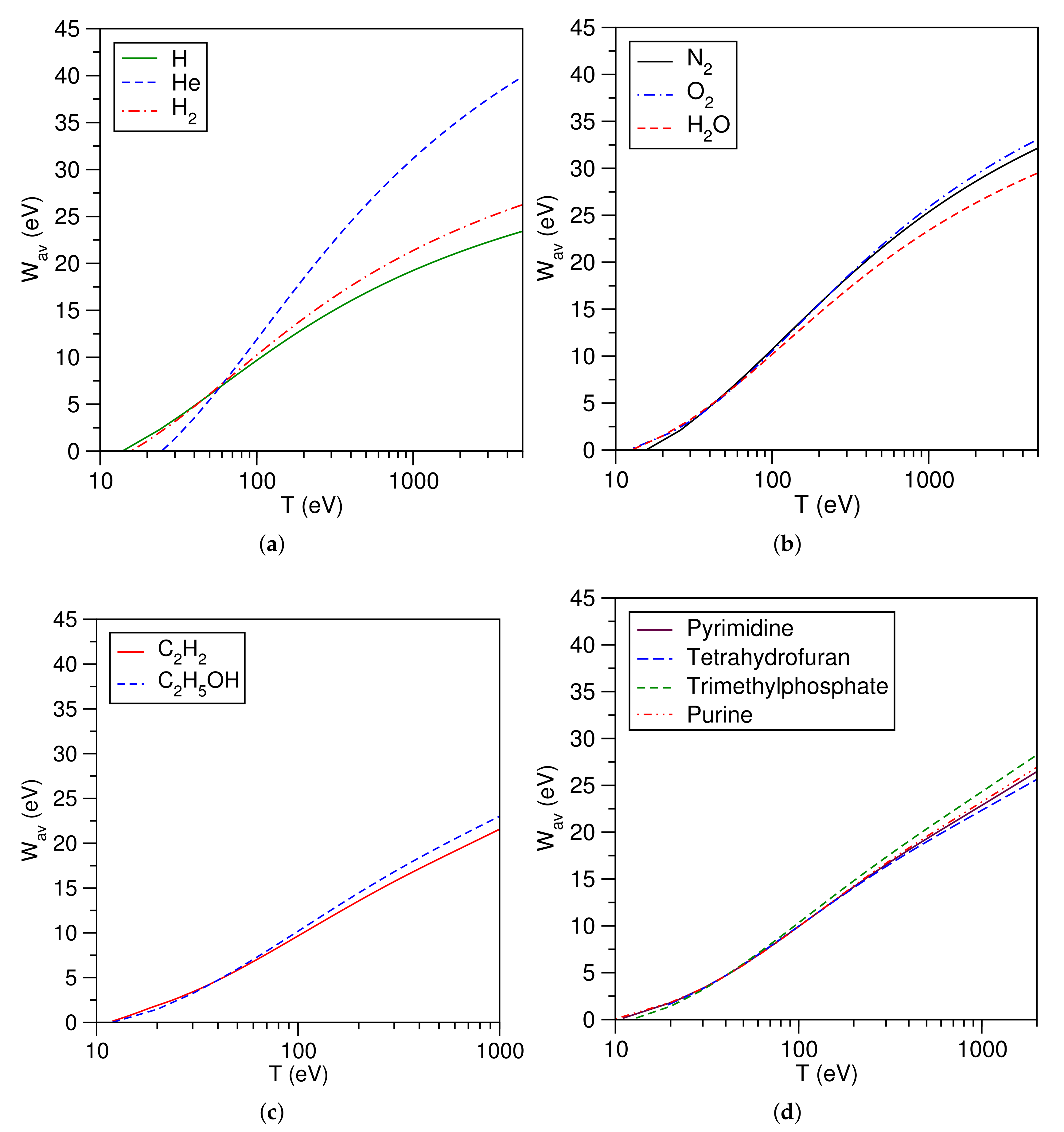
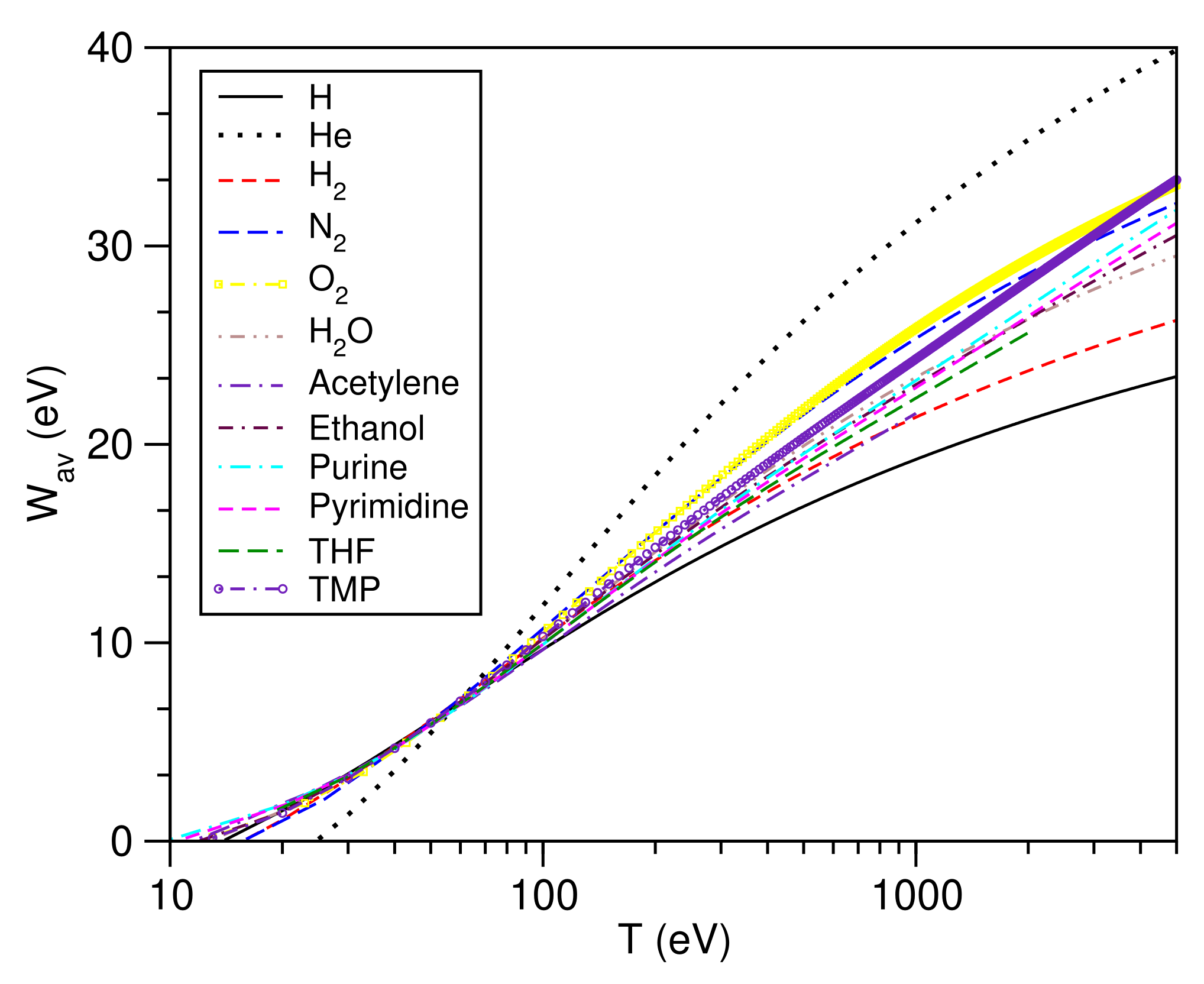
3.10. Average Secondary Electron Energy
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| BED | binary-encounter-dipole |
| BEB | binary-encounter-Bethe |
| SE | Static-Exchange |
| CC | Close Coupling |
| CCC | Convergent Close Coupling |
| SDCS | Singly Differentiated Cross Sections |
| PICS | Partial Ionization Cross Sections |
| TICS | Total Ionization Cross Sections |
| DOS | Differential Oscillator Strength |
| JK | Jain-Khare |
| MO | Molecular Orbitals |
| eV | electron volt |
References
- Joshipura, K.N.; Mason, N. Atomic-Molecular Ionization by Electron Scattering: Theory and Applications; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Märk, T.D.; Dunn, G.H. Electron Impact Ionization; Springer: Vienna, Austria, 1985. [Google Scholar] [CrossRef]
- Caleman, C.; Ortiz, C.; Marklund, E.; Bultmark, F.; Gabrysch, M.; Parak, F.; Hajdu, J.; Klintenberg, M.; Timneanu, N. Radiation damage in biological material: Electronic properties and electron impact ionization in urea. EPL 2008, 85, 18005. [Google Scholar] [CrossRef] [Green Version]
- Lillis, R.J.; Fang, X. Electron impact ionization in the Martian atmosphere: Interplay between scattering and crustal magnetic field effects. J. Geophys. Res. Planets 2015, 120, 1332–1345. [Google Scholar] [CrossRef]
- Campbell, L.; Brunger, M. Electron collisions in atmospheres. Int. Rev. Phys. Chem. 2016, 35, 297–351. [Google Scholar] [CrossRef]
- Adamovich, I.; Baalrud, S.D.; Bogaerts, A.; Bruggeman, P.J.; Cappelli, M.; Colombo, V.; Czarnetzki, U.; Ebert, U.; Eden, J.G.; Favia, P.; et al. The 2017 Plasma Roadmap: Low temperature plasma science and technology. J. Phys. D Appl. Phys. 2017, 50, 323001. [Google Scholar] [CrossRef]
- Christophorou, L.G.; Olthoff, J.K. Fundamental Electron Interactions with Plasma Processing Gases; Springer: New York, NY, USA, 2012. [Google Scholar]
- Kai, T. Single-differential and integral cross sections for electron-impact ionization for the damage of carbon clusters irradiated with X-ray free-electron lasers. Phys. Rev. A 2010, 81, 023201. [Google Scholar] [CrossRef]
- Sanche, L. Low Energy Electron-Driven Damage in Biomolecules. Eur. Phys. J. D 2005, 35, 367–390. [Google Scholar] [CrossRef]
- Boudaïffa, B.; Coultier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant Formation of DNA Strand Breaks by Low-Energy (3 to 20 eV) Electrons. Science 2000, 287, 1658–1660. [Google Scholar] [CrossRef]
- Bray, I. Convergent close-coupling approach to light and heavy projectile scattering on atomic and molecular hydrogen. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 202001. [Google Scholar] [CrossRef]
- Scarlett, L.H.; Savage, J.S.; Fursa, D.V.; Bray, I.; Zammit, M.C.; Schneider, B.I. Convergent close-coupling calculations of electrons scattering on electronically excited molecular hydrogen. Phys. Rev. A 2021, 103, 032802. [Google Scholar] [CrossRef]
- Tennyson, J. Electron–molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron– and positron–molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Graves, V.; Cooper, B.; Tennyson, J. The efficient calculation of electron impact ionization cross sections with effective core potentials. J. Chem. Phys. 2021, 154, 114104. [Google Scholar] [CrossRef]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, M.; Pal, S. (e,2e) ionization cross-sections for C4H4O, C4H8O and C6H8O. Int. J. Mass Spectrom. 2021, 468, 116665. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, M.; Pal, S. Electron impact ionization cross sections for methylamines. J. Electron Spectrosc. Relat. Phenom. 2018, 226, 22–25. [Google Scholar] [CrossRef]
- Deutsch, H.; Becker, K.; Probst, M.; Märk, T.D. Chapter 3 The Semiempirical Deutsch–Märk Formalism: A Versatile Approach for the Calculation of Electron-Impact Ionization Cross Sections of Atoms, Molecules, Ions, and Clusters. In Advances in Atomic, Molecular, and Optical Physics; Academic Press: Cambridge, MA, USA, 2009; Volume 57, pp. 87–155. [Google Scholar] [CrossRef]
- Deutsch, H.; Becker, K.; Matt, S.; Märk, T.D. Theoretical determination of absolute electron-impact ionization cross sections of molecules. Int. J. Mass Spectrom. 2000, 197, 37–69. [Google Scholar] [CrossRef]
- Bharadvaja, A.; Bassi, M.; Arora, A.; Baluja, K.L. Electron interactions with Tetramethylsilane from ionization threshold upto 5000 eV. Plasma Sources Sci. Technol. 2021, 30, 095012. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Tennyson, J.; Huang, S.; Kushner, M.J. Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 2017, 26, 065010. [Google Scholar] [CrossRef] [Green Version]
- Irikura, K.K. Semi-empirical estimation of ion-specific cross sections in electron ionization of molecules. J. Chem. Phys. 2016, 145, 224102. [Google Scholar] [CrossRef]
- Tanaka, H.; Brunger, M.J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A.R.P. Scaled plane-wave Born cross sections for atoms and molecules. Rev. Mod. Phys. 2016, 88, 025004. [Google Scholar] [CrossRef]
- Vriens, L. Binary-Encounter Electron-Atom Collision Theory. Phys. Rev. 1966, 141, 88–92. [Google Scholar] [CrossRef]
- Stone, P.; Kim, Y.-K. An Overview of the BEB Method for Electron-Impact Ionization of Atoms and Molecules. Surf. Interface Anal. 2005, 37, 966–968. [Google Scholar] [CrossRef]
- Denifl, S.; Märk, T.; Scheier, P. The Role of Secondary Electrons in Radiation Damage. Radiat. Damage Biomol. Syst. 2012, 45–58. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Janev, R.K.; Samm, U.; Reiter, D. Collision Processes in Low-Temperature Hydrogen Plasmas; Technical report; TIB Hannover: Hannover, Germany, 2003. [Google Scholar]
- Barklem, P.; Belyaev, A.; Guitou, M.; Feautrier, N.; Gadéa, F.; Spielfiedel, A. On inelastic hydrogen atom collisions in stellar atmospheres. Astron. Astrophys. 2011, 530, 9. [Google Scholar] [CrossRef]
- Feldman, W.C.; Phillips, J.L.; Gosling, J.T.; Isenberg, P.A. Electron impact ionization rates for interstellar H and He atoms near interplanetary shocks: Ulysses observations. AIP Conf. Proc. 1996, 382, 622–625. [Google Scholar] [CrossRef]
- Shyn, T.W.; Sharp, W.E.; Kim, Y.K. Doubly differential cross sections of secondary electrons ejected from gases by electron impact: 25–250 eV on H2. Phys. Rev. A 1981, 24, 79–88. [Google Scholar] [CrossRef]
- Mori, N.A.; Utamuratov, R.; Fursa, D.V.; Zammit, M.C.; Bray, I. Calculation of the single differential cross section for electron-impact ionization of atoms and molecules. J. Phys. B At. Mol. Opt. Phys. 2020, 54, 015205. [Google Scholar] [CrossRef]
- Shyn, T.W. Doubly differential cross sections of secondary electrons ejected from atomic hydrogen by electron impact. Phys. Rev. A 1992, 45, 2951–2956. [Google Scholar] [CrossRef]
- Opal, C.; Beaty, E.; Peterson, W. Tables of secondary-electron-production cross sections. At. Data Nucl. Data Tables 1972, 4, 209–253. [Google Scholar] [CrossRef]
- Röder, J.; Ehrhardt, H.; Bray, I.; Fursa, D.V. Absolute double differential cross sections for electron-impact ionization of helium. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 1309–1322. [Google Scholar] [CrossRef]
- Hunten, D.M. The production of in the atmosphere. Planet. Space Sci. 1963, 10, 37–45. [Google Scholar] [CrossRef]
- Broadfoot, A.; Hunten, D. emission in the twilight. Planet. Space Sci. 1966, 14, 1303–1319. [Google Scholar] [CrossRef]
- Pal, S.; Kumar, J.; Bhatt, P. Electron impact ionization cross-sections for the N2 and O2 molecules. J. Electron Spectrosc. Relat. Phenom. 2003, 129, 35–41. [Google Scholar] [CrossRef]
- Seki, K.; Elphic, R.C.; Hirahara, M.; Terasawa, T.; Mukai, T. On atmospheric loss of oxygen ions from earth through magnetospheric processes. Science 2001, 291, 1939–1941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newson, K.A.; Price, S.D. The formation and dissociation of the ozone dication. Int. J. Mass Spectrom. Ion Process. 1996, 153, 151–159. [Google Scholar] [CrossRef]
- Itikawa, Y.; Mason, N. Cross Sections for Electron Collisions with Water Molecules. J. Phys. Chem. Ref. Data 2005, 34, 1–22. [Google Scholar] [CrossRef]
- Verkhovtsev, A.; Traore, A.; Muñoz, A.; Blanco, F.; García, G. Modeling secondary particle tracks generated by intermediate- and low-energy protons in water with the Low-Energy Particle Track Simulation code. Radiat. Phys. Chem. 2017, 130, 371–378. [Google Scholar] [CrossRef]
- Wiklund, K.; Fernández-Varea, J.; Lind, B. A Monte Carlo program for the analysis of low-energy electron tracks in liquid water. Phys. Med. Biol. 2011, 56, 1985–2003. [Google Scholar] [CrossRef]
- Bolorizadeh, M.A.; Rudd, M.E. Angular and energy dependence of cross sections for ejection of electrons from water vapor. I. 50–2000-eV electron impact. Phys. Rev. A 1986, 33, 882–887. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, H.; Zhu, Y.; Yu, D.; Tang, Z.; He, Y.; Wu, C.; Wang, J. A new method of fullerene production: Pyrolysis of acetylene in high-frequency thermal plasma. Mater. Sci. Eng. B 2002, 95, 29–32. [Google Scholar] [CrossRef]
- De Bleecker, K.; Bogaerts, A.; Goedheer, W. Detailed modeling of hydrocarbon nanoparticle nucleation in acetylene discharges. Phys. Rev. E 2006, 73, 026405. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, R.I. Experimental Investigation on the formation of Carbon-Bearing Molecules in the Interstellar Medium via Neutral-Neutral Reaction. Chem. Rev. 2002, 102, 1309–1358. [Google Scholar] [CrossRef]
- Stein, T.; Bera, P.P.; Lee, T.J.; Head-Gordon, M. Molecular growth upon ionization of van der Waals clusters containing HCCH and HCN is a pathway to prebiotic molecules. Phys. Chem. Chem. Phys. 2020, 22, 20337–20348. [Google Scholar] [CrossRef]
- Huber, S.E.; Seebacher, J.; Kendl, A.; Reiter, D. Assessment of Hydrocarbon Electron-Impact Ionization Cross Section Measurements for Magnetic Fusion. Contrib. Plasma Phys. 2011, 51, 931–943. [Google Scholar] [CrossRef] [Green Version]
- Pal, S.; Singh, R.; Kumar, M.; Kumar, N. Ionization cross-sections for C2H2 and C2H5OH by electron- impact. Radiat. Phys. Chem. 2020, 173, 108877. [Google Scholar] [CrossRef]
- Lopes, M.C.; Pires, W.; Nixon, K.L.; Amorim, R.; Silva, D.; Fernandes, A.; Ghosh, S.; Jones, D.; Campbell, L.; Neves, R.; et al. Electron impact ionization and fragmentation of biofuels. Eur. Phys. J. D 2020, 74, 88. [Google Scholar] [CrossRef]
- Perrero, J.; Enrique-Romero, J.; Martínez-Bachs, B.; Ceccarelli, C.; Balucani, N.; Ugliengo, P.; Rimola, A. Non-energetic Formation of Ethanol via CCH Reaction with Interstellar H2O Ices. A Computational Chemistry Study. ACS Earth Space Chem. 2022, 6, 496–511. [Google Scholar] [CrossRef]
- Nixon, K.L.; Pires, W.A.D.; Neves, R.; Duque, H.; Jones, D.B.; Brunger, M.J.; Lopes, M. Electron Impact Ionisation and Fragmentation of Methanol and Ethanol. Int. J. Mass Spectrom. 2016, 404, 48–59. [Google Scholar] [CrossRef]
- Rejoub, R.; Morton, C.D.; Lindsay, B.G.; Stebbings, R.F. Electron-impact ionization of the simple alcohols. J. Chem. Phys. 2003, 118, 1756–1760. [Google Scholar] [CrossRef]
- Bug, M.U.; Gargioni, E.; Nettelbeck, H.; Baek, W.Y.; Hilgers, G.; Rosenfeld, A.B.; Rabus, H. Ionization cross section data of nitrogen, methane, and propane for light ions and electrons and their suitability for use in track structure simulations. Phys. Rev. E 2013, 88, 043308. [Google Scholar] [CrossRef] [Green Version]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascialino, B.; Moretto, P.; et al. The GEANT4-DNA Project. Int. J. Model. Simul. Sci. Comput. 2010, 1, 157–178. [Google Scholar] [CrossRef]
- Champion, C.; Quinto, M.A.; Weck, P.F. Electron- and proton-induced ionization of pyrimidine. Eur. Phys. J. D 2015, 69, 127. [Google Scholar] [CrossRef]
- Bug, M.U.; Woon, Y.B.; Rabus, H.; Villagrasa, C.; Meylan, S.; Rosenfeld, A.B. An electron-impact cross section data set (10 eV–1 keV) of DNA constituents based on consistent experimental data: A requisite for Monte Carlo simulations. Radiat. Phys. Chem. 2017, 130, 459–479. [Google Scholar] [CrossRef]
- Fuss, M.C.; Sanz, A.G.; Blanco, F.; Limão-Vieira, P.; Brunger, M.J.; García, G. Differential and integral electron scattering cross sections from tetrahydrofuran (THF) over a wide energy range: 1–10,000 eV. Eur. Phys. J. D 2014, 68, 161. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar] [CrossRef]
- Goswami, K.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Electron impact partial ionization cross sections of methyl alcohol up to 5 keV using the mass spectrometry data. Eur. Phys. J. D 2021, 75, 228. [Google Scholar] [CrossRef]
- Arora, A.K.; Gupta, K.K.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. A binary-encounter-Bethe approach to compute electron-impact partial ionization cross sections of plasma relevant molecules such as hexamethyldisiloxane and silane. Plasma Sources Sci. Technol. 2022, 31, 015008. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G.P. Binary-encounter dipole model for positron-impact direct ionization. Phys. Rev. A 2019, 100, 062702. [Google Scholar] [CrossRef]
- Sahgal, V.; Bharadvaja, A.; Baluja, K.L. Positron-induced scattering of acetone from 0.1 eV to 5 keV. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 075202. [Google Scholar] [CrossRef]
- Arora, A.K.; Sahgal, V.; Gupta, K.K.; Bharadvaja, A.; Baluja, K.L. Positron-induced scattering from pentane isomers beyond ionization threshold. Eur. Phys. J. D 2021, 75, 259. [Google Scholar] [CrossRef]
- Arora, A.K.; Sahgal, V.; Bharadvaja, A.; Baluja, K.L. Positron-impact scattering off 1-1 C2H2F2 from 0.1 eV to 4 keV. Phys. Rev. A 2021, 104, 022816. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garkoti, P.; Luthra, M.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization. Atoms 2022, 10, 60. https://doi.org/10.3390/atoms10020060
Garkoti P, Luthra M, Goswami K, Bharadvaja A, Baluja KL. The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization. Atoms. 2022; 10(2):60. https://doi.org/10.3390/atoms10020060
Chicago/Turabian StyleGarkoti, Pankaj, Meetu Luthra, Kanupriya Goswami, Anand Bharadvaja, and Kasturi Lal Baluja. 2022. "The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization" Atoms 10, no. 2: 60. https://doi.org/10.3390/atoms10020060
APA StyleGarkoti, P., Luthra, M., Goswami, K., Bharadvaja, A., & Baluja, K. L. (2022). The Binary-Encounter-Bethe Model for Computation of Singly Differential Cross Sections Due to Electron-Impact Ionization. Atoms, 10(2), 60. https://doi.org/10.3390/atoms10020060






