Low-Energy Electron Scattering from c-C4F8
Abstract
:1. Introduction
2. Theoretical Methodology
Target Models
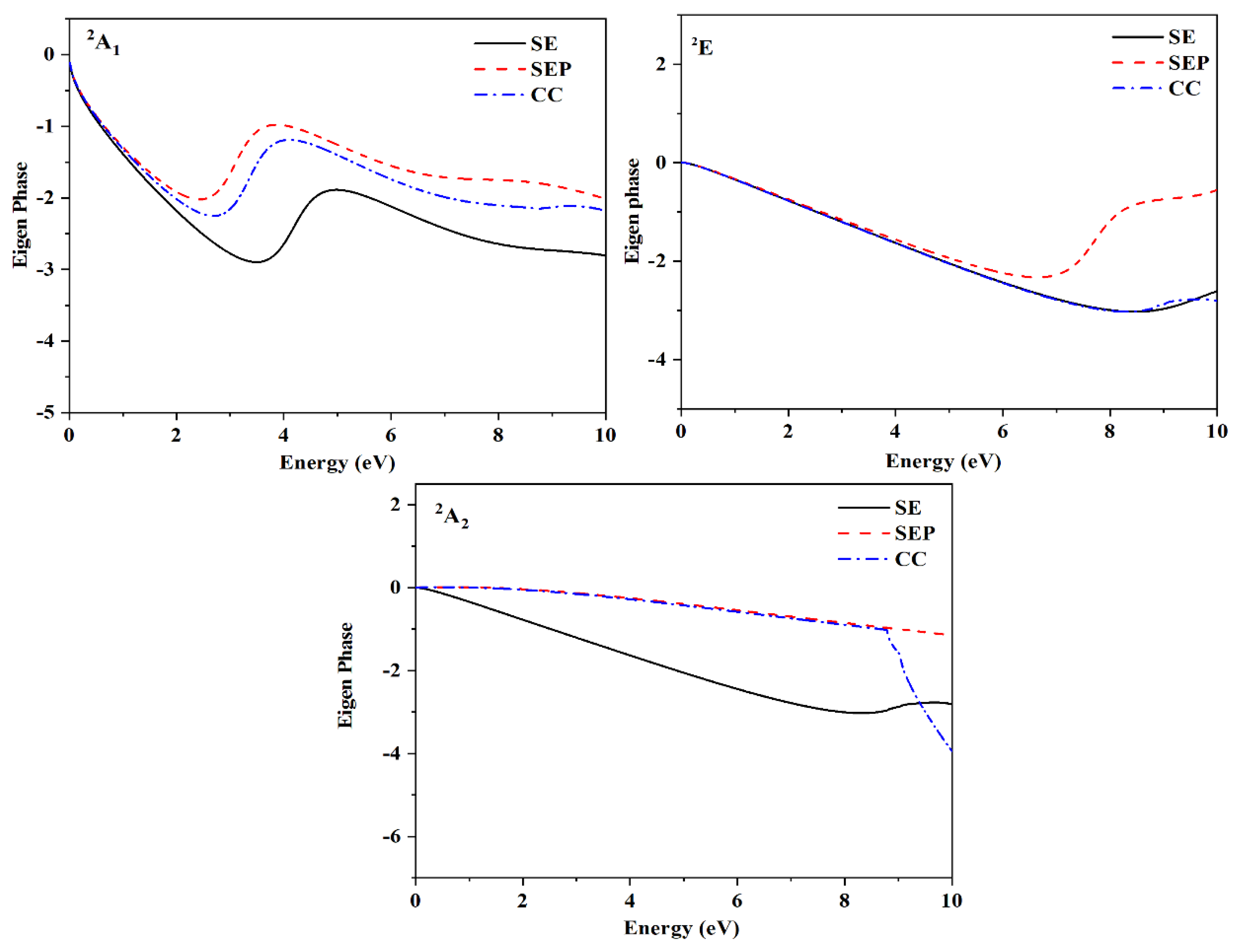
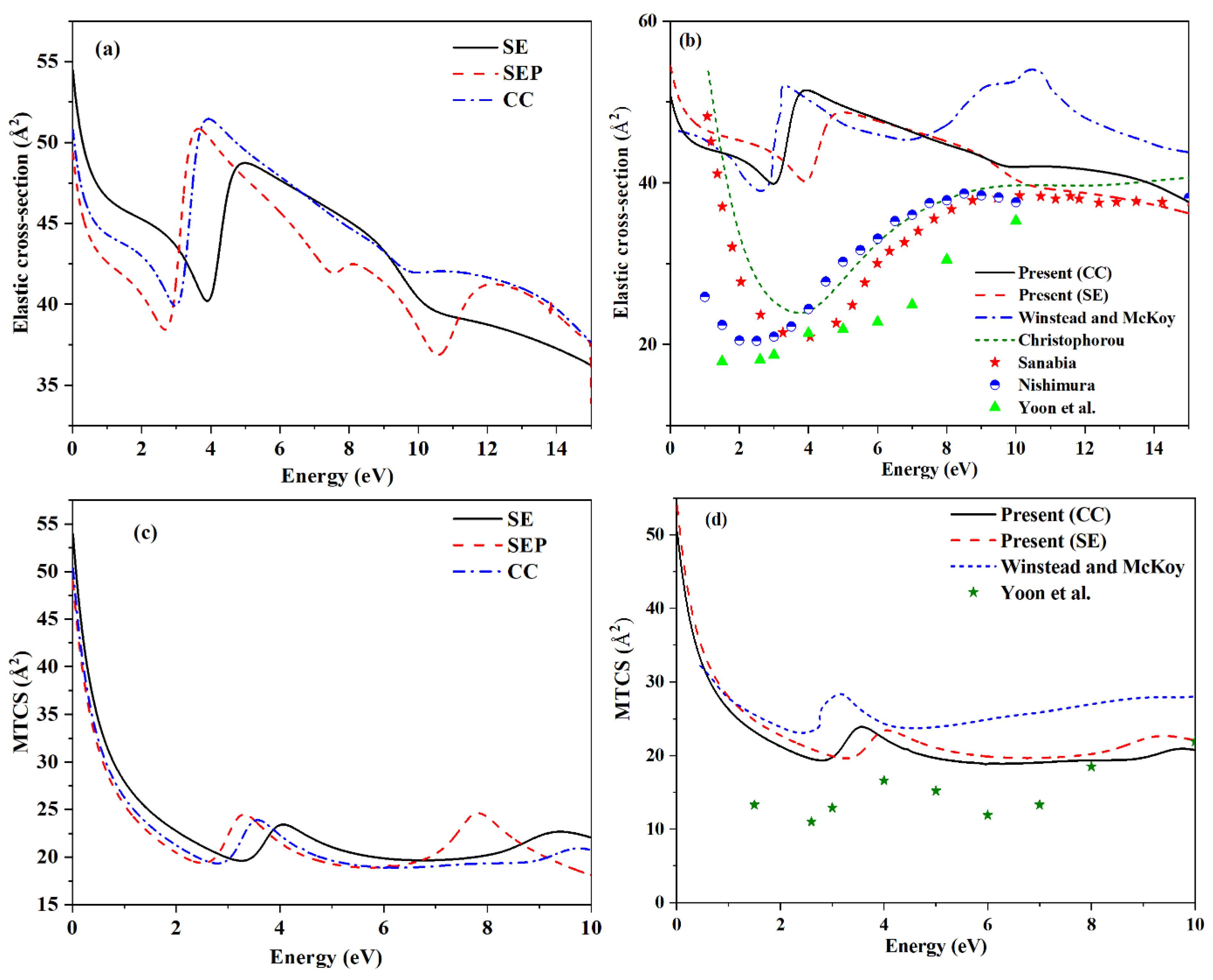
3. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartschat, K.; Kushner, M.J. Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology. Proc. Natl. Acad. Sci. USA 2016, 113, 7026–7034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rauf, S.; Dauksher, W.J.; Clemens, S.B.; Smith, K.H. Model for a multiple-step deep Si etch process. J. Vac. Sci. Technol. A Vac. Surf. Film. 2002, 20, 1177–1190. [Google Scholar] [CrossRef]
- Li, X.; Ling, L.; Hua, X.; Oehrlein, G.S.; Wang, Y.; Anderson, H.M. Characteristics of C4F8 plasmas with Ar, Ne, and He additives for SiO2 etching in an inductively coupled plasma (ICP) reactor. J. Vac. Sci. Technol. A Vac. Surf. Film. 2003, 21, 1955–1963. [Google Scholar] [CrossRef] [Green Version]
- Metzler, D.; Bruce, R.L.; Engelmann, S.; Joseph, E.A.; Oehrlein, G.S. Fluorocarbon assisted atomic layer etching of SiO2 using cyclic Ar/C4F8 plasma. J. Vac. Sci. Technol. A Vac. Surf. Film. 2014, 32, 020603. [Google Scholar] [CrossRef] [Green Version]
- Hua, X.; Wang, X.; Fuentevilla, D.; Oehrlein, G.S.; Celii, F.G.; Kirmse, K.H.R. Study of C4F8/N2 and C4F8/Ar/N2 plasmas for highly selective organosilicate glass etching over Si3N4 and SiC. J. Vac. Sci. Technol. A Vac. Surf. Film. 2003, 21, 1708–1716. [Google Scholar] [CrossRef]
- Takahashi, K.; Ono, K.; Setsuhara, Y. Etching characteristics of high-k dielectric HfO2 thin films in inductively coupled fluorocarbon plasmas. J. Vac. Sci. Technol. A Vac. Surf. Film. 2005, 23, 1691–1697. [Google Scholar] [CrossRef]
- Rauf, S.; Balakrishna, A. SiO2 etching in an Ar/c-C4F8/O2 dual frequency capacitively coupled plasma. J. Vac. Sci. Technol. A Vac. Surf. Film. 2017, 35, 021308. [Google Scholar] [CrossRef]
- Huang, S.; Huard, C.; Shim, S.; Nam, S.K.; Song, I.-C.; Lu, S.; Kushner, M.J. Plasma etching of high aspect ratio features in SiO2 using Ar/C4F8/O2 mixtures: A computational investigation. J. Vac. Sci. Technol. A 2019, 37, 031304. [Google Scholar] [CrossRef] [Green Version]
- Capitelli, M.; Colonna, G.; D’Ammando, G.; Laporta, V.; Laricchiuta, A. The role of electron scattering with vibrationally excited nitrogen molecules on non-equilibrium plasma kinetics. Phys. Plasmas 2013, 20, 101609. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Kwon, D.C.; Yoon, J.S.; Antony, B.; Song, M.Y. Cross sections for electron collision with difluoroacetylene. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 085202. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Song, M.Y.; Chakrabarti, K.; Yoon, J.S. Low energy cross sections for electron scattering from tetrafluoroallene. Eur. Phys. J. D 2017, 71, 213. [Google Scholar] [CrossRef]
- Gupta, D.; Song, M.Y.; Baluja, K.L.; Choi, H.; Yoon, J.S. Electron impact elastic and excitation cross-sections of the isomers of C4F6 molecule for plasma modeling. Phys. Plasmas 2018, 25, 063504. [Google Scholar] [CrossRef]
- Gupta, D. Brief review of electron collision studies of molecules relevant to plasma. Appl. Sci. Converg. Technol. 2020, 29, 125–132. [Google Scholar] [CrossRef]
- Christophorou, L.G.; Olthoff, J.K. Electron Interactions with c-C4F8. J. Phys. Chem. Ref. Data 2001, 30, 449–473. [Google Scholar] [CrossRef]
- Jelisavcic, M.; Panajotovic, R.; Kitajima, M.; Hoshino, M.; Tanaka, H.; Buckman, S.J. Electron scattering from perfluorocyclobutane (c-C4F8). J. Chem. Phys. 2004, 121, 5272–5280. [Google Scholar] [CrossRef]
- Yoon, J.S.; Song, M.Y.; Kato, H.; Hoshino, M.; Tanaka, H.; Brunger, M.J.; Buckman, S.J.; Cho, H. Elastic cross sections for electron collisions with molecules relevant to plasma processing. J. Phys. Chem. Ref. Data 2010, 39, 033106. [Google Scholar] [CrossRef] [Green Version]
- Makochekanwa, C.; Sueoka, O.; Kimura, M.; Kitajima, M.; Tanaka, H. Electron and positron scattering from perfluorocyclobutane (c-C4F8) molecules. Phys. Rev. A—At. Mol. Opt. Phys. 2005, 71, 032717. [Google Scholar] [CrossRef]
- Sanabia, J.E.; Cooper, G.D.; Tossell, J.A.; Moore, J.H. Total electron-scattering cross sections for CHF3, C2F6, C3F8, and c-C4F8. J. Chem. Phys. 1998, 108, 389–391. [Google Scholar] [CrossRef]
- Nishimura, H.; Hamada, A. Total Electron Scattering Cross Sections for Cylofluorobutane. J. Phys. Soc. Jpn. 2007, 76, 014301. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V. Electron collisions with octafluorocyclobutane, c-C4F8. J. Chem. Phys. 2001, 114, 7407–7412. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J. Electron-molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Carr, J.M.; Galiatsatos, P.G.; Gorfinkiel, J.D.; Harvey, A.G.; Lysaght, M.A.; Madden, D.; Masin, Z.; Plummer, M.; Tennyson, J. UKRmol: A low-energy electron- and positron-molecule scattering suite. Eur. J. Phys. D 2012, 66, 58. [Google Scholar] [CrossRef]
- Cooper, B.; Tudorovskaya, M.; Mohr, S.; O’Hare, A.; Hanicinec, M.; Dzarasova, A.; Gorfinkiel, J.D.; Benda, J.; Mašín, Z.; Al-Refaie, A.; et al. Quantemol Electron Collisions (QEC): An Enhanced Expert System for Performing Electron Molecule Collision Calculations Using the R-matrix Method. Atoms 2019, 7, 97. [Google Scholar] [CrossRef] [Green Version]
- Werner, H.-J.; Knowles, P.J.; Lindh, R.; Manby, F.R.; Schütz, M.; Celani, P.; Györffy, W.; Kats, D.; Korona, T.; Lindh, R.; et al. MOLPRO, Version 2009.1, a Package of ab Initio Programs. Available online: http://www.molpro.net (accessed on 1 October 2021).
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J.; Brown, D.B.; Munro, J.J.; Rozum, I.; Varambhia, H.N.; Vinci, N. Quantemol-N: An expert system for performing electron molecule collision calculations using the R-matrix method. J. Phys. Conf. Ser. 2007, 86, 012001. [Google Scholar] [CrossRef]
- Harrison, S.; Tennyson, J. Electron collisions with the CN radical: Bound states and resonances. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 035204. [Google Scholar] [CrossRef]
- Barot, A.; Gupta, D.; Vinodkumar, M.; Antony, B. Computation of electron-impact total and differential cross sections for allene (C3H4) in the energy range 0.1–2000 eV. Phys. Rev. A—At. Mol. Opt. Phys. 2013, 87, 062701. [Google Scholar] [CrossRef]
- Gupta, D.; Song, M.Y.; Choi, H.; Kwon, D.C.; Baluja, K.L.; Tennyson, J. R-matrix study for electron scattering of beryllium dihydride for fusion plasma. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 065204. [Google Scholar] [CrossRef]
- Singh, S.; Gupta, D.; Antony, B. Plasma-relevant electron scattering cross sections of propene. Plasma Sources Sci. Technol. 2018, 27, 105014. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Song, M.Y.; Singh, S.; Antony, B.; Chakrabarti, K.; Yoon, J.S.; Tennyson, J. Electron scattering studies of BF and BF2. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 225203. [Google Scholar] [CrossRef]
- Arthurs, A.M.; Dalgarno, A. The theory of scattering by a rigid rotator. Proc. R. Soc. A 1960, 256, 540–551. [Google Scholar] [CrossRef]
- Faure, A.; Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. GTOBAS: Fitting continuum functions with Gaussian-type orbitals. Comput. Phys. Commun. 2002, 144, 224–241. [Google Scholar] [CrossRef] [Green Version]
- Gailitis, M. New forms of asymptotic expansions for wavefunctions of charged-particle scattering. J. Phys. B At. Mol. Phys. 1976, 9, 843–854. [Google Scholar] [CrossRef]
- Tennyson, J.; Noble, C.J. RESON-A program for the detection and fitting of Breit-Wigner resonances. Comput. Phys. Commun. 1984, 33, 421–424. [Google Scholar] [CrossRef]
- Breit, G.; Wigner, E. Capture of slow electrons. Phys. Rev. 1936, 49, 519. [Google Scholar] [CrossRef] [Green Version]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Lifshitz, C.; Grajower, R. Dissociative electron capture and dissociative ionization in perfluorocyclobutane. Int. J. Mass Spectrom. Ion Phys. 1973, 10, 25. [Google Scholar] [CrossRef]
- Bibby, M.M.; Carter, G. C—F bond dissociation energies in perfluorocarbon gases using negative ion appearance potential data. Trans. Faraday Soc. 1963, 59, 2455. [Google Scholar] [CrossRef]
- Harland, P.W.; Thynne, J.C.J. Ionisation of perfluorocyclobutane by electron impact. Int. J. Mass Spectrom. Ion Phys. 1973, 10, 11. [Google Scholar] [CrossRef]
- Sauers, I.; Christophorou, L.G.; Carter, J.G. Electron attachment to perfluorocarbon compounds. III. Fragmentation of aliphatic perfluorocarbons of interest to gaseous dielectrics. J. Chem. Phys. 1979, 71, 3016. [Google Scholar] [CrossRef]



| State | Present | Theory [20] |
|---|---|---|
| 1A1 | 0 | |
| 3A2 | 8.80 | 8.52 |
| 1A2 | 9.04 | 9.13 |
| 3A2 | 11.54 | |
| 3E | 12.23 | |
| 1A2 | 12.45 | |
| 1E | 13.53 |
| States | Present (SE) | Present (SEP) | Present (CC) | Winstead and Mckoy [20] | Experimental DEA Results | ||||
|---|---|---|---|---|---|---|---|---|---|
| Position | Width | Position | Width | Position | Width | Position | Width | Position | |
| 2A1 | 4.21 | 1.01 | 3.12 | 0.95 | 3.37 | 0.92 | 3.0 | 0.33 | 3.75 [41] |
| 2E | 7.73 | 1.07 | 8.1 | 1.2 | 8.0 [41], 8.2 [42], 8.5~8.8 [43], 7.9 [44] | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, D.; Choi, H.; Kwon, D.-C.; Su, H.; Song, M.-Y.; Yoon, J.-S.; Tennyson, J. Low-Energy Electron Scattering from c-C4F8. Atoms 2022, 10, 63. https://doi.org/10.3390/atoms10020063
Gupta D, Choi H, Kwon D-C, Su H, Song M-Y, Yoon J-S, Tennyson J. Low-Energy Electron Scattering from c-C4F8. Atoms. 2022; 10(2):63. https://doi.org/10.3390/atoms10020063
Chicago/Turabian StyleGupta, Dhanoj, Heechol Choi, Deuk-Chul Kwon, He Su, Mi-Young Song, Jung-Sik Yoon, and Jonathan Tennyson. 2022. "Low-Energy Electron Scattering from c-C4F8" Atoms 10, no. 2: 63. https://doi.org/10.3390/atoms10020063
APA StyleGupta, D., Choi, H., Kwon, D.-C., Su, H., Song, M.-Y., Yoon, J.-S., & Tennyson, J. (2022). Low-Energy Electron Scattering from c-C4F8. Atoms, 10(2), 63. https://doi.org/10.3390/atoms10020063







