Abstract
In this work, we direct our attention to the study of the effect of a nonuniform and strong magnetic field on the quantum properties of ions in plasma. We have assumed that the strong magnetic field is a sum of two magnetic fields: one, the most intense, has a toroidal geometry, whereas the other of less intensity (about the third of the first) is poloidal. Regarding the quantum properties, we have focused our attention on obtaining the corresponding eigenenergy of n hydrogen-like ion in this nonuniform magnetic field. Using the obtained eigenenergy, we investigated the spectral line shape (Lyman-alpha) of three types of ions: He, C, and Ar for different magnetic field magnitudes. In this study, we considered only Doppler and electronic Stark broadening of the spectral line shapes.
1. Introduction
The confinement of plasmas by adequate magnetic fields is the most highly developed and reached technique to obtain a controlled fusion. A large part of the problem of confinement has been obtaining a magnetic field geometry that effectively confines the plasma. To reach this goal, a toroidal field is created by a set of toroidal magnets. It ensures the confinement of the charged particles in the torus. However, it is shown that this confinement is not quite sufficient and to further minimize the leakage of particles towards the walls, the field lines must be helical along the torus. This is achieved by adding to the toroidal field another magnetic field, called a poloidal field, which is perpendicular to it. To guarantee these requirements, several devices and experiments must be prepared before the startup of the fusion. In that sense, Feldman et al. discussed the measurement of the poloidal magnetic field in a tokamak plasma from the Zeeman splitting and polarization of the magnetic dipole radiation from heavy ions [1,2].
In the same year (1985), a dye laser induced resonant fluorescence scattering system was installed on the Toroidal Cusp Experiment (TCX) by P. Gao et al. [3].
Measurements were made of the line shapes of the Balmer series of hydrogen/deuterium in the edge and divertor regions of the Alcator C-Mod tokamak by Welch et al. [4] in 1996. In 2002, J. D. Hey et al. [5,6], discussed the Zeeman spectroscopy method to diagnose the tokamak. Koubiti et al. [7] analyzed the Dalpha/Halpha spectra to obtain several neutral populations with different temperatures (about 1–3 eV and 10–30 eV). To improve the analysis, Y. Marandet et al. [8], used an efficient fitting technique based on a genetic algorithm (GA), to fit the model to the experimental spectra. The results of this analysis, suggested the existence of a population of neutrals of several hundreds of electron volts. On the other hand, the positions of emission of beryllium-like oxygen ions in the core region as well as the hydrogen atoms in the boundary region of the limiter shadow were measured by means of the difference of the Zeeman patterns in the spectral shape in the poloidal section of the TRIAM-M1 fusion device [9]. To determine magnetic field strength, Shikama et al. resolved the components of the Zeeman spectra by a linear polarizer, and they also measured the bulk ion temperature in the core region [10]. In 2008, M F Gu et al. [11], presented detailed atomic physics models for the motional Stark effect (MSE) diagnostic on magnetic fusion devices. In the same year J. Rosato et al. [12], presented calculations of hydrogen Zeeman-Stark line profiles and discussed when the conditions for impact ion broadening were almost satisfied [12]. Measurements were made using spectra emitted parallel to the magnetic field by carbon impurities in high-temperature plasma. In 2011, A Iwamae et al. [13], presented the intensity of emission lines in the ITER divertor: the intensity of hydrogen isotopes and impurities was observed with the divertor central optical system. In 2012, M Koubiti et al. [14] investigated the broadening mechanisms affecting carbon lines emitted from tokamak divertor plasmas with an emphasis on the C IV n = 6–7 ( = 772.6 nm) line. For simplicity, they ignored the Zeeman effect by considering only Doppler and Stark broadenings in the calculations. Therefore, these calculations, which ignored the magnetic field effect, could be compared to spectra measured with the use of a linear polarizer transmitting only the component whose polarization is parallel to the toroidal magnetic field. Comparison of theoretical profiles to high-resolution measured C IV n = 6–7 line spectra allowed the determination of the several plasma parameters [14]. In the same year, J Rosato et al, calculated line shapes and S-matrix elements for the first Lyman lines of hydrogen with two models proposed for retaining simultaneously the Stark and Zeeman effects in the impact limit [15]. The Lorentz electric field present in the emitters’ frame of reference yielded a perturbation of the atomic energy levels, commonly referred to as a ‘motional’ Stark effect [16,17]. In 2017, and based on passive spectroscopy, the D atomic emission spectra in the boundary region of the plasma were measured by a high resolution Optical Spectroscopic Multichannel Analysis (OSMA) system in EAST tokamak by Wei Gao et al. [18].
In our study, limiting ourselves to hydrogen-like ions, we are interested, firstly, in the influence of a nonuniform magnetic field on the quantum dynamics of ions located in fusion plasma. The choice of this type of ion is didacted by its simple atomic structure. Secondly we have used the obtained eigenenergy to determine the spectral line shape (Lyman-alpha) of three types of ions, namely: He, C, and Ar for different magnetic field magnitudes. Moreover, as we will see, the Zeeman separation, for large values of , is much larger than the separation of the fine structure (for example, the latter is about 5 eV, while the Zeeman separation is much larger for large values of ). This leads us to work in the following without fine structure.
Our paper is organized in four sections. The next section is devoted to presenting the quantum mechanical equations that describe the ions in the presence of the nonuniform magnetic field. We have obtained a new removal of the degeneracy by the magnetic field. In Section 3, we present some spectral line shapes for Ly-alpha of three hydrogen-like ions, for different magnetic fields and temperatures. In this same section, we conduct a discussion. The fourth section is devoted to a conclusion.
2. Quantum Dynamics of the Confined Ions
Let start our work by considering the quantum dynamics of an ion embedded in a strong nonuniform magnetic field. In this case, we will work with the Schroedinger equation for a particle of spin of 1/2 (the electron) and an electric charge (-e) moving in the nucleus field (Coulomb interaction) and in the nonuniform magnetic field. The equation of this type of problem is commonly known as the Pauli equation. The dynamics of this problem must be seen in the relativistic quantum mechanics via the Dirac equation; however, it has been shown in many papers, such as [16,19], that in the presence of a strong magnetic field, it is a good approximation to work with the Pauli equation and to neglect the fine structure effect. The main objective in this section is to obtain the eigenenergy of that system. So, the Pauli Hamiltonian [20] is:
such that
and
where we have used cartesian coordinates () and spherical coordinates (). The choice of in (3) is made such that we obtain the desired geometry of the resulting magnetic field in the tore. is the reduced mass, is Bohr’s magneton, and is the spin of the electron interacting with the magnetic field (the spin–orbit coupling is neglected here). is the strength of the magnetic along the z-axis, responsible to the poloidal field. In this form of the magnetic field (4), we have implicitly considered that the observation will be done in the direction parallel to the component of the magnetic field along z (the other component of the magnetic field rotates along inducing a zero average polarization). Before we proceed, following the symmetry of the problem, we must express the two fields ( and ) in the spherical coordinates
The dynamics of the ion in the magnetic field is governed by the time independent Schrodinger given by (), that is to say
or equivalently
where the momentum operator must be expressed in spherical coordinates too, as
We must express at first the products and : it easy to show that
then
and
We substitute them into the above Pauli equation and neglecting the term of order:
On the other hand, we have
where are the components of along azumital angle and z, respectively, whereas Pauli Spin Matrices are given by
We put
or also
We separate the real part and the imaginary part in the first equation
Dividing member by member, we obtain
but ():
We replace the term in brackets by its average in the ground state (without magnetic field) ():
where
and the subscript (100) stands for the principal quantum numbers (nlm). The term with appears from the factor , whereas the factor with disappears because its average over in cancels, then
Now, we choose as:
where is a factor in the toroidal magnetic field along ; it has the magnetic field unit, whereas “a” is a constant (that can be assimilated to Bohr radius); then, we obtain
Now, we separate the radial part from the angular one
or equivalently
which is valid when each term is a constant
We multiply by to obtain a more adequate equation
We separate the equation with respect the angles and :
where
By solving these equations we obtain the eigenenergy as
where
Here, () play the role of the quantum numbers (). We can check that, when the magnetic fields are zero, we recover the Bohr levels of energy. We have now the eigenenergy of the system; we will use it in the study of the spectral radiative properties of the fusion plasma in the next section.
3. Spectral Line Shape
Before presenting the main results (mainly in figures), we must mention two things: the first concerns the strong magnetic field that is encountered also in certain stars and a white dwarf. The second thing is to say we have considered, in order to make the figures (Figure 1, Figure 2 and Figure 3) readable, that, in one part the Stark broadening is (overestimated), and that the Doppler broadening is Lorentzian on other part. Only in the last figure (Figure 4) we have considered, as it must be, a convolution between the Doppler (gaussian) and the Stark (Lorentzian) broadening. The choice of the values of and is arbitrary, but we have made them large enough to hide the fine structure effect and kept much larger than (), because the poloidal field is small in front of the toroidal field.
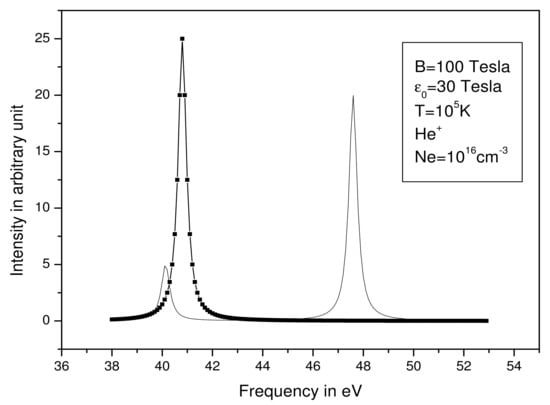
Figure 1.
Ly-alpha line for Hydrogen-like Helium for = 10 cm, T = K, Tesla, and Tesla. The line + symbol is for B = 0 Tesla.
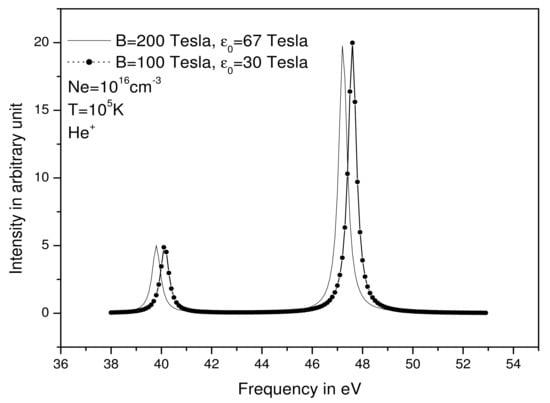
Figure 2.
Ly-alpha line for Hydrogen-like Helium for = 10 cm, T = K, Tesla, and Tesla and for Tesla and Tesla.
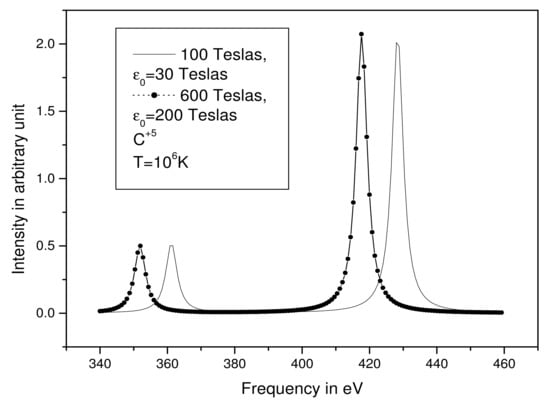
Figure 3.
Ly-alpha line for Hydrogen-like Carbon for = 10 cm, T = K, Tesla, and Tesla and for Tesla and Tesla.
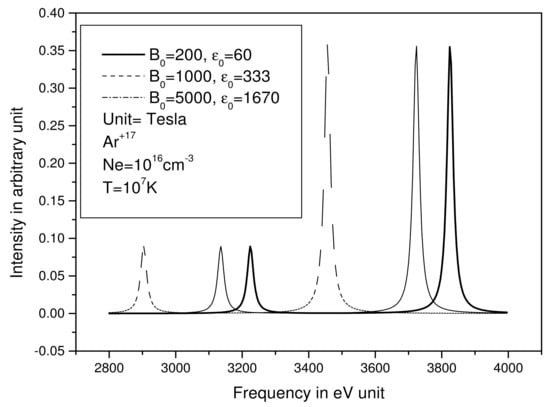
Figure 4.
Ly-alpha line for Hydrogen-like Argon for = 10 cm, T = K, Tesla, and Tesla, Tesla and , and Tesla and Tesla.
In Figure 1 and Figure 2 (Figure 1 contains the line without magnetic field, B = 0), we present the Ly-alpha line for Hydrogen-like Helium for = 10 cm, 10 K, = 100 Tesla, and = 30 Tesla and for = 200 Tesla and = 67. The presence of the magnetic field enhances the degeneracy removal and the gives the profile two peaks; increasing the value of the field ( = 200 Tesla and = 67 Teslas), we notice a shift of the centers of the two peaks towards the small frequencies towards the red). We can interpret the shift as follows: from Equation (43), it is clear that the effect of the magnetic field on the energy levels makes these levels far from each other when increasing the value of this field. Consequently, the center of the line, which is the energy difference between these levels, moves with the increasing magnetic field. Then, the center of the line undergoes a shift.
In Figure 3, we have the Ly-alpha line for Hydrogen-like Carbon for = 10 cm, T = K, = 100 Tesla, and = 30 Teslas and = 600 Tesla and = 200 Teslas, we notice the same as the previous remarks, but the shift increases between the two peaks of the line.
For the Ly-alpha line for Hydrogen-like Argon for = 10 cm, K, = 200 Tesla, and = 68 Teslas, = 1000 Teslas and = 333 Teslas, and = 5000 Tesla and = 1670, in this case, we observe a noticeable shift towards the red, going from 1000 Tesla to 5000 Tesla; the second peak is shifted about 267 eV (Figure 4). In all figures, we used a convolution product to introduce the Doppler broadening, and the final profile will not be a Gaussian profile but a convolution between the Gaussian and the Zeeman effect.
4. Conclusions
In conclusion, in this paper, we have solved the quantum problem of hydrogen-like ions in a nonuniform and intense magnetic field. We have assumed that the intense magnetic field is a sum of two magnetic fields: the most intense field has a toroidal geometry, whereas the less intense field (about the third) is poloidal. The obtained results allowed us to investigate the spectral line shape (Lyman-alpha) of three types of ions: He , C, and Ar for different magnetic field magnitudes. We remark that, the Zeeman separation is as large as the magnetic field is large, and the charge number Z is great. Another feature must be noticed: the left Zeeman component is near the line without a magnetic field (see Figure 1). In future studies, this model of magnetic field geometry can be studied in relativistic quantum mechanics via the Dirac equation.
Author Contributions
Conceptualization, S.F.; Data curation, M.T.M.; Formal analysis, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feldman, U.; Seely, J.F.; Sheeley, N.R., Jr.; Suckewer, S.; Title, A.M. Magnetic field measurements in tokamak plasmas. J. Appl. Phys. 1984, 56, 2512–2518. [Google Scholar] [CrossRef]
- Feldman, U.; Seely, J.F.; Sheeley, N.R., Jr.; Suckewer, S.; Title, A.M. Magnetic field measurements based on the Zeeman splitting of forbidden transitions. Rev. Sci. Instrum. 1985, 56, 855–856. [Google Scholar]
- Gao, P.; Rhodes, M.; Peebles, W.A. Laser resonant fluorescence scattering in the Toroidal Cusp Experiment. Rev. Sci. Instrum. 1985, 56, 1071. [Google Scholar] [CrossRef]
- Welch, B.L.; Griem, H.R.; Terry, J.L.W.L.; Boivin, R.L.; Lipschultz, B.; Lumma, D.; Marmar, E.S.; McCracken, G.; Rost, J.C. Line shape measurements of visible light emission from the Alcator C-Mod tokamak. AIP Conf. Proc. 1996, 381, 159–166. [Google Scholar]
- Hey, J.D.; Chu, C.C.; Mertens, P. Zeeman Spectroscopy of Tokamak Edge Plasmas. AIP Conf. Proc. 2002, 645, 26–39. [Google Scholar]
- Hey, J.D.; Chu, C.C.; Mertens, P.; Brezinsek, S.; Unterberg, B. Atomic collision processes with ions at the edge of magnetically confined fusion plasmas. J. Phys. B At. Mol. Opt. Phys. 2004, 37, 2543–2567. [Google Scholar] [CrossRef]
- Koubiti, M.; Marandet, Y.; Escarguel, A.; Capes, H.; Godbert-Mouret, L.; Stamm, R.; Michelis, C.D.; Guirlet, R.; Mattioli, M. Analysis of asymmetric Dα spectra emitted in front of a neutralizer plate of the Tore-Supra ergodic divertor. Plasma Phys. Control. Fusion 2002, 44, 261. [Google Scholar] [CrossRef]
- Marandet, Y.; Genesio, P.; Koubiti, M.; Godbert-Mouret, L.; Felts, B.; Stamm, R.; Guirlet, H.C.R. Characterization of tokamak edge plasmas using spectroscopic line profiles. J. Nucl. Fusion 2004, 44, S118–S122. [Google Scholar] [CrossRef]
- Zushi, H.; Itoh, S.; Hanada, K.; Nakamura, K.; Sakamoto, M.; Jotaki, E.; Hasegawa, M.; Pan, Y.D.; Kulkarni, S.V.; Iyomasa, A.; et al. Overview of steady state tokamak plasma experiments in TRIAM-1M. Nucl. Fusion 2003, 43, 1600. [Google Scholar] [CrossRef]
- Shikama, T.; Kado, S.; Zushi, H.; Iwamae, A.; Tanaka, S. Application of the Zeeman patterns in Ov and H-alpha spectra to the local plasma diagnostics of the TRIAM-1M tokamak. Phys. Plasmas 2004, 11, 4701–4708. [Google Scholar] [CrossRef]
- Gu, M.F.; Holcomb, C.T.; Jayakuma, R.J.; Allen, S.L. Atomic models for the motional Stark effect diagnostic. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 095701. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Ferri, S.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Stamm, R. Zeeman-Stark Profiles of Low-n Hydrogen Lines in Near Impact Regime. AIP Conf. Proc. 2008, 1058, 213–215. [Google Scholar]
- Iwamae, A.; Sugie, T.; Ogawa, H.; Kusama, Y. Synthesized intensity of emission lines of hydrogen isotopes and impurities in the ITER divertor plasma. Plasma Phys. Control. Fusion 2011, 53, 045005. [Google Scholar] [CrossRef]
- Koubiti, M.; Nakano, T.; Marandet, Y.; Mouret, L.; Rosato, J.; Stamm, R. Contribution of Stark-Doppler broadening of carbon impurity lines to the analysis of tokamak divertor plasmas. J. Phys. 2012, 397, 012025. [Google Scholar] [CrossRef] [Green Version]
- Rosato, J.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Stamm, Y.M.R. Accuracy of impact broadening models in low-density magnetized hydrogen plasmas. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 165701. [Google Scholar] [CrossRef] [Green Version]
- Touati, K.A.; Chenini, K.; Meftah, M.T. Profils de raies spectrales dans les plasmas magnétisés: Effet Stark Motionnel. Can. J. Phys. 2018, 96, 241–248. [Google Scholar] [CrossRef]
- Rosato, J.; Marandet, Y.; Stamm, R. Stark broadening by Lorentz fields in magnetically confined plasmas. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 105702. [Google Scholar] [CrossRef]
- Gao, W.; Huang, J.; Wu, C.; Xu, Z.; Hou, Y.; Jin, Z.; Chen, Y.; Zhang, P.; Zhang, L.; Wu, Z.; et al. Analysis of the Zeeman effect on D-alpha spectra on the EAST tokamak. Chin. Phys. B 2017, 26, 045203. [Google Scholar] [CrossRef]
- Godbert-Mouret, L.; Koubiti, M.; Stamm, R.; Touati, K.; Felts, B.; Capes, H.; Corre, Y.; Guirlet, R.; De Michelis, C. Spectroscopy of magnetized plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 365–372. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics; Mir Edition; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).