Collisional Broadening within a Hadronic Transport Approach
Abstract
:1. Introduction
2. SMASH Transport Approach
3. Results
3.1. Hadron Gas in Equilibrium
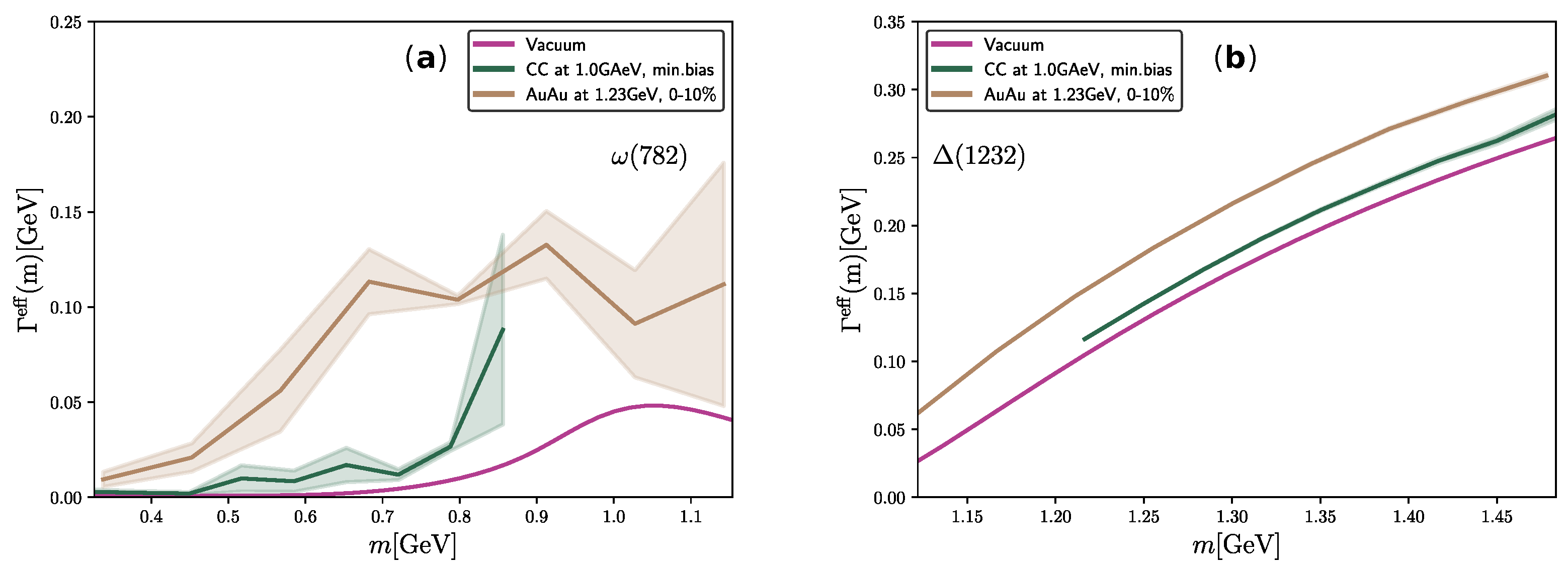
3.2. Heavy-Ion Collisions
3.3. Collisional Broadening under Different Vacuum Assumptions
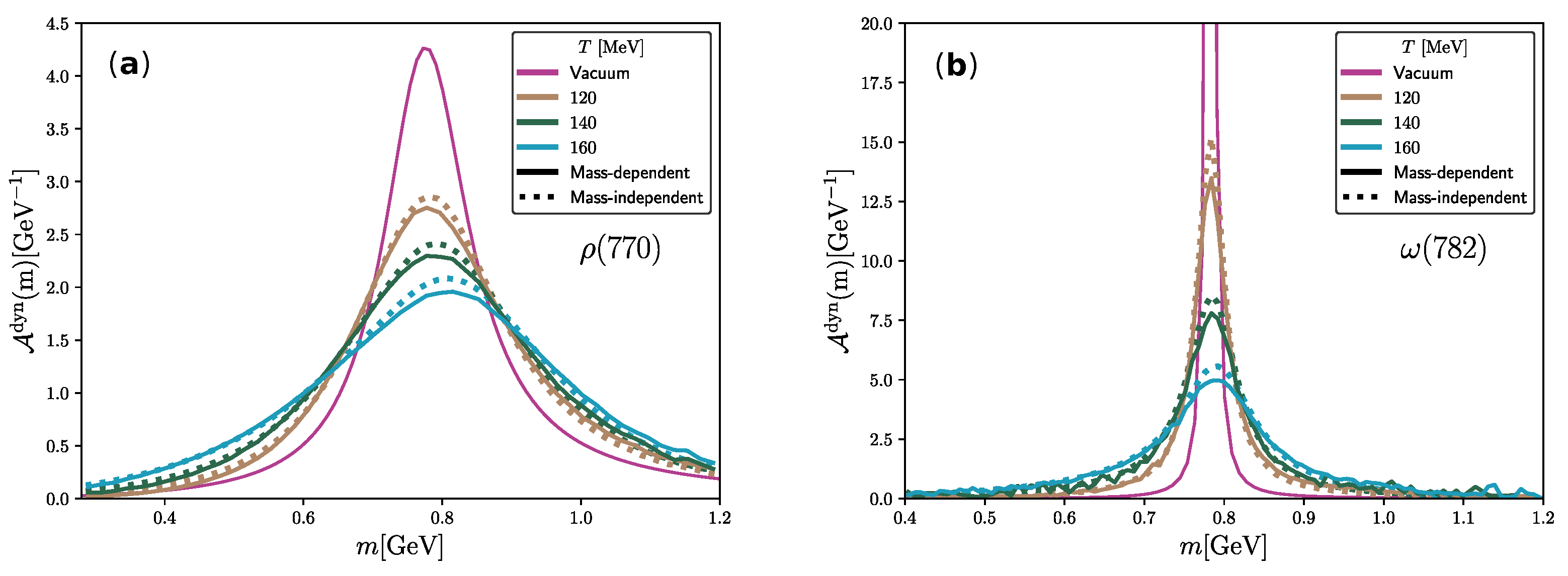
- Particles that decay cannot be absorbed, so a larger vacuum width suppresses collisional broadening. At low masses, the vacuum decay width tapers down to 0 in the mass-dependent assumption. This makes the particles more prone to be absorbed by the medium in comparison with the mass-independent case.
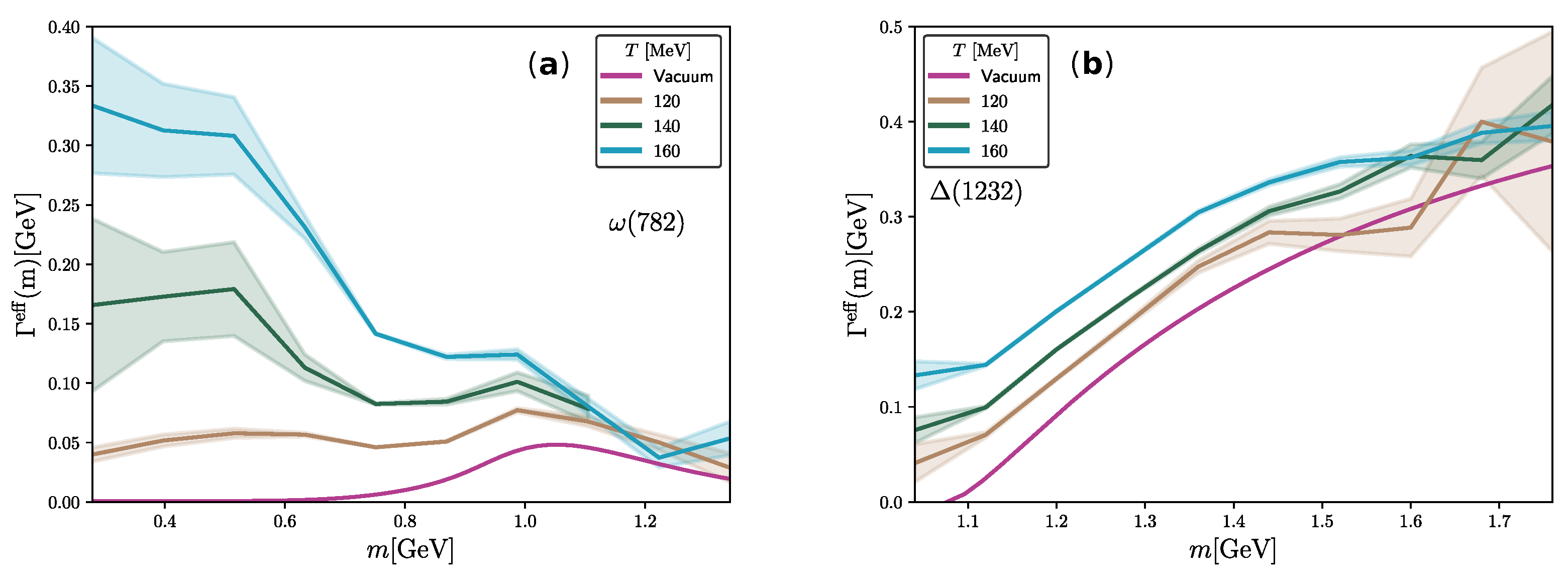
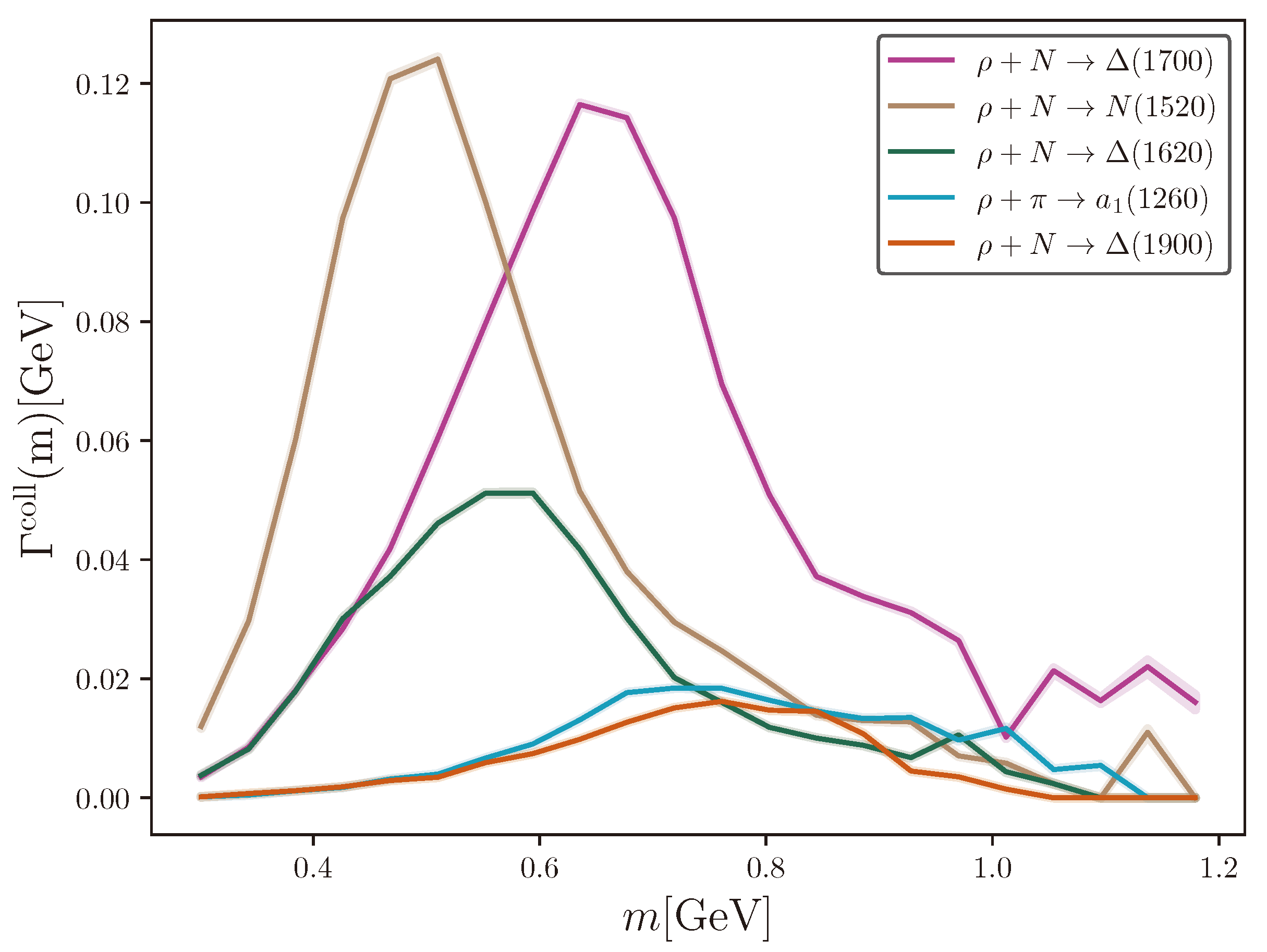
- Inelastic cross-section affects the broadening of both a and b, since it determines how much one absorbs the other. It has peaks around the pole mass () of possible resonances [10]. The masses of the incoming particles control the off-shell mass of the outgoing resonance (), so such peaks lead to structures in the collisional width of a and b, as exemplified by Figure 6; the contribution of the process is higher and close3 to , and heavier resonances lead to peaks in larger . This effect is not relevant for very small masses, when .
- Absorption cross-section is also proportional to , so that different mass assumptions give different weights to the resonance peaks.
- At high enough masses, the absorption cross-section decreases so much that particles stop undergoing collisional broadening, as detailed in Appendix A, such that the vacuum assumption has no effect.
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Interaction Cross-Sections

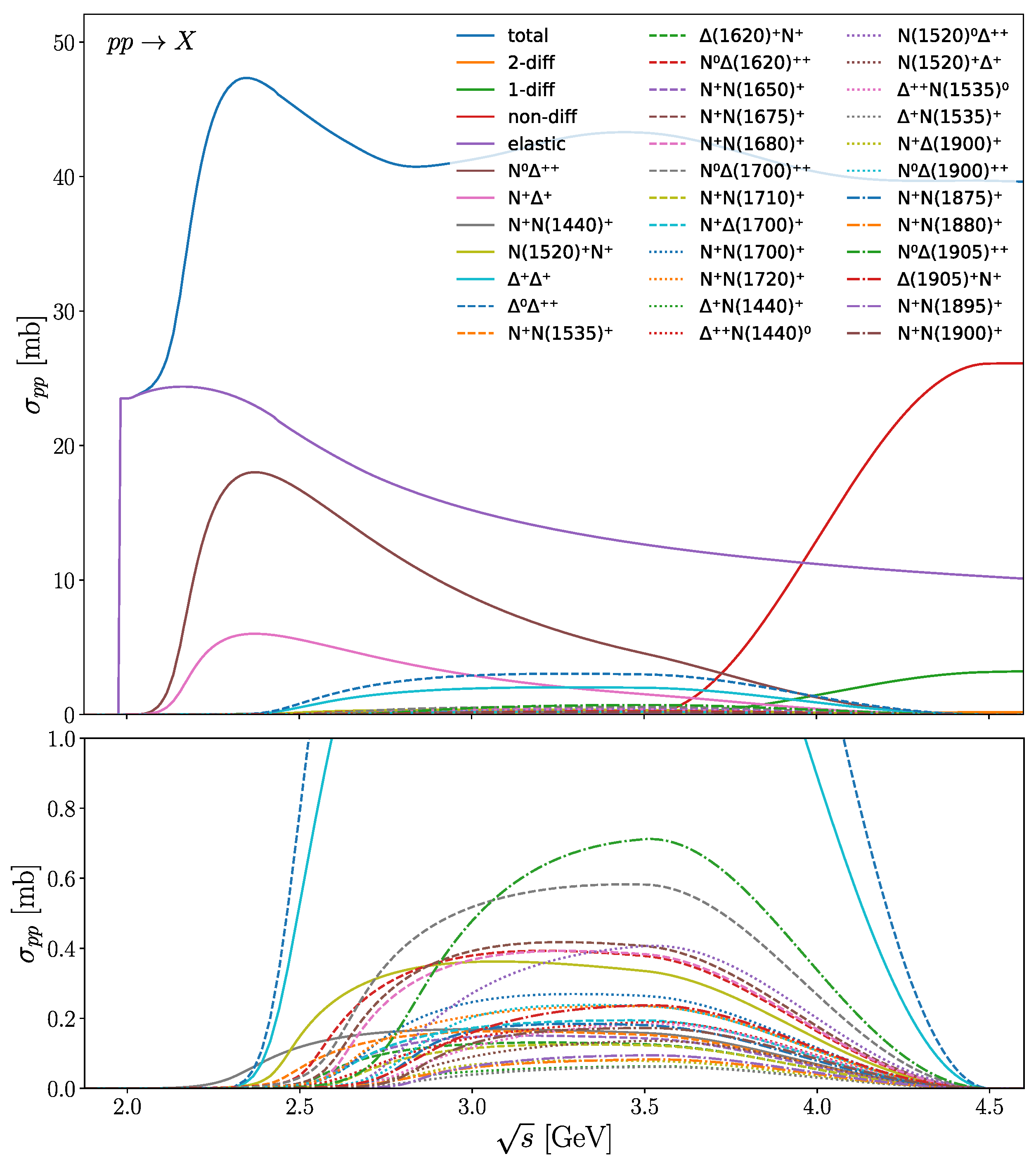
| 1 | We consider stable the hadrons with . |
| 2 | In collisions with energies higher than , strange hadrons also come from string fragmentation (see Appendix A). |
| 3 | The difference from the actual peak is due to the kinetic energy given to the created resonance. |
References
- Larionov, A.B.; Effenberger, M.; Leupold, S.; Mosel, U. Resonance lifetime in BUU: Observable consequences. Phys. Rev. C 2002, 66, 054604. [Google Scholar] [CrossRef]
- Rapp, R.; Wambach, J. Low mass dileptons at the CERN SPS: Evidence for chiral restoration? Eur. Phys. J. A 1999, 6, 415–420. [Google Scholar] [CrossRef]
- van Hees, H.; Rapp, R. Dilepton Radiation at the CERN Super Proton Synchrotron. Nucl. Phys. A 2008, 806, 339–387. [Google Scholar] [CrossRef]
- Buss, O.; Gaitanos, T.; Gallmeister, K.; van Hees, H.; Kaskulov, M.; Lalakulich, O.; Larionov, A.B.; Leitner, T.; Weil, J.; Mosel, U. Transport-theoretical Description of Nuclear Reactions. Phys. Rept. 2012, 512, 1–124. [Google Scholar] [CrossRef]
- Linnyk, O.; Bratkovskaya, E.L.; Ozvenchuk, V.; Cassing, W.; Ko, C.M. Dilepton production in nucleus-nucleus collisions at top SPS energy within the Parton-Hadron-String Dynamics (PHSD) transport approach. Phys. Rev. C 2011, 84, 054917. [Google Scholar] [CrossRef]
- Endres, S.; van Hees, H.; Weil, J.; Bleicher, M. Coarse-graining approach for dilepton production at energies available at the CERN Super Proton Synchrotron. Phys. Rev. C 2015, 91, 054911. [Google Scholar] [CrossRef]
- Endres, S.; van Hees, H.; Weil, J.; Bleicher, M. Dilepton production and reaction dynamics in heavy-ion collisions at SIS energies from coarse-grained transport simulations. Phys. Rev. C 2015, 92, 014911. [Google Scholar] [CrossRef]
- Staudenmaier, J.; Weil, J.; Steinberg, V.; Endres, S.; Petersen, H. Dilepton production and resonance properties within a new hadronic transport approach in the context of the GSI-HADES experimental data. Phys. Rev. C 2018, 98, 054908. [Google Scholar] [CrossRef]
- Hirayama, R.; Staudenmaier, J.; Elfner, H. Effective spectral function of vector mesons via lifetime analysis. Phys. Rev. C 2023, 107, 025208. [Google Scholar] [CrossRef]
- Weil, J.; Steinberg, V.; Staudenmaier, J.; Pang, L.G.; Oliinychenko, D.; Mohs, J.; Kretz, M.; Kehrenberg, T.; Goldschmidt, A.; Bauchle, B.; et al. Particle production and equilibrium properties within a new hadron transport approach for heavy-ion collisions. Phys. Rev. C 2016, 94, 054905. [Google Scholar] [CrossRef]
- Olive, K.A.; et al.; [Particle Data Group] Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Manley, D.M.; Saleski, E.M. Multichannel resonance parametrization of pi N scattering amplitudes. Phys. Rev. D 1992, 45, 4002–4033. [Google Scholar] [CrossRef] [PubMed]
- Danielewicz, P.; Pratt, S. Delays associated with elementary processes in nuclear reaction simulations. Phys. Rev. C 1996, 53, 249–266. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Li, Q.; Bleicher, M. A Model comparison of resonance lifetime modifications, a soft equation of state and non-Gaussian effects on pi-pi correlations at FAIR/AGS energies. J. Phys. G 2009, 36, 015111. [Google Scholar] [CrossRef]
- Schumacher, D.; Vogel, S.; Bleicher, M. Theoretical analysis of dilepton spectra in heavy ion collisions at GSI-FAIR energies. Acta Phys. Hung. A 2006, 27, 451–458. [Google Scholar] [CrossRef]
- Reichert, T.; Bleicher, M. Kinetic mass shifts of ρ(770) and K*(892) in Au+Au reactions at Ebeam = 1.23 AGeV. Nucl. Phys. A 2022, 1028, 122544. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Agakishiev, G.; et al.; [HADES Collaboration] Study of dielectron production in C+C collisions at 1-A-GeV. Phys. Lett. B 2008, 663, 43–48. [Google Scholar] [CrossRef]
- Adamczewski-Musch, J.; et al.; [HADES Collaboration] Centrality determination of Au + Au collisions at 1.23A GeV with HADES. Eur. Phys. J. A 2018, 54, 85. [Google Scholar] [CrossRef]
- Vogel, S.; Bleicher, M. Reconstructing ρ 0 and ω mesons from nonleptonic decays in C+ C collisions at 2 GeV/nucleon in transport model calculations. Phys. Rev. C 2006, 74, 014902. [Google Scholar] [CrossRef]
- Rapp, R.; Gale, C. ρ properties in a hot meson gas. Phys. Rev. C 1999, 60, 024903. [Google Scholar] [CrossRef]


| 120 | 140 | 160 | |
|---|---|---|---|
| N | 0.063 (1) | 0.1082 (8) | 0.1789 (7) |
| 0.0802 (4) | 0.2033 (5) | 0.4376 (6) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balinovic, B.; Hirayama, R.; Elfner, H. Collisional Broadening within a Hadronic Transport Approach. Universe 2023, 9, 414. https://doi.org/10.3390/universe9090414
Balinovic B, Hirayama R, Elfner H. Collisional Broadening within a Hadronic Transport Approach. Universe. 2023; 9(9):414. https://doi.org/10.3390/universe9090414
Chicago/Turabian StyleBalinovic, Branislav, Renan Hirayama, and Hannah Elfner. 2023. "Collisional Broadening within a Hadronic Transport Approach" Universe 9, no. 9: 414. https://doi.org/10.3390/universe9090414
APA StyleBalinovic, B., Hirayama, R., & Elfner, H. (2023). Collisional Broadening within a Hadronic Transport Approach. Universe, 9(9), 414. https://doi.org/10.3390/universe9090414








