Phase Transitions in the Interacting Relativistic Boson Systems
Abstract
:1. Introduction
2. Canonical Ensemble: Condensation in Ideal Boson Gas
3. Self-Interacting Scalar Field
3.1. The Effective Lagrangian in the Mean-Field Approximation
3.2. Hamiltonian Density in the Mean-Field Approximation
3.3. Bosonic System with Self-Interaction
4. An Interacting Boson System within the Thermodynamic Mean-Field Model
4.1. Parametrization of the Interaction
5. Condensation of Interacting Bosons at Finite Temperatures
6. Particle–Antiparticle System with Conserved Isospin (Charge) Density
6.1. Derivation of Basic Equations
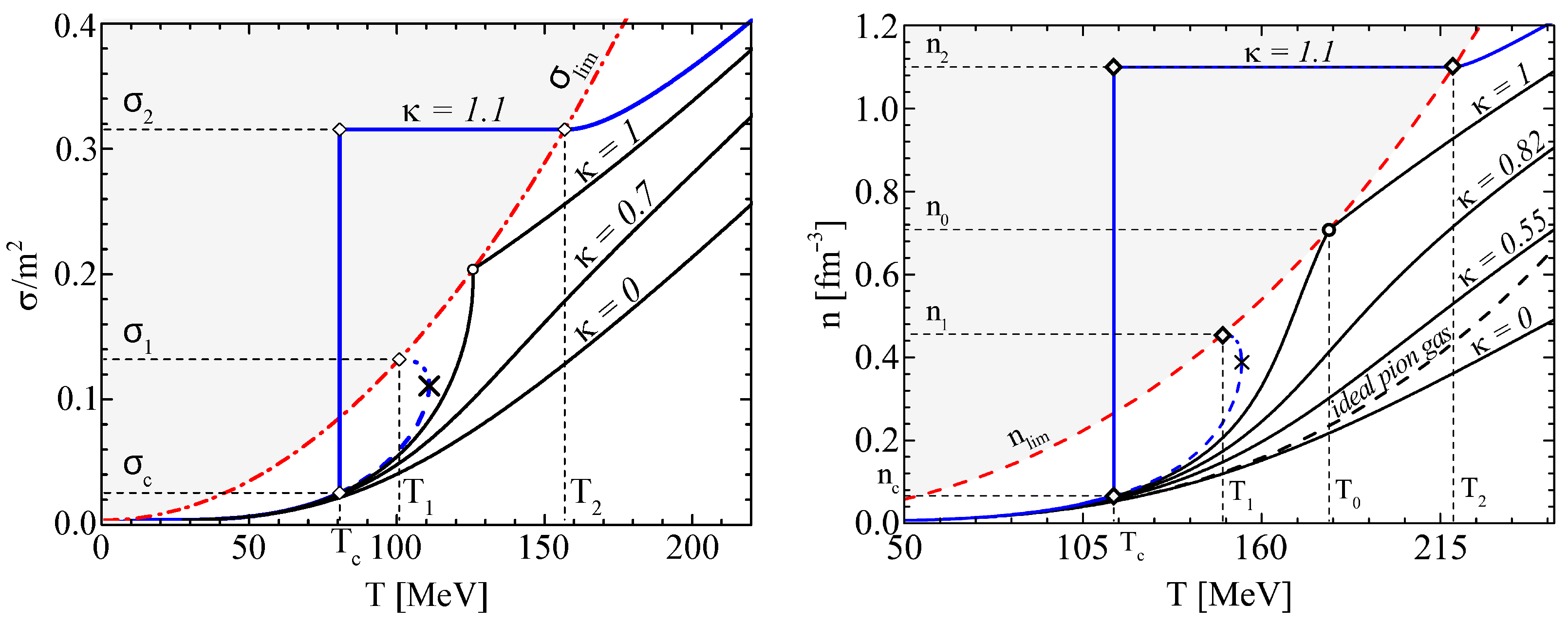
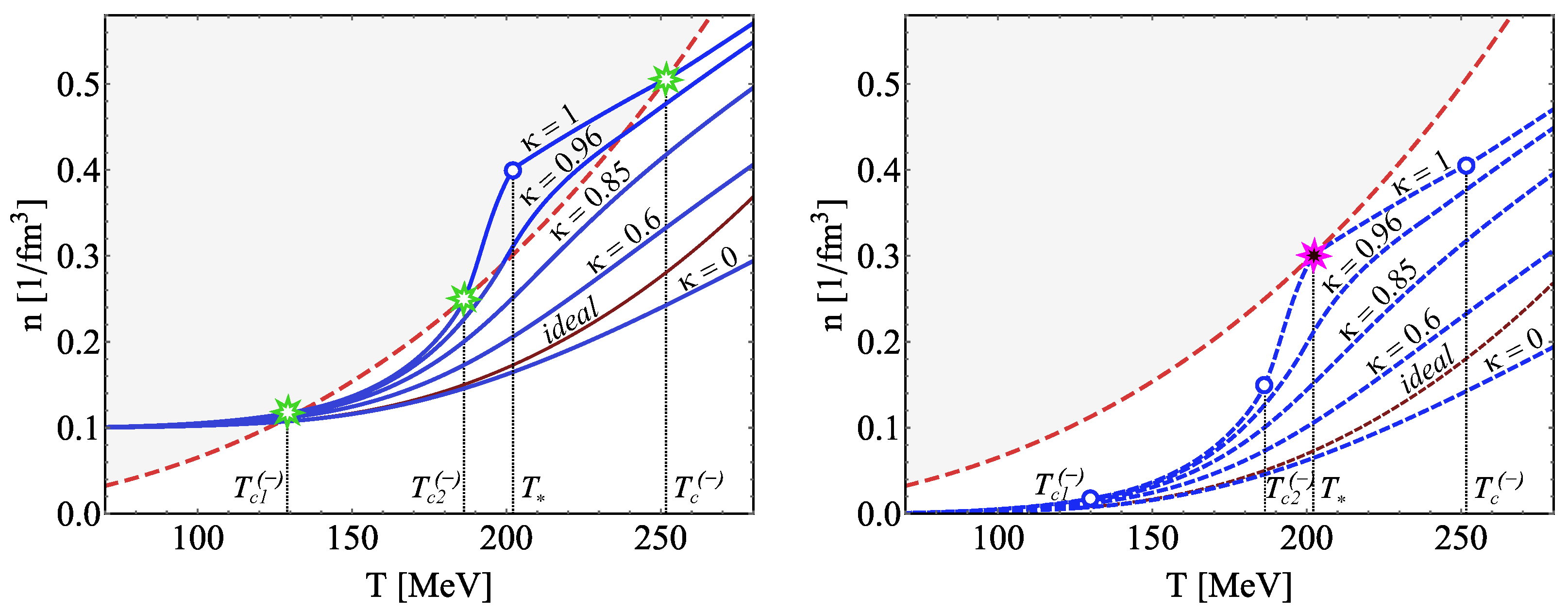
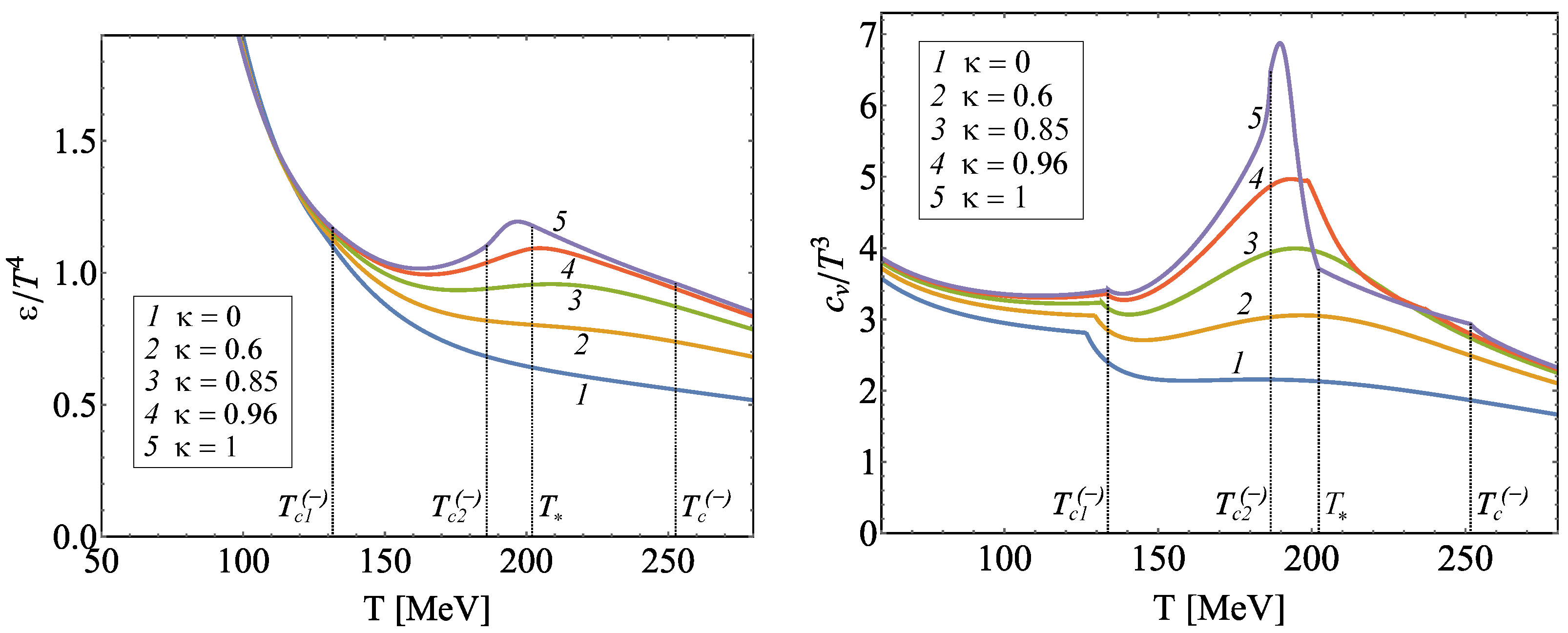
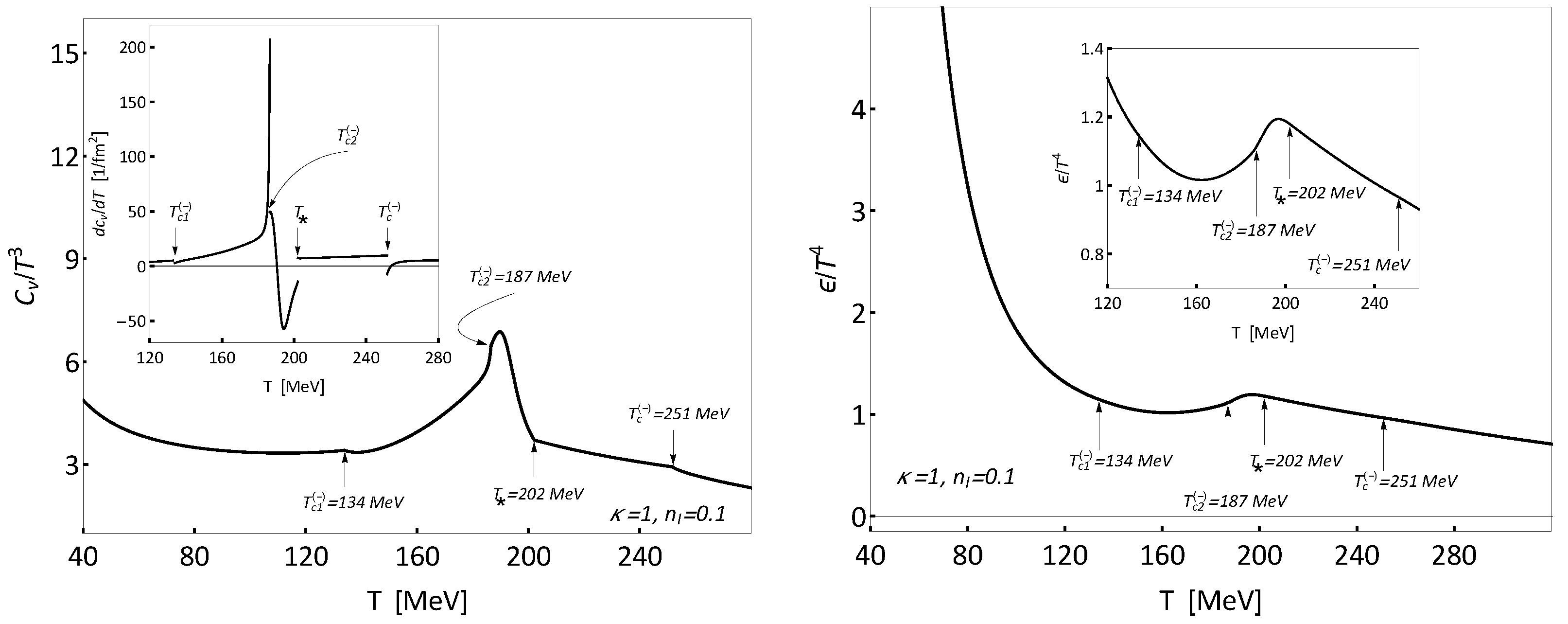
6.2. Numerical Results: Second-Order Phase Transitions Generated by the Particles That Carry Dominant Charge
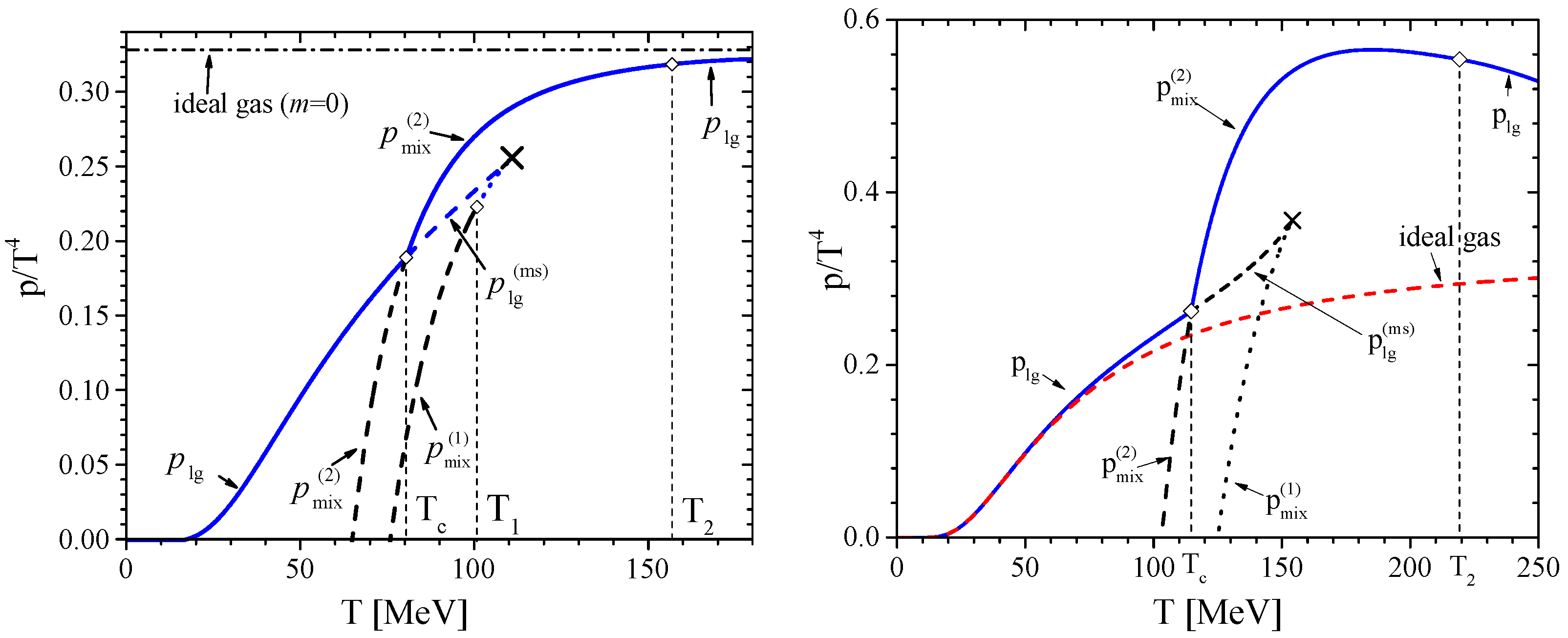
7. Canonical Ensemble vs. Grand Canonical Ensemble: Description of the Boson Systems in the Presence of a Condensate
7.1. Particle-Number Conservation in an Ideal Single-Component Bosonic System
7.2. Charge Conservation in an Interacting Particle–Antiparticle Boson System
- (a)
- (b)
- when both components, i.e., mesons and , are in the condensate phase, it is necessary to modify set (a), see hereinafter;
- (c)
7.3. Other Examples
8. Conclusions
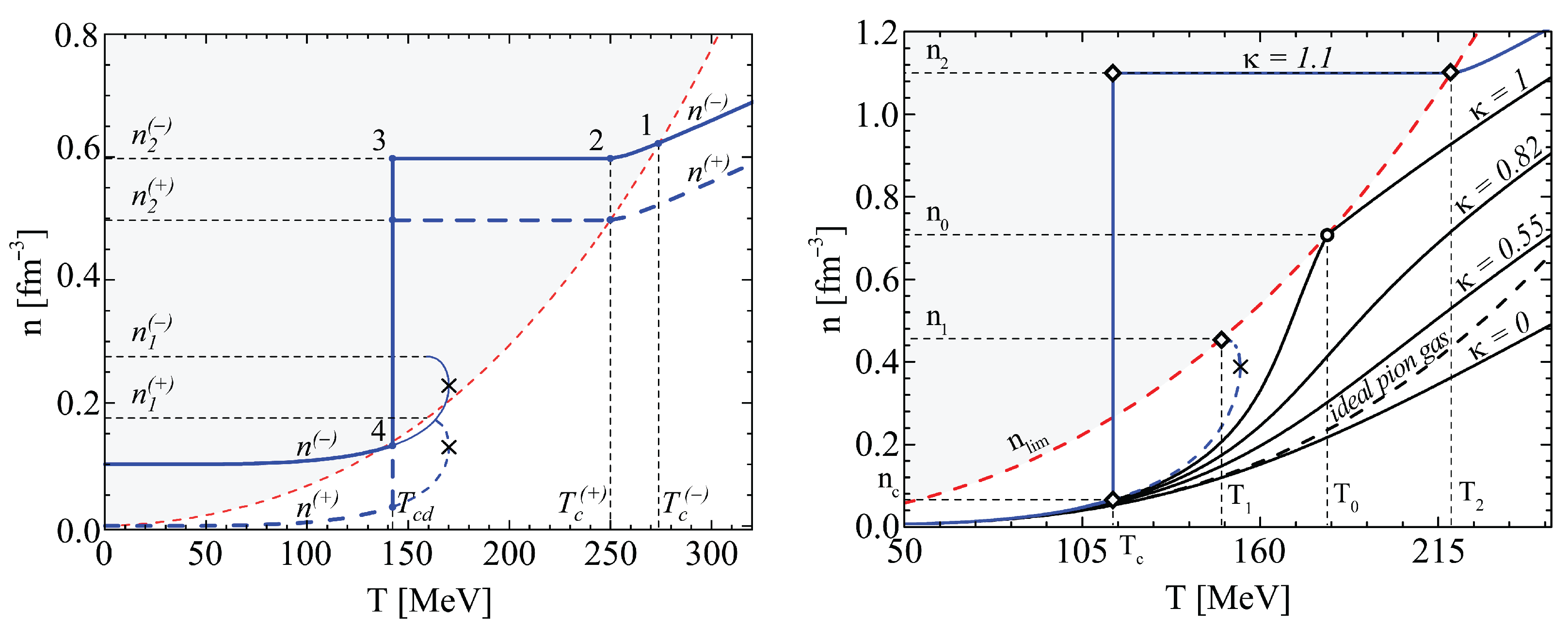
- The intersections of the particle density curves with the critical curve indicate second-order phase transitions in the system.
- At the point where the particle density of mesons touches the critical curve, the virtual phase transition of second order, i.e., a phase transition without setting the order parameter, appears.
- The meson system develops a first-order phase transition for sufficiently strong attractive interactions via forming a Bose condensate, thus releasing the latent heat. The model predicts that the condensed phase is characterized by a constant total density of particles.
- The grand canonical ensemble cannot describe the state of the condensate since the chemical potential is significantly affected by the conditions of condensate formation, so it cannot be used as a free variable if the system is in the condensed phase. That is why the grand canonical ensemble is not suitable for describing a multi-component system in the condensate phase, even if only one of the components is in the condensate.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMF | Scalar mean-field model |
| TMF | Thermodynamic mean-field model |
| FED | Free energy density |
Appendix A. Thermodynamically Consistent Mean-Field Model for the Interacting Particle–Antiparticle System
The System of Particles and Antiparticles
| 1 | In the nonrelativistic case, where , the maximum value of the thermal-particle density is achieved at zero chemical potential. |
| 2 | It should be noted that we just conventionally say “condensate phase”. In fact, it is the thermodynamic state of a system that contains thermal particles and condensed particles at the same time. |
| 3 | In fact, the name “condensate phase” is just a conventional one because this phase is a mixture of the thermal (kinetic) particles and the condensed particles. |
| 4 | For our choice of the total charge of the system, it is the mesons. |
| 5 | Because we named it as the virtual phase transition of the second order. |
| 6 | For our choice of the total charge of the system, these are mesons. |
| 7 |
References
- Bogolubov, N. On the theory of superfluidity. Sov. J. Phys. 1947, 11, 23. [Google Scholar]
- Bogolyubov, N.N. Energy levels of the imperfect Bose-Einstein gas. Bull. Moscow State Univ. 1947, 7, 43. [Google Scholar]
- Bogolyubov, M.M. Lectures on Quantum Statistics; Gordon and Breach: Kyiv, Ukraine; New York, NY, USA, 1947. [Google Scholar]
- Ginzburg, V.L.; Pitaevskii, L.P. On the theory of Superfluidity. Sov. Phys. JETP 1958, 7, 858. [Google Scholar]
- Gross, E.P. Hydrodynamics of a Superfluid Condensate. J. Math. Phys. 1963, 4, 195–207. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics; John Wiley and Sons: Hoboken, NJ, USA, 1987; p. 294. [Google Scholar]
- Haber, H.E.; Weldon, H.A. Thermodynamics of an Ultrarelativistic Ideal Bose Gas. Phys. Rev. Lett. 1981, 46, 1497. [Google Scholar] [CrossRef]
- Anchishkin, D.; Gnatovskyy, V.; Zhuravel, D.; Karpenko, V. Self-interacting particle-antiparticle system of bosons. Phys. Rev. C 2022, 105, 045205. [Google Scholar] [CrossRef]
- Bzdak, A.; Esumi, S.; Koch, V.; Liao, J.; Stephanov, M.; Xu, N. Mapping the phases of quantum chromodynamics with beam energy scan. Phys. Rep. 2020, 853, 1–87. [Google Scholar] [CrossRef]
- Anchishkin, D.; Mishustin, I.; Stoecker, H. Phase transition in an interacting boson system at finite temperatures. J. Phys. G 2019, 46, 035002. [Google Scholar] [CrossRef]
- Anselm, A.; Ryskin, M. Production of classical pion field in heavy ion high energy collisions. Phys. Lett. B 1991, 226, 482. [Google Scholar] [CrossRef]
- Blaizot, J.-P.; Krzwitski, A. Soft-pion emission in high-energy heavy-ion collisions. Phys. Rev. D 1992, 46, 246. [Google Scholar] [CrossRef]
- Bjorken, J.D. A full-acceptance detector for SSC physics at low and intermediate mass scales: An expression of interest to the SSC. Int. J. Mod. Phys. A 1992, 7, 4189. [Google Scholar] [CrossRef]
- Mishustin, I.N.; Greiner, W. Multipion droplets. J. Phys. G Nucl. Part. Phys. 1993, 19, L101. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at Finite Isospin Density. Phys. Rev. Lett. 2001, 86, 592. [Google Scholar] [CrossRef] [PubMed]
- Kogut, J.; Toublan, D. QCD at small nonzero quark chemical potentials. Phys. Rev. D 2001, 64, 034007. [Google Scholar] [CrossRef]
- Toublan, D.; Kogut, J. Isospin chemical potential and the QCD phase diagram at nonzero temperature and baryon chemical potential. Phys. Lett. B 2001, 564, 212. [Google Scholar] [CrossRef]
- Mammarella, A.; Mannarelli, M. Intriguing aspects of meson condensation. Phys. Rev. D 2015, 92, 085025. [Google Scholar] [CrossRef]
- Carignano, S.; Lepori, L.; Mammarella, A.; Mannarelli, M.; Pagliaroli, G. Scrutinizing the pion condensed phase. Eur. Phys. J. A 2017, 53, 35. [Google Scholar] [CrossRef]
- Kapusta, J. Bose-Einstein condensation, spontaneous symmetry breaking, and gauge theories. Phys. Rev. D 1981, 24, 426. [Google Scholar] [CrossRef]
- Haber, H.E.; Weldon, H.A. Finite-temperature symmetry breaking as Bose-Einstein condensation. Phys. Rev. D 1982, 25, 502. [Google Scholar] [CrossRef]
- Bernstein, J.; Dodelson, S. Relativistic Bose gas. Phys. Rev. Lett. 1991, 66, 683. [Google Scholar] [CrossRef]
- Shiokawa, K.; Hu, B.L. Finite number and finite size effects in relativistic Bose-Einstein condensation. Phys. Rev. D 1999, 60, 105016. [Google Scholar] [CrossRef]
- Salasnich, L. Particles and Anti-Particles in a Relativistic Bose Condensate. Il Nuovo C. B 2002, 117, 637. [Google Scholar] [CrossRef]
- Begun, V.V.; Gorenstein, M.I. Bose-Einstein condensation in the relativistic pion gas: Thermodynamic limit and finite size effects. Phys. Rev. C 2008, 77, 064903. [Google Scholar] [CrossRef]
- Markó, G.; Reinosa, U.; Szép, Z. Bose-Einstein condensation and Silver Blaze property from the two-loop Φ-derivable approximation. Phys. Rev. D 2014, 90, 25021. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G. QCD phase diagram with isospin chemical potential. arXiv 2016, arXiv:1611.06758. [Google Scholar]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD at finite isospin chemical potential. arXiv 2017, arXiv:1709.10487. [Google Scholar] [CrossRef]
- London, F. The λ-Phenomenon of Liquid Helium and the Bose-Einstein Degeneracy. Nature 1938, 141, 643. [Google Scholar] [CrossRef]
- Ehrenfest, P. Phasenumwandlungen im ueblichen und erweiterten Sinn, Classifiziert nach dem Entsprechenden Singularitaeten des Thermodynamischen Potentiales; Communications from the Physical Laboratory of the University of Leiden, Supplement No. 75b; Kamerlingh Onnes-Institut: Leiden, The Netherlands, 1933. [Google Scholar]
- Jaeger, G. The Ehrenfest Classification of Phase Transitions: Introduction and Evolution. Arch. Hist. Exact Sci. 1998, 53, 51. [Google Scholar] [CrossRef]
- Mishustin, I.N.; Anchishkin, D.V.; Satarov, L.M.; Stashko, O.S.; Stoecker, H. Condensation of interacting scalar bosons at finite temperatures. Phys. Rev. C 2019, 100, 022201. [Google Scholar] [CrossRef]
- Anchishkin, D.; Vovchenko, V. Mean-field approach in the multi-component gas of interacting particles applied to relativistic heavy-ion collisions. J. Phys. G Nucl. Part. Phys. 2015, 42, 105102. [Google Scholar] [CrossRef]
- Anchishkin, D.; Mishustin, I.; Stashko, O.; Zhuravel, D.; Stoecker, H. Relativistic selfinteracting particle -antiparticle system of bosons. Ukranian J. Phys. 2019, 64, 1110–1116. [Google Scholar] [CrossRef] [PubMed]
- Anchishkin, D.; Suhonen, E. Generalization of mean-field models to account for effects of excluded volume. Nucl. Phys. A 1995, 586, 734–754. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anchishkin, D.; Gnatovskyy, V.; Zhuravel, D.; Karpenko, V.; Mishustin, I.; Stoecker, H. Phase Transitions in the Interacting Relativistic Boson Systems. Universe 2023, 9, 411. https://doi.org/10.3390/universe9090411
Anchishkin D, Gnatovskyy V, Zhuravel D, Karpenko V, Mishustin I, Stoecker H. Phase Transitions in the Interacting Relativistic Boson Systems. Universe. 2023; 9(9):411. https://doi.org/10.3390/universe9090411
Chicago/Turabian StyleAnchishkin, Dmitry, Volodymyr Gnatovskyy, Denys Zhuravel, Vladyslav Karpenko, Igor Mishustin, and Horst Stoecker. 2023. "Phase Transitions in the Interacting Relativistic Boson Systems" Universe 9, no. 9: 411. https://doi.org/10.3390/universe9090411
APA StyleAnchishkin, D., Gnatovskyy, V., Zhuravel, D., Karpenko, V., Mishustin, I., & Stoecker, H. (2023). Phase Transitions in the Interacting Relativistic Boson Systems. Universe, 9(9), 411. https://doi.org/10.3390/universe9090411








