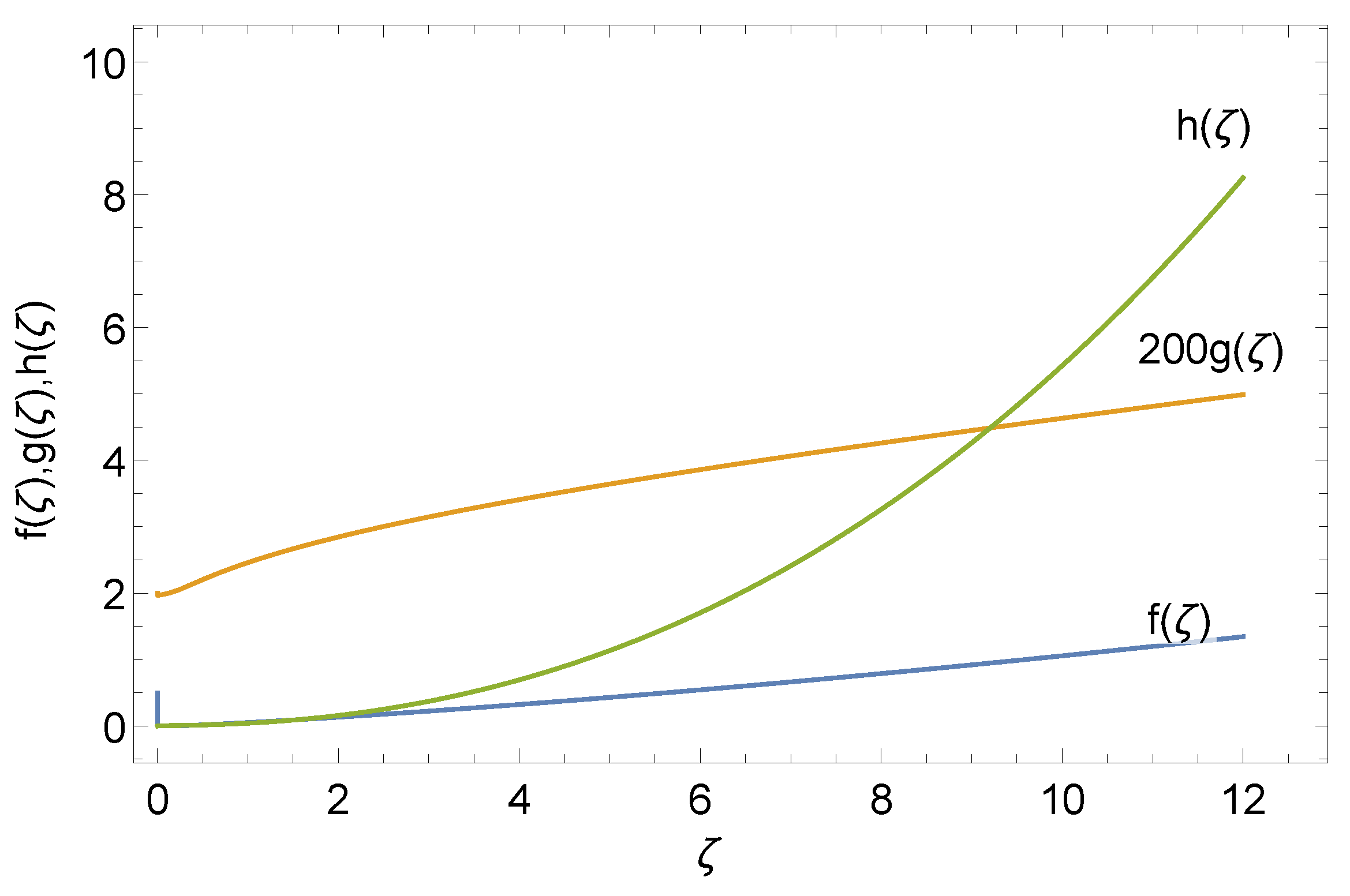1. Introduction
In the second half of the 20th century, various self-similar solutions have been found following Gottfried Gurderley’s famous discovery of spherically symmetric self-similar solutions that describe an imploding gas that collapses to the center [
1]. In this paper, we use the kinds of self-similar solutions that were independently found by Leonid Ivanovich Sedov and Sir Geoffrey Ingram Taylor during the 1940s [
2,
3]. Despite the fact that such models have been well-known for decades, they have recently received attention again. This
ansatz has been already applied successfully in several hydrodynamical systems, such as in the context of the three-dimensional Navier–Stokes and Euler equations [
4], heat equations [
5,
6], and star formation [
7]. In addition, the concept of self-similarity has a wide range of applications in general relativity. Homothetic solutions were first introduced by Cahill and Taub [
8], and have been studied extensively for such different topics as asymptotic solutions in cosmology [
9] and the gravitational collapse of black holes [
10].
The existence of the dark matter was first proposed by the Dutch astronomer Jacobus Cornelius Kapteyn [
11], and became widely known through Zwicky’s famous work from 1933 [
12]. During the second half of the century, solid experimental evidence was provided by Vera Rubin, Ken Ford, and others [
13,
14]. However, the general existence and specified properties of dark matter remain one of the most disputed topics in theoretical astrophysics. Dark fluid is a theoretical attempt to describe the properties of dark matter and its unification with dark energy into one hypothesized substance [
15].
Our goal is to use the Sedov–Taylor
ansatz to describe the time evolution of a dark fluid-like material characterized by a coupled nonlinear partial differential equation system. In our model, we study one of the simplest dark fluid materials, described by a polytropic (linear) equation of state. The dynamical evolution of the dark fluid is governed by the Euler equation and the gravitational field is described by the corresponding Poisson equation. We find time-dependent scaling solutions of the velocity flow, density flow, and gravitational fields, which can be good candidates to describe the evolution of the gravitationally coupled dust-like dark matter in the universe. We show that these kinds of solutions are consistent with the Newtonian Friedmann equations. They satisfy the mass conservation and acceleration equations and provide a similar expansion rate of the universe as the traditional solutions. The aim of this study is to broaden the knowledge of time-dependent self-similar solutions in these dark fluid models by improving upon and extending our previous model [
16]. We tested our model on cosmological scales; moreover, we studied how the obtained evolution of the Hubble parameter and the ratio of the density parameters resemble other physical models.
2. The Model
We consider a set of coupled nonlinear partial differential equations which describe the non-relativistic dynamics of a compressible fluid with zero thermal conductivity and zero viscosity [
17],
These equations are the continuity, Euler equation, and equation of state (EoS), respectively. We assume that the system has spherical symmetry, and we are interested in solving it in one dimension. If we assume the fluid is ideal and the system has spherical symmetry, we can reduce the multi-dimensional partial differential equation (PDE) system into the one-dimensional radial-dependent one:
Here, the dynamical variables are
,
, and
, respectively referring to the density, radial velocity flow, and pressure field distributions, with
g being the radial component of an exterior force density. As we noted briefly in the introduction, we use the following general linear equation of state:
Several forms of the EOS are available in astrophysics, and polytropic ones have been successfully used in the past; see Emden’s famous book [
18]. A great variety of applications can be found [
19]. In Equation (
3), the
w parameter can vary depending on the type of matter that governs the system’s evolution. Traditionally,
is used; this value corresponds to the EoS for ordinary non-relativistic matter or cold dust. For our case, we choose a negative value for
w which leads to different kinds of dark-fluid scenarios, as was presented in detail by Perkovic [
20]. In this paper, we choose
which represents the simplest case of an expanding universe governed by dark matter. Smaller values could cause a “big rip”. The adiabatic speed of sound can be evaluated from Equation (
3), and it is easy to show that it is constant:
which is a necessary physical condition. Furthermore, let us assume that we have an additional self-gravitating term in Equation (2b). In this case, the exterior force density
g can be expressed in the following way:
where
is the Newtonian gravitational potential and satisfies the Poisson equation, which is coupled to the previously proposed PDE system [
21]
where
G is the universal gravitational constant, which is set to unity in our further calculations. Note that we can add an additional constant term
to Equation (1b) which plays a similar role to the cosmological constant in Einstein’s equations:
Below, we show that this constant cannot be used, as it does not lead to a consistent self-similar solution, which is what we are looking for here. Note that this observation in our model can be an
indirect proof of the nonexistence of the static Universe picture. We can extend the exterior force density further with a rotating term. In this case, we add a phenomenological rotation term to Equation (2b), meaning that the equation takes the following modified form:
where
is a dimensionless parameter that describes the strength of the rotational effect and
is the polar angle. We assume that the rotation is slow; therefore, we can expect that the spherical symmetry is not broken. This statement is satisfied if the
parameter is sufficiently small, implying that the rotational energy is negligible compared to the gravitational energy. The self-similar analysis of various rotating and stratified incompressible ideal fluids was investigated in two Cartesian coordinates in [
22]. Note that the geometrized unit system (
,
) was applied for the calculations below, which can be converted to other units as well. See
Appendix A for more details and unit conversations.
3. Scaling Solution and Sedov–Taylor Ansatz
We would like to find and study analytic solutions of equations by applying the long-established self-similar
ansatz by Sedov and Taylor [
2,
3], which can be expressed in the following form:
where
r means radial and
t means time dependence. Note that the so-called shape functions
only depend on
; thus, we introduce a new variable
where
is a dimensionless quantity in geometrized units. The (not yet determined) exponents are called similarity exponents (
,
,
, and
), and have physical relevance;
describes the rate of spread of the spatial distribution during the time evolution (if the exponent is positive) or contraction (if
). In addition, the other exponents describe the rate of decay of the intensity of the corresponding field. Solutions with integer exponents are called self-similar solutions of the first kind, while the second kind denotes the non-integer ones. Self-similarity is based on the concept that physical quantities preserve their shape during time evolution. A general description of the properties of these types of scaling solutions can be found in our previous publication [
16].
We assume that the shape functions are sufficiently smooth and continuously differentiable at least twice in
over the entire domain. Thus, we calculate the relevant time and space derivatives of the shape functions and substitute them into Equation (2). As a consequence, we usually obtain an overdetermined algebraic equation system for the similarity exponents. Other possible scenarios may play out as well; these have been presented in detail in [
16]. We obtain the following numerical value for the exponents for both the non-rotating and rotating cases:
,
,
, and
. If we add the
constant to the Euler equation, such a solution for the similarity equation cannot be found. From these results, it is evident that the dynamical variables such as the velocity, gravitational potential, and density flow have spreading properties. Our physical intuition says that spreading is somehow similar to expansion, which is a basic property of the universe at astronomical or cosmological scales.
By substituting the obtained numerical values of the similarity exponents, we can reduce the induced PDE system into an ordinary differential equation (ODE) system that depends only on the
independent variable. We find that the obtained equation system has the following form:
It can easily be noticed that the ordinary differential equation system presented in Equation (11) cannot be solved analytically. For linearized nonautonomous ordinary differential equation systems, the stationary point of the phase space can be found, and we can say something about the general asymptotic behavior of the solutions as well [
23]. Nonetheless, there is no generally known method for nonlinearized nonautonomous differential equation systems. Moreover, the existence and uniqueness of smooth solutions has not yet been proven in multiple dimensions. Therefore, it is a reasonable approach to solve the obtained ordinary differential equation system in Equation (11) numerically for a large number of parameter sets (based on physical considerations) in order to explore the behavior of the solution of the system with different boundary and initial conditions. One example of such a numerical solution can be seen in
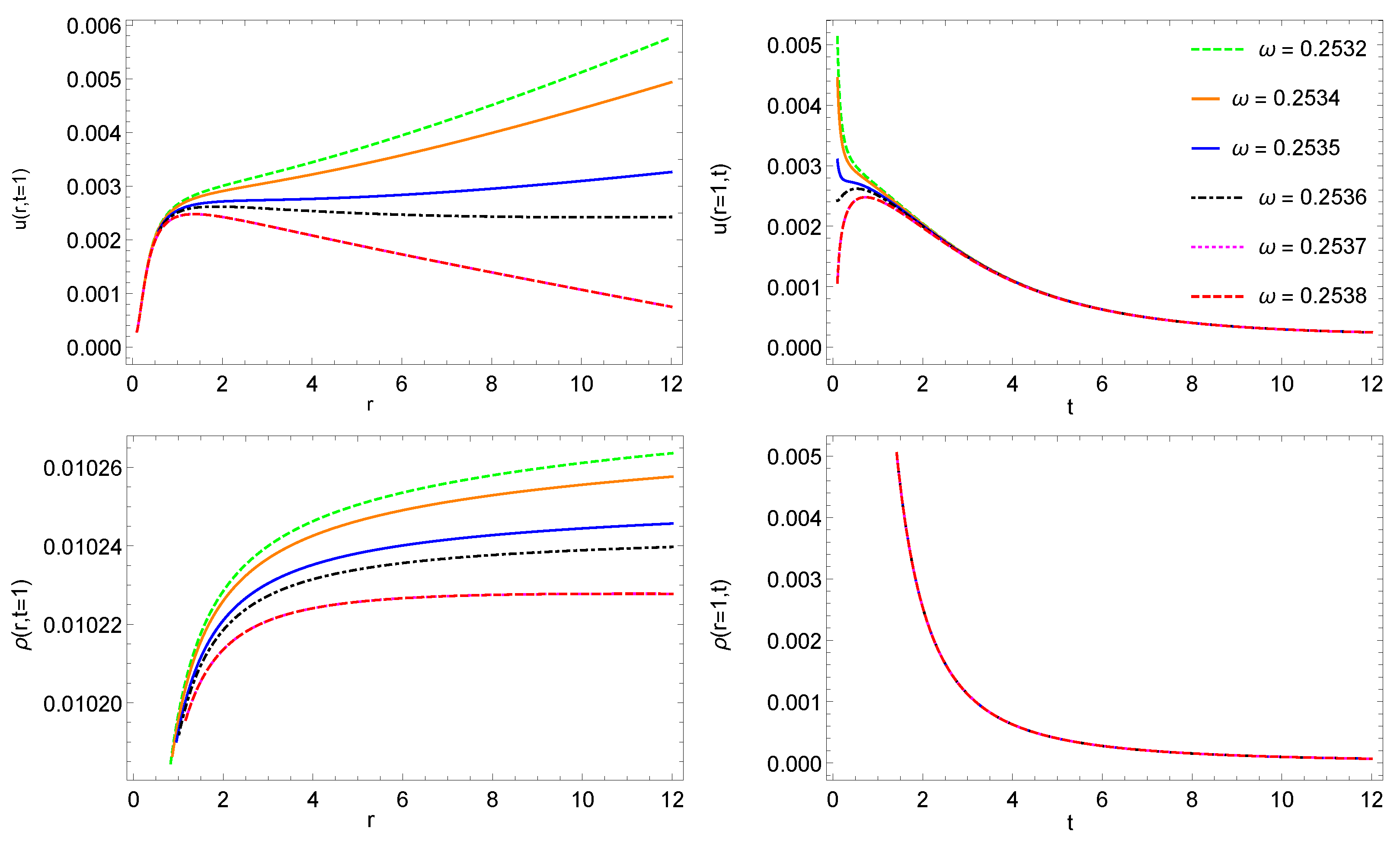
Figure 1.
As an example, at a specific parameter and initial condition set, the shape function of the velocity
is almost linear and increasing after a short decrease, providing a hint of Hubble expansion-like behavior. The shape function
is asymptotically flat after a quick ramp-up, corresponding to the conservation of matter. The last shape function
has an increasing polynomial trend with a slight positive exponent, which is connected to the gravitational potential. To obtain a sufficiently smooth numerical solution, we solved the ODE system using an adaptive numerical integration provided by
Wolfram Mathematica 13.1 [
24]. For all of our calculations, the integration limits were
and
, the same as in [
16]. As has been said before, we established initial conditions to obtain the numerical solution; for this reason, we use ranges
of
and
, while for the second-order differential equation we have
and
.
This choice of initial conditions reflects that, first it is physically reasonable that the density flow range is
and finite. Recent results suggest that dark fluid could possibly have negative mass [
25]; however, in the present model this leads to singular solutions. Second, our choice of initial velocity flow
makes for an initially radially expanding fluid. We have seen that if the initial value for
and
is set outside of the previously given range, the solution of the differential equation becomes singular. Moreover, we have seen that the variation in the initial condition corresponding to the shape function of the gravitational potential does not affect the trend of the time evolution of the system, as it only causes vertical shifts. Therefore, we set the initial numerical value equal to zero.
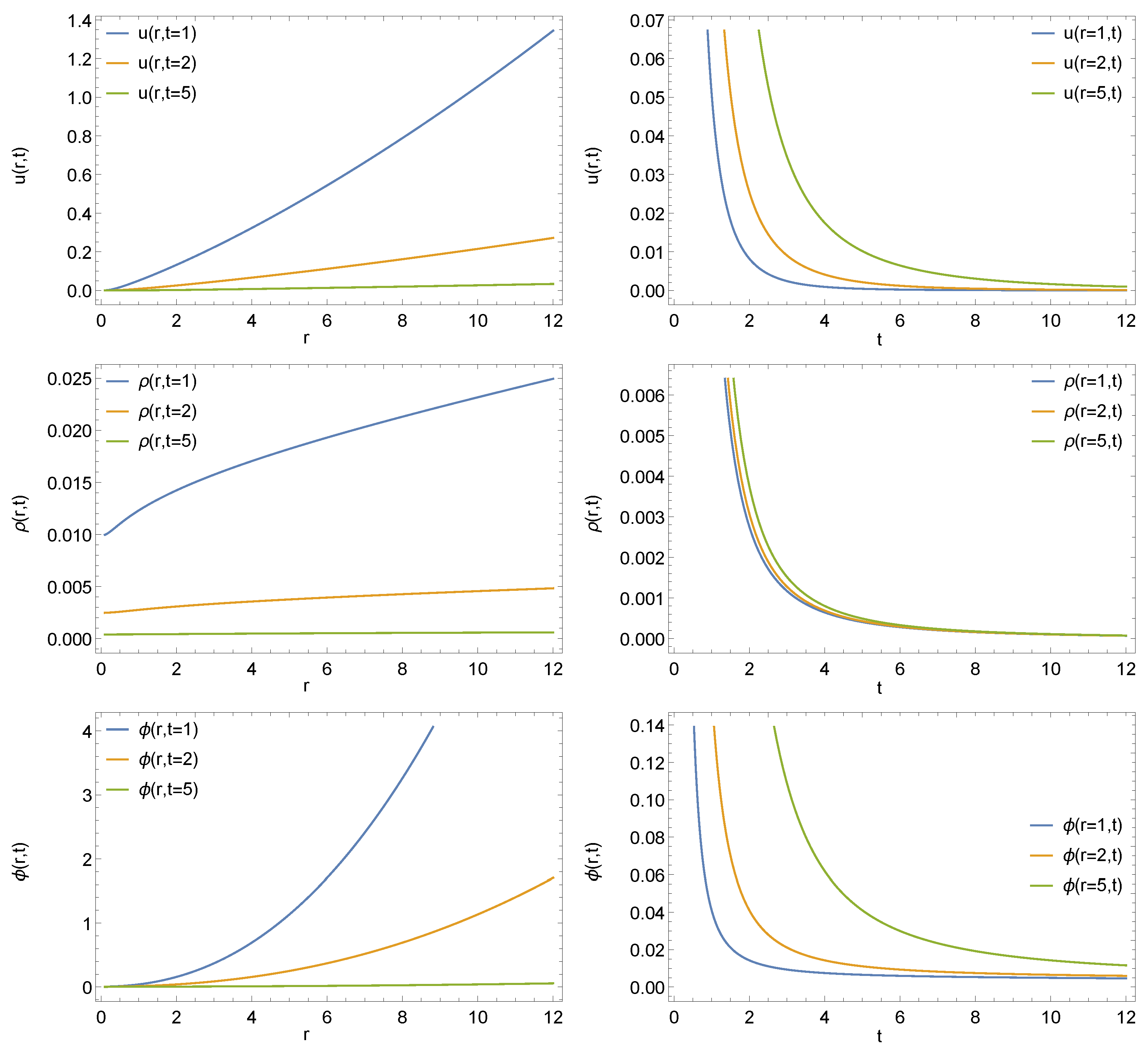
We are interested in finding the solution of the ODE system as a function of the spatial and time coordinates. We transform our single-variable numerical solutions into two-variable functions, for which we use the inverted form of Equation (
10). It can easily be noticed that if we look at the shape of the
ansatz, the solution has a singularity at
. Thus, we use the
and
domains to obtain the space- and time-dependent initial dynamical functions
,
, and
.
6. Discussion
According to current scientific understanding, dark matter and dark energy make up about 95% of the total energy density of the observable universe today. The dark fluid theory suggests that a single substance may explain both dark matter and dark energy. The behaviour of the hypothetical dark fluid is believed to resemble that of cold dark matter on galactic scales while exhibiting similar characteristics to dark energy at larger scales [
25]. Predictions can be obtained from our Sedov–von Neumann–Taylor blast wave-inspired nonrelativistic dark fluid model on galactic and cosmological scales. A useful feature of this model is that the initial value problem of the reduced ordinary differential equation system is easier to handle than the boundary and initial condition problem of the original partial differential equations. To provide a reliable practical basis for our dark fluid model, we have tested the theoretical results on astrophysical scales in order to demonstrate the similar nature of the solutions on the cosmological scale.
Our solution was developed based on cosmological observations, using the Hubble law to scale the expansion of the universe. Our model includes various scaling mechanisms through the use of a Sedov-type self-similar
ansatz, which allows for describing different time decay scenarios [
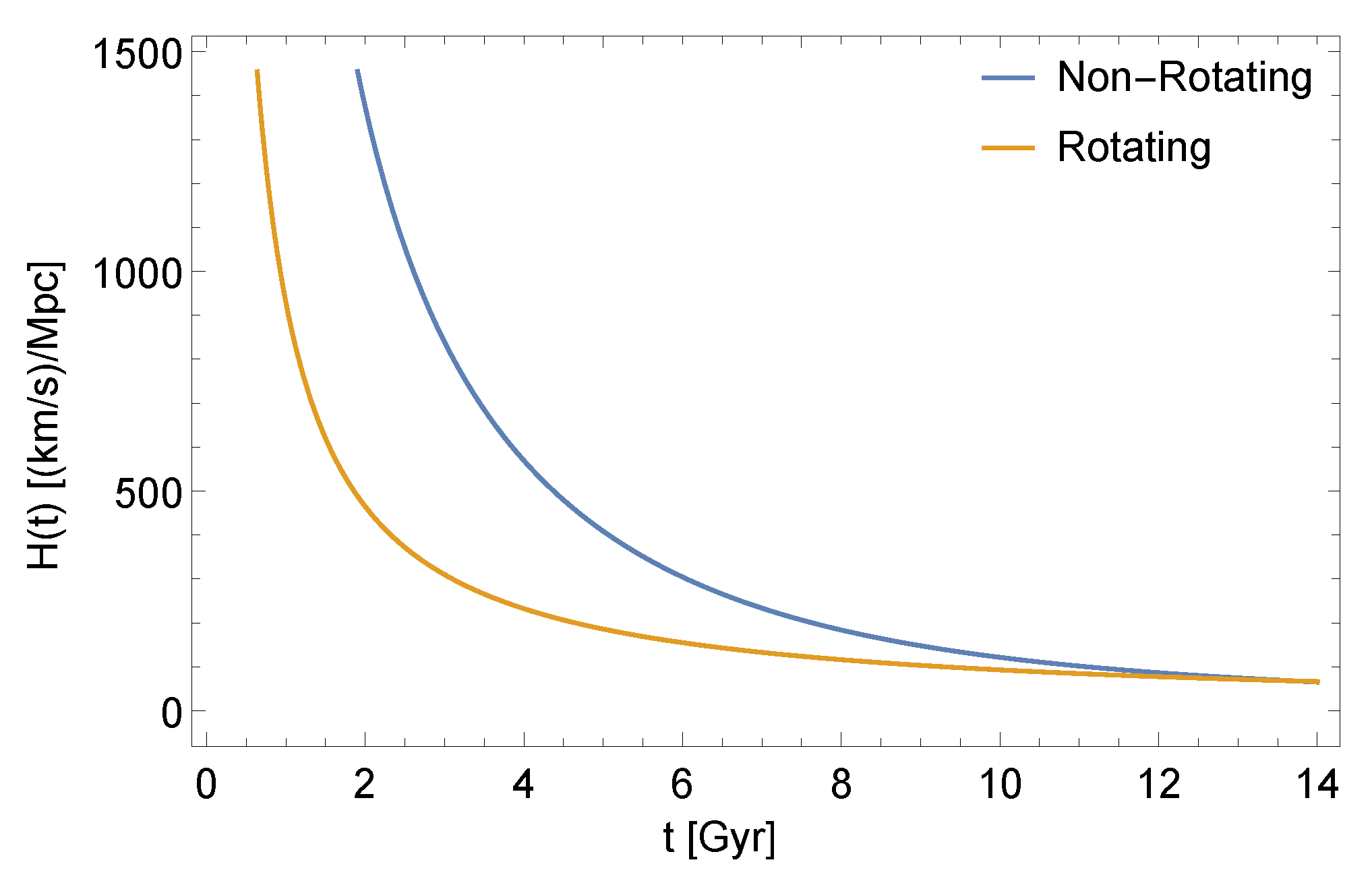
33]. In the case of a non-rotating system, we can conclude that the radial velocity profile of the solution provides Hubble-like expansion, while the non-rotating model provides inflation-like behavior
on a long-range timescale, which cannot be physical (causal). We have seen that the high initial velocity of the dark fluid relaxes to a small, constant, and non-relativistic value on long timescales (
billion years). Another interesting feature of the model is that the gravitation potential is a negative polynomial in time, which is consistent with the distribution of the density of the dark fluid.
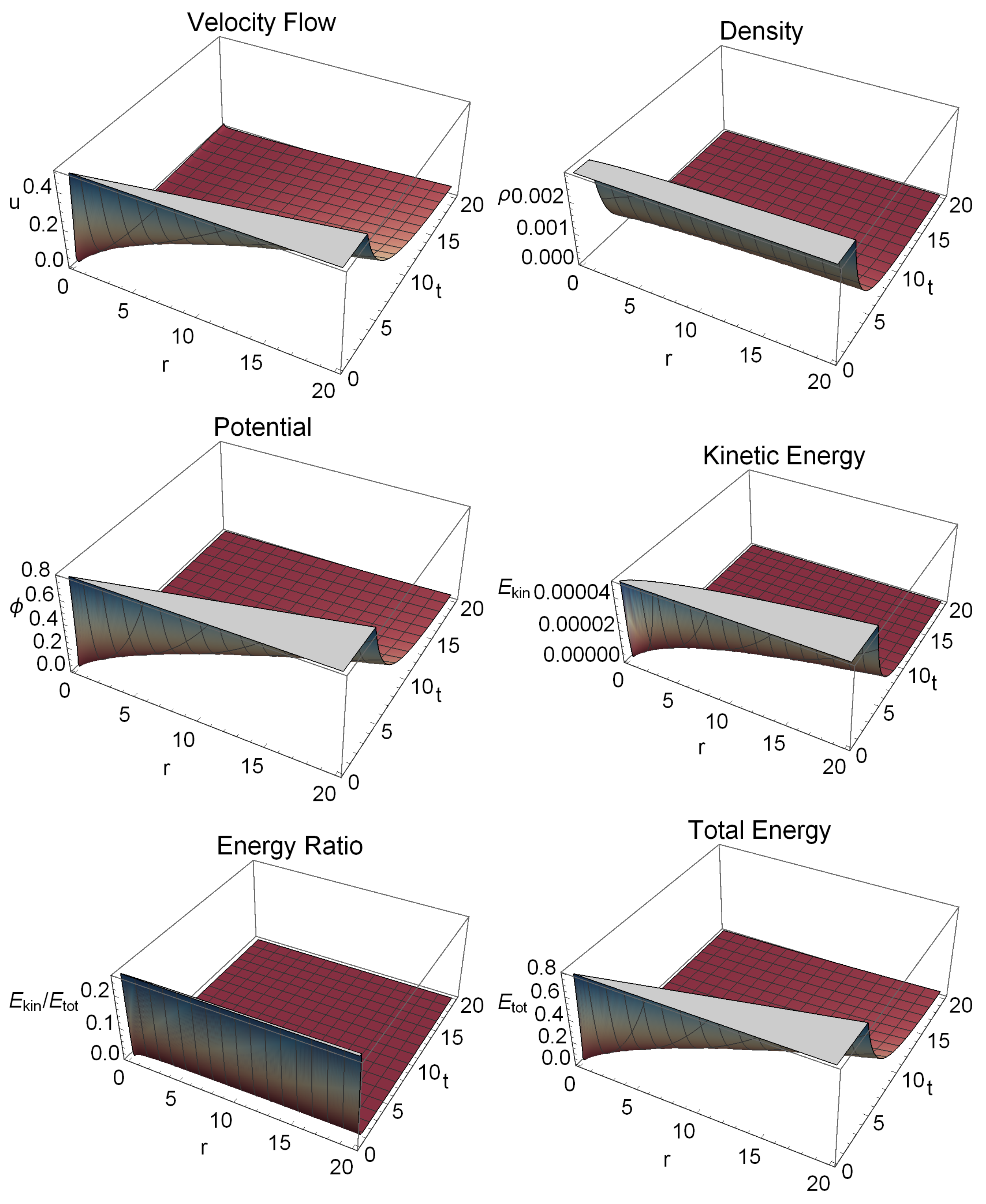
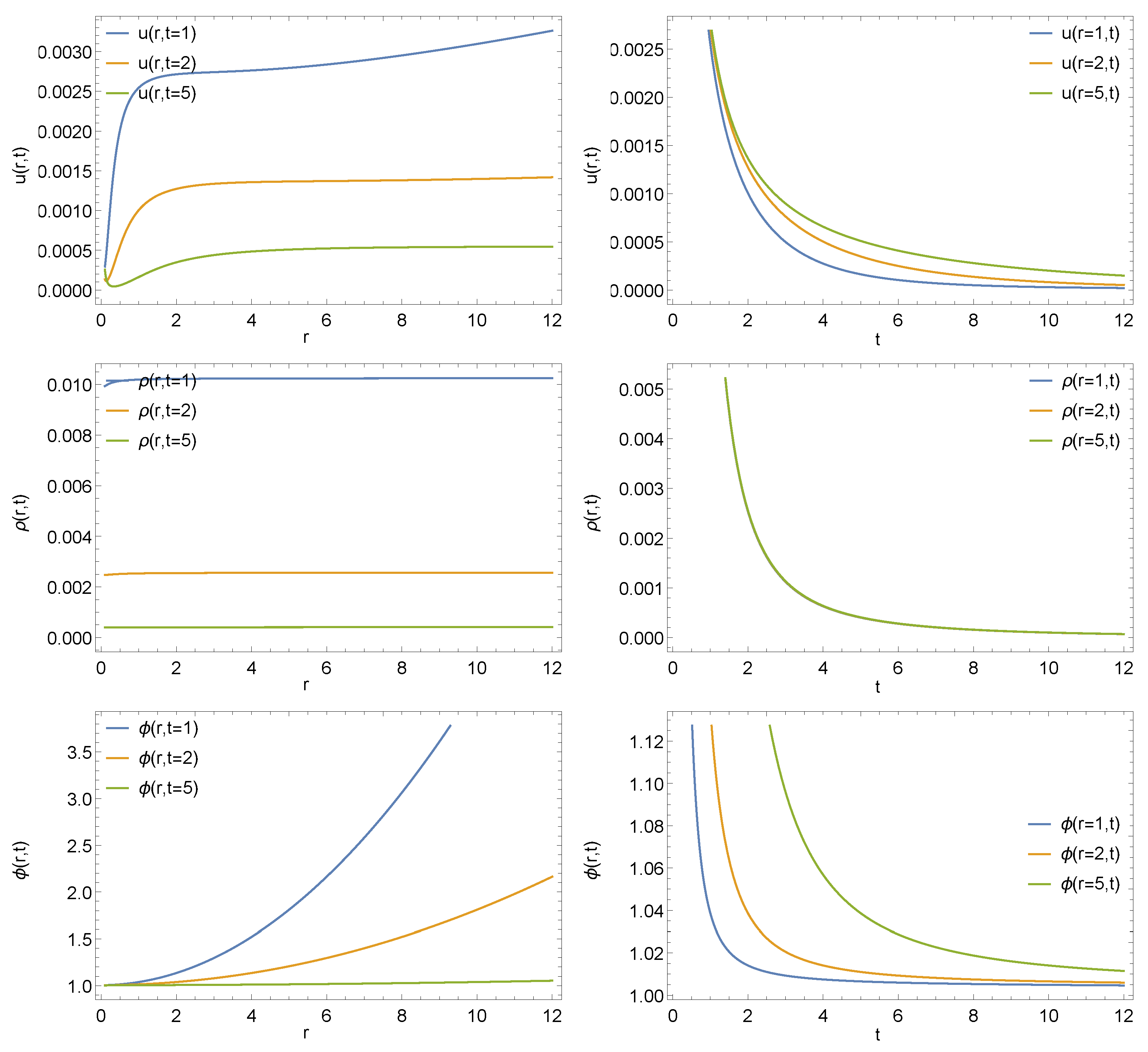
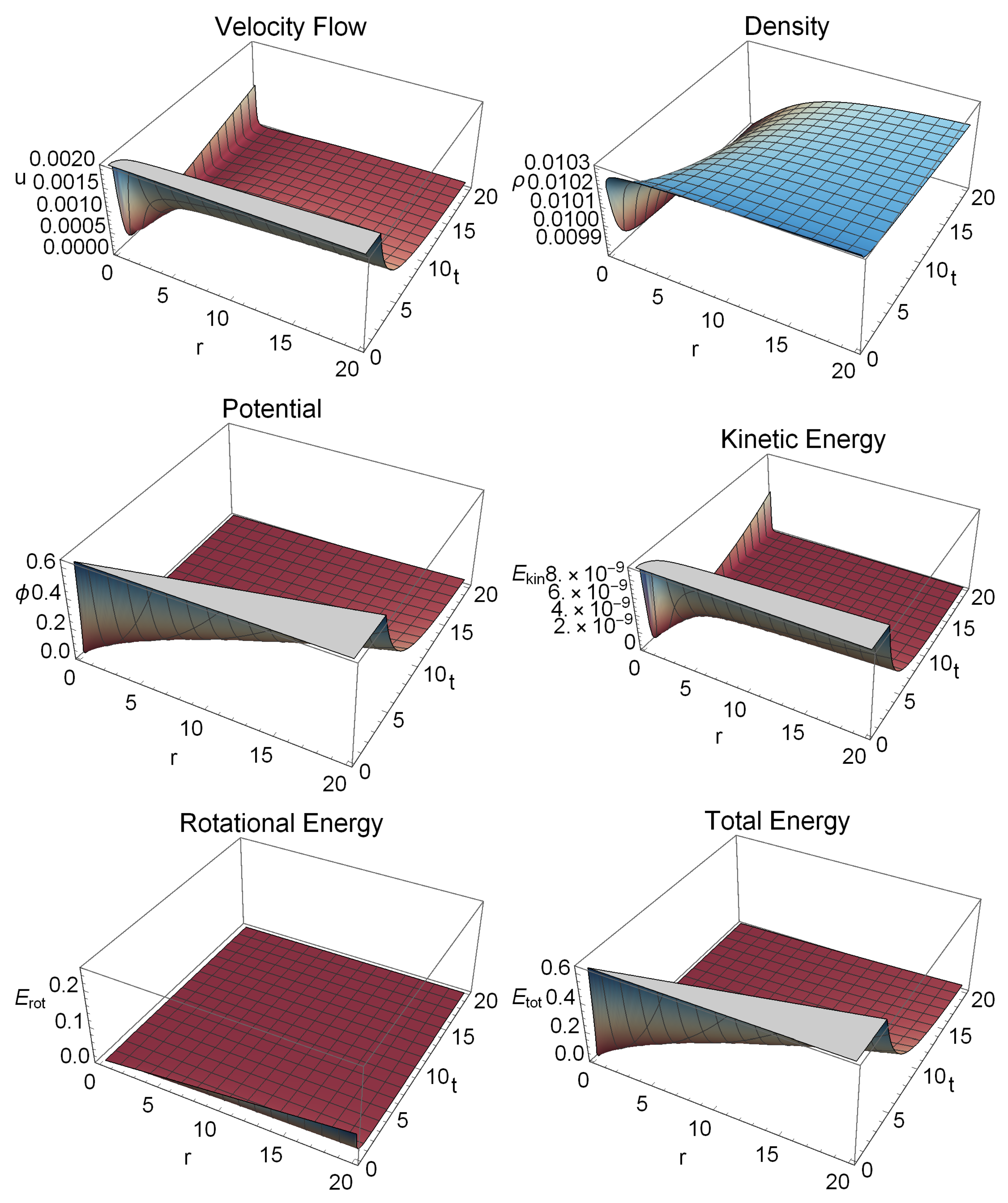
One notable aspect in the case of the rotating model is that it does not show superluminous behavior in the expected time range, contrary to the non-rotating model. Simultaneously, we have found that the radial profile of the density becomes saturated and close to flat at far distances from the initial point; see the top right panel of
Figure 6. In addition, it is possible to set the initial conditions such that the universe today is observed as flat Euclidean with the density parameter
being the critical density corresponding to the Hubble parameter
. The flatness of the universe is indicated by the recent measurements of WMAP [
34]. The sum index uses the baryonic energy
, dark energy (DE), and cold dark matter (CDM). We can define the matter part of
along with the full
and
[
35]. If the
relation is correct, then we can assume the following identity:
Accordingly, we can determine the relevant time and radial coordinates from the obtained results, which correspond to this specific energy relation evaluated at
and
. In the absence of dark fluid, the universe continues to expand indefinitely, though at a gradually slowing rate that eventually approaches zero. This causes an open-topology universe. In this case, the ultimate fate of the universe is that the temperature asymptotically approaches absolute zero in a so-called “big freeze”. At the same time, it is essential to mention that a weakness of our non-relativistic model is that its results are not as precise as those of relativistic Friedmann equation-based models [
25].
7. Conclusions and Outlook
In this paper, we have studied the behaviour of self-similar time-dependent solutions in a coupled nonlinear partial differential equation system describing a non-viscous, non-relativistic, and self-gravitating fluid (Euler–Poisson system). The reason behind the applied self-similar solutions is that they provide a very efficient method to analyze various kinds of physical systems, particularly as concerns the hydrodynamical description of systems that involve collapse and explosion.
The analysis presented in this paper is a Euler–Poisson extension of our previous model [
16]. We found that a Sedov–Taylor type solutions exists and that the algebraic equation obtained for the similarity exponents has only one unique solution. We have used the obtained solution to describe the behaviour of a non-relativistic dark fluid on cosmological scales, and have presented the relevant kinematical and dynamical quantities. In addition, we have shown that our model based on self-similarity is in agreement with the Newtonian Friedmann equations.
It can easily be noticed that this model has certain limitations due to its classical nature, although it does provide relatively adequate results on the cosmological scale. We have shown that the obtained quasi-analytical solution for the evolution of the Hubble parameter is in agreement with the standard cosmological model, e.g., [
28]. Moreover, in the previous section we have shown that the energy ratio from our model closely resembles the ratio of
, i.e., the relevant density parameters as of today.
This model has the additional practical benefit that the calculation does not require high computing performance and resources. Therefore, it can be used to estimate the physical value of the initial and boundary values when more sophisticated theoretical or numerical simulations are used. Moreover, it can provide a reliable basis for comparing for two- and three-dimensional hydrodynamical simulations. In future research, through reasonable effort it would be possible to improve this model in order to describe relativistic matter [
36], Chaplygin gas [
37], and two-fluid models.