Binary Neutron-Star Mergers with a Crossover Transition to Quark Matter
Abstract
:1. Introduction
2. Equations of State
3. Simulation Details
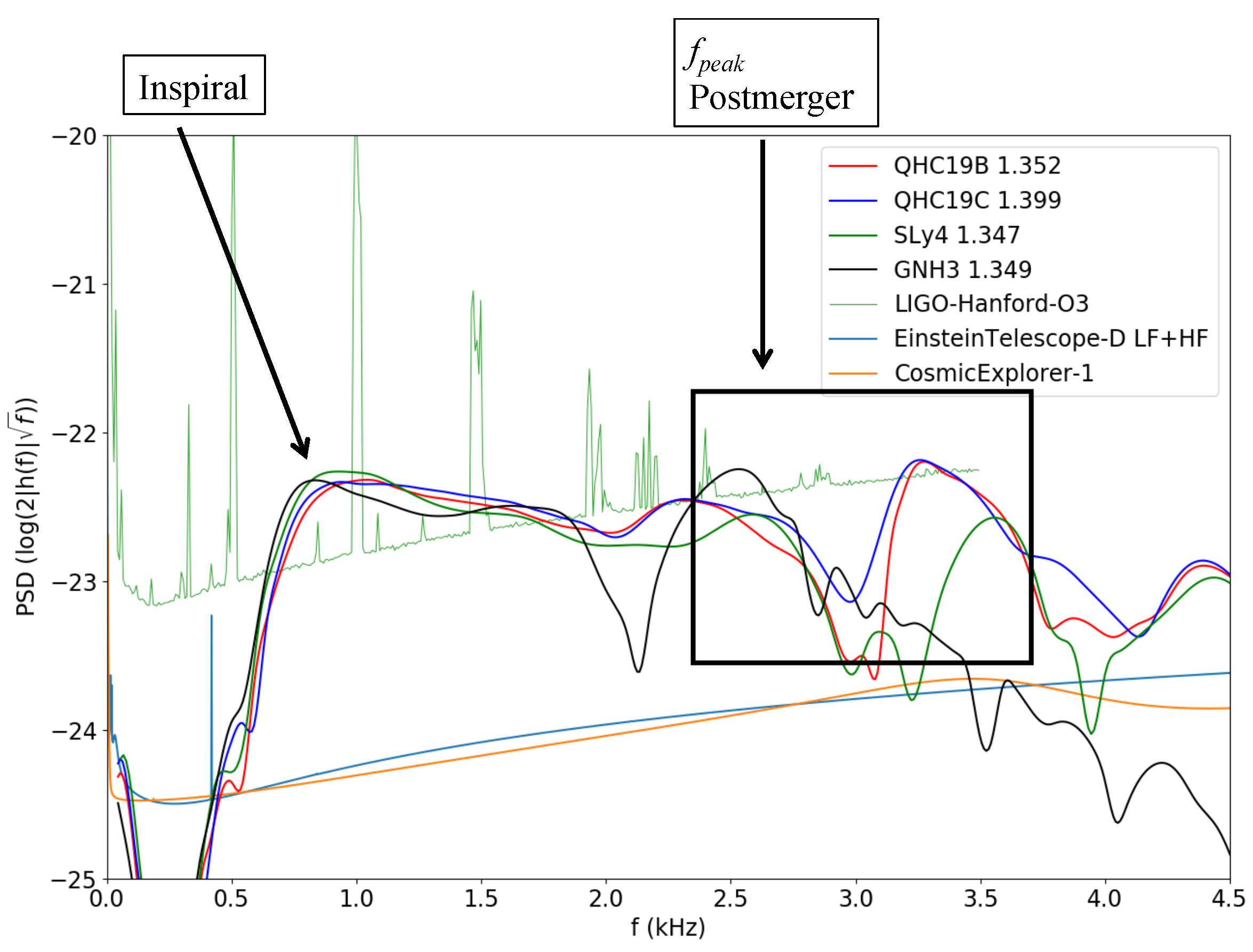
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruffini, R.; Karlica, M.; Sahakyan, N.; Rueda, J.A.; Wang, Y.; Mathews, G.J.; Bianco, C.L.; Muccino, M. A GRB Afterglow Model Consistent with Hypernova Observations. Astrophys. J. 2018, 869, 101. [Google Scholar] [CrossRef]
- Ruffini, R.; Moradi, R.; Rueda, J.A.; Li, L.; Sahakyan, N.; Chen, Y.C.; Wang, Y.; Aimuratov, Y.; Becerra, L.; Bianco, C.L.; et al. The morphology of the X-ray afterglows and of the jetted GeV emission in long GRBs. MNRAS 2021, 504, 5301–5326. [Google Scholar] [CrossRef]
- Kedia, A.; Kim, H.I.; Suh, I.S.; Mathews, G.J. Binary neutron star mergers as a probe of quark-hadron crossover equations of state. Phys. Rev. D 2022, 106, 103027. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A. The Dynamics of Binary Neutron Star Mergers and GW170817. Annu. Rev. Nucl. Part. Sci. 2020, 70, 95–119. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Annu. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Bogdanov, S.; Guillot, S.; Ray, P.S.; Wolff, M.T.; Chakrabarty, D.; Ho, W.C.G.; Kerr, M.; Lamb, F.K.; Lommen, A.; Ludlam, R.M.; et al. Constraining the Neutron Star Mass-Radius Relation and Dense Matter Equation of State with NICER. I. The Millisecond Pulsar X-ray Data Set. Astrophys. J. Lett. 2019, 887, L25. [Google Scholar] [CrossRef]
- Bogdanov, S.; Dittmann, A.J.; Ho, W.C.G.; Lamb, F.K.; Mahmoodifar, S.; Miller, M.C.; Morsink, S.M.; Riley, T.E.; Strohmayer, T.E.; Watts, A.L.; et al. Constraining the Neutron Star Mass-Radius Relation and Dense Matter Equation of State with NICER. III. Model Description and Verification of Parameter Estimation Codes. Astrophys. J. Lett. 2021, 914, L15. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Weih, L.R.; Hanauske, M.; Rezzolla, L. Postmerger Gravitational-Wave Signatures of Phase Transitions in Binary Mergers. Phys. Rev. Lett. 2020, 124, 171103. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a First-Order Phase Transition in Neutron-Star Mergers through Gravitational Waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef] [PubMed]
- Blacker, S.; Bastian, N.U.F.; Bauswein, A.; Blaschke, D.B.; Fischer, T.; Oertel, M.; Soultanis, T.; Typel, S. Constraining the onset density of the hadron-quark phase transition with gravitational-wave observations. Phys. Rev. D 2020, 102, 123023. [Google Scholar] [CrossRef]
- Radice, D. General-relativistic Large-eddy Simulations of Binary Neutron Star Mergers. Astrophys. J. Lett. 2017, 838, L2. [Google Scholar] [CrossRef]
- Breschi, M.; Bernuzzi, S.; Zappa, F.; Agathos, M.; Perego, A.; Radice, D.; Nagar, A. Kilohertz gravitational waves from binary neutron star remnants: Time-domain model and constraints on extreme matter. Phys. Rev. D 2019, 100, 104029. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.T. Measuring Neutron-Star Properties via Gravitational Waves from Neutron-Star Mergers. Phys. Rev. Lett. 2012, 108, 011101. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Muranushi, T.; Sekiguchi, Y.i.; Shibata, M.; Taniguchi, K. Remnant massive neutron stars of binary neutron star mergers: Evolution process and gravitational waveform. Phys. Rev. D 2013, 88, 044026. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Nagar, A.; Balmelli, S.; Dietrich, T.; Ujevic, M. Quasiuniversal Properties of Neutron Star Mergers. Phys. Rev. Lett. 2014, 112, 201101. [Google Scholar] [CrossRef]
- Rezzolla, L.; Takami, K. Gravitational-wave signal from binary neutron stars: A systematic analysis of the spectral properties. Phys. Rev. D 2016, 93, 124051. [Google Scholar] [CrossRef]
- Zappa, F.; Bernuzzi, S.; Radice, D.; Perego, A.; Dietrich, T. Gravitational-Wave Luminosity of Binary Neutron Stars Mergers. Phys. Rev. Lett. 2018, 120, 111101. [Google Scholar] [CrossRef] [PubMed]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of Quark-Hadron Phase Transitions in General-Relativistic Neutron-Star Mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef] [PubMed]
- Most, E.R.; Jens Papenfort, L.; Dexheimer, V.; Hanauske, M.; Stoecker, H.; Rezzolla, L. On the deconfinement phase transition in neutron-star mergers. Eur. Phys. J. A 2020, 56, 59. [Google Scholar] [CrossRef]
- Liebling, S.L.; Palenzuela, C.; Lehner, L. Effects of high density phase transitions on neutron star dynamics. Class. Quantum Gravity 2021, 38, 115007. [Google Scholar] [CrossRef]
- Prakash, A.; Radice, D.; Logoteta, D.; Perego, A.; Nedora, V.; Bombaci, I.; Kashyap, R.; Bernuzzi, S.; Endrizzi, A. Signatures of deconfined quark phases in binary neutron star mergers. Phys. Rev. D 2021, 104, 083029. [Google Scholar] [CrossRef]
- Sebastian Blacker and Hristijan Kochankovski and Andreas Bauswein and Angels Ramos and Laura Tolos Thermal behavior as indicator for hyperons in binary neutron star merger remnants. arXiv 2023, arXiv:2307.03710.
- Mallick, R. Gravitational wave signatures of phase transition from hadronic to quark matter in isolated neutron stars and binaries. Eur. Phys. J. Web Conf. 2022, 274, 07002. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, C. Hybrid stars may have an inverted structure. arXiv 2022, arXiv:2211.12043. [Google Scholar]
- Tajima, H.; Tsutsui, S.; Doi, T.M.; Iida, K. Density-Induced Hadron–Quark Crossover via the Formation of Cooper Triples. Symmetry 2023, 15, 333. [Google Scholar] [CrossRef]
- Kohsuke, S.; Toru, K.; Shun, F. Equation of State in Neutron Stars and Supernovae. In Handbook of Nuclear Physics; Springer: Singapore, 2023; pp. 1–51. [Google Scholar]
- Sebastian, B.; Andreas, B.; Stefan, T. Exploring thermal effects of the hadron-quark matter transition in neutron star mergers. arXiv 2023, arXiv:2304.01971. [Google Scholar]
- Bauswein, A.; Janka, H.T.; Hebeler, K.; Schwenk, A. Equation-of-state dependence of the gravitational-wave signal from the ring-down phase of neutron-star mergers. Phys. Rev. D 2012, 86, 063001. [Google Scholar] [CrossRef]
- Bauswein, A.; Blacker, S.; Vijayan, V.; Stergioulas, N.; Chatziioannou, K.; Clark, J.A.; Bastian, N.U.F.; Blaschke, D.B.; Cierniak, M.; Fischer, T. Equation of State Constraints from the Threshold Binary Mass for Prompt Collapse of Neutron Star Mergers. Phys. Rev. Lett. 2020, 125, 141103. [Google Scholar] [CrossRef] [PubMed]
- Pisarski, R.D.; Skokov, V.V. Chiral matrix model of the semi-QGP in QCD. Phys. Rev. D 2016, 94, 034015. [Google Scholar] [CrossRef]
- Steinheimer, J.; Schramm, S. The problem of repulsive quark interactions - Lattice versus mean field models. Phys. Lett. B 2011, 696, 257–261. [Google Scholar] [CrossRef]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N.; Baym, G. New Critical Point Induced By the Axial Anomaly in Dense QCD. Phys. Rev. Lett. 2006, 97, 122001. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Baym, G.; Furusawa, S.; Hatsuda, T.; Kojo, T.; Togashi, H. New Neutron Star Equation of State with Quark-Hadron Crossover. Astrophys. J. 2019, 885, 42. [Google Scholar] [CrossRef]
- Kojo, T.; Baym, G.; Hatsuda, T. Implications of NICER for Neutron Star Matter: The QHC21 Equation of State. Astrophys. J. 2022, 934, 46. [Google Scholar] [CrossRef]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Ajith, P.; Allen, B.; Amaro-Seoane, P.; Andersson, N.; Aoudia, S.; Arun, K.; Astone, P.; et al. Scientific objectives of Einstein Telescope. Class. Quantum Gravity 2012, 29, 124013. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the sensitivity of next generation gravitational wave detectors. Class. Quantum Gravity 2017, 34, 044001. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densitiesPart II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter [review article]. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Etienne, Z.; Brandt, S.R.; Diener, P.; Gabella, W.E.; Gracia-Linares, M.; Haas, R.; Kedia, A.; Alcubierre, M.; Alic, D.; Allen, G.; et al. The Einstein Toolkit. Zenodo (The "Lorentz" release, ET_2021_05) 2021. [Google Scholar] [CrossRef]
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. 1987, 90, 1–218. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef] [PubMed]
- Baumgarte, T.W.; Shapiro, S.L. Numerical integration of Einstein’s field equations. Phys. Rev. D 1998, 59, 024007. [Google Scholar] [CrossRef]
- Alcubierre, M.; Brügmann, B.; Dramlitsch, T.; Font, J.A.; Papadopoulos, P.; Seidel, E.; Stergioulas, N.; Takahashi, R. Towards a stable numerical evolution of strongly gravitating systems in general relativity: The conformal treatments. Phys. Rev. D 2000, 62, 044034. [Google Scholar] [CrossRef]
- Alcubierre, M.; Brügmann, B.; Diener, P.; Koppitz, M.; Pollney, D.; Seidel, E.; Takahashi, R. Gauge conditions for long-term numerical black hole evolutions without excision. Phys. Rev. D 2003, 67, 084023. [Google Scholar] [CrossRef]
- Baiotti, L.; Hawke, I.; Montero, P.J.; Löffler, F.; Rezzolla, L.; Stergioulas, N.; Font, J.A.; Seidel, E. Three-dimensional relativistic simulations of rotating neutron-star collapse to a Kerr black hole. Phys. Rev. D 2005, 71, 024035. [Google Scholar] [CrossRef]
- Hawke, I.; Löffler, F.; Nerozzi, A. Excision methods for high resolution shock capturing schemes applied to general relativistic hydrodynamics. Phys. Rev. D 2005, 71, 104006. [Google Scholar] [CrossRef]
- Mösta, P.; Mundim, B.C.; Faber, J.A.; Haas, R.; Noble, S.C.; Bode, T.; Löffler, F.; Ott, C.D.; Reisswig, C.; Schnetter, E. GRHydro: A new open-source general-relativistic magnetohydrodynamics code for the Einstein toolkit. Class. Quantum Gravity 2014, 31, 015005. [Google Scholar] [CrossRef]
- Banyuls, F.; Font, J.A.; Ibáñez, J.M.; Martí, J.M.; Miralles, J.A. Numerical {3 + 1} General Relativistic Hydrodynamics: A Local Characteristic Approach. Astrophys. J. 1997, 476, 221–231. [Google Scholar] [CrossRef]
- Font, J.A. Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity. Living Rev. Relativ. 2008, 11, 7. [Google Scholar] [CrossRef]
- Gourgoulhon, E.; Grandclément, P.; Taniguchi, K.; Marck, J.A.; Bonazzola, S. Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity: Method and tests. Phys. Rev. D 2001, 63, 064029. [Google Scholar] [CrossRef]
- Grandclément, P.; Novak, J. Spectral Methods for Numerical Relativity. Living Rev. Relativ. 2009, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Schnetter, E.; Hawley, S.H.; Hawke, I. Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Gravity 2004, 21, 1465–1488. [Google Scholar] [CrossRef]
- Schnetter, E.; Diener, P.; Dorband, E.N.; Tiglio, M. A multi-block infrastructure for three-dimensional time-dependent numerical relativity. Class. Quantum Gravity 2006, 23, S553–S578. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Maione, F.; Löffler, F. Modeling equal and unequal mass binary neutron star mergers using public codes. Phys. Rev. D 2016, 93, 064047. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Spectral properties of the post-merger gravitational-wave signal from binary neutron stars. Phys. Rev. D 2015, 91, 064001. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathews, G.J.; Kedia, A.; Kim, H.I.; Suh, I.-S. Binary Neutron-Star Mergers with a Crossover Transition to Quark Matter. Universe 2023, 9, 410. https://doi.org/10.3390/universe9090410
Mathews GJ, Kedia A, Kim HI, Suh I-S. Binary Neutron-Star Mergers with a Crossover Transition to Quark Matter. Universe. 2023; 9(9):410. https://doi.org/10.3390/universe9090410
Chicago/Turabian StyleMathews, Grant J., Atul Kedia, Hee Il Kim, and In-Saeng Suh. 2023. "Binary Neutron-Star Mergers with a Crossover Transition to Quark Matter" Universe 9, no. 9: 410. https://doi.org/10.3390/universe9090410
APA StyleMathews, G. J., Kedia, A., Kim, H. I., & Suh, I.-S. (2023). Binary Neutron-Star Mergers with a Crossover Transition to Quark Matter. Universe, 9(9), 410. https://doi.org/10.3390/universe9090410







