A First Analysis of the Ensemble of Local Maxima of Maximal Center Gauge
Abstract
:1. Introduction
2. Methods and Formalism
2.1. The Problem of the Gauge Functional
2.2. The Importance of the Ensemble
3. Numerical Results and Discussion
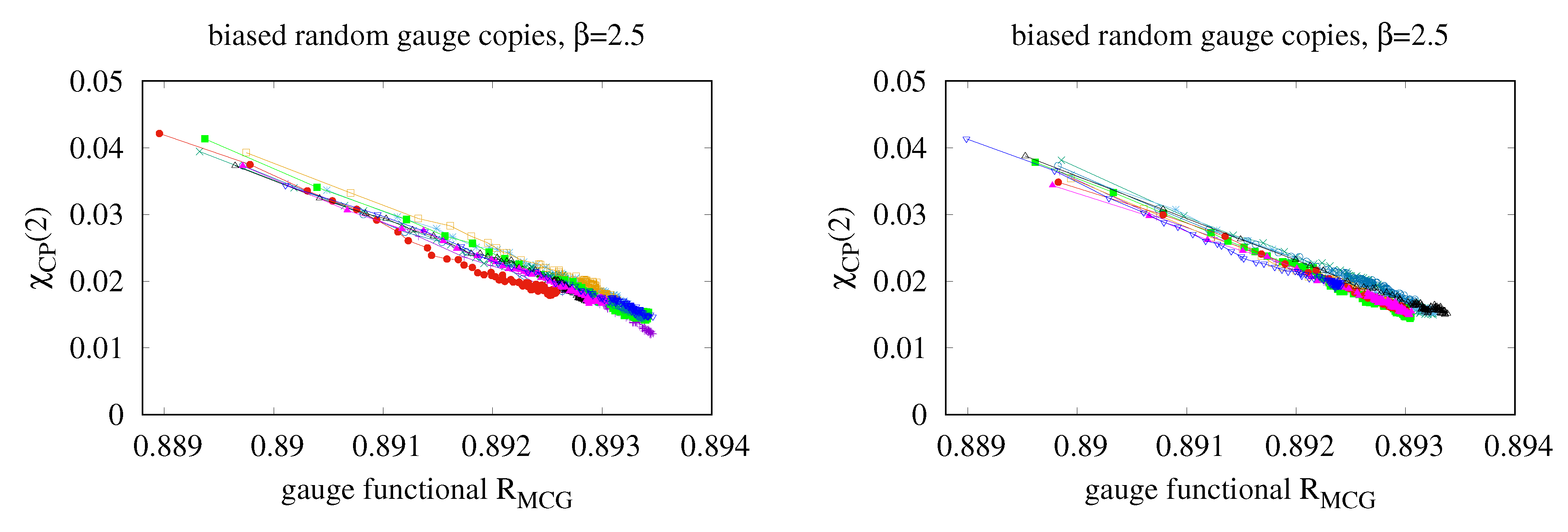
3.1. Gauge Functional Distributions and Creutz Ratios
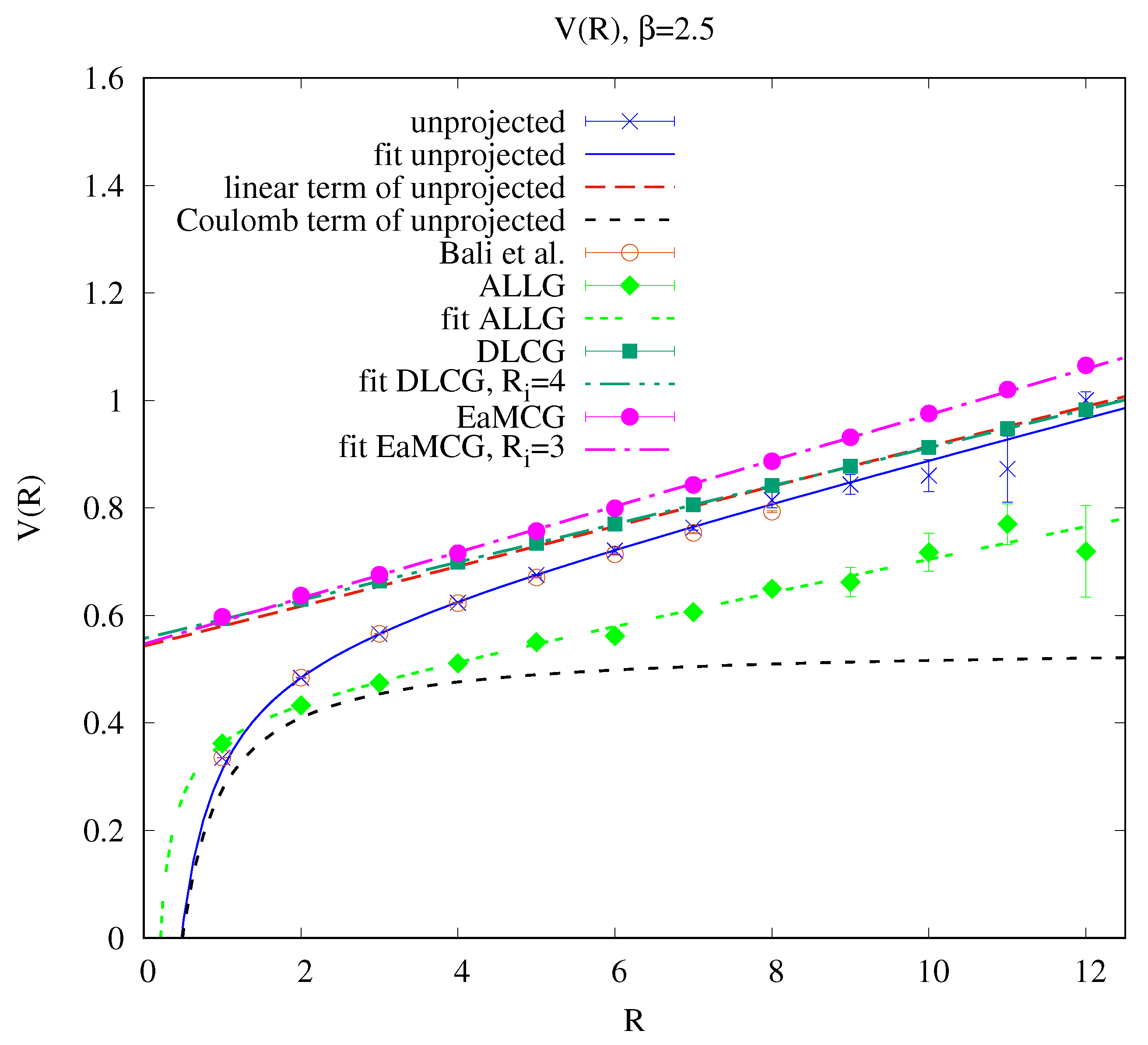
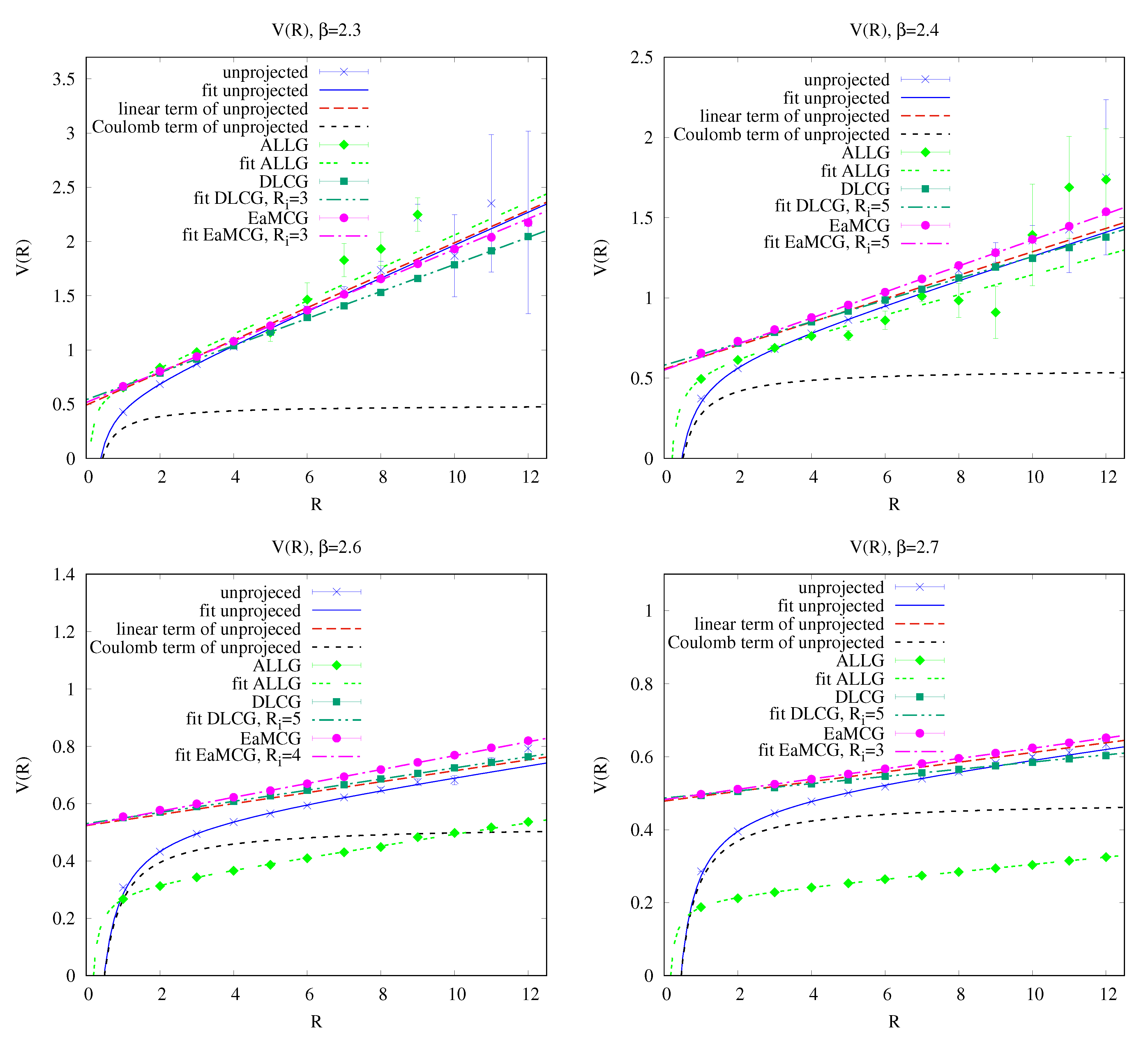
3.2. Center Dominance and Precocious Linearity
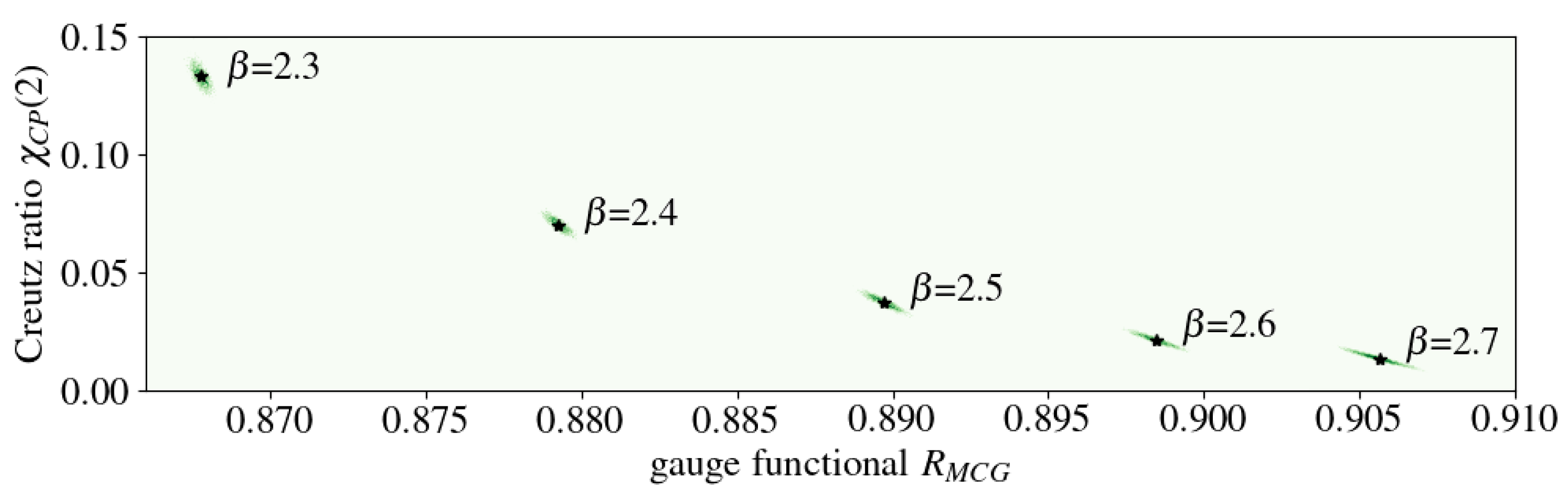
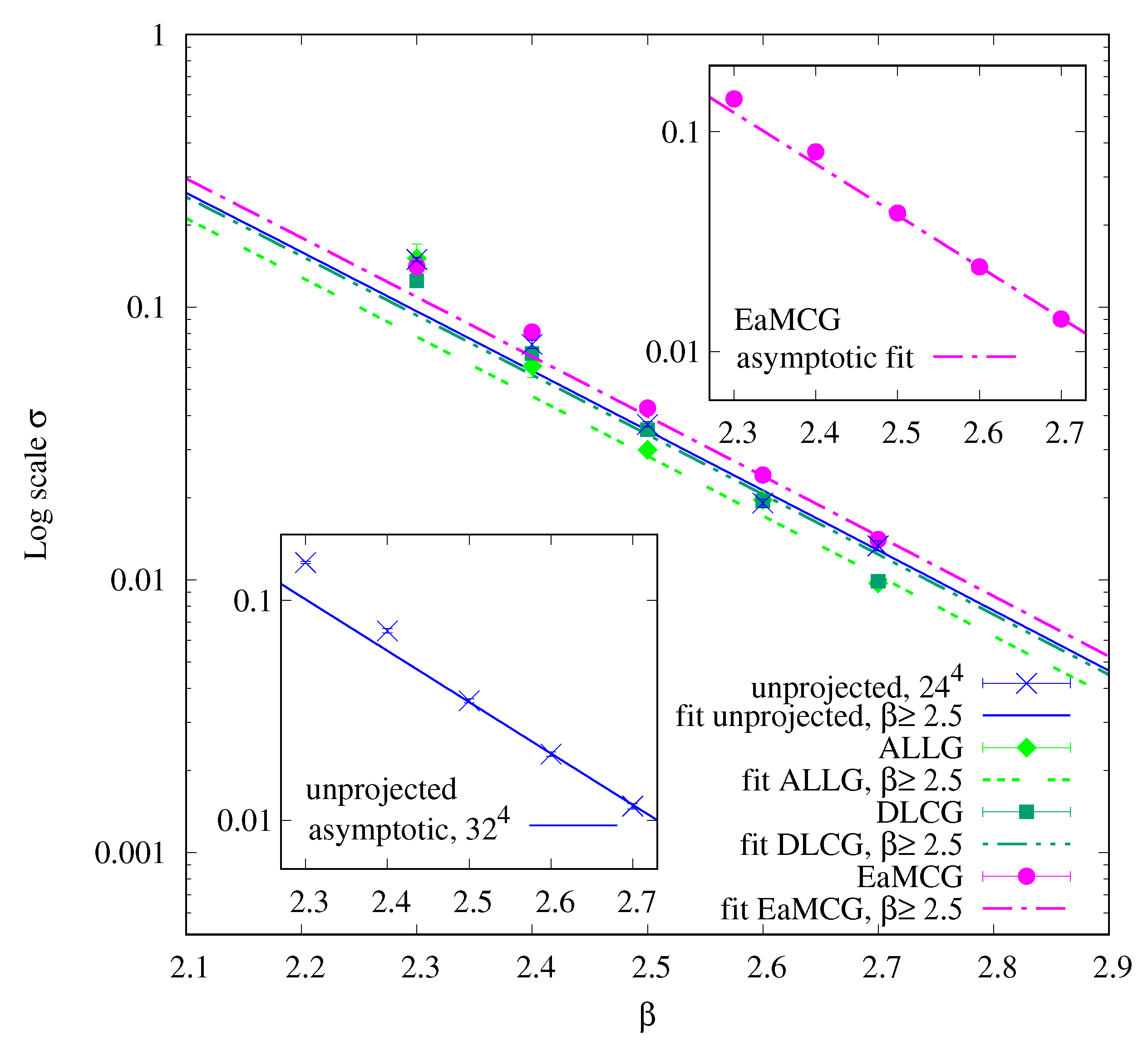
3.3. Scaling Behavior
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hooft, G. On the Phase Transition Towards Permanent Quark Confinement. Nucl. Phys. B 1978, 138, 1–25. [Google Scholar] [CrossRef]
- Hooft, G. A Property of Electric and Magnetic Flux in Nonabelian Gauge Theories. Nucl. Phys. B 1979, 153, 141–160. [Google Scholar] [CrossRef]
- Cornwall, J.M. Quark confinement and vortices in massive gauge-invariant QCD. Nucl. Phys. B 1979, 157, 392–412. [Google Scholar] [CrossRef]
- Debbio, L.D.; Faber, M.; Greensite, J.; Olejník, Š. Center dominance and Z(2) vortices in SU(2) lattice gauge theory. Phys. Rev. D 1997, 55, 2298–2306. [Google Scholar] [CrossRef]
- Faber, M.; Greensite, J.; Olejnik, S. Casimir scaling from center vortices: Towards an understanding of the adjoint string tension. Phys. Rev. D 1998, 57, 2603–2609. [Google Scholar] [CrossRef]
- Del Debbio, L.; Faber, M.; Giedt, J.; Greensite, J.; Olejnik, S. Detection of center vortices in the lattice Yang-Mills vacuum. Phys. Rev. D 1998, 58, 094501. [Google Scholar] [CrossRef]
- Bertle, R.; Faber, M.; Greensite, J.; Olejnik, S. The Structure of projected center vortices in lattice gauge theory. JHEP 1999, 03, 019. [Google Scholar] [CrossRef]
- Faber, M.; Greensite, J.; Olejnik, S.; Yamada, D. The Vortex finding property of maximal center (and other) gauges. JHEP 1999, 12, 012. [Google Scholar] [CrossRef]
- Engelhardt, M.; Reinhardt, H. Center projection vortices in continuum Yang-Mills theory. Nucl. Phys. B 2000, 567, 249. [Google Scholar] [CrossRef]
- Bertle, R.; Faber, M.; Greensite, J.; Olejnik, S. P vortices, gauge copies, and lattice size. JHEP 2000, 10, 007. [Google Scholar] [CrossRef]
- Greensite, J. The Confinement problem in lattice gauge theory. Prog. Part. Nucl. Phys. 2003, 51, 1. [Google Scholar] [CrossRef]
- Engelhardt, M.; Quandt, M.; Reinhardt, H. Center vortex model for the infrared sector of SU(3) Yang-Mills theory: Confinement and deconfinement. Nucl. Phys. B 2004, 685, 227–248. [Google Scholar] [CrossRef]
- Greensite, J. Confinement from Center Vortices: A review of old and new results. EPJ Web Conf. 2017, 137, 01009. [Google Scholar] [CrossRef]
- de Forcrand, P.; D’Elia, M. On the relevance of center vortices to QCD. Phys. Rev. Lett. 1999, 82, 4582–4585. [Google Scholar] [CrossRef]
- Alexandrou, C.; de Forcrand, P.; D’Elia, M. The Role of center vortices in QCD. Nucl. Phys. A 2000, 663, 1031–1034. [Google Scholar] [CrossRef]
- Reinhardt, H.; Engelhardt, M. Center vortices in continuum Yang-Mills theory. In Quark Confinement and the Hadron Spectrum IV; Lucha, W., Maung, K.M., Eds.; World Scientific: Singapore, 2002; pp. 150–162. [Google Scholar]
- Engelhardt, M. Center vortex model for the infrared sector of Yang-Mills theory: Quenched Dirac spectrum and chiral condensate. Nucl. Phys. B 2002, 638, 81–110. [Google Scholar] [CrossRef]
- VBornyakov, G.; Ilgenfritz, E.-M.; Martemyanov, B.V.; Morozov, S.M.; Müller-Preussker, M.; Veselov, A.I. Interrelation between monopoles, vortices, topological charge and chiral symmetry breaking: Analysis using overlap fermions for SU(2). Phys. Rev. D 2008, 77, 074507. [Google Scholar] [CrossRef]
- Höllwieser, R.; Faber, M.; Greensite, J.; Heller, U.M.; Olejník, Š. Center Vortices and the Dirac Spectrum. Phys. Rev. D 2008, 78, 054508. [Google Scholar] [CrossRef]
- Höllwieser, R.; Faber, M.; Heller, U.M. Intersections of thick Center Vortices, Dirac Eigenmodes and Fractional Topological Charge in SU(2) Lattice Gauge Theory. JHEP 2011, 06, 052. [Google Scholar] [CrossRef]
- Schweigler, T.; Höllwieser, R.; Faber, M.; Heller, U.M. Colorful SU(2) center vortices in the continuum and on the lattice. Phys. Rev. D 2013, 87, 054504. [Google Scholar] [CrossRef]
- Höllwieser, R.; Faber, M.; Heller, U.M. Critical analysis of topological charge determination in the background of center vortices in SU(2) lattice gauge theory. Phys. Rev. D 2012, 86, 014513. [Google Scholar] [CrossRef]
- Höllwieser, R.; Schweigler, T.; Faber, M.; Heller, U.M. Center Vortices and Chiral Symmetry Breaking in SU(2) Lattice Gauge Theory. Phys. Rev. D 2013, 88, 114505. [Google Scholar] [CrossRef]
- Höllwieser, R.; Faber, M.; Schweigler, T.; Heller, U.M. Chiral Symmetry Breaking from Center Vortices. arXiv 2014, arXiv:1410.2333. [Google Scholar]
- Höllwieser, R.; Engelhardt, M. Smearing Center Vortices. arXiv 2015, arXiv:1411.7097. [Google Scholar]
- Höllwieser, R.; Altarawneh, D.; Engelhardt, M. Random center vortex lines in continuous 3D space-time. AIP Conf. Proc. 2016, 1701, 030007. [Google Scholar] [CrossRef]
- Greensite, J.; Höllwieser, R. Double-winding Wilson loops and monopole confinement mechanisms. Phys. Rev. D 2015, 91, 054509. [Google Scholar] [CrossRef]
- Höllwieser, R.; Engelhardt, M. Approaching SU(2) gauge dynamics with smeared Z(2) vortices. Phys. Rev. D 2015, 92, 034502. [Google Scholar] [CrossRef]
- Trewartha, D.; Kamleh, W.; Leinweber, D. Evidence that centre vortices underpin dynamical chiral symmetry breaking in SU(3) gauge theory. Phys. Lett. B 2015, 747, 373–377. [Google Scholar] [CrossRef]
- Höllwieser, R.; Altarawneh, D. Center Vortices, Area Law and the Catenary Solution. Int. J. Mod. Phys. A 2015, 30, 1550207. [Google Scholar] [CrossRef]
- Altarawneh, D.; Höllwieser, R.; Engelhardt, M. Confining Bond Rearrangement in the Random Center Vortex Model. Phys. Rev. D 2016, 93, 054007. [Google Scholar] [CrossRef]
- Altarawneh, D.; Engelhardt, M.; Höllwieser, R. Model of random center vortex lines in continuous 2+1-dimensional spacetime. Phys. Rev. D 2016, 94, 114506. [Google Scholar] [CrossRef]
- Trewartha, D.; Kamleh, W.; Leinweber, D. Centre vortex removal restores chiral symmetry. J. Phys. G 2017, 44, 125002. [Google Scholar] [CrossRef]
- Faber, M.; Höllwieser, R. Chiral symmetry breaking on the lattice. Prog. Part. Nucl. Phys. 2017, 97, 312–355. [Google Scholar] [CrossRef]
- Biddle, J.C.; Kamleh, W.; Leinweber, D.B. Gluon propagator on a center-vortex background. Phys. Rev. D 2018, 98, 094504. [Google Scholar] [CrossRef]
- Langfeld, K.; Reinhardt, H.; Tennert, O. Confinement and scaling of the vortex vacuum of SU(2) lattice gauge theory. Phys. Lett. B 1998, 419, 317–321. [Google Scholar] [CrossRef]
- Langfeld, K. Vortex structures in pure SU(3) lattice gauge theory. Phys. Rev. D 2004, 69, 014503. [Google Scholar] [CrossRef]
- Golubich, R.; Faber, M. A Possible Resolution to Troubles of SU(2) Center Vortex Detection in Smooth Lattice Configurations. Universe 2021, 7, 122. [Google Scholar] [CrossRef]
- Golubich, R.; Faber, M. Properties of SU(2) Center Vortex Structure in Smooth Configurations. Particles 2021, 4, 93–105. [Google Scholar] [CrossRef]
- Golubich, R.; Faber, M. Center Regions as a Solution to the Gribov Problem of the Center Vortex Model. Acta Phys. Pol. B Proc. Suppl. 2021, 14, 87. [Google Scholar] [CrossRef]
- Golubich, R.; Faber, M. Thickness and Color Structure of Center Vortices in Gluonic SU(2) QCD. Particles 2020, 3, 444–455. [Google Scholar] [CrossRef]
- Golubich, R. The Road to Solving the Gribov Problem of the Center Vortex Model in Quantum Chromodynamics. Acta Phys. Pol. B Proc. Suppl. 2020. [Google Scholar] [CrossRef]
- Golubich, R.; Faber, M. Improving Center Vortex Detection by Usage of Center Regions as Guidance for the Direct Maximal Center Gauge. Particles 2019, 2, 491–498. [Google Scholar] [CrossRef]
- Golubich, R.C.F. Improvement of Vortex Detection in SU (2)-QCD. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2022. [Google Scholar] [CrossRef]
- Dehghan, Z.; Deldar, S.; Faber, M.; Golubich, R.; Höllwieser, R. Influence of Fermions on Vortices in SU(2)-QCD. Universe 2021, 7, 130. [Google Scholar] [CrossRef]
- Langfeld, K.; Engelhardt, M.; Reinhardt, H.; Tennert, O. Quantum gauge fixing and vortex dominance. Nucl. Phys. B Proc. Suppl. 2000, 83–84, 506–508. [Google Scholar] [CrossRef]
- Vink, J.C.; Wiese, U.J. Gauge fixing on the lattice without ambiguity. Phys. Lett. 1992, B289, 122–126. [Google Scholar] [CrossRef]
- de Forcrand, P.; Pepe, M. Center vortices and monopoles without lattice Gribov copies. Nucl. Phys. B 2001, 598, 557–577. [Google Scholar] [CrossRef]
- Faber, M.; Greensite, J.; Olejník, S. Direct Laplacian Center Gauge. J. High Energy Phys. 2001, 2001, 053. [Google Scholar] [CrossRef]
- Faber, M.; Greensite, J.; Olejník, Š. Center dominance recovered: Direct Laplacian center gauge. Nucl. Phys. B Proc. Suppl. 2002, 106–107, 652–654. [Google Scholar] [CrossRef]
- Kovacs, T.G.; Tomboulis, E.T. Vortices and confinement at weak coupling. Phys. Rev. D 1998, 57, 4054–4062. [Google Scholar] [CrossRef]
- Bornyakov, V.; Komarov, D.; Polikarpov, M. P-vortices and drama of Gribov copies. Phys. Lett. B 2001, 497, 151–158. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A Note on the Generation of Random Normal Deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Bali, G.S.; Schilling, K.; Schlichter, C. Observing long color flux tubes in SU(2) lattice gauge theory. Phys. Rev. D 1995, 51, 5165. [Google Scholar] [CrossRef] [PubMed]
- Rothe, H. Lattice Gauge Theories: An Introduction, 3rd ed.; World Scientific Lecture Notes In Physics; World Scientific Publishing Company: Singapore, 2005. [Google Scholar]
- Heinzl, T.; Ilderton, A.; Langfeld, K.; Lavelle, M.; McMullan, D. The Ice-limit of Coulomb gauge Yang-Mills theory. Phys. Rev. D 2008, 78, 074511. [Google Scholar] [CrossRef]
- Höllwieser, R.; Knechtli, F.; Korzec, T.; Peardon, M.; Urrea-Niño, J.A. Constructing static quark-anti-quark creation operators from Laplacian eigenmodes. arXiv 2022. [Google Scholar] [CrossRef]
- Höllwieser, R.; Knechtli, F.; Peardon, M. The static energy of a quark-antiquark pair from Laplacian eigenmodes. In Proceedings of the 39th International Symposium on Lattice Field Theory, Bonn, Germany, 8–13 August 2022. [Google Scholar]
- Höllwieser, R.; Knechtli, F.; Peardon, M. The static potential using trial states from Laplacian eigenmodes. EPJ Web Conf. 2022, 274, 02008. [Google Scholar] [CrossRef]
| Method | c | ||
|---|---|---|---|
| unprojected, | |||
| unprojected, , fix c | |||
| unprojected, | |||
| , ALLG | |||
| , DLCG | − | ||
| , EaMCG | − | ||
| unprojected, | |||
| unprojected, , fix c | |||
| unprojected, | |||
| , ALLG | |||
| , DLCG | − | ||
| , EaMCG | − | ||
| unprojected, | |||
| unprojected, , fix c | |||
| unprojected, | |||
| , ALLG | |||
| , DLCG | − | ||
| , EaMCG | − | ||
| unprojected, | |||
| unprojected, , fix c | |||
| unprojected, | |||
| , ALLG | |||
| , DLCG | − | ||
| , EaMCG | − | ||
| unprojected, | |||
| unprojected, , fix c | |||
| unprojected, | |||
| , ALLG | |||
| , DLCG | − | ||
| , EaMCG | − | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghan, Z.; Golubich, R.; Höllwieser, R.; Faber, M. A First Analysis of the Ensemble of Local Maxima of Maximal Center Gauge. Universe 2023, 9, 389. https://doi.org/10.3390/universe9090389
Dehghan Z, Golubich R, Höllwieser R, Faber M. A First Analysis of the Ensemble of Local Maxima of Maximal Center Gauge. Universe. 2023; 9(9):389. https://doi.org/10.3390/universe9090389
Chicago/Turabian StyleDehghan, Zeinab, Rudolf Golubich, Roman Höllwieser, and Manfried Faber. 2023. "A First Analysis of the Ensemble of Local Maxima of Maximal Center Gauge" Universe 9, no. 9: 389. https://doi.org/10.3390/universe9090389
APA StyleDehghan, Z., Golubich, R., Höllwieser, R., & Faber, M. (2023). A First Analysis of the Ensemble of Local Maxima of Maximal Center Gauge. Universe, 9(9), 389. https://doi.org/10.3390/universe9090389







