Confronting Strange Stars with Compact-Star Observations and New Physics
Abstract
1. Introduction
2. EOS of SQM
3. SSs without the Consideration of the New Physics
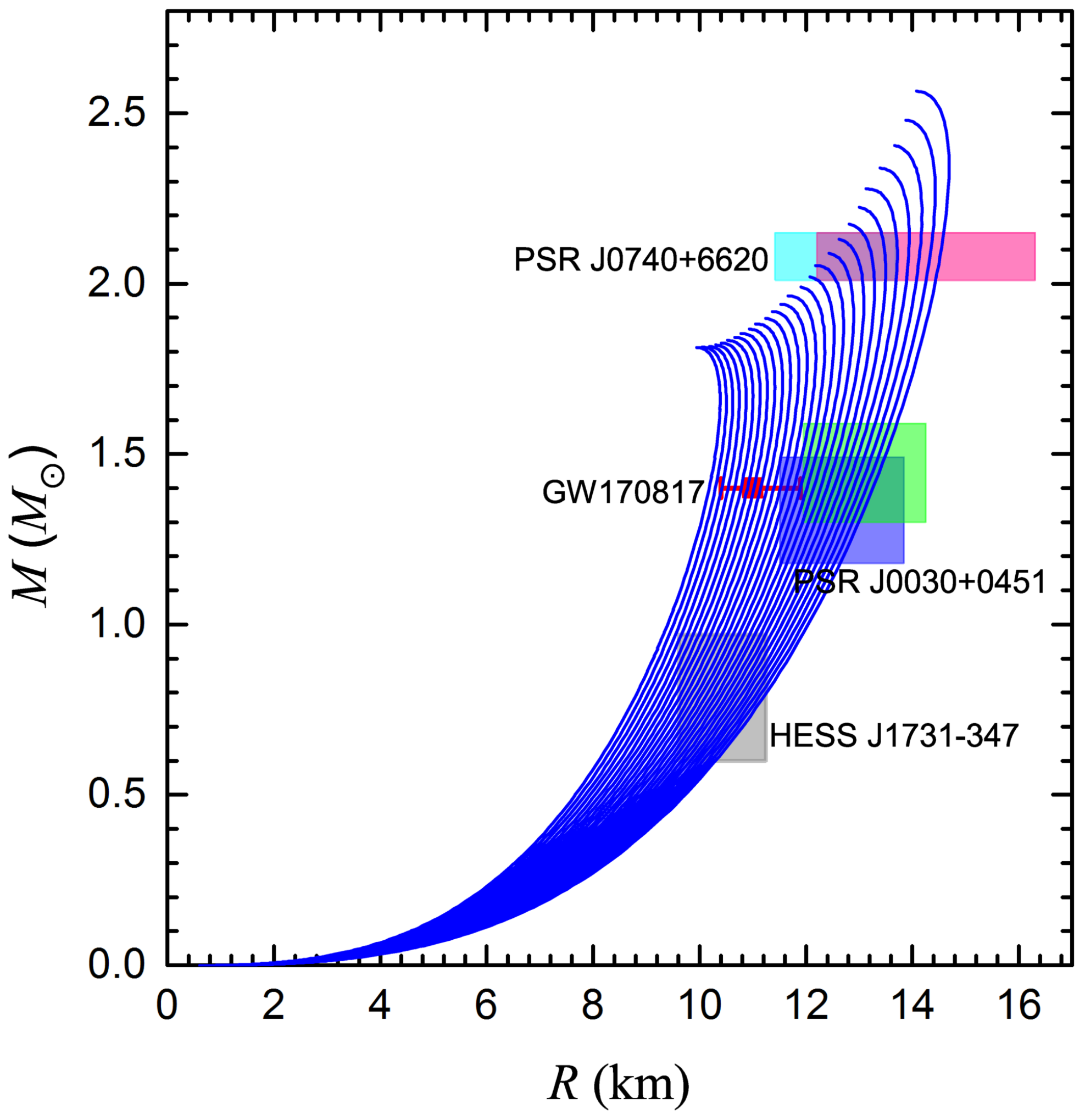
3.1. The Global Properties of SSs
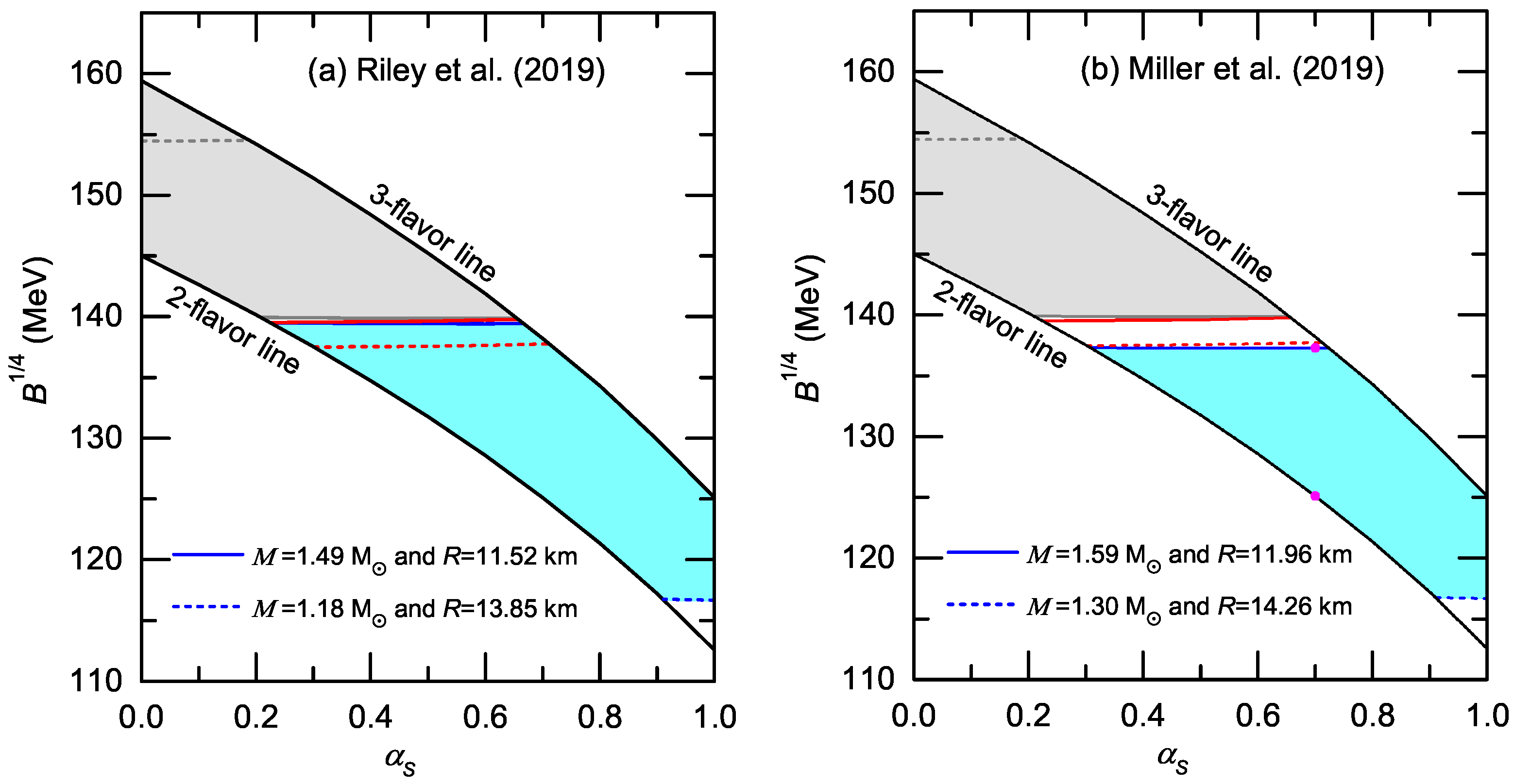
3.2. Parameter Space of SQM
4. SSs in the Framework of Non-Newtonian Gravity
4.1. EOS of SQM in the Framework of Non-Newtonian Gravity
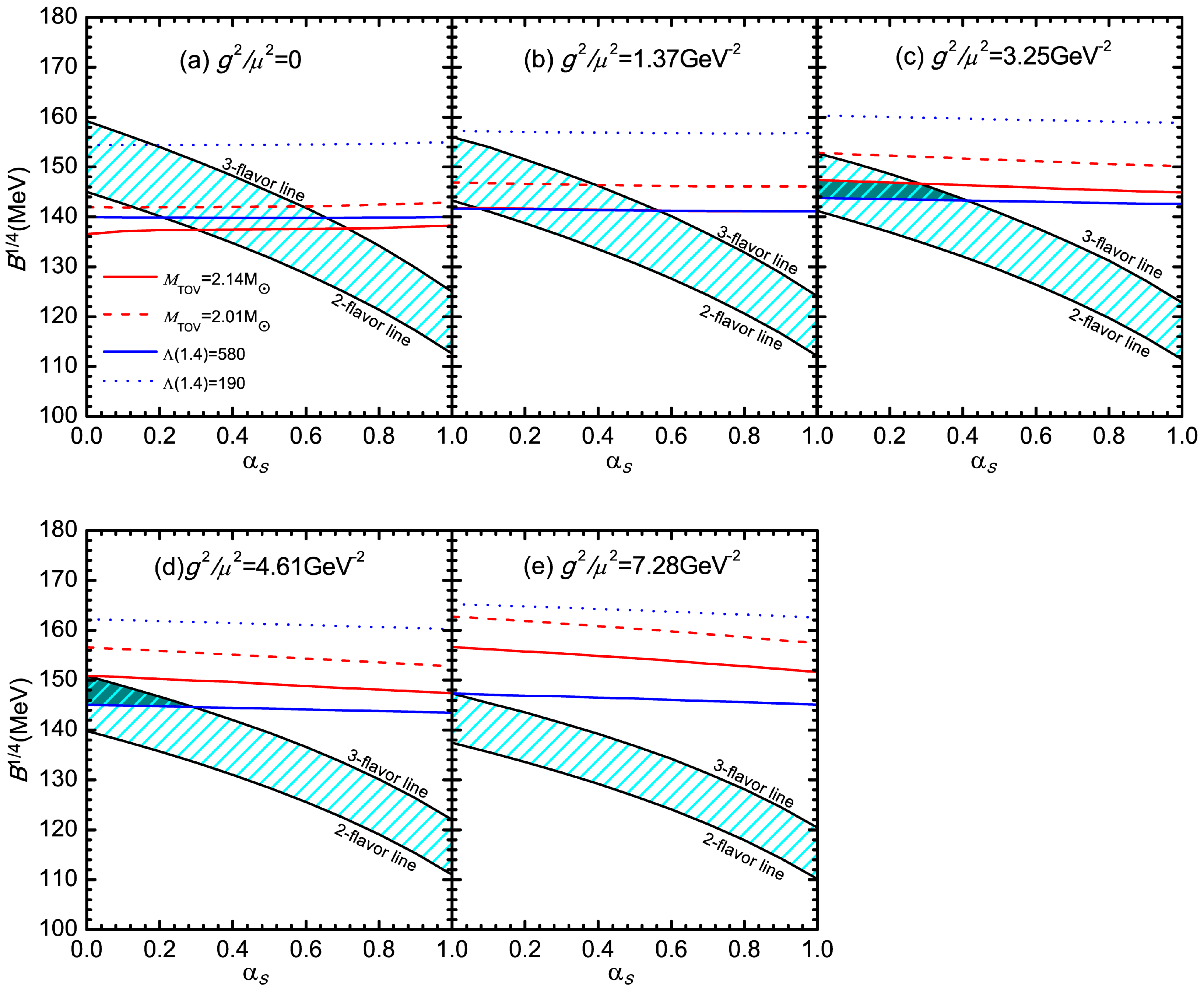
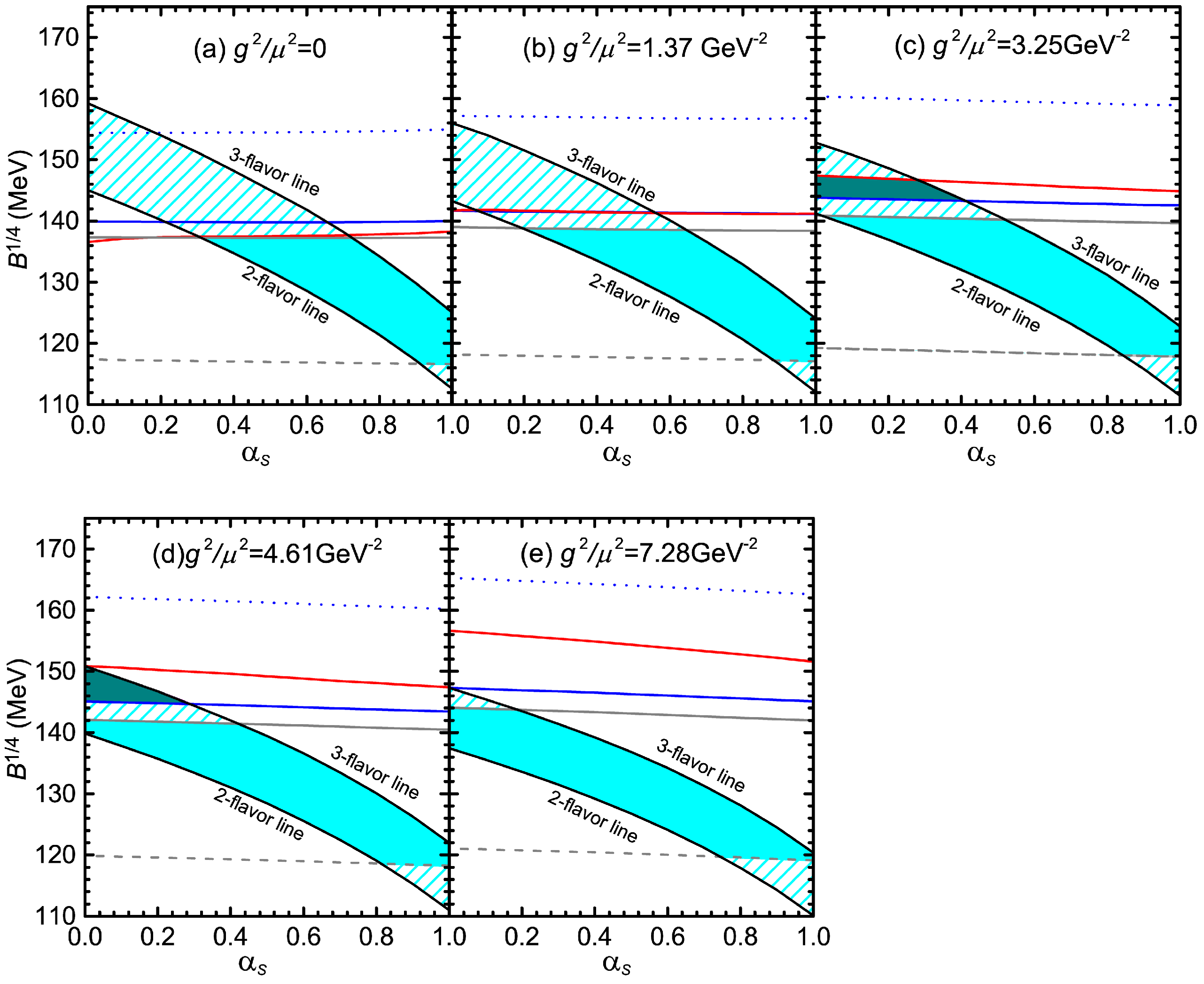
4.2. The Allowed Parameter Space of SQM in the Framework of Non-Newtonian Gravity
5. SSs with a Mirror-Dark-Matter Core
5.1. EOS of MDM
5.2. The Properties of SSs with an MDM Core
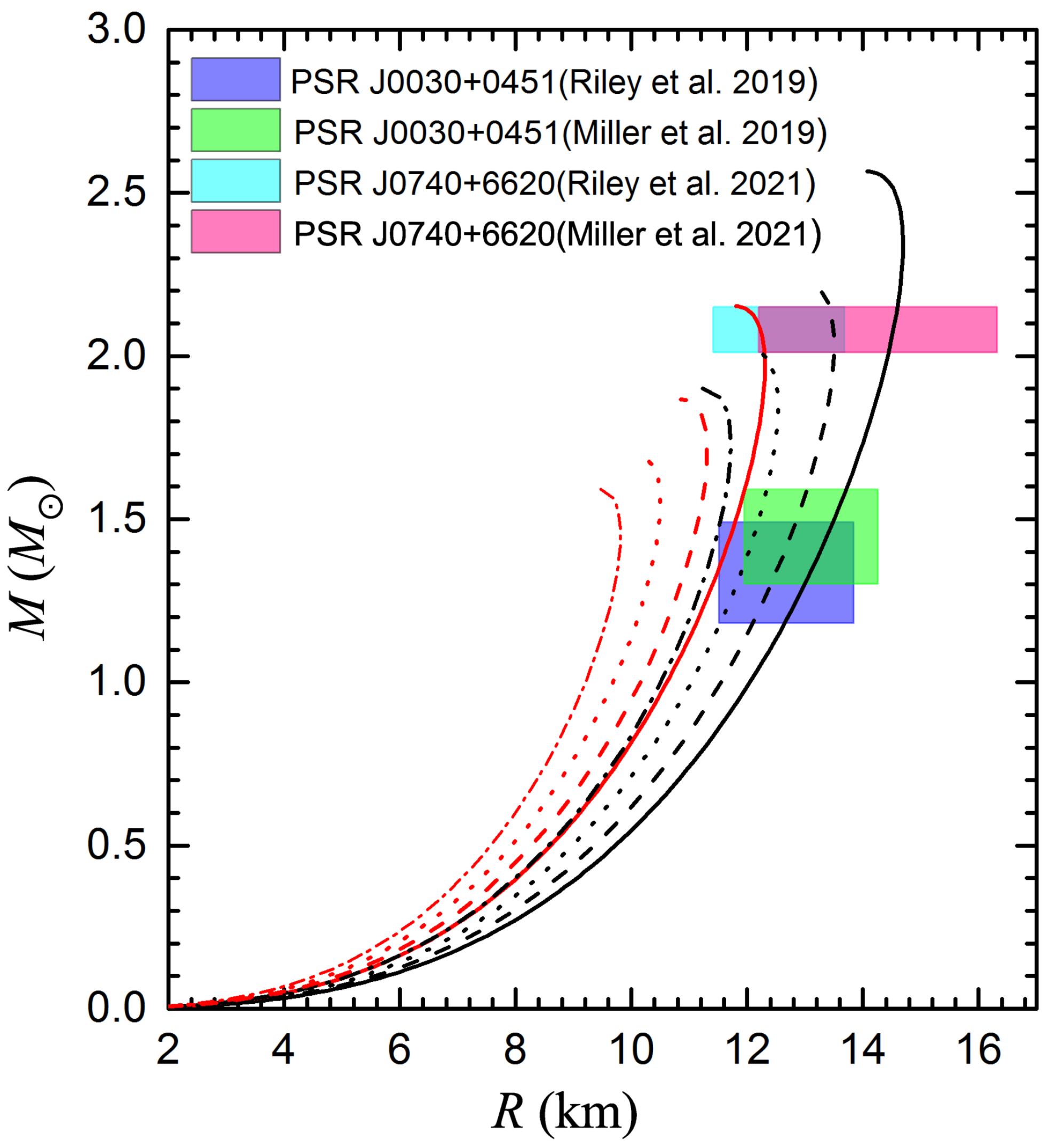

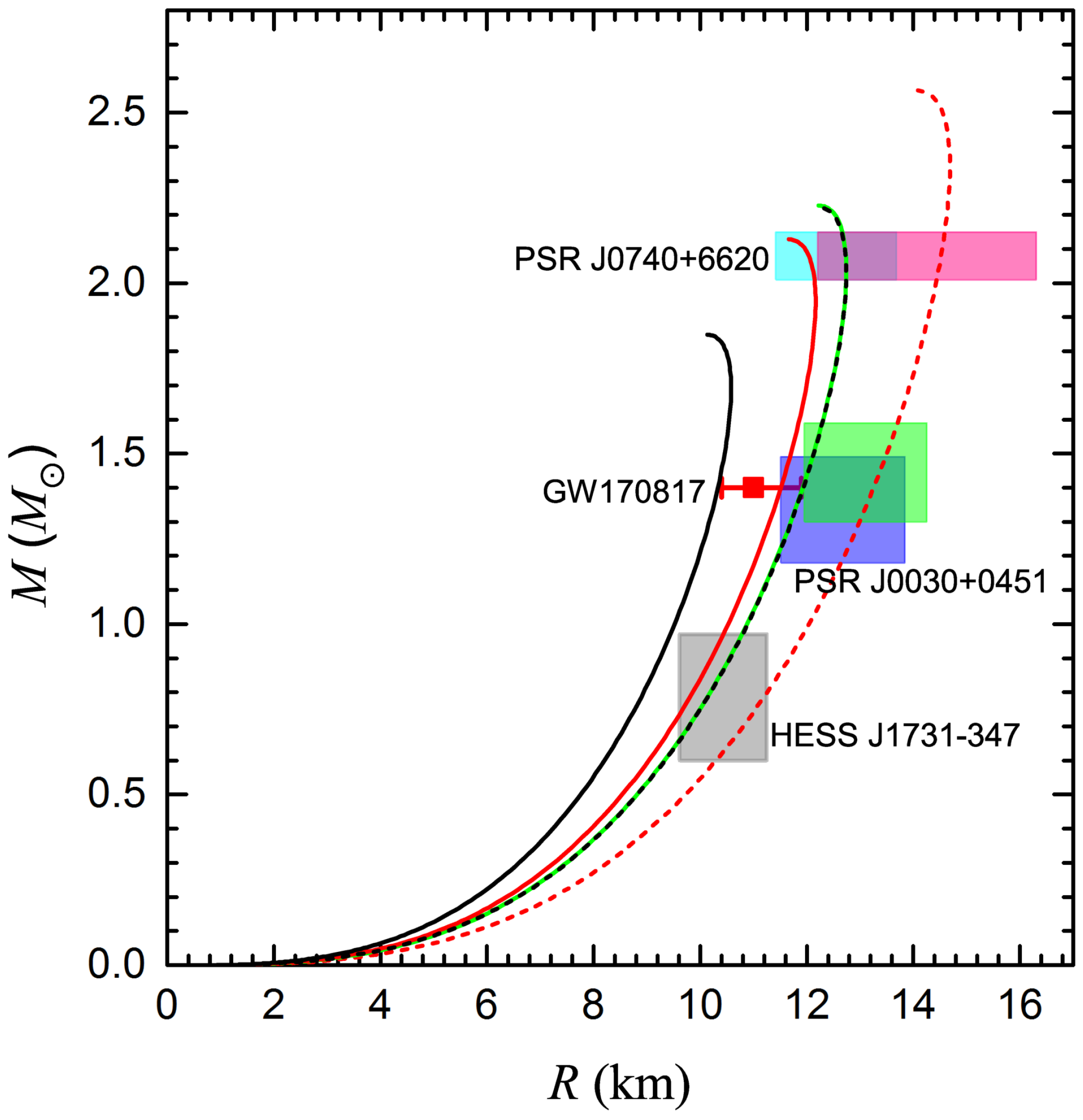
5.3. The Allowed Parameter Space of SQM for SSs with an MDM Core
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DM | dark matter |
| EOS | equation of state |
| eXTP | enhanced X-ray timing and polarimetry mission |
| GR | general relativity |
| LIGO | laser interferometer gravitational wave observatory |
| MDM | mirror dark matter |
| MIT | Massachusetts Institute of Technology |
| NICER | Neutron star Interior Composition Explorer |
| NS | neutron star |
| SM | Standard Model |
| SQM | strange quark matter |
| SS | strange star |
| STROBE-X | Spectroscopic Time-Resolving Observatory for Broadband Energy X-rays |
| SKA | Square Kilometre Array observatory |
| TOV | Tolman–Oppenheimer–Volkoff |
| Virgo | Virgo interferometer |
| 1 | For the standard MIT model, this is true considering the constraints from the observations of PSR J0740+6620 and GW170817, which are mentioned in the previous paragraph. However, if the observation data of PSR J0030+0451 are also considered, SSs will be ruled out even if we consider the effects of non-Newtonian gravity [62]. The details can be seen in Section 4.2 of this review. |
| 2 | |
| 3 | |
| 4 | |
| 5 | in the weak-field limit, a Yukawa term also appears in alternative theories of gravity such as f(R), the nonsymmetric gravitational theory, and modified gravity [6]. |
| 6 | Scalar bosons lead to a softer EOS of dense matter, while vector bosons make the EOS stiffer [71]. In the following section of this review, we will focus on vector bosons. This is necessary because a stiff EOS is needed to explain the large mass of PSR J0740+6620, with g being the boson–baryon coupling constant and being the baryon mass. |
| 7 |
References
- Mann, A. The golden age of neutron-star physics has arrived. Nature 2020, 579, 20–22. [Google Scholar] [CrossRef] [PubMed]
- Özel, F.; Freire, P. Masses, radii, and the equation of state of neutron stars. Annu. Rev. Astron. Astrophys. 2016, 88, 401–440. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Star Mass and Radius Measurements. Universe 2019, 5, 159. [Google Scholar] [CrossRef]
- Raithel, C.A. Constraints on the Neutron Star Equation of State from GW170817. Eur. Phys. J. A 2019, 55, 80. [Google Scholar] [CrossRef]
- Li, B.-A.; Krastev, P.G.; Wen, D.-H.; Zhang, N.-B. Towards understanding astrophysical effects of nuclear symmetry energy. Eur. Phys. J. A 2019, 55, 117. [Google Scholar] [CrossRef]
- Orsaria, M.G.; Malfatti, G.; Mariani, M.; Ranea-Sandoval, I.F.; Garcá, F.; Spinella, W.M.; Contrera, G.A.; Lugones, G.; Weber, F. Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G: Nucl. Part. Phys. 2019, 46, 073002. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Li, A.; Zhu, Z.-Y.; Zhou, E.-P.; Dong, J.-M.; Hu, J.-N.; Xia, C.-J. Neutron star equation of state: Quark mean-field (QMF) modeling and applications. J. High Energy Astrophys. 2020, 28, 19. [Google Scholar] [CrossRef]
- Burgio, G.F.; Vidaña, I. The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe 2020, 6, 119. [Google Scholar] [CrossRef]
- Chatziioannou, K. Neutron-star tidal deformability and equation-of-state constraints. Gen. Rel. Grav. 2020, 52, 109. [Google Scholar] [CrossRef]
- Lattimer, J.M. Neutron Stars and the Nuclear Matter Equation of State. Annu. Rev. Nucl. Part. Sci. 2021, 71, 433–464. [Google Scholar] [CrossRef]
- Li, B.-A.; Cai, B.-J.; Xie, W.-J.; Zhang, N.-B. Progress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables Since GW170817. Universe 2021, 7, 182. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange matter. Phys. Rev. D 1984, 30, 2379–2390. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaefer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Alcock, C.; Farhi, E.; Olinto, A. Strange Stars. Astrophys. J. 1986, 310, 261. [Google Scholar] [CrossRef]
- Alcock, C.; Olinto, A. Exotic phases of hadronic matter and their astrophysical application. Annu. Rev. Nucl. Part. Sci. 1988, 38, 161–184. [Google Scholar] [CrossRef]
- Madsen, J. Physics and Astrophysics of Strange Quark Matter. Lect. Notes Phys. 1999, 516, 162–203. [Google Scholar]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. J. Phys. Soc. Jpn. 1989, 58, 3555–3563. [Google Scholar] [CrossRef]
- Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. II. J. Phys. Soc. Jpn. 1989, 58, 4388–4393. [Google Scholar] [CrossRef]
- Glendenning, N.K. Fast Pulsars, Strange Stars:. An Opportunity in Radio Astronomy. Mod. Phys. Lett. A 1990, 5, 2197–2207. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Friedman, J.L. Evidence against a strange ground state for baryons. Phys. Lett. B 1991, 264, 143–148. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Bombaci, I.; Logoteta, D.; Thampan, A.V. Fast spinning strange stars: Possible ways to constrain interacting quark matter parameters. Mon. Not. R. Astron. Soc. 2016, 457, 3101–3114. [Google Scholar] [CrossRef]
- Di Clemente, F.; Drago, A.; Pagliara, G. Is the compact object associated with HESS J1731-347 a strange quark star? arXiv 2022, arXiv:2211.07485. [Google Scholar]
- Horvath, J.E.; Rocha, L.S.; de Sá, L.M.; Moraes, P.H.R.S.; Barão, L.G.; de Avellar, M.G.B.; Bernardo, A.; Bachega, R.R.A. A light strange star in the remnant HESS J1731-347: Minimal consistency checks. arXiv 2023, arXiv:2303.10264. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star within a supernova remnant. Nat. Astron. 2022, 6, 1444–1451. [Google Scholar] [CrossRef]
- Suwa, Y.; Yoshida, T.; Shibata, M.; Umeda, H.; Takahashi, K. On the minimum mass of neutron stars. Mon. Not. Roy. Astron. Soc. 2018, 481, 3305–3312. [Google Scholar] [CrossRef]
- Li, X.-D.; Bombaci, I.; Dey, M.; Dey, J.; van den Heuvel, E.P.J. Is SAX J1808.4-3658 a Strange Star? Phys. Rev. Lett. 1999, 83, 3776–3779. [Google Scholar] [CrossRef]
- Li, X.-D.; Ray, S.; Dey, J.; Dey, M.; Bombaci, I. On the Nature of the Compact Star in 4U 1728-34. Astrophys. J. 1999, 527, L51–L54. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.J.; Marshall, H.L.; Dreizler, S.; Freeman, P.E.; Fruscione, A.; Juda, M.; Kashyap, V.; Nicastro, F.; Pease, D.O.; Wargelin, B.J.; et al. Is RX J1856.5-3754 a Quark Star? Astrophys. J. 2002, 572, 996–1001. [Google Scholar] [CrossRef]
- Burwitz, V.; Haberl, F.; Neuhäuser, R.; Predehl, P.; Trümper, J.; Zavlin, V.E. The thermal radiation of the isolated neutron star RX J1856.5-3754 observed with Chandra and XMM-Newton. Astron. Astrophy. 2003, 399, 1109–1114. [Google Scholar] [CrossRef]
- Li, Z.; Qu, Z.; Chen, L.; Guo, Y.; Qu, J.; Xu, R. An Ultra-low-mass and Small-radius Compact Object in 4U 1746-37? Astrophys. J. 2015, 798, 56. [Google Scholar] [CrossRef]
- Yue, Y.L.; Cui, X.H.; Xu, R.X. Is PSR B0943+10 a Low-Mass Quark Star? Astrophys. J. 2006, 649, L95–L98. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: New York, NY, USA, 2000; pp. 337–362. [Google Scholar]
- Blaschke, D.; Chamel, N. Phases of Dense Matter in Compact Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2018; pp. 337–400. [Google Scholar]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Bombaci, I.; Drago, A.; Frontera, F.; Lavagno, A. Gamma-Ray Bursts from Delayed Collapse of Neutron Stars to Quark Matter Stars. Astrophys. J. 2003, 586, 1250–1253. [Google Scholar] [CrossRef]
- Bombaci, I.; Parenti, I.; Vidaña, I. Quark Deconfinement and Implications for the Radius and the Limiting Mass of Compact Stars. Astrophys. J. 2004, 614, 314–325. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G. The Supernova-GRB connection. Eur. Phys. J. A 2004, 19, 197–201. [Google Scholar] [CrossRef]
- Bombaci, I.; Drago, A.; Logoteta, D.; Pagliara, G.; Vidaña, I. Was GW190814 a Black Hole-Strange Quark Star System? Phys. Rev. Lett. 2021, 126, 162702. [Google Scholar] [CrossRef] [PubMed]
- Bombaci, I. The Equation of State of Neutron Star Matter. In Millisecond Pulsars; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2022; pp. 281–317. [Google Scholar]
- Xu, R.X. Solid Quark Stars? Astrophys. J. Lett. 2003, 596, L59. [Google Scholar] [CrossRef]
- Miao, Z.-Q.; Xia, C.-J.; Lai, X.-Y.; Maruyama, T.; Xu, R.-X.; Zhou, E.-P. A bag model of matter condensed by the strong interaction. Int. J. Mod. Phys. E 2022, 31, 2250037. [Google Scholar] [CrossRef]
- Lai, X.; Xia, C.; Xu, R. Bulk strong matter: The trinity. Adv. Phys. X 2023, 8, 2137433. [Google Scholar] [CrossRef]
- Holdom, B.; Ren, J.; Zhang, C. Quark Matter May Not Be Strange. Phys. Rev. Lett. 2018, 120, 222001. [Google Scholar] [CrossRef]
- Zhao, T.; Zheng, W.; Wang, F.; Li, C.-M.; Yan, Y.; Huang, Y.-F.; Zong, H.-S. Do current astronomical observations exclude the existence of nonstrange quark stars? Phys. Rev. D 2019, 100, 043018. [Google Scholar] [CrossRef]
- Zhang, C. Probing up-down quark matter via gravitational waves. Phys. Rev. D 2020, 101, 043003. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, L.-W.; Chu, P.-C.; Zhou, Y. GW190814: Circumstantial evidence for up-down quark star. Phys. Rev. D 2022, 106, 083007. [Google Scholar] [CrossRef]
- Weissenborn, S.; Sagert, I.; Pagliara, G.; Hempel, M.; Schaffner-Bielich, J. Quark matter in massive compact stars. Astrophys. J. Lett. 2011, 740, L14. [Google Scholar] [CrossRef]
- Wei, W.; Zheng, X.-P. Quark stars with the density-dependent quark mass model. Astropart. Phys. 2012, 37, 1–4. [Google Scholar] [CrossRef]
- Pi, C.-M.; Yang, S.-H.; Zheng, X.-P. R-mode instability of strange stars and observations of neutron stars in LMXBs. Res. Astron. Astrophys. 2015, 15, 871–878. [Google Scholar] [CrossRef]
- Zhou, E.-P.; Zhou, X.; Li, A. Constraints on interquark interaction parameters with GW170817 in a binary strange star scenario. Phys. Rev. D 2018, 97, 083015. [Google Scholar] [CrossRef]
- Yang, S.-H.; Pi, C.-M.; Zheng, X.-P.; Weber, F. Non-Newtonian Gravity in Strange Quark Stars and Constraints from the Observations of PSR J0740+6620 and GW170817. Astrophys. J. 2020, 902, 32. [Google Scholar] [CrossRef]
- Yang, S.-H.; Pi, C.-M.; Zheng, X.-P. Strange stars with a mirror-dark-matter core confronting with the observations of compact stars. Phys. Rev. D 2021, 104, 083016. [Google Scholar] [CrossRef]
- Yang, S.-H.; Pi, C.-M.; Zheng, X.-P.; Weber, F. Constraints from compact star observations on non-Newtonian gravity in strange stars based on a density dependent quark mass model. Phys. Rev. D 2021, 103, 043012. [Google Scholar] [CrossRef]
- Cai, W.-H.; Wang, Q.-W. Strange quark star and the parameter space of the quasi-particle model. Commun. Theor. Phys. 2021, 73, 105202. [Google Scholar] [CrossRef]
- Backes, B.C.; Hafemann, E.; Marzola, I.; Menezes, D.P. Density-dependent quark mass model revisited: Thermodynamic consistency, stability windows and stellar properties. J. Phys. G: Nucl. Part. Phys. 2021, 48, 055104. [Google Scholar] [CrossRef]
- Pi, C.-M.; Yang, S.-H. Non-Newtonian gravity in strange stars and constraints from the observations of compact stars. New Astron. 2022, 90, 101670. [Google Scholar] [CrossRef]
- Pi, C.-M.; Yang, S.-H. Strange stars confronting with the observations: Non-Newtonian gravity effects, or the existence of a dark-matter core. Astron. Nachr. 2023, e20220083. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2018; pp. 737–806. [Google Scholar]
- Krivoruchenko, M.I.; Šimkovic, F.; Faessler, A. Constraints for weakly interacting light bosons from existence of massive neutron stars. Phys. Rev. D 2009, 79, 125023. [Google Scholar] [CrossRef]
- Wen, D.-H.; Li, B.-A.; Chen, L.W. Supersoft symmetry energy encountering non-Newtonian gravity in neutron stars. Phys. Rev. Lett. 2009, 103, 211102. [Google Scholar] [CrossRef]
- Cooney, A.; Dedeo, S.; Psaltis, D. Neutron stars in f(R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Arapoǧlu, S.; Deliduman, C.; Ekşi, K.Y. Constraints on perturbative f(R) gravity via neutron stars. J. Cosmol. Astropart. Phys. 2011, 07, 020. [Google Scholar] [CrossRef]
- Pani, P.; Cardoso, V.; Delsate, T. Compact Stars in Eddington Inspired Gravity. Phys. Rev. Lett 2011, 107, 031101. [Google Scholar] [CrossRef] [PubMed]
- Pani, P.; Berti, E.; Cardoso, V.; Read, J. Compact stars in alternative theories of gravity: Einstein-Dilaton-Gauss-Bonnet gravity. Phys. Rev. D 2011, 84, 104035. [Google Scholar] [CrossRef]
- Rahaman, F.; Sharma, R.; Ray, S.; Maulick, R.; Karar, I. Strange stars in Krori-Barua space-time. Eur. Phys. J. C 2012, 72, 2071. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K.; Sushkov, S.V. Structure of neutron, quark, and exotic stars in Eddington-inspired Born-Infeld gravity. Phys. Rev. D 2013, 88, 044032. [Google Scholar] [CrossRef]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. Slowly rotating neutron and strange stars in R2 gravity. J. Cosmol. Astropart. Phys. 2014, 10, 6. [Google Scholar] [CrossRef]
- Sham, Y.-H.; Lin, L.-M.; Leung, P.T. Testing Universal Relations of Neutron Stars with a Nonlinear Matter-Gravity Coupling Theory. Astrophys. J. 2014, 781, 66. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Arbañil, J.D.V.; Malheiro, M. Stellar equilibrium configurations of compact stars in f(R, T) theory of gravity. J. Cosmol. Astropart. Phys. 2016, 6, 5. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate universal relations for neutron stars and quark stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Yazadjiev, S.S.; Doneva, D.D.; Kokkotas, K.D. Tidal Love numbers of neutron stars in f(R) gravity. Eur. Phys. J. C 2018, 78, 818. [Google Scholar] [CrossRef]
- Lopes, I.; Panotopoulos, G. Dark matter admixed strange quark stars in the Starobinsky model. Phys. Rev. D 2018, 97, 024030. [Google Scholar] [CrossRef]
- Deb, D.; Ketov, S.V.; Khlopov, M.; Ray, S. Study on charged strange stars in f(R, T) gravity. J. Cosmol. Astropart. Phys. 2019, 10, 070. [Google Scholar] [CrossRef]
- Salako, I.G.; Khlopov, M.; Ray, S.; Arouko, M.Z.; Saha, P.; Debnath, U. Study on Anisotropic Strange Stars in f(T, T) Gravity. Universe 2020, 6, 167. [Google Scholar] [CrossRef]
- Majid, A.; Sharif, M. Quark Stars in Massive Brans-Dicke Gravity with Tolman-Kuchowicz Spacetime. Universe 2020, 6, 124. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended gravity description for the GW190814 supermassive neutron star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Danchev, V.I.; Doneva, D.D. Constraining the equation of state in modified gravity via universal relations. Phys. Rev. D 2021, 103, 024049. [Google Scholar] [CrossRef]
- Saffer, A.; Yagi, K. Tidal deformabilities of neutron stars in scalar-Gauss-Bonnet gravity and their applications to multimessenger tests of gravity. Phys. Rev. D 2021, 104, 124052. [Google Scholar] [CrossRef]
- Banerjee, A.; Tangphati, T.; Channuie, P. Strange Quark Stars in 4D Einstein-Gauss-Bonnet Gravity. Astrophys. J. 2021, 909, 14. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Maximum baryon masses for static neutron stars in f(R) gravity. Europhys. Lett. 2021, 136, 59001. [Google Scholar] [CrossRef]
- Prasetyo, I.; Maulana, H.; Ramadhan, H.S.; Sulaksono, A. 2.6 M⊙ compact object and neutron stars in Eddington-inspired Born-Infeld theory of gravity. Phys. Rev. D 2021, 104, 084029. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Tangphati, T.; Banerjee, A.; Jasim, M.K. Anisotropic quark stars in R2 gravity. Phys. Lett. B 2021, 817, 136330. [Google Scholar] [CrossRef]
- Xu, R.; Gao, Y.; Shao, L. Neutron stars in massive scalar-Gauss-Bonnet gravity: Spherical structure and time-independent perturbations. Phys. Rev. D 2022, 105, 024003. [Google Scholar] [CrossRef]
- Tangphati, T.; Hansraj, S.; Banerjee, A.; Pradhan, A. Quark stars in f(R, T) gravity with an interacting quark equation of state. Phys. Dark Universe 2022, 35, 100990. [Google Scholar] [CrossRef]
- Lin, R.-H.; Chen, X.-N.; Zhai, X.-H. Realistic neutron star models in f(T) gravity. Eur. Phys. J. C 2022, 82, 308. [Google Scholar] [CrossRef]
- Jiménez, J.C.; Pretel, J.M.Z.; Fraga, E.S.; Jorás, S.E.; Reis, R.R.R. R2-gravity quark stars from perturbative QCD. J. Cosmol. Astropart. Phys. 2022, 7, 17. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Arbañil, J.D.V.; Duarte, S.B.; Jorś, S.E.; Reis, R.R.R. Charged quark stars in metric f(R) gravity. J. Cosmol. Astropart. Phys. 2022, 9, 58. [Google Scholar] [CrossRef]
- Shao, L.; Yagi, K. Neutron stars as extreme laboratories for gravity tests. Sci. Bull. 2022, 67, 1946–1949. [Google Scholar] [CrossRef]
- El Hanafy, W. Impact of Rastall Gravity on Mass, Radius, and Sound Speed of the Pulsar PSR J0740+6620. Astrophys. J. 2022, 940, 51. [Google Scholar] [CrossRef]
- Yang, R.-X.; Xie, F.; Liu, D.-J. Tidal Deformability of Neutron Stars in Unimodular Gravity. Universe 2022, 8, 576. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Lobato, R.V.; Deb, D.; Moraes, P.H.R.S.; Malheiro, M. Quark stars with 2.6 M⊙ in a non-minimal geometry-matter coupling theory of gravity. Eur. Phys. J. C 2022, 82, 1096. [Google Scholar] [CrossRef]
- Maurya, S.K.; Singh, K.N.; Govender, M.; Ray, S. Observational constraints on maximum mass limit and physical properties of anisotropic strange star models by gravitational decoupling in Einstein-Gauss-Bonnet gravity. Mon. Not. R. Astron. Soc. 2023, 519, 4303–4324. [Google Scholar] [CrossRef]
- Shao, L. Degeneracy in studying the supranuclear equation of state and modified gravity with neutron stars. AIP Conf. Proc. 2019, 2127, 020016. [Google Scholar]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rep. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational Evidence for Self-Interacting Cold Dark Matter. Phys. Rev. Lett. 2000, 84, 3760. [Google Scholar] [CrossRef] [PubMed]
- Tulin, S.; Yu, H.-B. Dark matter self-interactions and small scale structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M.P. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278–284. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Leung, S.-C.; Chu, M.-C.; Lin, L.-M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Li, A.; Huang, F.; Xu, R.-X. Too massive neutron stars: The role of dark matter? Astropart. Phys. 2012, 37, 70–74. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, F.Y.; Cheng, K.S. Gravitational effects of condensate dark matter on compact stellar objects. J. Cosmol. Astropart. Phys. 2012, 10, 031. [Google Scholar] [CrossRef]
- Xiang, Q.-F.; Jiang, W.-Z.; Zhang, D.-R.; Yang, R.-Y. Effects of fermionic dark matter on properties of neutron stars. Phys. Rev. C 2014, 89, 025803. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Atta, D.; Imam, K.; Basu, D.N.; Samanta, C. Compact bifluid hybrid stars: Hadronic matter mixed with self-interacting fermionic asymmetric dark matter. Eur. Phys. J. C 2017, 77, 440. [Google Scholar] [CrossRef]
- Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark matter effects on neutron star properties. Phys. Rev. D 2018, 97, 123007. [Google Scholar] [CrossRef]
- Deliyergiyev, M.; Del Popolo, A.; Tolos, L.; Le Delliou, M.; Lee, X.; Burgio, F. Dark compact objects: An extensive overview. Phys. Rev. D 2019, 99, 063015. [Google Scholar] [CrossRef]
- Bezares, M.; Vigano, D.; Palenzuela, C. Gravitational wave signatures of dark matter cores in binary neutron star mergers by using numerical simulations. Phys. Rev. D 2019, 100, 044049. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Sagun, V.; Lopes, I. Neutron stars: New constraints on asymmetric dark matter. Phys. Rev. D 2020, 102, 063028. [Google Scholar] [CrossRef]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. Eur. Phys. J. C 2021, 81, 1036. [Google Scholar] [CrossRef]
- Ciancarella, R.; Pannarale, F.; Addazi, A.; Marciano, A. Constraining mirror dark matter inside neutron stars. Phys. Dark Universe 2021, 32, 100796. [Google Scholar] [CrossRef]
- Emma, M.; Schianchi, F.; Pannarale, F.; Sagun, V.; Dietrich, T. Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles 2022, 5, 273–286. [Google Scholar] [CrossRef]
- Rafiei Karkevandi, D.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Di Giovanni, F.; Sanchis-Gual, N.; Cerdá-Durán, P.; Font, J.A. Can fermion-boson stars reconcile multimessenger observations of compact stars? Phys. Rev. D 2022, 105, 063005. [Google Scholar] [CrossRef]
- Leung, K.-L.; Chu, M.-C.; Lin, L.-M. Tidal deformability of dark matter admixed neutron stars. Phys. Rev. D 2022, 105, 123010. [Google Scholar] [CrossRef]
- Das, A.; Malik, T.; Nayak, A.C. Dark matter admixed neutron star properties in light of gravitational wave observations: A two fluid approach. Phys. Rev. D 2022, 105, 123034. [Google Scholar] [CrossRef]
- Gleason, T.; Brown, B.; Kain, B. Dynamical evolution of dark matter admixed neutron stars. Phys. Rev. D 2022, 105, 023010. [Google Scholar] [CrossRef]
- Dengler, Y.; Schaffner-Bielich, J.; Tolos, L. Second Love number of dark compact planets and neutron stars with dark matter. Phys. Rev. D 2022, 105, 043013. [Google Scholar] [CrossRef]
- Miao, Z.; Zhu, Y.; Li, A.; Huang, F. Dark Matter Admixed Neutron Star Properties in the Light of X-Ray Pulse Profile Observations. Astrophys. J. 2022, 936, 69. [Google Scholar] [CrossRef]
- Collier, M.; Croon, D.; Leane, R.K. Tidal Love numbers of novel and admixed celestial objects. Phys. Rev. D 2022, 106, 123027. [Google Scholar] [CrossRef]
- Rutherford, N.; Raaijmakers, G.; Prescod-Weinstein, C.; Watts, A. Constraining bosonic asymmetric dark matter with neutron star mass-radius measurements. arXiv 2022, arXiv:2208.03282. [Google Scholar]
- Giangrandi, E.; Sagun, V.; Ivanytskyi, O.; Providência, C.; Dietrich, T. The effects of self-interacting bosonic dark matter on neutron star properties. arXiv 2022, arXiv:2209.10905. [Google Scholar]
- Shakeri, S.; Rafiei Karkevandi, D. Bosonic Dark Matter in Light of the NICER Precise Mass-Radius Measurements. arXiv 2022, arXiv:2210.17308. [Google Scholar]
- Hippert, M.; Dillingham, E.; Tan, H.; Curtin, D.; Noronha-Hostler, J.; Yunes, N. Dark Matter or Regular Matter in Neutron Stars? How to tell the difference from the coalescence of compact objects. arXiv 2022, arXiv:2211.08590. [Google Scholar]
- Fynn Diedrichs, R.; Becker, N.; Jockel, C.; Christian, J.-E.; Sagunski, L.; Schaffner-Bielich, J. Tidal Deformability of Fermion-Boson Stars: Neutron Stars Admixed with Ultra-Light Dark Matter. arXiv 2023, arXiv:2303.04089. [Google Scholar]
- Mukhopadhyay, P.; Schaffner-Bielich, J. Quark stars admixed with dark matter. Phys. Rev. D 2016, 93, 083009. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Gravitational effects of condensed dark matter on strange stars. Phys. Rev. D 2017, 96, 023002. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with fermionic dark matter. Phys. Rev. D 2018, 98, 083001. [Google Scholar] [CrossRef]
- Jiménez, J.C.; Fraga, E.S. Radial Oscillations of Quark Stars Admixed with Dark Matter. Universe 2022, 8, 34. [Google Scholar] [CrossRef]
- Ferreira, O.; Fraga, E.S. Strange magnetars admixed with fermionic dark matter. J. Cosmol. Astropart. Phys. 2023, 4, 12. [Google Scholar] [CrossRef]
- Lopes, L.L.; Das, H.C. Strange Stars within Bosonic and Fermionic Admixed Dark Matter. arXiv 2023, arXiv:2301.00567. [Google Scholar]
- Zyla, P.A. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625–632. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Schaab, C.; Hermann, B.; Weber, F.; Weigel, M.K. Are strange stars distinguishable from neutron stars by their cooling behaviour? J. Phys. G: Nucl. Part. Phys. 1997, 23, 2029–2037. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Reddy, S.; Wilczek, F. Minimal color-flavor-locked-nuclear interface. Phys. Rev. D 2001, 64, 074017. [Google Scholar] [CrossRef]
- Oertel, M.; Urban, M. Surface effects in color superconducting strange-quark matter. Phys. Rev. D 2008, 77, 074015. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.; Ajmi, M.A. Surface tension and curvature energy of quark matter in the Nambu-Jona-Lasinio model. Phys. Rev. C 2013, 88, 045803. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Sun, T.T.; Guo, W.L.; Lu, D.H.; Jaikumar, P. Interface effects of strange quark matter with density dependent quark masses. Phys. Rev. D 2018, 98, 034031. [Google Scholar] [CrossRef]
- Fraga, E.S.; Hippert, M.; Schmitt, A. Surface tension of dense matter at the chiral phase transition. Phys. Rev. D 2019, 99, 014046. [Google Scholar] [CrossRef]
- Lugones, G.; Grunfeld, A.G. Surface tension of hot and dense quark matter under strong magnetic fields. Phys. Rev. C 2019, 99, 035804. [Google Scholar] [CrossRef]
- Wang, L.; Hu, J.; Xia, C.-J.; Xu, J.-F.; Peng, G.-X.; Xu, R.-X. Stable Up-Down Quark Matter Nuggets, Quark Star Crusts, and a New Family of White Dwarfs. Galaxies 2021, 9, 70. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Konstantinou, A.; Morsink, S.M. Universal Relations for the Increase in the Mass and Radius of a Rotating Neutron Star. Astrophys. J. 2022, 934, 139. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102–134. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Nelson, A.E. Tests of the gravitational inverse-square law. Annu. Rev. Nucl. Part. Sci. 2003, 53, 77–121. [Google Scholar] [CrossRef]
- Fischbach, E.; Talmadge, C.L. The Search for Non-Newtonian Gravity; Springer: New York, NY, USA, 1999. [Google Scholar]
- Fayet, P. Effects of the spin-1 partner of the goldstino (gravitino) on neutral current phenomenology. Phys. Lett. B 1980, 95, 285–289. [Google Scholar] [CrossRef]
- Fayet, P. A la recherche d’un nouveau boson de spin un. Nucl. Phys. B 1980, 187, 184–204. [Google Scholar] [CrossRef]
- Murata, J.; Tanaka, S. A review of short-range gravity experiments in the LHC era. Class. Quant. Grav. 2015, 32, 033001. [Google Scholar] [CrossRef]
- Wen, D.-H.; Li, B.-A.; Chen, L.-W. Can the maximum mass of neutron stars rule out any equation of state of dense stellar matter before gravity is well understood? arXiv 2011, arXiv:1101.1504. [Google Scholar]
- Sulaksono, A.; Marliana; Kasmudin. Effects of In-Medium Modification of Weakly Interacting Light Boson Mass in Neutron Stars. Mod. Phys. Lett. A 2011, 26, 367–375. [Google Scholar] [CrossRef]
- Zhang, D.-R.; Yin, P.-L.; Wang, W.; Wang, Q.-C.; Jiang, W.-Z. Effects of a weakly interacting light U boson on the nuclear equation of state and properties of neutron stars in relativistic models. Phys. Rev. C 2011, 83, 035801. [Google Scholar] [CrossRef]
- Wen, D.-H.; Yan, J. R-mode Instability of Neutron Star with Non-Newtonian Gravity. Commun. Theor. Phys. 2013, 59, 47–52. [Google Scholar]
- Lin, W.; Li, B.-A.; Chen, L.-W.; Wen, D.-H.; Xu, J. Breaking the EOS-gravity degeneracy with masses and pulsating frequencies of neutron stars. J. Phys. G: Nucl. Part. Phys. 2014, 41, 075203. [Google Scholar] [CrossRef]
- Lu, Z.-Y.; Peng, G.-X.; Zhou, K. Effects of non-Newtonian gravity on the properties of strange stars. Res. Astron. Astrophys. 2017, 17, 11. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, Y.; Zhang, G.-Q.; Hu, T.-P. Effects of a Weakly Interacting Light U Boson on Protoneutron Stars Including the Hyperon-Hyperon Interactions. Commun. Theor. Phys. 2018, 69, 417–424. [Google Scholar] [CrossRef]
- Fujii, Y. Dilaton and Possible Non-Newtonian Gravity. Nat. Phys. Sci. 1971, 234, 5–7. [Google Scholar] [CrossRef]
- Kamyshkov, Y.; Tithof, J.; Vysotsky, M. Bounds on new light particles from high-energy and very small momentum transfer np elastic scattering data. Phys. Rev. D 2008, 78, 114029. [Google Scholar] [CrossRef]
- Xu, J.; Li, B.-A.; Chen, L.-W.; Zheng, H. Nuclear constraints on non-Newtonian gravity at femtometer scale. J. Phys. G: Nucl. Part. Phys. 2013, 40, 035107. [Google Scholar] [CrossRef]
- Pokotilovski, Y.N. Constraints on new interactions from neutron scattering experiments. Phys. At. Nucl. 2006, 69, 924–931. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Kuusk, P.; Mostepanenko, V.M. Constraints on non-Newtonian gravity and axionlike particles from measuring the Casimir force in nanometer separation range. Phys. Rev. D 2020, 101, 056013. [Google Scholar] [CrossRef]
- Kamiya, Y.; Itagaki, K.; Tani, M.; Kim, G.N.; Komamiya, S. Constraints on New Gravitylike Forces in the Nanometer Range. Phys. Rev. Lett. 2015, 114, 161101. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger Limits on Hypothetical Yukawa Interactions in the 30-8000 nm Range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef]
- Yong, G.-C.; Li, B.-A. Effects of nuclear symmetry energy on η meson production and its rare decay to the dark U-boson in heavy-ion reactions. Phys. Lett. B 2013, 723, 388–392. [Google Scholar] [CrossRef]
- Jean, P.; Knödlseder, J.; Lonjou, V.; Allain, M.; Roques, J.-P.; Skinner, G.K.; Teegarden, B.J.; Vedrenne, G.; von Ballmoos, P.; Cordier, B.; et al. Early SPI/INTEGRAL measurements of 511 keV line emission from the 4th quadrant of the Galaxy. Astron. Astrophys. 2003, 407, L55–L58. [Google Scholar] [CrossRef]
- Boehm, C.; Fayet, P.; Silk, J. Light and heavy dark matter particles. Phys. Rev. D 2004, 69, 101302. [Google Scholar] [CrossRef]
- Boehm, C.; Hooper, D.; Silk, J.; Casse, M.; Paul, J. MeV Dark Matter: Has It Been Detected? Phys. Rev. Lett. 2004, 92, 101301. [Google Scholar] [CrossRef]
- Long, J.C.; Chan, H.W.; Churnside, A.B.; Gulbis, E.A.; Varney, M.C.M.; Price, J.C. Upper limits to submillimetre-range forces from extra space-time dimensions. Nature 2003, 421, 922–925. [Google Scholar] [CrossRef]
- Fujii, Y. Cosmological Implications of the Fifth Force. In Proceedings of the 130th Symposium of the International Astronomical Union, Balatonfured, Hungary, 15–20 June 1987. [Google Scholar]
- Abbott, R. et al. [LIGO Scientific and Virgo Collaborations] GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Uryū, K.; Xu, R.; Shibata, M. Differentially rotating strange star in general relativity. Phys. Rev. D 2019, 100, 043015. [Google Scholar] [CrossRef]
- Foot, R.; Lew, H.; Volkas, R.R. A model with fundamental improper spacetime symmetries. Phys. Lett. B 1991, 272, 67–70. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Foot, R. Mirror Matter-Type Dark Matter. Int. J. Mod. Phys. D 2004, 13, 2161–2192. [Google Scholar] [CrossRef]
- Berezhiani, Z. Mirror World and its Cosmological Consequences. Int. J. Mod. Phys. A 2004, 19, 3775–3806. [Google Scholar] [CrossRef]
- Berezhiani, Z. Through the Looking-Glass Alice’s Adventures in Mirror World. In From Fields to Strings: Circumnavigating Theoretical Physics; Shifman, M., Vainshtein, A., Wheater, J., Eds.; World Scientific: Singapore, 2005; pp. 2147–2195. [Google Scholar]
- Okun, L.B. Mirror particles and mirror matter: 50 years of speculation and searching. Phys. Usp. 2007, 50, 380–389. [Google Scholar] [CrossRef]
- Foot, R. Mirror dark matter: Cosmology, galaxy structure and direct detection. Int. J. Mod. Phys. A 2014, 29, 1430013. [Google Scholar] [CrossRef]
- Pavsic, M. External inversion, internal inversion, and reflection invariance. Int. J. Theor. Phys. 1974, 9, 229–244. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Bento, L. Neutron-Mirror-Neutron Oscillations: How Fast Might They Be? Phys. Rev. Lett. 2006, 96, 081801. [Google Scholar] [CrossRef]
- Berezhiani, Z. More about neutron-mirror neutron oscillation. Eur. Phys. J. C 2009, 64, 421–431. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S. Bounds on neutron-mirror neutron mixing from pulsar timing. Phys. Rev. D 2019, 100, 123021. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Raj, N. Neutron Star Internal Heating Constraints on Mirror Matter. Phys. Rev. Lett. 2021, 127, 061805. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S.; Zhang, Y. Neutron-Mirror-Neutron Oscillation and Neutron Star Cooling. Phys. Rev. Lett. 2022, 129, 061103. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Raha, S.; Sinha, B. Strange quark matter and the mechanism of confinement. Phys. Lett. B 1989, 229, 112–116. [Google Scholar] [CrossRef]
- Benvenuto, O.G.; Lugones, G. Strange matter equation of state in the quark mass-density-dependent model. Phys. Rev. D 1995, 51, 1989–1993. [Google Scholar] [CrossRef] [PubMed]
- Lugones, G.; Benvenuto, O.G. Strange matter equation of state and the combustion of nuclear matter into strange matter in the quark mass-density-dependent model at T>0. Phys. Rev. D 1995, 52, 1276–1280. [Google Scholar] [CrossRef]
- Peng, G.X.; Chiang, H.C.; Zou, B.S.; Ning, P.Z.; Luo, S.J. Thermodynamics, strange quark matter, and strange stars. Phys. Rev. C 2000, 62, 025801. [Google Scholar] [CrossRef]
- Xia, C.J.; Peng, G.X.; Chen, S.W.; Lu, Z.Y.; Xu, J.F. Thermodynamic consistency, quark mass scaling, and properties of strange matter. Phys. Rev. D 2014, 89, 105027. [Google Scholar] [CrossRef]
- Peshier, A.; Kämpfer, B.; Pavlenko, O.P.; Soff, G. An effective model of the quark-gluon plasma with thermal parton masses. Phys. Lett. B 1994, 337, 235–239. [Google Scholar] [CrossRef]
- Gorenstein, M.I.; Yang, S.N. Gluon plasma with a medium-dependent dispersion relation. Phys. Rev. D 1995, 52, 5206–5212. [Google Scholar] [CrossRef]
- Peshier, A.; Kämpfer, B.; Soff, G. Equation of state of deconfined matter at finite chemical potential in a quasiparticle description. Phys. Rev. C 2000, 61, 045203. [Google Scholar] [CrossRef]
- Zong, H.-S.; Sun, W.-M. A Model Study of the Equation of State of QCD. Int. J. Mod. Phys. A 2008, 23, 3591–3612. [Google Scholar] [CrossRef]
- Li, B.-L.; Cui, Z.-F.; Yu, Z.-H.; Yan, Y.; An, S.; Zong, H.-S. Structures of the strange quark stars within a quasiparticle model. Phys. Rev. D 2019, 99, 043001. [Google Scholar] [CrossRef]
- Rüster, S.B.; Rischke, D.H. Effect of color superconductivity on the mass and radius of a quark star. Phys. Rev. D 2004, 69, 045011. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Menezes, D.P.; Providência, C.; Melrose, D.B. Quark stars within relativistic models. J. Phys. G: Nucl. Part. Phys. 2006, 32, 1081–1095. [Google Scholar] [CrossRef]
- Klähn, T.; Lastowiecki, R.; Blaschke, D. Implications of the measurement of pulsars with two solar masses for quark matter in compact stars and heavy-ion collisions: A Nambu-Jona-Lasinio model case study. Phys. Rev. D 2013, 88, 085001. [Google Scholar] [CrossRef]
- Chu, P.-C.; Wang, B.; Ma, H.-Y.; Dong, Y.-M.; Chang, S.-L.; Zheng, C.-H.; Liu, J.-T.; Zhang, X.-M. Quark matter in an SU(3) Nambu-Jona-Lasinio model with two types of vector interactions. Phys. Rev. D 2016, 93, 094032. [Google Scholar] [CrossRef]
- Freedman, B.; Mclerran, L. Fermions and gauge vector mesons at finite temperature and density. III. The ground-state energy of a relativistic quark gas. Phys. Rev. D 1977, 16, 1169–1185. [Google Scholar] [CrossRef]
- Freedman, B.; Mclerran, L. Quark star phenomenology. Phys. Rev. D 1978, 17, 1109–1122. [Google Scholar] [CrossRef]
- Kurkela, A.; Romatschke, P.; Vuorinen, A. Cold quark matter. Phys. Rev. D 2010, 81, 105021. [Google Scholar] [CrossRef]
- Chu, P.-C.; Chen, L.-W. Quark Matter Symmetry Energy and Quark Stars. Astrophys. J. 2014, 780, 135. [Google Scholar] [CrossRef]
- Liu, H.; Xu, J.; Chen, L.-W.; Sun, K.-J. Isospin properties of quark matter from a 3-flavor NJL model. Phys. Rev. D 2016, 94, 065032. [Google Scholar] [CrossRef]
- Chen, L. Symmetry Energy in Nucleon and Quark Matter. Nucl. Phys. Rev. 2017, 34, 20–28. [Google Scholar]
- Chu, P.-C.; Zhou, Y.; Qi, X.; Li, X.-H.; Zhang, Z.; Zhou, Y. Isospin properties in quark matter and quark stars within isospin-dependent quark mass models. Phys. Rev. C 2019, 99, 035802. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Wilczek, F. QCD at finite baryon density: Nucleon droplets and color superconductivity. Phys. Lett. B 1998, 422, 247–256. [Google Scholar] [CrossRef]
- Rapp, R.; Schäfer, T.; Shuryak, E.V.; Velkovsky, M. Diquark Bose Condensates in High Density Matter and Instantons. Phys. Rev. Lett. 1998, 81, 53–56. [Google Scholar] [CrossRef]
- Rapp, R.; Schäfer, T.; Shuryak, E.V.; Velkovsky, M. High-Density QCD and Instantons. Ann. Phys. 2000, 280, 35–99. [Google Scholar] [CrossRef]
- Rajagopal, K.; Wilczek, F. The Condensed Matter Physics of QCD, In At the Frontier of Particle Physics: Handbook of QCD; Shifman, M., Ed.; World Scientific: Singapore, 2001; pp. 2061–2151. [Google Scholar]
- Alford, M. Color-Superconducting Quark Matter. Ann. Rev. Nucl. Part. Sci. 2001, 51, 131–160. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Alford, M.; Rajagopal, K.; Wilczek, F. Color-flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef]
- Rajagopal, K.; Wilczek, F. Enforced Electrical Neutrality of the Color-Flavor Locked Phase. Phys. Rev. Lett. 2001, 86, 3492–3495. [Google Scholar] [CrossRef]
- Lugones, G.; Horvath, J.E. Color-flavor locked strange matter. Phys. Rev. D 2002, 66, 074017. [Google Scholar] [CrossRef]
- Roupas, Z.; Panotopoulos, G.; Lopes, I. QCD color superconductivity in compact stars: Color-flavor locked quark star candidate for the gravitational-wave signal GW190814. Phys. Rev. D 2021, 103, 083015. [Google Scholar] [CrossRef]
- Horvath, J.E.; Moraes, P.H.R.S. Modeling a 2.5 M⊙ compact star with quark matter. Int. J. Mod. Phys. D 2021, 30, 2150016. [Google Scholar] [CrossRef]
- Miao, Z.; Jiang, J.-L.; Li, A.; Chen, L.-W. Bayesian Inference of Strange Star Equation of State Using the GW170817 and GW190425 Data. Astrophys. J. Lett. 2021, 917, L22. [Google Scholar] [CrossRef]
- Pagliara, G.; Herzog, M.; Röpke, F.K. Combustion of a neutron star into a strange quark star: The neutrino signal. Phys. Rev. D 2013, 87, 103007. [Google Scholar] [CrossRef]
- Geng, J.; Li, B.; Huang, Y. Repeating fast radio bursts from collapses of the crust of a strange star. Innovation 2021, 2, 100152. [Google Scholar] [CrossRef]
- Kuerban, A.; Geng, J.-J.; Huang, Y.-F.; Zong, H.-S.; Gong, H. Close-in Exoplanets as Candidates for Strange Quark Matter Objects. Astrophys. J. 2020, 890, 41. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Pi, C.; Zheng, X.; Weber, F. Confronting Strange Stars with Compact-Star Observations and New Physics. Universe 2023, 9, 202. https://doi.org/10.3390/universe9050202
Yang S, Pi C, Zheng X, Weber F. Confronting Strange Stars with Compact-Star Observations and New Physics. Universe. 2023; 9(5):202. https://doi.org/10.3390/universe9050202
Chicago/Turabian StyleYang, Shuhua, Chunmei Pi, Xiaoping Zheng, and Fridolin Weber. 2023. "Confronting Strange Stars with Compact-Star Observations and New Physics" Universe 9, no. 5: 202. https://doi.org/10.3390/universe9050202
APA StyleYang, S., Pi, C., Zheng, X., & Weber, F. (2023). Confronting Strange Stars with Compact-Star Observations and New Physics. Universe, 9(5), 202. https://doi.org/10.3390/universe9050202






