Abstract
We review conceptual aspects of inflationary scenarios able to produce primordial black holes by amplifying the size of curvature fluctuations to the level required to trigger black hole formation. We identify general mechanisms to do so, both for single- and multiple-field inflation. In single-field inflation, the spectrum of curvature fluctuations is enhanced by pronounced gradients of background quantities controlling the cosmological dynamics, which can induce brief phases of non-slow-roll inflationary evolution. In multiple-field inflation, the amplification occurs through appropriate couplings with additional sectors characterized by tachyonic instabilities that enhance the size of their fluctuations. As representative examples, we consider axion inflation and two-field models of inflation with rapid turns in field space. We develop our discussion in a pedagogical manner by including some of the most relevant calculations and by guiding the reader through the existing theoretical literature, emphasizing general themes common to several models.
1. Introduction
- Primordial black holes: history of the concept
Inflation, a short period of accelerated expansion in the very early moments of the universe, has become one of the main pillars of modern cosmology [1,2]. Leaving aside its success in addressing the puzzles of the standard hot Big Bang cosmology, inflation provides an explanation for the quantum mechanical origin of structures such as galaxies (including our own) and the anisotropies in the cosmic microwave background (CMB) radiation [3]. In the last two decades, advances in observational cosmology and, in particular, observations of the CMB and of the large-scale structure (LSS) of our universe have confirmed the predictions of inflation and arguably established its status as the main theoretical framework describing the very early universe [4,5]. These successes notwithstanding, CMB and LSS probes only provide us with information on the early universe at the largest cosmological scales () corresponding to a small fraction of the early stages of inflationary dynamics. Hence, while inflation provides us with a consistent, testable framework to understand the initial conditions in the universe at the largest scales, we do not have direct access to most of the inflationary dynamics or to the evolution of the universe in the early post-inflationary era. Importantly, these stages could be host to a number of interesting phenomena, including the production of stable relics such as dark matter (see, e.g., [6] for a historical review of dark matter), which is essential in understanding the world we observe today, as well as for establishing new physics. Indeed, the existence of non-luminous, cold dark matter (CDM) that constitutes a quarter of the total energy budget in the universe [7] is one of the most glaring pieces of evidence beyond Standard Model physics [8]. The absence of signatures from collider experiments, along with unsuccessful direct and indirect detection searches, have all made the DM puzzle particularly compelling [9].
An intriguing and economical explanation that might account for DM density in our universe is a scenario wherein DM is made of compact objects such as primordial black holes (PBHs). Pioneered by the works of Y. Zel’dovic and I. Novikov [10] and S. Hawking [11], the initial ideas in this direction began with the realization that PBHs could form as a result of the gravitational collapse of over-dense inhomogeneities in the early universe. In the mid 1970s, it was realized in the works of B. Carr [12,13] and G. Chapline [14] that PBHs could contribute to DM density and provide the seeds for the supermassive BHs populating our universe [15]. Following these theoretical progressions, the interest of the scientific community in PBHs increased in the mid 1990s with the reported detection of microlensing events from the MACHO collaboration [16]. An immediate interpretation of these results suggested the possibility that a significant fraction of mass density in our galaxy could be composed of subsolar-mass PBHs. However, these considerations were later rendered invalid by the findings of the EROS [17] and OGLE [18,19] collaborations, concluding that only a small fraction of mass in the Milky Way could be in the form of PBHs.
Stimulated both by the absence of signals for well-motivated particle DM candidates and the first detection of gravitational waves (GWs) from merging BHs by the the LIGO/VIRGO collaboration [20], a second surge of interest in PBHs was ignited (see Figure 1). In particular, different groups suggested that merging PBHs could be responsible for the observed GW signals, constituting a significant fraction of DM density in our universe [21,22,23]. Since the first appearance of these articles, a significant amount of effort has been pushed forward by the community to search for and constrain the abundance of PBHs by utilizing their gravitational and electromagnetic effects on the environment at small scales. Various experiments set stringent constraints on PBH abundance for the solar- and subsolar-mass range, leaving a viable window for this scenario of tiny PBH masses ( ()) as the totality of DM (see, e.g., [24,25,26]).
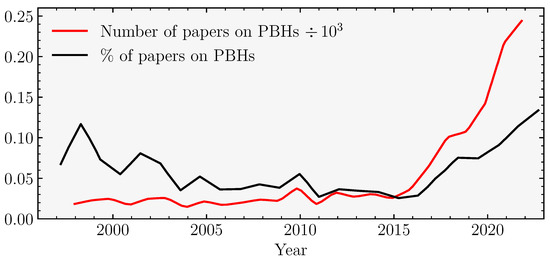
Figure 1.
Total and relative number of manuscripts in the literature on arXiv from 1996 until today related to various aspects regarding primordial black holes. Spikes of activity in the literature, particularly after the mid 1990s due to claimed lensing events by the the MACHO collaboration and GW detection by LIGO in 2015, are clearly visible. Data were extracted from https://www.benty-fields.com/trending (accessed on 24 January 2023).
It should be noted that some of the constraints derived in the literature make specific assumptions about the formation process and the subsequent evolution of PBHs (such as monochromatic mass functions, clustering and accretion processes, etc.) and about other model-dependent specifics (such as non-Gaussianity) that could relax or tighten these constraints1. Since we mostly focus on the subject of inflationary model building, we will not review these issues and aforementioned constraints, but the interested reader can find more details in excellent reviews published recently, see e.g., [28,29,30,31,32,33,34].
PBHs are likely to form well before the end of the radiation-dominated era (i.e., before the so-called matter–radiation equality) and behave like cold and collision-less matter. Therefore, they constitute an interesting DM candidate if they are massive enough () to ensure a lifetime comparable with the age of the universe [35]2. In this context, a particularly appealing aspect of PBH dark matter is its economical and minimal structure in the sense that this scenario does not require any additional beyond-Standard-Model (BSM) physics (such as new particles and interactions), provided that one alters the not-so-well-constrained early universe at small scales by introducing a viable mechanism to account for the production of large density fluctuations required for PBH formation.
Similar to the generation of CMB anisotropies, a compelling and natural source of these perturbations in the early universe could be the quantum fluctuations that are stretched outside the horizon during inflation. However, in order to generate such over-dense regions that can collapse to form PBHs in the post-inflationary universe, one needs to devise a mechanism to enhance, by several orders of magnitude, the inflationary scalar perturbations at small scales () (corresponding to late stages of inflation) far above the values required to match CMB observations. As the observed temperature anisotropies prefer a red-tilted power spectrum at CMB scales, this situation generally requires a blue-tilted power spectrum or some specific features at scales associated with PBH formation.
In the context of canonical single scalar field inflation, the first ideas in this direction appeared in works by P. Ivanov, P. Naselsky and I. Novikov [38] (see also [39]). In particular, these authors showed that if the inflation potential has a very flat plateau-like region for field ranges corresponding to the late stages of accelerated expansion, the inflationary dynamics enters a “non-attractor” regime called ultra-slow-roll (USR) inflation [40]. This leads to super-horizon growth of scalar perturbations [41,42,43] that can eventually trigger PBH formation in the post-inflationary universe3. Many explicit single-field inflationary models that exhibit similar local features were subsequently studied in the literature; for a partial list of popular works, see, e.g., [46,47,48,49,50,51,52,53,54,55,56] (see also [57,58,59,60,61,62,63] for earlier constructions). In the context of single scalar field inflation, another possibility to generate an enhancement in the scalar power spectrum is to invoke a variation of the sound speed of scalar fluctuations, for example, through a reduction in the speed of sound () [52,64,65] or through rapid oscillation (), which triggers a resonant instability in the scalar sector [66,67].
From a top-down model-building perspective, a rich particle content during inflation is not just an interesting possibility, but appears to be a common outcome of many BSM theories [68]. Since the early days of research on PBHs, multifield inflationary scenarios have also attracted considerable attention as a natural way to realize enhancement in the scalar perturbations at small scales. For instance, large scalar perturbations may arise through instabilities arising in the scalar sector, e.g., during the waterfall phase of hybrid inflation [57,69,70] or due to turning trajectories in the multiscalar inflationary landscape, as reported recently in [71,72,73,74,75,76,77,78]. Another intriguing possibility in this context is to employ axion-gauge field dynamics during inflation [79,80,81,82,83,84,85,86]. In these models, particle production in the gauge field sector act as a source for the scalar fluctuations and can therefore be responsible for PBH formation.
A common feature of all inflationary scenarios capable of producing PBH populations is the inevitable production of a stochastic GW background (SGWB) induced through higher-order gravitational interactions between enhanced scalar and tensor fluctuations of the metric [87,88,89]. Interestingly, this signal may carry crucial information about the properties of its sources, including the amplitude, statistics and spectral shape of scalar perturbations (see, e.g., [90,91,92,93,94,95,96,97,98]) and could provide invaluable information about the underlying inflationary production mechanism. Furthermore, since the resulting GW background interacts very weakly with the intervening matter between the time of its formation and today, it leads to a rather clean probe of the underlying PBH formation scenario. This allows us to access inflationary dynamics on scales much smaller than those currently probed with CMB and LSS experiments through space- and ground-based GW interferometers including the Laser Interferometer Space Antenna (LISA) [99,100], Pulsar Timing Array (PTA) experiments [101,102] and DECIGO [103,104]. For a detailed review of induced SGWB and the dependence of its properties on the post-inflationary expansion history, see [105].
- The structure of this review
If their origin is attributed to the large primordial fluctuations, PBHs may offer us a unique window to probe inflationary dynamics at sub-CMB scales. In this work, focusing mainly on the activity in the literature within the last few years, we aim to revisit and review different inflationary production mechanisms of PBHs4 and their main predictions, in a heuristic and pedagogical manner. The audience we have in mind is graduate students or researchers in related fields who wish to learn about inflation and primordial black holes and to be guided through the large literature on the subject by emphasizing common conceptual themes behind many different realizations.
This review is organized as follows. In Section 2, we present a simplified, intuitive picture of PBH formation in the inflationary universe and provide an approximate estimate of the required conditions to produce PBHs from the perspective of inflationary dynamics. In Section 3, we discuss ideas to enhance the curvature power spectrum within single-field inflation, as required for PBH formation. These mechanisms exploit large gradients in background quantities that are converted into an amplification of fluctuations. Besides reviewing analytic findings, we also develop numerical analysis and provide a link to a code for reproducing our results (see Notes 21). In Section 4, we focus on multifield inflationary scenarios that can generate PBH populations including particle production during axion inflation or sudden turns in the multiscalar inflationary landscape. Finally, we end with a discussion on future directions in Section 5. We supplement this work with several technical appendices, where we provide useful formulas and calculations used in the main body of this work.
- Conventions
Throughout this review, we work with natural units (). We use the reduced Planck mass defined as and retain it in the equations unless otherwise stated. For time-dependent quantities, over dots and primes denote derivatives with respect to cosmological time (t) and conformal time (), respectively, where is the scale factor of the background FLRW metric ().
2. PBH Formation in the Early Universe
We start by providing a physical description of PBH formation in the early universe, as comprised of an early stage of inflation, followed by radiation and matter domination (for a mini review of background cosmology, see Appendix A). Our aim is to set the stage and relate basic properties of a PBH population—as their mass and abundance—with the features of primordial curvature fluctuations originating from inflation. For this purpose, in Section 2.1, we describe the mechanism of PBH formation in the post-inflationary universe, emphasizing its nature as a causal process controlled by inflationary quantum fluctuations. In Section 2.2, we discuss relevant concepts such as the threshold for collapse into black holes and the corresponding mass and collapse fraction of PBHs relevant for a computation of their abundance. Finally, in Section 2.3, we relate the PBH abundance to primordial physics during inflation with the aim of determining the amplitude of scalar fluctuations required to produce a population of PBHs with interesting consequences for cosmology. All the concepts we discuss form the basis and motivations for our analysis of inflationary mechanisms for PBH production, which we develop in Section 3 and Section 4.
 Main References: In compiling the materials for this section and to set the main framework for our discussion, we benefited from the ideas presented in the reviews by C. Byrnes and P. Cole [126] and M. Sasaki et al. [30], as well as the Ph.D. thesis of G. Franciolini [127].
Main References: In compiling the materials for this section and to set the main framework for our discussion, we benefited from the ideas presented in the reviews by C. Byrnes and P. Cole [126] and M. Sasaki et al. [30], as well as the Ph.D. thesis of G. Franciolini [127].
2.1. PBH Formation as a Causal Process
An important concept in an expanding space–time is the horizon scale, which is crucial for understanding the causal properties of the dynamics of perturbations that are responsible for PBH formation. As an indicator of the rate of expansion of our universe, the Hubble rate () has dimensions of inverse length (or time in natural units). This makes the quantity (Hubble horizon) a natural candidate for a physical length scale in an expanding universe. Commonly referred to as the Hubble distance, the quantity (or if one wishes to recover physical units) measures the distance that light travels within one unit of Hubble time. Therefore, it can be considered a good proxy for a (time-dependent) length scale controlling the size of a causal patch in our universe. Bearing in mind that we relate physical quantities to comoving quantities by the scale factor (), a useful quantity that guides us in this direction is the comoving Hubble horizon () and, in particular, its time evolution. When expressed in terms of the second derivative of the scale factor, the time derivative of the comoving horizon can be written as
Notice that during inflation, ; hence, the comoving horizon scale is a decreasing function of time, whereas in a decelerating universe with (i.e., in the post-inflationary universe before dark energy domination), this quantity is an increasing function of time. The property that the comoving horizon decreases during an accelerated expansion is perhaps the most important element to understand inflation as a solution of the horizon problem of hot Big Bang cosmology and a framework for the quantum mechanical origin of structures in our universe5. The time dependence of the comoving Hubble horizon is controlled by the value of the background equation of state (w) (EoS) as (see Appendix A)
Therefore, during inflation, and , while during the subsequent phases of the radiation-dominated (RDU) and matter-dominated universe (MDU), the comoving horizon evolves as and , respectively. The evolution of the comoving horizon with respect to the logarithm-of-scale factor () is illustrated in Figure 2.
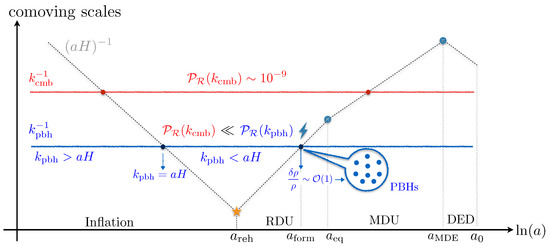
Figure 2.
A sketch of the time evolution of curvature fluctuations () (labeled by a comoving scale ()) with respect to the comoving Hubble horizon (dotted lines) () in the early universe. In the post-inflationary universe, denotes the reheating time, refers to the time of matter–radiation equality, refers to matter–dark energy equality and denotes the value of the scale factor today. The blue horizontal line indicates the comoving size of a representative small-scale perturbation responsible for PBH formation. If the power spectrum associated with these modes is enhanced during inflation, they can transfer their energy to density perturbations during radiation domination and ignite PBH formation upon horizon re-entry at .
When we study the statistical properties of fluctuations in Fourier space, we often label a given perturbation mode with a comoving length scale () measured in units of megaparsecs (). Therefore, a crucial quantity to conceptualize the behavior of perturbations in the inflationary universe is the ratio of the wavelength of a given mode with respect to the size of the comoving Hubble horizon, i.e., . Fluctuations with wavelengths larger than the comoving horizon are referred to as superhorizon modes (), while subhorizon perturbations satisfy . Each mode crosses the horizon at . As shown in Figure 2, a typical fluctuation with a comoving size of (horizontal lines) begins its life deep inside the horizon (typically as a quantum fluctuation); then, it leaves the horizon to become a superhorizon mode, and, finally, it re-enters the comoving horizon in the post-inflationary universe. Large-scale modes (with smaller k) exit the horizon earlier than small-scale modes and re-enter the horizon at a later time in the post-inflationary era. For definiteness, in Figure 2, we represent the behavior of the comoving curvature perturbation () [129,130] (see [128] for a textbook discussion), which plays an important role in our discussion.
In fact, apart from providing seeds for the observed cosmic microwave background (CMB) anisotropies at large scales, the dynamics of curvature fluctuations () may also be at play for PBH formation, provided that cosmological fluctuations exhibit specific ‘initial conditions’ at small scales. For this purpose, denoting as the comoving momentum associated with PBH formation, we assume that the curvature power spectrum at these small scales acquires an amplification well above the level required to match CMB observations: [4] (more on this later). Soon after the end of inflation, i.e., after reheating6, the modes associated with the enhancement (e.g., modes with a comoving size of ) become the seeds of density perturbations in the RDU:
Since the comoving Hubble scale grows with respect to comoving scales in the RDU, the characteristic scale of perturbations eventually becomes comparable to the comoving horizon at , where (the subscript indicates PBH formation time). At this point, gravitational interactions can trigger the collapse of over-dense regions if the latter have a sufficient over-density above a certain collapse threshold (see the discussion below).
Notice that at subhorizon scales, the radiation pressure can overcome the gravitational collapse. Therefore, the production of PBHs effectively occurs around horizon re-entry. This implies that the concept of horizon re-entry is crucial for our understanding of PBH formation as a causal process. In fact, only when the physical wavelength of a perturbation becomes comparable to the causal distance () is gravity able to communicate the presence of an over-density and to initiate gravitational collapse. A schematic diagram that summarizes the discussion presented above is illustrated in Figure 2.
In what comes next, we briefly discuss relevant quantities such as the threshold for collapse and the mass and collapse fractions of PBHs, which are important for the computation of the current PBH abundance.
2.2. The Relevant Quantities for PBH Abundance
- The threshold for collapse
The first criterion of the collapse threshold—defined as hereafter—for PBH formation was formulated by B. Carr in 1975 using a Jeans-type instability argument within Newtonian gravity [13]. In Carr’s estimate, an over-density in RDU would collapse upon horizon re-entry if the fractional over-density of the perturbation is larger than the sound speed square of density perturbations (), which is a measure of how fast a pressure wave caused by the over-density can travel from the center to the edge of a local fluctuation. In the RDU, the speed of sound of perturbations satisfies so that its square is directly related to EoS. This result implies that a perturbation can collapse to form PBHs if its over-density is larger than the pressure exerted by the radiation pressure7. Implementing general relativistic effects, the second analytical estimate was derived in [132], obtaining during the RDU. These results notwithstanding, further studies in this direction have found that the threshold depends on the initial profile of curvature perturbation [133,134,135,136]8.
At this point, we emphasize that a more precise criterion for the threshold of collapse is provided in terms of the so-called compaction function (which is a measure of excess mass within a given spatial volume; see, e.g., [135,139]) the maximum value of which results in . In this prescription, we note that contrary to the simplistic argument presented in Appendix B, there is no one-to-one correspondence between the threshold value and the peak over-density ((3) ), although they are related; see, e.g., [140]. Keeping this in mind, in the rest of this work, we will continue to refer to the threshold using the notation as commonly practiced in the literature.
An accurate characterization of the threshold requires a dedicated analysis of the evolution of perturbations in the non-linear regime after horizon re-entry, which can be done with the help of numerical simulations (see, e.g., [141] for a review). Utilizing the peak of the criterion of compaction function as the definition of the threshold (), simulations performed in the radiation fluid for different primordial perturbation profiles lead to a range of values () depending on the shape of the density peak [135,142]. Although in general, threshold depends on the shape of the primordial perturbation, refs. [142,143] showed the existence of an approximate universal value for the threshold that depends only on the type of ambient fluid and geometry. For a detailed account of the threshold and its history, we refer the reader to a recent review [141].
- The mass of PBHs
The characteristic mass of PBHs can be related to the mass contained within the Hubble horizon at the time of formation () through an efficiency factor (), as suggested by the analytical model developed in [13]:
In this formula, is the time-dependent horizon mass, where the sub/superscripts “f” and “eq” denote quantities evaluated at the time of PBH formation and matter–radiation equality, respectively; we use the standard relations during the RDU. Noting that the horizon mass at the time of equality is given by [90], Equation (4) informs us that PBHs, contrary to astrophysical black holes, can, in principle, span a wide range of masses, depending on their formation time with respect to matter–radiation equality.
Making use of the time-dependent horizon mass as above, we can relate the PBH mass at formation to the characteristic size of the perturbations that leave the horizon during inflation and are responsible for PBH formation. For this purpose, we first rewrite the PBH mass at formation as
Using the property of entropy conservation () and the scaling property of the energy density with respect to the temperature of the plasma during the RDU (), Equation (5) can be re-expressed as the following relation
In the second line, we assume that the effective number of relativistic degrees of freedom in energy density and entropy are equal, i.e., we set and take 9 with , accordingly with the latest Planck results [7]. Equation (6) indicates that for masses of PBHs that can be associated with recent LIGO observations (), the peak scale of perturbations responsible for PBH formation is much smaller compared to CMB scales (). For subsolar-mass PBHs, the corresponding peak scale for PBH formation becomes progressively smaller. For example, considering the currently allowed sublunar range () of PBH masses (), which are objects that can account for the totality of dark matter, the range of scales associated with PBH formation is quite small: . See Table 1 for an easier-to-visualize summary of these considerations.

Table 1.
Range of PBH mass(es) vs. the corresponding wave number(s) () (see Equation (6)) of the primordial modes, together with the approximate horizon crossing time measured with respect to e-folding number of the pivot scale leaves the horizon during inflation, (see Equation (7)). The first row refers to the corresponding quantities for a typical supermassive black hole (SMBH), such as in the center of our galaxy [144]. The third row refers to asteroid-mass PBHs that can still account for a significant fraction (or all) of DM density today [26]. The corresponding mass of the PBHs in terms of the Earth’s mass () and the mass of Mount Everest () are given in the last two columns on the right.
Elaborating on Equation (6), we can also derive a rough relation between the PBH mass at formation with the the number of e-folds () at which the PBH-forming modes leave the horizon during inflation. For this purpose, we first notice that , where the values of the Hubble rate and scale factor should be evaluated at the scales of horizon exit during inflation (see Figure 2). Assuming a roughly constant slow-roll parameter () between the horizon exit time of modes associated with CMB and PBH formation, respectively, we can relate the Hubble and the scale factor as and , where so that we count e-folds forward in time with respect to the horizon exit of the CMB mode10. Using the last two relations, we find ; once plugged into Equation (6), assuming , we find
Modes that leave the horizon much later compared to CMB scales have ; therefore, the exponential in Equation (7) can considerably reduce the overall large normalization, leading to small PBH masses.
- PBH abundance
After discussing possible masses for PBHs and how they depend on the dynamics of inflation, we analyze the notion of abundance of PBHs relative to the energy density of other species. We can compute this quantity during two epochs: today and at PBH formation.
When considering the present-day fraction of PBH density, it is a common practice to relate the PBH abundance to present-day dark matter density, introducing the quantity
where for each species (i), we define , with subscript “0” denoting quantities evaluated today and representing the critical density. Planck measurements provide the following value for the dark matter abundance [7],
in terms of , which measures the Hubble rate () in units of .
We can then relate today to the density fraction of PBHs at the epoch of their formation, denoting this quantity with . In fact, since we assume that PBH formation takes place during the RDU and sinc after formation, the PBH density scales as , we can write
where is the current matter density in the universe. In (10), we normalize the scale factor today as and use the fact that the total energy density evolves as for and . Using the conservation of total entropy (), we can re-express the factor appearing in Equation (10) as follows:
where we make use of Equation (5) to relate to the mass of PBHs at formation, and, as before, we assume . Finally, plugging (11) into (10) and implementing Planck measurements on (9) and (see Equation (A18)), we directly relate the abundance of PBHs at formation () to their present-day fraction () in terms of the PBH mass at formation:
Therefore, we learn that in the case in which PBH abundance accounts for the total DM density today (), the fraction of the total density in the form of PBHs () at the time of their formation takes extremely small values when considering an interesting range of masses (). This situation reflects the fact that PBH formation in the early universe is a very rare event. There is also another way to parameterize in terms of the (relative) number of collapsing regions to form PBHs. This approach is especially useful to relate the PBH abundance to the statistical properties of primordial fluctuations, as we discuss below.
- Collapse fraction of PBHs at formation
The PBH abundance at formation can also be interpreted as the fraction () of local regions in the universe that has a density larger than a certain threshold. The standard treatment for estimating is based on the so-called Press–Schechter model of gravitational collapse, which is widely used in the literature on large-scale structure formation [145]11,
where is the probability distribution function (PDF), which describes the likelihood that a given fluctuation has an over-density ; we assume that a perturbation will collapse to form a BH if its amplitude is larger than a critical value (). Notice that is the critical density contrast and, in general, cannot be identified with the threshold , where the latter can be defined as the peak value of the compaction function and can be related to an averaged density contrast [141]. Note also that an alternative, more accurate approach to compute the PBH abundance requires the use of the PDF of the compaction function (see, e.g., [149]). A discussion of this approach and the actual relation between and would bring us outside the pedagogical purposes of this review. For a detailed account of the use the PDF of the compaction function and the influence of resulting non-linearities on the PBH abundance, we refer the reader to [149] and references therein. For more details on the relation between and , see also the review [141]. Keeping an eye on the recent progress in the literature on these issues, we will continue to identify for estimates of in this and the next section and continue to work with a PDF on over-density .
Let us assume that the latter follows a Gaussian distribution,
where is the mean and is the variance of the distribution. In Figure 3, we represent two Gaussian PDFs that have the same mean value and two different variances satisfying . As the second distribution is more “spread” with a larger variance compared to the first one, the probability of an over-density larger than the critical threshold () is larger, as is PBH abundance at formation, since the integral in Equation (13) has more support within the integration limits . Hence, we can expect that the quantity () plays an important role in estimating the PBH abundance.
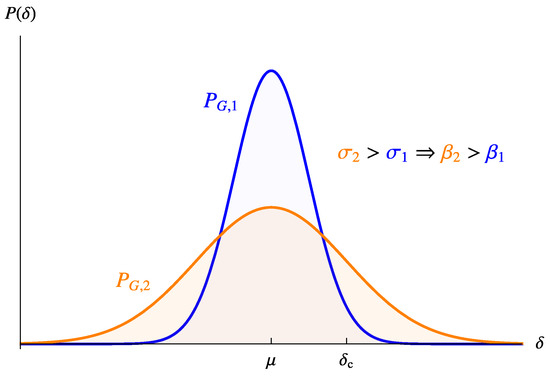
Figure 3.
Two Gaussian PDFs of the over-density field () with different variances (). Since the second distribution has a larger variance, the area under the curve above the critical threshold () is larger, leading to larger PBH abundance () (13) at formation.
Using (12) and (13), we can estimate the required variance () of (14) that can give rise to a large population of PBH today, as controlled by the quantity (). Focusing on a distribution with zero mean in (14) and integrating (13), we have
where is the complementary error function, and in the last equality, we take . As we will learn shortly, this is a good approximation for all practical purposes. As concrete examples, substituting Equation (15) into Equation (12), we infer that a solar mass PBH population with requires , whereas for a population with and , we need . Assuming a threshold of , these results translate into and , respectively. Notice also from (15) that the PBH abundance at the time of formation is exponentially sensitive to the variance of the distribution. We will dwell more on this dependence below. However, first, we discuss the implications of these findings in terms of the amplitude of scalar fluctuations generated during the phase of cosmic inflation.
2.3. Relating PBH Properties to Primordial Scalar Fluctuations
We now examine how to relate the notion of PBH abundance to the properties of the comoving curvature fluctuation () [129,130], as produced in the early universe by cosmic inflation. is conserved on super Hubble scales as the modes evolve from the inflationary phase to the RDU. We start by connecting the amplitude of with the fractional over-density (), which triggers PBH formation, as we learned in our previous discussion. Working in Fourier space with Taylor expansion at the leading order in a gradient expansion (controlled by the small parameter ) and at a linear order in , one finds [135]:
where is used during the RDU, and … denotes terms of higher order () in the curvature perturbation12. Defining the power spectrum of a Fourier variable () as
the relation between the power spectrum of over-density and curvature perturbation is then given by
In the computation of the density contrast, one should typically use a window function () to smooth on a scale () (e.g., on scales of size at horizon re-entry, as shown in Figure 2) relevant to PBH formation. Therefore, the variance of density contrast can be related to the primordial power spectrum as [30,152]13
where is the Fourier transform of a real space-window function. Popular choices for include a volume-normalized Gaussian or a top-hat window function, the Fourier transforms of are respectively given by
When selecting a curvature power spectrum () characterized by a narrow peak around the wave number , the integral in (19) can be approximated as . Then, utilizing (18) at horizon entry () (i.e., at the time of PBH formation), since , we can roughly relate the variance () to the primordial curvature power spectrum as
Finally, recall our considerations after Equation (15): a Gaussian PDF of requires () for () to generate a population of () today. Hence, we can estimate the amplitude of the scalar power spectrum needed at scales relevant for PBH formation:
This estimate holds for a wide range of subsolar PBH masses. This implies that we need a very large amplification of the curvature spectrum between large CMB and small PBH formation scales:
and the task is to produce such amplification in a controllable way by an appropriate inflationary mechanism.
It is worth pointing out that this estimate does not change much for even smaller-mass PBHs with because the power spectrum has a logarithmic sensitivity to the PBH fraction (). In order to see this, we can invert the expression (15) and use (22) to relate the primordial power spectrum of curvature perturbations to as
Now, as an extreme case, we can consider the smallest PBHs () that can survive until today (not yet eliminated by Hawking radiation), which have the tightest available observational constraints, restricting their current abundance to [32]. Plugging these values into (12), PBH fraction at formation gives , which, in turn, leads to the constraint in (24) for a threshold of . Therefore, we conclude that for Gaussian perturbations and for any PBH mass of interest, the amplitude of the scalar power spectrum relevant for PBH formation requires for any potentially observable PBH fraction () today. The discussion presented above informs us that a small change in the amplitude of the power spectrum leads to a difference of many orders of magnitude in the fraction of regions collapsing into PBHs, as clearly implied by the exponential dependence of on in (24). Similarly, a small change in the choice of threshold () could lead to very different estimates in terms of . For example, focusing on a fixed value of variance () as relevant for PBH formation, (15) can change by various orders of magnitude if we reduce the threshold () by about . In fact,
demonstrating how tuned the conditions are for producing a cosmologically interesting population of PBHs.
- Collapse fraction vs. curvature perturbation
While it is customary to use the smoothed density contrast at horizon crossing to estimate the number of collapsing regions, it is also possible to work directly with the comoving curvature perturbation to approximately compute the PBH fraction () at the time of formation. In this case, there is no need of to rely on the smoothing procedure of subhorizon fluctuations provided by the window functions [152,153]. Interestingly, as we will see later, this approach also provides a way to assess the effects of large primordial non-Gaussianity that might be present in some of the PBH-forming inflationary scenarios.
To understand the role of the primordial curvature fluctuation (), we approximate its variance with the power spectrum . Using the Press–Schechter approach with a Gaussian PDF for the curvature fluctuation spectrum, the fraction of collapsing regions at formation can be estimated as
where is the threshold. To roughly estimate , we can assume an almost scale-invariant power spectrum of for a logarithmic range of wave numbers relevant to PBH formation. Making use of a Gaussian window function in (19) gives, in this case, . Finally, plugging the latter into (15), and comparing the resulting expression with (26), we obtain [152]:
For a density threshold of , the relation presented above gives , which we set as the fiducial value for the estimates below. Following these considerations and using the formulas derived so far—in particular Equations (12) and (26)—we can then repeat the previous estimates and determine the approximate amplitude of the power spectrum required for PBH formation. The result is that for Gaussian primordial fluctuations, a sensible PBH population today requires . These findings confirm our earlier results of Equation (22).
- The case of non-Gaussian curvature fluctuations
So far, we have assumed that primordial fluctuations obey Gaussian statistics in order to estimate the amplitude of the power spectrum required for PBH formation. Since PBHs are expected to form through extremely rare large fluctuations (see Figure 3), any small deviations in the shape of the tail of the fluctuation distribution—which essentially depend on the amount of non-Gaussianity (i.e., skewness of the PDF)—can have a significant impact on the PBH abundance [153,154,155,156,157,158,159,160,161]. For the sake of obtaining a lower limit on the amplitude of the PBH-forming curvature power spectrum, we now consider scenarios with large primordial non-Gaussianity. A particularly interesting case of this type occurs if the main source of the curvature perturbation results from a higher-order interaction, where the distribution of can be modeled as a distribution (see, e.g., [79,153,162]):
where g is a Gaussian random variable () with variance . The PDF of in this case can be determined by making a change of variable , which takes the following form
Making a change of variable to a quantity t through the definition , the fraction of regions in the universe that can collapse to form PBHs can be estimated as
where in the last step, we approximate the variance as , in order to express in terms of the curvature power spectrum14. We can now compute the amplitude of the curvature power spectrum required for PBH formation when the statistics of fluctuations are strongly non-Gaussian. Using (12), together with (30), a population of solar mass PBHs with requires , whereas for a population of PBHs with and , we find . Hence, we conclude that the required amplitude of the power spectrum is roughly given by
Compared to the case of Gaussian distributed curvature perturbation (see Equation (22)), we learn that the required amplitude of the power spectrum is reduced by about one order of magnitude. Therefore, a curvature perturbation with a smaller amplitude can produce the same amount of PBH abundance if non-Gaussianity is present (see Equation (28)). In particular, for , which is typically satisfied by a satisfactory approximation, we can disregard the factor in (30). Compared with Equation (26), the power spectrum required to generate the same collapse fraction of PBHs in both cases can be related as
To further illustrate these points, in Figure 4, we show the quantity () both for Gaussian and non-Gaussian cases, represented as a function of the curvature power spectrum. We learn from the figure that in the non-Gaussian case, within a phenomenologically relevant interval of (see, e.g., (12)), a given value of the power spectrum leads to a much larger value of . We emphasize that we focus on a specific type of non-Gaussian distribution (namely ) to estimate the amplitude of the power spectrum required for PBH formation; therefore, the derived results could change for milder cases depending on the amplitude and sign of the non-Gaussianity (i.e., depending on whether the PDF in (26) is positively or negatively skewed) [153].
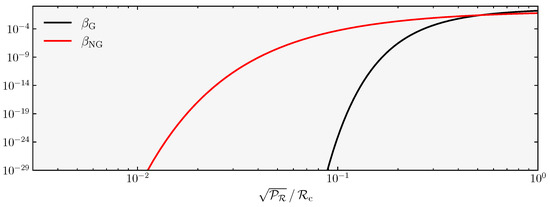
Figure 4.
Fraction of the universe that collapses into PBHs as a function of the power spectrum. For a phenomenologically interesting interval of (see, e.g., (12)) values, in the non-Gaussian case, we need a smaller amplitude of the power spectrum in order to generate the same amount of PBHs at horizon re-entry.
2.4. Brief Summary and the Path Ahead
Let us summarize the arguments that we have reviewed so far. We computed the required amplitude of the small-scale primordial power spectrum () required to generate a sizable population of PBHs that can account for all or a fraction of DM density. The typical small scale of PBH formation () is related to the BH mass through Equation (6) (see Table 1 for examples). Compared with the power spectrum at large CMB scales, we need a
enhancement in the spectrum amplitude between small and large scales, depending on the statistics obeyed by the primordial curvature perturbation (see Equations (22) and (31)).
We also learned that the PBH abundance is extremely sensitive to the amplitude of the primordial curvature spectrum. Notice that the results we reviewed are derived for the case of PBHs produced during the RDU; if early phase transitions or early phases of non-standard cosmology occur, the corresponding modified equations of state can also considerably influence the properties of the PBH population [143,163]. An interesting example is the QCD phase transition, which can lead to a high peak in the distribution of solar-mass PBHs several orders of magnitude larger than the corresponding values in the RDU [164,165].
There are various opportunities to improve and elaborate on these results. In our considerations, we assumed that PBHs form at a particular mass (Equations (4) and (6)), for example, by means of a sharply peaked primordial power spectrum; moreover, we ignored the effects of clustering [22,166,167,168,169] and mergers [170,171,172] on the PBH abundance and evolution. As shown in [140,173,174], assumptions about the shape of the primordial spectrum may alter the PBH abundance and the corresponding clustering properties. Another topic of debate concerns the use of over-density () versus the curvature perturbation () when computing the PBH abundance (see, e.g., [175] for a discussion on these issues). In light of the discussion presented above, we emphasize that the calculations we carried out in this section should be regarded as rough order-of-magnitude estimates, requiring more precise numerical analysis. Furthermore, in discussing the effects of non-Gaussianities on PBH formation, we stress that we computed the corresponding power spectrum only for an extreme example of non-Gaussian statistics. For a detailed analysis of the impact of primordial non-Gaussianity on PBH formation and abundance, we refer the reader to the general discussion in [176]. An additional phenomenological consequence of PBH-forming inflationary scenarios is the inevitable production of a stochastic gravitational wave (GW) background [87,88]. In fact, an enhanced spectrum of curvature fluctuations, as needed to produce PBH, acts as a source of GW [89]. The characterization of this GW background (see, e.g., [93,94,96]), along with the properties of its scalar sources (see, e.g., [92,97,177]) and the corresponding forecasts for its detection, is an important avenue for the experimental probing of PBH-forming inflationary models. We refer the reader to [105] for a detailed recent review of scalar-induced GW backgrounds.
All the topics mentioned above are being actively developed by the PBH community. The arguments and results we reviewed in this section are sufficient for introducing our specific purpose, which is to review the theoretical foundation of inflationary scenarios leading to PBHs. In the following sections, we discuss different conceptual ideas and concrete inflationary mechanisms for obtaining the enhancement (33) of the curvature power spectrum, as needed to generate PBHs. We focus on the inflationary theory aspects only, without computing the resulting PBH abundance, as well as other phenomenological properties that are already covered in various recent complementary reviews [28,29,30,31,32,33,34].
3. Enhancement of Scalar Perturbations during Single-Field Inflation
We now focus our attention on inflationary scenarios able to lead to PBH formation. As we learned in the previous section, such scenarios are characterized by a significant enhancement in the curvature power spectrum at a scale () (which depends on the PBH mass) much smaller with respect to CMB scales (). The condition to satisfy is Equation (23), which we rewrite here as:
We classify inflationary models as single-field (this section) or multifield type (next section) depending on whether the mechanism responsible for the enhancement in the scalar fluctuations relies on a single- or multifield scenario. In general, existing inflationary mechanisms amplify the spectrum of curvature fluctuations by means of significant gradients in the background evolution of fields responsible for inflation. In this section, we phrase our discussion as model-independently as possible, mostly focusing on conceptual aspects of the problem. We aim to discuss the dynamics and the general properties of curvature fluctuations in inflationary models leading to PBHs and refer to specific representative scenarios when necessary.
 Main References: Our discussion in this section is based on [41,42,52,64].
Main References: Our discussion in this section is based on [41,42,52,64].
3.1. The Dynamics of Curvature Perturbation
In order to analyze the behavior of the scalar power spectrum in single-field scenarios, we consider the second-order action of scalar perturbations around an inflationary phase of evolution. The background metric corresponds to a (quasi) de Sitter background with a nearly constant Hubble parameter (H). Cosmological inflation is controlled by a slow-roll parameter () satisfying , with corresponding to the condition required to conclude the inflationary process. We work with conformal time () during inflation (see, e.g., [178] for a classic survey of inflationary models).
The dynamics of scalar fluctuations can be formulated in terms of the comoving curvature perturbation () [129,130], the second-order action (at the lowest order in derivatives)15 of which takes the following form (see, e.g., [64])
In this formula, is the sound speed of the curvature perturbation, M is an effective time-dependent Planck mass and is the aforementioned slow-roll parameter.
First, we present a few initial words to contextualize single-field models aimed to produce PBHs, leading to a set of dynamics of curvature perturbation controlled by action (35). The simplest option to consider is PBH-forming models with unit sound speed and constant Planck mass characterized only by the shape of the potential (). As mentioned in the Introduction, models in this class require a potential characterized by a flat, plateau-like region (see, e.g., [46,47,48,49,50,51,52,53,55] for a choice of works studying this possibility; we will discuss its implications for the dynamics of curvature perturbations in the next subsection). PBH-forming potentials with the required characteristics can find explicit realizations, for example, in models of Higgs inflation [47,185,186,187],alpha attractors [188,189] and string inflation [51,52,190]. Considering more complex possibilities, PBH-generating models that exploit a time dependence for the sound speed are based on non-canonical kinetic terms for the inflation scalar, such as K-inflation [191,192] (see, e.g., [64,65,66,67,193,194,195,196,197] for concrete examples and Section 3.3 for some of their implications). Finally, scenarios with a time-dependent effective Planck mass can be generated by non-minimal couplings of the inflation scalar with gravity, as in the Horndeski action [198] and its cosmological applications to G-inflation scenarios [199]. Realizations of PBH-forming models in setups with non-minimal couplings belonging to the Horndeski sector include [200,201,202,203]. To the best of our knowledge, early universe models based on the more recent covariant DHOST actions [204,205,206] have not yet been explored in the context of PBH model building.
Interestingly, despite the many distinct concrete realizations, all single-field scenarios rely on a few common mechanisms to enhance the spectrum of curvature fluctuations, which exploit the behavior of background quantities. We are now going to discuss these mechanisms in a model-independent way. We treat M, and as appearing in action (35) as time-dependent quantities controlled by the single scalar background profile that drives inflation. To start with, it is convenient to redefine the time variable in action (35) to adsorb the time-dependent into a rescaled conformal time and impose an equal-scaling condition of time and space coordinates:
with a prime indicating a derivative with respect to , the rescaled conformal time. Importantly, we introduce a so-called time-dependent ‘pump field’ () as
The dynamics of are strongly tied to the time dependence of the pump field () and, more generally, to the behavior of the background quantities () that constitute it.
To analyze the evolution mode by mode, we work in Fourier space and write the Euler–Lagrange mode equation for curvature perturbation derived from the action (36):
where is the magnitude of the wave number that labels a given mode. This is a differential equation involving derivatives along the time direction acting on the function depending on both time and momentum (k).
To express its solution, we implement a gradient expansion approach (see, e.g., [41,42,52]), starting from the solution in the limit of small and including its momentum-dependent corrections, which solve (38) order by order in a expansion. This approach is particularly suitable for our purpose of describing scenarios in which the size of small-scale curvature fluctuations (, large) differs considerably from that of large-scale curvature fluctuations (, small) (see condition (23)). Indeed, a gradient expansion allows us to better understand the physical origin of possible mechanisms that raise the curvature spectrum at small scales.
The most general solution of Equation (38), up to second order in powers of , is formally given by the following integral equation16
where the sub- and superscripts 0 denote a reference time, and a tilde over a time-dependent quantity indicates that it is normalized with respect to its value at .
Typically, we are interested in relating the late time curvature perturbation at to the same quantity computed at some earlier time (). For this purpose, it is convenient to identify as the time coordinate evaluated soon after horizon crossing and as the mode function computed at . In order to enhance the spectrum of curvature fluctuations at small scales (recall the PBH-forming condition of Equation (23)), we can envisage two possibilities. One option is to exploit the structure of Equation (39), making sure that its contributions within the square parentheses become increasingly important as time proceeds after modes leave the horizon. In this way, we generate a sizable scale dependence for after horizon crossing, with the possibility of amplifying the small-scale curvature spectrum. Alternatively, we can design methods that lead to significant scale dependence already at horizon crossing, i.e., for the quantity , which then maintains its value at superhorizon scales. We explore both these options in Section 3.2 and Section 3.3, respectively.
To develop a quantitative discussion, it is convenient to introduce the so-called slow-roll parameters as
where, in our definition, we make use of the relation between e-foldings and the time coordinate (: ).
In standard models of inflation based on inflationary attractor dynamics, one imposes the so-called slow-roll conditions throughout the entire inflationary period, corresponding to the requirements
which imply that the pump field always grows in time as (see Equation (37)). As a consequence, the second and third terms in the general solution (39) decay as and , respectively in the late time limit (). Hence, they can be identified as decaying modes17 that rapidly cease to play any role in the dynamics of curvature perturbations. This is a regime of a slow-roll attractor, wherein soon after horizon crossing, the curvature perturbation settles into a nearly-constant configuration (), the spectrum of which is almost scale-invariant. In this case, the momentum-dependent terms in Equation (39) do not have the opportunity to raise the curvature spectrum at small scales.
Hence, in order to produce PBHs, we need to go beyond the slow-roll conditions of Equation (41), as first emphasized in [207]. Before discussing concrete ideas to do so, in view of numerical implementations, as well to improve our physical understanding, it is convenient to express the curvature perturbation (Equation (38)) in a way that makes more manifest the role of slow-roll parameters in controlling the mode evolution. We introduce a canonical variable () defined as
Plugging this definition into Equation (38), we obtain the so-called Mukhanov–Sasaki equation, which reads
where
Expanding the derivatives of z (37) in terms of the slow-roll parameters of Equation (40), we define
Standard slow-roll attractor scenarios correspond to situations in which is negligibly small; the quantity in Equation (44) then reads , leading to a scale-invariant curvature power spectrum. To break the scale invariance of curvature perturbation, we need to consider a sizable time-dependent . We note that the expression (45) is exact and does not assume any slow-roll hierarchy as Equation (41). Hence, it can be used to study the system beyond slow roll, as we will do in the following section.
3.2. Enhancement through the Resurrection of the Decaying Mode
- The idea
An interesting mechanism to enhance the curvature perturbation at superhorizon scales is suggested by the structure of the integrals within the square parentheses of Equation (39). Suppose that for a brief time interval, a given mode (k) experiences a background evolution during which the pump field (z) rapidly decreases after the horizon exit epoch (). Then, the ‘decaying’ mode can increase, and the integrals in the parentheses of Equation (39) can contaminate the nearly constant solution (), eventually leading to a late-time value () on superhorizon scales. This situation signals a significant departure from the attractor slow-roll regime discussed after Equation (41). In fact, in this case, the criterion for the enhancement of the curvature perturbation can be explicitly phrased in terms of the derivative of the pump-field transiently changing sign during a short time interval during inflation:
This condition implies that the combination of the slow-roll parameters () should be of order and negative during some e-folds during inflation, violating the slow-roll conditions (41). In particular, we require
If Equation (46) is satisfied, the slow-roll conditions (41) are not satisfied, and the contributions within parentheses in Equation (39) can increase. Strong time gradients of homogeneous background quantities, which lead to condition (47), can then be converted into a small-scale amplification of the curvature power spectrum. As discussed in [64], the expression (46), along with the considerations mentioned above, generalizes to a time-dependent sound speed and Planck mass according to the arguments first developed in [41,42].
- Model building parameterization of the non-attractor phase
To illustrate a viable model that can generate a seven-order-of-magnitude enhancement required for PBH formation—see Equation (23)—we focus on canonical single-field models ( and ) in order to simplify our analysis. The background evolution for the single scalar field driving inflation is
where is the scalar potential, and the time derivatives are carried on in coordinate time (t). The non-slow-roll dynamics are controlled by the properties of the potential (V), as we are going to discuss, and by its consequences for the behavior of the inflation velocity ().
Since in these scenarios, the pump field can be parameterized purely in terms of the slow-roll parameter () as (see, e.g., Equation (37)), the linear dynamics of (Equation (39)) are dictated by the first slow-roll parameter, the evolution of which is, in turn, determined by the sign and amplitude of the slow-roll parameter . Hence, the criterion required to realize the desired growth in the spectrum can be simply parameterized as a condition of the second slow-roll parameter as in (47).
From a concrete model-building perspective, scalar potentials () that can induce this type of dynamics include a characteristic ‘plateau’ within a non-vanishing field range () [38,39,208]. This property gives rise to phases of transient non-attractor dynamics of ultra slow-roll (USR) [40,43,44] or constant-roll (CR) [45,209,210] evolution, depending on the shape profile of the potential around the aforementioned feature. In particular, for USR evolution, the potential typically has a very flat plateau with , whereas for constant-roll evolution, so that the field climbs a hill by overshooting a local minimum18. As the scalar field, during its evolution, traverses such a flat region with negligible potential gradient, the acceleration term () is balanced by the Hubble damping term in the Klein–Gordon Equation (48), and the inflation speed is no longer controlled by the scalar potential. This phenomenon significantly changes the values of the inflation velocity () during the transient non-attractor phase and inevitably leads to the violation of one of the slow-roll conditions:
hence, () for transient USR () and CR () phases 19. We emphasize that since the non-slow-roll inflationary era is characterized by a large negative for a brief interval of e-folds, the pump field, as well as the first slow-roll parameter (), quickly decays during this stage as required for the activation of the decaying modes. In fact,
where, for simplicity, we assume a constant during the non-attractor phase. For explicit inflationary scenarios that can realize such transient phases in the context of PBH formation, see, e.g., [49,51,52,211]. Nevertheless, it is worth pointing out that, although possible, explicit constructions of suitable inflationary potentials involve a high degree of tuning to render the potentials extremely flat for a small region in the field range and ensure an appropriate transition for the scalar velocity among different epochs (see, e.g., the discussion in [50], as well as the comments at the end of this section).
After this general discussion of model building, in the analysis that follows, we do not need to work with an explicit form of potential () to analyze the enhancement through the non-attractor dynamics. Instead, we exploit the general idea we are discussing in a model-independent way and model PBH-forming inflationary scenarios as a succession of distinct phases that connect smoothly with one another, each parameterized by a constant (related approaches are developed in [212,213,214,215,216]). Our perspective encompasses the important features of scenarios based on the idea of transient resurrection of the decaying mode at superhorizon scales, satisfying Equations (46) and (47). In order to capture the transitions among phases, we multiply each phase by the smoothing function [217]:
where N denotes e-folds; and are the e-folding numbers at the beginning and end of the constant phase, respectively; and signifies the duration of the smoothing procedure. Keeping this smoothing prescription in mind, the inflationary evolution can be divided into three phases:
- Phase I. The initial phase of inflationary evolution is characterized by a standard slow-roll (SR) regime, where and at the pivot scale () (assuming that modes at the pivot scale exit the horizon at the beginning of evolution ()) in order to match Planck observations [4];
- Phase II. As the scalar field starts to traverse the flat plateau-like region in its potential, its dynamics eventually enter the non-attractor era, lasting a given number of e-folds of evolution. This phase is characterized by a large negative , during which the first slow-roll parameter () decays exponentially:
- Phase III. The final phase of evolution ensures a graceful exit from the non-attractor phase into a final slow-roll epoch, leading to the end of inflation. Since decays quickly in the non-attractor era, this final phase is characterized by a hierarchy between the slow-roll parameters:where . We typically require a large positive to bring back from its tiny values at the end of the non-attractor era, towards the value () needed to conclude inflation. To capture this behavior accurately, we split the final phase of evolution into two parts, parameterizing asThe relevant parameter choices to model the dynamics can be found in the third column of Table 2.
 Table 2. Parameter choices that characterize the background evolution of smoothed by the function (51) in each phase. Note that the final phase of evolution is divided into two in orders to accommodate the end of inflation with at .We note that our choice of in the initial stage of the Phase III and in Phase II is not a coincidence; in most of the single-field modes, there exists a correspondence that relates the values in Phase II and Phase III, i.e., , which is a consequence of Wands’ duality [218]. We will elaborate the consequence of this correspondence in the context of the power spectrum below, in particular for modes that exit the horizon as the background evolves from Phase II to Phase III.
Table 2. Parameter choices that characterize the background evolution of smoothed by the function (51) in each phase. Note that the final phase of evolution is divided into two in orders to accommodate the end of inflation with at .We note that our choice of in the initial stage of the Phase III and in Phase II is not a coincidence; in most of the single-field modes, there exists a correspondence that relates the values in Phase II and Phase III, i.e., , which is a consequence of Wands’ duality [218]. We will elaborate the consequence of this correspondence in the context of the power spectrum below, in particular for modes that exit the horizon as the background evolves from Phase II to Phase III.
In light of the discussion presented above, we can characterize the full background evolution using the Hubble hierarchy in (52) and , where denotes the Hubble rate at the end of inflation, where .
For a representative set of parameter choices (see Table 2), in Figure 5, we show an example of background evolution in which we plot and . The right panel of the figure makes manifest that the background evolution leads to for a short interval of e-folds (), as highlighted by the red region in the plot. In accordance with our discussion so far, this behavior is appropriate for triggering a significant enhancement in the power spectrum of curvature perturbation through the resurrection of the decaying mode.
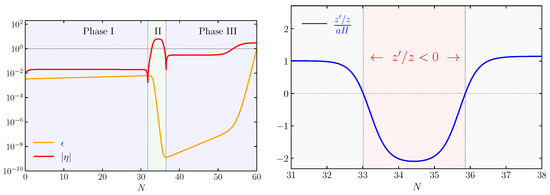
Figure 5.
(Left) panel: evolution of and in e-folds through the successive phases outlined in the main text. The green region indicates the range of e-fold numbers where , corresponding roughly to the beginning and end of the non-attractor phase. (Right) panel: the time evolution of , with in the region highlighted in red.
- Numerical analysis
Having obtained the background evolution, we are ready to describe mode evolution to obtain the power spectrum of curvature perturbation towards the end of inflation20:
where to study the evolution of curvature perturbations, we make use of the canonical variable () and consider the Mukhanov–Sasaki system of Equations (43)–(45) after setting . In general, it is not possible to find full analytic solutions for this system of equations, and a numerical analysis is needed. However, as we will explain soon, interesting properties of the resulting curvature spectrum can be derived and understood analytically. We implement the numerical procedure explained in detail in the technical Appendix C, which solves the Mukhanov–Sasaki equation with Bunch–Davies initial conditions, and we provide a Python code that reproduces our numerical findings21. The resulting power spectrum is represented in Figure 6; it manifestly grows in amplitude towards small scales, exhibiting a peak at around . Notice that the spectrum grows as towards its peak and is characterized by a dip preceding the phase of steady growth [212]. We will have more to say soon about these features.
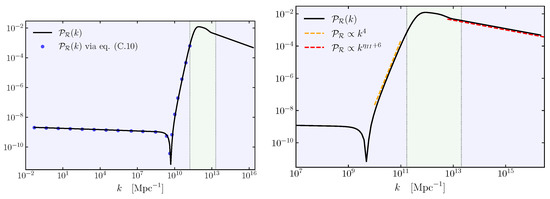
Figure 6.
Power spectrum of curvature perturbation in the three-phase model described in the main text. The pale green region separated by the vertical lines denotes the range of modes that exit the horizon during the non-attractor era, whereas the light blue regions denote the range of modes that cross the horizon during the initial and final slow-roll era, respectively.
Interestingly, for the system under consideration, the bulk of the enhancement can be attributed to the active dynamics of the would-be ‘decaying modes’, i.e., the second and third terms of Equation (39). To show this explicitly, we study superhorizon solution of the curvature perturbation in Appendix C by applying the Formula (A38), which is a special case of Equation (39) applied to the canonical single-field scenario we discuss here. For a grid of wave numbers that exit the horizon during the initial slow-roll era, the amplitude of the power spectrum obtained in this way is shown by blue dots in Figure 6. The accuracy of these locations with respect to the full numerical result (black solid line) confirms our expectation that decaying modes in (39) play a crucial role for the enhancement of the curvature perturbation for this scenario. In the right panel of Figure 6, we zoom in on the growth and the subsequent decay of power spectrum following the peak.
- The features of the spectrum: analytic considerations
Besides the numerical findings presented above, we can derive general analytic results for the spectrum of curvature fluctuations in scenarios activating the would-be decaying modes through a brief non-attractor era.
We start by noticing that for modes that leave the horizon during the initial slow-roll stage (leftmost light blue region in Figure 6), the spectrum shows characteristic features such as the presence of a dip, followed by an enhancement parameterized by a spectral index of during the bulk of the growth [95,212,224,225,226]. The dip is physically caused by a disruptive interference between the ‘constant’ mode of curvature fluctuation at superhorizon scales and the ‘decaying’ mode that is becoming active and ready to contribute to the enhancement of the spectrum. The position and depth of the dip are analytically calculable in terms of other features of the spectrum, at least in a limit of short duration of the non-slow-roll epoch. It is found that the position of the dip in momentum space is proportional to the inverse fourth root of the enhancement of the spectrum, and the depth of the dip is proportional to the inverse square root of the enhancement of the spectrum [226]. These relations are valid for any single-field models that enhance the spectrum through a brief deviation from the standard attractor era, including cases with a time-varying sound speed and Planck mass. They are accompanied by consistency conditions on the squeezed limit of non-Gaussian higher-order point functions around the dip [227,228,229], as expected in single-field scenarios22.
While in the considerations of the previous paragraph, we considered modes leaving the horizon during the first stage of slow-roll evolution, we can also derive analytic results for what happens during the non-attractor epoch. In fact, for modes that exit the horizon deep in the non-attractor era (light green region in the middle of Figure 6) and the following final slow-roll era, the spectrum behaves as expected in a standard slow-roll phase, with spectral index
(Recall that the latin numbers and relate to the phases of evolution; see Equations (52) and (54).) This behavior is a manifestation of the duality invariance of perturbation spectra within distinct inflationary backgrounds, called Wands’ duality (see, e.g., [218,231]). Wands’ duality can be understood by noticing that the structure of the Mukhanov–Sasaki Equation (43) is unchanged by a redefinition of the pump field that leaves the combination invariant:
where are arbitrary constants. If controls a phase of the slow-roll attractor, , a dual phase whose pump field () as given by Equation (57) describes a non-attractor era. Although the statistics of the canonical variable () are identical in the two regimes, the amplitude of the curvature perturbation spectrum () increases in the non-attractor epoch. In scenarios in which the parameter is considerably larger than the other slow-roll parameters, Wands’ duality (57) analytically prescribes the relation (56), in agreement with the numerical findings plotted in Figure 6. Subtleties can arise in joining attractor and non-attractor phases, since consistency conditions can be violated [232] due to the effects of boundary conditions at the transitions between different epochs. All these considerations are relevant for our topic, given the sensitivity of PBH formation and properties on the shape of the spectrum near the peak.
For further detailed accounts of the characterization of the interesting features in the power spectrum of PBH-forming single-field scenarios, we refer the reader to [95,212,214,215,217,224,225,226,233].
- Stochastic inflation and quantum diffusion
While, so far, we have focused on the predictions of the second-order action (35), non-linearities and non-Gaussian effects can play an important role in the production of PBHs, as we learned in Section 2.3. For the case of ultra-slow-roll (USR) models based on non-attractor phases of inflation, there are sources of non-Gaussianity associated with stochastic effects during inflation.
The stochastic approach to inflation pioneered by Starobinsky [234] constitutes a powerful formalism for describing the evolution of coarse-grained superhorizon fluctuations during inflation. It is based on a classical (but stochastic) Langevin equation, which reads in canonical single-field inflation (N is the number of e-folds, and we assume constant sound speed and Planck mass):
Here, represents a coarse-grained version of superhorizon scalar fluctuations; is the derivative of the inflationary potential, which leads to a deterministic drift for the coarse-grained superhorizon mode; and is a source of stochastic noise acting on long-wavelength fluctuations caused by the continuous kicks of modes that cross the cosmological horizon and pass from sub- to superhorizon scales during inflation.
Besides the physical insights that it offers, the inflationary stochastic formalism [234,235,236,237,238,239,240,241,242] offers the opportunity to obtain accurate results for the probability distribution function controlling coarse-grained superhorizon modes beyond any Gaussian approximation. As a classic example, by solving the Fokker–Planck equation associated with (58), the seminal work [238] analytically obtained the full non-Gaussian distribution functions for certain representative inflationary potentials, going beyond the reach of a perturbative treatment of the problem.
Returning to the discussion of a USR inflationary evolution for PBH scenarios, we can expect that stochastic effects can be very relevant in this context (see, e.g., [241,243,244,245,246,247,248,249,250,251]). In fact, since the amplitude of scalar fluctuations are amplified, the stochastic noise can increase relative to that under slow-roll inflation. Moreover, during USR, the derivative of the potential (), the classical drift is absent, and the stochastic evolution is driven by stochastic effects only. Various researchers have studied this topic by solving the stochastic evolution equations [252,253,254,255] and found that non-Gaussian effects can change the predictions of PBH formation, depending on the duration of the USR phase. In fact, the stochastic noise modifies the tails for the curvature probability distribution function, which decays with an exponential (instead of a Gaussian) profile23 and, consequently, tends to overproduce PBHs. Refs. [252,253,254,255] set constraints on the duration of the USR phase, which (depending on the scenario) can last, at most, a few e-folds before overproducing PBHs. There has been increased activity surrounding these subjects, and we refer the reader to the aforementioned literature for details on the state of the art with respect to this important topic.
3.3. Growth in the Power Spectrum When the Decaying Modes Are Slacking
- Slow-roll violation without triggering decaying modes
We learned in the previous subsections that a possible way to enhance the spectrum of fluctuations at small scales with respect to its large-scale counterpart is to amplify the k-dependent corrections to the constant-mode solution () within the parentheses of Equation (39).
However, as we anticipated in the paragraph following Equation (39), we can also design scenarios in which an enhanced time dependence of the slow-roll parameters leads to a scale-dependent curvature power spectrum at horizon crossing, even without exciting the decaying mode at superhorizon scales. The idea is to still make sure that the pump field () increases with time—hence, conditions (46) and (47) are not satisfied, the decaying mode remains inactive and the terms within parentheses in Equation (39) can be neglected. However, at the same time, each individual slow-roll parameter changes considerably during a short time interval during inflation. The derivatives of slow-roll parameters can be large; they can contribute significantly to the quantity () controlling the Mukhanov–Sasaki equation, and they can influence the scale dependence of the curvature spectrum at horizon crossing (see Equations (43) and (45)).
We start this section by setting the stage and derive formulas to describe this possibility. We then present an explicit realization of this scenario. It is convenient to work with the canonical variable () defined through Equation (42), and solve the Mukhanov–Sasaki system in the form of the set of Equations (43)–(59). We assume that the pump field (z) is monotonic and always increasing with time, and we identify the sound horizon of fluctuations as 24. We can identify two asymptotic regimes for each mode k: (i) an early-time regime, when each mode is deep inside the horizon; and (ii) a late-time regime, when the modes are stretched to become a superhorizon. On the one hand, in the former regime, the modes satisfy and behave as the standard vacuum fluctuations in Minskowski space time
On the other hand, later during inflation, the fluctuations are stretched outside the horizon, entering the second regime and eventually satisfying , with a solution given by
where the finite corrections to this solution can be derived in a similar fashion as in (39). Recall that we are now interested in attractor background configurations; hence, we can neglect the last two terms in Equation (60) that rapidly decay. Shortly after horizon crossing, the canonical variable settles into the solution . Using the field redefinition (42), we can identify the constant mode as the curvature perturbation at late times (). In order to determine its expression, we match the solutions sometime around horizon crossing (), and we obtain
The horizon-crossing time can be conveniently expressed as a leading contribution in a WKB approximation [64]:
with given in Equation (45). Collecting there results, we can write the late-time power spectrum for curvature fluctuations as
From (63), we observe that rapid changes in the background quantities () and slow-roll parameters constituting the quantity () of Equation (45) as a function of can then translate into a scale-dependent amplification of the power spectrum. As we will see, this situation leads to a scale-dependent enhancement in the power spectrum realized through the ‘constructive interference’ of the time-dependent background parameters ().
- An explicit realization
We now review a possible realization of this scenario, closely following the discussion presented in [64]. We focus on the generalized single-field framework discussed in Section 3.1, and we consider background dynamics that include simultaneous pronounced dips in the time-dependent profiles for the parameters . We then study the power spectrum by numerically solving numerically the Mukhanov–Sasaki equation for curvature perturbations (see Appendix C), and we compare the result with the analytical expressions discussed in Section 3.1 (see, e.g., (63)).
To analyze a representative scenario in this category, we parameterize the three time-dependent quantities () as [64]
Each of these quantities tends to asymptotically away from in both directions, and becomes equal to at while staying around the neighborhood of this value for a number of e-folds determined by . Notice that we are interested in features of the inflationary dynamics that affect modes at scales much smaller than the CMB pivot scale. Hence, we can assume , where modes associated with CMB scales leave the horizon at , while inflation ends at . A representative set of parameter choices that leads to a localized decrease in the slow-roll parameters is presented in Table 3. The resulting background evolution and the behavior of are shown in the left and right panels of Figure 7, respectively. We observe from the right panel of the figure that is always satisfied during inflation, suggesting (as expected) that the decaying modes do not grow over time. Using the parameterization (64), we then numerically solve the Mukhanov–Sasaki equation, following Appendix C.

Table 3.
Parameter choices that characterize the background evolution of the time-dependent parameters (, , ).
Our results for are presented in Figure 8. In the left panel, we notice that the expression (63) accurately describes the behavior of the power spectrum towards its peak, confirming our expectation that the constant growing mode is responsible for the enhancement. Notice the absence of a dip proceeding the growth (which characterizes the scenario shown in Figure 6). This is in agreement with our interpretation presented in the previous section; the dip is due to disruptive interference between ‘growing’ and ‘decaying’ modes, while in this context, the decaying mode is not active. On the other hand, as shown in the right panel of the figure, the power spectrum exhibits oscillations for scales following the peak. As we discussed in Note 24, this is due to multiple horizon crossing of modes within certain momentum scales, leading to excited states and oscillations in the spectrum. We illustrate this phenomenon in Figure 9—for two neighboring modes labeled by red and purple dots in Figure 8—where we plot k versus as a function of e-folds. As shown in the right panel of Figure 9, although these modes are neighboring, they exhibit non-trivial behavior before their final horizon exit () so that their asymptotic values () differ considerably, giving rise to the sizable modulations in the late-time power spectrum (see Figure 8), as discussed in [64].
Figure 8.
The full power spectrum of curvature perturbation for the background model presented in Figure 7 (left). The blue dots represent the accuracy of the Formula (63) in describing the rise of towards its peak. As shown by the red dotted line, the spectral index on the rise satisfies . The power spectrum for scales following the peak illustrates the oscillations in the amplitude at those scales (right).
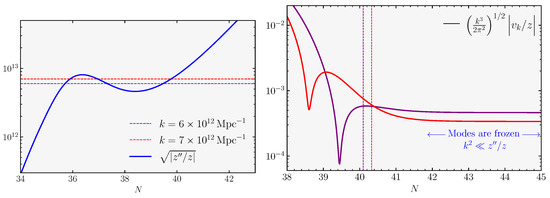
Figure 9.
(Left): The occurrence of multiple horizon crossing for the neighboring modes labeled by red and purple dot in Figure 8. (Right): Evolution of the modes that exhibit multiple horizon crossing (same color coding as in the left panel). The vertical lines illustrate the final horizon crossing time for each mode.
Besides [64], the ideas discussed in this subsection for enhancing the spectrum at small scales are further realized in [65]. Conceptually similar frameworks include a sound speed resonance scenario proposed in [66]—which can be explicitly realized within a DBI inflation model [67]—and a parametric resonance model discussed within the single-field canonical inflation framework [257].
3.4. Brief Summary
We find it remarkable that many distinct single-field models of inflation built with the aim of producing PBHs share common features in the properties of the resulting power spectrum because the enhancement of the curvature spectrum at small scales is the result of few mechanisms common to several scenarios. We identified the idea of resurrecting the decaying mode of curvature fluctuations at super Hubble scales by increasing the absolute value of the slow-roll parameter ()—see Section 3.2—and the idea of having very rapid changes in the values of slow-roll parameters (keeping them relatively small)—see Section 3.3.
The resulting properties of the curvature spectrum might be essential for testing single-field models of inflation at small scales, thanks to their predictions for the PBH population properties, as well as for the spectrum of gravitational waves induced at the second order in perturbations [87,88]. In fact, the latter is a very interesting topic that is relevant and well-studied for single-field models; we refer the reader to [105] for a detailed review.
Nevertheless, the existing explicit scenarios of single-field inflation, which are able to generate an appreciable PBH abundance, typically suffer from severe fine-tunings on the choices of the parameters characterizing their Lagrangians, for example, in producing sufficiently flat plateau regions of their potential and in ensuring regular transitions between attractor and non-attractor eras during the inflation process (see e.g., the discussion in [50] and [258] for a scenario that can partially ameliorate the tuning involved). Moreover, as we learned in Section 2.2, the resulting PBH population can be very sensitive to the details of the spectrum profile and to the presence of primordial non-Gaussianities. The latter should, to a certain extent, be generated in many concrete single-field realizations (see Section 3.2) and render particularly delicate the task of making precise theoretical predictions. In fact, large non-Gaussianities might not only change the predictions for PBH production but can also impose restrictions on single-field model building due to large one-loop corrections [259,260,261,262] (see [263]).
It is then interesting to try to consider PBH inflationary scenarios in contexts in which more than one field acquires dynamics during inflation. The hope is to find qualitatively new ideas for the production of PBHs or, alternatively, more natural realizations of known mechanisms in order to amplify the primordial curvature spectrum at small scales. It is possible that multiple fields affect the predictions on the statistics of curvature fluctuations with respect to single-field models, with important implications for PBH formation. We review this topic in the following section.
4. Enhanced Primordial Power Spectrum in Multifield Models
Despite the remarkable agreement of single-field, slow-roll inflation with the CMB and the LSS data [4], the fundamental nature of inflation continues to elude us. In particular, it is very important to know whether additional fields took part in the dynamics of inflation, besides the scalar driving cosmic expansion. In fact, while current cosmological observations do not provide hints of isocurvature fluctuations associated with extra inflationary degrees of freedom, it might also be the case that additional fields play a role during epochs of inflation that are not well probed by current large-scale surveys. The formation of PBHs occurring at small scales can be sensitive to isocurvature fluctuations and represent a valuable probe of inflationary multifield dynamics. Multifield inflation can offer new possibilities for the production of PBHs, exploiting novel, distinctive ways of converting large gradients of background quantities into the spectrum of curvature fluctuations. Moreover, when used in tandem with the techniques discussed in the previous section, multifield models might alleviate some of the fine-tuning issues the occur in single-field scenarios (see the discussion in Section 3.4). For these reasons, in this section, we review a selected set of theoretical frameworks aimed at enhancing the curvature spectrum at small scales25 by using tools that specifically involve more than one field during inflation, in particular the tachyonic behavior of field dynamics in some extra sectors during inflation.
First, in Section 4.1, we review PBH scenarios based on axions interacting with gauge fields during inflation, exploiting a mechanism based on particle production during inflation. This possibility is well-motivated by particle physics constructions, and it has been thoroughly explored in the literature; we make efforts to carefully review the state of the art, discussing opportunities and challenges for PBH formation in this context. Then, in Section 4.2, we review multifield inflationary scenarios in which the rise in the spectrum is a result of large isocurvature perturbations induced by a curved inflationary trajectory traversing a rich multifield moduli space.
 Main References: In the discussion presented in Section 4.1, we benefit from the works presented in [79,80,81,82,85,86], while the material presented in Section 4.2 is based on [72,73].
Main References: In the discussion presented in Section 4.1, we benefit from the works presented in [79,80,81,82,85,86], while the material presented in Section 4.2 is based on [72,73].
4.1. Enhanced Scalar Perturbations from Axion-Gauge Field Dynamics
Axions [269,270] are pseudoscalar particles theoretically introduced in studies of particle physics theories beyond the Standard Model. First motivated by scenarios addressing the strong CP problem in terms of a Peccei–Quinn mechanism [271,272], they find natural realizations in string theory (see, e.g., [273]), as well as many useful applications in cosmology—see, e.g., [274] for a comprehensive review. The possibility of using the physics of axions to produce PBHs is very interesting, given their strong theoretical and experimental motivations that enable connections between particle physics, quantum gravity and cosmology. In this section, we review several representative ideas and their realizations in this context.
Axion fields, denoted here as , correspond to Goldstone bosons of Peccei–Quinn (PQ) global symmetry spontaneously broken at a scale dubbed f. Their Goldstone nature equips axions with a shift symmetry constant, which is valid at all orders in perturbations. The shift symmetry makes them interesting inflation candidates, as their potential is naturally very flat [275]. The PQ symmetry suffers from a chiral anomaly, which breaks the shift symmetry and assigns axions a potential () through non-perturbative contributions in field theory, or monodromy effects in string theory (see, e.g., [68] for a review). The chiral anomaly implies that axions interact with gauge vectors through higher-dimensional operators. This property is essential for our arguments. The typical structure of an axion Lagrangian considered for cosmological purposes reads
The axion is equipped by a kinetic term and a potential term (). The potential is often a polynomial function of the axion field, at least for small values of 26. As anticipated, the Lagrangian (65) also includes a gauge field () with field strength (), coupling to the axion through a dimension-5 gauge-preserving operator
where f is the PQ symmetry-breaking scale, and is a dimensionless coupling constant. The dual field strength appearing in Equation (66) is , and the alternating symbol is 1 for even permutations of its indices and otherwise (starting with ). The dimension-5 operator (66) is especially important for our arguments. As we review below, this axion–vector coupling leads to a tachyonic instability in the gauge sector, which exponentially enhances one of the helicities of the gauge vector modes and produces a large amount of gauge quanta [280]. The energy adsorbed in the production of vector modes is carried away from the axion kinetic energy, which slows down its evolution; this is good news for axion inflationary models, since the axion can slowly roll, even along steep potentials [281]. Moreover, the inverse decay of enhanced gauge quanta into axion fluctuations (schematically, ) can amplify curvature perturbations [282,283] and lead to a large curvature spectrum at small scales at a level able to produce PBHs [79]. We refer the reader to [284] for a review on axion inflation written one decade ago, which includes many of the topics mentioned above. We now focus on reviewing the consequences of these ideas for scenarios amplifying curvature fluctuations, in addition to covering opportunities and challenges put forward in the most recent literature on this subject.
- Amplification of gauge field fluctuations
When considering a dynamical axion field with a time-dependent background profile (), the dimension-5 axion-vector interaction of Equation (66) leads to a copious production of vector fluctuations. This property can be understood by considering the equation of motion (EoM) for the gauge field mode functions (See Appendix D) [281]
where corresponds to the gauge vector polarizations, and we define a dimensionless time variable (), as well as the effective dimensionless coupling () between the spectator axion and the gauge field. Without loss of generality, we work within the following conditions
Hence, the axion rolls along its potential from large positive to small values of .
Notice from (67) that the dimension-5 operator of Equation (66) introduces a time-dependent mass term in the dispersion relation of the field, which changes sign depending on the helicity (). This property reflects the parity-violating nature of the dimension-5 interaction. When the gauge modes are deep inside the horizon (), the time-dependent correction term is negligible, and both vector polarizations obey a standard dispersion relation as in Minkowski space. However, as the modes stretch outside the horizon, the correction becomes dominant for , leading to an instability for one of the circular polarizations of the gauge fields. In our conventions (68), only the state experiences a tachyonic instability, while is unaffected. The dynamics of the axion-like field controlled by the axion velocity (), therefore induces a significant production of helical vector fields.
The nature of gauge field production and its consequences as a source for scalar perturbations are sensitive to the scalar potential (), since this quantity determines the profile of the axion background velocity (). The dynamics of the curvature perturbations, as generated through the axion-gauge field dynamics, depend on whether we identify the axion field as the inflation or whether it belongs to some extra spectator sector during inflation. In what comes next, we arrange our discussion so as to clearly distinguish between these possibilities. We consider the following scenarios:
- 1.
- Section 4.1.1 As a first possibility, we identify the axion () with that drives inflation: . Then, the order parameter () controlling the gauge-field production increases over time, generating scalar perturbations through an inverse vector decay: . We refer to this scenario as “Smooth Axion Inflation”; models that can be considered in this category are studied in [79,80,81,82]. Such scenarios suffer from dynamical instabilities associated with large back-reaction effects from the gauge fields on the axion evolution.
- 2.
- Section 4.1.2 In certain axion-inflation models, the axion potential has special features located far away from the field range corresponding to scales affecting CMB physics. A sudden increase in the axion inflation velocity occurs at their location, with enhanced scalar perturbations amplified at small PBH scales through inverse vector decay. This possibility was first discussed in [81], while further developments were studied in [83,86]. We refer to scenarios producing PBHs by exploiting localized particle production as “Bumpy Axion Inflation”, and we analyze how they address the instabilities mentioned above.
- 3.
- Section 4.1.3 A final possibility corresponds to gauge field production in a hidden sector through the dynamics of an axion spectator field. This case also allows one to address the aforementioned dynamical instabilities, given that the back-reaction effects from the vector sector can be placed under control. Depending on the shape of the spectator axion potential, such a scenario can lead to localized peaks in the scalar curvature power spectrum [81,85]. We refer to this scenario as “Spectator axion-gauge field dynamics”.
We build our discussion mainly in terms of representative, concrete examples, presenting the main results and relegating technical details to appendices.
4.1.1. Smooth Axion Inflation
In the first scenario, we identify the axion () as the inflaton : to study the behavior of scalar perturbations in a setup described by Lagrangian (65). We assume that the profile for the scalar potential () is sufficiently flat to support inflation. In this case, the effective coupling (), as defined in Equation (67), adiabatically increases during the inflationary process:
where is the standard slow-roll parameter. The amplified gauge-field mode function can be analytically expressed as [281] (recall that the axion speed has a negative sign; see Equation (68)):
The slowly changing time-dependent parameters ( and H) in Equation (70) are evaluated at the epoch of horizon crossing. The amplification of gauge field modes is maximized when the size of the mode is comparable to the horizon, .
In fact, the analytic expression in (70) is valid within the interval . For the values ) we are be interested in, this range corresponds to a phase during which the gauge modes grow and then remain frozen to their maximal value before being diluted away by universe expansion. We proceed by discussing the time evolution of the relevant quantities in this setup. For concreteness, we focus on a representative example. For a more detailed account of the gauge field amplification by the slowly rolling scalar, we refer the reader to Section 2.1 of [285] or Appendix B of [286].
- Background evolution in a concrete example
As the effective coupling () of Equation (70) increases during inflation, the enhanced vector modes eventually lead to a sizable back-reaction on the background evolution of the axionic inflation field. This fact can significantly affect the homogeneous dynamics of the system.
The back-reaction is mainly controlled by the vector-dependent friction term in the equation of motion for the homogeneous inflation field [281]. This phenomenon implies that the gauge field amplification occurs at the expense of the inflation velocity (). We consider a situation characterized by a transition between standard slow-roll dynamics in the early stages of inflation and a new attractor regime at late stages, when the gauge field enhancement dominates the Hubble friction [287] (see the cautionary remark towards the end of this section).
The aforementioned friction effect induced by the gauge-mode production can be analyzed considering modified Klein–Gordon and Friedmann equations:
where we introduced ‘electric’ and ‘magnetic’ field contributions27, as discussed in detail in Appendix D (see, in particular, Equation (A63)). Using the solutions (70) for gauge-field modes, the expectation values for the electric and magnetic fields can be computed analytically [281,286], finding (see Appendix D)
The quantity () corresponds the total energy density contained in the gauge field fluctuations. Using the evolution Equation (71), we can identify the conditions corresponding to a small back-reaction of the vector modes into the background evolution. They are and , which can be expressed as
Assuming that inflation starts in a standard slow-roll regime, the relation implies that the first condition in (73) is more demanding than the second. When these conditions are not met, we enter into an inflationary phase characterized by a strong back-reaction of gauge modes, which goes beyond the standard slow-roll inflationary attractor.
To concretely illustrate the back-reaction of the gauge field production on the homogeneous background evolution of inflation, we focus on a modified version of the linear monodromy-type potential [276] that interpolates between and from large to small field values around the global minimum:
where is a dimensionless parameter that fixes the overall amplitude of the potential. Assuming negligible back-reaction in the beginning of inflation, can determined by enforcing the standard normalization of the power spectrum in the slow-roll regime for a given choice of using
We then numerically solve Equation (71) utilizing (72) by setting the coupling between the inflation and the gauge fields to its maximally allowed value28 by Planck: (see e.g., [289]). Note that for a given initial value of the scalar field, this number can be translated to an initial value of the effective coupling, which we label as :
For (), the results of the numerical computation are shown in Figure 10. In the left panel, we show the inflation profile as a function of e-folds until the end of inflation, where . We can clearly observe that in the absence of coupling to the gauge fields () (black dashed line with ), inflation lasts for about ≈48 e-folds. Turning on the interactions with gauge fields at the beginning of inflation (solid orange line with ), the back-reaction induced by the vector fluctuations become noticeable around ≈36 e-folds, which, in turn, has the overall effect of extending the duration of inflation for about ≈12 e-folds compared to the standard slow-roll case ().
Figure 10.
Field profile () with respect to e-folding number (N) in smooth-axion inflation for the initial choice () (left). At early stages, the dynamics are in the standard slow-roll regime (light blue region), but as increases, they enter into a stage dominated by the friction generated due to gauge field production (light red region), which has the effect of prolonging inflation with respect to the background evolution with . For the choice of , the behavior of the Hubble damping term () and the friction induced by the source term () are shown in the (right) panel.
These findings are also supported by the right panel of Figure 10, where we compare the standard Hubble damping term () with the friction term () induced by the gauge field production as a function of e-folds until the end of inflation. We observe that the standard Hubble friction dominates the dynamics at early times, but as the effective coupling () increases, the dynamics gradually evolve into a regime dominated by the back-reaction of the produced gauge quanta. For the parameter choices we adopt, the onset of this regime starts around e-folds, and at around the system enters into a strong back-reaction regime wherein the dynamics become completely controlled by the gauge modes [281].
Therefore, in any viable model of axion inflation, back-reaction effects induced by gauge field production become important only towards the latest stages of inflation. For example, for a rough estimate of the orders of magnitude involved, we can adopt a linear potential (). Assuming the dynamics are initially in the slow-roll regime, we have and . For typical initial field values that can sustain enough inflationary evolution, we have , which implies that . Hence, back-reaction becomes dominant in the latest stages but before the end of inflation corresponding to .
- Scalar fluctuations sourced by gauge fields
As inflation progresses, particle production becomes increasingly efficient. Hence, the vector modes start to act as an additional source of inflation fluctuations () due to the presence of trilinear coupling () (see Appendix D.2 and references therein). In particular, a tachyonic amplification of the vector fields leads—at the second order in perturbations—to an enhancement in the scalar sector. Since these contributions to the scalar fluctuations are statistically independent of their vacuum counterpart, the resulting curvature power spectrum acquires two separate contributions (see Appendix E) that can be parameterized as [79,281]
The first term in the second line denotes the standard vacuum contribution to the curvature power spectrum. The second accounts for the vector part, with the time-dependent quantities ( and ) defined in Equations (A81) and (A99). In the weak back-reaction regime, the power spectrum of the curvature perturbation is dominated by the vacuum contribution in the first term of Equation (77). As inflation progresses, the effective coupling between the inflation and the vector fields increases; the source contribution to the power spectrum starts to kick in, and the power spectrum grows as (the system is still in the weak back-reaction regime, where ). Then, the scalar fluctuations grow; they start influencing the gauge fields sources and lead to an increase in the damping factor (). Therefore, the sourced contribution to the power spectrum eventually saturates towards late times during inflation. In fact, the time-dependent factor () is introduced to capture the modified definition of the curvature perturbation in the strong back-reaction regime. As discussed in detail in [81], this factor is responsible for an order-one correction to the power spectrum amplitude towards the end of inflation.
We summarize these arguments with a plot (Figure 11) of the total power spectrum with respect to the e-folding number. We notice that as the effective coupling ( between the scalar and the gauge fields increases along the inflationary trajectory, the power spectrum acquires a large contribution from the vector source. As desired, it grows towards smaller scales, eventually saturating towards a constant value. Since the source of the peak in the power spectrum originates from a trilinear coupling between the inflation and the gauge fields, the statistics of the curvature perturbation at those scales is non-Gaussian (see also [290]). The values of the curvature spectrum amplitude at the peak appearing in Figure 11 are sufficiently large to generate a sizable population of PBHs (recall the discussion in Section 2.3).
- Cautionary remarks: an instability in the inflation dynamics
We warn the reader that the findings reviewed in this section have been recently questioned. In particular, the authors of [290,291,292,293,294] studied the axion-gauge field dynamics for different choices of potentials and parameters, focusing on the strong back-reaction regime. By implementing sophisticated numerical techniques, these works go beyond the constant-velocity approximation assumed in our discussion above. Their findings indicate that after entering the strong back-reaction regime, the inflation velocity is characterized by oscillations of increasing amplitude, in sharp contrast to analytical studies approximating (and ) as constant. Finally, the recent analytic study reported in [295] fully supports the numerical results. The physical source of this instability seems to be a delayed response of the vector source to changes in the axion velocity () when the system enters a strong back-reaction regime. This phenomenon causes the aforementioned oscillations with increasing amplitude in the inflation velocity.
It is not clear at the moment whether these secular effects can be tamed by adding ingredients to the setup discussed in this section. A potential way out is to modify the inflationary dynamics in such a way as to push the strong vector back-reaction regime towards an epoch that does not affect the predictions of PBH formation in the scalar sector. This possibility can be achieved in scenarios in which the gauge field production is localized, leading to a pronounced peak in the scalar power spectrum before entering into a strong back-reaction regime (see Section 4.1.2). Such a way out does not avoid the instability but at least moves it towards epochs that do not affect our predictions for the production and properties of curvature perturbations. In Section 4.1.3, we instead discuss the possibility of avoiding a strong vector back-reaction regime altogether in scenarios in which the axion is a spectator field and does not drive inflation. Appropriate choices of the axion potential nevertheless lead to an enhancement of the scalar sector at a level sufficient for producing PBHs. All the opportunities we review next are possible in scenarios of inflation including axion–vector couplings, which have very rich ramifications and are well studied, given their particle physics motivations.
4.1.2. Bumpy Axion Inflation
In this section, motivated by the instability arguments discussed above, we consider scenarios with localized production of gauge fields able to enhance the curvature spectrum and produce PBHs before entering any strong back-reaction regime. As we will see, the mechanism is based on the ideas discussed in the previous Section 4.1.1 but also uses tools for the activation of the decaying mode that we introduced in Section 3.2.
For definiteness, we focus on a representative example, discussing its properties in the main text and referring to appendices for technical details. We assume that the shift symmetry of the axion is broken both by non-perturbative instanton corrections, as well as by a non-periodic monomial term in the potential29 (see, e.g., [276,278,279,297,298,299,300,301]),
where are parameters of unit mass dimension. In fact, potentials such as those mentioned above characterized by modulations on top of a smooth profile are well-motivated and studied in theoretical constructions of axion inflation models in a variety of situations. For these reasons, we find it interesting to review their useful applications for our aim of producing PBHs.
We are interested in obtaining noticeable modulations of the functional form of the potential within the regime (which we refer to as the “bumpy” regime in what follows). In particular, we exploit the aforementioned non-perturbative corrections to generate a roller-coaster profile to the otherwise smooth potential, where plateau-like regions are connected to each other by steep cliffs (see Figure 12). While plateau-like regions are suitable to sustain long enough inflation—and to generate nearly scale-invariant fluctuations at CMB scales—when reaching the cliff-like regions, the scalar velocity speeds up intermittently.
Figure 12.
The shape of the potential (78) in the bumpy regime (orange curve) for . The red stars on the potential denotes the locations in field space where axion velocity and the slope of the potential are maximal.
During such brief stages, a localized production of gauge fields occurs. To illustrate this phenomenon explicitly, we rely on a numerical procedure along the same lines as that discussed with respect to single-field models of inflation. We numerically solve the background Equation (71) in the bumpy regime of the potential (78), neglecting possible back-reaction effects induced by gauge fields30. The resulting background evolution during inflation is represented in Figure 13 in terms of the first two slow-roll parameters () for the parameter choices used in Figure 12.
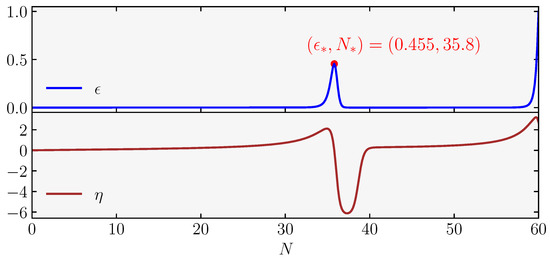
Adopting the initial condition , the scalar field completes a total of 60 e-foldings of its evolution when traversing a single bump-like region, around which the slow-roll parameter () reaches its maximal value of at . Following the stage of maximal velocity for the scalar field, the background dynamics enter into a short non-attractor phase with , during which slows down before the dynamics re-enter into a final inflationary slow-roll stage (). Since the inflationary background proceeds through an epoch of slow-roll violation, in our calculations, we compute the vacuum contribution to the scalar power spectrum using the numerical methods discussed in Section 3.2 Appendix C. In fact, as anticipated above, in developing this example, we make use both of ideas based on the conversion into curvature fluctuations of gauge-field modes (as in the previous section) and on the activation of the would-be decaying mode of the inflation scalar sector (as discussed in Section 3.2).
Since while traveling the plateau-like regions, the scalar velocity is small, the only contributions to the scalar power spectrum arise from the cliff-like region of the potential (see Figure 12). Around the cliff, the scalar field velocity and the effective coupling () acquire the following profile [86]:
where denotes the maximal value of the effective coupling. The dimensionless parameter () determines the number of e-folds during which the parameter maintains its maximal value, i.e., . For , the duration of such an epoch is inversely proportional to the restoring force provided by the potential; hence, it inversely depends on the mass parameter (m). A time-dependent profile for the effective coupling gives rise to a scale-dependent amplification of the gauge fields whose growing solutions correspond to the real part of the mode functions (see Equation (A61)), using Equation (A62) (see Appendix D.1 for more details).
As expected, the resulting sourced contribution to the power spectrum induced by the inherits the scale dependence of the gauge fields, and the curvature power spectrum can be parameterized as [86],
The vacuum contribution () can be numerically calculated following some of the methods explained in Section 3. Due to the presence of a brief non-attractor phase, it is amplified by the activation of the would-be scalar decaying mode (see Section 3.2). The dimensionless function () characterizes the contributions from the gauge fields and has a log-normal shape [86],
As suggested by the expression (81), the information about the location, width and height of the sourced signals in (80) depends on the motion of through the step-like features of its wiggly potential, particularly through and dependence of the functions (). We learn from (81) that the sourced signal is maximal at , where it is elevated to , whereas controls the width of the signal. For the background evolution presented in Figure 13, the fitting functions describing the height, width and location of the sourced signal is calculated in [85] using the semianalytical techniques developed in [302].
Collecting all the results above, we present in Figure 14 the full power spectrum in Equation (80) in terms of the e-folding number by converting the scale dependence to e-fold dependence using the horizon crossing condition (). Due to non-trivial background evolution during which the slow-roll conditions are briefly violated, the vacuum contribution to the power spectrum (dotted lines) acquires a non-trivial shape, which shares the characteristic features of the single-field scenarios we discussed in Section 3.2. Notice in the presence of the dip due to the interference between growing and decaying modes of the curvature perturbation that immediately precedes a phase of steady growth of the spectrum.
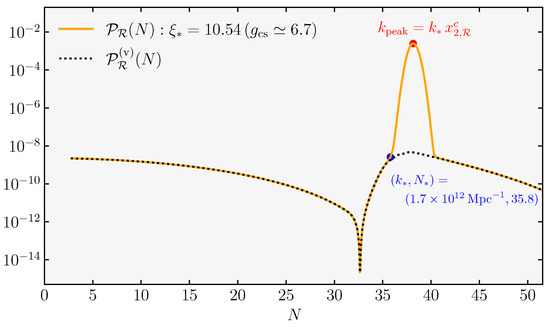
However, in the present example, the duration of the non-attractor era is not sufficient to provide a prominent peak in the power spectrum solely given the presence of vacuum fluctuations of the curvature perturbation. At this point, the additional source provided by the gauge fields come to the rescue, giving rise to extra-steep growth, leading to the required power to generate a sizable peak at wave numbers corresponding to peak PBH mass at the time of formation (see Equation (6)). Hence, in the presence of couplings to the Abelian gauge fields, the roller-coaster architecture of the potential provides an assisted amplification mechanism of the power spectrum. The curvature perturbation sourced by the vector fields and its vacuum counterpart help each another to generate a sufficiently pronounced peak to produce PBHs. Interestingly, the profile of the curvature spectrum as a function of momenta, in particular its growth rate and the details of the peak, are quite different from the corresponding predictions of single-field inflation, as investigated in Section 3. These differences make the two scenarios distinguishable.
In conclusion, the localized production scenario we presented in this section might be considered a possible way to address the instability issues associated with the background of the smooth-axion inflation discussed in Section 4.1.1. In fact, for the model we considered in this section, back-reaction effects become prominent for —see [86] for details—a much larger value than the phenomenological value () needed for the amplification of the power spectrum. Hence, we make predictions in a safe region of cosmological evolution.
Although this is promising in terms of building workable models of PBH production in axion inflation, the issue regarding the stability of the background is likely to reappear towards the end of bumpy axion inflation—in particular towards its final stages, when , where . In the next section, we discuss an extension of the model presented here, in which a spectator axion sector generates a localized scalar enhancement through its coupling to an Abelian gauge sector. Since in this model, the dynamical evolution of the axion field stops long before inflation ends, we can avoid a strong back-reaction regime that leads to instabilities of the background configuration.
4.1.3. Spectator Axion-Gauge Field Dynamics
We continue to discuss possible methods to locally enhance the spectrum of scalar fluctuations in axion-gauge field models, with an eye to solving the dynamical instability problems mentioned above. We focus on scenarios in which the axion is a spectator field, i.e., does not directly drive inflation. We call the spectator axion field and couple it to an Abelian gauge sector. The Lagrangian is
where is the inflation Lagrangian, and is its potential. We are interested in an inflationary setup whereby the spectator sector provides a subleading contribution to the total energy density during inflation. This implies that the energy densities of the scalar fields in the model (82) satisfy . Assuming small back-reaction from the gauge field fluctuations () (more on this later), the Friedmann equation simplifies to
so that the inflationary background is completely dictated by the inflation potential. We assume that is flat enough to support sufficient inflation, but otherwise, we leave it unspecified, as the fine details of the inflation dynamics are not essential for what follows. Since we are working in a weak back-reaction system, we can avoid instabilities in the inflation sector such as that reviewed in Section 4.1.1.
From now on, we consider representative examples of axion potentials and their corresponding dynamics. The choice of our examples is motivated by their interesting ramifications for PBH production and for their motivations from high-energy physics. If the spectator axion () is displaced from its global minimum, it can be dynamically active during inflation. Thanks to the perturbative shift symmetry of the axion sector, we expect the axion potential to be nearly flat; hence, the axion dynamics should occur in a slow-roll regime (). In such a case, we can neglect back-reaction effects induced by gauge field fluctuations31, and the background evolution of the spectator axion can be studied through the following equation,
To realize localized gauge field production through the last term in (82), we consider two class of transiently rolling spectator axion models characterized by the following potentials [85,302]
where and are parameters of mass dimension one.
The first model (M1) features a standard (discrete) shift symmetric potential akin to natural inflation [275], where the size of the axion modulations is set by . In this model, the axion dynamics span an interval bounded by the maximum () and the minimum () of the potential. Therefore, for large and small field values (early and late times, respectively), the axion rolls with small velocities. However, obtains relatively large values at an intermediate time when passes through an inflection point () with , where the slope of the potential () becomes maximal.
In the second model (M2), the axion field range is extended via a linear term [276,278] proportional to a soft symmetry breaking mass parameter (). We assume that the axion () can probe the corresponding bumpy potential32 in the regime, similar to the axion inflation model we discussed in Section 4.1.3. In the plateau-like region(s) and towards the global minimum ()33, the spectator axion acquires very small velocities, but obtains a relatively large transient peak when the slope of the potential () becomes maximal in the cliff-like region(s), in particular at the inflection point(s) denoted by * in Figure 15.
Figure 15.
The shape of spectator axion potentials for M1 (left) and M2 (right). For both panels, the red stars indicate the location of the inflection point(s) at which the slope of the potential () and, hence, the background velocity () of become maximal (see e.g., Equation (84)).
The background evolution () can be analytically derived in the slow-roll regime (84), starting from the expressions for the scalar potentials of Equation (85). For typical field ranges dictated by these potentials34, the spectator axion velocity () and the effective coupling strength () obtain a peaked time-dependent profile [85,302]:
where denotes the e-fold number when the axion passes through the inflection point (see Figure 15), and is the maximal value of the effective coupling parameter at . As in the bumpy axion inflation model, the width of the time-dependent peak in depends on the dimensionless ratio (), which characterizes the mass of the spectator axion in its global minimum (). For a heavier axion (corresponding to larger ), the restoring force towards the global minimum becomes very relevant; the axion traverses the inflection point faster, the result being a sharper peak in . In other words, controls the acceleration () of as it rolls down on its potential. Notice that given our slow-roll approximation, we require .
The peaked structure of the profile controls a critical scale () characterizing the equation of motion (A56) corresponding to the scale of momenta leaving the horizon at an epoch when the axion velocity is maximal (i.e, when ). Since the mass of the field in (A56) is as tachyonic as possible around this scale, it gives rise to a scale-dependent growth of the gauge field fluctuations, where only modes with a size comparable to the horizon size at , i.e , are efficiently amplified. In Appendix D.1, we briefly review the parametric amplification of the gauge field modes corresponding to both models (M1,2) we are presenting in this section; for more details, we refer the reader to [85,285,302].
In the spectator axion models we are focusing on, the impact of the vector field production on the visible scalar fluctuations is encoded only indirectly by the presence of gravitational interactions [303]. In fact, although we consider a matter Lagrangian (82) where the spectator axion-gauge field sector is decoupled from the visible inflation sector, when integrating the non-dynamical lapse and shift metric fluctuations, we find a mass mixing between inflation () and spectator axion () fluctuations. This phenomenon introduces the possibility that the gauge fields influence the curvature perturbation () through a succession of inverse decays: (see Appendix E).
Therefore, the dynamics of this sourced contribution can be understood by first studying the influence of particle production on the spectator axion fluctuations () and then by computing their conversion to curvature perturbation (). We sketch some of the steps in Appendix D.3; more detailed computations can be found in [85,302].
Taking into account the vacuum fluctuations within the inflation sector, the total power spectrum of curvature perturbation in the spectator axion-gauge field model can be expressed as [85,302],
where with and the sum over i denotes contributions from each particle production location, e.g., for model M1, the sum is over only one of such regions, while for M2, there are two of them (due to our assumptions about the initial conditions of in the bumpy regime of the potential in (85)), as the spectator rolls along the potential towards its global minimum. Equation (87) teaches us that the part of the spectrum sourced by the gauge fields has an extra slow-roll suppression (), in particular with respect to the direct coupling model we discussed in the previous section (see Equation (80)). However, the part that parameterizes the scale dependence of the sourced contribution, i.e., in (87), exhibits the same log-normal scale dependence of the bumpy axion model in (81), the peak height, width and location () of which are calculated in [85,302] in terms of for phenomenologically interesting values of that characterize the background evolution of the spectator axion.
To understand the full-scale dependence of the power spectrum (and, in particular, its vacuum contribution ()), we need to specify the scalar potential () in the inflationary sector. Instead of specifying , we take a phenomenological approach to determine the important set of parameters summarizing the inflationary dynamics. For this purpose, first notice that assuming the effects introduced by the rolling of is negligible at CMB scales (early times during inflation), we have and . Considering the latest Planck results, we adopt at CMB scales [4] to obtain . However, the observed value of the spectral tilt gives [4]. Furthermore, neglecting higher-order slow-roll parameters, we assume that remains constant throughout the inflation. These simplifying approximations enable us the describe the total power spectrum in the multifield scenarios we described above. Denoting the e-fold dependence of the Hubble parameter during slow-roll inflation as (where the subscript denotes the time at which the CMB pivot scale () exits the horizon), we can turn the the scale dependence of the vacuum scalar power spectrum into e-fold dependence as
where , where and , as discussed above. Collecting all the information we presented above, we plot in Figure 16 the total scalar power spectrum (Equation (87)) for a representative set of parameter choices describing both of the spectator axion-gauge field models (M1 and M2).
Figure 16.
Total scalar power spectrum (black curves) as a function of e-folds during inflation for the spectator axion-gauge field models M1 (Left) and M2 (Right). In the left panel, we assume that is maximal at , where the effective coupling reaches corresponding to using Equation (85). In the right panel, the spectator traverses two bumps before it settles to its minimum, and we set the inflection points at and , where ().
We learn from Figure 16 that since the spectator dynamics do not significantly influence the inflationary background, the vacuum contribution (dotted lines) has a smooth red tilted power law form, which should be contrasted with the bumpy axion inflation model we discussed in the previous section. However, the transient roll of the spectator axion () before settling to its global minimum triggers gauge field production as it probes the inflection point(s) on its potential (see Figure 15). This phenomenon generates an additional Gaussian bump in the scalar power spectrum. Notice that for larger values, the width of the corresponding bump decreases because is maximal for a shorter time interval, during which it can affect fewer gauge field modes. This explains why the sourced signals in the second model (M2) has a narrower width. As in the direct coupling cases with the gauge fields we considered earlier, the peak in the power spectrum originates from a cubic term, i.e., the last term in (82); therefore, the statistics of the curvature perturbation are expected to be non-Gaussian. This explains why the exemplifying scenarios we present in Figure 16 with a peak power of are sufficient to generate large populations of PBHs at masses corresponding to the peak scales in Equation (7).
To close this section on axion-vector inflationary systems with the aim of producing PBHs, we can conclude that this possibility requires a fair amount of complex model building. Nevertheless, the physics of axion reached so far have a high degree of theoretical sophistication, thanks to the input and motivations from particle physics, quantum gravity and cosmology. The distinctive predictions we explored with respect to the properties of the curvature power spectrum, in particular its profile as a function of momenta and its shape around the peak, make these scenarios distinguishable from single-field inflation, with relevant ramifications for PBH phenomenology. It is certainly worthwhile to explore and apply existing efforts to explore their consequences with respect to the physics of PBH formation.
4.2. Strong Turns in the Multiscalar Field Space
An alternative approach to enhance scalar fluctuations at small scales is to exploit the dynamics of multifield inflation. Multifield inflation is a topic that has been thoroughly studied in the inflationary literature with a variety of motivations (see e.g., [304] for a review). In reviewing the applications to PBH production, we focus on a general class of non-linear sigma models that are well-motivated when embedding inflation high-energy physics. Although we go through representative concrete examples, the essence of the mechanism is again associated with a transient tachyonic instability in the scalar sector—along a direction orthogonal to the inflationary one—which is converted through suitable couplings into an amplification of curvature perturbations.
The generic two-derivative Lagrangian describing the dynamics of such a system of scalar fields () minimally coupled to gravity is given by (),
where the fields may interact through the potential () and the field field space metric (). For an FLRW background characterized by the scale factor () and Hubble parameter (), the equation of motion of the homogeneous fields is described by
where the time field space covariant derivative of any field space vector () is defined as . Considering a two-field case for simplicity, the background trajectory can be split into adiabatic () and entropic () field bases that are orthogonal to each other. Here, , which is related to the Hubble slow-roll parameter as .
We find it worth mentioning that the vanilla multifield slow-roll trajectory corresponds to fields following standard gradient flow of the potential () corresponding to a field space trajectory that is approximately geodesic with (see, e.g., (90)). However, a sufficiently long phase of inflation only requires a small acceleration along the unit vector tangent to the inflationary trajectory (), and the acceleration pointing in the perpendicular direction—which parameterizes the “bending” of the inflationary trajectory—is generically not constrained and can therefore be large. The level of “bending” can be described by the dimensionless parameter () so that the orthogonal field bases evolve as
where measures the acceleration of the trajectory perpendicular to its velocity [305,306]. In combination with the Hubble rate, a “turning rate” associated with the trajectory can be defined as . Therefore, an inflationary background with a strong turn () satisfies . As we will show below, this is the regime of interest for the amplification of the scalar fluctuations in this multifield setup.
For this purpose, we consider the linear fluctuations around the background we described above, which is given by the following action [306,307,308]
where is the comoving curvature perturbation35, and is the instantaneous entropy perturbation, the mass of which is given by
were is the projection of the covariant Hessian of the potential along the entropic direction, and is the field space curvature. As should be clear from the action (92), the dynamics of the fluctuations in this two-field model are completely dictated by three functions of time (), namely the Hubble rate (), the turning rate () and the mass () of the entropy mode. To demonstrate the amplification in the power spectrum via strong turns in curved multifield space, we follow the effective approach presented in [73] to consider a field space that undergoes a strong turn () around an e-folding number () during inflation corresponding to a time well after CMB scales exited the horizon and assume a featureless Hubble rate (). We also assume that the time dependence of entropic mass is mainly controlled by the bending parameter, taking , where b is chosen as a constant for simplicity.
The behavior of the bending parameter (and that of the entropic mass ()) for typical strong turn cases is shown in Figure 17. An important quantity that determines the behavior of the fluctuations is the duration of the turn, which leads to either broad (left panel) or rapid turn (right panel) cases, as shown in the figure. Although the dynamics of the scalar perturbations are qualitatively different for broad and sudden (strong) turn cases, their behaviors share some common characteristics that can be attributed to the transient nature of the strong turn in field space. First of all, the modes that are still deep in the horizon at the end of the turn do not feel the presence of the feature; hence, their dynamics are of standard single-field type, where the power spectrum is given by
with a slight red-tilted scale dependence. For this purpose, we utilize the phenomenological model we discussed in the previous section to parameterize the scale dependence (time dependence) of the power spectrum as in Equation (88), with a constant and , along with . On the other hand, large scales that leave the horizon well before the turn experience typical multifield dynamics, resulting in a transfer of power from entropic to curvature perturbations and enhancement in the power spectrum [304]. The corresponding amplification is sensitive to the value of the entropic mass () from the time of horizon exit until the turn. In the following, we assume a sizable (i.e., b) before the turn so that the entropic fluctuations have decayed sufficiently before the onset of the turn so that the power spectrum is given by the standard result (94) for these scales. For scales that exit the horizon around the time of the turn, the entropic fluctuations exhibit transient (exponential) growth due to their tachyonic mass () around the turn, which is eventually transferred to the curvature perturbation through the kinetic coupling in (92) proportional to the bending () parameter. The exponential amplification of associated with these scales is a typical observational feature of strong turns, which we discuss briefly, focusing on broad and sharp turn cases separately.
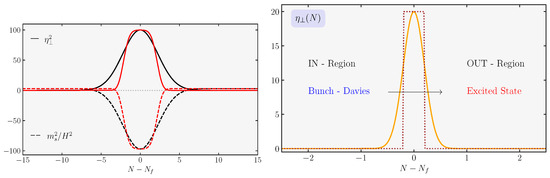
Figure 17.
(Left): schematic time evolution of the bending parameter () and entropic mass () for a broad turn using a Gaussian (, ) and smoothed top-hat profile (, ) with . (Right): time dependence of the bending parameter () for representative sharp (rapid) turn examples with Gaussian and top-hat profiles.
- Broad turns
For a strong turn in field space that lasts a sufficiently long time so that modes of interest (i.e., modes that are enhanced) have already exited the Hubble radius at the end of the turn, the dynamics of the curvature perturbation can be described by the single-field effective theory with an imaginary sound speed parameterizing the growth of the fluctuations [309,310]. From the perspective of two-field description, imaginary sound speed is just a manifestation of the transient instability induced by the strong non-geodesic motion in field space and the associated transient negative entropic mass () [311]. Therefore, the dynamics of mode functions are mainly characterized by two time scales: (i) , corresponding to entropic mass crossing and the onset of instability; and (ii) , denoting the sound horizon crossing of fluctuations after which the curvature perturbation () becomes frozen:
where denotes the absolute value of the imaginary speed of sound describing the instability/growth in the fluctuations () in the single EFT language. Since the background dynamics change mildly between the time of entropic mass crossing () and freeze-out () in the broad turn case, the exponential enhancement in the power spectrum can be parameterized as [73,311]
for all k modes that satisfies , while . Notice that exponential enhancement in the power spectrum with respect to the base spectrum is proportional to the bending parameter ().
In Figure 18, we show the power spectrum profile as a function of e-folds (left panel) using the analytic Formula (96) for Gaussian bending profiles () with (orange curve, Model 1) and (black curve, Model 2) and . For both models, the range of scales and times affected by the turn where are highlighted by red and correspond to (Model 1) (Model 2). As should be clear from the expression (96), the power spectrum reaches its maximal value for the scale for which entropic mass crossing overlaps with the peak of the bending parameter, i.e., when corresponding to
where is the scale that exits the horizon at . To determine the slope of the power spectrum on the rise, one can compute the spectral index with respect to the base power spectrum to obtain
which shows that stronger and/or less broad turns in field space lead to a steeper power spectrum. In particular, the expression (98) tells us that for broad and strong turn in field space, the slope of the power spectrum towards its peak can be much larger than the single-field models, where [95,212,217,224].
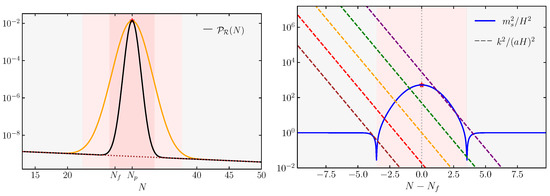
Figure 18.
(Left): curvature power spectrum (normalized to ) for broad strong turns and for two representative parameter choices using a Gaussian bending profile (see main text). (Right): migration of modes for equally spaced values around the turn to confirm the expectation that the power spectrum should fall more quickly after the peak (as compared to the left panel) because more modes experience entropic mass crossing for than for in the region highlighted in red.
We would like to note that for scales affected by the turn, the analytic profile presented in (96) is symmetric around the peak; however, numerical computations carried out in [73] show that the power spectrum typically exhibits a much quicker fall of behavior for scales following the peak compared to those preceding it. This can be understood by first recalling that the modes that are enhanced are those that go through entropic mass crossing (95) while the entropic mass is negative (). The right panel of Figure 18 can then guide us for an intuitive understanding for the expected asymmetry in the power spectrum following its peak because a larger range of modes enjoys entropic mass crossing before the peak of 36 than afterwards. We therefore conclude that the expression (96), along with the power spectrum shown in the left panel of Figure 18, only characterizes the behavior of the fluctuations qualitatively, and for more accurate results, numerical methods are required, as shown in [73].
- Sudden turns
When the duration of the turn is shorter (a statement that we will make more precise below), the scales that are maximally enhanced are still those that experience entropic mass crossing during the turn; therefore, they are of order (see, e.g., Equation (97)). However, in contrast to the broad turn case, these modes get caught in the (rapid turn) feature while they are still deep inside the horizon, i.e., they satisfy at the end of the turn. This situation effectively generates an initial excited state for these modes that can be studied analytically in the regime of sudden and strong (constant) turns () [72,312]. Along with a localized exponential amplification, the resulting power spectrum of curvature perturbation exhibits order-one oscillations in k, which is a common characteristic of sharp features [313,314], with a frequency set by the time of the turn. We will review these features below by focusing on the analytic model presented in [312]37. For this purpose, we consider an inflationary trajectory with a top-hat38sudden turn profile (see, e.g., the right panel in Figure 17) characterized by three parameters: , the central time of its location (measured with respect to the horizon exit time of the CMB pivot scale); its duration () and typical (constant) value () around :
along with an entropic mass profile during the turn that is given by
where is a constant parameter. Note from the parameterization of the bending parameter (99) that the sudden turn case we consider corresponds to .
In this setup, one can determine the power spectrum generated by sharp turns by studying the scattering problem of the two-field system using WKB methods [72]. In particular, this procedure includes matching operators (and their derivatives) describing the perturbations from the IN region, where the Bunch–Davies vacuum is assumed, passing through the turn and to the OUT region, resulting in an excited “initial” state as sketched in the right panel of Figure 17. The behavior of the entropic and curvature perturbations in both regions (IN and OUT) are standard, where the fields are dynamically decoupled from each other, while the turn sandwiched between the IN and OUT regions results in their exponential growth. Following this procedure, an analytic expression for the power spectrum was derived in [312] for scales satisfying as:
where
where and denote the typical constant value of the bending parameter corresponding to in the top-hat profile (99).
For the choice of —which corresponds to an effectively massless entropy mode on superhorizon scales (see Section 2 of [312] for a detailed discussion on this)—the profile of the curvature power spectrum39 for two representative parameter choices characterizing the turn is shown in Figure 19. As described by the analytic expression (101), the power spectrum features characteristic oscillations ( term) modulated by an envelope that is described as highlighted in the equation. The peak value of the envelope (see, e.g., the blue dashed lines in Figure 19) controls the maximal enhancement of the power spectrum with respect to the baseline power spectrum (94) (we assume it to be scale invariant for simplicity) which will occur roughly at the maximum of the function defined in (102). Arguably, the oscillatory pattern of the power spectrum around the peak is much more interesting. In particular, the term changes much faster than the envelope. On the other hand, in a sharp turn regime so that the first term in the argument of the term also changes much faster than the second. These two observations imply that oscillations in the power spectrum are periodic to a considerable degree. The period of the maxima in the oscillations occurs roughly in , corresponding to a linear frequency of
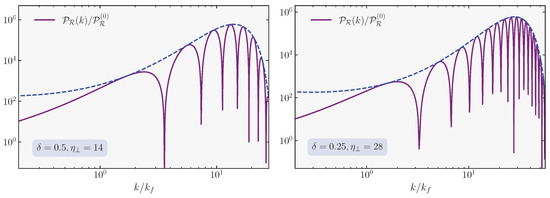
Figure 19.
Shape of the curvature power spectrum using the analytic formula in Equation (101) for two representative sharp turn cases, where the turn in parameterized with a top-hat bending parameter of Equation (99). The dashed blue line represents the envelope characterized by the terms highlighted in Equation (101).
Therefore, the scale () that exits the horizon at the center of the feature roughly set the frequency of oscillations in the power spectrum.
In summary, strong sudden turns in field space lead to a power spectrum that exhibits order-one oscillations, the amplitude of which is modulated by an exponentially enhanced envelope (101). The oscillations are fast, making their peaks almost periodic with a frequency given by (103). We note that these oscillations do not have an impact on the PBH mass spectrum () (see, e.g., (15)) because the calculation of the variance () (of the density contrast) involves a smoothing procedure over scales comparable to the width of peaks in the power spectrum () [73]. Another issue of interest from the perspective of model building is the influence of non-Gaussianity. The periods of strong turns during inflation are known to generate non-Gaussianity of the flattened type [310,316,317]. The implications of this on the PBH distribution and model building (i.e., the required peak amplitude of ) is not known and subject to future research. We therefore would like to emphasize that in the strong turn examples we discussed in this section (see Figure 18 and Figure 19), the peak amplitudes we provided are not chosen based on a particular bias on the basis of non-Gaussianity present in these models.
5. Outlook
Primordial black holes (PBHs), if they exist, can shed light on long-standing questions with respect to the nature of dark matter and on the mechanisms driving cosmic inflation. They can provide distinctive sources of gravitational waves that are potentially detectable with current or forthcoming gravitational wave experiments. For these reasons, the physics of PBHs offer promising opportunities for collaboration between cosmologists, astronomers and gravitational wave scientists.
In this review, we focused on theoretical aspects of PBH inflationary model building. We learned that generating PBHs from inflation is difficult but possible. We reviewed conceptual ideas for amplifying the primordial curvature spectrum at a level sufficient to trigger black hole formation. These mechanisms find realizations within single-field inflation through a conversion of pronounced gradients of homogeneous quantities into curvature perturbations or within multifield inflation, where curvature fluctuations are instead amplified through appropriate couplings with additional sectors, which are characterized by tachyonic instabilities. The required tuning of model parameters, or the degree of model sophistication required to realize these ideas can be demanding. However, it is certainly a worthwhile effort, given that experimental probes of PBHs are sensitive to the details of the curvature power spectrum, for example, through the properties of the resulting PBH population or through an induced stochastic gravitational wave background sourced by curvature fluctuations. In fact, different categories of models lead to distinct, potentially distinguishable predictions for the statistics of primordial fluctuations. Hence, a detailed analysis relating theoretical scenarios to cosmological and gravitational wave probes offers new precise tests of inflationary mechanisms complementary to traditional ones associated with the physics of the cosmic microwave background and of the large-scale structures of our universe.
Although much theoretical work has been done so far by the community, much more is needed to further investigate and clarify different aspects of the physics of inflation leading to PBH. At the level of model building, it will be important to clarify and address challenges associated with a severe tuning of model parameters or with the dynamical stability of PBH models requiring non-attractor, non-slow-roll phases of inflationary evolution. It will also be crucial to continue to characterize the rich and subtle properties of primordial fluctuations in PBH models of inflation with large enhancements of the primordial power spectrum at small scales. The to-do list includes a deeper analytic understanding of the properties of the curvature spectrum profile, as well as non-linearities and non-Gaussianities and their consequences for observable quantities. Such theoretical analysis will have relevant ramifications for designing appropriate cosmological probes of the physics of PBHs. Hopefully, a concerted effort of theory and experiments motivated by a deeper understanding of PBH physics will allow us to set new bounds or possibly make new discoveries with respect to the mechanisms driving inflation and the nature of dark matter.
Author Contributions
Conceptualization, O.Ö. and G.T.; formal analysis, O.Ö.; writing—original draft preparation, O.Ö.; writing—review and editing, O.Ö. and G.T.; visualization, O.Ö. All authors have read and agreed to the published version of the manuscript.
Funding
O.Ö. is supported by the “Juan de la Cierva” fellowship IJC2020-045803-I, the European Structural and Investment Funds and the Czech Ministry of Education, Youth and Sports (Project CoGraDS-CZ.02.1.01/0.0/0.0/15003/0000437) and by the Spanish Research Agency (Agencia Estatal de Investigación) through the Grant IFT Centro de Excelencia Severo Ochoa No CEX2020-001007-S funded by MCIN/AEI/10.13039/501100011033. G.T. is partially funded by the STFC grant ST/T000813/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data is reported.
Acknowledgments
We would like to thank Cristiano Germani and Shi Pi for discussions and comments. For the purpose of open access, the authors have applied a Creative Commons Attribution license to any author-accepted manuscript version arising from this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Background Cosmology: A Mini Review
Space-time metric. The central premise in modern cosmology is that as we look at the universe on large enough scales, it appears to be simpler and more uniform compared to the small scales. In other words, if we focus on sufficiently large scales, clumpy regions such as the distribution of galaxies appear to be isotropic and homogeneous. The large-scale spatial homogeneity and isotropy of the universe have been tested by a variety of observations such as large-scale structure (LSS) surveys [318,319]. However, perhaps the most important evidence supporting this claim comes from the almost uniform temperature of the CMB originating from different parts of the sky. For a first approximation, we can therefore assume the universe to be isotropic and homogeneous. The high degree of spatial symmetry uniquely determines the structure of space–time geometry, where physical distances are measured by the so-called Friedmann [320], Lemaître [321], Robertson [322] and Walker [323] (FLRW) line element40,
where is the line element on the two-dimensional sphere (), and represent negative, zero and positive curvature of constant-time hypersurfaces respectively. Note that the symmetries of the universe allow us to describe the metric using just a single function of time () and a constant parameter (K). The function is called the scale factor, which parameterizes the size of the spatial slices at a given moment in time, and the Hubble rate () describes the speed of expansion at a given moment in time. Here, an expanding universe () corresponds to a monotonically increasing scale factor ().
Dynamics of the universe. Dynamics of space–time are governed by the Einstein field equation,
where is the Ricci tensor build-out of Christoffel symbols, is the Ricci scalar and in terms of the metric and Christoffel symbols are given by
The Einstein equation in (A2) relates the geometry of space–time on the l.h.s to the matter content in the universe through the appearance of an energy momentum tensor () on the r.h.s. As in the case of the space–time metric, homogeneity and isotropy restrict the possible choices of matter content and enforce the energy–momentum tensor to take the perfect fluid form,
where and are the background energy density and the pressure in the rest frame of the fluid, respectively, and is its time-like 4-velocity of the fluid relative to the observer. The evolution equation for the energy density deriving the expansion of the universe can be derived from the component of covariant conservation law of the energy momentum tensor:
On the other hand, using the FLRW metric (A1), Einstein field equations give us information about how space–time reacts to the matter content in the universe through the Friedmann,
and acceleration equation,
The Equations (A5)–(A7) are the key in determining the evolution of the universe and its constituents at large scales, namely and (assuming knowledge of spatial curvature (K)). An important aspect of these equations is that they are not independent; for example, it is possible to combine the last two to obtain the first one. In practice, this implies that we need another ingredient to solve for three variables, i.e., , and —or, equivalently, . A quantity that comes to the rescue in this context is the equation of state (EoS) parameter, which provides a linear relation between the pressure and energy density of the fluid(s) constituting the universe:
where for each fluid contributing to the total pressure. Although this relation is not the most general form of that is available to us, this parameterization is perfectly adequate in providing an accurate coarse-grained description of our universe through most of its history. In particular, it provides a simple analytic control for determining the dynamics of the different components of the universe and the evolution of the Hubble parameter (scale factor). In order to describe the history of the universe in a continuous manner, we typically consider multiple fluids that contribute to the energy density of the universe while satisfying the relation (A8). For example, labeling each EoS with and assuming that a single component dominates the energy density for a given moment of time in the universe, one can easily integrate (A5) to obtain
Cosmological inventory. We can classify different sources of cosmological evolution by their contribution to the pressure: (i) For relativistic gas of particles (radiation), pressure is about one-third of the energy density, with . Popular constituents of such a fluid are photons, neutrinos and gravitons. (ii) Non-relativistic pressureless dust (matter) () such as dark matter (e.g., PBHs) and baryons. (iii) Cosmological constants () such as vacuum energy. According to Equation (A9), the energy density of each of these fluids therefore evolves as . Therefore, in the future, the cosmological constant will dominate, while in the far past (), the universe was radiation-dominated, and in between these two stages, there is a matter-dominated stage. Due to the inadequacy of explaining initial conditions of the observed CMB anisotropies, cosmologists tend to complete the picture we described above with a very early phase of accelerated expansion () called inflation (see, e.g., [324] for a comprehensive review). During this phase, the EoS parameter also closely mimics the behavior of a cosmological constant (). More precisely, the departure of the EoS from its value () during inflation is characterized by a time-dependent slow-roll parameter (, where ). In this framework, during inflation, , while inflation terminates when . After this stage, it is generically assumed that the constituent(s) (i.e., a scalar field or fields) that drive inflation decay to relativistic particles in a process called (p)reheating [121,122]. In this review, we assume that this process proceeds very efficiently so that soon after inflation ends, the universe is filled with relativistic particles and, consequently, evolves through the radiation-dominated (RD), matter-dominated (MD) and, finally, dark-energy-dominated (DED) phases. On the other hand, we refer to the full picture that arises by the inclusion of an early accelerated expansion as the inflationary universe, which is composed of the following consequent phases: inflation → RD → MD → DED.
Evolution of the comoving Hubble horizon. As we described in the main text, the evolution of the comoving horizon is crucial to understanding the causal evolution of fluctuation modes in the inflationary universe. To understand its time evolution in the picture we described above, we focus on its time derivative
where we used the acceleration Equation (A7), together with the Friedmann Equation (A6), focusing on flat FLRW slicing ()41. The expression mentioned above can be shaped into a form suitable for integration as , which immediately gives
where we normalized the scale factor today as . Notice that during inflation, , and the comoving horizon decreases, while during the subsequent RD () and MD () phases, it grows with a scale factor.
Density parameters (). To describe different energy components in the universe, cosmologists often parameterize radiation, matter and dark energy density relative to the critical energy density of spatially flat hypersurfaces using the following definitions (and dropping the over-bar notation to describe background quantities)
where subscript “0” denotes quantities evaluated today, and “i” indicates different kinds of fluids. Focusing on the post-inflationary era, we can then rewrite the Friedmann equation in terms of dimensionless density parameters as
According to the latest observations of the CMB anisotropies by the Planck collaboration, matter and dark energy density are determined to be [7],
On the other hand, we can infer radiation density today by utilizing the transition time of the universe from RD to MD. This moment in our universe is commonly referred to as matter–radiation equality, which is defined by
Noting the relation between the red-shift parameter42 () and scale factor () and Planck’s prediction () [7], together with Equation (A14), therefore gives
where we used the central values of the quantities () determined by Planck.
Making a two-component fluid approximation around the time of matter radiation equality (), the total energy density of the universe at can be related to matter density today via
Cosmological parameters. Other cosmological parameters determined by the latest Planck data (2018) (TT,TE,EE + low E + lensing, % 68 CL) are as follows [7]:
So far, have not mentioned thermodynamical properties such as temperature and entropy in the universe following inflation. In what follows, we will note some of the key formulas we will use in Section 2 without getting into the details of the derivation of these formulas. For an in-depth discussion on the contents we will introduce below, we refer the reader to Chapter 3 of the seminal books by Kolb and Turner [325] and Mukhanov [326] or to Baumann’s recent book [128].
The total energy density of relativistic degrees of freedom that are in thermal equilibrium with the plasma can be related to the temperature of the plasma (T) (i.e., temperature of the photon gas) as
where is the effective number of relativistic degrees of freedom at the temperature (T) which is defined as
where and denote the intrinsic degree of freedom (i.e., spin) for bosonic and fermionic species, respectively. The total entropy density of relativistic species is defined as
where is the effective number of degrees of freedom in entropy. For species in thermal equilibrium (i.e., species that have the same temperature (), ) because for each bosonic/fermionic degree of freedom, the entropy density is defined as with a common denominator.
A very useful formula can be derived by using the conservation of total entropy in the universe (), which can be utilized to relate the scale factor and the temperature of the plasma as
Appendix B. A Simple Estimate for the Threshold of Collapse
In this short appendix, we present a simple analytic estimate of the characteristic value of the collapse threshold for PBH formation during the RDU based on the Jeans length argument in Newtonian gravity as first discussed in [13], closely following [30,127]. For this purpose, we take the background space–time after inflation to have the spatially flat () FLRW form (A1) and therefore the evolution of the scale factor described by the Friedmann equation: . Now consider a locally perturbed, spherically symmetric region in the universe that is initially outside the horizon and could eventually collapse to form a PBH upon horizon re-entry. The metric describing such a region can be written as
where is the scale factor, and is the non-linear generalization of the conserved comoving curvature perturbation defined on a super-Hubble scale [327]. At large distances (), curvature perturbation is assumed to vanish () so that the universe is described by the spatially flat FLRW metric. By making a coordinate redefinition (), the metric describing the spherical perturbed region (A23) can be transformed into the one describing a closed universe with positive spatial curvature (as in (A1)),
where the relation between perturbations of the two metrics is given by , showing that the local spatial curvature is given in terms of the first-order spatial (leading-order) derivatives of the curvature perturbation (). Ignoring higher-order spatial derivatives of K () on sufficiently large scales, the evolution of the spherical region is given by the 00 component of the Einstein Equation (A2)
which is equivalent to the evolution of a closed universe (see e.g., (A6)) with a perturbation () induced by spatial curvature ():
where we make use of . According to (A26), since during the RDU, perturbations are initially () small, i.e., . As the universe evolves, a local spherical region with will eventually stop expanding and collapse to form a PBH. This happens precisely when the right-hand side of (A25) becomes negative, i.e., at , where , corresponding to in (A26), assuming a homogeneous and isotropic universe. In the RDU, since perturbation modes that have a length scale smaller than the Jeans length () cannot collapse, the smallest comoving scale that can undergo collapse at is given by , where is the speed propagation of perturbation. Therefore, we have
which suggests the identification of . Therefore, at the time of horizon re-entry (), the perturbations relevant for PBH formation should have a density contrast larger than
Appendix C. Solving the Mukhanov–Sasaki Equation: Numerical Procedure
In this appendix, we discuss important steps for the numerical evaluation of the Mukhanov–Sasaki (MS) equation. The aim is to obtain the power spectrum of curvature perturbation in the inflationary scenarios we discussed in Section 3.2 and Section 3.3. Note that scenarios discussed in those sections can be captured by the generalized MS Equation (43) utilizing (44) and (59), as we describe below.
We start by scaling away the highly oscillatory contributions from the Bunch–Davies (BD) initial conditions (59). For this purpose, we define a dimensionless variable () through
to rewrite the MS Equation (43) as
For mode-by-mode evaluation, the e-folds (N) are more suitable variable for numerical integration, so we turn the derivatives with respect to in (A30) into e-folds using and obtain
We parameterize the scale factor and Hubble rate as
and note that
In terms of the new variable, the Bunch–Davies initial conditions simplify considerably and can described as
Provided that the background evolution (i.e., , etc.) is known in terms of e-fold number, the MS equation can be solved numerically for each k mode in terms of the rescaled variable (A31) using the initial conditions (A34). In this respect, some care must be taken for the initialization time of individual modes because deep inside the horizon (), the solution to (A31) is highly oscillatory, which would be costly for the numerical computation. Typically, it is enough to initialize the modes at some time such that they are sufficiently inside the horizon. For this purpose, we choose to evolve each mode by setting the initial time as
where the “k” superscript indicates the intrinsic mode dependence for the choice of , and denotes the horizon crossing time43. As argued in the main text (see the discussion around (62)), the latter can be obtained via
using (A33) (or, equivalently, (44)), provided the background solution is known. Having obtained the individual mode evaluation from to , the power spectrum (55) can be described as
where we defined , while is the mode that exits the horizon at the end of inflation.
In order to set the overall normalization of the power spectrum, we need to determine with respect to . We do so by requiring the normalization of the power spectrum indicated by Planck at the pivot scale () using . Notice that, from the general formulas we presented above, canonical single-field scenarios (see Section 3.2) can be recovered by making the following replacements: , and and . A pedagogical Python notebook file that calculates the power spectrum using the prescription described above can be found through the github link.
The role of decaying modes in the canonical single-field scenarios. We can now verify whether the general expression (39) provides an accurate description for the enhancement of the power spectrum in the canonical single-field model discussed in Section 3.2. For this purpose, we assume that the leading solution to the curvature perturbation at superhorizon scales is given by the constant solution at horizon crossing () and plugging it into the last term in (39). We can then generate an iterative solution for the curvature perturbation as
where we switched to e-folds as a time variable, is the fractional velocity of curvature perturbation at the horizon crossing epoch () and a tilde over quantities denotes a normalization with respect to their values at , i.e., . Using the standard solution to the curvature perturbation during the initial slow-roll era, an analytic formula for the fractional velocity of curvature perturbation is obtained [95], which is valid for modes that leave the horizon during the initial slow-roll era:
Similarly, for modes that cross the horizon during the initial slow-roll era, the amplitude of the curvature perturbation at horizon crossing results in
Combining these results with a given background evolution (i.e., ), the power spectrum of curvature perturbation for modes that leave the horizon can be described via the following definition
using (A38)–(A40). For a set of modes that exit the horizon during Phase 1 (the initial slow-roll era), the amplitude of the power spectrum obtained using the procedure we outlined is shown by blue dots in Figure 6.
Appendix D. Details of the Axion-Gauge Field Dynamics
In this appendix, we focus on the dynamics of the gauge fields according to the presence of a rolling scalar () and the influence of these dynamics on the scalar perturbations for the models we discussed in Section 4.1.1, Section 4.1.2 and Section 4.1.3. The part of the action (65) relevant for this purpose is given by
where, using the definition of the field strength tensor () and the totally antisymmetric nature of the symbol (), we note the following identities
Notice that apart from the gauge fields, these expressions involve the metric. Therefore, it is convenient to characterize the metric fluctuations in their most general form using ADM decomposition as
where is the three spatial metrics on constant-time hypersurfaces, N is the lapse function and is the shift vector. In terms of these variables, the component of the metric with the upper indices can be expressed as
where is the inverse of the spatial metric. Including the Einstein–Hilbert term () with the action (A42) and the matter action associated with the scalar field(s) (), one can show that the second-order terms that include do not contain more than one time derivative, implying that they can be identified as Lagrange multipliers to be solved in terms of the physical fluctuations of and [286,330].
To characterize the dynamics of gauge fields, we assume that vector fields start the linear order in perturbations (so that they do not exhibit a time-dependent background vev ()) and adopt the Coulomb gauge44 in the gauge sector along with the flat gauge choice in the scalar—gravitational sector
where is the transverse, traceless tensor fluctuation of the metric, . In this appendix, we will present the dynamics of the gauge fields by expanding the action (A42) up to the third order in fluctuations. Noting that the shift vector is order-one in perturbations and expanding the lapse (), we compile all the information mentioned above to obtain the second- and third-order action involving gauge field fluctuations as
where we introduced electric and magnetic field notation using , . Note that we artificially introduced tadpole terms proportional to the expectation values involving and fields in the expressions (A49) and (A50). Later, we will subtract these terms in the action describing inflation (gravity plus inflation sector) in (A72) to consistently take into account the modifications that might arise in the background equations of the scalar field(s) () and the Friedmann equation (see, e.g., Equation (71)).
The action labeled by parameterizes the cubic interactions (see, e.g., the first and the third term in (A50)) induced by the gravitational fluctuations. The influence of these terms on the observable scalar sector was studied in [283,332] with the conclusion that they can be neglected compared to the direct interaction term in (A49). This is because the vertices associated with the gravitationally induced cubic terms in (A50) is suppressed () with respect to that in (A49) unless and 45 and therefore can be safely ignored compared to the latter. Finally, the cubic action in (A51) parameterizes the influence of the gauge fields on the tensor part of the metric. In this review, we will not study these effects. For the impact of gauge field production on the tensor fluctuations during inflation and its interesting parity violating effects, see [85,86,302,333,334,335,336] and the references therein.
To summarize, in the presence of rolling axion-like fields during inflation and the interaction (), the dynamics of the gauge fields can be studied by focusing on the second-order action () (A48). On the other hand, the influence of the gauge fields on the scalar sector depends on whether we identify as the inflation (Section 4.1.1 and Section 4.1.2) or as a spectator scalar rolling during inflation (Section 4.1.3). In the following, we will first introduce the basics of the gauge field production in the presence of a rolling scalar, discussing the different cases we cover in this review. The nature of the subsequent sourcing of (visible sector) scalar fluctuations by the vector fields depends on whether the scalar () directly interacts with fields or not. We will cover each case following our discussion on the vector field production.
Appendix D.1. Gauge Field Production by Rolling Scalars
To understand the gauge field production by a rolling scalar (either an inflation or a spectator scalar), we focus on the second-order action (A48) and decompose the gauge field into its helicity modes () in Fourier space using conformal time () as
where the polarization vectors obey
and we defined
which satisfies so that is a hermitian operator. Finally, annihilation and creation operators satisfy the standard commutation relations
Plugging the decomposition into (A48) and varying the action, the mode functions of the gauge field can be shown to satisfy
It is clear from Equation (A56) that the dispersion relation of the gauge fields are modified in the presence of the last term in (A42). More importantly, the negative helicity modes () can experience a tachyonic instability for modes satisfying , while positive helicity modes stay in their vacuum. These facts reflect the parity-violating nature of the interaction (). The behavior of the solutions according to Equation (A56) is sensitive to the velocity profile () of the rolling scalar. In what follows, we discuss the different cases and the corresponding solutions within the context of Section 4.1.1, Section 4.1.2 and Section 4.1.3.
Production by a slowly rolling scalar. For a slowly rolling scalar field, we can treat as constant per Hubble time. In terms of the effective coupling (), this adiabaticity condition can be parameterized as
In this case, the solution to the Equation (A56) that reduces to the Bunch–Davies vacuum solutions () deep inside the horizon () can be written in terms of the Coulomb functions
where and . Another simplification can be made, focusing on the regime (as we will see, particle production is only efficient for and takes place as )
where and are modified Bessel functions of the first and second kind, respectively. According to the solution presented above, one can realize that for the interesting case of , field amplification occurs shortly after horizon crossing (). Therefore, for a final simplification we can take the large argument limit () of the Bessel functions in (A59) to obtain
The real part of the solution (A60) is the growing solution, as and encodes the physical amplification of the negative helicity mode by the presence of a slowly rolling axion-like field. Within the approximations we undertake, the imaginary part of the solution (A60) represents the UV-divergent part as grows, which should precede the vacuum solution deep inside the horizon. Therefore, ignoring the imaginary part typically amounts to throwing away the standard divergent (also present in flat space) peace of quantities such as and (see below). For a detailed discussion of these issues, we refer the reader to [285] and the appendices of [85].
Production by a transiently rolling scalar. For the models we discuss in Section 4.1.2, the potential of the scalar () has a feature around which the background velocity () and the effective coupling () in the equation of motion of the gauge field modes (A56) have a transient peak with a maximal value () at . A peaked time-dependent profile of , in turn, translates into a scale-dependent growth of the mode functions( ), where only modes that are in the vicinity of the scale () that exits the horizon at are maximally amplified. For the time-dependent profiles we study in Section 4.1.2 and Section 4.1.3, it is difficult to obtain a fully analytic solution describing the amplification of the gauge modes. However, an accurate description of the mode function at late times can be obtained by employing WKB approximation methods supplemented with numerical analysis [302], as we mention below. In particular, at late times (), the amplification of the mode functions can be parameterized in terms of a (real and positive) normalization factor as
where we defined and as a time-dependent function that asymptotes to zero at late times (), the functional form of which depends on the model under consideration. For example, for the bumpy axion inflation discussed in Section 4.1.2 and its cousin spectator model (see Section 4.1.3), it is given by . On the other hand, for the transiently rolling axion model with the standard cosine potential, one obtains . Notice that the solution (A61) reduces to (A60) of constant if we make the following replacements: and . An important point that should be observed from the form of the solution (A61) is the dependence of the normalization (amplification) factor on the dimensionless parameter (), which can be derived in terms of the physical model parameters (see Section 4.1.2 and Section 4.1.3). As we explain in the main text, this parameter is a measure of the scalar’s mass around a global minimum () and therefore determines the rate at which the field rolls towards its minimum. In this sense, it determines the width of gauge field modes that take part in particle production; the faster the scalar traverses the region in its potential where the velocity is maximal (i.e., with larger acceleration( )), the less time each gauge field mode spends in the tachyonic region and the fewer of them will be excited by the rolling scalar, leading to a sharper distribution of excited modes. These arguments clarify the dependence of the normalization factor () in (A61) on the parameter (), along with and , which characterize the amplification and scale dependence of the particle production process, respectively.
At fixed and , the scale dependence of the normalization factor can be obtained by numerically solving (A56) for a grid of values and matching these solutions to the WKB solution given at late times. In this way, one can confirm that is given by a log-normal distribution for the models we consider in Section 4.1.2 and Section 4.1.3:
where the functions and parameterizes the background dependence of gauge field production through their dependence on and . In particular, accurate fitting formulas for these quantities can be obtained at fixed values in terms of . For the parameter choices we adopt in this review, these formulas can be found in [85,86,285].
The “Electric” and “Magnetic” fields as sources. For future reference, we also note the electric and magnetic fields, which are related to the auxiliary potential () as
Utilizing the decomposition (A52), together with (A53) and (A54), we take into account only the growing part (i.e., the real part) of the solutions (corresponding to the physical amplification of vector fields caused by a rolling scalar) we derived in (A60) and (A61) to express the Fourier decomposition of the and fields as follows
where
where we defined the short-hand notation . Note that the case of particle production through a slowly rolling scalar with can be recovered from the formulas by making the following replacements: , and . Having studied the particle production in the gauge field sector, we now study the expectation values including electromagnetic fields before we discuss how these sources influence the fluctuations of the scalar sector.
Expectation values involving gauge fields. Noting again the decomposition of the vector fields (A52) (along with (A53) and (A54)) and the definition of their electromagnetic counterparts (A63), the energy density of the gauge fields ( and ) can be expressed as
Taking into account only the amplified mode function () of the gauge field, the energy density ( and ) per logarithmic wave number is given by
where we utilized [285],
defining the the following dimensionless variables: and . Employing the solutions for we derived in (A60) and (A61), one can use Formulas (A66) and (A67) to obtain and . In particular, for the localized gauge field production models presented in Section 4.1.2 (see [86]) and Section 4.1.3 (see [85]), these formulas can be used to justify the negligible back-reaction of the gauge fields on the background evolution. We will not repeat these calculations here for the localized production case; however, below, we will derive the relevant formulas for the slowly rolling smooth axion inflation described in Section 4.1.1. For this purpose, we focus on the real part of the solution (A60) that corresponds to the physical amplification of the gauge field fluctuations. Plugging the solution into (A67) and (A66), we obtain
where we send the lower limits of the integrals to zero as the integrands converge in the limit. Similarly, since we are only focusing on the physical amplification of the gauge fields by throwing away the imaginary part of the solution (A60), the integrands vanish quickly deep in the UV (), so we can also send the upper limit of the integrals in (A69) to infinity (). Finally, by making a change of variable to , one can realize that the resulting integrals can be carried analytically; in fact, they are proportional to Gamma functions with integer arguments. In particular, we obtain
Inserting the numerical values of the Gamma functions, these expressions give rise to Equation (72), which we provide in the main text.
Appendix D.2. Scalars Sourced by Vector Fields and the Direct Coupling Case: χ=ϕ
To understand the sourcing of scalar fluctuations by the gauge fields, we should consider the gravitational and inflation (that we refer to as ) action, in addition to : , where
Expanding the action in terms of the scalar fluctuations (, and ) around a background solution, one obtains the following linear and second-order actions,
Notice that in (A72), we subtracted the tadpole terms () that we introduced earlier in Equations (49) and (50). By virtue of the background equations presented in Equation (71), these terms precisely cancel. The terms that contain gravitational fluctuations ( and ) in the second-order action () (A73) induce additional mass contributions to the inflation fluctuations, which can be seen by varying this action with respect to and and solving them in terms of as
where we defined the Hubble slow-roll parameters as
Similar to our discussion regarding the cubic terms induced by gravity within the gauge field sector (see e.g., (50)), the influence of the lapse and shift on the second-order action of the inflation fluctuations can be typically ignored in the slow-roll regime (as well as for the non-attractor era associated with the model in Section 4.1.2, where , ), which is a situation that is generically referred as the decoupling limit of gravity within the literature. However, for completeness, we will keep them here. Plugging (A74) into the action (A73), we perform several integrations by parts, and by taking into account the source terms induced by the gauge fields ( in Equation (49)), the equation of motion obeyed by the inflation fluctuations can be written as
where is the Laplacian in flat Euclidean space, and the effective time-dependent mass is defined as . Noting the second derivative of the potential in terms of the slow-roll parameters:
the effective time-dependent mass can be described fully in terms of the slow-roll parameters as
In (A76), the last term is introduced to parameterize the additional sources that might arise in the strong back-reaction regime. In particular, as grows during inflation (i.e., as the effective coupling increases during inflation; see Equation (72)), this will first have the effect of sourcing the inflation perturbations through the first term on the right-hand side of (A76). As a result, the inflation perturbations start to grow, and eventually, the solution of the gauge field modes obtained by assuming a homogeneous inflation will no longer be valid and are expected to go from the solution (A60) to a more general solution (). The additional term on the right-hand side of (A76) is precisely introduced to capture the influence of this modified solution of the gauge fields on the inflation perturbations. Since gauge field production (and ) is sensitive to the velocity of the homogeneous inflation mode, it is reasonable to expect the influence of this additional source to be proportional to , as shown in (A76) (see also [79,81,281] for a detailed discussion of this point). Recalling and (72), we note
so the influence of the source term can be parameterized as an additional damping term in the equation of motion of the inflation fluctuations as
where
Assuming that amounts to neglecting the influence back-reaction effects of the inflation fluctuations on the gauge field solutions. This is, for example, the approach taken in [86] for the bumpy axion inflation we discussed in Section 4.1.2 with the reasoning that back-reaction effects are mild due to the localized nature of gauge field production (as is the resulting increase in inflation fluctuations) in the presence of a transiently increasing effective coupling () between scalar and gauge field sectors. However, in smooth axion inflation (Section 4.1.1), gauge field sources and the resulting scalar fluctuations continuously grow, which can eventually influence the dynamics of the fluctuations through an additional (positive) friction term in (A81) as soon as the homogeneous dynamics of the inflation enter into the back-reaction regime with .
Armed with the equations of motion in real space, one can study vacuum and sourced solutions of the inflation perturbations in Fourier space by using the splitting () and utilizing the standard Green function methods. We will not repeat these computations here; for the calculation of the scalar power spectrum relevant to PBH formation, interested readers can consult [79,81,281,283] in the context of smooth axion inflation and [86] in the context of bumpy axion inflation as discussed in Section 4.1.1 and Section 4.1.2.
Appendix D.3. Scalars Sourced by Vector Fields and the Indirect Coupling Case: χ = σ
To capture the dynamics of scalar fluctuations in the models studied in Section 4.1.3, we extend the inflationary action with a spectator sector () that interacts with the gauge fields as in (A42). The action that describes inflation is therefore given by
where we assume that the spectator axion-like field does not contribute significantly to the background evolution during inflation, which is mainly driven by a sufficiently flat inflation potential (V) that we will leave unspecified.
Expanding the action in terms of the scalar fluctuations (, and ) around a background solution, we obtain the following linear and second-order actions,
where the summation over a runs over fluctuations and background values of the following two fields: and . Varying (A84) with respect to Lagrange multipliers and , we obtain
Plugging these solutions back into the actions, we obtain the following second-order action for scalar fluctuations [286,303],
where summation over repeated indices () is implied and with . We note that in deriving the expressions presented above, we used background equations of motion, ignoring the artificially introduced mean field expectation values involving gauge fields (noticing that these terms that appear in (A49), (A50) and (A83) sum up to zero):
Indeed, for the spectator models discussed in Section 4.1.3, due to the localized nature of the gauge field production, the back-reaction effect is small and can be ignored [81,85,285]; therefore, the background evolution can be studied in a consistent way by focusing on the equations in (A89), along with the Friedmann equation (). Taking into account the effects of gauge field sources ( in Equation (A49)) on the spectator scalar fluctuations, the equations of motion for the scalar perturbations read as
where and . Notice that since we consider sum separable potentials (), the first term in the mass matrix (A88) makes a diagonal contribution to the mass of each field in the equations of motion (A91). However, the presence of the second term in the mass matrix (A88), which is induced by the presence of gravitational fluctuations ( and ) introduces mass mixing between scalar fluctuations ( ()) (i.e., through the last term in (A91)). In other words, although we consider a Lagrangian (A82) where the two scalar fields appear to be decoupled from each other, gravitational interaction will inevitably introduce a minimal communication channel between the physical fluctuations of the two scalar sectors. At leading order in the slow-roll expansion, the mass mixing () originates from the following terms in the Lagrangian
where is the slow-roll parameter of each field. Therefore, as long as both fields roll with a non-vanishing velocity () during inflation, their fluctuations can be converted to one another. In the presence of particle production in the gauge field sector, the mixing between the two scalar sectors is crucial in understanding the influence of the gauge field sources on the visible scalar sector fluctuations (). In order to see this explicitly, we focus on the leading order mixing in the slow-roll expansion to rewrite the system of equations in (A91) as
where at leading order in the slow-roll expansion. We note that in the second line of (A93), we ignored mixing terms that can source spectator fluctuations () through , which is a subleading effect compared to the sourcing of by the enhanced gauge fields. This amounts to considering the main production channel of the observable scalar fluctuations schematically as . Using the equations of motion in real space (A93) and considering their sources in (A65), the observable power spectrum of scalar fluctuations can be carried out using Green’s function methods in Fourier space following the detailed calculations presented in [85,302], along with the prescription we present in Appendix E regarding the curvature perturbation.
Appendix E. Curvature Perturbation
In this short appendix, we define the curvature perturbation () on comoving slices and study its parametric dependence on the matter fluctuations for some of the scenarios we consider in the main text. We begin by noting the definition of comoving curvature perturbation in flat gauge, which reads as [324,337]:
where and are the total background energy density and pressure (see Appendix A), respectively, and is the scalar momentum density in flat gauge. In terms of the perturbed energy momentum tensor, is given by
where the definition of the unperturbed energy momentum tensor provided on the right-hand side of (A95) can be used for a given matter action describing the system. We note that in this definition, represents the variation of the matter action with respect to the metric field. Anticipating that we will focus on different limits of a more complicated/general model, we start by parameterizing perturbed for the spectator axion model we discussed in Section 4.1.3 with the matter action given by the sum of (A82) and (A42). Noting that the last term in (A42) is topological and does not gravitate, we have
where the last term characterizes the contribution from gauge fields, which is second-order in fluctuations. Following (A94)–(A96), it is clear that for a multisector inflationary model, curvature perturbation can, in principle, obtain contributions from all fields present in the matter Lagrangian. In what follows, we take (A96) as the main reference point to study different limits to derive an expression for the curvature perturbation () relevant to some of the models we studied in the main text.
Canonical single-field inflation. This case corresponds to neglecting terms proportional to spectator and gauge field fluctuations in (A96). Noting that for single-field canonical inflation to linear order in inflation fluctuations, the curvature perturbation (A94) is given by
where we made the connection between the MS variable (see Section 3.1) and inflation fluctuations clear () using the definition of pump field in this case (). Upon canonical quantization of (and hence ), their corresponding Fourier space variables satisfy the same relation in (A97), and the dimensionless power spectrum at the end of inflation can be computed via (A41).
Smooth Axion Inflation and Bumpy Axion Inflation. For the models we studied in Section 4.1.1 and Section 4.1.2, we instead focus on the curvature perturbation () on uniform-density gauge, which can be related to the density perturbation in flat gauge () and comoving curvature perturbation () on superhorizon scales as [337]
where is the total energy density of the axion gauge field system. Using background equations of the system, the time derivative of the total energy density is given by [338] where is the energy density of the gauge field as defined in (72). Noting this relation, to linear order46 in the cosmological fluctuations, the comoving curvature perturbation () can be obtained as [81]
where we used , neglecting contributions to the total energy proportional to the kinetic energy of the inflation, as they should be small both in the slow-roll and the inflationary regime dominated by the friction provided by the gauge fields. In (A99), the factor parameterizes the correction to the definition of the curvature perturbation in the strong back-reaction regime, which must be taken into account in the smooth axion inflation model we presented in the main text. On the other hand, the standard relation in (A97) applies to the regime of negligible back-reaction of the gauge field on the evolution of the inflation and expansion of the universe, i.e., when is negligible and the relation is satisfied. This situation applies both at early times during the considered smooth axion model, as well as within the bumpy axion inflation model described in Section 4.1.2, where back-reaction effects were shown to be small around the peak of the scalar power spectrum. To summarize, in the strong back-reaction regime, the power spectrum of curvature perturbation can be computed using the standard relation (A97) times a factor of correction.
Spectator axion-gauge field model. In the model presented in Section 4.1.3, in principle, we need to consider all the contributions to the curvature perturbation using Formulas (A94)–(A96). However, as explicitly checked in [85], the contribution to the curvature perturbation that is bilinear in the gauge fields can be safely ignored at late times during which we are interested in the correlators of . Further simplifications of the functional form of arise due to the spectator nature of the axion sector () and due to the assumption that it settles back to its global minimum long before the end of inflation, where . Noting and the fact that long before inflation ends, the late-time curvature perturbation obtains the following form
Therefore, the standard expression , which is valid in single-field inflation, still provides a very good approximation of the computation of late-time correlators of the curvature perturbation in this model.
Notes
| 1 | See, e.g., the impact of extended mass functions on the PBH abundance constraints [27]. |
| 2 | Ultralight PBHs with —although they cannot account for the DM density—may also have interesting observational effects if they come to dominate the energy budget of the universe before BBN (see, e.g., [36,37]). |
| 3 | Another inflationary background that exhibits similar features is called constant-roll inflation (see, e.g., [44,45]). |
| 4 | PBHs could also form in the post-inflationary universe through the collapse of cosmic strings [106,107,108] and domain walls [109,110,111,112], phase transitions [113,114], bubble collisions [115,116] or scalar-field fragmentation via instabilities [117,118]. We note that PBH formation in the post-inflationary universe can be triggered by bubble nucleation during inflation or instabilities generated in the final stage of inflation commonly referred as (p)reheating [119,120,121,122]. We will not dwell on these possibilities here; for a partial list of recent works in this line of research, see [123,124,125]. |
| 5 | A detailed discussion on these topics can be found in Chapter 4 of Baumann’s book [128]. |
| 6 | Throughout this work, we assume an efficient reheating process at the end of inflation such that the universe becomes radiation-dominated shortly after inflation terminates. For a collage of interesting physics that might arise through the reheating stage and alternative post-inflationary histories, see the recent review [131]. |
| 7 | A simple analytic argument that leads to this result is presented in Appendix B. |
| 8 | Other effects such as anisotropies [137] in the radiation fluid and a time-dependent equation of state parameter (w) [138] may also impact the estimate of the threshold for collapse. |
| 9 | Strictly speaking, is only satisfied when species are in thermal equilibrium at the same temperature. For a comprehensive overview of the thermal history of the universe after inflation, see Chapter 3 of [128]. |
| 10 | We note that another common convention is to count e-folds with respect to the end of inflation, denoting the end point as . |
| 11 | In contrast to the original approach by Press and Schechter [145], we do not take into account a symmetry factor of two on the right-hand side of (13), which accounts for all the mass in the universe, since it is not clear whether such a factor makes sense when considering non-symmetric PDFs of (e.g., non-Gaussian cases). Furthermore, the error introduced by omitting this factor is comparable to the other uncertainties in the computation of , such as the fraction of the horizon mass that collapses to form a PBH (see, e.g., [146,147,148]). |
| 12 | Non-linearities that we neglect in the expression (16) can be important to understand intrinsic non-Gaussianity present in the PBH formation process (see, e.g., [150,151] and references therein.) |
| 13 | |
| 14 | Note that the power spectrum is the variance of curvature perturbation per logarithmic interval in k, i.e., . Therefore, the approximate signs (≃) in the expressions in (26) and (30) can be turned into an equality if we consider the values defined in those expressions as the collapse fraction per in the spectrum, namely . |
| 15 | One can also introduce a time-dependent mass in the action (35) which may arise through broken spatial translations as in solid [179] and supersolid [180,181] inflation. Another possibility is to include higher derivative terms in the quadratic action to modify the dispersion relation of curvature perturbation (see, e.g., [182]) as in ghost inflation [183]. We will not consider these possibilities here. For a discussion of PBH formation in solid and ghost inflation, see Sections 4 and 6 of [64,184]. |
| 16 | In fact, if the time evolution of the pump field is known, up to second order in the gradient expansion, we can generate a solution for the curvature perturbation by replacing in the last integral of Equation (39) with the leading growing-mode solution of the homogeneous part of Equation (38), which we can identify as . |
| 17 | In particular, the standard decaying mode is given by the last term in (39), as it decays slowly, i.e., , compared to the second term. |
| 18 | Here, we assume that field rolls down on its potential from large to small values () with before it encounters the feature required for the enhancement. Since during the feature, there must be a point in the potential where the second derivative of the field vanishes (). |
| 19 | |
| 20 | Note that evaluating the power spectrum at the end of inflation is necessary when modes evolve outside the horizon, as in the example background we are focusing on in this section. |
| 21 | In fact, the general procedure outlined in Appendix C can be generalized to accurately solve the Mukhanov–Sasaki equation using a broad class of single-field models of inflation. In the context of phenomenological models we discuss in this and the next section, jupyter notebook files that compute the power spectrum is are available at https://github.com/oozsoy/SingleFieldINF_Powerspec_PBH (accessed on 24 January 2023). We acknowledge the use of the following Python libraries: matplotlib [219], numpy [220], scipy [221], pandas [222] along with jupyter notebooks [223]. |
| 22 | The distinct behavior of the cosmological correlators around the dip feature may also be probed by the 21 cm signal of the Hydrogen atom [230]. |
| 23 | Notice that an exponential tail in the PDF of curvature fluctuations, similar to the tailarising in the context of a stochastic approach to inflation, has been recently shown [256] to be a property of all single-field models with potential up to quadratic. Such a feature is physically caused by the logarithmic relation between curvature fluctuation and the (Gaussian) inflation field fluctuations (see [256] for details). |
| 24 | Notice that if the background dynamics have localized features, phases of slow-roll violation might occur for some time interval, and this exact identification ceases to be valid. In particular, in this case, might lose its monotonic nature for some time interval, leading to multiple horizon crossings for a range of modes, resulting in oscillations of the spectrum [64]. For the time being, we set a discussion on this possibility aside and continue identifying the quantity as an effective horizon for the slow-roll violating scenarios we are interested in. |
| 25 | Some other notable models we do not cover in this context utilize (i) dissipative dynamics as in warm inflation-type scenarios discussed in [264,265,266], (ii) the conversion of resonantly produced spectator fluctuations to curvature perturbation during [75] or after inflation, e.g., in curvaton-type scenarios discussed in [267,268]. |
| 26 | See e.g., [276,277,278,279] for string-theory-motivated constructions in the context of inflation. |
| 27 | Be aware that despite the terminology we adopt, the gauge fields () do not need to correspond to Standard Model photons. |
| 28 | At large CMB scales described by modes leaving the horizon in the early stages of inflation, the value of the effective coupling () is restricted by existing information and constraints on the scalar power spectrum and non-Gaussianity [282,283,288]. Depending on priors and on the shape of the inflation potential, these constraints give [289]. |
| 29 | In fact, the potential (78) is not unique for the purpose of generating a localized particle production scenario. In this context, any potential that exhibits (a) step-like feature(s) is sufficient (see e.g., [83,296]. However, the choice of the potential in (78) does provide some useful analytic control over the background evolution of the axion and the resulting amplification of the power spectrum, as discussed in [86]. |
| 30 | As discussed in [86], this assumption is actually self-consistent due to the localized nature of the particle production. |
| 31 | For the phenomenological examples we will present in this section, this statement can be made precise, and back-reaction can be shown to be negligible [85,285]. |
| 32 | In this work, by an appropriate choice of initial conditions and model parameters, we assume that traverses two step-like features on its potential before it settles to its global minimum. |
| 33 | The roll of towards the global minimum can be captured by modifying the monomial term as so that the axion potential (85) interpolates between and from large to small field () values, respectively. |
| 34 | For M2, this translates into a single step-like region in the potential (see Figure 15). |
| 35 | In the comoving gauge with which we are operating, the field fluctuations are proportional to entropy fluctuation (), while the spatial part of the metric takes the form . |
| 36 | Recall from our discussion above that entropic mass crossing at corresponds to the peak of the power spectrum. |
| 37 | For a detailed analytic/numerical analysis of the behavior of the power spectrum from strong sharp turns, see [72,73]. |
| 38 | More realistic models of the turn are expected to have a smooth time dependence of such as the Gaussian profile we considered earlier. As shown by the numerical evaluations in [312], the choice of top-hat profile does not introduce any qualitative difference but appears to be a convenient choice for analytic manipulations. For a detailed study of sudden turn trajectories in conjunction with PBH formation, see [315]. |
| 39 | We also note that the presence of very light entropy mode (for the case) leads to a non-negligible contribution to the power spectrum for scales that cross the horizon before the turn, i.e., for . In particular, the analytic expression (101) does not perform well on these scales. For a more complete analytic formula including numerical analysis, see [312]. |
| 40 | Note that for flat spatial hypersurfaces (), we can define new coordinates as , and to turn the metric into a form that is commonly used in the literature (). |
| 41 | Indeed, CMB data inform us that the spatial geometry of our universe is flat on large cosmological scales (see (A18)). On the other hand, since it dilutes slowly () compared to radiation and matter, we would expect it to dominate the energy density before DED, but this did not happen. This implies that the initial value of the curvature must either be tuned to be extremely small or that it should relax to small values through a dynamical mechanism. Inflation could be also a solution to this puzzle because during such an exponential expansion, any initially large curvature would be inflated away. |
| 42 | The red-shift parameter can be defined as the fractional shift in the physical wavelength () of a photon emitted at a distant point and time (t) in the universe until today, i.e., . |
| 43 | Unless modes undergo resonance and are excited deep inside the horizon, the choice of initial conditions in Equations (A34) and (A35) provide an accurate prescription for the initialization of the numerical evaluation. For the models we consider in Section 3.2 and Section 3.3, this is indeed the case. For a model that leads to excited states inside the horizon, see [328,329]. |
| 44 | We note that at linear order in fluctuations, the Coulomb gauge condition () is equivalent to setting the temporal component of the gauge field to zero, i.e., . This can be seen by explicitly expanding the gauge field action (A42) to second order in and , then solving for the non-dynamical mode (see also the discussion in Section 3 of [331]). |
| 45 | This regime is not interesting from a phenomenological point of view, as the gauge field production will be very weak in this case. |
| 46 | We note that also takes up a contribution bilinear in gauge fields proportional to the absolute value of the Poynting vector (). We expect this contribution to be negligible at the end of inflation (i.e., at the time for we are interested in the correlators of ) because the gauge field production saturates on superhorizon scales, and the corresponding electromagnetic fields decay as . See, e.g., the discussion presented in [85,339] within similar contexts. |
References
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. 1981, D23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. 1982, B108, 389–393. [Google Scholar] [CrossRef]
- Penzias, A.A.; Wilson, R.W. A Measurement of excess antenna temperature at 4080-Mc/s. Astrophys. J. 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. IX. Constraints on primordial non-Gaussianity. Astron. Astrophys. 2020, 641, A9. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Aghanim, N.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2021, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Bergström, L. Nonbaryonic dark matter: Observational evidence and detection methods. Rep. Prog. Phys. 2000, 63, 793. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Sov. Astron. AJ (Engl. Transl.) 1967, 10, 602. [Google Scholar]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S.W. Black holes in the early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Chapline, G.F. Cosmological effects of primordial black holes. Nature 1975, 253, 251–252. [Google Scholar] [CrossRef]
- Carr, B.J.; Rees, M.J. Can pregalactic objects generate galaxies? Mon. Not. R. Astron. Soc. 1984, 206, 801–818. [Google Scholar] [CrossRef]
- Aubourg, E.; Bareyre, P.; Brehin, S.; Gros, M.; Lachieze-Rey, M.; Laurent, B.; Lesquoy, E.; Magneville, C.; Milsztajn, A.; Moscoso, L.; et al. Evidence for gravitational microlensing by dark objects in the galactic halo. Nature 1993, 365, 623–625. [Google Scholar] [CrossRef]
- Tisserand, P.; Le Guillou, L.; Afonso, C.; Albert, J.N.; Andersen, J.; Ansari, R.; Aubourg, É.; Bareyre, P.; Beaulieu, J.P.; Charlot, X.; et al. Limits on the Macho Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. Astron. Astrophys. 2007, 469, 387–404. [Google Scholar] [CrossRef]
- Wyrzykowski, L.; Kozlowski, S.; Skowron, J.; Udalski, A.; Szymanski, M.K.; Kubiak, M.; Pietrzynski, G.; Soszynski, I.; Szewczyk, O.; Ulaczyk, K.; et al. The OGLE View of Microlensing towards the Magellanic Clouds. III. Ruling out sub-solar MACHOs with the OGLE-III LMC data. Mon. Not. R. Astron. Soc. 2011, 413, 493. [Google Scholar] [CrossRef]
- Wyrzykowski, L.; Kozlowski, S.; Skowron, J.; Udalski, A.; Szymanski, M.K.; Kubiak, M.; Pietrzynski, G.; Soszynski, I.; Szewczyk, O.; Ulaczyk, K.; et al. The OGLE View of Microlensing towards the Magellanic Clouds. IV. OGLE-III SMC Data and Final Conclusions on MACHOs. Mon. Not. R. Astron. Soc. 2011, 416, 2949. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO detect dark matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef] [PubMed]
- Clesse, S.; García-Bellido, J. The clustering of massive Primordial Black Holes as Dark Matter: Measuring their mass distribution with Advanced LIGO. Phys. Dark Univ. 2017, 15, 142–147. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2018, 117, 061101, Erratum in Phys. Rev. Lett. 2018, 121, 059901. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yasuda, N.; Lupton, R.H.; Sumi, T.; More, S.; Kurita, T.; Sugiyama, S.; More, A.; Oguri, M.; et al. Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations. Nat. Astron. 2019, 3, 524–534. [Google Scholar] [CrossRef]
- Katz, A.; Kopp, J.; Sibiryakov, S.; Xue, W. Femtolensing by Dark Matter Revisited. J. Cosmol. Astropart. Phys. 2018, 2018, 005. [Google Scholar] [CrossRef]
- Montero-Camacho, P.; Fang, X.; Vasquez, G.; Silva, M.; Hirata, C.M. Revisiting constraints on asteroid-mass primordial black holes as dark matter candidates. J. Cosmol. Astropart. Phys. 2019, 2019, 031. [Google Scholar] [CrossRef]
- Carr, B.; Raidal, M.; Tenkanen, T.; Vaskonen, V.; Veermäe, H. Primordial black hole constraints for extended mass functions. Phys. Rev. D 2017, 96, 023514. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Primordial Black Holes. Res. Astron. Astrophys. 2010, 10, 495–528. [Google Scholar] [CrossRef]
- García-Bellido, J. Massive Primordial Black Holes as Dark Matter and their detection with Gravitational Waves. J. Phys. Conf. Ser. 2017, 840, 012032. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes: Perspectives in gravitational wave astronomy. Class. Quant. Grav. 2018, 35, 063001. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on primordial black holes. Rep. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef]
- Green, A.M.; Kavanagh, B.J. Primordial Black Holes as a dark matter candidate. J. Phys. G 2021, 48, 043001. [Google Scholar] [CrossRef]
- Escrivà, A.; Kuhnel, F.; Tada, Y. Primordial Black Holes. arXiv 2022, arXiv:2211.05767. [Google Scholar]
- Page, D.N. Particle Emission Rates from a Black Hole: Massless Particles from an Uncharged, Nonrotating Hole. Phys. Rev. D 1976, 13, 198–206. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Vennin, V.; Langlois, D. Gravitational waves from a universe filled with primordial black holes. J. Cosmol. Astropart. Phys. 2021, 2021, 053. [Google Scholar] [CrossRef]
- Papanikolaou, T. Gravitational waves induced from primordial black hole fluctuations: The effect of an extended mass function. J. Cosmol. Astropart. Phys. 2022, 2022, 089. [Google Scholar] [CrossRef]
- Ivanov, P.; Naselsky, P.; Novikov, I. Inflation and primordial black holes as dark matter. Phys. Rev. 1994, D50, 7173–7178. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of adiabatic perturbations in the universe when there are singularities in the inflation potential. JETP Lett. 1992, 55, 489–494. [Google Scholar]
- Dimopoulos, K. Ultra slow-roll inflation demystified. Phys. Lett. 2017, B775, 262–265. [Google Scholar] [CrossRef]
- Leach, S.M.; Liddle, A.R. Inflationary perturbations near horizon crossing. Phys. Rev. 2001, D63, 043508. [Google Scholar] [CrossRef]
- Leach, S.M.; Sasaki, M.; Wands, D.; Liddle, A.R. Enhancement of superhorizon scale inflationary curvature perturbations. Phys. Rev. 2001, D64, 023512. [Google Scholar] [CrossRef]
- Kinney, W.H. Horizon crossing and inflation with large eta. Phys. Rev. 2005, D72, 023515. [Google Scholar] [CrossRef]
- Martin, J.; Motohashi, H.; Suyama, T. Ultra Slow-Roll Inflation and the non-Gaussianity Consistency Relation. Phys. Rev. 2013, D87, 023514. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Inflation with a constant rate of roll. J. Cosmol. Astropart. Phys. 2015, 2015, 018. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Garcia-Bellido, J.; Ruiz Morales, E. Primordial Black Hole production in Critical Higgs Inflation. Phys. Lett. B 2018, 776, 345–349. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Ballesteros, G.; Taoso, M. Primordial black hole dark matter from single field inflation. Phys. Rev. 2018, D97, 023501. [Google Scholar] [CrossRef]
- Hertzberg, M.P.; Yamada, M. Primordial Black Holes from Polynomial Potentials in Single Field Inflation. Phys. Rev. D 2017, 97, 083509. [Google Scholar] [CrossRef]
- Cicoli, M.; Diaz, V.A.; Pedro, F.G. Primordial Black Holes from String Inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 034. [Google Scholar] [CrossRef]
- Özsoy, O.; Parameswaran, S.; Tasinato, G.; Zavala, I. Mechanisms for Primordial Black Hole Production in String Theory. J. Cosmol. Astropart. Phys. 2018, 2018, 005. [Google Scholar] [CrossRef]
- Mishra, S.S.; Sahni, V. Primordial Black Holes from a tiny bump/dip in the inflation potential. J. Cosmol. Astropart. Phys. 2020, 2020, 007. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Markkanen, T.; Racioppi, A.; Vaskonen, V. Primordial Black Holes from Thermal Inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 046. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Taoso, M.; Urbano, A. Primordial black holes as dark matter and gravitational waves from single-field polynomial inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 025. [Google Scholar] [CrossRef]
- Inomata, K.; McDonough, E.; Hu, W. Amplification of primordial perturbations from the rise or fall of the inflation. J. Cosmol. Astropart. Phys. 2022, 2022, 031. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Linde, A.D.; Wands, D. Density perturbations and black hole formation in hybrid inflation. Phys. Rev. D 1996, 54, 6040–6058. [Google Scholar] [CrossRef]
- Kawasaki, M.; Sugiyama, N.; Yanagida, T. Primordial black hole formation in a double inflation model in supergravity. Phys. Rev. D 1998, 57, 6050–6056. [Google Scholar] [CrossRef]
- Yokoyama, J. Chaotic new inflation and formation of primordial black holes. Phys. Rev. D 1998, 58, 083510. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Kawasaki, M.; Takayama, T.; Yamaguchi, M.; Yokoyama, J. Formation of intermediate-mass black holes as primordial black holes in the inflationary cosmology with running spectral index. Mon. Not. R. Astron. Soc. 2008, 388, 1426–1432. [Google Scholar] [CrossRef]
- Kohri, K.; Lyth, D.H.; Melchiorri, A. Black hole formation and slow-roll inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 038. [Google Scholar] [CrossRef]
- Frampton, P.H.; Kawasaki, M.; Takahashi, F.; Yanagida, T.T. Primordial Black Holes as All Dark Matter. J. Cosmol. Astropart. Phys. 2010, 2010, 023. [Google Scholar] [CrossRef]
- Drees, M.; Erfani, E. Running Spectral Index and Formation of Primordial Black Hole in Single Field Inflation Models. J. Cosmol. Astropart. Phys. 2012, 2012, 035. [Google Scholar] [CrossRef]
- Ballesteros, G.; Beltran Jimenez, J.; Pieroni, M. Black hole formation from a general quadratic action for inflationary primordial fluctuations. J. Cosmol. Astropart. Phys. 2019, 2019, 016. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Venturi, G. DBI inflation and warped black holes. J. Cosmol. Astropart. Phys. 2022, 2022, 051. [Google Scholar] [CrossRef]
- Cai, Y.F.; Tong, X.; Wang, D.G.; Yan, S.F. Primordial Black Holes from Sound Speed Resonance during Inflation. Phys. Rev. Lett. 2018, 121, 081306. [Google Scholar] [CrossRef]
- Chen, C.; Ma, X.H.; Cai, Y.F. Dirac-Born-Infeld realization of sound speed resonance mechanism for primordial black holes. Phys. Rev. D 2020, 102, 063526. [Google Scholar] [CrossRef]
- Baumann, D.; McAllister, L. Inflation and String Theory; Cambridge Monographs on Mathematical Physics, Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Randall, L.; Soljacic, M.; Guth, A.H. Supernatural inflation: Inflation from supersymmetry with no (very) small parameters. Nucl. Phys. B 1996, 472, 377–408. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive Primordial Black Holes from Hybrid Inflation as Dark Matter and the seeds of Galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef]
- Brown, A.R. Hyperbolic Inflation. Phys. Rev. Lett. 2018, 121, 251601. [Google Scholar] [CrossRef] [PubMed]
- Palma, G.A.; Sypsas, S.; Zenteno, C. Seeding primordial black holes in multifield inflation. Phys. Rev. Lett. 2020, 125, 121301. [Google Scholar] [CrossRef]
- Fumagalli, J.; Renaux-Petel, S.; Ronayne, J.W.; Witkowski, L.T. Turning in the landscape: A new mechanism for generating Primordial Black Holes. arXiv 2020, arXiv:2004.08369. [Google Scholar] [CrossRef]
- Braglia, M.; Hazra, D.K.; Finelli, F.; Smoot, G.F.; Sriramkumar, L.; Starobinsky, A.A. Generating PBHs and small-scale GWs in two-field models of inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 001. [Google Scholar] [CrossRef]
- Zhou, Z.; Jiang, J.; Cai, Y.F.; Sasaki, M.; Pi, S. Primordial black holes and gravitational waves from resonant amplification during inflation. Phys. Rev. D 2020, 102, 103527. [Google Scholar] [CrossRef]
- Iacconi, L.; Assadullahi, H.; Fasiello, M.; Wands, D. Revisiting small-scale fluctuations in α-attractor models of inflation. J. Cosmol. Astropart. Phys. 2021, 2022, 007. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. Dilaton-Axion Inflation with PBHs and GWs. J. Cosmol. Astropart. Phys. 2022, 2022, 037. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes and gravitational waves from nonminimally coupled supergravity inflation. Phys. Rev. 2022, 107, 043523. [Google Scholar] [CrossRef]
- Linde, A.; Mooij, S.; Pajer, E. Gauge field production in supergravity inflation: Local non-Gaussianity and primordial black holes. Phys. Rev. D 2013, 87, 103506. [Google Scholar] [CrossRef]
- Bugaev, E.; Klimai, P. Axion inflation with gauge field production and primordial black holes. Phys. Rev. D 2014, 90, 103501. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Peloso, M.; Unal, C. Gravitational waves at interferometer scales and primordial black holes in axion inflation. J. Cosmol. Astropart. Phys. 2016, 2016, 031. [Google Scholar] [CrossRef]
- Domcke, V.; Muia, F.; Pieroni, M.; Witkowski, L.T. PBH dark matter from axion inflation. J. Cosmol. Astropart. Phys. 2017, 2017, 048. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lee, W.; Ng, K.W. Primordial black holes and associated gravitational waves in axion monodromy inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 001. [Google Scholar] [CrossRef]
- Kawasaki, M.; Nakatsuka, H.; Obata, I. Generation of Primordial Black Holes and Gravitational Waves from Dilaton-Gauge Field Dynamics. J. Cosmol. Astropart. Phys. 2020, 2020, 007. [Google Scholar] [CrossRef]
- Özsoy, O. Synthetic Gravitational Waves from a Rolling Axion Monodromy. J. Cosmol. Astropart. Phys. 2021, 2021, 040. [Google Scholar] [CrossRef]
- Özsoy, O.; Lalak, Z. Primordial black holes as dark matter and gravitational waves from bumpy axion inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 040. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. 2007, D75, 123518. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. 2007, D76, 084019. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. 2018, D97, 123532. [Google Scholar] [CrossRef]
- Nakama, T.; Silk, J.; Kamionkowski, M. Stochastic gravitational waves associated with the formation of primordial black holes. Phys. Rev. D 2017, 95, 043511. [Google Scholar] [CrossRef]
- Cai, R.G.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef] [PubMed]
- Unal, C. Imprints of Primordial Non-Gaussianity on Gravitational Wave Spectrum. Phys. Rev. D 2019, 99, 041301. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, Z.C.; Huang, Q.G. Log-dependent slope of scalar induced gravitational waves in the infrared regions. Phys. Rev. D 2020, 101, 043019. [Google Scholar] [CrossRef]
- Cai, R.G.; Pi, S.; Sasaki, M. Universal infrared scaling of gravitational wave background spectra. Phys. Rev. D 2020, 102, 083528. [Google Scholar] [CrossRef]
- Özsoy, O.; Tasinato, G. On the slope of the curvature power spectrum in non-attractor inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 048. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Gravitational Waves Induced by Scalar Perturbations with a Lognormal Peak. J. Cosmol. Astropart. Phys. 2020, 2020, 037. [Google Scholar] [CrossRef]
- Yuan, C.; Huang, Q.G. Gravitational waves induced by the local-type non-Gaussian curvature perturbations. Phys. Lett. B 2021, 821, 136606. [Google Scholar] [CrossRef]
- Ragavendra, H.V. Accounting for scalar non-Gaussianity in secondary gravitational waves. Phys. Rev. D 2022, 105, 063533. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Barausse, E.; Berti, E.; Hertog, T.; Hughes, S.A.; Jetzer, P.; Pani, P.; Sotiriou, T.P.; Tamanini, N.; Witek, H.; Yagi, K.; et al. Prospects for Fundamental Physics with LISA. Gen. Relat. Grav. 2020, 52, 81. [Google Scholar] [CrossRef]
- Lentati, L.; Taylor, S.R.; Mingarelli, C.M.; Sesana, A.; Sanidas, S.A.; Vecchio, A.; Caballero, R.N.; Lee, K.J.; Van Haasteren, R.; Babak, S.; et al. European Pulsar Timing Array Limits On An Isotropic Stochastic Gravitational-Wave Background. Mon. Not. R. Astron. Soc. 2015, 453, 2576–2598. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Chen, S.; Cordes, J.M.; et al. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.I.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Polnarev, A.; Zembowicz, R. Formation of Primordial Black Holes by Cosmic Strings. Phys. Rev. D 1991, 43, 1106–1109. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, R.R.; Casper, P. Formation of black holes from collapsed cosmic string loops. Phys. Rev. D 1996, 53, 3002–3010. [Google Scholar] [CrossRef]
- Helfer, T.; Aurrekoetxea, J.C.; Lim, E.A. Cosmic String Loop Collapse in Full General Relativity. Phys. Rev. D 2019, 99, 104028. [Google Scholar] [CrossRef]
- Rubin, S.G.; Khlopov, M.Y.; Sakharov, A.S. Primordial black holes from nonequilibrium second order phase transition. Grav. Cosmol. 2000, 6, 51–58. [Google Scholar]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. J. Cosmol. Astropart. Phys. 2016, 2016, 064. [Google Scholar] [CrossRef]
- Deng, H.; Garriga, J.; Vilenkin, A. Primordial black hole and wormhole formation by domain walls. J. Cosmol. Astropart. Phys. 2017, 2017, 050. [Google Scholar] [CrossRef]
- Kusenko, A.; Sasaki, M.; Sugiyama, S.; Takada, M.; Takhistov, V.; Vitagliano, E. Exploring Primordial Black Holes from the Multiverse with Optical Telescopes. Phys. Rev. Lett. 2020, 125, 181304. [Google Scholar] [CrossRef] [PubMed]
- Kodama, H.; Sasaki, M.; Sato, K. Abundance of Primordial Holes Produced by Cosmological First Order Phase Transition. Prog. Theor. Phys. 1982, 68, 1979. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871–5875. [Google Scholar] [CrossRef]
- Moss, I.G. Singularity formation from colliding bubbles. Phys. Rev. D 1994, 50, 676–681. [Google Scholar] [CrossRef]
- Kitajima, N.; Takahashi, F. Primordial Black Holes from QCD Axion Bubbles. J. Cosmol. Astropart. Phys. 2020, 2020, 060. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A. Primordial black holes from supersymmetry in the early universe. Phys. Rev. Lett. 2017, 119, 031103. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A.; Sasaki, M.; Takhistov, V. Analytic Description of Primordial Black Hole Formation from Scalar Field Fragmentation. J. Cosmol. Astropart. Phys. 2019, 2019, 077. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef]
- Shtanov, Y.; Traschen, J.H.; Brandenberger, R.H. Universe reheating after inflation. Phys. Rev. D 1995, 51, 5438–5455. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. 1997, D56, 3258–3295. [Google Scholar] [CrossRef]
- Amin, M.A.; Hertzberg, M.P.; Kaiser, D.I.; Karouby, J. Nonperturbative Dynamics Of Reheating After Inflation: A Review. Int. J. Mod. Phys. D 2014, 24, 1530003. [Google Scholar] [CrossRef]
- Ashoorioon, A.; Rostami, A.; Firouzjaee, J.T. Examining the end of inflation with primordial black holes mass distribution and gravitational waves. Phys. Rev. D 2021, 103, 123512. [Google Scholar] [CrossRef]
- Martin, J.; Papanikolaou, T.; Vennin, V. Primordial black holes from the preheating instability in single-field inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 024. [Google Scholar] [CrossRef]
- Auclair, P.; Vennin, V. Primordial black holes from metric preheating: Mass fraction in the excursion-set approach. J. Cosmol. Astropart. Phys. 2021, 2021, 038. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Cole, P.S. Lecture notes on inflation and primordial black holes. arXiv 2021, arXiv:2112.05716. [Google Scholar]
- Franciolini, G. Primordial Black Holes: From Theory to Gravitational Wave Observations. Ph.D. Thesis, University of Geneva, Department of Theoretical Physics, Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]
- Baumann, D. Cosmology; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- Sasaki, M. Large Scale Quantum Fluctuations in the Inflationary Universe. Prog. Theor. Phys. 1986, 76, 1036. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Allahverdi, R.; Amin, M.A.; Berlin, A.; Bernal, N.; Byrnes, C.T.; Delos, M.S.; Erickcek, A.L.; Escudero, M.; Figueroa, D.G.; Freese, K.; et al. The First Three Seconds: A Review of Possible Expansion Histories of the Early Universe. arXiv 2020, arXiv:2006.16182. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. 2014, D88, 084051, Erratum in Phys. Rev. 2014, D89, 029903. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Dynamics of primordial black hole formation. Phys. Rev. D 1999, 59, 124013. [Google Scholar] [CrossRef]
- Nakama, T.; Harada, T.; Polnarev, A.G.; Yokoyama, J. Identifying the most crucial parameters of the initial curvature profile for primordial black hole formation. J. Cosmol. Astropart. Phys. 2014, 2014, 037. [Google Scholar] [CrossRef]
- Musco, I. Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations. Phys. Rev. D 2019, 100, 123524. [Google Scholar] [CrossRef]
- Musco, I.; De Luca, V.; Franciolini, G.; Riotto, A. Threshold for primordial black holes. II. A simple analytic prescription. Phys. Rev. D 2021, 103, 063538. [Google Scholar] [CrossRef]
- Musco, I.; Papanikolaou, T. Primordial black hole formation for an anisotropic perfect fluid: Initial conditions and estimation of the threshold. Phys. Rev. D 2022, 106, 083017. [Google Scholar] [CrossRef]
- Papanikolaou, T. Toward the primordial black hole formation threshold in a time-dependent equation-of-state background. Phys. Rev. D 2022, 105, 124055. [Google Scholar] [CrossRef]
- Shibata, M.; Sasaki, M. Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity. Phys. Rev. D 1999, 60, 084002. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef] [PubMed]
- Escrivà, A. PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review. Universe 2022, 8, 66. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Universal threshold for primordial black hole formation. Phys. Rev. D 2020, 101, 044022. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. J. Cosmol. Astropart. Phys. 2021, 2021, 030. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of galaxies and clusters of galaxies by selfsimilar gravitational condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Evans, C.R.; Coleman, J.S. Observation of critical phenomena and selfsimilarity in the gravitational collapse of radiation fluid. Phys. Rev. Lett. 1994, 72, 1782–1785. [Google Scholar] [CrossRef] [PubMed]
- Niemeyer, J.C.; Jedamzik, K. Near-critical gravitational collapse and the initial mass function of primordial black holes. Phys. Rev. Lett. 1998, 80, 5481–5484. [Google Scholar] [CrossRef]
- Koike, T.; Hara, T.; Adachi, S. Critical behavior in gravitational collapse of radiation fluid: A Renormalization group (linear perturbation) analysis. Phys. Rev. Lett. 1995, 74, 5170–5173. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Kehagias, A.; Peloso, M.; Riotto, A.; Ünal, C. The Ineludible non-Gaussianity of the Primordial Black Hole Abundance. J. Cosmol. Astropart. Phys. 2019, 2019, 048. [Google Scholar] [CrossRef]
- Young, S.; Musco, I.; Byrnes, C.T. Primordial black hole formation and abundance: Contribution from the non-linear relation between the density and curvature perturbation. J. Cosmol. Astropart. Phys. 2019, 2019, 012. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T.; Sasaki, M. Calculating the mass fraction of primordial black holes. J. Cosmol. Astropart. Phys. 2014, 2014, 045. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Copeland, E.J.; Green, A.M. Primordial black holes as a tool for constraining non-Gaussianity. Phys. Rev. 2012, D86, 043512. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Primordial black holes in non-Gaussian regimes. J. Cosmol. Astropart. Phys. 2013, 2013, 052. [Google Scholar] [CrossRef]
- Passaglia, S.; Hu, W.; Motohashi, H. Primordial black holes and local non-Gaussianity in canonical inflation. Phys. Rev. D 2019, 99, 043536. [Google Scholar] [CrossRef]
- Biagetti, M.; De Luca, V.; Franciolini, G.; Kehagias, A.; Riotto, A. The formation probability of primordial black holes. Phys. Lett. B 2021, 820, 136602. [Google Scholar] [CrossRef]
- Atal, V.; Germani, C. The role of non-gaussianities in Primordial Black Hole formation. Phys. Dark Univ. 2019, 24, 100275. [Google Scholar] [CrossRef]
- Taoso, M.; Urbano, A. Non-gaussianities for primordial black hole formation. J. Cosmol. Astropart. Phys. 2021, 2021, 016. [Google Scholar] [CrossRef]
- Young, S. Peaks and primordial black holes: The effect of non-Gaussianity. J. Cosmol. Astropart. Phys. 2022, 2022, 037. [Google Scholar] [CrossRef]
- Ferrante, G.; Franciolini, G.; Iovino, A.J.; Urbano, A. Primordial non-gaussianity up to all orders: Theoretical aspects and implications for primordial black hole models. Phys. Rev. D 2023, 107, 043520. [Google Scholar] [CrossRef]
- Gow, A.D.; Assadullahi, H.; Jackson, J.H.P.; Koyama, K.; Vennin, V.; Wands, D. Non-perturbative non-Gaussianity and primordial black holes. arXiv 2022, arXiv:2211.08348. [Google Scholar]
- Lyth, D.H. The hybrid inflation waterfall and the primordial curvature perturbation. J. Cosmol. Astropart. Phys. 2012, 2012, 022. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C. Primordial black hole formation in the early universe: Critical behaviour and self-similarity. Class. Quant. Grav. 2013, 30, 145009. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. J. Cosmol. Astropart. Phys. 2018, 2018, 041. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic conundra explained by thermal history and primordial black holes. Phys. Dark Univ. 2021, 31, 100755. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y. Correlation Function of High-Threshold Regions and Application to the Initial Small-Scale Clustering of Primordial Black Holes. Phys. Rev. Lett. 2018, 121, 081304. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Initial clustering and the primordial black hole merger rate. J. Cosmol. Astropart. Phys. 2020, 2020, 004. [Google Scholar] [CrossRef]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Riotto, A. The clustering evolution of primordial black holes. J. Cosmol. Astropart. Phys. 2020, 2020, 028. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Riotto, A.; Veermäe, H. Ruling Out Initially Clustered Primordial Black Holes as Dark Matter. Phys. Rev. Lett. 2022, 129, 191302. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Kovetz, E.D.; Kamionkowski, M. Merger rate of primordial black-hole binaries. Phys. Rev. D 2017, 96, 123523. [Google Scholar] [CrossRef]
- Ballesteros, G.; Serpico, P.D.; Taoso, M. On the merger rate of primordial black holes: Effects of nearest neighbours distribution and clustering. J. Cosmol. Astropart. Phys. 2018, 2018, 043. [Google Scholar] [CrossRef]
- Vaskonen, V.; Veermäe, H. Lower bound on the primordial black hole merger rate. Phys. Rev. D 2020, 101, 043015. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Riotto, A. On the Primordial Black Hole Mass Function for Broad Spectra. Phys. Lett. B 2020, 807, 135550. [Google Scholar] [CrossRef]
- Moradinezhad Dizgah, A.; Franciolini, G.; Riotto, A. Primordial Black Holes from Broad Spectra: Abundance and Clustering. J. Cosmol. Astropart. Phys. 2019, 2019, 001. [Google Scholar] [CrossRef]
- De Luca, V.; Riotto, A. A note on the abundance of primordial black holes: Use and misuse of the metric curvature perturbation. Phys. Lett. B 2022, 828, 137035. [Google Scholar] [CrossRef]
- Young, S. Constraining the Early Universe with Primordial Black Holes. Ph.D. Thesis, University of Sussex, Sussex, UK, 2016. [Google Scholar]
- Garcia-Bellido, J.; Peloso, M.; Unal, C. Gravitational Wave signatures of inflationary models from Primordial Black Hole Dark Matter. J. Cosmol. Astropart. Phys. 2017, 2017, 013. [Google Scholar] [CrossRef]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rep. 1999, 314, 1–146. [Google Scholar] [CrossRef]
- Endlich, S.; Nicolis, A.; Wang, J. Solid Inflation. J. Cosmol. Astropart. Phys. 2013, 2013, 011. [Google Scholar] [CrossRef]
- Cannone, D.; Tasinato, G.; Wands, D. Generalised tensor fluctuations and inflation. J. Cosmol. Astropart. Phys. 2015, 2015, 029. [Google Scholar] [CrossRef]
- Bartolo, N.; Cannone, D.; Ricciardone, A.; Tasinato, G. Distinctive signatures of space-time diffeomorphism breaking in EFT of inflation. J. Cosmol. Astropart. Phys. 2016, 2016, 044. [Google Scholar] [CrossRef]
- Ashoorioon, A.; Rostami, A.; Firouzjaee, J.T. EFT compatible PBHs: Effective spawning of the seeds for primordial black holes during inflation. J. High Energy Phys. 2021, 2021, 087. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Creminelli, P.; Mukohyama, S.; Zaldarriaga, M. Ghost inflation. J. Cosmol. Astropart. Phys. 2004, 2004, 001. [Google Scholar] [CrossRef]
- Ballesteros, G.; Céspedes, S.; Santoni, L. Large power spectrum and primordial black holes in the effective theory of inflation. J. High Energy Phys. 2022, 2022, 074. [Google Scholar] [CrossRef]
- Drees, M.; Xu, Y. Overshooting, Critical Higgs Inflation and Second Order Gravitational Wave Signatures. Eur. Phys. J. C 2021, 81, 182. [Google Scholar] [CrossRef]
- Cheong, D.Y.; Lee, S.M.; Park, S.C. Primordial black holes in Higgs-R2 inflation as the whole of dark matter. J. Cosmol. Astropart. Phys. 2021, 2021, 032. [Google Scholar] [CrossRef]
- Rasanen, S.; Tomberg, E. Planck scale black hole dark matter from Higgs inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 038. [Google Scholar] [CrossRef]
- Dalianis, I.; Kehagias, A.; Tringas, G. Primordial black holes from α-attractors. J. Cosmol. Astropart. Phys. 2019, 2019, 037. [Google Scholar] [CrossRef]
- Dalianis, I.; Tringas, G. Primordial black hole remnants as dark matter produced in thermal, matter, and runaway-quintessence postinflationary scenarios. Phys. Rev. D 2019, 100, 083512. [Google Scholar] [CrossRef]
- Cicoli, M.; Pedro, F.G.; Pedron, N. Secondary GWs and PBHs in string inflation: Formation and detectability. J. Cosmol. Astropart. Phys. 2022, 2022, 030. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. 1999, B458, 219–225. [Google Scholar] [CrossRef]
- Solbi, M.; Karami, K. Primordial black holes and induced gravitational waves in k-inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 056. [Google Scholar] [CrossRef]
- Solbi, M.; Karami, K. Primordial black holes formation in the inflationary model with field-dependent kinetic term for quartic and natural potentials. Eur. Phys. J. C 2021, 81, 884. [Google Scholar] [CrossRef]
- Teimoori, Z.; Rezazadeh, K.; Rasheed, M.A.; Karami, K. Mechanism of primordial black holes production and secondary gravitational waves in α-attractor Galileon inflationary scenario. J. Cosmol. Astropart. Phys. 2021, 2021, 018. [Google Scholar] [CrossRef]
- Ahmed, W.; Junaid, M.; Zubair, U. Primordial black holes and gravitational waves in hybrid inflation with chaotic potentials. Nucl. Phys. B 2022, 984, 115968. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Vardanyan, T.; Venturi, G. Non-Canonical Inflation and Primordial Black Holes Production. Phys. Lett. B 2019, 791, 201–205. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized G-inflation: Inflation with the most general second-order field equations. Prog. Theor. Phys. 2011, 126, 511–529. [Google Scholar] [CrossRef]
- Frolovsky, D.; Ketov, S.V.; Saburov, S. Formation of primordial black holes after Starobinsky inflation. Mod. Phys. Lett. A 2022, 37, 2250135. [Google Scholar] [CrossRef]
- Fu, C.; Wu, P.; Yu, H. Primordial Black Holes from Inflation with Nonminimal Derivative Coupling. Phys. Rev. D 2019, 100, 063532. [Google Scholar] [CrossRef]
- Heydari, S.; Karami, K. Primordial black holes in nonminimal derivative coupling inflation with quartic potential and reheating consideration. Eur. Phys. J. C 2022, 82, 83. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes from Gauss-Bonnet-corrected single field inflation. Phys. Rev. D 2021, 104, 083545. [Google Scholar] [CrossRef]
- Langlois, D.; Noui, K. Degenerate higher derivative theories beyond Horndeski: Evading the Ostrogradski instability. J. Cosmol. Astropart. Phys. 2016, 2016, 034. [Google Scholar] [CrossRef]
- Crisostomi, M.; Koyama, K.; Tasinato, G. Extended Scalar-Tensor Theories of Gravity. J. Cosmol. Astropart. Phys. 2016, 2016, 044. [Google Scholar] [CrossRef]
- Ben Achour, J.; Crisostomi, M.; Koyama, K.; Langlois, D.; Noui, K.; Tasinato, G. Degenerate higher order scalar-tensor theories beyond Horndeski up to cubic order. J. High Energy Phys. 2016, 2016, 100. [Google Scholar] [CrossRef]
- Motohashi, H.; Hu, W. Primordial Black Holes and Slow-Roll Violation. Phys. Rev. 2017, D96, 063503. [Google Scholar] [CrossRef]
- Pi, S.; Wang, J. Primordial Black Hole Formation in Starobinsky’s Linear Potential Model. arXiv 2022, arXiv:2209.14183. [Google Scholar]
- Inoue, S.; Yokoyama, J. Curvature perturbation at the local extremum of the inflation’s potential. Phys. Lett. B 2002, 524, 15–20. [Google Scholar] [CrossRef]
- Tzirakis, K.; Kinney, W.H. Inflation over the hill. Phys. Rev. 2007, D75, 123510. [Google Scholar] [CrossRef]
- Motohashi, H.; Mukohyama, S.; Oliosi, M. Constant Roll and Primordial Black Holes. J. Cosmol. Astropart. Phys. 2020, 2020, 002. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Cole, P.S.; Patil, S.P. Steepest growth of the power spectrum and primordial black holes. J. Cosmol. Astropart. Phys. 2019, 2019, 028. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Saha, P.; Sriramkumar, L.; Silk, J. Primordial black holes and secondary gravitational waves from ultraslow roll and punctuated inflation. Phys. Rev. D 2021, 103, 083510. [Google Scholar] [CrossRef]
- Ng, K.W.; Wu, Y.P. Constant-rate inflation: Primordial black holes from conformal weight transitions. J. High Energy Phys. 2021, 2021, 076. [Google Scholar] [CrossRef]
- Karam, A.; Koivunen, N.; Tomberg, E.; Vaskonen, V.; Veermäe, H. Anatomy of single-field inflationary models for primordial black holes. J. Cosmol. Astropart. Phys. 2023, 2023, 013. [Google Scholar] [CrossRef]
- Franciolini, G.; Urbano, A. Primordial black hole dark matter from inflation: The reverse engineering approach. Phys. Rev. D 2022, 106, 123519. [Google Scholar] [CrossRef]
- Cole, P.S.; Gow, A.D.; Byrnes, C.T.; Patil, S.P. Steepest growth re-examined: Repercussions for primordial black hole formation. arXiv 2022, arXiv:2204.07573. [Google Scholar]
- Wands, D. Duality invariance of cosmological perturbation spectra. Phys. Rev. 1999, D60, 023507. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks ? A publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas; Loizides, F., Scmidt, B., Eds.; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar]
- Carrilho, P.; Malik, K.A.; Mulryne, D.J. Dissecting the growth of the power spectrum for primordial black holes. Phys. Rev. D 2019, 100, 103529. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.K.; Cai, R.G. Analytical approximation of the scalar spectrum in the ultraslow-roll inflationary models. Phys. Rev. D 2020, 101, 083535. [Google Scholar] [CrossRef]
- Tasinato, G. An analytic approach to non-slow-roll inflation. Phys. Rev. D 2021, 103, 023535. [Google Scholar] [CrossRef]
- Özsoy, O.; Tasinato, G. CMB μT cross correlations as a probe of primordial black hole scenarios. Phys. Rev. D 2021, 104, 043526. [Google Scholar] [CrossRef]
- Özsoy, O.; Tasinato, G. Consistency conditions and primordial black holes in single field inflation. Phys. Rev. D 2022, 105, 023524. [Google Scholar] [CrossRef]
- Zegeye, D.; Inomata, K.; Hu, W. Spectral distortion anisotropy from inflation for primordial black holes. Phys. Rev. D 2022, 105, 103535. [Google Scholar] [CrossRef]
- Balaji, S.; Ragavendra, H.V.; Sethi, S.K.; Silk, J.; Sriramkumar, L. Observing Nulling of Primordial Correlations via the 21-cm Signal. Phys. Rev. Lett. 2022, 129, 261301. [Google Scholar] [CrossRef]
- Morse, M.J.P.; Kinney, W.H. Large-η constant-roll inflation is never an attractor. Phys. Rev. 2018, D97, 123519. [Google Scholar] [CrossRef]
- Suyama, T.; Tada, Y.; Yamaguchi, M. Revisiting non-Gaussianity in non-attractor inflation models in the light of the cosmological soft theorem. Prog. Theor. Exp. Phys. 2021, 2021, 073E02. [Google Scholar] [CrossRef]
- Davies, M.W.; Carrilho, P.; Mulryne, D.J. Non-Gaussianity in inflationary scenarios for primordial black holes. J. Cosmol. Astropart. Phys. 2022, 2022, 019. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Stochastic de Sitter (inflationary) stage in the early universe. Lect. Notes Phys. 1986, 246, 107–126. [Google Scholar] [CrossRef]
- Nambu, Y.; Sasaki, M. Stochastic Stage of an Inflationary Universe Model. Phys. Lett. B 1988, 205, 441–446. [Google Scholar] [CrossRef]
- Kandrup, H.E. Stochastic inflation as a time dependent random walk. Phys. Rev. D 1989, 39, 2245. [Google Scholar] [CrossRef]
- Nambu, Y. Stochastic Dynamics of an Inflationary Model and Initial Distribution of Universes. Prog. Theor. Phys. 1989, 81, 1037. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Yokoyama, J. Equilibrium state of a selfinteracting scalar field in the De Sitter background. Phys. Rev. 1994, D50, 6357–6368. [Google Scholar] [CrossRef]
- Finelli, F.; Marozzi, G.; Starobinsky, A.A.; Vacca, G.P.; Venturi, G. Generation of fluctuations during inflation: Comparison of stochastic and field-theoretic approaches. Phys. Rev. D 2009, 79, 044007. [Google Scholar] [CrossRef]
- Burgess, C.P.; Holman, R.; Tasinato, G.; Williams, M. EFT Beyond the Horizon: Stochastic Inflation and How Primordial Quantum Fluctuations Go Classical. J. High Energy Phys. 2015, 2015, 090. [Google Scholar] [CrossRef]
- Vennin, V.; Starobinsky, A.A. Correlation Functions in Stochastic Inflation. Eur. Phys. J. C 2015, 75, 413. [Google Scholar] [CrossRef]
- Burgess, C.P.; Holman, R.; Tasinato, G. Open EFTs, IR effects \& late-time resummations: Systematic corrections in stochastic inflation. J. High Energy Phys. 2016, 2016, 153. [Google Scholar] [CrossRef]
- Ando, K.; Vennin, V. Power spectrum in stochastic inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 057. [Google Scholar] [CrossRef]
- Biagetti, M.; Franciolini, G.; Kehagias, A.; Riotto, A. Primordial Black Holes from Inflation and Quantum Diffusion. J. Cosmol. Astropart. Phys. 2018, 2018, 032. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; García-Bellido, J. Quantum diffusion beyond slow-roll: Implications for primordial black-hole production. J. Cosmol. Astropart. Phys. 2018, 2018, 018. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Taoso, M.; Urbano, A. Stochastic inflationary dynamics beyond slow-roll and consequences for primordial black hole formation. J. Cosmol. Astropart. Phys. 2020, 2020, 043. [Google Scholar] [CrossRef]
- Cruces, D.; Germani, C.; Prokopec, T. Failure of the stochastic approach to inflation beyond slow-roll. J. Cosmol. Astropart. Phys. 2019, 2019, 048. [Google Scholar] [CrossRef]
- Firouzjahi, H.; Nassiri-Rad, A.; Noorbala, M. Stochastic Ultra Slow Roll Inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 040. [Google Scholar] [CrossRef]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. Stochastic inflation beyond slow roll. J. Cosmol. Astropart. Phys. 2019, 2019, 031. [Google Scholar] [CrossRef]
- Vennin, V. Stochastic Inflation and Primordial Black Holes. Habilitation Thesis, Universite Paris-Saclay, Bures-sur-Yvette, France, 2020. [Google Scholar]
- Rigopoulos, G.; Wilkins, A. Inflation is always semi-classical: Diffusion domination overproduces Primordial Black Holes. J. Cosmol. Astropart. Phys. 2021, 2021, 027. [Google Scholar] [CrossRef]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. Quantum diffusion during inflation and primordial black holes. J. Cosmol. Astropart. Phys. 2017, 2017, 046. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; García-Bellido, J.; Vennin, V. The exponential tail of inflationary fluctuations: Consequences for primordial black holes. J. Cosmol. Astropart. Phys. 2020, 2020, 029. [Google Scholar] [CrossRef]
- Figueroa, D.G.; Raatikainen, S.; Rasanen, S.; Tomberg, E. Non-Gaussian Tail of the Curvature Perturbation in Stochastic Ultraslow-Roll Inflation: Implications for Primordial Black Hole Production. Phys. Rev. Lett. 2021, 127, 101302. [Google Scholar] [CrossRef]
- Figueroa, D.G.; Raatikainen, S.; Rasanen, S.; Tomberg, E. Implications of stochastic effects for primordial black hole production in ultra-slow-roll inflation. J. Cosmol. Astropart. Phys. 2022, 2022, 027. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Logarithmic Duality of the Curvature Perturbation. arXiv 2022, arXiv:2211.13932. [Google Scholar]
- Cai, R.G.; Guo, Z.K.; Liu, J.; Liu, L.; Yang, X.Y. Primordial black holes and gravitational waves from parametric amplification of curvature perturbations. J. Cosmol. Astropart. Phys. 2020, 2020, 013. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Rompineve, F. Detuning primordial black hole dark matter with early matter domination and axion monodromy. J. Cosmol. Astropart. Phys. 2020, 2020, 014. [Google Scholar] [CrossRef]
- Kristiano, J.; Yokoyama, J. Why Must Primordial Non-Gaussianity Be Very Small? Phys. Rev. Lett. 2022, 128, 061301. [Google Scholar] [CrossRef]
- Meng, D.S.; Yuan, C.; Huang, Q.G. One-loop correction to the enhanced curvature perturbation with local-type non-Gaussianity for the formation of primordial black holes. Phys. Rev. D 2022, 106, 063508. [Google Scholar] [CrossRef]
- Kristiano, J.; Yokoyama, J. Ruling Out Primordial Black Hole Formation From Single-Field Inflation. arXiv 2022, arXiv:2211.03395. [Google Scholar]
- Inomata, K.; Braglia, M.; Chen, X. Questions on calculation of primordial power spectrum with large spikes: The resonance model case. J. Cosmol. Astropart. Phys. 2023, 2023, 011. [Google Scholar] [CrossRef]
- Riotto, A. The Primordial Black Hole Formation from Single-Field Inflation is Not Ruled Out. arXiv 2023, arXiv:2301.00599. [Google Scholar]
- Arya, R. Formation of Primordial Black Holes from Warm Inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 042. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Díaz-Blanco, M.S. Gravity waves and primordial black holes in scalar warm little inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 052. [Google Scholar] [CrossRef]
- Ballesteros, G.; García, M.A.G.; Rodríguez, A.P.; Pierre, M.; Rey, J. Primordial black holes and gravitational waves from dissipation during inflation. J. Cosmol. Astropart. Phys. 2022, 2022, 006. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Primordial Black Hole Formation in Non-Minimal Curvaton Scenario. arXiv 2021, arXiv:2112.12680. [Google Scholar]
- Meng, D.S.; Yuan, C.; Huang, Q.G. Primordial black holes generated by the non-minimal spectator field. arXiv 2022, arXiv:2212.03577. [Google Scholar]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Svrcek, P.; Witten, E. Axions In String Theory. J. High Energy Phys. 2006, 2006, 051. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation with pseudo—Nambu-Goldstone bosons. Phys. Rev. Lett. 1990, 65, 3233–3236. [Google Scholar] [CrossRef] [PubMed]
- McAllister, L.; Silverstein, E.; Westphal, A. Gravity Waves and Linear Inflation from Axion Monodromy. Phys. Rev. 2010, D82, 046003. [Google Scholar] [CrossRef]
- Silverstein, E.; Westphal, A. Monodromy in the CMB: Gravity Waves and String Inflation. Phys. Rev. D 2008, 78, 106003. [Google Scholar] [CrossRef]
- McAllister, L.; Silverstein, E.; Westphal, A.; Wrase, T. The Powers of Monodromy. J. High Energy Phys. 2014, 2014, 123. [Google Scholar] [CrossRef]
- Flauger, R.; McAllister, L.; Silverstein, E.; Westphal, A. Drifting Oscillations in Axion Monodromy. J. Cosmol. Astropart. Phys. 2017, 2017, 055. [Google Scholar] [CrossRef]
- Anber, M.M.; Sorbo, L. N-flationary magnetic fields. J. Cosmol. Astropart. Phys. 2006, 2006, 018. [Google Scholar] [CrossRef]
- Anber, M.M.; Sorbo, L. Naturally inflating on steep potentials through electromagnetic dissipation. Phys. Rev. 2010, D81, 043534. [Google Scholar] [CrossRef]
- Barnaby, N.; Peloso, M. Large Nongaussianity in Axion Inflation. Phys. Rev. Lett. 2011, 106, 181301. [Google Scholar] [CrossRef]
- Barnaby, N.; Namba, R.; Peloso, M. Phenomenology of a Pseudo-Scalar Inflaton: Naturally Large Nongaussianity. J. Cosmol. Astropart. Phys. 2011, 2011, 009. [Google Scholar] [CrossRef]
- Pajer, E.; Peloso, M. A review of Axion Inflation in the era of Planck. Class. Quant. Grav. 2013, 30, 214002. [Google Scholar] [CrossRef]
- Peloso, M.; Sorbo, L.; Unal, C. Rolling axions during inflation: Perturbativity and signatures. J. Cosmol. Astropart. Phys. 2016, 2016, 001. [Google Scholar] [CrossRef]
- Özsoy, O. On Synthetic Gravitational Waves from Multi-field Inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 062. [Google Scholar] [CrossRef]
- Barnaby, N.; Pajer, E.; Peloso, M. Gauge Field Production in Axion Inflation: Consequences for Monodromy, non-Gaussianity in the CMB, and Gravitational Waves at Interferometers. Phys. Rev. 2012, D85, 023525. [Google Scholar] [CrossRef]
- Meerburg, P.D.; Pajer, E. Observational Constraints on Gauge Field Production in Axion Inflation. J. Cosmol. Astropart. Phys. 2013, 2013, 017. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Caravano, A.; Komatsu, E.; Lozanov, K.D.; Weller, J. Lattice Simulations of Axion-U(1) Inflation. arXiv 2022, arXiv:2204.12874. [Google Scholar]
- Cheng, S.L.; Lee, W.; Ng, K.W. Numerical study of pseudoscalar inflation with an axion-gauge field coupling. Phys. Rev. D 2016, 93, 063510. [Google Scholar] [CrossRef]
- Dall’Agata, G.; González-Martín, S.; Papageorgiou, A.; Peloso, M. Warm dark energy. J. Cosmol. Astropart. Phys. 2020, 2020, 032. [Google Scholar] [CrossRef]
- Domcke, V.; Guidetti, V.; Welling, Y.; Westphal, A. Resonant backreaction in axion inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 009. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Schmitz, K.; Sobol, O.O.; Vilchinskii, S.I. Gauge-field production during axion inflation in the gradient expansion formalism. Phys. Rev. D 2021, 104, 123504. [Google Scholar] [CrossRef]
- Peloso, M.; Sorbo, L. Instability in axion inflation with strong backreaction from gauge modes. J. Cosmol. Astropart. Phys. 2023, 2023, 038. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lee, W.; Ng, K.W. Production of high stellar-mass primordial black holes in trapped inflation. J. High Energy Phys. 2017, 2017, 008. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.; Vercnocke, B. Natural Inflation in Supergravity and Beyond. Phys. Rev. 2014, D90, 041303. [Google Scholar] [CrossRef]
- Kobayashi, T.; Oikawa, A.; Otsuka, H. New potentials for string axion inflation. Phys. Rev. 2016, D93, 083508. [Google Scholar] [CrossRef]
- Cabo Bizet, N.; Loaiza-Brito, O.; Zavala, I. Mirror quintic vacua: Hierarchies and inflation. J. High Energy Phys. 2016, 2016, 082. [Google Scholar] [CrossRef]
- Parameswaran, S.; Tasinato, G.; Zavala, I. Subleading Effects and the Field Range in Axion Inflation. J. Cosmol. Astropart. Phys. 2016, 2016, 008. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Zavala, I. Sharp turns in axion monodromy: Primordial black holes and gravitational waves. arXiv 2022, arXiv:2205.06065. [Google Scholar]
- Namba, R.; Peloso, M.; Shiraishi, M.; Sorbo, L.; Unal, C. Scale-dependent gravitational waves from a rolling axion. J. Cosmol. Astropart. Phys. 2016, 2016, 041. [Google Scholar] [CrossRef]
- Ferreira, R.Z.; Sloth, M.S. Universal Constraints on Axions from Inflation. J. High Energy Phys. 2014, 2014, 139. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Groot Nibbelink, S.; van Tent, B.J.W. Density perturbations arising from multiple field slow roll inflation. arXiv 2000, arXiv:hep-ph/0011325. [Google Scholar]
- Groot Nibbelink, S.; van Tent, B.J.W. Scalar perturbations during multiple field slow-roll inflation. Class. Quant. Grav. 2002, 19, 613–640. [Google Scholar] [CrossRef]
- Sasaki, M.; Stewart, E.D. A General analytic formula for the spectral index of the density perturbations produced during inflation. Prog. Theor. Phys. 1996, 95, 71–78. [Google Scholar] [CrossRef]
- Langlois, D.; Renaux-Petel, S. Perturbations in generalized multi-field inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 017. [Google Scholar] [CrossRef]
- Garcia-Saenz, S.; Renaux-Petel, S.; Ronayne, J. Primordial fluctuations and non-Gaussianities in sidetracked inflation. J. Cosmol. Astropart. Phys. 2018, 2018, 057. [Google Scholar] [CrossRef]
- Garcia-Saenz, S.; Renaux-Petel, S. Flattened non-Gaussianities from the effective field theory of inflation with imaginary speed of sound. J. Cosmol. Astropart. Phys. 2018, 2018, 005. [Google Scholar] [CrossRef]
- Bjorkmo, T.; Ferreira, R.Z.; Marsh, M.C.D. Mild Non-Gaussianities under Perturbative Control from Rapid-Turn Inflation Models. J. Cosmol. Astropart. Phys. 2019, 2019, 036. [Google Scholar] [CrossRef]
- Fumagalli, J.; Renaux-Petel, S.; Witkowski, L.T. Oscillations in the stochastic gravitational wave background from sharp features and particle production during inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 030. [Google Scholar] [CrossRef]
- Chluba, J.; Hamann, J.; Patil, S.P. Features and New Physical Scales in Primordial Observables: Theory and Observation. Int. J. Mod. Phys. D 2015, 24, 1530023. [Google Scholar] [CrossRef]
- Slosar, A.; Chen, X.; Dvorkin, C.; Green, D.; Meerburg, P.D.; Silverstein, E.; Wallisch, B. Scratches from the Past: Inflationary Archaeology through Features in the Power Spectrum of Primordial Fluctuations. Bull. Am. Astron. Soc. 2019, 51, 98. [Google Scholar]
- Anguelova, L. On Primordial Black Holes from Rapid Turns in Two-field Models. J. Cosmol. Astropart. Phys. 2021, 2021, 004. [Google Scholar] [CrossRef]
- Fumagalli, J.; Garcia-Saenz, S.; Pinol, L.; Renaux-Petel, S.; Ronayne, J. Hyper-Non-Gaussianities in Inflation with Strongly Nongeodesic Motion. Phys. Rev. Lett. 2019, 123, 201302. [Google Scholar] [CrossRef]
- Ferreira, R.Z. Non-Gaussianities in models of inflation with large and negative entropic masses. J. Cosmol. Astropart. Phys. 2020, 2020, 034. [Google Scholar] [CrossRef]
- Wu, K.K.S.; Lahav, O.; Rees, M.J. The large-scale smoothness of the Universe. Nature 1999, 397, 225–230. [Google Scholar] [CrossRef]
- Yadav, J.; Bharadwaj, S.; Pandey, B.; Seshadri, T.R. Testing homogeneity on large scales in the Sloan Digital Sky Survey Data Release One. Mon. Not. R. Astron. Soc. 2005, 364, 601–606. [Google Scholar] [CrossRef]
- Friedmann, A. On the Possibility of a world with constant negative curvature of space. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Lemaitre, G. The expanding universe. Ann. Soc. Sci. Brux. A 1933, 53, 51–85. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure. Astrophys. J. 1935, 82, 284–301. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s Theory of World-Structure. Proc. Lond. Math. Soc. 1937, 42, 90–127. [Google Scholar] [CrossRef]
- Baumann, D. Inflation. In Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics: Physics of the Large and the Small, Boulder, CO, USA, 1–26 June 2009; pp. 523–686. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; CRC Press: Boca Raton, FL, USA, 1990; Volume 69. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Oxford, UK, 2005. [Google Scholar]
- Lyth, D.H.; Malik, K.A.; Sasaki, M. A General proof of the conservation of the curvature perturbation. J. Cosmol. Astropart. Phys. 2005, 2005, 004. [Google Scholar] [CrossRef]
- Flauger, R.; McAllister, L.; Pajer, E.; Westphal, A.; Xu, G. Oscillations in the CMB from Axion Monodromy Inflation. J. Cosmol. Astropart. Phys. 2010, 2010, 009. [Google Scholar] [CrossRef]
- Flauger, R.; Pajer, E. Resonant Non-Gaussianity. J. Cosmol. Astropart. Phys. 2011, 2011, 017. [Google Scholar] [CrossRef]
- Maldacena, J.M. Non-Gaussian features of primordial fluctuations in single field inflationary models. J. High Energy Phys. 2003, 2003, 013. [Google Scholar] [CrossRef]
- Adshead, P.; Giblin, J.T.; Scully, T.R.; Sfakianakis, E.I. Gauge-preheating and the end of axion inflation. J. Cosmol. Astropart. Phys. 2015, 2015, 034. [Google Scholar] [CrossRef]
- Barnaby, N.; Moxon, J.; Namba, R.; Peloso, M.; Shiu, G.; Zhou, P. Gravity waves and non-Gaussian features from particle production in a sector gravitationally coupled to the inflaton. Phys. Rev. 2012, D86, 103508. [Google Scholar] [CrossRef]
- Sorbo, L. Parity violation in the Cosmic Microwave Background from a pseudoscalar inflaton. J. Cosmol. Astropart. Phys. 2011, 2011, 003. [Google Scholar] [CrossRef]
- Cook, J.L.; Sorbo, L. Particle production during inflation and gravitational waves detectable by ground-based interferometers. Phys. Rev. D 2012, 85, 023534. [Google Scholar] [CrossRef]
- Özsoy, O. Parity violating non-Gaussianity from axion-gauge field dynamics. Phys. Rev. D 2021, 104, 123523. [Google Scholar] [CrossRef]
- Campeti, P.; Özsoy, O.; Obata, I.; Shiraishi, M. New constraints on axion-gauge field dynamics during inflation from Planck and BICEP/Keck data sets. J. Cosmol. Astropart. Phys. 2022, 2022, 039. [Google Scholar] [CrossRef]
- Malik, K.A.; Wands, D. Cosmological perturbations. Phys. Rep. 2009, 475, 1–51. [Google Scholar] [CrossRef]
- Notari, A.; Tywoniuk, K. Dissipative Axial Inflation. J. Cosmol. Astropart. Phys. 2016, 2016, 038. [Google Scholar] [CrossRef]
- Caprini, C.; Guzzetti, M.C.; Sorbo, L. Inflationary magnetogenesis with added helicity: Constraints from non-gaussianities. Class. Quantum Gravity 2018, 35, 124003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).