Dark Energy Is the Cosmological Quantum Vacuum Energy of Light Particles—The Axion and the Lightest Neutrino

Abstract

We uncover the general mechanism and the nature of today’s dark energy (DE). This is only based on well-known quantum physics and cosmology. We show that the observed DE today originates from the cosmological quantum vacuum of light particles, which provides a continuous energy distribution able to reproduce the data. Bosons give positive contributions to the DE, while fermions yield negative contributions. As usual in field theory, ultraviolet divergences are subtracted from the physical quantities. The subtractions respect the symmetries of the theory, and we normalize the physical quantities to be zero for the Minkowski vacuum. The resulting finite contributions to the energy density and the pressure from the quantum vacuum grow as $loga\left(t\right)$, where $a\left(t\right)$ is the scale factor, while the particle contributions dilute as $1/a^3\left(t\right)$, as it must be for massive particles. We find the explicit dark energy equation of state of today to be $P=w\left(z\right)\mathcal{H}$: it turns to be slightly $w\left(z\right)<-1$ with $w\left(z\right)$ asymptotically reaching the value $-1$ from below. A scalar particle can produce the observed dark energy through its quantum cosmological vacuum provided that (i) its mass is of the order of ${10}^{-3}$ eV = 1 meV, (ii) it is very weakly coupled, and (iii) it is stable on the time scale of the age of the universe. The axion vacuum thus appears as a natural candidate. The neutrino vacuum (especially the lightest mass eigenstate) can give negative contributions to the dark energy. We find that $w(z=0)$ is slightly below $-1$ by an amount ranging from $(-1.5\times {10}^{-3})$ to $(-8\times {10}^{-3})$ and we predict the axion mass to be in the range between 4 and 5 $\mathrm{meV}$. We find that the universe will expand in the future faster than the de Sitter universe as an exponential in the square of the cosmic time. Dark energy today arises from the quantum vacuum of light particles in FRW cosmological space-time in an analogous way to the Casimir vacuum effect of quantum fields in Minkowski space-time with non-trivial boundary conditions.

1. Introduction and Results

Since the discovery of dark energy in the present universe [1,2,3,4], intense observational activity has improved our knowledge about it [5,6,7,8,9,10,11,12,13,14,15], and more activity is expected to provide new data and understanding, e.g., [16,17]. Many different approaches and models have been proposed to explain dark energy [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. For reviews on and approaches to dark energy, see, for example, refs. [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

As is, by now, well known, let us mention that there exist current discordances between different cosmological probes, mainly the discrepancy in the value of the Hubble constant $H_0:5.0\sigma$ between early universe indirect $H_0$ determinations and late universe direct measurements of $H_0$. Regarding other stresses and anomalies of lower statistical significance, which are interesting in their own but are not the subject of this paper, see, for example, ref. [35] and references therein. As is well known too, there also exist theoretical discordances, such as the fine adjustment of the cosmological constant $\mathsf{\Lambda }$, seen, for example, in refs. [22,34] and references therein. Clarification to this problem has been provided recently [36,37]: The huge difference between the observed value of $\mathsf{\Lambda }$ today and the particle physics-evaluated value ${\mathsf{\Lambda }}_Q$ is correct and must be physically like that because the two values correspond to the same physical magnitude but to two different vacuum states and cosmic eras—the observed $\mathsf{\Lambda }$ value today corresponds to the classical/semiclassical, large and dilute (mostly empty) universe of today, consistent with the very low observed $\mathsf{\Lambda }$ value (${10}^{-122}$ in Planck units), while the computed value ${\mathsf{\Lambda }}_Q$ (${10}^{+122}$ in Planck units) corresponds to the small, highly dense and energetic quantum gravity universe in its far (trans-Planckian) past, and this is consistent with its extremely high, trans-Planckian value. The two values are classical-quantum duals of each other in the sense of the classical-quantum (wave-particle) duality including gravity and independently agree with a path integral gravity derivation [36,37,38].

In this paper, we study the cosmological Quantum Field Theory (QFT) vacuum as dark energy within a fundamental analytic framework with explicit and analytic results, e.g., the derivation of the dark energy equation of state and the future evolution of the universe. Moreover, from these results, we also extract the implications and determination of the particles contributing to dark energy and compute their masses.

We show that the dark energy present today in the universe originates from the cosmological quantum vacuum of light particles in the meV mass scale. This is a vacuum effect that unavoidably appears when quantum fields evolve in a cosmological space-time. That is, dark energy today is generated by a mechanism based on well-known quantum physics and cosmology. Bosons yield positive contributions to the dark energy, while fermions give negative contributions.

We find that the scale of the contributions to the dark energy is of the order of

$$\frac{M^4}{2{\left(4\pi \right)}^2}log{z}_{\mathrm{dec}},$$

(1)

where M is the particle mass and $z_{\mathrm{dec}}$ is the redshift when it is decoupled from the early universe plasma.

Generally speaking, the energy of a quantum field is the sum of the vacuum contribution plus particle contributions. It is known that the vacuum energy of a quantum field dissipates into particles when the field evolves coupled to other fields or to itself [39,40,41,42,43]. Dissipation into fermions is reduced by Pauli blocking [41,42]. Electrons, protons and photons are coupled to photons and, therefore, their vacuum energy dissipates through photon production well before recombination, that is, when the temperature of the universe is 1 MeV or more. Unstable particles cannot produce long-lasting vacuum effects. Only a very weakly coupled stable particle can produce a vacuum energy contribution lasting for times of the order of the age of the universe, that is, a vacuum energy contribution measurable today.

Since dark energy is known to be positive, bosons must dominate the cosmological vacuum energy. The scale of the boson mass must be in the meV range because the observed dark energy density has the value [15,44,45,46]

$${\rho }_{\mathsf{\Lambda }}={\mathsf{\Omega }}_{\mathsf{\Lambda }}{\rho }_c={\left(2.39\mathrm{meV}\right)}^4,1\mathrm{meV}={10}^{-3}\mathrm{eV}.$$

(2)

Spontaneous symmetry breaking of continuous symmetries is a natural way to produce massless scalars (Goldstone bosons) in particle physics. Furthermore, a slight violation of the corresponding symmetry can give a small mass to such a scalar particle. Axions, majorons and familons have been proposed on these grounds [47,48,49,50,51,52,53,54,55,56].

In addition, the lightest neutrino can give a negative contribution to dark energy.

Neutrinos are, by now, very well-motivated particles from the point of view of particle physics, cosmology and astrophysics, e.g., [57,58,59]. For Majorana-type neutrinos, neutrinos and antineutrinos coincide, while, for Dirac neutrinos, neutrinos and antineutrinos are distinct. It is not yet clear whether neutrinos are of Majorana or Dirac type, and, in this paper, we discuss the implications for dark energy of both of them. Interestingly enough, light meV neutrinos and the meV axion do appear here as a consequence of our results for the dark energy computed from first principles. For constraints on other types of neutrinos and other relativistic species or “dark radiation”, see, for example, [60,61] and references therein.

Neutrinos in the universe are known to be free for temperatures $T\lesssim 1$ Mev, which correspond to redshifts $z\lesssim 6\times {10}^9$ [57,58,59]. That is, we can describe their evolution as free fermions in the cosmological FRW universe.

Axions with masses $M\sim 1$ meV are free for temperatures $T\lesssim {10}^6$ GeV, which correspond to redshifts $z\lesssim {10}^{19}$ [62,63,64,65,66]. They can be considered as free scalars in the cosmological FRW universe. Both the axion and neutrino decoupling happen during the radiation-dominated era. Before decoupling, the non-negligeable interaction of the corresponding particles made dissipation important, therefore the vacuum energy can only become significant after decoupling. Therefore, we can restrict ourselves to study free quantum field evolution in the cosmological space-time after decoupling.

• We investigate the evolution of scalars and fermions as an initial value problem (Cauchy problem) for the corresponding quantum fields on a cosmological space-time.
• We find that the initial temperature has a negligible effect on the vacuum energy for late times.
• Both axions and neutrinos can lead to vacuum effects lasting cosmological time scales. Any of the two heavier neutrino mass eigenstates, ${\nu }_2$ and ${\nu }_3$, would produce a large negative dark energy in the ${\left(50\mathrm{meV}\right)}^4$ range. Hence:

  (i)

  either the heavier neutrinos, ${\nu }_2$ and ${\nu }_3$, annihilate with their respective anti-neutrinos in a time scale of the age of the universe, or

  (ii)

  a stable scalar particle with mass in the $\gtrsim 50$ meV range must be present in order to reproduce the observed value of the dark energy Equation (2).

  However, we find in this paper that possibility (ii) is inconsistent with the observed dark energy equation of state.

An effective four-fermions interaction with strength characterized by $M^{\prime }{}^{-2}$, where $M^{\prime }$ is a mass scale, can make the heavier neutrinos unstable. The mass scale $M^{\prime }$ should be $M^{\prime }\lesssim 1$ MeV or $M^{\prime }\lesssim 10$ MeV for the direct and inverse neutrino mass hierarchies.

As shown in Section 8, the lightest meV neutrino remains the only neutrino contribution to dark energy. The heavier neutrinos dissipate at the time of the age of the universe.

As shown in Section 7, the meV axion lifetime to decay into photons is much longer than the age of the universe. Dissipation of the energy in the cosmological quantum axion vacuum takes longer than the age of the universe too.

These results are unified in Section 9, with both light meV particles, meV axions and meV light neutrinos, contributing to dark energy together.

Table 1. The Equation of state today, w(0) + 1, computed from Equation (80) in three relevant cases, which all describe the dark energy observed today (Equation (89)): (i) no neutrino contribution to the dark energy; (ii) a Majorana neutrino contribution with mass $m=3.2$ meV; (iii) a Dirac neutrino contribution with mass $m=3.2$ meV. See the discussion in Section 9.

Neutrino Type	Scalar Mass	Equation of State Today
No vacuum neutrino energy	$M=3.96$ meV	$w\left(0\right)+1=-0.00794$
Majorana neutrino	$M=4.35$ meV	$w\left(0\right)+1=-0.00473$
$m=3.2$ meV
Dirac neutrino	$M=4.66$ meV	$w\left(0\right)+1=-0.00156$
$m=3.2$ meV

summarizes their contributions together with the computed equation of state.

On the other hand, let us mention that a global analysis of cosmological constraints on decaying axion-like particles (ALPs) performed recently ref. [67] shows that ALPs are stable on cosmological time scales unless they are heavy enough, with masses >300 keV. This is an independent confirmation that ${10}^{-3}$ eV axions, as shown in this paper, are safely stable enough to be considered as the source of dark energy. Previously, ALPs have been proposed, among other proposals, to be constituents of the cosmological energy density, i.e., ref. [68].

In conformal time $\left(\eta \right)$, the scalar and fermion fields rescaled by the scale factor $a\left(\eta \right)$ turn out to obey equations of motion similar to those in Minkowski space-time but with time-dependent masses

$$\begin{array}{ccc}\hfill & & {\chi }^{″}-{\nabla }^2\chi +\left[M^2{a}^2\left(\eta \right)-\frac{a^{″}\left(\eta \right)}{a\left(\eta \right)}\right]\chi (\overrightarrow{x},\eta )=0,\hfill \end{array}$$

$$\begin{array}{ccc}& & \left[i\cancel{\partial }-ma(\eta )\right]\psi (\overrightarrow{x},\eta )=0.\hfill \end{array}$$

(3)

Here, $\chi$ and $\psi$ are, respectively, rescaled scalar and fermion fields, ${\nabla }^2$ is the usual flat space Laplacian and $i\cancel{\partial }$ is the usual Dirac differential operator in Minkowski space-time in terms of flat space-time Dirac matrices.

There are two widely separate scales in the field evolution in cosmological space-times:

• The fast scale is the microscopic quantum evolution scale,
  typically $\sim 1/M\sim 1/m$, where M and m are the scalar and fermion masses, respectively.
• The slow scale is the Hubble scale $1/H$ of the universe expansion.
  When $M\sim m\gg H,M^2\gg a^{″}\left(\eta \right)/a^3\left(\eta \right)$, and hence the scale factor can be considered as constant.
• Therefore, the cosmological quantum field evolution for the fields $\chi$ and $\psi$ is just the Minkowski evolution with effective masses $\left(M^2{a}^2\right)$ and $\left(ma\right)$, respectively, as seen from Equation (3).

Energy density, pressure and field density are expressed in field theory as products of the field operators and their derivatives at equal space-time points. Such expressions are ultraviolet divergent and need to be subtracted. The subtractions respect the symmetries of the theory, and we normalize them such that the physical quantities are zero for the vacuum in Minkowski space-time. The finite resulting quantities grow as $loga\left(\eta \right)$. This is analogous to the high-energy growth of renormalized one-loop Feynman graphs.

That is, the energy density and the pressure receive contributions from the quantum vacuum that grow as $loga\left(\eta \right)$, while the particle contributions are as dilute as $1/a^3\left(\eta \right)$, as it must be for massive particles.

We obtain for the vacuum energy density and pressure of scalar and fermion fields with mass M and m, respectively, the following results:

$$<\mathcal{H}>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}\frac{M^4}{2{\left(4\pi \right)}^2}\left[loga\left(\eta \right)+b_S-\frac{1}{4}\right]-\frac{m^4}{{\left(4\pi \right)}^2}\mathcal{N}\left[loga\left(\eta \right)+b_F-\frac{1}{4}\right],$$

(4)

$$<P>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\frac{M^4}{2{\left(4\pi \right)}^2}\left[loga\left(\eta \right)+b_S+\frac{1}{12}\right]+\frac{m^4}{{\left(4\pi \right)}^2}\mathcal{N}\left[loga\left(\eta \right)+b_F+\frac{1}{12}\right]$$

(5)

where $b_S$ and $b_F$ take into account the initial values of the scale factor $a_{\mathrm{dcs}}$ and $a_{\mathrm{dcf}}$ (at the decoupling time) of the scalars and fermions, respectively. $\mathcal{N}=1$ for Majorana fermions and $\mathcal{N}=2$ for Dirac fermions.

Therefore, we obtain for the equation of state the explicit expression:

$$w\left(\eta \right)\equiv \frac{<P>\left(\eta \right)}{<\mathcal{H}>\left(\eta \right)}\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-1-\frac{1}{3}{\left[loga\left(\eta \right)-\frac{1}{4}+\frac{b_S-(2\mathcal{N}{m}^4/M^4)b_F}{1-(2\mathcal{N}{m}^4/M^4)}\right]}^{-1}.$$

(6)

That is, we find $w\left(\eta \right)<-1$ with $w\left(\eta \right)$ asymptotically reaching the value $-1$ from below.

It is convenient to express the scale factor in terms of the redshift. Taking into account that $b_S$ and $b_F$ contain the initial values of the scale factor yields

$$a\left(\eta \right)e^{b_S}=\frac{1+z_S}{1+z},a\left(\eta \right)e^{b_F}=\frac{1+z_F}{1+z},$$

(7)

where $z_S$ ($z_F$) is the redshift when the scalar (fermion) field is decoupled. For neutrinos, $z_F\sim 6\times {10}^9$, while, for axions with mass $\sim 1$ meV, $z_S\sim 2.2\times {10}^{18}$.

We find from Equations (4) and (7),

$$\begin{array}{ccc}\hfill & & <\mathcal{H}>\left(z\right)=\frac{1}{2{\left(4\pi \right)}^2}\left\{M^{4}log{z}_S-2\mathcal{N}{m}^{4}log{z}_F-(M^4-2\mathcal{N}{m}^4)\left[log(1+z)+\frac{1}{4}\right]\right\}\hfill \end{array}$$

(8)

$$\begin{array}{c}\\ & & <P>\left(z\right)=-\frac{1}{2{\left(4\pi \right)}^2}\left\{M^{4}log{z}_S-2\mathcal{N}{m}^{4}log{z}_F-(M^4-2\mathcal{N}{m}^4)\left[log(1+z)-\frac{1}{12}\right]\right\},\hfill \end{array}$$

where we used the conditions $z_S\gg 1,z_F\gg 1$.

We identify the vacuum energy density today $<\mathcal{H}>(z=0)$ with the observed dark energy ${\rho }_{\mathsf{\Lambda }}$. We can then write Equations (4), (6) and (8) as:

$$\begin{array}{ccc}& & {\rho }_{\mathsf{\Lambda }}=\frac{1}{2{\left(4\pi \right)}^2}\left[M^4\left(log{z}_S-\frac{1}{4}\right)-2\mathcal{N}{m}^4\left(log{z}_F-\frac{1}{4}\right)\right],\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & <\mathcal{H}>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}{\rho }_{\mathsf{\Lambda }}\left[1+{\beta }_{\mathcal{N}}log\frac{a\left(\eta \right)}{a_0}\right],\hfill \end{array}$$

$$\begin{array}{ccc}& & w\left(\eta \right)+;1\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\frac{\left(M^4-2\mathcal{N}{m}^4\right)}{6{\left(4\pi \right)}^2{\rho }_{\mathsf{\Lambda }}\left[1+{\beta }_{\mathcal{N}}log\frac{a\left(\eta \right)}{a_0}\right]},\hfill \end{array}$$

(10)

where $a_0$ is the scale factor today and

$${\beta }_{\mathcal{N}}=\frac{{\displaystyle \left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)}}{{\displaystyle log{z}_S-\frac{1}{4}-\left(2\frac{\mathcal{N}{m}^4}{M^4}\right)\left[log{z}_F-\frac{1}{4}\right]}}.$$

(11)

That is, the vacuum energy density at late times after decoupling grows as the logarithm of the scale factor and the equation of state asymptotically approaches $-1$ from below.

The equation of state as a function of z takes the form:

$$w\left(z\right)+1=-\frac{1}{3}\frac{{\displaystyle \left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)}}{{\displaystyle log{z}_S-\left(\frac{2\mathcal{N}{m}^4}{M^4}\right)log{z}_F-\left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)\left[log(1+z)+\frac{1}{4}\right]}}.$$

(12)

For $z=0$, it becomes, today:

$$w\left(0\right)+1=-\frac{1}{3}\frac{{\displaystyle \left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)}}{{\displaystyle log{z}_S-\frac{1}{4}-\left(\frac{2\mathcal{N}{m}^4}{M^4}\right)\left[log{z}_F-\frac{1}{4}\right]}}=-\frac{1}{6{\left(4\pi \right)}^2{\rho }_{\mathsf{\Lambda }}}\left(M^4-2\mathcal{N}{m}^4\right).$$

(13)

The scalar and fermion masses are constrained by the value of the dark energy today Equation (2). This gives the positivity requirement:

$$M>{\left(2\mathcal{N}\right)}^{\frac{1}{4}}m,$$

as well as the expression for the mass of the scalar particle:

$${\displaystyle M=\frac{10.1\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}{\left[1+\mathcal{N}{\left(\frac{m}{3.90\mathrm{meV}}\right)}^4\right]}^{\frac{1}{4}}.}$$

(14)

The neutrino contribution to dark energy can be ignored when $m\ll 1$ meV and when the vacuum neutrino contribution dissipates in the time scale of the age of the universe, as mentioned before. The mass of the lightest neutrino is not yet known (only neutrino mass differences are known). We will consider that the lightest neutrino mass is either $m=3.2$ meV [69,70] or zero [71,72].

More specifically, we set $z_S\sim 2.2\times {10}^{18}$, assuming the scalar field to be an axion with mass $\sim 1$ meV in Equations (13) and (14).

• We therefore obtain for the axion mass M and for the equation of state today the following values:

  $$\begin{array}{ccc}\hfill & & 3.96\mathrm{meV}<M<4.66\mathrm{meV},\hfill \end{array}$$

  $$\begin{array}{ccc}& & -0.00794<w\left(0\right)+1<-0.00156.\hfill \end{array}$$

  (15)
  The left and right ends of the intervals in Equation (15) correspond to no neutrino contribution and to the lightest neutrino contribution, respectively, as a Dirac fermion with mass $m=3.2$ meV.
• We see that $w\left(0\right)$ is slightly below $-1$ by an amount ranging from $(-1.5\times {10}^{-3})$ to $(-8\times {10}^{-3})$, while the axion mass results are between 4 and 5 meV, which is within the range of axion masses allowed by astrophysical and cosmological constraints, e.g., [73,74,75].
  If the scalar particle is not the axion, the value of $z_S\gg 1$ will depend on the dynamics of such scalar particle.
• In general, we express the contribution of the quantum vacuum of light particles to dark energy and pressure in terms of two parameters: the particle masses and the redshifts when they are decoupled. There is also a dependence on the number of states per particle (1 for a scalar, $2\mathcal{N}$ for a fermion).
• We uncover in this paper the general mechanism producing the dark energy today. This mechanism is only based on well-known quantum physics and cosmology. The observed dark energy in the universe today appears as a quantum vacuum effect only due to the (classical) cosmological space-time expansion. That is to say, dark energy in the present universe is a semiclassical gravity effect.
• The dark energy arises for a quantum field in the cosmological context in an analogous way to how the Casimir effect arises for a quantum field in Minkowski space-time with non-trivial boundary conditions in space.
• All physical (finite) results are independent of any energy cutoff as well as of the regularization method used.
• We obtain and solve in this paper the self-consistent Einstein–Friedmann equation for the scale factor when dark energy dominates and the universe expansion accelerates. The growth of the energy density Equation (4) as the logarithm of the scale factor implies an expansion faster than in de Sitter space-time. More precisely, we find that the Universe will reach in the future an asymptotic phase where it expands exponentially as

  $$a\left(t\right)\stackrel{H_{0}t\gtrsim 1}{\simeq }a\left(\mathrm{today}\right)exp[c_1{H}_{0}t+c_2{\left(H_{0}t\right)}^2],$$

  (16)

  where

  $$\begin{array}{ccc}\hfill & & c_1\equiv \sqrt{{\mathsf{\Omega }}_{\mathsf{\Lambda }}}=0.87,0.00452<c_2<0.00872,\hfill \end{array}$$

  (17)

  and $H_0$ stands for the Hubble parameter today. The left and right ends of the interval for $c_2$ in Equation (17) correspond to no neutrino contribution and to the lightest neutrino contribution, respectively, as a Dirac fermion with mass $m=3.2$ meV.
• Notice that the time scale of the accelerated expansion is huge: $\sim 1/H_0=13.4$ Gyr. In the exponent of Equation (16), the quadratic term dominates over the linear term by a time $t\sim 100/H_0$ to $200/H_0$.
  In this accelerated universe, we see from the Friedman equation and Equation (4) that the Hubble radius $1/H$ decreases with time as $1/\left[H_0\sqrt{loga\left(t\right)}\right]$.

This paper is organized as follows: In Section 2 and Section 3, we review the dynamics of scalar and fermion fields on cosmological space-times, respectively. In Section 4, we discus the quantum cosmological vacuum and the two point functions and compute the main physical quantities from them. In Section 5, we find the vacuum energy density and pressure and the equation of state for late times, and in Section 6 we discuss their quantum nature. In Section 7, we find dark energy as a result of the cosmological quantum vacuum contributions from meV light particles, and the properties, masses and stabilities of axions are treated.. In Section 8, we compute and analyze the neutrino contributions to dark energy: the lightest neutrino remains the only contribution. In Section 9, we unify these results with both light meV particles together. We obtain the future self-consistent evolution of the universe in Section 10. We discuss relevant related issues in Section 11, and we present our conclusions in Section 12. Appendix A is devoted to the equivalence between different regularization methods.

2. Scalar Fields in Cosmological Space-Times

We consider a massive neutral scalar field $\phi$ in an FRW geometry defined by the invariant distance

$$d{s}^2=d{t}^2-a^2\left(t\right)d{\overrightarrow{x}}^2.$$

(18)

The Lagrangian density is taken to be

$$\mathcal{L}=\frac{1}{2}\sqrt{-g}\left[{\dot{\phi }}^2-{\left(\frac{\overrightarrow{\nabla }\phi }{a}\right)}^2-M^2{\phi }^2\right].$$

(19)

It is convenient to use the conformal time $\eta$,

$$\eta =\int \frac{dt}{a\left(t\right)},$$

and the conformally rescaled field $\chi (\overrightarrow{x},\eta )$,

$$\chi (\overrightarrow{x},\eta )\equiv a\left(t\right)\phi (\overrightarrow{x},t).$$

(20)

The action (after discarding surface terms that do not affect the equations of motion) reads:

$$A\left(\chi ,\delta \right)=\frac{1}{2}\int d^{3}xd\eta \left[{{\chi }^{\prime }}^2-{(\nabla \chi )}^2-{\mathcal{M}}^2\left(\eta \right){\chi }^2\right],$$

(21)

where primes denote derivatives with respect to the conformal time $\eta$ and where

$${\mathcal{M}}^2\left(\eta \right)=M^2{a}^2\left(\eta \right)-\frac{a^{″}\left(\eta \right)}{a\left(\eta \right)}$$

(22)

plays the role of an effective mass squared. Therefore, the rescaled field $\chi (\overrightarrow{x},\eta )$ obeys the equation of motion,

$${\chi }^{″}-{\nabla }^2\chi +{\mathcal{M}}^2\left(\eta \right)\chi =0.$$

(23)

The evolution of $\chi (\overrightarrow{x},\eta )$ is similar to that of a scalar field in Minkowski space-time with a time-dependent mass squared ${\mathcal{M}}^2\left(\eta \right)$.

The solution for the field $\phi (\overrightarrow{x},t)$ can be Fourier expanded as follows,

$$\phi (\overrightarrow{x},\eta )=\frac{1}{a\left(\eta \right)}\int \frac{d^{3}k}{{\left(2\pi \right)}^{3}2E_0}\left[a_{\overrightarrow{k}}{\varphi }_k\left(\eta \right)e^{i\overrightarrow{k}·\overrightarrow{x}}+a_{\overrightarrow{k}}^{†}{\varphi }_k^{*}\left(\eta \right)e^{-i\overrightarrow{k}·\overrightarrow{x}}\right],$$

(24)

where

$$E_0\equiv \sqrt{k^2+{\mathcal{M}}_i^2}$$

and ${\mathcal{M}}_i$ is the effective mass $\mathcal{M}\left(\eta \right)$ at the decoupling time (initial time) for the scalar field evolution. The mode functions ${\varphi }_k\left(\eta \right)$ obey the evolution equations,

$$\left[\frac{d^2}{d{\eta }^2}+k^2+M^2{a}^2\left(\eta \right)-\frac{a^{″}\left(\eta \right)}{a\left(\eta \right)}\right]{\varphi }_k\left(\eta \right)=0.$$

(25)

We choose the initial state as the vacuum state, which, here (at decoupling), is a thermal equilibrium state at temperature T. However, as we see below (Equation (70)), the effect of the initial temperature on the vacuum energy is negligible for late times. The Fock vacuum state $|0>$ is annihilated by the operators $a_{\overrightarrow{k}}$. Therefore, we have as initial conditions for the mode functions

$${\varphi }_k\left(0\right)=1,{\varphi }_k^{\prime }\left(0\right)=-i{E}_0.$$

(26)

These initial conditions describe the Bunch–Davies vacuum when they are applied at asymptotically earlier times in the past ($\eta \to -\infty$) [76,77]. See the discussion in Section 11 below.

The time-dependent creation and annihilation operators obey the canonical commutation rules,

$$\left[a_{\overrightarrow{k}},a_{{\overrightarrow{k}}^{\prime }}^{†}\right]=2E_0{\left(2\pi \right)}^3\delta (\overrightarrow{k}-\overrightarrow{k^{\prime }}).$$

The energy-momentum tensor for a scalar field is given by [76],

$$T_{\mu \nu }={\partial }_{\mu }\phi {\partial }_{\nu }\phi -\frac{1}{2}{g}_{\mu \nu }\left[{\partial }_{\lambda }\phi {\partial }^{\lambda }\phi -M^2{\phi }^2\right].$$

(27)

Its expectation value has the fluid form

$$<T_{S0}^0>=<{\mathcal{H}}_S>\left(\eta \right),<T_i^j>=-{\delta }_i^j<P_S>\left(\eta \right)$$

since we consider homogeneous and isotropic quantum states and density matrices. In conformal time, the hamiltonian density and the pressure take the form

$$\begin{array}{ccc}\hfill & & {\mathcal{H}}_S\left(\eta \right)=\frac{1}{2a^4\left(\eta \right)}\left\{{\left[{\chi }^{\prime }(\overrightarrow{x},\eta )-a\left(\eta \right)H\left(\eta \right)\chi (\overrightarrow{x},\eta )\right]}^2+{(\nabla \chi (\overrightarrow{x},\eta ))}^2+a^2\left(\eta \right)M^2{\chi }^2(\overrightarrow{x},\eta )\right\},\hfill \end{array}$$

$$\begin{array}{ccc}& & {\mathcal{H}}_S+P_S\left(\eta \right)=\frac{1}{a^4\left(\eta \right)}\left\{{\left[{\chi }^{\prime }(\overrightarrow{x},\eta )-a\left(\eta \right)H\left(\eta \right)\chi (\overrightarrow{x},\eta )\right]}^2+\frac{1}{3}{\left(\nabla \chi (\overrightarrow{x},\eta )\right)}^2\right\},\hfill \end{array}$$

(28)

where $H\left(\eta \right)$ stands for the Hubble parameter

$$H\left(\eta \right)\equiv \frac{dlna\left(t\right)}{dt}=\frac{1}{a^2\left(\eta \right)}\frac{da}{d\eta }.$$

(29)

It is convenient to consider the conformal energy and pressure,

$${\epsilon }_S\left(\eta \right)\equiv a^4\left(\eta \right)<{\mathcal{H}}_S>\left(\eta \right),p_S\left(\eta \right)\equiv a^4\left(\eta \right)<P_S>\left(\eta \right).$$

(30)

We find the trace of the energy-momentum tensor from Equations (28),

$$a^4\left(\eta \right)\left[{\mathcal{H}}_S\left(\eta \right)-3P_S\left(\eta \right)\right]=a^2\left(\eta \right)M^2{\chi }^2-\left[{({\chi }^{\prime }-ah\chi )}^2-{(\nabla \chi )}^2-a^2\left(\eta \right)M^2{\chi }^2\right].$$

(31)

Ignoring the bracket term on the right hand side yields the virial theorem. Although this bracket term is non-zero, its space and time average is zero:

$$\frac{1}{\Delta }{\int }_{\eta }^{\eta +\Delta }d\eta \int d^{3}x\left[{({\chi }^{\prime }-ah\chi )}^2-{(\nabla \chi )}^2-a^2\left(\eta \right)M^2{\chi }^2\right]\stackrel{\Delta \gg 1/M}{=}0.$$

In addition, this bracket can be neglected for late times, as we shall see below.

Therefore, we have for the expectation values

$${\epsilon }_S\left(\eta \right)-3p_S\left(\eta \right)=M^2{a}^2\left(\eta \right){\mathsf{\Sigma }}_S\left(\eta \right)-a^4\left(\eta \right)V\left(\eta \right),$$

(32)

where

$${\mathsf{\Sigma }}_S\left(\eta \right)\equiv <{\chi }^2(\overrightarrow{x},\eta )>=a^2\left(\eta \right)<{\phi }^2(\overrightarrow{x},\eta )>$$

(33)

and V stands for the expectation value of the virial

$$V\left(\eta \right)\equiv <{({\chi }^{\prime }-ah\chi )}^2-{\left(\nabla \chi \right)}^2-a^2\left(\eta \right)M^2{\chi }^2>.$$

Using the equations of motion (23), we obtain for the time derivative of the energy density Equation (30),

$$\frac{d{\epsilon }_S}{d\eta }=\frac{1}{2}{M}^2\frac{d{a}^2\left(\eta \right)}{d\eta }{\mathsf{\Sigma }}_S\left(\eta \right)-a\left(\eta \right)H\left(\eta \right)V\left(\eta \right).$$

(34)

This relation in conformal time implies the usual continuity equation in cosmic time:

$$\frac{d}{dt}<{\mathcal{H}}_S>+3H\left(\eta \right)\left[<{\mathcal{H}}_S>+<P_S>\right]=0.$$

(35)

Therefore, from Equations (32) and (34), we see that there is only one independent quantity among ${\epsilon }_S\left(\eta \right),p_S\left(\eta \right)$ and ${\mathsf{\Sigma }}_S\left(\eta \right)$.

3. Fermion Fields in Cosmological Space-Times

The Lagrangian density for fermions is taken to be [77]

$$\mathcal{L}=\sqrt{-g}\overline{\mathsf{\Psi }}\left[i{\gamma }^{\mu }{\mathcal{D}}_{\mu }\mathsf{\Psi }-m\right]\mathsf{\Psi }.$$

(36)

The ${\gamma }^{\mu }$ are the curved space-time Dirac $\gamma$ matrices, and the fermionic covariant derivative is given by

$$\begin{array}{ccc}\hfill {\mathcal{D}}_{\mu }& =& {\partial }_{\mu }+\frac{1}{8}[{\gamma }^c,{\gamma }_{;}^d]V_c^{\nu }\left(D_{\mu }{V}_{d\nu }\right)\hfill \end{array}$$

$$\begin{array}{c}\\ \hfill D_{\mu }{V}_{d\nu }& =& {\partial }_{\mu }{V}_{d\nu }-{\mathsf{\Gamma }}_{\mu \nu }^{\lambda }{V}_{d\lambda },\hfill \end{array}$$

where the vierbein field is defined as

$$g^{\mu \nu }=V_a^{\mu }{V}_b^{\nu }{\eta }^{ab},$$

${\eta }_{ab}$ is the Minkowski space-time metric and the curved space-time matrices ${\gamma }^{\mu }$ are given in terms of the Minkowski space-time ones, ${\gamma }^a$ (Greek indices refer to curved space-time coordinates and Latin indices to the local Minkowski space-time coordinates):

$${\gamma }^{\mu }={\gamma }^a{V}_a^{\mu },\{{\gamma }^{\mu },{\gamma }^{\nu }\}=2g^{\mu \nu }.$$

In conformal time, the vierbeins $V_a^{\mu }$ are particularly simple:

$$V_a^{\mu }=a\left(\eta \right){\delta }_a^{\mu },$$

(37)

where $a\left(\eta \right)\equiv a\left(t\right(\eta \left)\right)$ is the scale factor as a function of the conformal time and we call $a(\eta =0)=a_{\mathrm{dc}}$. The Dirac Lagrangian density thus simplifies to the following expression:

$$\sqrt{-g}\overline{\mathsf{\Psi }}\left(i{\gamma }^{\mu }{\mathcal{D}}_{\mu }\mathsf{\Psi }-m\right)\mathsf{\Psi }=a^{\frac{3}{2}}\overline{\mathsf{\Psi }}\left[i\cancel{\partial }-ma\left(\eta \right)\right]\left(a^{\frac{3}{2}}\mathsf{\Psi }\right),$$

(38)

where $i\cancel{\partial }$ is the usual Dirac differential operator in Minkowski space-time in terms of flat space-time ${\gamma }^a$ matrices.

Therefore, the Dirac equation in the FRW geometry is given by

$$\left[i\cancel{\partial }-ma\left(\eta \right)\right]\left[a^{\frac{3}{2}}\mathsf{\Psi }(\overrightarrow{x},\eta )\right]=0.$$

(39)

The solution $\mathsf{\Psi }(\overrightarrow{x},\eta )$ can be expanded in spinor mode functions as

$$\mathsf{\Psi }(\overrightarrow{x},\eta )=\frac{1}{a^{\frac{3}{2}}\left(\eta \right)}\sum _{\lambda =\pm 1}\int \frac{d^{3}k}{{\left(2\pi \right)}^{3}2e_0}{e}^{i\overrightarrow{k}·\overrightarrow{x}}\left[b_{\overrightarrow{k},\lambda }{U}_{\lambda }(\overrightarrow{k},\eta )+d_{-\overrightarrow{k},\lambda }^{†}{V}_{\lambda }(-\overrightarrow{k},\eta )\right],$$

(40)

where

$$e_0\equiv \sqrt{k^2+m^2{a}_{\mathrm{dc}}^2}$$

and the spinor mode functions $U,V$ obey the Dirac equations

$$\begin{array}{ccc}\hfill \left[i{\gamma }^0{\partial }_{\eta }-\overrightarrow{\gamma }·\overrightarrow{k}-ma\left(\eta \right)\right]U_{\lambda }(\overrightarrow{k},\eta )& =& 0,\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill \left[i{\gamma }^0{\partial }_{\eta }+\overrightarrow{\gamma }·\overrightarrow{k}-ma\left(\eta \right)\right]V_{\lambda }(\overrightarrow{k},\eta )& =& 0.\hfill \end{array}$$

(42)

The time-independent creation and annihilation operators obey the canonical anticommutation rules

$$\begin{array}{ccc}& & \left\{b_{\overrightarrow{k},\lambda },b_{\overrightarrow{k^{\prime }},{\lambda }^{\prime }}^{†}\right\}=2e_0{\left(2\pi \right)}^3\delta (\overrightarrow{k}-\overrightarrow{k^{\prime }}){\delta }_{\lambda {\lambda }^{\prime }},\hfill \end{array}$$

$$\begin{array}{ccc}& & \left\{d_{\overrightarrow{k},\lambda },d_{\overrightarrow{k^{\prime }},{\lambda }^{\prime }}^{†}\right\}=2e_0{\left(2\pi \right)}^3\delta (\overrightarrow{k}-\overrightarrow{k^{\prime }}){\delta }_{\lambda {\lambda }^{\prime }}.\hfill \end{array}$$

(43)

Following the method of refs. [41,42], it proves convenient to write

$$\begin{array}{ccc}\hfill U_{\lambda }(\overrightarrow{k},\eta )& =& {(e_0+m{a}_{\mathrm{dc}})}^{-\frac{1}{2}}\left[i{\gamma }^0{\partial }_{\eta }-\overrightarrow{\gamma }·\overrightarrow{k}+ma\left(\eta \right)\right]f_k\left(\eta \right){\mathcal{U}}_{\lambda }\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill V_{\lambda }(\overrightarrow{k},\eta )& =& {(e_0+m{a}_{\mathrm{dc}})}^{-\frac{1}{2}}\left[i{\gamma }^0{\partial }_{\eta }+\overrightarrow{\gamma }·\overrightarrow{k}+ma\left(\eta \right)\right]g_k\left(\eta \right){\mathcal{V}}_{\lambda },\hfill \end{array}$$

(45)

with ${(e_0+m{a}_{\mathrm{dc}})}^{-\frac{1}{2}}$ being a normalization factor and $({\mathcal{U}}_{\lambda },{\mathcal{V}}_{\lambda })$ being constant spinors [41,42] obeying

$${\gamma }^0{\mathcal{U}}_{\lambda }={\mathcal{U}}_{\lambda },{\gamma }^0{\mathcal{V}}_{\lambda }=-{\mathcal{V}}_{\lambda },\lambda =\pm 1.$$

(46)

More explicitly,

$$\begin{array}{ccc}& & U_{\lambda }(\overrightarrow{k},\eta )={(e_0+m{a}_{\mathrm{dc}})}^{-\frac{1}{2}}\left(\begin{array}{cc}\left[i{f}_k^{\prime }\left(\eta \right)+ma\left(\eta \right)f_k\left(\eta \right)\right]& 0\\ 0& \lambda k{f}_k\left(\eta \right)\end{array}\right){\mathcal{U}}_{\lambda },\hfill \end{array}$$

$$\begin{array}{ccc}& & V_{\lambda }(-\overrightarrow{k},\eta )={(e_0+m{a}_{\mathrm{dc}})}^{-\frac{1}{2}}\left(\begin{array}{cc}\lambda k{g}_k\left(\eta \right)& 0\\ 0& \left[-i{g}_k^{\prime }\left(\eta \right)+ma\left(\eta \right)g_k\left(\eta \right)\right]\end{array}\right){\mathcal{V}}_{\lambda }.\hfill \end{array}$$

(47)

The mode functions $f_k\left(\eta \right),g_k\left(\eta \right)$ obey then the following equations of motion

$$\begin{array}{ccc}\hfill \left[\frac{d^2}{d{\eta }^2}+k^2+m^2{a}^2\left(\eta \right)-im{a}^{\prime }\left(\eta \right)\right]f_k\left(\eta \right)& =& 0\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill \left[\frac{d^2}{d{\eta }^2}+k^2+m^2{a}^2\left(\eta \right)+im{a}^{\prime }\left(\eta \right)\right]g_k\left(\eta \right)& =& 0.\hfill \end{array}$$

(49)

We choose the initial state for the fermion field as the vacuum state, which is a thermal equilibrium state at temperature T for the fermion. This Fock state $|0>$ is annihilated by the operators $b_{\overrightarrow{k},\lambda }$ and $d_{\overrightarrow{k},\lambda }$.

Therefore, we have as initial conditions for the mode functions [41,42]

$$\begin{array}{ccc}\hfill & & f_k\left(0\right)=1,f_k^{\prime }\left(0\right)=-i{e}_0,\hfill \end{array}$$

(50)

$$\begin{array}{c}\\ & & g_k\left(0\right)=1,g_k^{\prime }\left(0\right)=+i{e}_0.\hfill \end{array}$$

These initial conditions describe the Bunch–Davies vacuum when they are applied at asymptotically earlier times in the past ($\eta \to -\infty$) [76,77]. See the discussion in Section 11 below.

Equations (48)–(50) imply that

$$g_k\left(\eta \right)=f_k^{*}\left(\eta \right).$$

That is, we have only one independent and complex mode function.

The scalar products of the spinors $U_{\lambda }(\overrightarrow{k},\eta ),V_{\lambda }(\overrightarrow{k},\eta )$ take the values

$$\begin{array}{ccc}& & U_{\lambda }^{†}(\overrightarrow{k},\eta )U_{{\lambda }^{\prime }}(\overrightarrow{k},\eta )=2e_0{\delta }_{\lambda {\lambda }^{\prime }}\hfill \end{array}$$

$$\begin{array}{ccc}& & V_{\lambda }^{†}(\overrightarrow{k},\eta )V_{{\lambda }^{\prime }}(\overrightarrow{k},\eta )=2e_0{\delta }_{\lambda {\lambda }^{\prime }}.\hfill \end{array}$$

(51)

As a consequence, the mode functions obey the relation [41,42]

$$|f_k^{\prime }{\left(\eta \right)|}^2-ima\left(\eta \right)[f_k\left(\eta \right){f^{\prime }}_k^{*}\left(\eta \right)-f_k^{\prime }\left(\eta \right)f_k^{*}\left(\eta \right)]+[k^2+m^2{a}^2\left(\eta \right)]{\left|f_k\left(\eta \right)\right|}^2=2e_0(e_0+m{a}_{\mathrm{dc}}),$$

which provides a conserved quantity.

The energy momentum tensor for a spin $1/2$ field is given by [76]

$$T_{\mu \nu }^F=\frac{i}{2}\left[\overline{\mathsf{\Psi }}{\gamma }_{(\mu }{\overleftrightarrow{\mathcal{D}}}_{\nu )}\mathsf{\Psi }\right],$$

(52)

and its expectation value has the fluid form

$$<{T_F}_0^0>=<{\mathcal{H}}_F>\left(\eta \right),<{T_F}_i^j>=-{\delta }_i^j<P_F>\left(\eta \right)$$

since we consider homogeneous and isotropic quantum states and density matrices.

More explicitly, the energy density in conformal time takes the form

$$<{\mathcal{H}}_F>\left(\eta \right)=<\mathsf{\Psi }{(\overrightarrow{x},\eta )}^{†}{H}_F\mathsf{\Psi }(\overrightarrow{x},\eta )>,$$

(53)

where the fermion hamiltonian $H_F$ is defined by

$$a\left(\eta \right){\gamma }_0{H}_F=-i\overrightarrow{\gamma }·\overrightarrow{\nabla }+ma\left(\eta \right)=\overrightarrow{\gamma }·\overrightarrow{p}+ma\left(\eta \right).$$

(54)

An analogous expression can be written for the pressure,

$$<P_F>\left(\eta \right)=\frac{1}{3a\left(\eta \right)}<\overline{\mathsf{\Psi }}\overrightarrow{\gamma }·\overrightarrow{p}\mathsf{\Psi }>\left(\eta \right).$$

(55)

Here, too, it is convenient to consider the conformal energy and pressure,

$${\epsilon }_F\left(\eta \right)\equiv a^4\left(\eta \right)<{\mathcal{H}}_F>\left(\eta \right),p_F\left(\eta \right)\equiv a^4\left(\eta \right)<P_F>\left(\eta \right).$$

(56)

We find the trace of the energy-momentum tensor from Equations (54)–(56),

$$\begin{array}{ccc}\hfill & & {\epsilon }_F\left(\eta \right)-3p_F\left(\eta \right)=ma\left(\eta \right){\mathsf{\Sigma }}_F\left(\eta \right),\mathrm{or}\hfill \end{array}$$

(57)

$$\begin{array}{c}\\ & & <{\mathcal{H}}_F>\left(\eta \right)-3<P_F>\left(\eta \right)=m<\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right).\hfill \end{array}$$

This is the expression of the virial theorem in the present context and

$${\mathsf{\Sigma }}_F\left(\eta \right)\equiv a^3\left(\eta \right)<\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right).$$

(58)

The above expressions for the energy density and pressure obey the usual continuity equation in cosmic time:

$$\frac{d}{dt}<{\mathcal{H}}_F>+3H\left(\eta \right)\left(<{\mathcal{H}}_F>+<P_F>\right)=0,$$

(59)

In conformal time, by using Equations (57) and (58), the continuity Equation (59) becomes

$$\frac{d{\epsilon }_F}{d\eta }=m\frac{da\left(\eta \right)}{d\eta }{\mathsf{\Sigma }}_F\left(\eta \right).$$

(60)

We thus see from Equations (57) and (60) that there is only one independent quantity among ${\epsilon }_F\left(\eta \right),{\mathcal{P}}_F\left(\eta \right)$ and ${\mathsf{\Sigma }}_F\left(\eta \right)$.

4. The Cosmological Quantum Vacuum

There are two widely separate scales in the field evolution in the cosmological space-time. The fast scale is the microscopic quantum evolution scale, typically $\sim 1/M\sim 1/m$. The slow scale is the Hubble scale, $1/H$ of the universe expansion.

When $M\sim m\gg H$, we can consider that the scale factor is practically constant. Therefore, in conformal time, the quantum field evolution is similar to the evolution in Minkowski space-time with a mass $Ma\left(\eta \right)$ or $ma\left(\eta \right)$ for bosons or fermions, respectively (see Equations (22) and (39)).

The scalar and fermion densities follow as equal point limits of the scalar and fermion two-point functions. That is, we consider the scale factor a as a constant and obtain for the scalar two-point function

$$\begin{array}{ccc}\hfill G_S(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },Ma)& \equiv & <T\phi (\overrightarrow{x},\eta )\phi ({\overrightarrow{x}}^{\prime },{\eta }^{\prime })>=\frac{1}{a^2}\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{e}^{-ik·(x-y)}\frac{i}{k^2-a^2{M}^2+i0}=\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{1}{{\left(2\pi \right)}^2}\frac{M}{za}{K}_1\left(Maz\right),z\equiv \sqrt{{(\overrightarrow{x}-{\overrightarrow{x}}^{\prime })}^2-{(\eta -{\eta }^{\prime })}^2},\hfill \end{array}$$

(61)

where $K_1\left(x\right)$ is a modified Bessel function.

Equation (61) is the zeroth order adiabatic approximation. It differs from the exact two-point function by quantities of the order $\mathcal{O}\left(a^{\prime }\left(\eta \right)\right),\mathcal{O}\left(a^{″}\left(\eta \right)\right)$, etc.

We find from Equation (61) in the coincidence point limit:

$$G_S(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },Ma)\stackrel{z\to 0}{=}\frac{1}{{\left(2\pi \right)}^2}\left\{\frac{1}{z^2{a}^2}+\frac{1}{2}{M}^2\left[log\left(Maz\right)+\mathcal{C}-ln2-\frac{1}{2}\right]\right\}[1+\mathcal{O}\left(M^2{z}^2\right)],$$

(62)

where $\mathcal{C}=0.57721566\dots$ is the Euler–Mascheroni constant. Equations (61) and (62) display the two-point functions for the zero temperature vacuum. The effect of a non-zero temperature on the two-point function is negligible for $a\gg 1$, as we show below (Equation (70)).

The fermion two-point function takes the form

$$<T\mathsf{\Psi }{(\overrightarrow{x},\eta )}_{\alpha }\overline{\mathsf{\Psi }}{({\overrightarrow{x}}^{\prime },{\eta }^{\prime })}_{\beta }>=\frac{1}{a^3}\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{e}^{-ik·(x-y)}\frac{i{(\cancel{k}+am)}_{\alpha \beta }}{k^2-a^2{m}^2+i0},$$

(63)

and hence,

$$G_F(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },ma)\equiv <T\overline{\mathsf{\Psi }}(\overrightarrow{x},\eta )\mathsf{\Psi }({\overrightarrow{x}}^{\prime },{\eta }^{\prime })>=-4m{G}_S(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },ma),\mathrm{Dirac}\mathrm{fermions}.$$

(64)

The minus sign in front arose from the anticommutation of the fermion fields going from Equation (63) to Equation (64). Here, we used Equation (61) and

$$\mathrm{Tr}\cancel{k}=0,\mathrm{Tr}1=4.$$

(65)

That is, the factor $4=2\times 2$ in Equations (64) and (65) comes from the fermion and antifermion contributions times the number of helicities of a Dirac fermion. Hence, this factor 4 becomes a factor 2 for Majorana fermions:

$$G_F(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },ma)\equiv <\overline{\mathsf{\Psi }}(\overrightarrow{x},\eta )\mathsf{\Psi }({\overrightarrow{x}}^{\prime },{\eta }^{\prime })>=-2m{G}_S(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },ma).$$

(66)

We find in the coincidence point limit corrections up to $[1+\mathcal{O}\left(m^2{z}^2\right)]$:

$$\begin{array}{ccc}\hfill & & G_F(\overrightarrow{x}-{\overrightarrow{x}}^{\prime },\eta -{\eta }^{\prime },ma)\stackrel{z\to 0}{=}-\frac{2\mathcal{N}m}{{\left(2\pi \right)}^2}\left\{\frac{1}{z^2{a}^2}+\frac{1}{2}{m}^2\left[log\left(maz\right)+\mathcal{C}-ln2-\frac{1}{2}\right]\right\}.\hfill \end{array}$$

(67)

Here, $\mathcal{N}=1$ for Majorana fermions and $\mathcal{N}=2$ for Dirac fermions.

In order to define the vacuum densities as the coincidence limits,

$$<{\phi }^2>\left(\eta \right)\equiv <{\phi }^2(\overrightarrow{x},\eta )>,<\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right)\equiv <\overline{\mathsf{\Psi }}(\overrightarrow{x},\eta )\mathsf{\Psi }(\overrightarrow{x},\eta )>,$$

we have to subtract the singularities at $z=0$ in Equations (62) and (67). Subtracting the singularities leaves a finite z independent piece. Requiring that the vacuum densities vanish in Minkowski space-time ($a=1$), we obtain

$$<{\phi }^2>\left(\eta \right)=\frac{M^2}{2{\left(2\pi \right)}^2}\left[loga+b_S{f}_S\left(a\right)\right],<\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right)=-\frac{\mathcal{N}{m}^3}{{\left(2\pi \right)}^2}\left[loga+b_F{f}_F\left(a\right)\right].$$

(68)

The functions $f_S\left(a\right)$ and $f_F\left(a\right)$ are finite and vanish for Minkowski space-time,

$$f_S\left(1\right)=0,f_F\left(1\right)=0.$$

We compute the terms $b_S{f}_S\left(a\right)$ and $b_F{f}_F\left(a\right)$ with the result

$$f_S(\infty )\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}1+\mathcal{O}\left(\frac{1}{a^2}\right),f_F(\infty )\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}1+\mathcal{O}\left(\frac{1}{a^2}\right).$$

When one performs an infinite subtraction at $z=0$, an additional finite subtraction can always be done. We recognize that the additional terms containing $b_S$ and $b_F$ can be absorbed in a finite multiplicative renormalization of the scale factor. That is, introducing $b_S$ and $b_F$ amounts to a scale transformation. We compute the coefficients $b_S$ and $b_F$ in terms of the subtraction scale in momentum space $\left(xM\right)$ for scalars and $\left(xm\right)$ for fermions, with the result

$$b_S\left(x\right)=b_F\left(x\right)=-\frac{1}{2}-logx-log{a}_{\mathrm{dc}},$$

where $a_{\mathrm{dc}}$ stands for the scale factor at decoupling time (initial time). In summary, we have for the late time regime,

$$\begin{array}{ccc}\hfill & & <{\phi }^2>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}\frac{M^2}{2{\left(2\pi \right)}^2}\left[loga\left(\eta \right)+b_S\right]=\frac{M^2}{2{\left(2\pi \right)}^2}\left[log\frac{a\left(\eta \right)}{x{a}_{\mathrm{dcs}}}-\frac{1}{2}\right],\hfill \end{array}$$

$$\begin{array}{ccc}& & <\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\frac{\mathcal{N}{m}^3}{{\left(2\pi \right)}^2}\left[loga\left(\eta \right)+b_F\right]=-\frac{\mathcal{N}{m}^3}{{\left(2\pi \right)}^2}\left[log\frac{a\left(\eta \right)}{x{a}_{\mathrm{dcf}}}-\frac{1}{2}\right],\hfill \end{array}$$

(69)

where $a_{\mathrm{dcs}}$ and $a_{\mathrm{dcf}}$ stand for the scale factor at the decoupling times (initial times) for the scalar and the fermion, respectively.

The two-point function Equations (61) and (64) correspond to the zero-temperature case. The singular pieces for $z\to 0$ are temperature independent. We can disregard the temperature-dependent contributions to the two-point functions since for large a they decrease as

$$\sqrt{M}{\left(\frac{T}{2\pi a}\right)}^{\frac{3}{2}}{e}^{-\frac{Ma}{T}}\to 0,a\gg 1.$$

(70)

The scalar and fermion densities $<{\phi }^2>\left(\eta \right)$ and $<\overline{\mathsf{\Psi }}\mathsf{\Psi }>\left(\eta \right)$ can be also computed as momentum integrals over the mode functions ${\varphi }_k\left(\eta \right)$ and $f_k\left(\eta \right)$. In addition, the subdominant terms in $1/a^2\left(\eta \right),\dot{a}\left(\eta \right)/a^2\left(\eta \right),\dots$, etc., can be obtained.

The equal points behavior of the two-point function Equations (62) and (67) is generic for any curved space-time when expressed as a function of the geodesic (squared) distance $\sigma \equiv z^2{a}^2$ between the two points. That is, the short distance behavior is uniquely and universally determined by the local space-time geometry. It must be noticed that the divergences and finite pieces at $\sigma =0$ are of the same type as in Minkowski space-time. This is the so-called Hadamard expansion for $\sigma \to 0$ and is equivalent to the adiabatic expansion. The coefficients of the divergent and finite parts are called Hadamard coefficients and they are known for generic space-times.

5. Vacuum Energy Density and Pressure for Late Times

The total energy density $\epsilon \left(\eta \right)$ and pressure $\mathcal{P}\left(\eta \right)$:

$$<\mathcal{H}>\left(\eta \right)=<{\mathcal{H}}_S>\left(\eta \right)+<{\mathcal{H}}_F>\left(\eta \right),$$

(71)

$$<P>\left(\eta \right)=<P_S>\left(\eta \right)+<P_F>\left(\eta \right),$$

(72)

can be computed in the late-time regime using the virial theorem Equations (32) and (57), the continuity equation Equations (34) and (60) and the late-time behavior of the densities, Equation (69).

We obtain after calculation for the energy density and pressure,

$$<\mathcal{H}>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}\frac{M^4}{2{\left(4\pi \right)}^2}\left[loga\left(\eta \right)+b_S-\frac{1}{4}\right]-\frac{m^4}{{\left(4\pi \right)}^2}\mathcal{N}\left[loga\left(\eta \right)+b_F-\frac{1}{4}\right],$$

(73)

$$<P>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\frac{M^4}{2{\left(4\pi \right)}^2}\left[loga\left(\eta \right)+b_S+\frac{1}{12}\right]+\frac{m^4}{{\left(4\pi \right)}^2}\mathcal{N}\left[loga\left(\eta \right)+b_F+\frac{1}{12}\right].$$

(74)

The decoupling (initial) times for the evolution of scalars and fermions can be different from each other. We have absorbed in $b_S$ and $b_F$ the corresponding initial values of the scale factor for scalars and fermions, respectively.

The positivity of the energy density imposes the condition

$$M^4>2\mathcal{N}{m}^4.$$

Notice that

$$<P>\left(\eta \right)+<\mathcal{H}>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\frac{1}{6{\left(4\pi \right)}^2}\left[M^4-2\mathcal{N}{m}^4\right]$$

is time independent and independent of the finite subtraction coefficients $b_S$ and $b_F$ as well.

From Equation (73), we obtain for the equation of state,

$$w\left(\eta \right)\equiv \frac{<P>\left(\eta \right)}{<\mathcal{H}>\left(\eta \right)}\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-1-\frac{1}{3}{\left[{\displaystyle loga\left(\eta \right)-\frac{1}{4}+\frac{b_S-(2\mathcal{N}{m}^4/M^4)b_F}{1-(2\mathcal{N}{m}^4/M^4)}}\right]}^{-1}.$$

(75)

That is, we find $w\left(\eta \right)<-1$ with $w\left(\eta \right)$ asymptotically reaching the value $-1$ from below.

It is convenient to express the scale factor in terms of the redshift as

$$a\left(\eta \right)exp\left(b_S\right)=\frac{1+z_S}{1+z},a\left(\eta \right)exp\left(b_F\right)=\frac{1+z_F}{1+z},$$

(76)

where $z_S$ ($z_F$) is the redshift when the evolution of the scalar (fermion) becomes the one of a free field in cosmological space-time. In terms of $z_S$ and $z_F$, Equation (73) reads,

$$\begin{array}{c}\hfill \left[2{\left(4\pi \right)}^2\right]<\mathcal{H}>\left(z\right)=M^{4}log(1+z_S)-2\mathcal{N}{m}^{4}log(1+z_F)-\\ \hfill -(M^4-2\mathcal{N}{m}^4)\left[log(1+z)+\frac{1}{4}\right],\end{array}$$

(77)

$$\begin{array}{c}\hfill [-2{\left(4\pi \right)}^2]<P>\left(z\right)=M^{4}log(1+z_S)-2\mathcal{N}{m}^{4}log(1+z_F)-\\ \hfill -(M^4-2\mathcal{N}{m}^4)\left[log(1+z)-\frac{1}{12}\right].\end{array}$$

(78)

The equation of state (75) as a function of z takes the form:

$$\begin{array}{c}w\left(z\right)+1=-\frac{1}{3}\left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)\times \\ \times {\left\{log(1+z_S)-\left(\frac{2\mathcal{N}{m}^4}{M^4}\right)log(1+z_F)-\left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right)\left[log(1+z)+\frac{1}{4}\right]\right\}}^{-1}.\end{array}$$

(79)

The equation of state and the energy density of today become:

$$w(z=0)+1=-\frac{1}{3}\left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right){\left\{log(1+z_S)-\frac{1}{4}-\left(\frac{2\mathcal{N}{m}^4}{M^4}\right)\left[log(1+z_F)-\frac{1}{4}\right]\right\}}^{-1},$$

(80)

$$<\mathcal{H}>(z=0)=\frac{1}{2{\left(4\pi \right)}^2}\left\{M^4\left[log(1+z_S)-\frac{1}{4}\right]-2\mathcal{N}{m}^4\left[log(1+z_F)-\frac{1}{4}\right]\right\}.$$

(81)

The energy density at late times $\eta$ after decoupling and the energy density today are related by

$$<\mathcal{H}>\left(\eta \right)\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}<\mathcal{H}>(z=0)+\left(\frac{M^4-2\mathcal{N}{m}^4}{2{\left(4\pi \right)}^2}\right)log\left(\frac{a\left(\eta \right)}{a_0}\right),$$

(82)

where we used Equations (73) and (80) and $a_0$ stands for the scale factor today.

We identify the vacuum energy density today $<\mathcal{H}>(z=0)$ with the observed dark energy ${\rho }_{\mathsf{\Lambda }}$. We can then write,

$$<\mathcal{H}>\left(\eta \right)={\rho }_{\mathsf{\Lambda }}\left[1+{\beta }_{\mathcal{N}}log\frac{a\left(\eta \right)}{a_0}\right],$$

(83)

where

$${\beta }_{\mathcal{N}}\equiv \left(1-\frac{2\mathcal{N}{m}^4}{M^4}\right){\left\{log(1+z_S)-\frac{1}{4}-\left(\frac{2\mathcal{N}{m}^4}{M^4}\right)\left[log(1+z_F)-\frac{1}{4}\right]\right\}}^{-1}.$$

(84)

That is, the vacuum energy density at late times after decoupling grows as the logarithm of the scale factor. Moreover, the equation of state approaches $-1$ from below as:

$$w\left(\eta \right)+1\stackrel{a\left(\eta \right)\gg a_{\mathrm{dcs}},a_{\mathrm{dcf}}}{=}-\left(\frac{M^4-2\mathcal{N}{m}^4}{6{\left(4\pi \right)}^2{\rho }_{\mathsf{\Lambda }}}\right){\left[1+{\beta }_{\mathcal{N}}log\frac{a\left(\eta \right)}{a_0}\right]}^{-1}.$$

The previous equations in this subsection generalize when there are several scalar and fermion fields by just summing over their respective contributions. Let us consider the case of several scalars and fermions. This case is relevant to study whether the three neutrino mass eigenstates can contribute to dark energy. Equation (80) becomes for $z_S,z_F\gg 1$:

$$\begin{array}{ccc}\hfill & & w(z=0)+1=-\frac{{\sum }_j{M}_j^4-2\mathcal{N}{\sum }_i{m}_i^4}{6{\left(4\pi \right)}^2{\rho }_{\mathsf{\Lambda }}},\hfill \end{array}$$

(85)

$$\begin{array}{ccc}& & {\rho }_{\mathsf{\Lambda }}=\frac{1}{2{\left(4\pi \right)}^2}\left[\left(log{z}_S-\frac{1}{4}\right)\sum _j{M}_j^4-2\mathcal{N}\left(log{z}_F-\frac{1}{4}\right)\sum _i{m}_i^4\right],\hfill \end{array}$$

(86)

where j and i label the species of scalars and fermions, respectively.

It is convenient to eliminate the sum of scalar masses ${\sum }_j{M}_j^4$ between Equations (85) and (86), with the result,

$$w(z=0)+1=\frac{1}{(log{z}_S-\frac{1}{4})}\left[-\frac{1}{3}+\frac{\mathcal{N}}{3{\left(4\pi \right)}^2}\frac{{\sum }_i{m}_i^4}{{\rho }_{\mathsf{\Lambda }}}log\frac{z_S}{z_F}\right].$$

(87)

We see in Equation (87) that the scalar contributes to the equation of state today by the negative term $-1/\left[3(log{z}_S-\frac{1}{4})\right]$, while the fermions give for $z_S>z_F$ a positive contribution proportional to the sum of the fourth power of their masses.

6. The Quantum Nature of the Cosmological Vacuum

Local observables as $<{\phi }^2>,<\overline{\mathsf{\Psi }}\mathsf{\Psi }>$, the energy density and the pressure involve the product of field operators at equal points. This is identical to one-loop tadpole Feynman diagrams. Logarithmic dependence on the scale of the momenta is typical in one-loop renormalized Feynman diagrams [78]. Here, we analogously find a logarithm of the scale factor in Equations (69) and (73) through the same mechanisms at work in renormalized quantum field theory. Hence, dark energy follows here as a truly quantum field vacuum effect. We stress quantum field effect and not just quantum effect because the infinite number of filled momentum modes in the vacuum as well as the subtraction of UV divergences play a crucial role in the vacuum late-time behavior. Here, the quantum fields are neither coupled nor self-coupled, but they interact with the expanding space-time geometry.

Notice that these results from Equations (69), (73) and (75) are valid for any expanding universe. They do not depend on the specific time dependence of the scale factor $a\left(\eta \right)$, provided it grows with $\eta$.

The quantum nature of the vacuum cosmological effects in the physical observables here are manifested from Equations (69) and (73),

$$\begin{array}{ccc}\hfill <{\phi }^2>\left(\eta \right)& & \sim M^{2}loga\left(\eta \right)=\frac{M^2{c}^2}{\hslash }loga\left(\eta \right)=\frac{Mc}{{\lambda }_C}loga\left(\eta \right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill <\mathcal{H}>\left(\eta \right)& & \sim M^{4}loga\left(\eta \right)=M{c}^2{\left(\frac{Mc}{\hslash }\right)}^{3}loga\left(\eta \right)=\frac{M{c}^2}{{\lambda }_C^3}loga\left(\eta \right).\hfill \end{array}$$

(88)

These quantities are of quantum nature since they depend on ℏ. There is no ‘classical contribution’ to the vacuum energy. Equation (88) just means that the scale of the dark energy density is of one scalar rest mass per a volume equal to the cube of the Compton wavelength ${\lambda }_C$ for the scalar particle. Notice that ${\lambda }_C=[\hslash /\left(Mc\right)]\simeq 0.05$ mm is almost a macroscopic length, while the mass of the scalar particle $M\sim 4$ meV $=7.1{10}^{-36}$ g is extremely small (see below for the value of M).

7. Dark Energy from the Cosmological Quantum Vacuum

Let us recall the current value for the dark energy density

$${\rho }_{\mathsf{\Lambda }}={\mathsf{\Omega }}_{\mathsf{\Lambda }}{\rho }_c=3.28\times {10}^{-11}{\left(\mathrm{eV}\right)}^4={\left(2.39\mathrm{meV}\right)}^4,$$

(89)

corresponding to

$$h=0.73\mathrm{and}{\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.76\mathrm{and}\mathrm{where}1\mathrm{meV}={10}^{-3}\mathrm{eV}.$$

(90)

We take these values because they do correspond to direct, model-independent and late universe observations, refs. [1,4,5,8,13,79,80,81,82], and, accordingly, this paper deals directly with dark energy in the late universe; moreover, dark energy was discovered with such direct and model-independent measurements in the late universe, refs. [1,4,5,8]. Other determinations of h (e.g., ref. [46] Table 2, page 16) yield values $h=0.68$, ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.69$. However, these are indirect, model-dependent and early universe determinations of h and ${\mathsf{\Omega }}_{\mathsf{\Lambda }}$. The difference between the determinations of h in the late and in the early universe is an important problem on its own, e.g., ref. [82], although we do not treat this problem here.

Bosons give a positive contribution to dark energy through the cosmological quantum vacuum, while fermions give a negative contribution. Therefore, the boson contribution must dominate.

As discussed in Section 8, the lightest neutrino certainly contributes to the cosmological quantum vacuum unless it dissipates. Definitely, a boson contribution is needed. The photon and graviton contributions are irrelevant since their masses are most probably zero and at most $m_{\gamma }<6\times {10}^{-17}\mathrm{eV},m_{\mathrm{graviton}}<4.7\times {10}^{-23}\mathrm{eV}$ [83].

Massless particles contribute to the energy-momentum tensor through the trace anomaly [76,77]. This contribution is of the order of $H_0^4$, where $H_0$ is the Hubble parameter today:

$$H_0=1.558\times {10}^{-33}\mathrm{eV}.$$

(91)

As a consequence, the massless particles’ contribution to the energy-momentum tensor is exceedingly small to explain the observed value of the dark energy.

• A scalar particle can produce the dark energy today Equation (89) through its quantum cosmological vacuum provided:
• Its mass is of the order of 1 meV, and it is very weakly coupled.
• Its lifetime is of the order of the age of the universe.

Spontaneous symmetry breaking of continuous symmetries produces massless scalars as Goldstone bosons. If, in addition, this continuous symmetry is slightly violated, the Goldstone boson acquires a small mass. This is the natural mechanism that generates light scalars, and several particles have been proposed on these grounds in the past. The axion is certainly the one that has caught more attention in the literature. Other proposed particles are the familons and the majorons [56,84,85,86,87,88,89].

The (invisible) axion [51,52,53,54,55] (if it exists) is hence a candidate to be the source of dark energy.

Axions were proposed to solve the strong CP problem in QCD [47,48,49,50]. Axions acquire a mass after the breaking of the Peccei–Quinn (PQ) symmetry when the temperature of the universe was at the PQ symmetry breaking scale $\sim f_a$ [62,63,64,65,66]. All axion couplings are inversely proportional to $f_a$, and the axion mass is given by

$$M_a\simeq 6\times \left(\frac{{10}^9\mathrm{GeV}}{f_a}\right)\mathrm{meV}.$$

(92)

The following range (‘axion window’) is currently acceptable for the axion mass [63,73,74,75,90,91,92]:

$${10}^{-3}\mathrm{meV}\lesssim M_a\lesssim 10\mathrm{meV}.$$

(93)

Therefore, this pseudoscalar particle has extremely weak coupling to gluons and quarks, and hence it contributes to the cosmological quantum vacuum. For example, the axion–photon–photon coupling is given by

$$g_{a\gamma \gamma }\sim \frac{{10}^{-10}}{\mathrm{GeV}}\left(\frac{M_a}{1\mathrm{meV}}\right).$$

(94)

As a consequence, the axion lifetime to decay into photons is much longer than the age of the universe. Dissipation of the energy in the cosmological quantum axion vacuum takes longer than the age of the universe too.

• An axion with mass $\sim 1$ meV and hence $f_a\sim {10}^9$ GeV decouples from the plasma at a scale of energies $\sim 2\times {10}^5$ GeV, that is, at redshift $z_S\sim 2.2\times {10}^{18}$. The temperatures of the axions and neutrinos today are lower than that of photons today,

  $$T_{\nu \mathrm{today}}={\left(\frac{4}{11}\right)}^{\frac{1}{3}}{T}_{\mathrm{CMB}\mathrm{today}}=0.1676\mathrm{meV},T_{a\mathrm{today}}=0.078\mathrm{meV}.$$

  (95)
  Because the axion lifetime is of the order or larger than the age of the universe, no specific properties of the axion play a role in dark energy, except for its mass and decoupling redshift. However, the dark energy depends on the decoupling redshift rather weakly because it is through its logarithm (see Equation (77)).
• Neutrinos in the universe are believed to be effectively free particles when the temperature of the universe is below $\sim 1$ MeV. That is, neutrinos decouple at a redshift $z_F\sim 0.6\times {10}^{10}$. Before such time, electrons and neutrinos interacted, keeping them in thermal equilibrium.
• Therefore, we can treat the axion with mass $\sim 1$ meV and the lightest neutrino as free particles in the universe for redshifts $z<z_S\sim 2.2\times {10}^{18}$ and $z<z_F\sim 0.6\times {10}^{10}$, respectively.

8. Neutrino Mass Eigenstates

As is known, the two heavier neutrino mass eigenstates ${\nu }_2$ and ${\nu }_3$ with masses $m_2$ and $m_3$, respectively, annihilate with their respective anti-neutrinos, yielding the lightest neutrino eigenstate ${\nu }_1$ and its antiparticle through weak interactions. However, this process is too slow for nonrelativistic neutrinos even compared with the age of the universe. Their decay rates can be estimated to be

$${\mathsf{\Gamma }}_2\sim G_F^2{m}_2^5\sim \frac{1}{1.5\times {10}^{33}\mathrm{yr}},{\mathsf{\Gamma }}_3\sim G_F^2{m}_3^5\sim \frac{1}{5\times {10}^{29}\mathrm{yr}},$$

where $G_F=1.166\times {10}^{-23}{\left(\mathrm{eV}\right)}^{-2}$ stands for the Fermi coupling.

Neutrinos with masses $m_2\sim 0.01$ eV or $m_3\sim 0.05$ eV will produce through their cosmological quantum vacuum today a large negative contribution to dark energy.

Therefore, the heavier neutrinos (${\nu }_2$ and ${\nu }_3$) must annihilate with their respective anti-neutrinos into the lightest neutrino ${\nu }_1$ through a mechanism such that

$${\mathsf{\Gamma }}_3\gtrsim {\mathsf{\Gamma }}_2\gtrsim {\left(\mathrm{age}\mathrm{of}\mathrm{the}\mathrm{universe}\right)}^{-1}.$$

(96)

Our results for dark energy are independent of the details of the decay mechanism. All that counts is that the decay rates of the heavier neutrinos obey Equation (96).

As a minimal assumption, let us consider the following effective couplings between the neutrinos,

$$\frac{1}{M^{\prime }{}^2}{\overline{\mathsf{\Psi }}}_2{\mathsf{\Psi }}_2{\overline{\mathsf{\Psi }}}_1{\mathsf{\Psi }}_1,\frac{1}{M^{\prime }{}^2}{\overline{\mathsf{\Psi }}}_3{\mathsf{\Psi }}_3{\overline{\mathsf{\Psi }}}_1{\mathsf{\Psi }}_1,$$

(97)

where $M^{\prime }$ is a mass scale much larger than the neutrino masses. We thus find,

$${\mathsf{\Gamma }}_2\sim \frac{{\left(m_2\right)}^5}{M^{\prime }{}^4},{\mathsf{\Gamma }}_3\sim \frac{{\left(m_3\right)}^5}{M^{\prime }{}^4}.$$

Imposing Equation (96) yields,

$$M^{\prime }\lesssim 1\mathrm{MeV}\mathrm{for}{m}_2=0.01\mathrm{eV}\mathrm{and}{M}^{\prime }\lesssim 10\mathrm{MeV}\mathrm{for}{m}_3=0.05\mathrm{eV}.$$

(98)

The first estimated bound (1 MeV) applies for a direct hierarchy of neutrino masses ($m_3\sim 0.05\mathrm{eV}>m_2\sim 0.01\mathrm{eV}>m_1$), while the second estimate (10 MeV) is for an inverse hierarchy of neutrino masses ($m_3\sim m_2\sim 0.05\mathrm{eV}>m_1$).

Effective couplings of the type in Equation (97) can be obtained from different renormalizable models.

Notice that the two heavier neutrino decays contribute to the background of lighter neutrino particles but not to the neutrino quantum vacuum.

Lagrangians leading to effective couplings analogous to Equation (97) have been considered in the context of models to generate neutrino masses and to provide light dark matter candidates [93,94,95,96,97,98,99,100,101,102,103,104]. Moreover, mass ranges compatible with Equation (98) have been obtained from various and independent considerations [95,96,97,98,99,100,101,102,103,104,105]. This value also follows by setting $Q=0$ (neutrinos has no charge) in Equation (1) of Ref. [69]. In case the effective couplings of Equation (97) arise from Yukawa couplings of the neutrinos with a scalar particle of mass $M^{\prime }$, this scalar particle cannot be a dark matter candidate since it decays into neutrino–antineutrino pairs.

The lightest neutrino with mass $m_1$ can be self-coupled through the interaction

$$\frac{1}{M^{″}{}^2}{\left({\overline{\mathsf{\Psi }}}_1{\mathsf{\Psi }}_1\right)}^2.$$

Its decay rate,

$${\mathsf{\Gamma }}_1\sim \frac{{\left(m_1\right)}^5}{M^{″}{}^4},$$

is of the order or larger than the age of the universe when

$$M^{″}\lesssim {\left(\frac{m_1}{\mathrm{meV}}\right)}^{\frac{5}{4}}50\mathrm{keV}.$$

(99)

Hence, if Equation (99) is fulfilled, the energy in the neutrino vacuum dissipates into the lightest neutrino’s ${\nu }_1$, thus contributing to the neutrino background.

9. Light Particle Masses and the Dark Energy Density Today

Let us consider the case where only one light scalar field and one light fermion field contribute to the quantum vacuum energy. That is, a light scalar and the lightest neutrino. We obtain from Equation (80) for the mass of the scalar,

$$M=\frac{2^{\frac{5}{4}}\sqrt{\pi }{\rho }_{\mathsf{\Lambda }}^{\frac{1}{4}}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}{\left[1+\frac{\mathcal{N}{m}^4}{{\left(4\pi \right)}^2{\rho }_{\mathsf{\Lambda }}}\left(log{z}_F-\frac{1}{4}\right)\right]}^{\frac{1}{4}},$$

(100)

where we identified the vacuum energy density today $<\mathcal{H}>\left(0\right)$ with the observed dark energy ${\rho }_{\mathsf{\Lambda }}$.

We now obtain using the observed value of the dark energy Equation (89) and the decoupling redshift for the neutrino $z_F\sim 0.6\times {10}^{10}$,

$$M=\frac{10.1\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}{\left[1+\mathcal{N}{\left(\frac{m}{3.90\mathrm{meV}}\right)}^4\right]}^{\frac{1}{4}}.$$

(101)

If the lightest neutrino has a very small mass $m\ll 1$ meV or if it decays in the time scale of the age of the universe (see Equation (99)) so the neutrino vacuum dissipates, there is no neutrino contribution to the dark energy. In these cases, Equation (101) gives for the mass of the scalar:

$$M=\frac{10.1\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}:\mathrm{no}\mathrm{vacuum}\mathrm{neutrino}\mathrm{energy}.$$

(102)

Assuming the scalar field to be the axion, we can use the value $z_S\sim 2.2\times {10}^{18}$ for the axion decoupling redshift, and Equation (101) becomes,

$$M\left(m\right)=3.96\mathrm{meV}{\left[1+\mathcal{N}{\left(\frac{m}{3.90\mathrm{meV}}\right)}^4\right]}^{\frac{1}{4}}.$$

(103)

The values of the neutrino masses are not yet known, only their differences are experimentally constrained. Both in the direct and inverse mass hierarchies, the mass m of the lightest neutrino can be in the meV range (or even zero).

According to ref. [69], we have

$$m=\frac{1}{3}{m}_2,$$

where $m_2$ is the mass of the middle neutrino. Combining this with the known neutrino mass differences yields

$$m=3.2\pm 0.1\mathrm{meV}.$$

(104)

This value for the neutrino mass perfectly agrees in order of magnitude with the see-saw prediction,

$$\frac{M_{\mathrm{Fermi}}^2}{M_{\mathrm{GUT}}}\simeq 6\times {10}^{-3}\mathrm{eV},$$

for the typical values $M_{\mathrm{Fermi}}=250$ GeV and $M_{\mathrm{GUT}}={10}^{16}$ GeV of the Fermi and Grand Unified energy scales, respectively.

Equations (103) and (104) give for the axion mass:

$$M(m=3.2\mathrm{meV},\mathcal{N}=1)=4.35\mathrm{meV},M(m=3.2\mathrm{meV},\mathcal{N}=2)=4.66\mathrm{meV},$$

(105)

for Majorana and Dirac neutrinos, respectively.

If the lightest neutrino has a very small mass $m_1\ll 1$ meV or if it decays in the time scale of the age of the universe (see Equation (99)), e.g., there is no neutrino contribution to the dark energy, then the axion mass is given by

$$M=3.96\mathrm{meV}:\mathrm{no}\mathrm{vacuum}\mathrm{neutrino}\mathrm{energy}.$$

(106)

All the axion mass value Equation (103), (105) and (106) found here describe the dark energy observed today Equation (89). The numerical values for the axion mass in Equations (105) and (106) are within the astrophysical bound of Equation (93).

We compute the equation of state today from Equation (80) and display it in Table 1 in three relevant cases: (i) no neutrino contribution to the dark energy, (ii) a Majorana neutrino contribution and (iii) a Dirac neutrino contribution. In all three cases, the observed value Equation (89) of the dark energy is imposed. For the last two cases, we choose the neutrino mass $m=3.2$ meV and the scalar mass M given by Equation (105), e.g., $4.35$ meV and $4.66$ meV, respectively.

We see that $w\left(0\right)$ is slightly below $-1$ by an amount ranging from $(-1.5\times {10}^{-3})$ to $(-8\times {10}^{-3})$.

It can be noticed that the mass of the lightest neutrino (Equation (104)) turns to be much higher than today’s neutrino temperature:

$$\frac{m_{\mathrm{Dirac}}}{T_{\nu \mathrm{today}}}=19.6,\frac{m_{\mathrm{Majorana}}}{T_{\nu \mathrm{today}}}=23.3,$$

(107)

where we used Equation (95). That is to say, the neutrinos forming the neutrino background are, today, non-relativistic particles.

Let us now analyze the possibility in which all three neutrino eigenstates contribute to dark energy. This contribution crucially depends on the values of their masses to the power four through the dimensionless factor

$$\mathcal{F}\equiv \frac{1}{3{\left(4\pi \right)}^2}\frac{\sum {}_i{m}_i^4}{{\rho }_{\mathsf{\Lambda }}},$$

as we see from Equations (85)–(87).

For the normal hierarchy, we have

$$m_1=3.2\mathrm{meV},m_2=9.5\mathrm{meV},m_3=47\mathrm{meV},$$

and for the inverted hierarchy:

$$m_1=3.2\mathrm{meV},m_2=47\mathrm{meV},m_3=48\mathrm{meV}.$$

Thus, using Equation (89), the factor $\mathcal{F}$ takes the values

$${\mathcal{F}}_{\mathrm{normal}}=315,{\mathcal{F}}_{\mathrm{inverted}}=656.$$

Inserting these numbers in the equation of state today Equation (87) yields values for $w\left(0\right)$ in strong disagreement with the data unless we fine tune $z_S\simeq z_F$. Because there is no reason to have such equality, we conclude that the vacuum of the two heavier neutrinos must not contribute to the dark energy. Their quantum vacuum must dissipate, as discussed in Section 8.

10. The Future Evolution of the Universe

The future evolution of the universe follows by inserting the total energy density in the Einstein–Friedmann equation

$$H^2\left(t\right)=\frac{8\pi G}{3}{\mathcal{H}}_T,$$

where we use cosmic time $t,G$ is the gravitational constant and the total energy density ${\mathcal{H}}_T$ is the sum of the contributions from the dark energy, the matter and the radiation.

We obtain using the dark energy expression Equation (83) the self-consistent Einstein–Friedmann evolution equation,

$$H^2\left(t\right)=H_0^2\left[{\mathsf{\Omega }}_{\mathsf{\Lambda }}\left(1+{\beta }_{\mathcal{N}}log\frac{a\left(t\right)}{a_0}\right)+{\mathsf{\Omega }}_{\mathrm{matter}}\frac{a_0^3}{a^3\left(t\right)}+{\mathsf{\Omega }}_{\mathrm{rad}}\frac{a_0^4}{a^4\left(t\right)}\right],$$

(108)

where $a_0\equiv a\left(\mathrm{today}\right),{\beta }_{\mathcal{N}}$ is defined by Equation (84), ${\rho }_{\mathsf{\Lambda }}={\rho }_{\mathrm{crit}}{\mathsf{\Omega }}_{\mathsf{\Lambda }}$ is given by Equation (9) and $H_0$ is the Hubble parameter today, being

$${\rho }_{\mathrm{crit}}=\frac{\left(3H_0^2\right)}{\left(8\pi G\right)},H_0=\frac{h}{\left[9.77813\mathrm{Gyr}\right]},{\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.76=(1-{\mathsf{\Omega }}_{\mathrm{matter}}-{\mathsf{\Omega }}_{\mathrm{rad}}).$$

(109)

We use the explicit values for M and m for Equations (104)–(106):

$${\beta }_0=0.0238:\mathrm{No}\mathrm{vacuum}\mathrm{neutrino}\mathrm{energy};{\beta }_1=0.0347:\mathrm{Majorana}\mathrm{neutrino};$$

$${\beta }_2=0.0459:\mathrm{Dirac}\mathrm{neutrino}.$$

For $a\left(t\right)\gtrsim a_0$, the matter and radiation contributions can be neglected in Equation (108), and we have,

$${\left[\frac{dloga\left(t\right)}{dt}\right]}^2\simeq H_0^2{\mathsf{\Omega }}_{\mathsf{\Lambda }}\left[1+{\beta }_{\mathcal{N}}log\frac{a\left(t\right)}{a_0}\right].$$

This equation can be immediately integrated with the solution

$$a\left(t\right)\stackrel{H_{0}t\gtrsim 1}{\simeq }{a}_{0}exp[c_1{H}_{0}t+c_2{\left(H_{0}t\right)}^2],$$

(110)

where

$$\begin{array}{ccc}\hfill & & c_1=\sqrt{{\mathsf{\Omega }}_{\mathsf{\Lambda }}}=0.87,c_2=\frac{1}{4}{\mathsf{\Omega }}_{\mathsf{\Lambda }}{\beta }_{\mathcal{N}}=0.19{\beta }_{\mathcal{N}},\hfill \end{array}$$

$$\begin{array}{ccc}& & 0.00452<c_2<0.00872.\hfill \end{array}$$

(111)

The left and right ends of the interval in $c_2$ Equation (111) correspond to the cases in which there is no neutrino contribution and to the lightest neutrino being a Dirac fermion with mass $m=3.2$ meV, respectively.

We find that the Universe is presently reaching an asymptotic phase where it expands as indicated by Equation (110).

Equation (110) shows that the expansion of the Universe in the future is faster than in the de Sitter Universe.

Notice that the time scale of the accelerated expansion is huge, $\sim (1/H_0)=13.4$ Gyr. The quadratic term dominates over the linear term in the exponent of Equation (110) by a time $t\sim (100/H_0)$ to $(200/H_0)$.

In this accelerated universe, Equation (108) shows that the Hubble radius $(1/H)$ decreases with time as

$$\frac{1}{H}\sim \frac{1}{H_0\sqrt{loga\left(t\right)}}.$$

11. Discussion

The non-trivial energy and pressure that we have is an effect resulting from the expansion of space-time as it arises from the $loga\left(\eta \right)$ factor in Equation (73). No dark energy appears in Minkowski space-time. Namely, the formation and growth of the vacuum density, the vacuum energy density and pressure is an effect due to the presence of quantum fields in an expanding cosmological space-time.

Notice that the energy scale of the cosmological vacuum is given by the mass of the particle when this mass is larger than the Hubble constant (see Equation (91)). For massless particles, the energy scale of the cosmological vacuum is given by the Hubble constant.

The axion evolution for $z\ge {10}^{18}$ as well as the neutrino evolution for $z\ge {10}^{10}$ are beyond the scope of this article. Namely, the regime where the interaction of axions and neutrinos with the plasma particles cannot be neglected. We choose as the initial state for both the axions and the neutrinos the vacuum thermal equilibrium state. It must be remarked that the vacuum energy at late times is independent of the initial temperature, as shown by Equation (70).

Before decoupling, particle interaction is non-negligable and dissipation is important for depleting the vacuum energy [41,106]. Hence, the vacuum energy can only become significant after decoupling. Therefore, it is a good approximation to just study the free quantum field evolution in cosmological space-time after decoupling.

The initial conditions Equations (26) and (50) are imposed at the origin of the conformal time. We shall see now that they are equivalent to the Bunch–Davies vacuum conditions. Since the initial time corresponds to a large value of redshift, it corresponds to asymptotic times in the past in a very good approximation. More precisely, the conformal time is related to the redshift z by

$$\begin{array}{ccc}& & \eta =\frac{3t_0}{\sqrt{1+z}}:\mathrm{matter}-\mathrm{dominated}\mathrm{era},\hfill \end{array}$$

$$\begin{array}{ccc}& & \eta =\frac{2t_0\sqrt{1+z_{\mathrm{eq}}}}{1+z}+\frac{t_0}{\sqrt{1+z_{\mathrm{eq}}}}:\mathrm{radiation}-\mathrm{dominated}\mathrm{era},\hfill \end{array}$$

(112)

where $t_0=13.7$ Gyr is the age of the universe and $1+z_{\mathrm{eq}}=3048$ is the transition from the radiation-dominated to the matter-dominated era. ${\eta }_0=3t_0$ corresponds to the present time. For $z\gg z_{\mathrm{eq}}$, we see that,

$$\eta \simeq \frac{t_0}{\sqrt{1+z_{\mathrm{eq}}}}=0.018t_0.$$

Hence, the conformal time at decoupling differs from the conformal time today ${\eta }_0=3t_0$ by an amount $\sim 3t_0$. As a result, the initial time can be considered as an asymptotic time deep in the past. More precisely, the change in the phases of the mode functions is characterized by $\left(M{t}_0\right)\sim 3\times {10}^{30}$ for a typical mass $M\sim 4$ meV. Hence, the initial conditions for the mode functions Equations (26) and (50) are virtually identical to Bunch–Davies initial conditions.

The vacuum density and energy density Equations (69) and (73) are determined by the short distance behavior of the two-point function in coordinate space. In momentum space, it is the high energy behavior that dominates the vacuum density and energy density for late times. The physical quantities can be written as integrals of mode functions, as in Equations (24) and (40). One can see that the relevant comoving momenta k values contributing on a physical energy scale q take the value $k=qa\left(\eta \right)$. At late times (e.g., today), $a\left(\eta \right)\sim z_{\mathrm{decoupling}}$, therefore only large $k\sim z_{\mathrm{decoupling}}M$ are relevant. This fact decreases the effect of the initial conditions. Analogous effects take place for the initial conditions of inflationary fluctuations with the exception of the low multipoles, particularly the quadrupole [107,108,109,110,111].

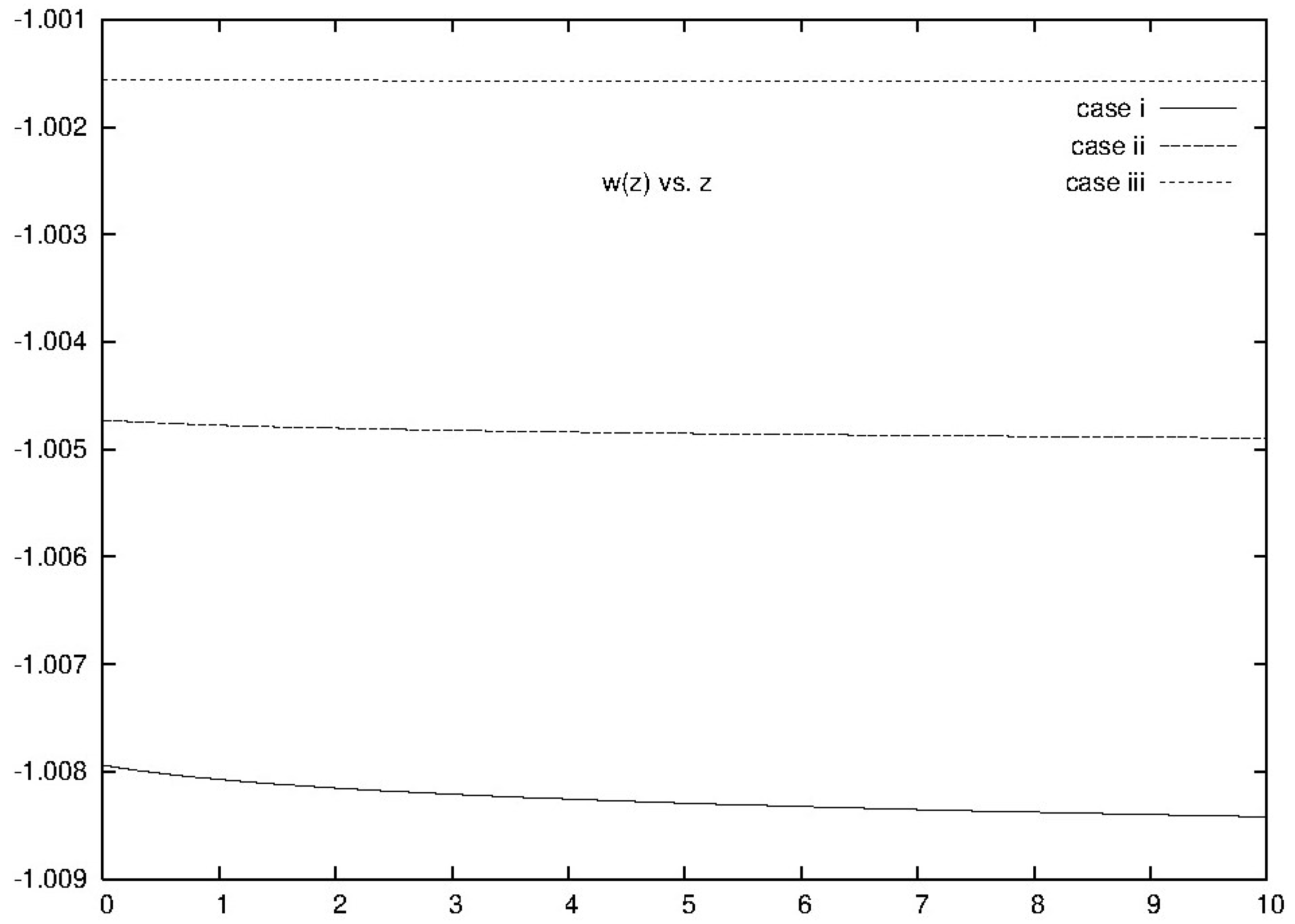
• In Figure 1, we plot the equation of state w(z) as a function of z for the three cases explicitly calculated in this paper:
• (i) No neutrino contribution to the dark energy and the scalar mass $M=3.96$ meV.
• (ii) A Majorana neutrino with mass $m=3.2$ meV and the scalar mass $M=4.35$ meV.
• (iii) A Dirac neutrino with mass $m=3.2$ meV and the scalar mass $M=4.66$ meV (see the discussion in Section 9).
• We see that the equation of state in all the three cases (i)–(iii) differs from the cosmological constant case $w=-1$ by less than $1\%$.
• The value of the lightest neutrino mass Equation (104) is well below the neutrino mass splittings $\sqrt{\Delta m_{sun}^2}$ and $\sqrt{\Delta m_{atm}^2}$ and consistent with both direct and inverse mass hierarchies. A quasi-degenerate mass spectrum will give a large negative contribution to the dark energy and will require a scalar particle with a mass $M\gtrsim 100$ meV to reproduce the observed dark energy data Equation (89). Such a particle can very well exist, but it cannot be the axion (see Equation (93)). Indeed, the scalar particle can have the mass value given by Equation (106) in case all three neutrinos decay in a time scale of the age of the universe in order to dissipate their cosmological vacuum energy, as discussed in Section 8.
• On the other hand, a range of neutrino masses from ${10}^{-3}$ eV to $0.1$ eV in agreement with neutrino mass differences from oscillations and the value Equation (104) for the mass of the lightest neutrinos is compatible with a consistent baryogenesis.

12. Conclusions

• We find that the presence of a cosmological quantum vacuum energy with an equation of state just below $-1$ is the unavoidable consequence of the existence of light particles with very weak couplings. Bosons yield positive contributions and fermions yield negative contributions to the vacuum energy.
• It must be noticed that there is a present lack of knowledge about the low-energy (energy $\sim 1$ meV) particle physics region. Actually, most of the constraints on this sector follow from astrophysics and cosmology, including the new constraints that we obtain here on the axion mass.
• No exotic physics need to be invoked to explain the dark energy. Since the observed energy scale of the dark energy is very low, we find it natural to explain it only through low-energy physics. The effects from energy scales higher than 1 eV or even 1 MeV arrive strongly suppressed to the dark energy scale of 1 meV.
• In summary, dark energy can be explained by a very light and very weakly coupled scalar particle, which decouples by redshift $z_S\gg 1$. If the scalar particle is the axion, then $z_S\sim 2.2\times {10}^{18}$.
  We have four main cases:

  (i)

  No neutrino contribution. This happens when the lightest neutrino has a mass $m\ll 1$ meV and when the vacuum neutrino contribution dissipates in the time scale of the age of the universe (see Equation (99)). The scalar mass must be

  $$M=\frac{10.1\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}:\mathrm{no}\mathrm{vacuum}\mathrm{neutrino}\mathrm{energy}.$$

  (113)

  If the scalar is the axion, then $M=3.96$ meV in this case.

  (ii)

  The lightest neutrino is Majorana and has a mass $m\simeq 3.2$ meV. Then, the scalar mass must be

  $$M=\frac{11.1\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}:\mathrm{the}\mathrm{Majorana}\mathrm{neutrino}\mathrm{contributes}.$$

  If the scalar is the axion, then $M=4.35$ meV in this case.

  (iii)

  The lightest neutrino is Dirac and has a mass $m\simeq 3.2$ meV. Then, the scalar mass must be

  $$M=\frac{11.9\mathrm{meV}}{{\left(log{z}_S-\frac{1}{4}\right)}^{\frac{1}{4}}}:\mathrm{the}\mathrm{Dirac}\mathrm{neutrino}\mathrm{contributes}.$$

  If the scalar is the axion, then $M=4.66$ meV in this case.

• Therefore, in all the three cases (i)–(iii) above where the axion explains the dark energy, we predict its mass in the range:

  $$3.96\mathrm{meV}<M<4.66\mathrm{meV}.$$

  (114)
  The left and right ends of the interval in Equation (114) correspond to no neutrino contribution and to the lightest neutrino as a Dirac fermion with mass $m=3.2$ meV, respectively.
• In short, we uncovered here the general mechanism producing the dark energy today. This mechanism has it grounds in well-known quantum physics and cosmology. The dark energy appears as a quantum vacuum effect arising when stable and weakly coupled quantum fields live in expanding cosmological space-times. That is to say, dark energy in the universe today is a QFT effect in (classical) curved space-times. That is to say, this is a semiclassical gravity effect.
• In addition, we have found here that the axion with mass in the meV range is a very serious candidate for dark energy, while we have shown already [112,113] that it is robustely excluded as a dark matter candidate. The cosmic dark energy today is on the meV scale, while the dark matter (cosmic and galactic) particle is on the keV scale [113,114,115,116,117,118,119,120].
• Many research avenues are open now connecting dark energy and light particles physics. The more immediate being:

  (1)

  The study of the radiative corrections to the axion and neutrino cosmological vacuum evolution from their interactions.

  (2)

  The study of the early neutrino and axion dynamics at temperatures $\gtrsim 1$ MeV and $\gtrsim {10}^6$ GeV, respectively.

  (3)

  The study of particle propagation in the media formed by the axion and the neutrino vacuum.

  (4)

  Last but not least: The probable deep connection between dark energy and dark matter through low-energy particle states beyond the standard model of particle physics.