Abstract
The unimodular theory of gravity is an alternative perspective to the traditional general relativity of Einstein and opens new possibilities for exploring its implications in cosmology. In this paper, we investigated Unimodular Gravity (UG) with the cosmological data from the Pantheon sample of Type Ia Supernovae (SNs) (2018), Baryon Acoustic Oscillations (BAOs), and the observational H(z) data from the Differential Age method (DA). We also used the Cosmic Microwave Background (CMB) distance priors from the Planck 2018 results. We considered a model consisting of a generalized cosmological constant, radiation, and a dark matter component along with normal matter. The considered theory respects only unimodular coordinate transformations. We first fit our model with low-redshift data from SNs and DA and determined the value of the model parameters . We found the best-fit value of parameter , which deviates slightly from 6, for which the theory becomes the standard general theory of relativity. We observed a small deviation in the value of the Hubble constant ( km s−1 Mpc−1) in the UG model compared with the standard CDM model ( km s−1 Mpc−1). Using the BAO + CMB constraint in the UG model, we obtained , and is ∼6.029. For the combined datasets (SN + DA + BAO + CMB), the estimated with 6.037, and in standard gravity, .
1. Introduction
There are many competing models to fit cosmological observations, such as the modified theory of gravity, the scalar field theory, the CDM model, etc. [1]. In these models, the CDM model is a plausible model for explaining current cosmological observations [2,3]. However, the cosmological constant has its own fine-tuning problem. Some of the proposals, such as supersymmetry, supergravity, anthropic considerations, the adjustment mechanism, changing gravity, etc., were discussed in [4] regarding the cosmological constant problem. In this review paper [4], Unimodular Gravity (UG) was discussed as a possible generalization of gravity. Unimodular gravity is an interesting model that was first proposed by Anderson and Finkelstein [5] following the closely related proposal given by Einstein [6]. It might solve the cosmological constant problem since is not a dynamical field in this theory. However, in [4], it was explained that the cosmological constant reappears as an integration constant, and the fine-tuning problem remains in the theory. This is because, within that unimodular model of gravity, the theory still maintains full General Coordinate Invariance (GCI). Several studies regarding the cosmological constant problem in unimodular gravity were performed in [7,8,9,10,11].
In [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], various other aspects of unimodular gravity were studied. In this work, we are interested in studying its implications in cosmology. The full metric can be broken into a scalar field and an unimodular metric [12,13]. In [15,16], the implication of unimodular gravity was studied thoroughly using such a decomposition. In these works and [12,13], the theory respects covariance under unimodular coordinate transformations instead of general coordinate invariance. Broken general coordinate invariance introduces a parameter [15,16] with a value other than 6, where corresponds to full general coordinate invariance, and the outcome of the theory is the same as that of general relativity. Other values of correspond to unimodular gravity and provide covariance under only unimodular coordinate transformations. In [15,16], the authors discussed the expansion of the universe considering the generalized non-relativistic matter and generalized cosmological constant separately. A model where only radiation was assumed was also discussed. The motivation for these models is to describe the current expansion of the universe by only one component, either dark matter or a cosmological constant, to solve the coincidence problem.
One of the challenging tasks in modern cosmology is to determine the precise value of the Hubble constant . Considering the standard CDM model, the value determined by the Cosmic microwave Background (CMB) experiments, such as WMAP and Planck, differs from the value determined by the local distance ladder approach, such as Supernovae and for the Equation of State (SH0ES) project. The Planck 2018 results gave the value [31]. The constraint of in CMB measurement is model-dependent. The most-recent results of the SH0ES program gave [32], which differ by from the final result of Planck. Since the local measurement of does not rely on any cosmological assumptions, it can be considered model-independent. To alleviate this tension in the measurement of from low- and high-redshift probes, primarily two methods are suggested in the literature: early universe modification and late universe modification [33,34,35,36,37]. Modified gravity might also be a solution for the Hubble tension [38,39].
In this paper, we investigated how the unimodular theory differs from the general theory of relativity and to what extent the Hubble tension problem can be addressed within this framework. Here, we took into account a unimodular gravity model [16] with a generalized cosmological constant term. We extended this model by including the dark matter and radiation energy components. In general relativity, it is well known that the radiation term has a small contribution at the lower redshift values. However, it is necessary to test if the same is true in unimodular gravity. The radiation term is added to check its contribution to the Hubble constant in our model. In addition, the value of the comoving sound horizon, which is the calibration scale for the BAO and CMB data, is sensitive to the radiation term. This might result in a change in the value of the Hubble constant when we consider the BAO and CMB data. For supernovae, we used the Pantheon datasets (2018) to estimate the parameters of the model. We further studied the Hubble constant problem in the theory by including the BAO data and CMB distance priors.
The manuscript is structured as follows. The review of the unimodular gravity model and unimodular field equations, with broken general coordinate invariance, is given in Section 2 and Section 3, respectively. In Section 4, we describe the unimodular gravity model having a generalized cosmological constant. In Section 5, we describe our methodology and datasets used for the analysis. In Section 6, we discuss our results, and then, we conclude in Section 7.
2. Field Decomposition in Unimodular Gravity
To begin, we decomposed the standard metric into a scalar field and unimodular metric as . We point out that, in the Cartesian coordinate system, the determinant of is unity. We can generalize it to any coordinate system, such that det [16], where is some specified function of space–time coordinates while keeping det as non-dynamical. The theory is supposed to be invariant under Unimodular General Coordinate Transformations (UGCTs), such that the Jacobian of the transformation is unity, i.e.,
Under this transformation, the determinant of and, hence, the field behaves as a scalar. Following the definition of , we have
where is the full affine connection, and the connection corresponds to the unimodular metric . contains all the terms of the scalar field and is given by
Similarly, under this definition, the Ricci curvature tensor and Ricci scalar R are decomposed. The first part of is made of the unimodular metric, and the second one contains the terms of the scalar field (see [16]). One can write the gravitational action as
where, if parameter , GCI is broken and the theory respects only unimodular coordinate invariance.
3. Field Equations in Unimodular Gravity
We considered the action as discussed in [15,16]. The action follows covariance under unimodular coordinate transformations. Considering both matter and the cosmological constant, the action is given as follows:
here , is the parameter of the theory, and and are the actions corresponding to matter and the cosmological constant. For the general theory of relativity, the parameter . Under this theory, the Einstein field equation and equation of motion for field are given by
and
respectively.
In this theory, the cosmological constant or vacuum energy term does not contribute to Equation (7); however, the term includes all the contribution due to the coupling of with matter fields and the cosmological constant. For the spatially flat Friedmann–Robertson–Walker (FLRW) metric, we can write and identify the scale factor with the scalar field .
4. Generalized Cosmological Constant with Radiation
In [16], the authors investigated a model for the coincidence problem based on a generalized cosmological constant in unimodular gravity, where only ordinary matter and the cosmological constant play a role. The action for the generalized cosmological constant term is defined as
In this model, the generalized cosmological constant term with a parameter appears in the action instead of the standard general relativity term . For a consistent solution, it is found that a term is required in the action and . We followed this model. We are interested in considering both the dark matter (CDM) and cosmological constant term, along with radiation. Thus, in place of ordinary matter, we took into account both cold dark matter and ordinary matter, and we also included radiation. We expect that minimally broken invariance may explain cosmological observations. The purpose of including radiation is that it might cause a deviation in the Hubble constant problem.
For radiation, the term and, also, since there is no direct coupling to the vector field with field [16]. The energy densities corresponding to matter and radiation still hold the same proportionality: and , respectively, as in standard general relativity [16]. Using Equations (7) and (8), we obtain
Here, we used . The equation of motion of gives
Integrating Equation (11), we obtain
where is the integration constant. For a consistent solution, we obtain
and
Now, we considered , where is the scale factor of the universe. Changing the conformal time “” to the cosmological time “t” using leads to
and simplifying, we obtain
Here, represents the current energy density of ordinary matter and CDM together, represents the current energy density of photons and neutrinos together, and is given by
5. Methodology and Datasets
We performed our analyses with the Hubble relation given in Equation (16), which can be written in standard notation as
where, for each component, we define with the critical energy density of the universe. For CDM model, we set , and in the unimodular gravity model, we set () as free parameters. We used the observational datasets including the Supernovae (SNs), measurements of the BAO, and observational H(z) data obtained from the Differential Age method (DA) to estimate the model parameters. We further constrained our parameters using the distance priors from the Planck 2018 data [40]. The MCMC exploration of the model parameter space was carried out using the Python ensemble sampling toolkit emcee [41].
We used the Pantheon dataset [42] for supernovae, which spans the redshift range and contains 1048 data points. These observations provide the apparent magnitude of the supernovae at peak brightness. The resulting apparent magnitude is related to the luminosity distance as
where the luminosity distance is
and is the supernova absolute magnitude. So, the distance modulus is given by
We also considered the 31 observed Hubble data points from the Differential Age (DA) method [43] to constrain the value of . The quantity measured in the differential age method is related to the Hubble parameter:
This method can be used to find the Hubble constant . Table 1 shows the 31 points of data given by differential age method [44].

Table 1.
The 31 observational data points of obtained from the differential age method.
In this work, we also wanted to test our model for the Hubble tension with the SH0ES observations. The determination of in the SH0ES observations [32,53] is based on the constraint on the absolute magnitude , which depends on the astrophysical properties of the sources. Furthermore, in the SH0ES observations, to determine the value of the Hubble constant , the data of Type Ia supernovae in the redshift range are used, and cosmography with and is considered. In [54], it was argued that the supernova absolute magnitude that is used to determine the value of the local is not compatible with the supernova, BAO, and CMB data, and it was shown that how the statistical analysis with the prior on is an alternative to the prior on . Further, in [54], it was shown that the statistical analysis is biased when the prior on is used instead of the prior on . A detailed analysis was performed in [54]. Therefore, we adopted this method of applying the prior on to determine the value of . The function for is given by
where is the calibration that corresponds to the latest constraint on by the SH0ES observation. For the Pantheon dataset, mag.
We performed the joint analysis of the SN and DA datasets by minimizing the chi-squared function, defined as
where
We took the values of and the full covariance matrix, , from the Pantheon catalog. To minimize the chi-squared function of supernovae, we adopted the methodology of marginalization over , as discussed in [54]. The marginalized chi-squared function will become
where
and
We further used the observational datasets of the BAO measurements including Galaxy BAO and BAO (eBOSS) to constrain the model parameters. BAO studies along the line of sight measure the combination , whereas investigations of the BAO feature in the transverse direction offer a value of and , where is the comoving size of the sound horizon at the baryon drag epoch [55]. Table 2 contains a list of the datasets we used.

Table 2.
BAO data measurements we used in our analysis. , , and are in units of Mpc, while is in units of km s Mpc.
The comoving angular diameter distance and volume averaged scale are related to as
The comoving sound horizon is given by
where is the speed of sound in the baryon–photon fluid, with and being the baryon and photon densities, respectively, and being the redshift at the drag epoch. The reference point used to calibrate the BAO observations is the sound horizon , also known as the standard ruler of BAO observations. From the BAO data, we can only constrain the combination of and sound horizon . In order to approximate the from BAO data, we used the analytic approximation of from [62] and took from the Planck 2018 results () [31].
Also, to constrain the model parameters with the physics of the early universe, we utilized the compressed likelihood of the CMB, which is based on distance priors [40]. Distance priors provide effective information on the CMB through the acoustic scale , which characterizes the variations of the peak spacing, and the shift parameter R, which affects the heights of the peaks.
Distance priors are defined as
where is the redshift at the photon decoupling epoch. At this epoch, the comoving sound horizon will be
here we used the analytic approximation of from [62] to estimate the model parameters.
Finally, we combined the BAO data and distance priors from the CMB with the DA and SN datasets and performed the joint analysis to explore the parameter space. We minimized the function, defined as
where
and are values predicted in the UG model, are set to their mean values, and is their covariance matrix in the CDM model [40].
6. Results and Discussion
In the unimodular gravity model, we set the uniform prior on all three parameters () in the range , and and performed the MCMC analysis of the joint SN + DA dataset, marginalized over . The mean values of the parameters we obtained were , and . For the standard (CDM) model (), the mean values of the parameters obtained for low redshift data are km s Mpc, and . In Figure 1, we show the results for the unimodular gravity and standard gravity models using the SN + DA datasets.
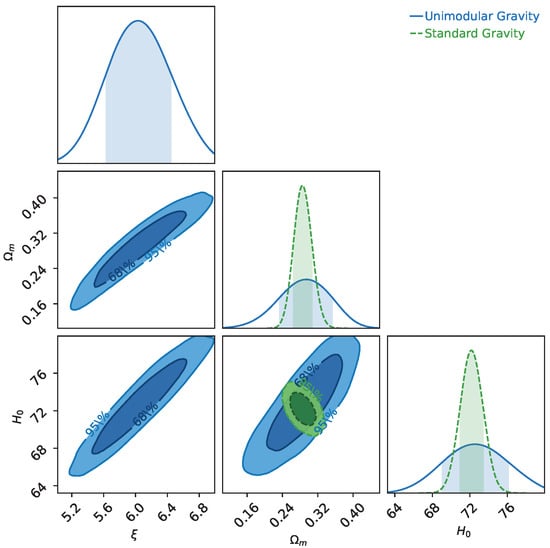
Figure 1.
The 2D contour plot and 1D marginalized posterior distributions of model parameters , , and in the unimodular gravity model () and the standard (CDM) model () using the SN + DA datasets.
We note that, while unimodular gravity theory can fit the low-redshift SN + DA data with a small deviation in the mean value of the parameters (), the constraints on and are not as tight as in the case of the standard CDM model.
We next used the BAO dataset combined with the CMB distance priors and set the uniform prior on , , and . We obtained the mean value of the parameters as , and . If we put these values in Equations (38) and (41), we find that the sound horizon at drag epoch () and at photon decoupling epoch () is Mpc and Mpc, respectively. The mean values of the parameters we found for the standard (CDM) model () are , km s Mpc, and in this case, Mpc and Mpc.
In this case, we found that the mean values of and are tightly constrained in the UG model and differ by ∼1 from the standard CDM model. Also, the value of and is consistent with the CDM model. In Figure 2, we show the comparison of the unimodular gravity model with the standard gravity model using the BAO + CMB data.
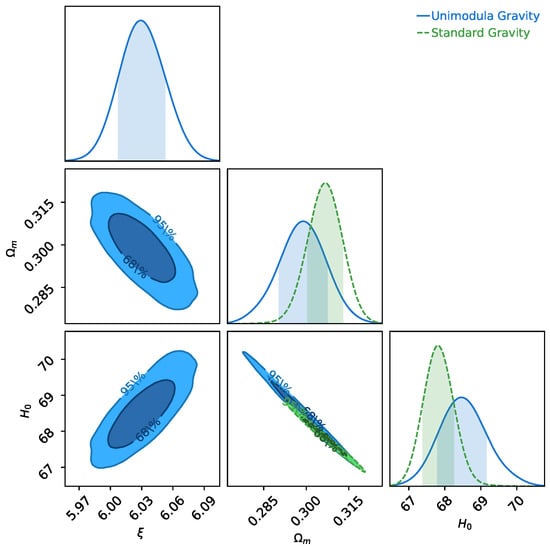
Figure 2.
The 2D contour plot and 1D posterior distributions of model parameters , and in the unimodular gravity model () and the standard (CDM) model () using the BAO data and distance priors from the Planck 2018 data.
Combining the SN + DA data with the BAO and CMB distance priors, we obtain , , and as the best-fit parameters for the unimodular gravity model and and for the standard (CDM) model. We found that the values of the model parameters in the unimodular gravity model using the SN + DA + BAO + CMB dataset are consistent with the Planck 2018 results. The results of both models are shown in Figure 3. In Table 3, we list the best-fit value of the parameters inferred from the CMB, BAO, DA, and SN datasets in the standard (CDM) model and the unimodular gravity model.
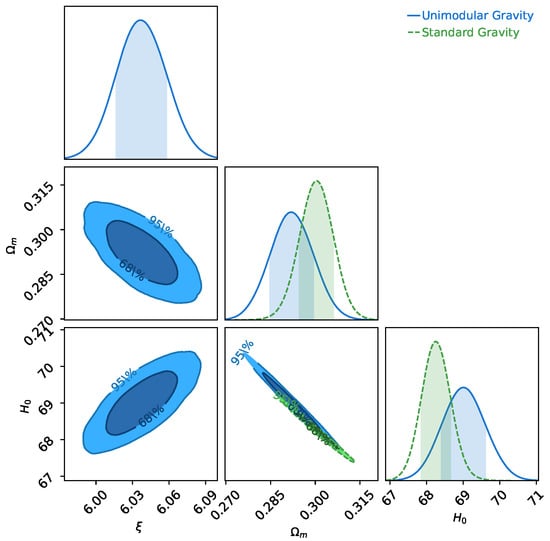
Figure 3.
The 2D contour plot and 1D posterior distributions of model parameters , and in the unimodular gravity model () and the standard (CDM) model () using the BAO + SN + DA + CMB data.

Table 3.
The results for the standard (CDM) model and the unimodular gravity model using the BAO, DA, and SN datasets.
In order to study the impact of unimodular gravity on the Hubble tension problem, in Figure 4, we plot the 1D posterior distribution of and the corresponding median along with the 1 error band plot for the unimodular gravity and standard (CDM) models. Here, we also compared our results with the Planck 2018 and SH0ES 2022 estimates of .
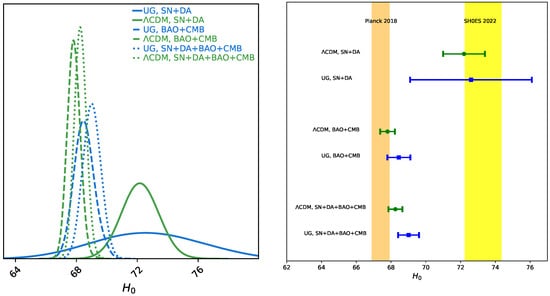
Figure 4.
The 1D posterior distribution and corresponding median along with the 1 error band plot of for the UG and standard (CDM) models in comparison with the Planck 2018 [31] and SH0ES 2022 [32] results.
From these results, one can note that the value of is sensitive to the value of . Here, we estimated from all datasets. The mean value of obtained from SN + DA data changed significantly after including the BAO + CMB data, and the constraint became more stringent. Furthermore, the tension with the SH0ES 2022 results remained almost the same in our results.
7. Conclusions
In this paper, we discussed the cosmological implication of the unimodular theory of gravity, which is an alternative approach to the general theory of relativity. The decomposition of the full metric in a scalar field and the unimodular metric led to the decomposition in the affine connection, Ricci tensor, and Ricci scalar. The general coordinate invariance was broken by introducing a parameter . We considered a unimodular gravity model with broken general coordinate invariance and focused on estimating the cosmological parameters of the current universe in this model. We found that the UG model can fit the cosmological data with , which is very close to that of general relativity (). We also observed a small increase in the mean value of obtained in unimodular gravity compared with the standard (CDM) model in all datasets.
We compared our theory of unimodular gravity with that studied in [28]. In this cosmological diffusion model, the unimodular constraint was applied to the full metric. In this way, a non-conservative current was established. Such a current can be due to the interaction of all matter. However, as the interaction of ordinary matter is well known, the authors explored the non-gravitational interaction of dark sector components. The cold dark matter interacts with dark energy, which appears as a time-dependent cosmological term . It was shown that, for some value of the diffusion parameter of the theory, it is possible to alleviate the Hubble tension by . On the other hand, in our theory, we applied the unimodular constraint only to the unimodular metric, and no such non-gravitational interacting term was considered. The introduced parameter is effective only in the gravitational sector and generalized cosmological constant. As a result, the theory does not reduce the Hubble tension as much as in the diffusion model of unimodular gravity.
In the current work, we studied the cosmological parameters at the background level. A study of cosmological perturbation can further give more-precise values of the parameters of the theory. In [25], a study of linear perturbation was performed under such a construction of unimodular gravity where the decomposition of the metric and the introduction of were performed in the same way. The power spectrum was derived, and the unimodular correction to the tensor-to-scalar ratio was obtained. It was shown that the unimodular correction can raise or lower the value of the tensor-to-scalar ratio. However, a detailed study is still required to know the shift in the peaks in the angular power spectrum in the CMB, which can further refine the value of the Hubble constant. One has to go for the complete study of cosmological perturbation assuming such a constraint of unimodular gravity.
A comparison with the model used in [16] is necessary. In that model, only the generalized cosmological constant or generalized non-relativistic matter was considered, whereas in our model, cold dark matter, the generalized cosmological constant, and radiation were all taken into account. Therefore, our model provides a more-satisfactory fit to the data. It could be a reliable model that consists of cold dark matter and the cosmological constant, similar to the CDM of standard gravity.
Author Contributions
Individual contributions of authors, N.K.S. and G.K., are equal and include the following: conceptualization, methodology, formal analysis, investigation, validation, visualization, writing original draft preparation, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created in this study. Data sharing is not applicable to this article.
Acknowledgments
We thank Pankaj Jain for valuable suggestions and comments on the draft.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Anderson, J.L.; Finkelstein, D. Cosmological Constant and Fundamental Length. Am. J. Phys. 1971, 39, 901–904. [Google Scholar] [CrossRef]
- Lorentz, H.A.; Einstein, A. The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity; Dover: New York, NY, USA, 1952. [Google Scholar]
- Henneaux, M.; Teitelboim, C. The cosmological constant and general covariance. Phys. Lett. B 1989, 222, 195–199. [Google Scholar] [CrossRef]
- Ng, Y.J.; van Dam, H. Unimodular theory of gravity and the cosmological constant. J. Math. Phys. 1991, 32, 1337–1340. [Google Scholar] [CrossRef]
- Finkelstein, D.R.; Galiautdinov, A.A.; Baugh, J.E. Unimodular relativity and cosmological constant. J. Math. Phys. 2001, 42, 340–346. [Google Scholar] [CrossRef]
- Smolin, L. Quantization of unimodular gravity and the cosmological constant problems. Phys. Rev. D 2009, 80, 084003. [Google Scholar] [CrossRef]
- Jiroušek, P. Unimodular Approaches to the Cosmological Constant Problem. Universe 2023, 9, 131. [Google Scholar] [CrossRef]
- Kursunoglu, B.; Mintz, S.L.; Perlmutter, A. (Eds.) High-Energy Physics, Proceedings of the 20th Annual Orbis Scientiae, Miami, FL, USA, 17–21 January 1983; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Buchmüller, W.; Dragon, N. Einstein gravity from restricted coordinate invariance. Phys. Lett. B 1988, 207, 292–294. [Google Scholar] [CrossRef]
- Unruh, W.G. Unimodular theory of canonical quantum gravity. Phys. Rev. D 1989, 40, 1048–1052. [Google Scholar] [CrossRef]
- Jain, P.; Karmakar, P.; Mitra, S.; Panda, S.; Singh, N.K. Testing unimodular gravity. J. Cosmol. Astropart. Phys. 2012, 2012, 020. [Google Scholar] [CrossRef]
- Jain, P.; Jaiswal, A.; Karmakar, P.; Kashyap, G.; Singh, N.K. Cosmological implications of unimodular gravity. J. Cosmol. Astropart. Phys. 2012, 2012, 003. [Google Scholar] [CrossRef]
- Álvarez, E. Can one tell Einstein’s unimodular theory from Einstein’s general relativity? J. High Energy Phys. 2005, 2005, 002. [Google Scholar] [CrossRef]
- Álvarez, E.; Faedo, A.F. Unimodular cosmology and the weight of energy. Phys. Rev. D 2007, 76, 064013. [Google Scholar] [CrossRef]
- Gao, C.; Brandenberger, R.; Cai, Y.; Chen, P. Cosmological perturbations in unimodular gravity. J. Cosmol. Astropart. Phys. 2014, 2014, 021. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unimodular-mimetic cosmology. Class. Quantum Gravity 2016, 33, 125017. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Saridakis, E.N. Inflationary cosmology in unimodular F(T) gravity. Mod. Phys. Lett. A 2017, 32, 1750114. [Google Scholar] [CrossRef]
- Rajabi, F.; Nozari, K. Unimodular f (R,T) gravity. Phys. Rev. D 2017, 96, 084061. [Google Scholar] [CrossRef]
- Rajabi, F.; Nozari, K. Energy condition in unimodular f(R, T) gravity. Eur. Phys. J. C 2021, 81, 247. [Google Scholar] [CrossRef]
- Costantini, A.; Elizalde, E. A reconstruction method for anisotropic universes in unimodular F(R)-gravity. Eur. Phys. J. C 2022, 82, 1127. [Google Scholar] [CrossRef]
- Cho, I.; Singh, N.K. Unimodular theory of gravity and inflation. Class. Quantum Gravity 2015, 32, 135020. [Google Scholar] [CrossRef]
- Singh, N.K. Unimodular constraint on global scale invariance. Mod. Phys. Lett. A 2013, 28, 1350130. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unimodular mimetic F(R) inflation. Astrophys. Space Sci. 2016, 361, 236. [Google Scholar] [CrossRef]
- Linares Cedeño, F.; Nucamendi, U. Revisiting cosmological diffusion models in Unimodular Gravity and the H0 tension. Phys. Dark Universe 2021, 32, 100807. [Google Scholar] [CrossRef]
- Agrawal, A.; Mishra, B.; Moraes, P. Unimodular gravity traversable wormholes. Eur. Phys. J. Plus 2023, 138, 275. [Google Scholar] [CrossRef]
- Landau, S.J.; Benetti, M.; Perez, A.; Sudarsky, D. Cosmological constraints on unimodular gravity models with diffusion. Phys. Rev. D 2023, 108, 043524. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Bay, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results—I. Overview and the cosmological legacy of Planck. A&A 2020, 641, A1. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; An, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy can Resolve the Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.Y.; Pinner, D.; Randall, L. Rock ’n’ Roll Solutions to the Hubble Tension. arXiv 2019, arXiv:astro-ph.CO/1904.01016. [Google Scholar] [CrossRef]
- Karwal, T.; Raveri, M.; Jain, B.; Khoury, J.; Trodden, M. Chameleon early dark energy and the Hubble tension. Phys. Rev. D 2022, 105, 063535. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Li, L.; Wang, S.J.; Yu, W.W. Chameleon dark energy can resolve the Hubble tension. Phys. Rev. D 2021, 103, 121302. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. J. Cosmol. Astropart. Phys. 2017, 10, 020. [Google Scholar] [CrossRef]
- Adi, T.; Kovetz, E.D. Can conformally coupled modified gravity solve the Hubble tension? Phys. Rev. D 2021, 103, 023530. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Q.G.; Wang, K. Distance priors from Planck final release. J. Cosmol. Astropart. Phys. 2019, 2019, 028. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Q.G. Hubble constant and sound horizon from the late-time universe. Phys. Rev. D 2021, 103, 043513. [Google Scholar] [CrossRef]
- Jimenez, R.; Verde, L.; Treu, T.; Stern, D. Constraints on the equation of state of dark energy and the Hubble constant from stellar ages and the CMB. Astrophys. J. 2003, 593, 622–629. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.J.; Sun, Y.C. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221–1233. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating Luminous Red Galaxies observed with the Southern African Large Telescope. Mon. Not. Roy. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 2010, 008. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the universe up to z ≈ 1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 006. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z~2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. On the use of the local prior on the absolute magnitude of Type Ia supernovae in cosmological inference. Mon. Not. R. Astron. Soc. 2021, 504, 5164–5171. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W. Baryonic features in the matter transfer function. Astrophys. J. 1998, 496, 605. [Google Scholar] [CrossRef]
- Lemos, P.; Lee, E.; Efstathiou, G.; Gratton, S. Model independent H(z) reconstruction using the cosmic inverse distance ladder. Mon. Not. Roy. Astron. Soc. 2019, 483, 4803–4810. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample—I. A 4 per cent distance measure at z = 0.15. Mon. Not. Roy. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. Roy. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Bautista, J.E.; Vargas-Magaña, M.; Dawson, K.S.; Percival, W.J.; Brinkmann, J.; Brownstein, J.; Camacho, B.; Comparat, J.; Gil-Marín, H.; Mueller, E.M.; et al. The SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations at Redshift of 0.72 with the DR14 Luminous Red Galaxy Sample. Astrophys. J. 2018, 863, 110. [Google Scholar] [CrossRef]
- Zhao, G.B.; Wang, Y.; Saito, S.; Gil-Marín, H.; Percival, W.J.; Wang, D.; Chuang, C.H.; Ruggeri, R.; Mueller, E.M.; Zhu, F.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: A tomographic measurement of cosmic structure growth and expansion rate based on optimal redshift weights. Mon. Not. R. Astron. Soc. 2018, 482, 3497–3513. [Google Scholar] [CrossRef]
- Blomqvist, M.; du Mas des Bourboux, H.; Busca, N.G.; de Sainte Agathe, V.; Rich, J.; Balland, C.; Bautista, J.E.; Dawson, K.; Font-Ribera, A.; Guy, J.; et al. Baryon acoustic oscillations from the cross-correlation of Lyorption and quasars in eBOSS DR14. A&A 2019, 629, A86. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N. Small-Scale Cosmological Perturbations: An Analytic Approach. Astrophys. J. 1996, 471, 542. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).