Analytical Approximate Solutions for Scalarized AdS Black Holes
Abstract
1. Introduction
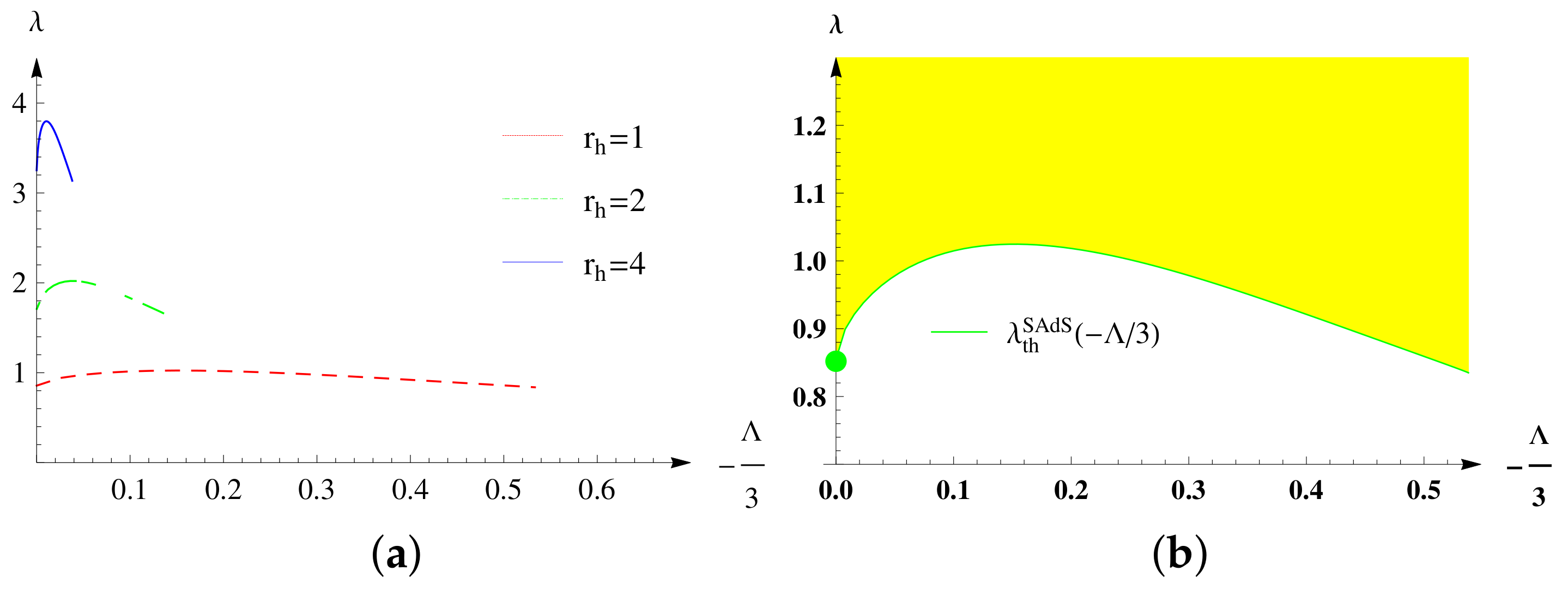
2. Instability of a SAdS Black Hole
3. Numerical Solutions for Scalarized AdS Black Holes
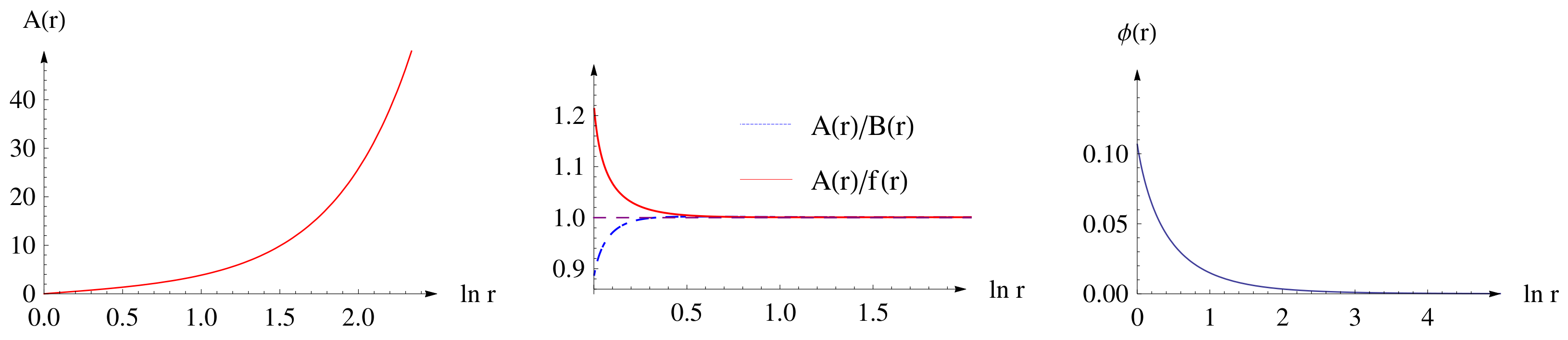
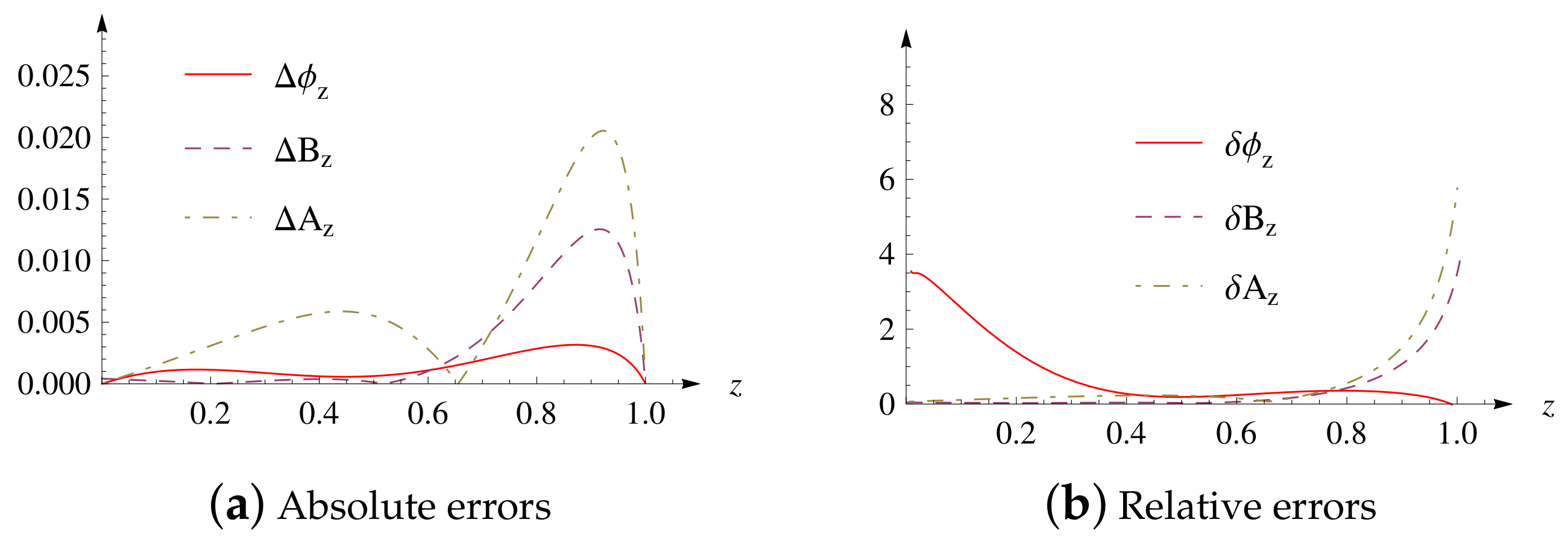
4. Analytical Approximate Solutions
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carter, B. Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 1971, 26, 331–333. [Google Scholar] [CrossRef]
- Ruffini, R.; Wheeler, J.A. Introducing the black hole. Phys. Today 1971, 24, 30. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Exact solutions of Einstein conformal scalar equations. Ann. Phys. 1974, 82, 535. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes with Scalar Charge. Ann. Phys. 1975, 91, 75. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Kireev, Y.N. Instability of Black Holes with Scalar Charge. Phys. Lett. A 1978, 67, 95. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Nonperturbative strong field effects in tensor—Scalar theories of gravitation. Phys. Rev. Lett. 1993, 70, 2220–2223. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Tensor-scalar gravity and binary pulsar experiments. Phys. Rev. D 1996, 54, 1474–1491. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss–Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss–Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss–Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef]
- Myung, Y.S.; Zou, D.C. Gregory-Laflamme instability of black hole in Einstein-scalar-Gauss–Bonnet theories. Phys. Rev. D 2018, 98, 024030. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Novel “no-scalar-hair” theorem for black holes. Phys. Rev. D 1995, 51, R6608. [Google Scholar] [CrossRef]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss–Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef]
- Doneva, D.D.; Kiorpelidi, S.; Nedkova, P.G.; Papantonopoulos, E.; Yazadjiev, S.S. Charged Gauss–Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. D 2018, 98, 104056. [Google Scholar] [CrossRef]
- Macedo, C.F.B.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Scalarized black holes. Arab. J. Math. 2022, 11, 17–30. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Beyond the spontaneous scalarization: New fully nonlinear mechanism for the formation of scalarized black holes and its dynamical development. Phys. Rev. D 2022, 105, L041502. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Axial perturbations of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2020, 101, 104006. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Polar quasinormal modes of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2020, 102, 024086. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Freedman, D.Z. Stability in Gauged Extended Supergravity. Ann. Phys. 1982, 144, 249. [Google Scholar] [CrossRef]
- Bakopoulos, A.; Antoniou, G.; Kanti, P. Novel Black-Hole Solutions in Einstein-Scalar-Gauss–Bonnet Theories with a Cosmological Constant. Phys. Rev. D 2019, 99, 064003. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B.; Aprile, N.P.; Urrestilla, J. Scalarization of asymptotically anti–de Sitter black holes with applications to holographic phase transitions. Phys. Rev. D 2020, 101, 124016. [Google Scholar] [CrossRef]
- Guo, H.; Kiorpelidi, S.; Kuang, X.M.; Papantonopoulos, E.; Wang, B.; Wu, J.P. Spontaneous holographic scalarization of black holes in Einstein-scalar-Gauss–Bonnet theories. Phys. Rev. D 2020, 102, 084029. [Google Scholar] [CrossRef]
- Guo, H.; Kuang, X.M.; Papantonopoulos, E.; Wang, B. Horizon curvature and spacetime structure influences on black hole scalarization. Eur. Phys. J. C 2021, 81, 842. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zhidenko, A. New parametrization for spherically symmetric black holes in metric theories of gravity. Phys. Rev. D 2014, 90, 084009. [Google Scholar] [CrossRef]
- Liao, S.J. On the Proposed Homotopy Analysis Techniques for Nonlinear Problems and Its Application. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Konoplya, R.; Rezzolla, L.; Zhidenko, A. General parametrization of axisymmetric black holes in metric theories of gravity. Phys. Rev. D 2016, 93, 064015. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Konoplya, R.A.; Zhidenko, A. Analytical approximation for the Einstein-dilaton-Gauss–Bonnet black hole metric. Phys. Rev. D 2017, 96, 064004. [Google Scholar] [CrossRef]
- Kokkotas, K.; Konoplya, R.A.; Zhidenko, A. Non-Schwarzschild black-hole metric in four dimensional higher derivative gravity: Analytical approximation. Phys. Rev. D 2017, 96, 064007. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Analytical representation for metrics of scalarized Einstein-Maxwell black holes and their shadows. Phys. Rev. D 2019, 100, 044015. [Google Scholar] [CrossRef]
- Sajadi, S.N.; Hendi, S.H. Analytically approximation solution to Einstein-Cubic gravity. Eur. Phys. J. C 2022, 82, 675. [Google Scholar] [CrossRef]
- Xu, H.; Lin, Z.; Liao, S.; Wu, J.; Majdalani, J. Homotopy based solutions of the Navier-CStokes equations for a porous channel with orthogonally moving walls. Phys. Fluids 2010, 22, 053601. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of the homotopy analysis method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 360, 109. [Google Scholar] [CrossRef]
- Yabushita, K.; Yamashita, M.; Tsuboi, K. An analytic solution of projectile motion with the quadratic resistance law using the homotopy analysis method. J. Phys. A Math. Theor. 2007, 40, 8403. [Google Scholar] [CrossRef]
- Song, H.; Tao, L. Homotopy analysis of 1d unsteady, nonlinear groundwater flow through porous media. J. Coast. Res. 2007, 50, 292. [Google Scholar]
- Palit, A.; Datta, D.P. Comparative Study of Homotopy Analysis and Renormalization Group Methods on Rayleigh and Van der Pol Equations. Differ. Equations Dyn. Syst. 2016, 24, 417–443. [Google Scholar] [CrossRef][Green Version]
- Rana, P.; Shukla, N.; Gupta, Y.; Pop, I. Homotopy analysis method for predicting multiple solutions in the channel flow with stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 183–193. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.; Yao, Y.; Liu, Q. Homotopy method for solving mathematical programs with bounded box-constrained variational inequalities. Optimization 2019, 68, 2297–2316. [Google Scholar] [CrossRef]
- Sultana, J. Obtaining analytical approximations to black hole solutions in higher-derivative gravity using the homotopy analysis method. Eur. Phys. J. Plus 2019, 134, 111. [Google Scholar] [CrossRef]
- Sultana, J. Gravitational Decoupling in Higher Order Theories. Symmetry 2021, 13, 1598. [Google Scholar] [CrossRef]
- Cho, G. Analytic expression of perturbations of Schwarzschild spacetime via Homotopy Analysis Method. arXiv 2020, arXiv:2008.12526. [Google Scholar]
- Cardoso, V.; Lemos, J.P.S. Quasinormal modes of Schwarzschild anti-de Sitter black holes: Electromagnetic and gravitational perturbations. Phys. Rev. D 2001, 64, 084017. [Google Scholar] [CrossRef]
- Ishibashi, A.; Kodama, H. Stability of higher dimensional Schwarzschild black holes. Prog. Theor. Phys. 2003, 110, 901. [Google Scholar] [CrossRef]
- Moon, T.; Myung, Y.S.; Son, E.J. Stability analysis of f(R)-AdS black holes. Eur. Phys. J. C 2011, 71, 1777. [Google Scholar] [CrossRef]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Gorder, R.A.; Vajravelu, K. On the selection of auxiliary functions, operators, and convergence control parameters in the application of the Homotopy Analysis Method to nonlinear differential equations: A general approach. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 4078–4089. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, D.-C.; Meng, B.; Zhang, M.; Li, S.-Y.; Lai, M.-Y.; Myung, Y.S. Analytical Approximate Solutions for Scalarized AdS Black Holes. Universe 2023, 9, 26. https://doi.org/10.3390/universe9010026
Zou D-C, Meng B, Zhang M, Li S-Y, Lai M-Y, Myung YS. Analytical Approximate Solutions for Scalarized AdS Black Holes. Universe. 2023; 9(1):26. https://doi.org/10.3390/universe9010026
Chicago/Turabian StyleZou, De-Cheng, Bo Meng, Ming Zhang, Sheng-Yuan Li, Meng-Yun Lai, and Yun Soo Myung. 2023. "Analytical Approximate Solutions for Scalarized AdS Black Holes" Universe 9, no. 1: 26. https://doi.org/10.3390/universe9010026
APA StyleZou, D.-C., Meng, B., Zhang, M., Li, S.-Y., Lai, M.-Y., & Myung, Y. S. (2023). Analytical Approximate Solutions for Scalarized AdS Black Holes. Universe, 9(1), 26. https://doi.org/10.3390/universe9010026





