Generalized Unitarity Method for Unstable Particles
Abstract
1. Introduction
2. Loop Amplitudes and the Unitarity Method
3. Unitarity Method for Unstable Particles
3.1. Possible Issues with Unstable Particles
3.2. When the Unitarity Method Works for Unstable Particles
3.3. Lee–Wick Theories
3.4. When the Unitarity Method Does Not Seem to Work for Unstable Particles
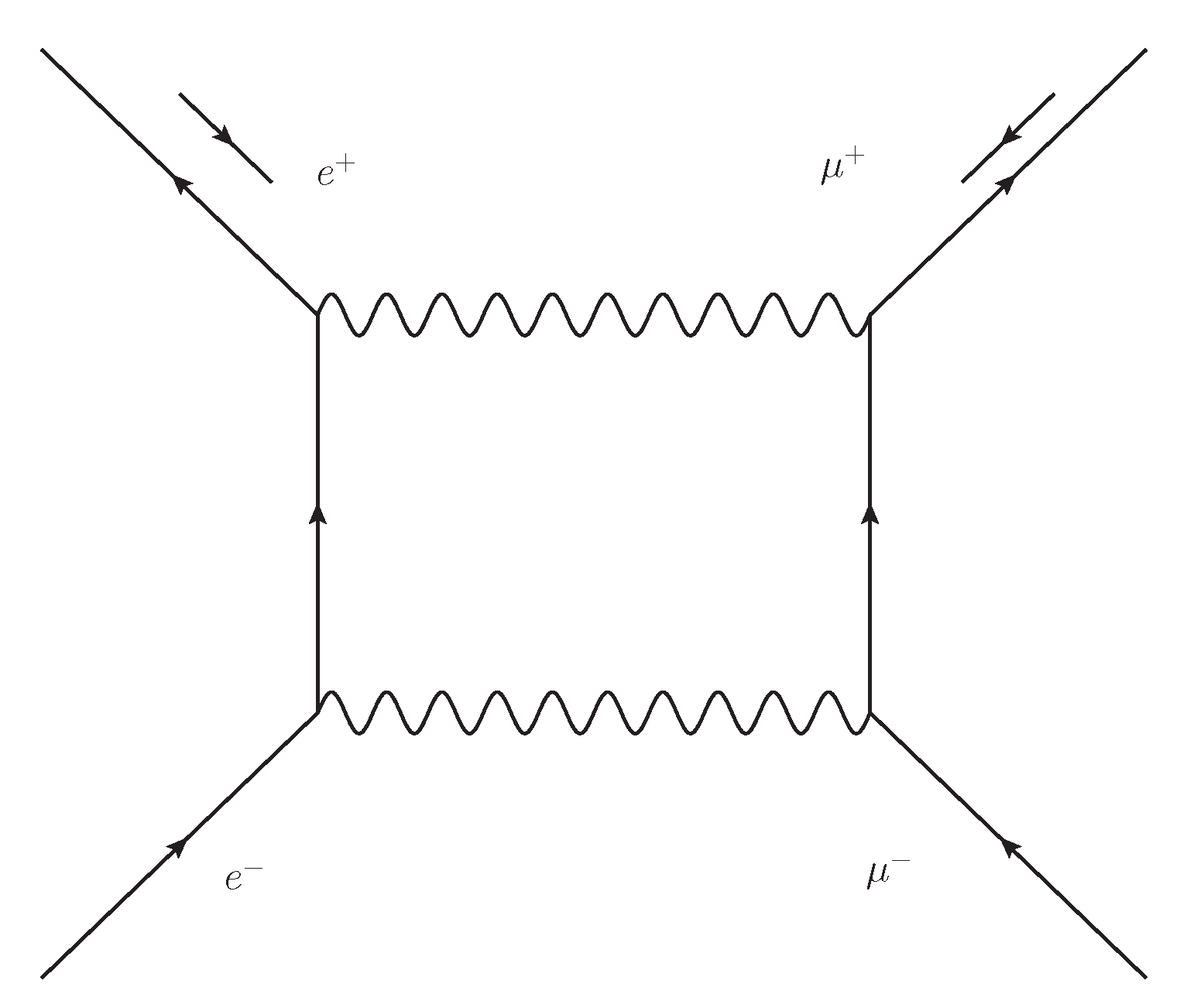
4. Examples of the Use of the Unitarity Method for Unstable Particles
4.1. Normal Unstable Particles
4.2. Lee–Wick QED
4.3. Non-Local Theories
5. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Quick Review of the Spinor-Helicity Formalism
| 1 | The terminology “unstable propagator” is actually a misnomer because what we mean by “unstable” is that the particle associated with this propagator. However, as the reader can easily check, this parlance is employed in the specialized literature. Therefore for brevity we will stick with this terminology. Henceforth, the expression “unstable propagator” will be understood as “propagator associated with an unstable particle/state”. |
| 2 | |
| 3 | For a nice discussion of some additional subtleties that can be encountered in this situation, see Ref. [42] and references cited therein. |
| 4 | Incidentally, this implies that the expansion (4) is also valid in the NWA as and the full energy dependence of the self-energy does not need to be taken into account. |
| 5 | Recall this is the narrow-width approximation we are using, not a fixed-width scheme, which is known to introduce gauge dependence. Indeed, fixed-width schemes are known to violate SU(2) × U(1) Ward identities—see for instance the discussion in Ref. [91]. Perhaps, in order to avoid further confusion, a better terminology for the narrow-width approximation would be “zero-width approximation”, as first suggested by John F. Donoghue in a private communication with the author, because after all it comes from taking the width to zero. |
| 6 | We recall that a four-scalar interaction is also possible in scalar QED and this interaction provides independent gauge-invariant data. As a consequence, the amplitude calculated with the BCFW recursion relation is the one associated with choosing the scalar self-coupling constant to be proportional to . For more details regarding this issue in scalar QED—which is independent of the addition of the non-local interaction—see Ref. [51]. |
References
- Evans, L.; Bryant, P. LHC Machine. J. Instrum. 2008, 3, S08001. [Google Scholar] [CrossRef]
- Cutkosky, R.E. Singularities and Discontinuities of Feynman Amplitudes. J. Math. Phys. 1960, 1, 429–433. [Google Scholar] [CrossRef]
- Eden, R.; Landshoff, P.; Olive, D.; Polkinghorne, J. The Analytic S-Matrix; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Landau, L. On analytic properties of vertex parts in quantum field theory. Nucl. Phys. 1959, 13, 181. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Kosower, D.A. One loop amplitudes for e+ e− to four partons. Nucl. Phys. B 1998, 513, 3. [Google Scholar] [CrossRef]
- Britto, R.; Cachazo, F.; Feng, B. Generalized unitarity and one-loop amplitudes in N = 4 super-Yang-Mills. Nucl. Phys. B 2005, 725, 275. [Google Scholar] [CrossRef]
- Forde, D. Direct extraction of one-loop integral coefficients. Phys. Rev. D 2007, 75, 125019. [Google Scholar] [CrossRef]
- Kosower, D.A.; Larsen, K.J. Maximal unitarity at two loops. Phys. Rev. D 2012, 85, 045017. [Google Scholar] [CrossRef]
- Caron-Huot, S.; Larsen, K.J. Uniqueness of two-loop master contours. J. High Energy Phys. 2012, 2012, 26. [Google Scholar] [CrossRef]
- Johansson, H.; Kosower, D.A.; Larsen, K.J. Two-Loop Maximal Unitarity with External Masses. Phys. Rev. D 2013, 87, 025030. [Google Scholar] [CrossRef]
- Johansson, H.; Kosower, D.A.; Larsen, K.J. Maximal Unitarity for the Four-Mass Double Box. Phys. Rev. D 2014, 89, 125010. [Google Scholar] [CrossRef]
- Abreu, S.; Britto, R.; Duhr, C.; Gardi, E. Cuts from residues: The one-loop case. J. High Energy Phys. 2017, 2017, 114. [Google Scholar] [CrossRef]
- Sogaard, M.; Zhang, Y. Elliptic Functions and Maximal Unitarity. Phys. Rev. D 2015, 91, 081701. [Google Scholar] [CrossRef]
- Larsen, K.J.; Zhang, Y. Integration-by-parts reductions from unitarity cuts and algebraic geometry. Phys. Rev. D 2016, 93, 041701. [Google Scholar] [CrossRef]
- Ita, H. Two-loop Integrand Decomposition into Master Integrals and Surface Terms. Phys. Rev. D 2016, 94, 116015. [Google Scholar] [CrossRef]
- Remiddi, E.; Tancredi, L. Differential equations and dispersion relations for Feynman amplitudes. The two-loop massive sunrise and the kite integral. Nucl. Phys. B 2016, 907, 400. [Google Scholar] [CrossRef]
- Primo, A.; Tancredi, L. On the maximal cut of Feynman integrals and the solution of their differential equations. Nucl. Phys. B 2017, 916, 94. [Google Scholar] [CrossRef]
- Frellesvig, H.; Papadopoulos, C.G. Cuts of Feynman Integrals in Baikov representation. J. High Energy Phys. 2017, 2017, 83. [Google Scholar] [CrossRef]
- Zeng, M. Differential equations on unitarity cut surfaces. J. High Energy Phys. 2017, 2017, 121. [Google Scholar] [CrossRef]
- Dennen, T.; Spradlin, M.; Volovich, A. Landau Singularities and Symbology: One− and Two-loop MHV Amplitudes in SYM Theory. J. High Energy Phys. 2016, 2016, 69. [Google Scholar] [CrossRef]
- Dennen, T.; Prlina, I.; Spradlin, M.; Stanojevic, S.; Volovich, A. Landau Singularities from the Amplituhedron. J. High Energy Phys. 2017, 2017, 152. [Google Scholar] [CrossRef]
- Veltman, M. Diagrammatica: The Path to Feynman Rules; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Remiddi, E. Dispersion Relations for Feynman Graphs. Helv. Phys. Acta 1982, 54, 364. [Google Scholar]
- Britto, R. Loop Amplitudes in Gauge Theories: Modern Analytic Approaches. J. Phys. A 2011, 44, 454006. [Google Scholar] [CrossRef]
- Abreu, S.; Britto, R.; Grönqvist, H. Cuts and coproducts of massive triangle diagrams. J. High Energy Phys. 2015, 2015, 111. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Dunbar, D.C.; Kosower, D.A. One loop n point gauge theory amplitudes, unitarity and collinear limits. Nucl. Phys. B 1994, 425, 217–260. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Dunbar, D.C.; Kosower, D.A. Fusing gauge theory tree amplitudes into loop amplitudes. Nucl. Phys. B 1995, 435, 59–101. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Kosower, D.A. Progress in one loop QCD computations. Ann. Rev. Nucl. Part. Sci. 1996, 46, 109–148. [Google Scholar] [CrossRef]
- Bern, Z.; Duca, V.D.; Dixon, L.J.; Kosower, D.A. All non-maximally-helicity-violating one-loop seven-gluon amplitudes in N = 4 super-yang-Mills theory. Phys. Rev. D 2005, 71, 045006. [Google Scholar] [CrossRef]
- Britto, R.; Feng, B.; Mastrolia, P. Closed-Form Decomposition of One-Loop Massive Amplitudes. Phys. Rev. D 2008, 78, 025031. [Google Scholar] [CrossRef]
- Bern, Z.; Huang, Y.-T. Basics of generalized unitarity. J. Phys. A Math. Theor. 2011, 44, 454003. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.; Dennen, T.; Huang, Y.T.; Ita, H. Generalized Unitarity and Six-Dimensional Helicity. Phys. Rev. D 2011, 83, 085022. [Google Scholar] [CrossRef]
- Drummond, J.M.; Henn, J.; Korchemsky, G.P.; Sokatchev, E. Generalized unitarity for N = 4 super-amplitudes. Nucl. Phys. B 2013, 869, 452–492. [Google Scholar] [CrossRef]
- Engelund, O.T.; McKeown, R.W.; Roiban, R. Generalized unitarity and the worldsheet S matrix in AdSn×Sn×M10−2n. J. High Energy Phys. 2013, 2013, 23. [Google Scholar] [CrossRef]
- Elvang, H.; Hadjiantonis, M.; Jones, C.R.T.; Paranjape, S. All-Multiplicity One-Loop Amplitudes in Born-Infeld Electrodynamics from Generalized Unitarity. J. High Energy Phys. 2020, 2020, 9. [Google Scholar] [CrossRef]
- Bern, Z.; Kosmopoulos, D.; Zhiboedov, A. Gravitational effective field theory islands, low-spin dominance, and the four-graviton amplitude. J. Phys. A 2021, 54, 344002. [Google Scholar] [CrossRef]
- Bern, Z.; Parra-Martinez, J.; Sawyer, E. Structure of two-loop SMEFT anomalous dimensions via on-shell methods. J. High Energy Phys. 2020, 2020, 211. [Google Scholar] [CrossRef]
- Cachazo, F. Sharpening The Leading Singularity. arXiv 2008, arXiv:0803.1988. [Google Scholar]
- Arkani-Hamed, N.; Cachazo, F.; Kaplan, J. What is the Simplest Quantum Field Theory? J. High Energy Phys. 2010, 2010, 16. [Google Scholar] [CrossRef]
- Veltman, M. Unitarity and causality in a renormalizable field theory with unstable particles. Physica 1963, 29, 186. [Google Scholar] [CrossRef]
- Hooft, G.; Veltman, M.J.G. Diagrammar. In Particle Interactions at Very High Energies; NATO Advanced Study Institutes: Series B; Speiser, D., Halzen, F., Weyers, J., Eds.; Plenum Press: New York, NY, USA, 1974; Volume 4, p. 177. [Google Scholar]
- Rodenburg, J. Unstable Particles and Resonances. Master’s Thesis, Institute for Theoretical Physics, University Utrecht, Utrecht, The Netherlands, 2015. [Google Scholar]
- Lang, J.-N.O. The Complex Mass Scheme, Gauge Dependence and Unitarity in Perturbative Quantum Field Theory. Master’s Thesis, Wurzburg University, Wurzburg, Germany, 2013. [Google Scholar]
- Denner, A.; Lang, J.N. The complex-mass scheme and unitarity in perturbative quantum field theory. Eur. Phys. J. C 2015, 75, 377. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Menezes, G. Unitarity, stability, and loops of unstable ghosts. Phys. Rev. D 2019, 100, 105006. [Google Scholar] [CrossRef]
- Ellis, R.K.; Kunszt, Z.; Melnikov, K.; Zanderighi, G. One-loop calculations in quantum field theory: From Feynman diagrams to unitarity cuts. Phys. Rep. 2012, 518, 141. [Google Scholar] [CrossRef]
- Frellesvig, H.A. Generalized Unitarity Cuts and Integrand Reduction at Higher Loop Orders. Ph.D. Thesis, Faculty of Science, University of Copenhagen, Copenhagen, Denmark, 2014. [Google Scholar]
- Brandhuber, A.; McNamara, S.; Spence, B.; Travaglini, G. Loop amplitudes in pure Yang-Mills from generalised unitarity. J. High Energy Phys. 2005, 2005, 11. [Google Scholar] [CrossRef][Green Version]
- Carrasco, J.J.M.; Johansson, H. Generic multiloop methods and application to = 4 super-Yang-Mills. J. Phys. A Math. Theor. 2011, 44, 454004. [Google Scholar] [CrossRef]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Elvang, H.; Huang, Y.-T. Scattering Amplitudes in Gauge Theory and Gravity; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Ossola, G.; Papadopoulos, C.G.; Pittau, R. Reducing full one-loop amplitudes to scalar integrals at the integrand level. Nucl. Phys. B 2007, 763, 147. [Google Scholar] [CrossRef]
- Giele, W.T.; Kunszt, Z.; Melnikov, K. Full one-loop amplitudes from tree amplitudes. J. High Energy Phys. 2008, 2008, 49. [Google Scholar] [CrossRef]
- Ellis, R.K.; Giele, W.T.; Kunszt, Z.; Melnikov, K. Masses, fermions and generalized D-dimensional unitarity. Nucl. Phys. B 2009, 822, 270. [Google Scholar] [CrossRef]
- Henn, J.M.; Plefka, J.C. Scattering Amplitudes in Gauge Theories; Springer: Berlin/Heidelberg, Germany, 2014; Volume 883. [Google Scholar]
- van Neerven, W.L.; Vermaseren, J.A.M. Large loop integrals. Phys. Lett. B 1984, 137, 241. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Kosower, D.A. Dimensionally regulated one loop integrals. Phys. Lett. B 1993, 302, 299, Erratum in Phys. Lett. B 1993, 318, 649. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.J.; Kosower, D.A. Dimensionally regulated pentagon integrals. Nucl. Phys. B 1994, 412, 75. [Google Scholar] [CrossRef]
- Brown, L.M.; Feynman, R.P. Radiative corrections to Compton scattering. Phys. Rev. 1952, 85, 231. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. Scalar one-loop integrals. Nucl. Phys. B 1979, 153, 365. [Google Scholar] [CrossRef]
- Passarino, G.; Veltman, M.J.G. One Loop Corrections for e+ e− Annihilation Into mu+ mu− in the Weinberg Model. Nucl. Phys. B 1979, 160, 151. [Google Scholar] [CrossRef]
- Ellis, R.K.; Zanderighi, G. Scalar one-loop integrals for QCD. J. High Energy Phys. 2008, 2008, 2. [Google Scholar] [CrossRef]
- Beenakker, W.; Denner, A. Infrared Divergent Scalar Box Integrals With Applications in the Electroweak Standard Model. Nucl. Phys. B 1990, 338, 349. [Google Scholar] [CrossRef]
- Denner, A.; Nierste, U.; Scharf, R. A Compact expression for the scalar one loop four point function. Nucl. Phys. B 1991, 367, 637. [Google Scholar] [CrossRef]
- Duplancic, G.; Nizic, B. Dimensionally regulated one loop box scalar integrals with massless internal lines. Eur. Phys. J. C 2001, 20, 357. [Google Scholar] [CrossRef][Green Version]
- Papavassiliou, J.; Pilaftsis, A. Gauge invariance and unstable particles. Phys. Rev. Lett. 1995, 75, 3060. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Pilaftsis, A. A Gauge independent approach to resonant transition amplitudes. Phys. Rev. D 1996, 53, 2128. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Pilaftsis, A. Gauge invariant resummation formalism for two point correlation functions. Phys. Rev. D 1996, 54, 5315. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Pilaftsis, A. Effective charge of the Higgs boson. Phys. Rev. Lett. 1998, 80, 2785. [Google Scholar] [CrossRef]
- Papavassiliou, J.; Pilaftsis, A. Gauge and renormalization group invariant formulation of the Higgs boson resonance. Phys. Rev. D 1998, 58, 53002. [Google Scholar] [CrossRef]
- Denner, A.; Dittmaier, S.; Roth, M.; Wackeroth, D. Predictions for all processes e+ e−—> 4 fermions + gamma. Nucl. Phys. B 1999, 560, 33. [Google Scholar] [CrossRef]
- Denner, A.; Dittmaier, S.; Roth, M.; Wieders, L.H. Electroweak corrections to charged-current e+ e−—> 4 fermion processes: Technical details and further results. Nucl. Phys. B 2005, 724, 247, Erratum in Nucl. Phys. B 2012, 854, 504. [Google Scholar] [CrossRef]
- Denner, A.; Dittmaier, S. The Complex-mass scheme for perturbative calculations with unstable particles. Nucl. Phys. B Proc. Suppl. 2006, 160, 22. [Google Scholar] [CrossRef]
- Willenbrock, S. Mass and width of an unstable particle. arXiv 2022, arXiv:2203.11056. [Google Scholar]
- Lee, T.D.; Wick, G.C. Negative Metric and the Unitarity of the S Matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Cutkosky, R.E.; Landshoff, P.V.; Olive, D.I.; Polkinghorne, J.C. A non-analytic S matrix. Nucl. Phys. B 1969, 12, 281–300. [Google Scholar] [CrossRef]
- Coleman, S. Acausality. In Erice 1969: Ettore Majorana Schoool on Subnuclear Phenomena; Zicchici, A., Ed.; Academic Press: New York, NY, USA, 1970; p. 282. [Google Scholar]
- Grinstein, B.; O’Connell, D.; Wise, M.B. The Lee-Wick standard model. Phys. Rev. D 2008, 77, 025012. [Google Scholar] [CrossRef]
- Grinstein, B.; O’Connell, D.; Wise, M.B. Causality as an emergent macroscopic phenomenon: The Lee-Wick O(N) model. Phys. Rev. D 2009, 79, 105019. [Google Scholar] [CrossRef]
- Modesto, L.; Calcagni, G. Tree-level scattering amplitudes in nonlocal field theories. J. High Energy Phys. 2021, 2021, 169. [Google Scholar] [CrossRef]
- Calcagni, G. Quantum scalar field theories with fractional operators. Class. Quant. Grav. 2021, 38, 165006. [Google Scholar] [CrossRef]
- Boudjema, F. The scattering of light by light in the non-linear gauge. Phys. Lett. B 1987, 187, 362. [Google Scholar] [CrossRef]
- Jiang, X.-D.; Zhou, X.-J. Calculation of the polarization tensors of Z→3γ and γγ→γγ via W-boson loops in the standard model. Phys. Rev. D 1993, 47, 214. [Google Scholar] [CrossRef] [PubMed]
- Dong, F.-X.; Jiang, X.-D.; Zhou, X.-J. Total cross section for photon-photon scattering via W loops. Phys. Rev. D 1993, 47, 5169. [Google Scholar] [CrossRef]
- Jikia, G.; Tkabladze, A. Photon-photon scattering at the photon linear collider. Phys. Lett. B 1994, 323, 453. [Google Scholar] [CrossRef][Green Version]
- Yang, M.-Z.; Zhou, X.-J. Analytical results for photon-photon scattering via bosonic loops and for the decay of Z→γγγ via W-boson loops. Phys. Rev. D 1995, 52, 5018. [Google Scholar] [CrossRef]
- Fanchiotti, H.; Girotti, H.O.; Sirlin, A. Convergence of the lowest-order photon-photon scattering amplitude in the gauge theories. Lett. Nuovo Cim. 1972, 4, 826. [Google Scholar] [CrossRef]
- Zyla, P.A. et al. [Particle Data Group]. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Costantini, V.; Tollis, B.D.; Pistoni, G. Nonlinear effects in quantum electrodynamics. Nuovo Cim. A 1971, 2, 733. [Google Scholar] [CrossRef]
- Durieux, G.; Kitahara, T.; Shadmi, Y.; Weiss, Y. The electroweak effective field theory from on-shell amplitudes. J. High Energy Phys. 2020, 2020, 119. [Google Scholar] [CrossRef]
- Argyres, E.N.; Beenakker, W.; van Oldenborgh, G.J.; Denner, A.; Dittmaier, S.; Hoogland, J.; Kleiss, R.; Papadopoulos, C.G.; Passarino, G. Stable calculations for unstable particles: Restoring gauge invariance. Phys. Lett. B 1995, 358, 339–346. [Google Scholar] [CrossRef]
- Bern, Z.; Cheung, C.; Roiban, R.; Shen, C.-H.; Solonc, M.P.; Zeng, M. Black hole binary dynamics from the double copy and effective theory. J. High Energy Phys. 2019, 2019, 206. [Google Scholar] [CrossRef]
- Bern, Z.; Kosower, D.A. The Computation of loop amplitudes in gauge theories. Nucl. Phys. B 1992, 379, 451. [Google Scholar] [CrossRef]
- Bern, Z.; Morgan, A.G. Massive Loop Amplitudes from Unitarity. Nucl. Phys. B 1996, 467, 479. [Google Scholar] [CrossRef]
- Bern, Z.; Dixon, L.; Dunbar, D.C.; Kosower, D.A. One-loop self-dual and N = 4 super Yang-Mills. Phys. Lett. B 1997, 394, 105. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Menezes, G. Ostrogradsky instability can be overcome by quantum physics. Phys. Rev. D 2021, 104, 045010. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Menezes, G. Arrow of Causality and Quantum Gravity. Phys. Rev. Lett. 2019, 123, 171601. [Google Scholar] [CrossRef] [PubMed]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Nikishov, A.I. Radiative corrections to the scattering of μ mesons on electrons. Zh. Eksp. Teor. Fiz. 1960, 39, 757, Erratum in Sov. Phys. JETP 1961, 12, 529. [Google Scholar]
- Eriksson, K.E. Radiative corrections to muon-electron scattering. Nuovo C. 1961, 19, 1029. [Google Scholar] [CrossRef]
- Eriksson, K.E.; Larsson, B.; Rinander, G.A. Radiative corrections to muon-electron scattering. Nuovo C. 1963, 30, 1434. [Google Scholar] [CrossRef]
- Van Nieuwenhuizen, P. Muon-electron scattering cross section to order α3. Nucl. Phys. B 1971, 28, 429. [Google Scholar] [CrossRef][Green Version]
- D’Ambrosio, G. Electron-muon scattering in the electroweak unified theory. Lett. Nuovo C. 1983, 38, 593. [Google Scholar] [CrossRef]
- Kukhto, T.V.; Shumeiko, N.M.; Timoshin, S.I. Radiative corrections in polarised electron-muon elastic scattering. J. Phys. G 1987, 13, 725. [Google Scholar] [CrossRef]
- Bardin, D.Y.; Kalinovskaya, L. QED Corrections for Polarized Elastic MU-E Scattering. arXiv 1997, arXiv:hep-ph/9712310. [Google Scholar]
- Kaiser, N. Radiative corrections to lepton-lepton scattering revisited. J. Phys. G 2010, 37, 115005. [Google Scholar] [CrossRef]
- Alacevich, M.; Calame, C.M.C.; Chiesa, M.; Montagna, G.; Nicrosini, O.; Piccinini, F. Muon-electron scattering at NLO. J. High Energy Phys. 2019, 2, 155. [Google Scholar] [CrossRef]
- Beenakker, W.; Berends, F.A.; Chapovsky, A.P. An effective Lagrangian approach for unstable particles. Nucl. Phys. B 2000, 573, 503. [Google Scholar] [CrossRef]
- Terning, J. Gauging nonlocal Lagrangians. Phys. Rev. D 1991, 44, 887. [Google Scholar] [CrossRef]
- Brivio, I.; Trott, M. The Standard Model as an Effective Field Theory. Phys. Rept. 2019, 793, 1–98. [Google Scholar] [CrossRef]
- Krause, C. Higgs Effective Field Theories—Systematics and Applications. Ph.D. Thesis, Faculty of Physics, Ludwig-Maximilians-Universität Munich, Munich, Germany, 2016. [Google Scholar]
- Menezes, G. Color-kinematics duality, double copy and the unitarity method for higher-derivative QCD and quadratic gravity. J. High Energy Phys. 2022, 2022, 74. [Google Scholar] [CrossRef]
- Menezes, G. Leading Singularities in Higher-Derivative Yang–Mills Theory and Quadratic Gravity. Universe 2022, 8, 326. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Huang, T.C.; Huang, Y.T. Scattering amplitudes for all masses and spins. J. High Energy Phys. 2021, 2021, 70. [Google Scholar] [CrossRef]
- Shadmi, Y.; Weiss, Y. Effective field theory amplitudes the on-shell way: Scalar and vector couplings to gluons. JHEP 2019, 2, 165. [Google Scholar] [CrossRef]
- Chung, M.-Z.; Huang, Y.-T.; Kim, J.-W.; Lee, S. The simplest massive S-matrix: From minimal coupling to black holes. J. High Energy Phys. 2019, 2019, 156. [Google Scholar] [CrossRef]
- Aoude, R.; Machado, C.S. The rise of SMEFT on-shell amplitudes. J. High Energy Phys. 2019, 2019, 58. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menezes, G. Generalized Unitarity Method for Unstable Particles. Universe 2023, 9, 28. https://doi.org/10.3390/universe9010028
Menezes G. Generalized Unitarity Method for Unstable Particles. Universe. 2023; 9(1):28. https://doi.org/10.3390/universe9010028
Chicago/Turabian StyleMenezes, Gabriel. 2023. "Generalized Unitarity Method for Unstable Particles" Universe 9, no. 1: 28. https://doi.org/10.3390/universe9010028
APA StyleMenezes, G. (2023). Generalized Unitarity Method for Unstable Particles. Universe, 9(1), 28. https://doi.org/10.3390/universe9010028





