Addressing Cosmological Tensions by Non-Local Gravity
Abstract
1. Introduction
2. Non-Local Gravity
2.1. The Deser–Woodard Model
2.2. The Ricci-Transverse Model
3. The Late-Time Cosmic Acceleration
3.1. The DW Case: Delayed Response to Cosmic Events
3.2. The RT Case: Dynamical Dark Energy
4. The Growth of Perturbations and the Tension
4.1. The Deser–Woodard Evolution of Scalar Perturbations
4.2. The Ricci-Transverse Evolution of Scalar Perturbations
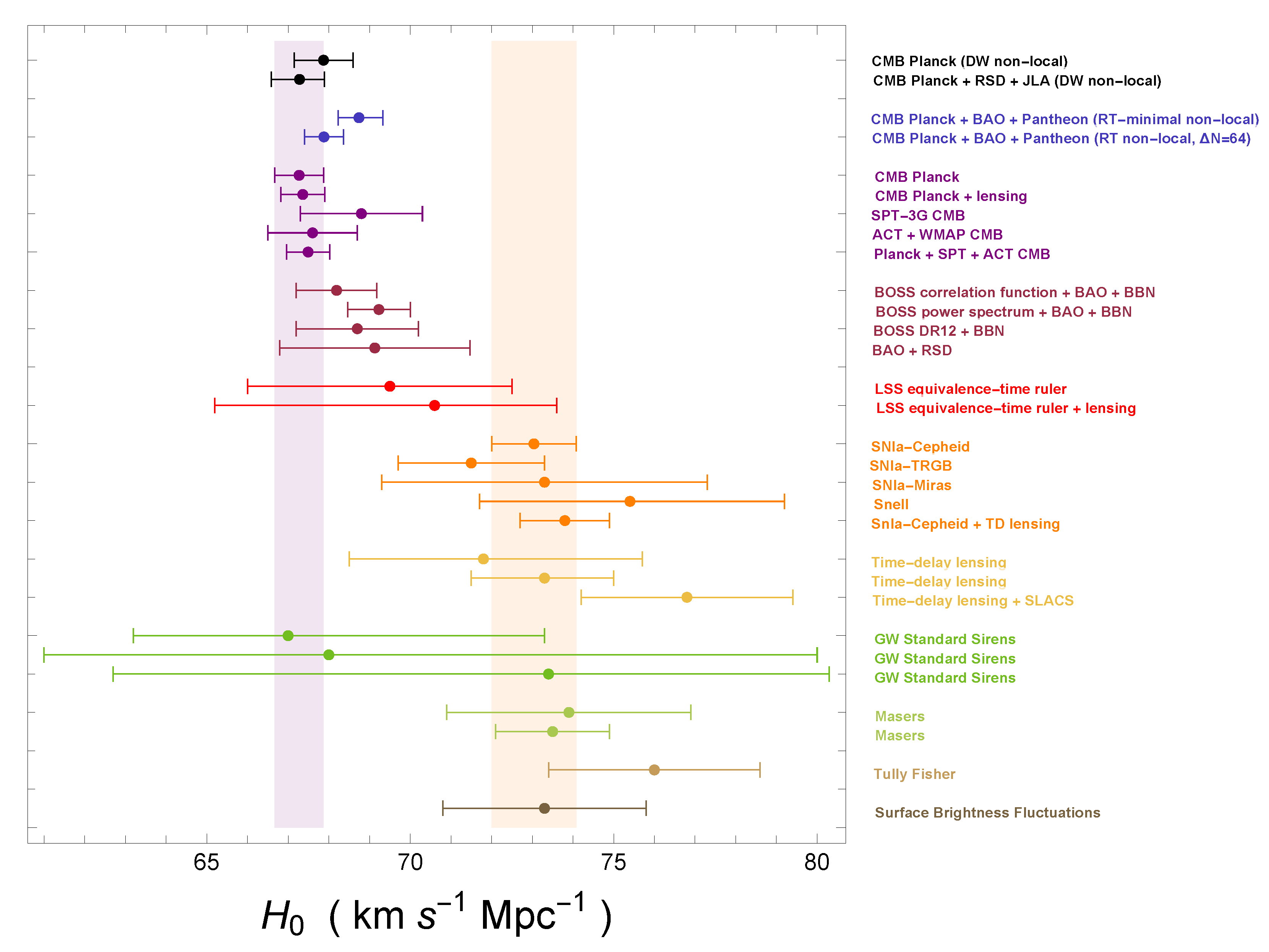
5. Hubble Tension in Light of the Non-Local Models
5.1. The Deser–Woodard Expansion History
5.2. The Ricci-Transverse Expansion History
6. Astrophysical Tests of Non-Local Gravity
6.1. Testing the Deser–Woodard Model by Galaxy Clusters, Elliptical Galaxies and the S2 Star
6.2. Testing the Ricci-Transverse Model by Solar System Observations and Gravitational Waves Detection
7. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BBN | Big Bang Nucleosynethesis |
| BAO | Baryon Acoustic Oscillations |
| CDM | Lambda Cold Dark Matter |
| GR | General Relativity |
| DE | Dark Energy |
| DM | Dark Matter |
| CMB | Cosmic Microwave Background |
| WL | Weak Lensing |
| CC | Cluster Counts |
| RSD | Redshift Space Distortion |
| DW | Deser–Woodard |
| RT | Ricci-Transverse |
| QFT | Quantum Field Theory |
| IDG | Infinite Derivative Theory of Gravity |
| IKG | Integral Kernel Theory of Gravity |
| UV | UltraViolet |
| IR | InfraRed |
| SNIa | Type Ia Supernovae |
| FLRW | Friedmann–Lemaitre–Robertson–Walker |
| MCMC | Markov Chain Monte Carlo |
| LLR | Lunar Laser Ranging |
| GW | Gravitational Waves |
| 1 |
References
- Hogg, D.W.; Eisenstein, D.J.; Blanton, M.R.; Bahcall, N.A.; Brinkmann, J.; Gunn, J.E.; Schneider, D.P. Cosmic homogeneity demonstrated with luminous red galaxies. Astrophys. J. 2005, 624, 54. [Google Scholar] [CrossRef]
- Labini, F.S.; Vasilyev, N.L.; Pietronero, L.; Baryshev, Y.V. Absence of self-averaging and of homogeneity in the large-scale galaxy distribution. Europhys. Lett. 2009, 86, 49001. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Abbott, T.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Jiménez, J.B.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Phys. Dark Universe 2016, 12, 56–99. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined II: The hubble constant tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Batista, R.A.; Amin, M.A.; Barenboim, G.; Bartolo, N.; Baumann, D.; Bauswein, A.; Bellini, E.; Benisty, D.; Bertone, G.; Blasi, P.; et al. EuCAPT White Paper: Opportunities and Challenges for Theoretical Astroparticle Physics in the Next Decade. arXiv 2021, arXiv:2110.10074. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stölzner, B.; Tröster, T.; van den Busch, J.L.; et al. KiDS-1000 cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Lesci, G.F.; Marulli, F.; Moscardini, L.; Sereno, M.; Veropalumbo, A.; Maturi, M.; Giocoli, C.; Radovich, M.; Bellagamba, F.; Roncarelli, M.; et al. AMICO galaxy clusters in KiDS-DR3: Cosmological constraints from counts and stacked weak lensing. Astron. Astrophys. 2022, 659, A88. [Google Scholar] [CrossRef]
- Chen, S.F.; Vlah, Z.; White, M. A new analysis of galaxy 2-point functions in the BOSS survey, including full-shape information and post-reconstruction BAO. J. Cosmol. Astropart. Phys. 2022, 2022, 8. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature Quintessence. Int. J. Mod. Phys. D 2002, 11, 483–491. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From a matter dominated epoch to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Fay, S.; Nesseris, S.; Perivolaropoulos, L. Can f(R) Modified Gravity Theories Mimic a ΛCDM Cosmology? Phys. Rev. D 2007, 76, 063504. [Google Scholar] [CrossRef]
- Lazkoz, R.; Ortiz-Baños, M.; Salzano, V. f(R) gravity modifications: From the action to the data. Eur. Phys. J. C 2018, 78, 213. [Google Scholar] [CrossRef] [PubMed]
- Bajardi, F.; D’Agostino, R.; Benetti, M.; De Falco, V.; Capozziello, S. Early and late time cosmology: The f(R) gravity perspective. Eur. Phys. J. Plus 2022, 137, 1239. [Google Scholar] [CrossRef]
- D’Agostino, R.; Nunes, R.C. Measurements of H0 in modified gravity theories: The role of lensed quasars in the late-time Universe. Phys. Rev. D 2020, 101, 103505. [Google Scholar] [CrossRef]
- Nesseris, S.; Basilakos, S.; Saridakis, E.N.; Perivolaropoulos, L. Viable f(T) models are practically indistinguishable from ΛCDM. Phys. Rev. D 2013, 88, 103010. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Golovnev, A.; Koivisto, T. Cosmological perturbations in modified teleparallel gravity models. J. Cosmol. Astropart. Phys. 2018, 11, 12. [Google Scholar] [CrossRef]
- Wang, D.; Mota, D. Can f(T) gravity resolve the H0 tension? Phys. Rev. D 2020, 102, 063530. [Google Scholar] [CrossRef]
- Bahamonde, S.; Dialektopoulos, K.F.; Escamilla-Rivera, C.; Farrugia, G.; Gakis, V.; Hendry, M.; Hohmann, M.; Said, J.L.; Mifsud, J.; Di Valentino, E. Teleparallel Gravity: From Theory to Cosmology. Rep. Prog. Phys. 2022. [Google Scholar] [CrossRef] [PubMed]
- Nojiri, S.; Odintsov, S.D. Modified Gauss-Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D.; Mota, D.F. The Cosmology of Modified Gauss-Bonnet Gravity. Phys. Rev. D 2007, 76, 044027. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Saez-Gomez, D.; Tureanu, A. On the ΛCDM Universe in f(G) gravity. Gen. Relativ. Gravit. 2011, 43, 1671–1684. [Google Scholar] [CrossRef]
- Bajardi, F.; Capozziello, S. f(G) Noether cosmology. Eur. Phys. J. C 2020, 80, 704. [Google Scholar] [CrossRef]
- Capozziello, S.; Nesseris, S.; Perivolaropoulos, L. Reconstruction of the Scalar-Tensor Lagrangian from a ΛCDM Background and Noether Symmetry. J. Cosmol. Astropart. Phys. 2007, 12, 009. [Google Scholar] [CrossRef]
- Heisenberg, L. A systematic approach to generalisations of General Relativity and their cosmological implications. Phys. Rept. 2019, 796, 1–113. [Google Scholar] [CrossRef]
- Langlois, D. Dark energy and modified gravity in degenerate higher-order scalar–tensor (DHOST) theories: A review. Int. J. Mod. Phys. D 2019, 28, 1942006. [Google Scholar] [CrossRef]
- D’Agostino, R.; Luongo, O. Growth of matter perturbations in nonminimal teleparallel dark energy. Phys. Rev. D 2018, 98, 124013. [Google Scholar] [CrossRef]
- Bajardi, F.; Capozziello, S. Equivalence of nonminimally coupled cosmologies by Noether symmetries. Int. J. Mod. Phys. D 2020, 29, 2030015. [Google Scholar] [CrossRef]
- Amendola, L.; Campos, G.C.; Rosenfeld, R. Consequences of dark matter-dark energy interaction on cosmological parameters derived from type Ia supernova data. Phys. Rev. D 2007, 75, 083506. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark matter and dark energy interactions: Theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Di Valentino, E.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H0 tension? Phys. Rev. D 2017, 96, 043503. [Google Scholar] [CrossRef]
- Asghari, M.; Jiménez, J.B.; Khosravi, S.; Mota, D.F. On structure formation from a small-scales-interacting dark sector. J. Cosmol. Astropart. Phys. 2019, 2019, 042. [Google Scholar] [CrossRef]
- Yang, W.; Vagnozzi, S.; Di Valentino, E.; Nunes, R.C.; Pan, S.; Mota, D.F. Listening to the sound of dark sector interactions with gravitational wave standard sirens. J. Cosmol. Astropart. Phys. 2019, 2019, 037. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Capozziello, S.; Bajardi, F. Nonlocal gravity cosmology: An overview. Int. J. Mod. Phys. D 2021, 31, 2230009. [Google Scholar] [CrossRef]
- Deser, S.; Woodard, R.P. Nonlocal Cosmology. Phys. Rev. Lett. 2007, 99, 111301. [Google Scholar] [CrossRef]
- Maggiore, M. Phantom dark energy from nonlocal infrared modifications of general relativity. Phys. Rev. D 2014, 89, 043008. [Google Scholar] [CrossRef]
- Buoninfante, L. Nonlocal Field Theories: Theoretical and Phenomenological Aspects. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Biswas, T.; Gerwick, E.; Koivisto, T.; Mazumdar, A. Towards Singularity- and Ghost-Free Theories of Gravity. Phys. Rev. Lett. 2012, 108, 031101. [Google Scholar] [CrossRef] [PubMed]
- Briscese, F.; Marcianò, A.; Modesto, L.; Saridakis, E.N. Inflation in (super-)renormalizable gravity. Phys. Rev. D 2013, 87, 083507. [Google Scholar] [CrossRef]
- Biswas, T.; Mazumdar, A.; Siegel, W. Bouncing universes in string-inspired gravity. J. Cosmol. Astropart. Phys. 2006, 2006, 009. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Finke, A.; Foffa, S.; Maggiore, M. Gravity in the infrared and effective nonlocal models. J. Cosmol. Astropart. Phys. 2020, 2020, 010. [Google Scholar] [CrossRef]
- Borka, D.; Borka Jovanović, V.; Capozziello, S.; Jovanović, P. Velocity distribution of elliptical galaxies in the framework of Non-local Gravity model. Adv. Space Res. 2022, in press. [CrossRef]
- Strominger, A. Lectures on the Infrared Structure of Gravity and Gauge Theory; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. A class of nonlocal truncations in quantum Einstein gravity and its renormalization group behavior. Phys. Rev. D 2002, 66, 125001. [Google Scholar] [CrossRef]
- Wetterich, C. Infrared limit of quantum gravity. Phys. Rev. D 2018, 98, 026028. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Gusev, Y.V.; Mukhanov, V.F.; Nesterov, D.V. Nonperturbative late time asymptotics for heat kernel in gravity theory. Phys. Rev. D 2003, 68, 105003. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Aspects of nonlocality in quantum field theory, quantum gravity and cosmology. Mod. Phys. Lett. A 2015, 30, 1540003. [Google Scholar] [CrossRef]
- Maggiore, M. Nonlocal Infrared Modifications of Gravity. A Review. In Gravity and the Quantum; Springer: Cham, Switzerland, 2017; pp. 221–281. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified non-local-F(R) gravity as the key for the inflation and dark energy. Phys. Lett. B 2008, 659, 821–826. [Google Scholar] [CrossRef]
- Kehagias, A.; Maggiore, M. Spherically symmetric static solutions in a nonlocal infrared modification of General Relativity. J. High Energy Phys. 2014, 2014, 29. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 47. [Google Scholar] [CrossRef]
- Tröster, T.; Asgari, M.; Blake, C.; Cataneo, M.; Heymans, C.; Hildebrandt, H.; Joachimi, B.; Lin, C.A.; Sá nchez, A.G.; Wright, A.H.; et al. KiDS-1000 Cosmology: Constraints beyond flat ΛCDM. Astron. Astrophys. 2021, 649, A88. [Google Scholar] [CrossRef]
- Pandey, S.; Krause, E.; DeRose, J.; MacCrann, N.; Jain, B.; Crocce, M.; Blazek, J.; Choi, A.; Huang, H.; To, C.; et al. Dark Energy Survey year 3 results: Constraints on cosmological parameters and galaxy-bias models from galaxy clustering and galaxy-galaxy lensing using the redMaGiC sample. Phys. Rev. D 2022, 106, 043520. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Deffayet, C.; Woodard, R. Reconstructing the distortion function for nonlocal cosmology. J. Cosmol. Astropart. Phys. 2009, 2009, 23. [Google Scholar] [CrossRef]
- Foffa, S.; Maggiore, M.; Mitsou, E. Cosmological dynamics and dark energy from nonlocal infrared modifications of gravity. Int. J. Mod. Phys. A 2014, 29, 1450116. [Google Scholar] [CrossRef]
- Calabrese, E.; Slosar, A.; Melchiorri, A.; Smoot, G.F.; Zahn, O. Cosmic microwave weak lensing data as a test for the dark universe. Phys. Rev. D 2008, 77, 123531. [Google Scholar] [CrossRef]
- Hildebrandt, H.; Viola, M.; Heymans, C.; Joudaki, S.; Kuijken, K.; Blake, C.; Erben, T.; Joachimi, B.; Klaes, D.; Miller, L.; et al. KiDS-450: Cosmological parameter constraints from tomographic weak gravitational lensing. Mon. Not. R. Astron. Soc. 2016, 465, 1454–1498. [Google Scholar] [CrossRef]
- Hildebrandt, H.; Köhlinger, F.; van den Busch, J.L.; Joachimi, B.; Heymans, C.; Kannawadi, A.; Wright, A.H.; Asgari, M.; Blake, C.; Hoekstra, H.; et al. KiDS+VIKING-450: Cosmic shear tomography with optical and infrared data. Astron. Astrophys. 2020, 633, A69. [Google Scholar] [CrossRef]
- Köhlinger, F.; Viola, M.; Joachimi, B.; Hoekstra, H.; van Uitert, E.; Hildebrandt, H.; Choi, A.; Erben, T.; Heymans, C.; Joudaki, S.; et al. KiDS-450: The tomographic weak lensing power spectrum and constraints on cosmological parameters. Mon. Not. R. Astron. Soc. 2017, 471, 4412–4435. [Google Scholar] [CrossRef]
- Wright, A.H.; Hildebrandt, H.; van den Busch, J.L.; Heymans, C.; Joachimi, B.; Kannawadi, A.; Kuijken, K. KiDS+VIKING-450: Improved cosmological parameter constraints from redshift calibration with self-organising maps. Astron. Astrophys. 2020, 640, L14. [Google Scholar] [CrossRef]
- Troxel, M.; MacCrann, N.; Zuntz, J.; Eifler, T.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; et al. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Joudaki, S.; Hildebrandt, H.; Traykova, D.; Chisari, N.E.; Heymans, C.; Kannawadi, A.; Kuijken, K.; Wright, A.H.; Asgari, M.; Erben, T.; et al. KiDS+VIKING-450 and DES-Y1 combined: Cosmology with cosmic shear. Astron. Astrophys. 2020, 638, L1. [Google Scholar] [CrossRef]
- Asgari, M.; Tröster, T.; Heymans, C.; Hildebrandt, H.; van den Busch, J.L.; Wright, A.H.; Choi, A.; Erben, T.; Joachimi, B.; Joudaki, S.; et al. KiDS+VIKING-450 and DES-Y1 combined: Mitigating baryon feedback uncertainty with COSEBIs. Astron. Astrophys. 2020, 634, A127. [Google Scholar] [CrossRef]
- Loureiro, A.; Whittaker, L.; Mancini, A.S.; Joachimi, B.; Cuceu, A.; Asgari, M.; Stölzner, B.; Tröster, T.; Wright, A.H.; Bilicki, M.; et al. KiDS and Euclid: Cosmological implications of a pseudo angular power spectrum analysis of KiDS-1000 cosmic shear tomography. Astron. Astrophys. 2022, 665. [Google Scholar] [CrossRef]
- Chang, C.; Omori, Y.; Baxter, E.J.; Doux, C.; Choi, A.; Pandey, S.; Alarcon, A.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; et al. Joint analysis of DES Year 3 data and CMB lensing from SPT and Planck II: Cross-correlation measurements and cosmological constraints. arXiv 2022, arXiv:2203.12440. [Google Scholar] [CrossRef]
- Amon, A.; Gruen, D.; Troxel, M.; MacCrann, N.; Dodelson, S.; Choi, A.; Doux, C.; Secco, L.; Samuroff, S.; Krause, E.; et al. Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to data calibration. Phys. Rev. D 2022, 105, 023514. [Google Scholar] [CrossRef]
- Secco, L.; Samuroff, S.; Krause, E.; Jain, B.; Blazek, J.; Raveri, M.; Campos, A.; Amon, A.; Chen, A.; Doux, C.; et al. Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to modeling uncertainty. Phys. Rev. D 2022, 105, 023515. [Google Scholar] [CrossRef]
- Heymans, C.; Tröster, T.; Asgari, M.; Blake, C.; Hildebrandt, H.; Joachimi, B.; Kuijken, K.; Lin, C.A.; Sá nchez, A.G.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Multi-probe weak gravitational lensing and spectroscopic galaxy clustering constraints. Astron. Astrophys. 2021, 646, A140. [Google Scholar] [CrossRef]
- Mantz, A.B.; von der Linden, A.; Allen, S.W.; Applegate, D.E.; Kelly, P.L.; Morris, R.G.; Rapetti, D.A.; Schmidt, R.W.; Adhikari, S.; Allen, M.T.; et al. Weighing the giants—IV. Cosmology and neutrino mass. Mon. Not. R. Astron. Soc. 2014, 446, 2205–2225. [Google Scholar] [CrossRef]
- Salvati, L.; Douspis, M.; Aghanim, N. Constraints from thermal Sunyaev-Zel’dovich cluster counts and power spectrum combined with CMB. Astron. Astrophys. 2018, 614, A13. [Google Scholar] [CrossRef]
- Costanzi, M.; Rozo, E.; Simet, M.; Zhang, Y.; Evrard, A.E.; Mantz, A.; Rykoff, E.S.; Jeltema, T.; Gruen, D.; Allen, S.; et al. Methods for cluster cosmology and application to the SDSS in preparation for DES Year 1 release. Mon. Not. R. Astron. Soc. 2019, 488, 4779–4800. [Google Scholar] [CrossRef]
- Bocquet, S.; Dietrich, J.P.; Schrabback, T.; Bleem, L.E.; Klein, M.; Allen, S.W.; Applegate, D.E.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; et al. Cluster Cosmology Constraints from the 2500 deg2 SPT-SZ Survey: Inclusion of Weak Gravitational Lensing Data from Magellan and the Hubble Space Telescope. Astrophys. J. 2019, 878, 55. [Google Scholar] [CrossRef]
- Abbott, T.; Aguena, M.; Alarcon, A.; Allam, S.; Allen, S.; Annis, J.; Avila, S.; Bacon, D.; Bechtol, K.; Bermeo, A.; et al. Dark Energy Survey Year 1 Results: Cosmological constraints from cluster abundances and weak lensing. Phys. Rev. D 2020, 102, 023509. [Google Scholar] [CrossRef]
- Abdullah, M.H.; Klypin, A.; Wilson, G. Cosmological Constraints on ΩM and σ8 from Cluster Abundances Using the GalWCat19 Optical-spectroscopic SDSS Catalog. Astrophys. J. 2020, 901, 90. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. D 2018, 97, 103503. [Google Scholar] [CrossRef]
- Benisty, D. Quantifying the S8 tension with the Redshift Space Distortion data set. Phys. Dark Universe 2021, 31, 100766. [Google Scholar] [CrossRef]
- Nunes, R.C.; Vagnozzi, S. Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions. Mon. Not. R. Astron. Soc. 2021, 505, 5427–5437. [Google Scholar] [CrossRef]
- Philcox, O.H.; Ivanov, M.M. BOSS DR12 full-shape cosmology: ΛCDM constraints from the large-scale galaxy power spectrum and bispectrum monopole. Phys. Rev. D 2022, 105, 043517. [Google Scholar] [CrossRef]
- Nersisyan, H.; Cid, A.F.; Amendola, L. Structure formation in the Deser-Woodard nonlocal gravity model: A reappraisal. J. Cosmol. Astropart. Phys. 2017, 2017, 46. [Google Scholar] [CrossRef]
- Park, S. Revival of the Deser-Woodard nonlocal gravity model: Comparison of the original nonlocal form and a localized formulation. Phys. Rev. D 2018, 97, 044006. [Google Scholar] [CrossRef]
- Amendola, L.; Dirian, Y.; Nersisyan, H.; Park, S. Observational constraints in nonlocal gravity: The Deser-Woodard case. J. Cosmol. Astropart. Phys. 2019, 2019, 45. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Heymans, C.; Choi, A.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Johnson, A.; Mead, A.; Parkinson, D.; et al. CFHTLenS revisited: Assessing concordance with Planck including astrophysical systematics. Mon. Not. R. Astron. Soc. 2016, 465, 2033–2052. [Google Scholar] [CrossRef]
- Ivanov, M.M. Cosmological constraints from the power spectrum of eBOSS emission line galaxies. Phys. Rev. D 2021, 104, 103514. [Google Scholar] [CrossRef]
- Ivanov, M.M.; Simonović, M.; Zaldarriaga, M. Cosmological parameters from the BOSS galaxy power spectrum. J. Cosmol. Astropart. Phys. 2020, 2020, 42. [Google Scholar] [CrossRef]
- White, M.; Zhou, R.; DeRose, J.; Ferraro, S.; Chen, S.F.; Kokron, N.; Bailey, S.; Brooks, D.; Garcí a-Bellido, J.; Guy, J.; et al. Cosmological constraints from the tomographic cross-correlation of DESI Luminous Red Galaxies and Planck CMB lensing. J. Cosmol. Astropart. Phys. 2022, 2022, 7. [Google Scholar] [CrossRef]
- Jeffreys, H. The Theory of Probability; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Nesseris, S.; Tsujikawa, S. Cosmological perturbations and observational constraints on nonlocal massive gravity. Phys. Rev. D 2014, 90, 024070. [Google Scholar] [CrossRef]
- Dutcher, D.; Balkenhol, L.; Ade, P.; Ahmed, Z.; Anderes, E.; Anderson, A.; Archipley, M.; Avva, J.; Aylor, K.; Barry, P.; et al. Measurements of the E-mode polarization and temperature-E-mode correlation of the CMB from SPT-3G 2018 data. Phys. Rev. D 2021, 104, 022003. [Google Scholar] [CrossRef]
- Wang, K.; Huang, Q.G. Implications for cosmology from ground-based Cosmic Microwave Background observations. J. Cosmol. Astropart. Phys. 2020, 2020, 045. [Google Scholar] [CrossRef]
- Balkenhol, L.; Dutcher, D.; Ade, P.; Ahmed, Z.; Anderes, E.; Anderson, A.; Archipley, M.; Avva, J.; Aylor, K.; Barry, P.; et al. Constraints on ΛCDM extensions from the SPT-3G 2018 EE and TE power spectra. Phys. Rev. D 2021, 104, 083509. [Google Scholar] [CrossRef]
- Addison, G.E. High H0 values from CMB E-mode Data: A Clue for Resolving the Hubble Tension? Astrophys. J. Lett. 2021, 912, L1. [Google Scholar] [CrossRef]
- D’Amico, G.; Gleyzes, J.; Kokron, N.; Markovic, K.; Senatore, L.; Zhang, P.; Beutler, F.; Gil-Marín, H. The cosmological analysis of the SDSS/BOSS data from the Effective Field Theory of Large-Scale Structure. J. Cosmol. Astropart. Phys. 2020, 2020, 5. [Google Scholar] [CrossRef]
- Colas, T.; d’Amico, G.; Senatore, L.; Zhang, P.; Beutler, F. Efficient cosmological analysis of the SDSS/BOSS data from the Effective Field Theory of Large-Scale Structure. J. Cosmol. Astropart. Phys. 2020, 2020, 1. [Google Scholar] [CrossRef]
- Cooke, R.J.; Pettini, M.; Steidel, C.C. One Percent Determination of the Primordial Deuterium Abundance. Astrophys. J. 2018, 855, 102. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Abbott, T.; Abdalla, F.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Krause, E.; Eifler, T.F.; Zuntz, J.; Friedrich, O.; Troxel, M.A.; Dodelson, S.; Blazek, J.; Secco, L.F.; MacCrann, N.; Baxter, E.; et al. Dark Energy Survey Year 1 Results: Multi-Probe Methodology and Simulated Likelihood Analyses. arXiv 2017, arXiv:1706.09359. [Google Scholar] [CrossRef]
- Riess, A.G. The expansion of the Universe is faster than expected. Nat. Rev. Phys. 2019, 2, 10–12. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% solution: Determination of the Hubble constant with the Hubble Space Telescope and the Wide Field Camera 3. Astrophys. J. 2011, 730, 119. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; et al. Gaia Early Data Release 3—Summary of the contents and survey properties. Astron. Astrophys. 2021, 649. [Google Scholar] [CrossRef]
- Lindegren, L.; Bastian, U.; Biermann, M.; Bombrun, A.; de Torres, A.; Gerlach, E.; Geyer, R.; Hernández, J.; Hilger, T.; Hobbs, D.; et al. Gaia Early Data Release 3 - Parallax bias versus magnitude, colour, and position. Astronomy & Astrophysics 2021, 649, A1. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW - XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2019, 498, 1420–1439. [Google Scholar] [CrossRef]
- Shajib, A.J.; Birrer, S.; Treu, T.; Agnello, A.; Buckley-Geer, E.J.; Chan, J.H.H.; Christensen, L.; Lemon, C.; Lin, H.; Millon, M.; et al. STRIDES: A 3.9 per cent measurement of the Hubble constant from the strong lens system DES J0408-5354. Mon. Not. R. Astron. Soc. 2020, 494, 6072–6102. [Google Scholar] [CrossRef]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D.M. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Re-determination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the SN Ia Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. Astrophys. J. 2020, 889, 5. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. Astrophys. J. 2019, 886, L27. [Google Scholar] [CrossRef]
- Zhang, P.; D’Amico, G.; Senatore, L.; Zhao, C.; Cai, Y. BOSS Correlation Function analysis from the Effective Field Theory of Large-Scale Structure. J. Cosmol. Astropart. Phys. 2022, 2022, 036. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, L.; Zhao, G.B. A Measurement of the Hubble Constant Using Galaxy Redshift Surveys. Astrophys. J. 2017, 849, 84. [Google Scholar] [CrossRef]
- Farren, G.S.; Philcox, O.H.; Sherwin, B.D. Determining the Hubble constant without the sound horizon: Perspectives with future galaxy surveys. Phys. Rev. D 2022, 105, 063503. [Google Scholar] [CrossRef]
- Philcox, O.H.; Sherwin, B.D.; Farren, G.S.; Baxter, E.J. Determining the Hubble constant without the sound horizon: Measurements from galaxy surveys. Phys. Rev. D 2021, 103, 023538. [Google Scholar] [CrossRef]
- Anand, G.S.; Tully, R.B.; Rizzi, L.; Riess, A.G.; Yuan, W. Comparing Tip of the Red Giant Branch Distance Scales: An Independent Reduction of the Carnegie-Chicago Hubble Program and the Value of the Hubble Constant. Astrophys. J. 2022, 932, 15. [Google Scholar] [CrossRef]
- de Jaeger, T.; Galbany, L.; Riess, A.G.; Stahl, B.E.; Shappee, B.J.; Filippenko, A.V.; Zheng, W. A 5% measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2022, 514, 4620–4628. [Google Scholar] [CrossRef]
- Denzel, P.; Coles, J.P.; Saha, P.; Williams, L.L.R. The Hubble constant from eight time-delay galaxy lenses. Mon. Not. R. Astron. Soc. 2020, 501, 784–801. [Google Scholar] [CrossRef]
- Chen, G.C.F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; Chan, J.H.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. R. Astron. Soc. 2019, 490, 1743–1773. [Google Scholar] [CrossRef]
- Mukherjee, S.; Krolewski, A.; Wandelt, B.D.; Silk, J. Cross-correlating dark sirens and galaxies: Measurement of H0 from GWTC-3 of LIGO-Virgo-KAGRA. arXiv 2022, arXiv:2203.03643. [Google Scholar] [CrossRef]
- The LIGO Scientific, Collaboration; The Virgo, Collaboration; The KAGRA, Collaboration; Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Adkins, V.K.; et al. Constraints on the cosmic expansion history from GWTC-3. arXiv 2021, arXiv:2111.03604. [Google Scholar] [CrossRef]
- Gayathri, V.; Healy, J.; Lange, J.; O’Brien, B.; Szczepanczyk, M.; Bartos, I.; Campanelli, M.; Klimenko, S.; Lousto, C.; O’Shaughnessy, R. Hubble Constant Measurement with GW190521 as an Eccentric Black Hole Merger. arXiv 2020, arXiv:2009.14247. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophys. J. 2020, 891, L1. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B.; Anand, G.S.; Courtois, H.M.; Dupuy, A.; Neill, J.D.; Rizzi, L.; Seibert, M. Cosmicflows-4: The Calibration of Optical and Infrared Tully—Fisher Relations. Astrophys. J. 2020, 896, 3. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. Astrophys. J. 2021, 911, 65. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Borka, D.; Capozziello, S.; Borka Jovanović, V.; Jovanović, P. Constraining nonlocal gravity by S2 star orbits. Phys. Rev. D 2019, 99, 044053. [Google Scholar] [CrossRef]
- Bouchè, F.; Capozziello, S.; Salzano, V.; Umetsu, K. Testing non-local gravity by clusters of galaxies. Eur. Phys. J. C 2022, 82, 652. [Google Scholar] [CrossRef]
- Capozziello, S.; De Ritis, R.; Rubano, C.; Scudellaro, P. Noether symmetries in cosmology. La Rivista del Nuovo Cimento 1996, 19N4, 1–114. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. The phase-space view of non-local gravity cosmology. Phys. Lett. B 2022, 834, 137475. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G. PeV IceCube signals and H0 tension in the framework of Non-Local Gravity. arXiv 2022, arXiv:2206.03690. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Capozziello, S. Noether symmetries as a geometric criterion to select theories of gravity. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1840007. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the massive black hole in the galactic centre. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Postman, M.; Coe, D.; Benítez, N.; Bradley, L.; Broadhurst, T.; Donahue, M.; Ford, H.; Graur, O.; Graves, G.; Jouvel, S.; et al. The Cluster Lensing And Supernova survey with Hubble: An overview. Astrophys. J. Suppl. Ser. 2012, 199, 25. [Google Scholar] [CrossRef]
- Umetsu, K.; Zitrin, A.; Gruen, D.; Merten, J.; Donahue, M.; Postman, M. CLASH: Joint analysis of strong-lensing, weak-lensing shear, and magnification data for 20 galaxy clusters. Astrophys. J. 2016, 821, 116. [Google Scholar] [CrossRef]
- Burstein, D.; Bender, R.; Faber, S.; Nolthenius, R. Global Relationships Among the Physical Properties of Stellar Systems. Astron. J. 1997, 114. [Google Scholar] [CrossRef]
- Belgacem, E.; Finke, A.; Frassino, A.; Maggiore, M. Testing nonlocal gravity with Lunar Laser Ranging. J. Cosmol. Astropart. Phys. 2019, 2019, 35. [Google Scholar] [CrossRef]
- Vainshtein, A. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Gravitational-wave luminosity distance in modified gravity theories. Phys. Rev. D 2018, 97, 104066. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Modified gravitational-wave propagation and standard sirens. Phys. Rev. D 2018, 98, 023510. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouché, F.; Capozziello, S.; Salzano, V. Addressing Cosmological Tensions by Non-Local Gravity. Universe 2023, 9, 27. https://doi.org/10.3390/universe9010027
Bouché F, Capozziello S, Salzano V. Addressing Cosmological Tensions by Non-Local Gravity. Universe. 2023; 9(1):27. https://doi.org/10.3390/universe9010027
Chicago/Turabian StyleBouché, Filippo, Salvatore Capozziello, and Vincenzo Salzano. 2023. "Addressing Cosmological Tensions by Non-Local Gravity" Universe 9, no. 1: 27. https://doi.org/10.3390/universe9010027
APA StyleBouché, F., Capozziello, S., & Salzano, V. (2023). Addressing Cosmological Tensions by Non-Local Gravity. Universe, 9(1), 27. https://doi.org/10.3390/universe9010027





