Abstract
The dark energy from virtual gravitons is consistent with observational data on supernovas with the same accuracy as the ΛCDM model. The fact that virtual gravitons are capable of producing a de Sitter accelerated expansion of the FLRW universe was established in 2008 (see references). The combination of conformal non-invariance with zero rest mass of gravitons (unique properties of the gravitational field) leads to the appearance of graviton dark energy in a mater-dominated era; this fact explains the relatively recent appearance of the dark energy and answers the question “Why now?”. The transition redshifts (where deceleration is replaced by acceleration) that follow from the graviton theory are consistent with model-independent transition redshifts derived from observational data. Prospects for testing the GCDM model (the graviton model of dark energy where G stands for gravitons) and comparison with the ΛCDM model are discussed.
1. Introduction
As is known, more than 20 years ago, two research groups independently discovered the accelerated expansion of the universe [1,2]. This effect was called dark energy (DE). The nature of DE is still unknown. A big number of approaches were considered, including quite unusual ones [3,4]. The most popular, apparently, is the hypothesis about scalar fields of different kinds, filling the universe. A fairly complete bibliography (comprising reviews) can be found, e.g., in [5,6,7,8,9,10,11]. One of the most popular theories based on the idea of a scalar field is so-called quintessence [8,12,13,14]. The quintessence is dark energy in the form of a time-varying scalar field which is slowly rolling down toward the minimum of its potential. Another direction of the search attempted to generalize Einstein’s theory in the classical and quantum way (see e.g., [11], and indeed an interesting attempt by [15] to construct an emergent gravity in which “the space-time and gravity emergent together from entanglement structure of an underlining microscopic theory”. Another interesting direction of modern research is associated with attempts to construct a cosmology with a variable cosmological constant [16].
For now, despite the large number of DE models, the community has settled on the simplest choice, which is the hypothesis that the cause of acceleration is the cosmological constant, which was introduced by Einstein himself into his theory more than 100 years ago. Later, he gave up on it; however, after in [17] it was shown that the cosmological constant is the energy of a non-gravitational vacuum, it again acquired the “rights of citizenship”. In the last hundred years, the cosmological constant has appeared every time astrophysics and cosmology have been faced with problems that, it seemed, could not be solved otherwise. For example, at the end of 60-th, when quasars were discovered, and at one time it seemed that they were concentrated near z = 2 [18,19,20], this effect was attempted to be explained by the fact that there is a positive cosmological constant ([21,22,23,24,25]). Later, quasars with large redshifts were discovered, and this hypothesis was dropped. As V. Petrosian remarked [26]: “In the absence of strong evidence in favor of Lemaître models, we must again send back the Lemaître models and along with them the cosmological constant until their next reappearance”. (page 28) 1 The next reappearance took place in 1998–1999 in connection with the discovery of dark energy. The next reappearance took place in 1998–1999 in connection with the discovery of dark energy [1,2] 2. The community has now opted for the ΛCDM model despite known problems with it. As is known, two main problems with it are the 122 order of magnitude difference between the theoretical and observational value of the cosmological constant and the coincidence problem (why dark energy has appeared recently, why now?). A very significant argument in favor of ΛCDM is the fact that it describes the observational data very well, despite these theoretical contradictions. On the other hand, all observational data (with no exceptions) based on the attempts to find the equation of state parameter , where and are the pressure and density of matter filling the universe. In the case of cosmological constant , all observational data show that , and this fact is considered by the community as confirmation of the validity of the ΛCDM model; however, the virtual gravitons also produce the de Sitter expansion with (Appendix B). To find the difference between the models, it is necessary to measure w(z) (Section 5).
The dark energy at the epoch of last scattering can contribute to the observed CMB anisotropies. We discuss it in Appendix E.
As we already mentioned, the goal of this paper is to compare the ΛCDM model with the GCDM model where G stands for gravitons. To do so, we are going to calculate distance modules for both models and compare them (Section 3 and Section 4). We will see that the GCDM model is consistent with SNe Ia observations with the same accuracy as the ΛCDM model. At the same time, the GCDM model is free from the contradictions that the ΛCDM model encounters.
2. Dark Energy from Virtual Gravitons
A graviton theory of dark energy was presented in [27]. A rigorous mathematical foundation of the theory was given in [28,29]. The present paper is dedicated to the comparison of graviton theory with supernova observations only, so we do not touch upon any theoretical problems. Nevertheless, we believe that it is necessary to remind the reader of at least basic information of graviton theory. It was shown in [28] that quantum fluctuations of the metric (gravitons) and their back reaction on the isotropic and homogeneous (on average) background provide the mechanism for cosmological acceleration (Appendix A). The dark energy effect is a consequence of the vacuum polarization and graviton creation by the non-stationary gravitational field of the Universe. The energy density of gravitons is a functional of the background geometry. In the non-empty Universe, the background geometry is defined by all contributing cosmological subsystems—by gravitons, matter, and radiation. The combination of conformal non-invariance with zero rest mass of gravitons (unique properties of the gravitational field) leads to a macroscopic quantum effect: condensation of gravitons in a quantum state with the wavelength of the order of the distance to the horizon. The same unique properties of the gravitational field are the causes for the appearance of dark energy in our era (Appendix D), and it answers the old unanswered question “Why now?”.
In the process of the evolution of the Universe, the density of gravitons, because of their condensation, starts dominating over the sum of the energy density of other subsystems of the cosmological media. The self-consistent state of background and gravitons, which evolves asymptotically, represents a self-polarized vacuum in the de Sitter space. The regime of the de Sitter-like expansion is beginning to form in the current Universe. Three new exact solutions for the one-loop quantum gravity were presented in [28]. The de Sitter solution is one of these. All exact solutions can be found when the theory is presented as Bogoliubov–Born–Green–Kirkwood–Yvon (BBGKY) hierarchy equations for moments of the graviton spectral function (Appendix B).
In this paper, we show that dark energy of graviton origin, with the case of a zero cosmological constant, is consistent with SNe Ia observational data with the same accuracy as the ΛCDM model. In terms of observational data, the difference between these models lies beyond the accuracy of observations (Section 4). We show also that the appearance of graviton DE during the modern epoch of the Universe evolution is a direct consequence of the combination of conformal non-invariance with zero rest mass of gravitons, which are unique features of the gravitational field (Appendix C). In Section 5 and Section 6, we discuss observational tests that might distinguish GCDM and ΛCDM models.
3. Distance Modules
To fit supernova data, we use distance modulus as follows
where is distance modules, the Hubble constant . The first term in Formula (3) represents the energy density of non-relativistic matter, and the second one represents the energy density of DE as a function of z. In the case of cosmological constant, . In the case of DE, is the fraction of DE in the total energy balance. Let us denote distance modules for the cosmological constant case as Our program is to compare runs for to show that the difference between them is smaller than observational errors. We do not include CMB input into Formula (3). The input of radiation into the current energy balance is very small, it is of the order of [30]. For example, for the Planck case with the input of radiation to the region z = 1000 is about 8%; it is reasonable to assume that the effect of radiation on the dynamics of expansion can be neglected when its contribution to the dynamics becomes no more than 8%.
The usual practice is to use the parameter of the equation of state and determine it from the observational data (see e.g., [1]). The equation of the state of dark energy is unknown, therefore for lack of a better option, the dark energy equation of state can be taken in the form (sometimes in more general forms such as ). After that, one can look for the w parameter which provides the best fit. Usually, the supernova data are used in combination with other data. All of them show that , and this fact, as it is generally accepted, leads to the idea that the DE effect is due to the cosmological constant. In the case of dynamical DE (and in the case of gravitons, particularly), the second term of Formula (3) must follow from the solution of Einstein’s equations for the model. In the case of cosmological constant, the Friedmannian equations for the flat Universe have a well-known exact analytical solution (see e.g., [31])
This allows us to calculate all values of interest analytically. Unlike the cosmological constant case, there is no exact analytical solution to the system consisting of gravitons and non-relativistic matter; thus, we must go for the numerical integration of Einstein’s equations (in our case they are the equations of the BBGKY chain) for the graviton model.
4. GCDM vs. ΛCDM
In this section, we will show that the difference between and for all cases of interest is less than the observational errors in SNe Ia database. In other words, we will show that both ΛCDM and GCDM are statistically indistinguishable. As it was mentioned by the Planck team [32], there is a “tension” between WMAP and Planck data. In accordance with WMAP, today’s value of DE is [33]; meanwhile, Plank’s data give [32]. Recent data obtained from the analysis of the large-scale structure give for the ΛCDM model [34]. The combination of these data with available baryon acoustic oscillation, redshift space distortion, SNe Ia data and with Planck CMB lensing leads to the following content of the nonrelativistic matter and Hubble constant in the universe for ΛCDM model [34] ; this leads to the following DE contents, which we need for our calculations: . We consider three cases (Bennett et al., 2012), [32] and [34]. In this work, we use Union 2.1 compilation from the Supernova Cosmology project [35,36]. A direct link to the observed supernova data used in calculations is shown in the reference [35].
We calculate distance modules using Formula (3). As we already mentioned, in the distinction of the generally accepted method of calculation of which uses the hypothesis on the equation of state parameter of DE , with the following determination of , we calculate directly by numerical integration of Einstein equations presented in the form of BBGKY chain (Equations (A7) and (A8)). In such an approach, the cosmological constant case corresponds to in Formula (3); thus, we must compare calculated for (cosmological constant) with calculated for , i.e., graviton dark energy.
Our computational model has only one free parameter which is a fraction of the graviton energy in the total energy balance at the start of the calculation run, (Appendix C). Each run started from some value of and finished when Ω(z) becomes equal to Ω0. Attention. In our calculations, the scale factor is increasing from the past to the future, i.e., from a = 1 to , where corresponds to the observed today DE fraction of the full energy, which we denote as . First, we conducted a series of runs to localize the interval of where the statistical deviation between calculated distance modulus and their values from the database for SNe Ia (Formulas (1)–(3) above) is minimal. We found that the interval 0.000125 < < 0.000162 provide the statistical deviation is about 1 sigma. Second, we found the best fitting separately for the three cases Ω0 = (0.721, 0.694, 0.685).
We ran our numerical simulations for the following initial conditions, ; these runs automatically lead to the following initial for all chosen (see Table 1).

Table 1.
Calculated and for different initial .
The SLS is situated at with the width of this region [37]; thus, we get the initial conditions for such runs in the following regions of interest.
The right column in the Table 1 shows what the initial values are for the observational values of dark energy (second column). The first column shows four randomly selected EDEs, each markedly less than 0.009. We present here the results of numerical simulation for the for all three cases . The results for all three other cases are similar.
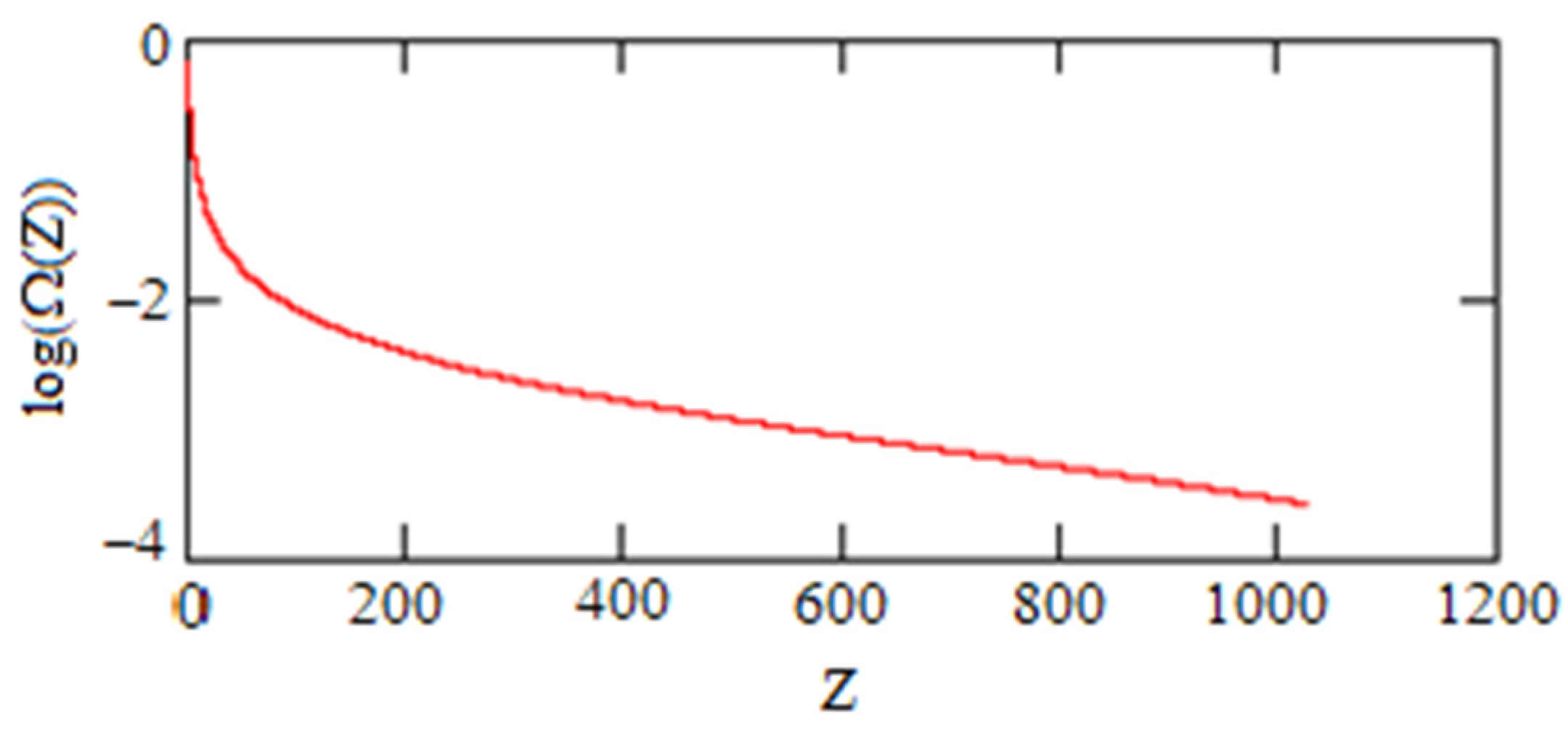
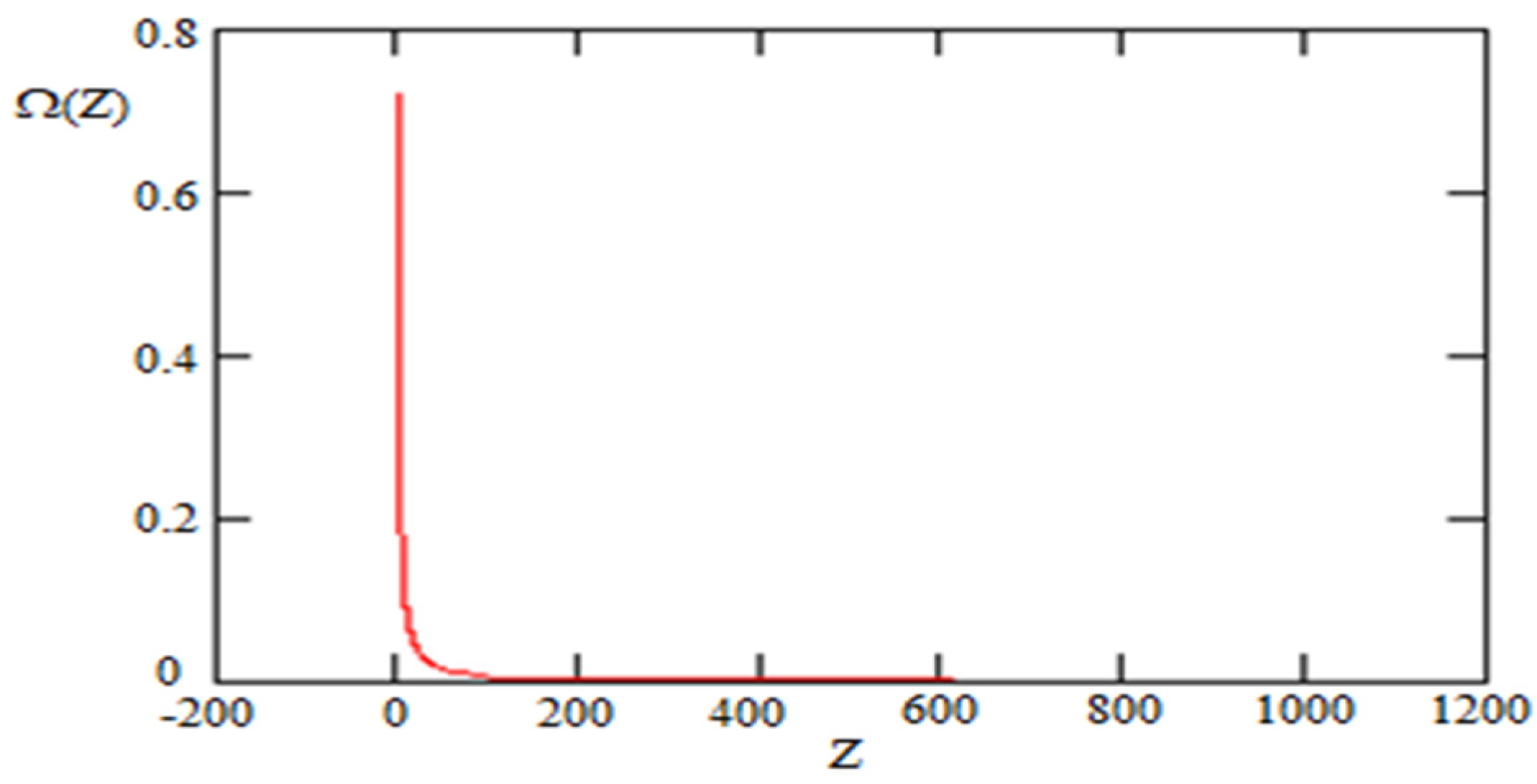
To start with, we choose the initial value of the energy density of DE as at the initial point for . Such a run produces shown on the Figure 1. For all figures below is the fraction of DE in the total energy balance.
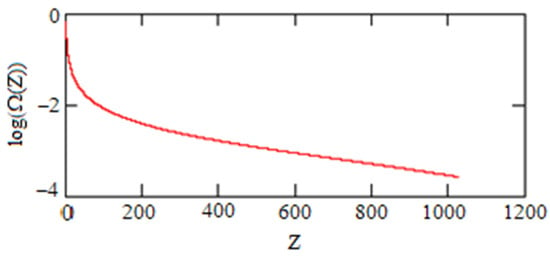
Figure 1.
Graviton DE as a function of z for the case.
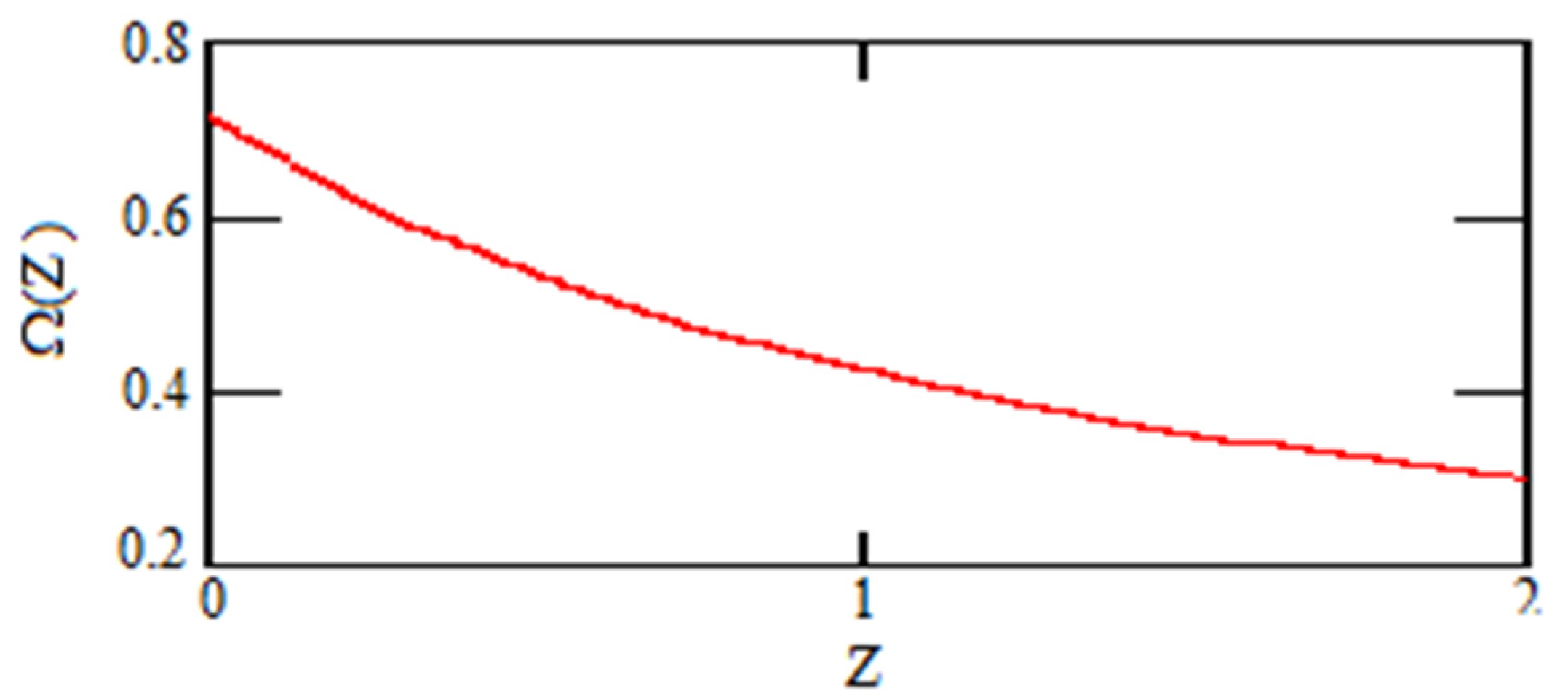
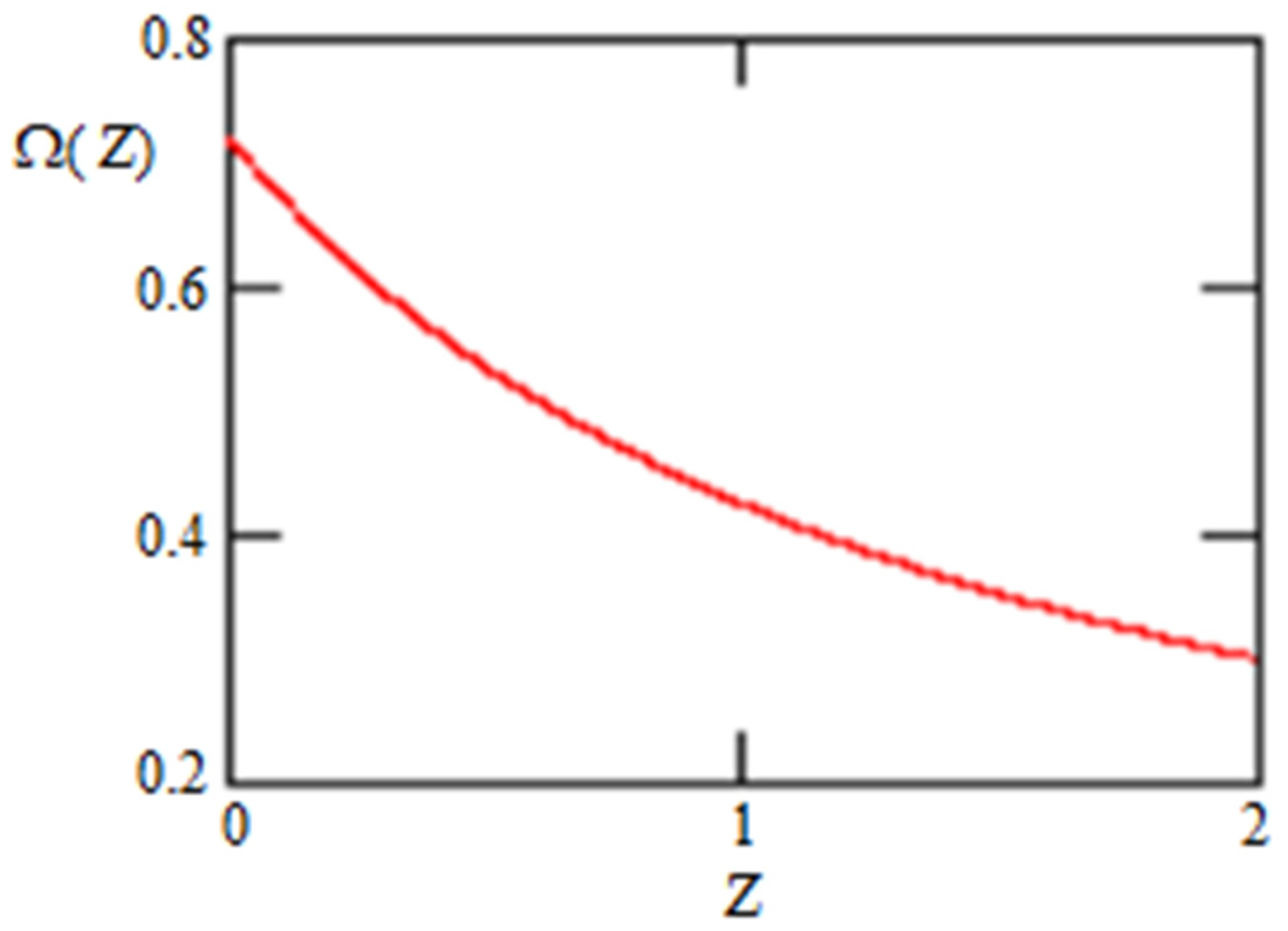
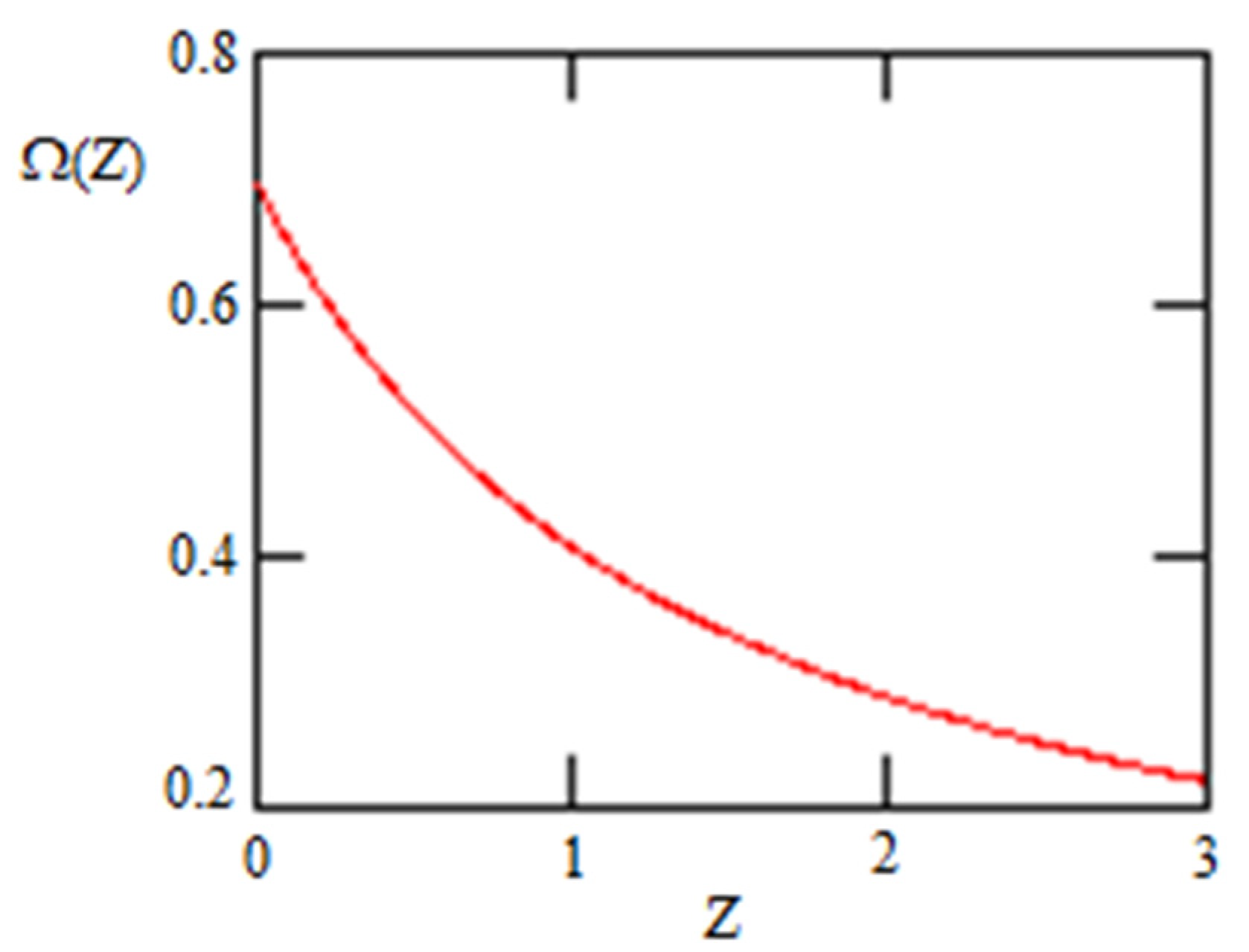
Graviton DE as a function of z is shown in Figure 2 for the region of interest, i.e., from z = 0 to z = 2, where supernovas observed are situated:
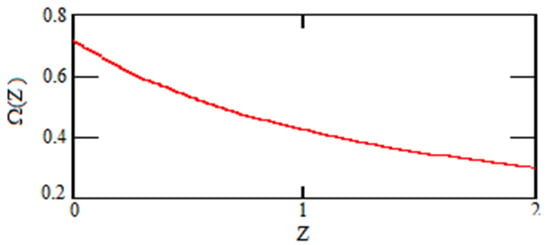
Figure 2.
Graviton DE as a function of z for in the region .
To compare , obtained by numerical integration of BBGKY chain Equations (A7) and (A8) with the observational data, a high accuracy analytical approximation of it in the whole interval was obtained in the form of
where
= 0.685, = 0.62974, = −0.046398, = 0.10038, = 0.109381, = 0.115417, = 0.0058062, = 0.0057869, = −4.135292 × 10−6
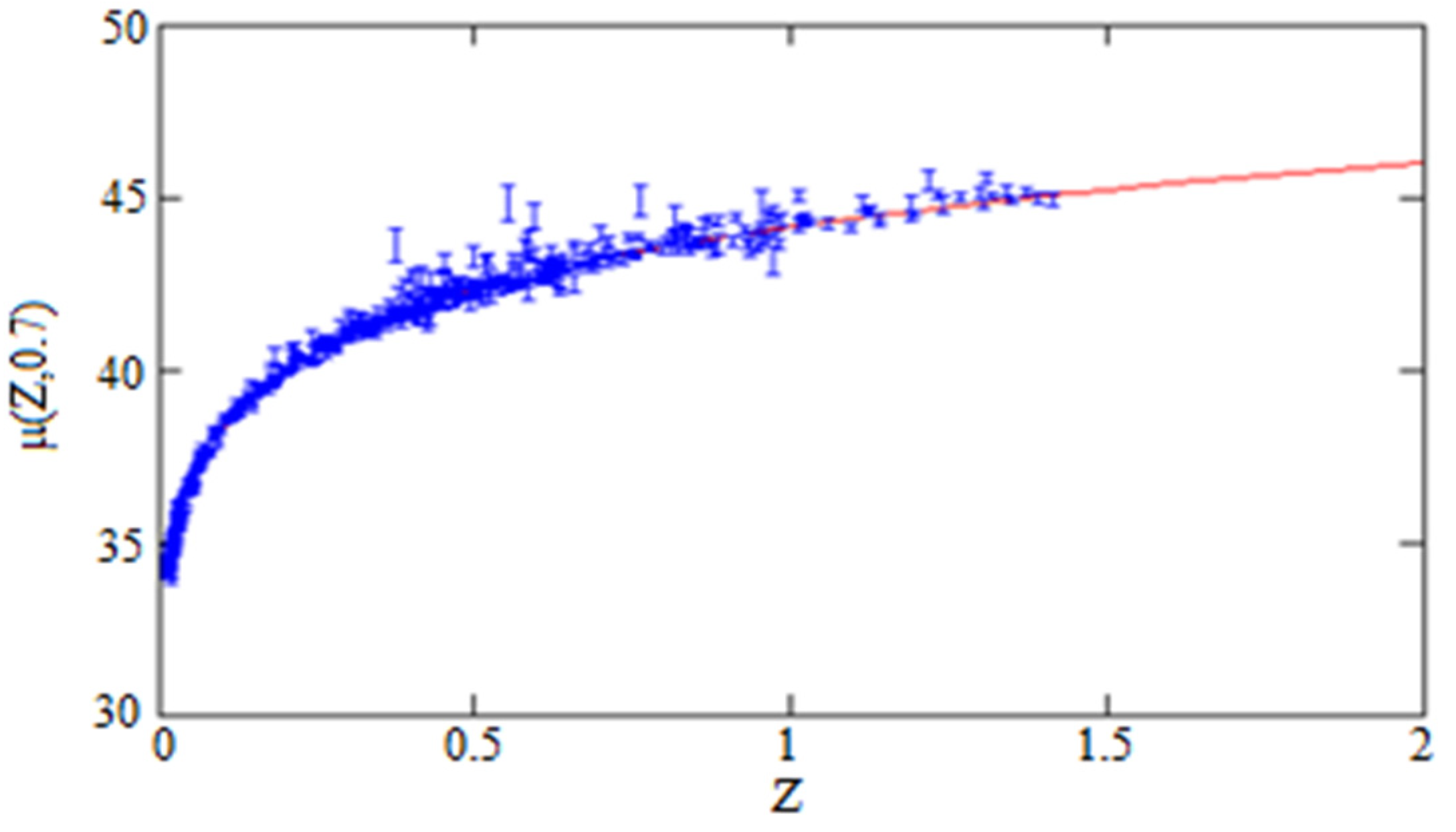
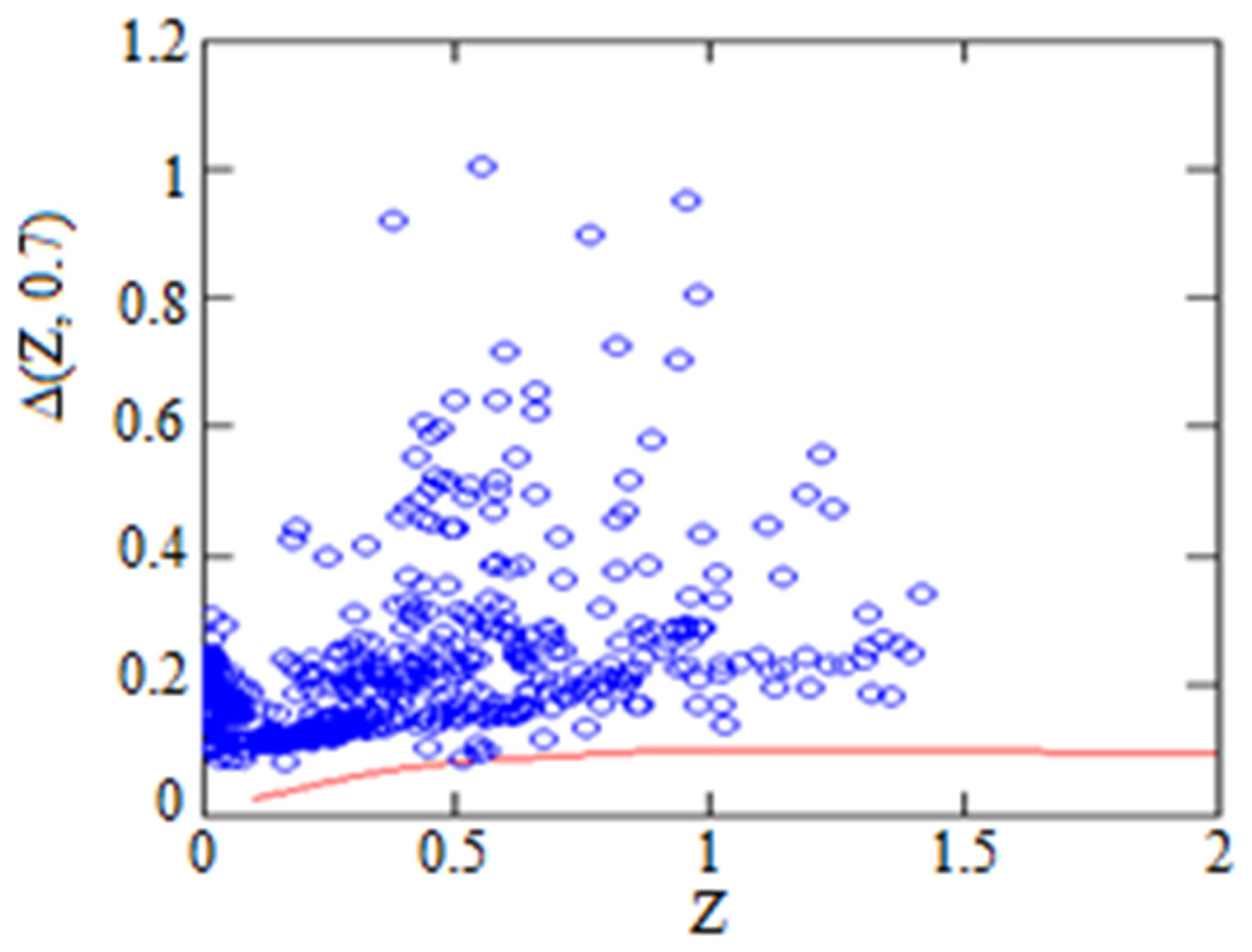
Such generates distance modules which are showed together with the observational errors in Figure 3.
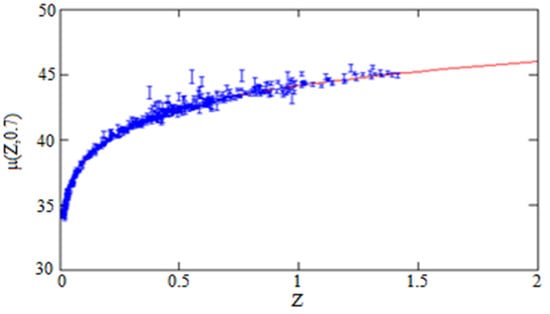
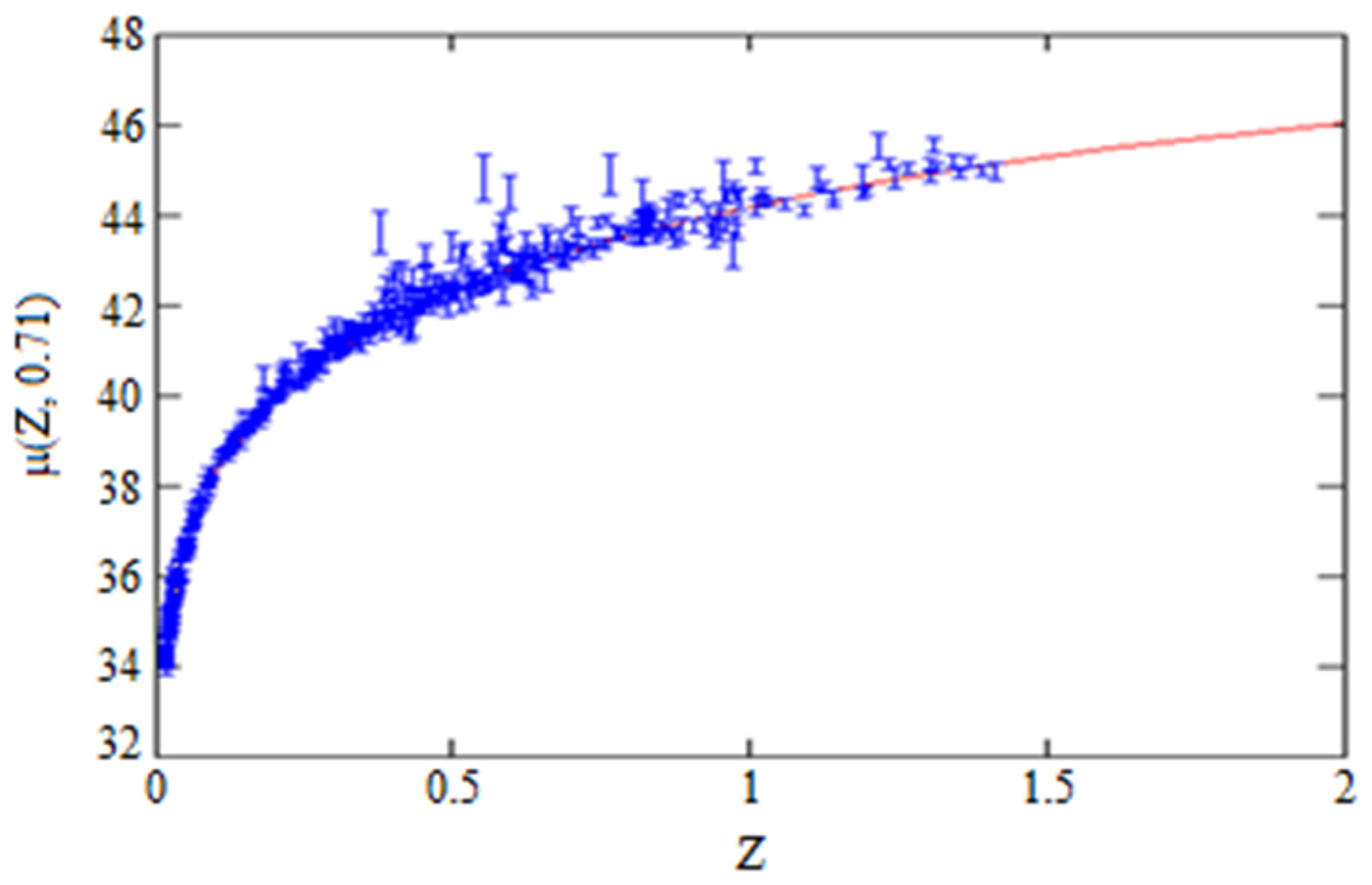
Figure 3.
Solid curve is the distance modules for graviton DE run with h = 0.7 for the case . The blue bars show supernova positions together with observational errors.
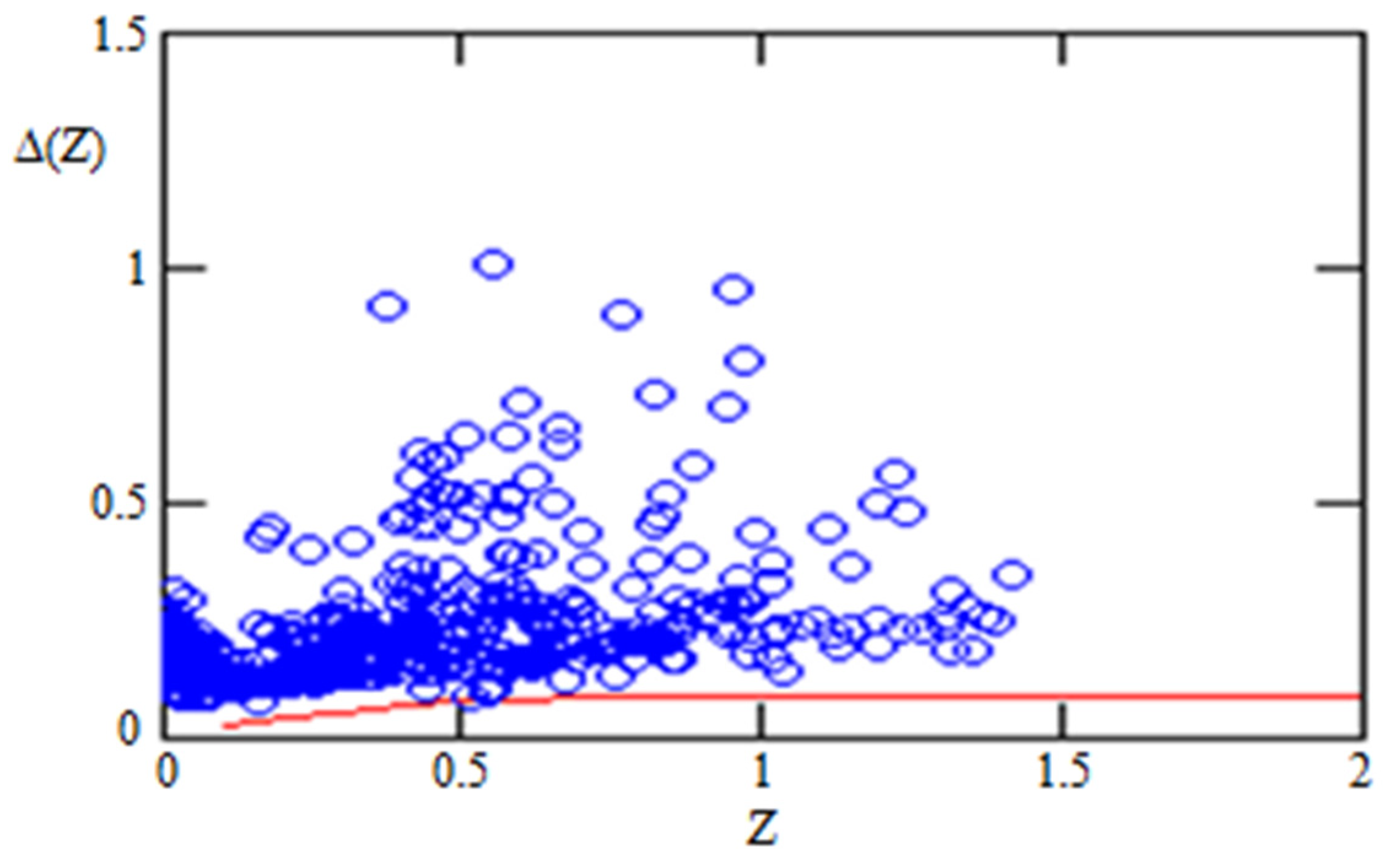
The Figure 4 below visually demonstrates the fact that the difference between ΛCDM and GCDM models is less than observational errors. The same fact follows from the consideration of statistical sums (chi-square criterions). The fit proceeds by minimizing the χ2 statistical criterion
where the sum is over all supernova defined in the Union 2.1 compilation [35,36]; is the ‘observed’ distance modulus to the i-th supernova in the Union 2.1 of supernovas; is the observational error (standard deviation) in the value estimation ; is a theoretical estimation for the same distance as . The statistical sum S is defined as
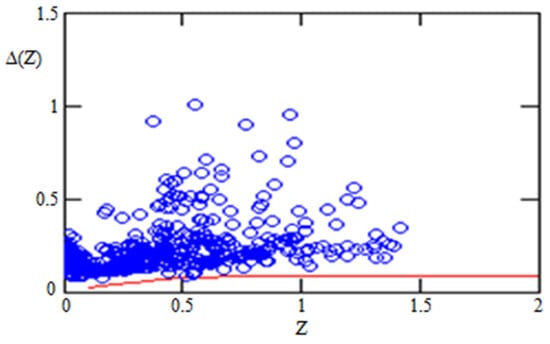
Figure 4.
The solid curve is difference between distance modules of GCDM and ΛCDM models for . The circles are the observational errors. One can see that the difference between these models is below all observational errors. The distance modules for the cosmological constant and for gravitons were calculated by Formulas (1)–(3) for = 0.7 3.
If the theoretical estimation is correct, and experimental errors of observed values are also correct (being independent of each other), and normally distributed, then follows the Chi-squared distribution [38]. When the number of members in the sum is equal N, the average (mean) value of is equal to N, and the variance is equal to 2 N [39]. Practically, if N ≥ 50, at its extremum, the Chi-squared distribution becomes very close to the normal distribution. In other words, the probability that the estimated will deviate from the average value, N, on more than three-sigma, ±3·sqrt (2 N), is about 100% − 99.7% = 0.3%. Mostly, with the probability 68%, the deviation should be observed within one-sigma interval about the mean value. To be exact, when one is fitting experimental data with a model having m free parameters, the value of χ2 in average reduces by the factor (N − m)/N [40]. In our case we used models with only one fitting parameter (m = 1) and many observations (N = 580), so we can safely neglect this factor in the chi-squared statistics. For the case of cosmological constant we get the minimal statistical sum for h = 0.7.
In this case the standard deviation of the statistical sum for ΛCDM model is equal to
The calculated statistical sum for GCDM model and its standard deviation here are
The difference << , . In other words, these two models (ΛCDM and GCDM) are indistinguishable, so that the visual result shown on the Figure 5 is confirmed by direct calculation of statistical sums.
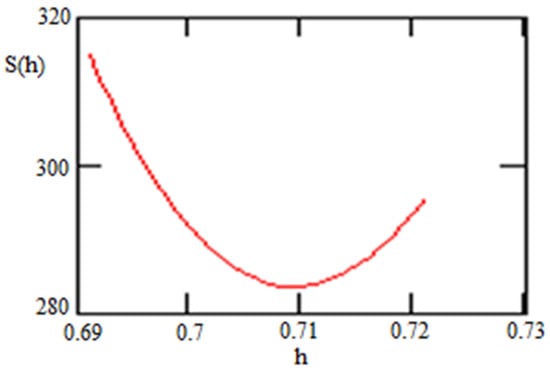
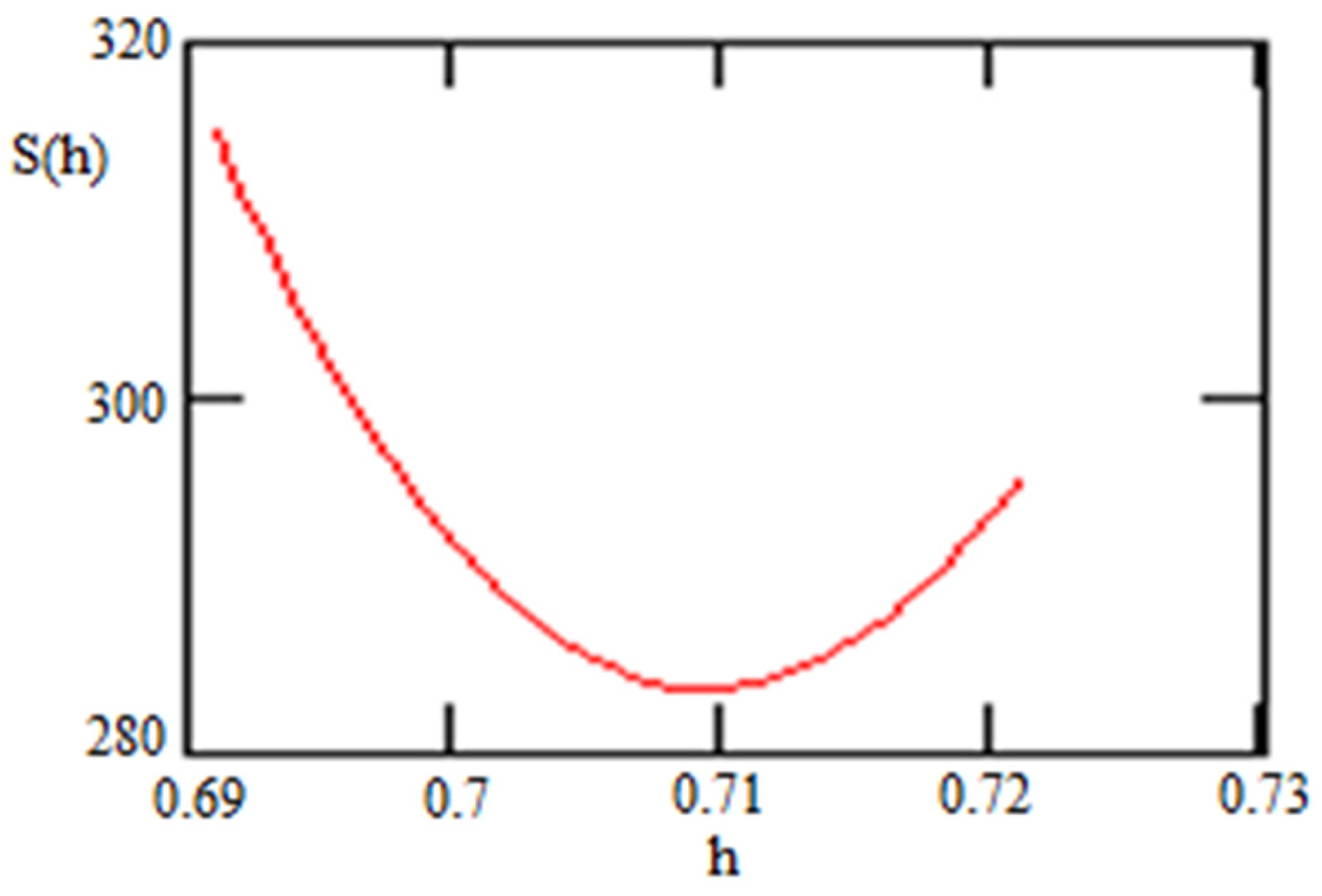
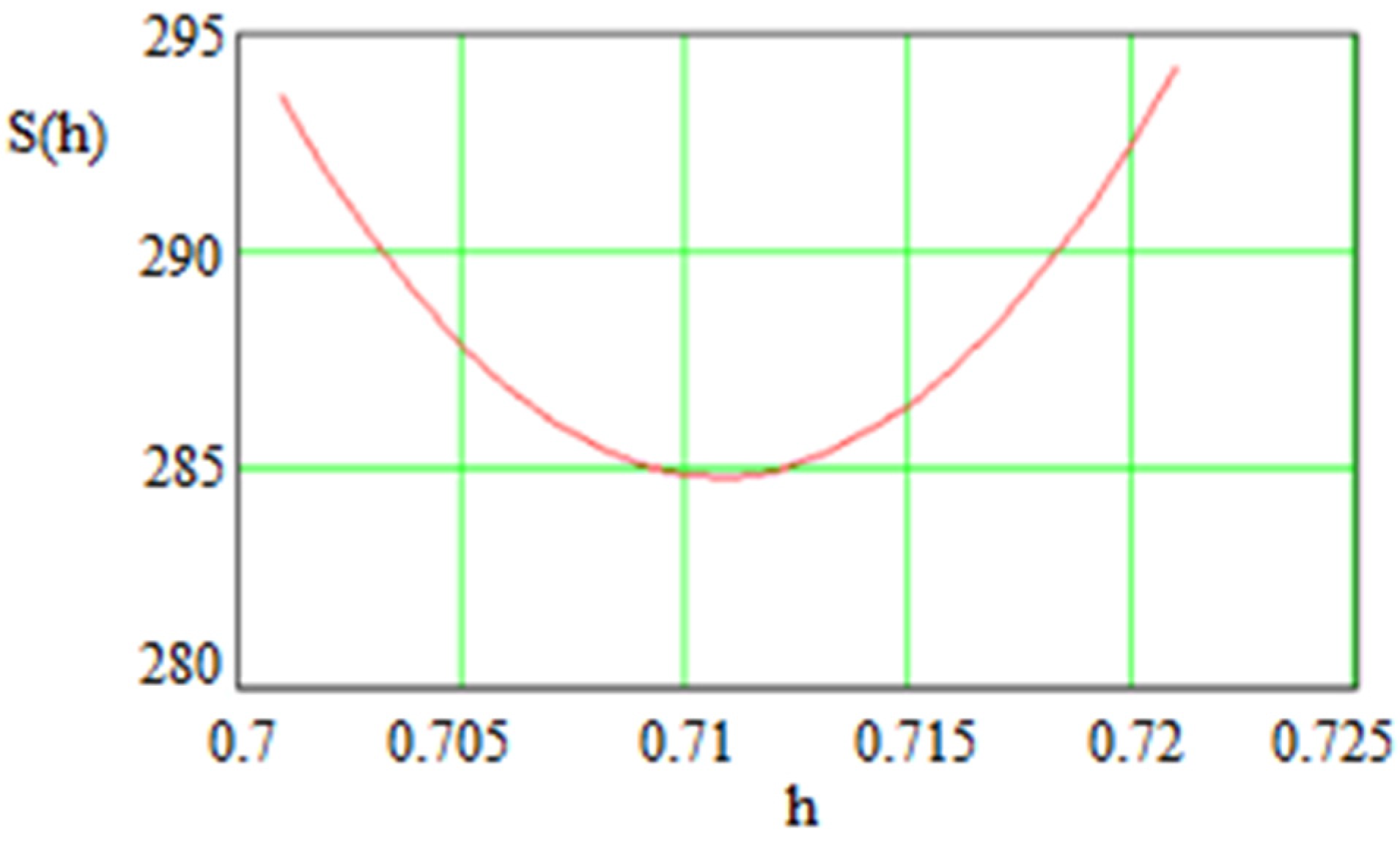
Figure 5.
Statistical sum as a function of h. The minimal statistical sum for DE in this case is with . Such h occupies an intermediate position between the typical values of h given in the Hubble tension problem [32,41,42].
The best fit to the cosmological constant model and 4 leads to statistical sum and the standard deviation as follows:
For the case, the calculations started at the point . Numerical integration leads to the dark energy distribution showed on the Figure 5.
Graviton DE if Figure 6 shown for the same region of interest 0 < z < 2 as in Figure 4 but for ; this dependence obtained by numerical integration of the BBGKY chain may be described by the following simple approximation
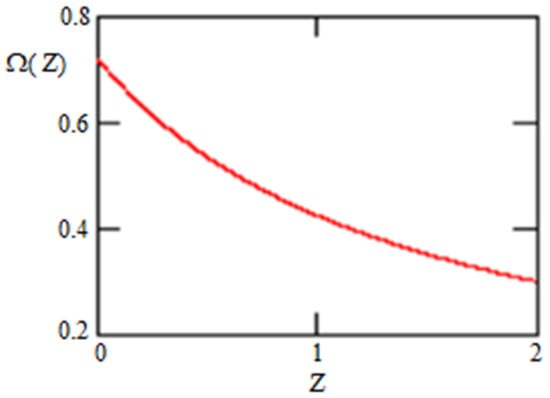
Figure 6.
Graviton DE for .
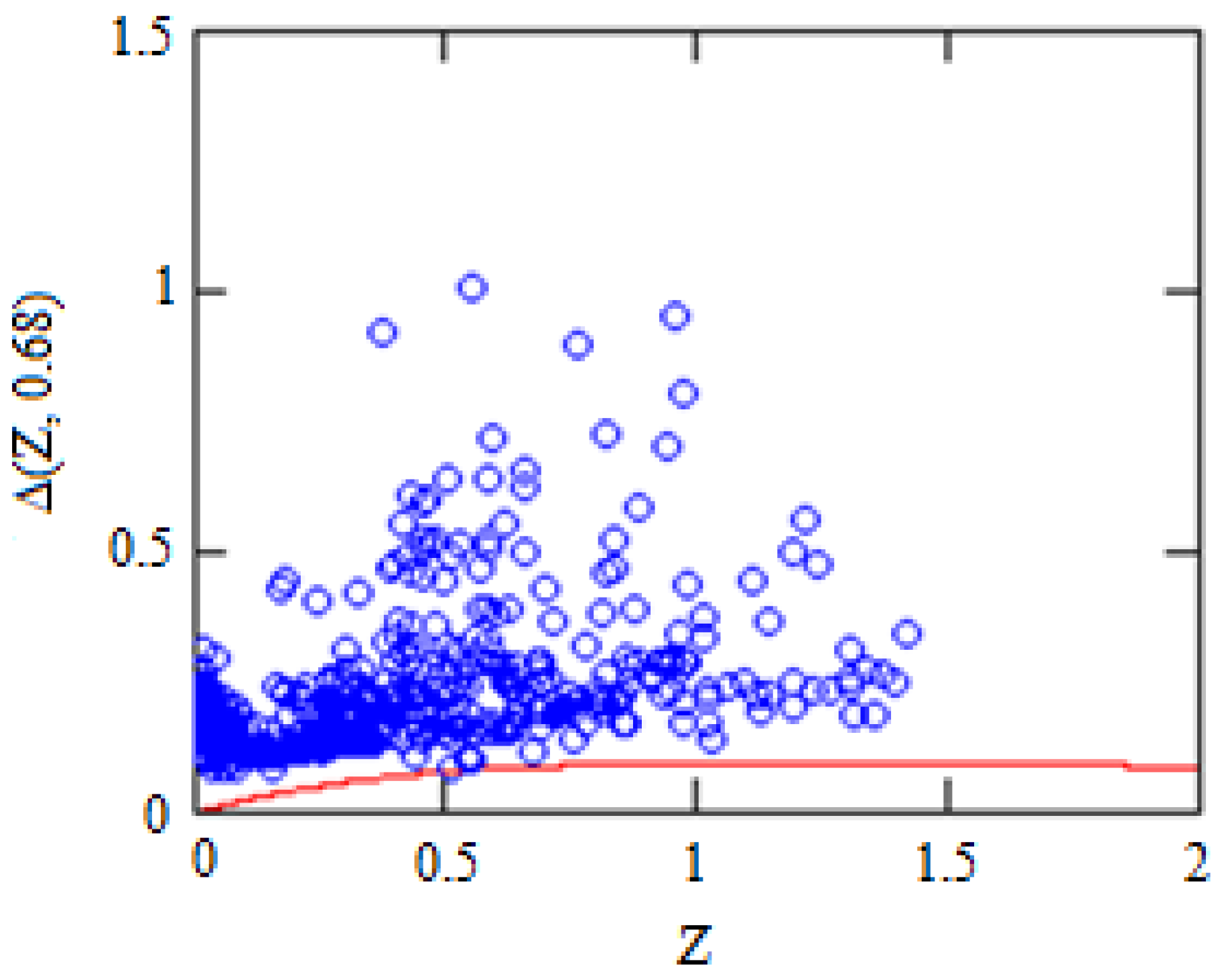
Figure 7 (similar to Figure 3) shows the calculated fitting curve for the graviton DE model but with h = 0.7 and .
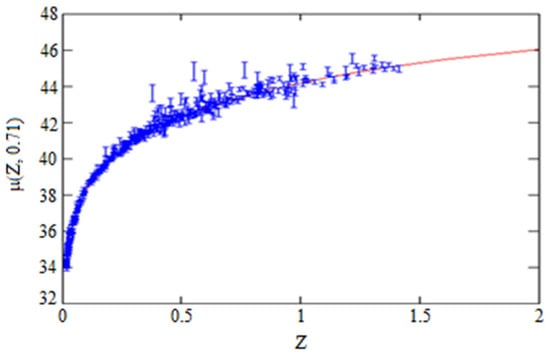
Figure 7.
Solid curve is the distance modules Same as on the as a function of z for graviton DE model run with h = 0.7 and . The blue bars show supernova positions together with observational errors.
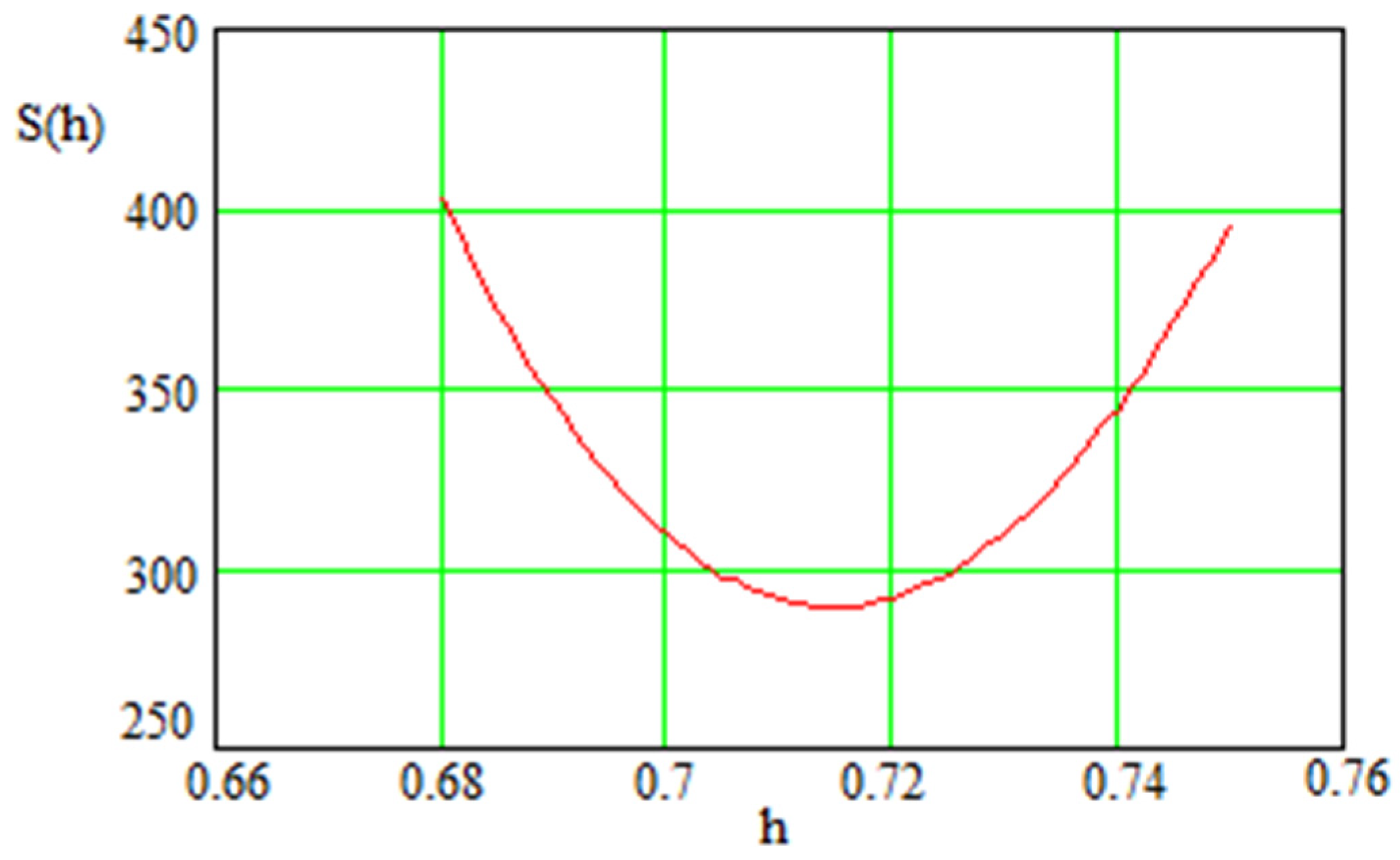
The statistical sum for the Ω0 = 0.721 is calculated the same way as for Ω0 = 0.685 case. The dependence of the statistical sum on the Hubble constant is illustrated in Figure 8 for the case.
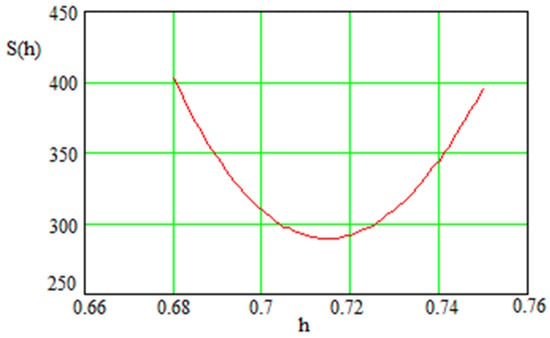
Figure 8.
Depiction of how the statistical sum depends on Hubble constant for the case. The minimal statistical sum here is with h = 0.714.
In this case, we get
Comparing Formulas (4) and (5) with Formula (6), we get an expected result of
Again, the difference between statistical sums less than standard deviations which means that both cases statistically indistinguishable. Visually, this fact can be seen in Figure 9.
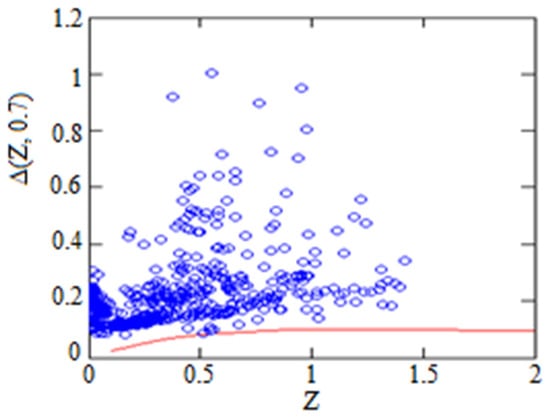
Figure 9.
Same as in Figure 3 but for case of . Again, one can see that the difference between graviton and cosmological constant distance modules is less than observational errors.
Similar to the Figure 9, in the Figure 10 below shown the case from the Table 1, corresponding to , Again the difference between ΛCDM and GCDM models is less than the observational errors shown as circles.
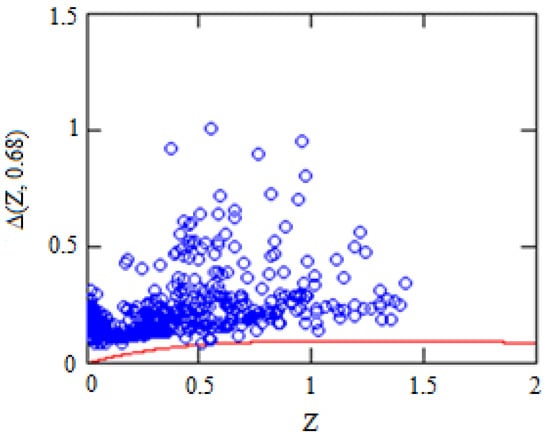
Figure 10.
is the difference between ΛCDM and GCDM models for the case .
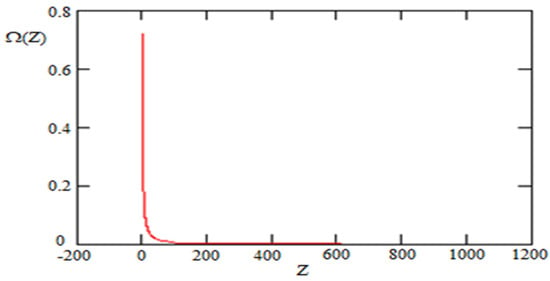
Figure 11.
Graviton DE as a function of z within the whole observable interval of redshifts z for the case .
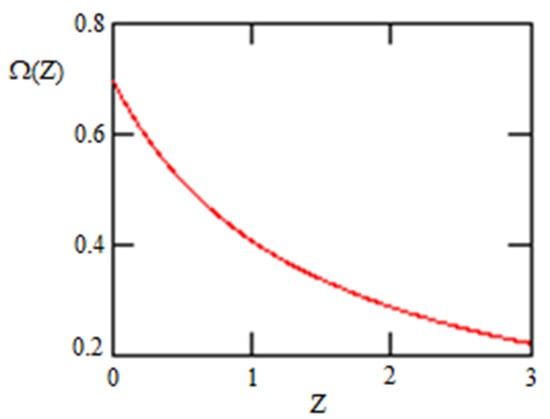
Figure 12.
Same as Figure 11 but a zoom-in for the area of interest 0 < z < 3 for .
The behavior of on the interval is shown in Figure 12.
The minimal statistical sums for the case are and , respectively. Obviously, , where 1 = 16.8 and . Thus, in this case we also have observational errors greater than the difference between models.
Thus, the results of this section confirm the fact that ΛCDM and GCDM models are statistically indistinguishable; moreover, they show that the Hubble constants h providing minimums for statistical sums are 0.709, 0.711, 0.714 for the cases considered which are close to the [43] result Ho = 69.8 ± 0.6 (stat) ± 1.6 (sys) km/s Mpc.
5. What Are the Prospects for the GCDM Testing and Comparison with ΛCDM Model?
We see at least two possible ways to test the difference between GCDM and ΛCDM models in the frame of supernova data. One of them is comparison of equations of state for GCDM and ΛCDM models. And the second one is comparison of transition redshifts at which the deceleration of expansion changes to acceleration.
Our program computes both energy density and pressure of GCDM from the start to the end when . So, we can get the dependence for GCDM and compare it with for ΛCDM model. Figure 13 shows this comparison for the Planck case .
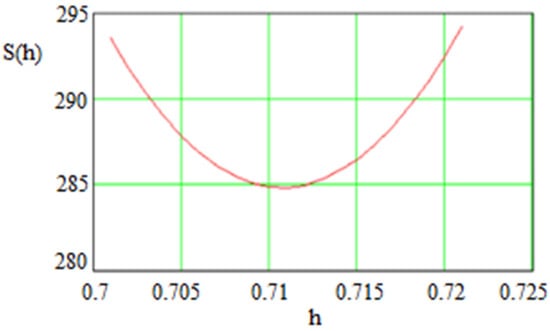
Figure 13.
Statistical sum as function of h for the case of . Here, minimal value of the statistical sum located at h = 0.711.
Below, in the Figure 14 shown the differences in the equation of state between GCDM and ΛCDM models.
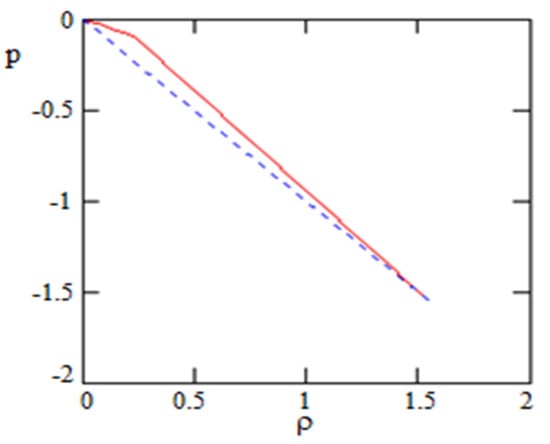
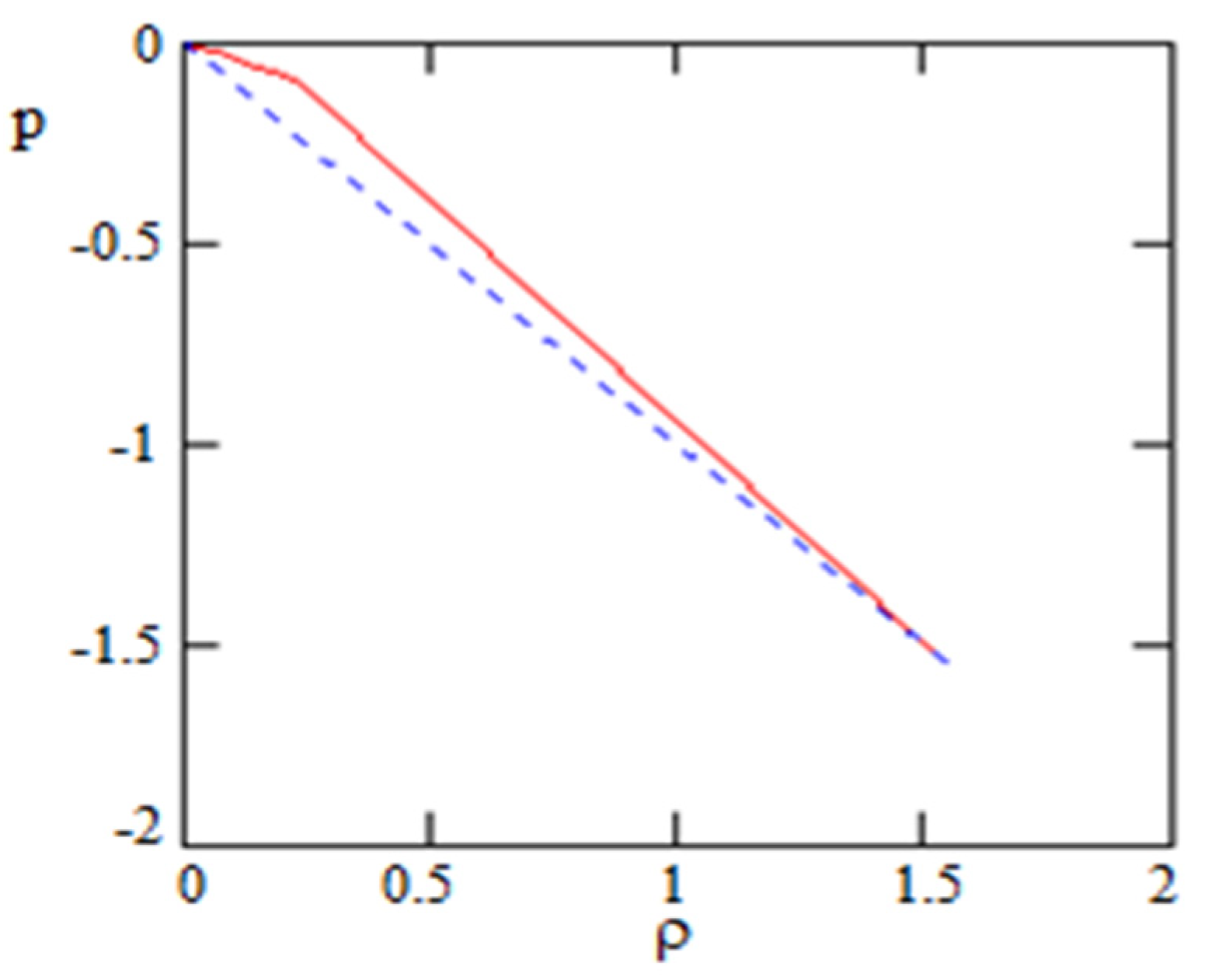
Figure 14.
The solid line is the equation of the state of the GCDM model and dash-line is that for ΛCDM model. Both start from the same point where (in accordance with our choice of initial conditions).
Obviously, to compare these two models we must have w(z) determined observationally. Usual practice is to suggest that w = const and to look for this constant from observational data.
In attempt to consider , Planck Collaboration [32] tested the model where a is a scale factor [44]. In z terms it reads
It was found in [32] that
As we see from Equation (8), w(0) can significantly differ from −1. Thus, even light modification of the model Equation (7) can be used for the successful determination w(z) and comparison GCDM and ΛCDM models.
6. Transition Redshifts
Recall that the Friedmannian equation for deceleration/acceleration in our case reads
In the case of cosmological constant, , Equation (9) leads to the well-known result that the redshift where deceleration is changed for the acceleration, i.e., where reads
For parameters that we use in our simulations one gets . For the Planck parameters , we obtain . So, for the ΛCDM model one gets considering a tension between WMAP and Planck data. For the GCDM model we have to expect [28]
Which leads to for WMAP data and for the Planck data. Now what we get from our numerical simulations. Figure 15 shows the case .
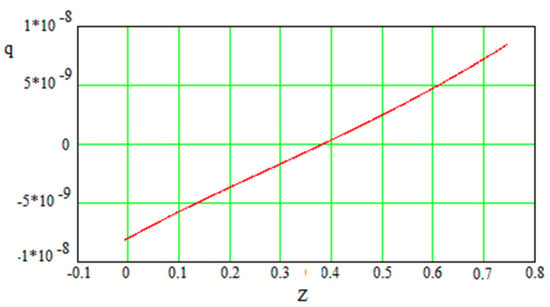
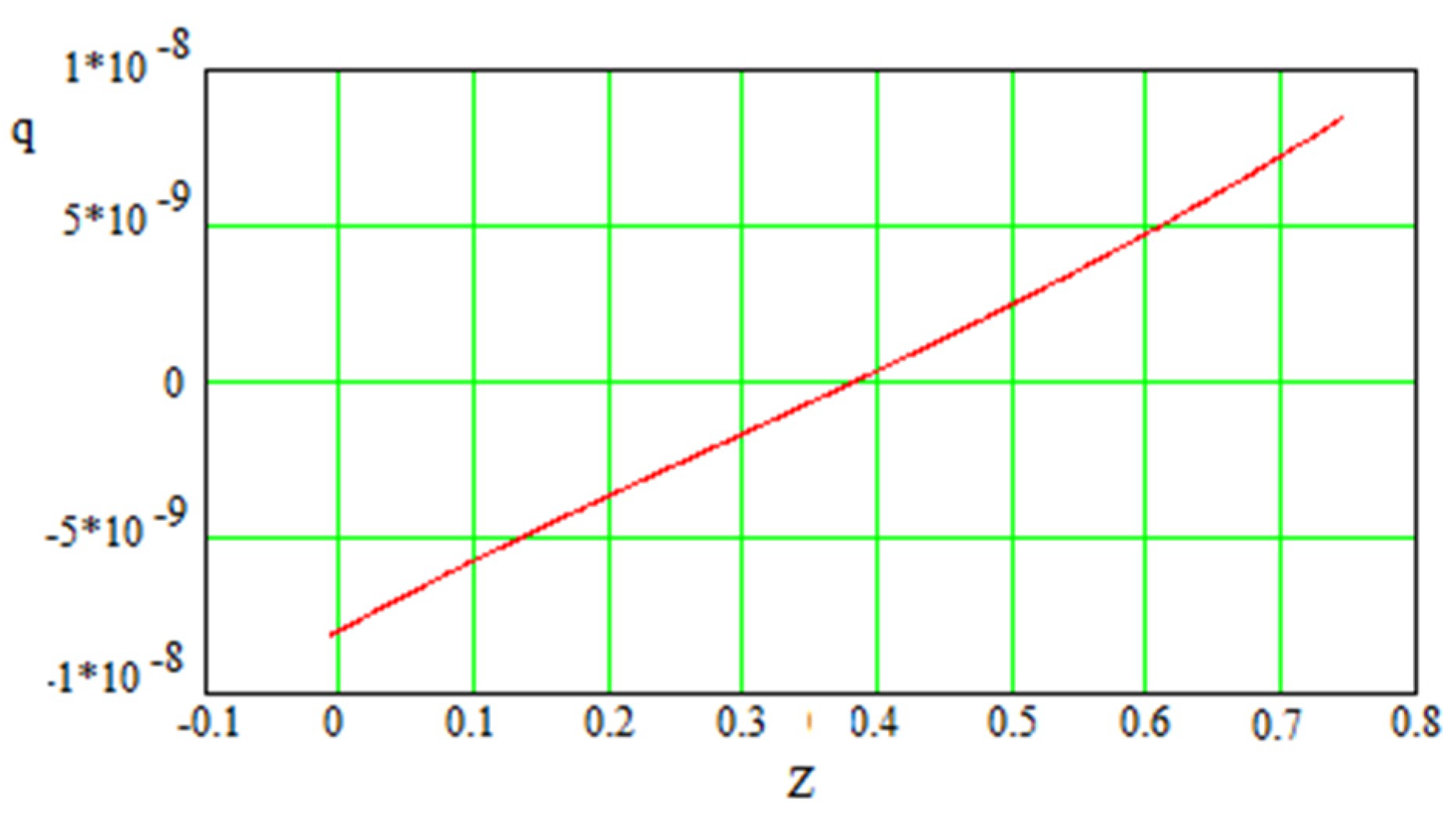
Figure 15.
One can see that the transition redshift is for .
Below, in Figure 16 shown the case .
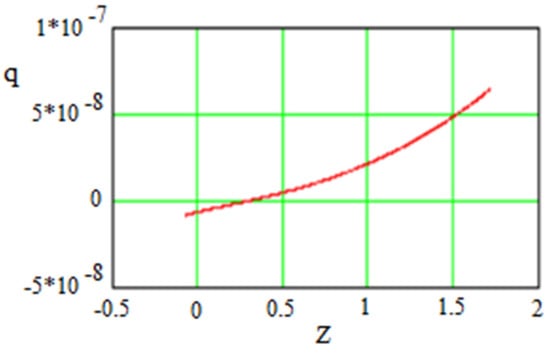
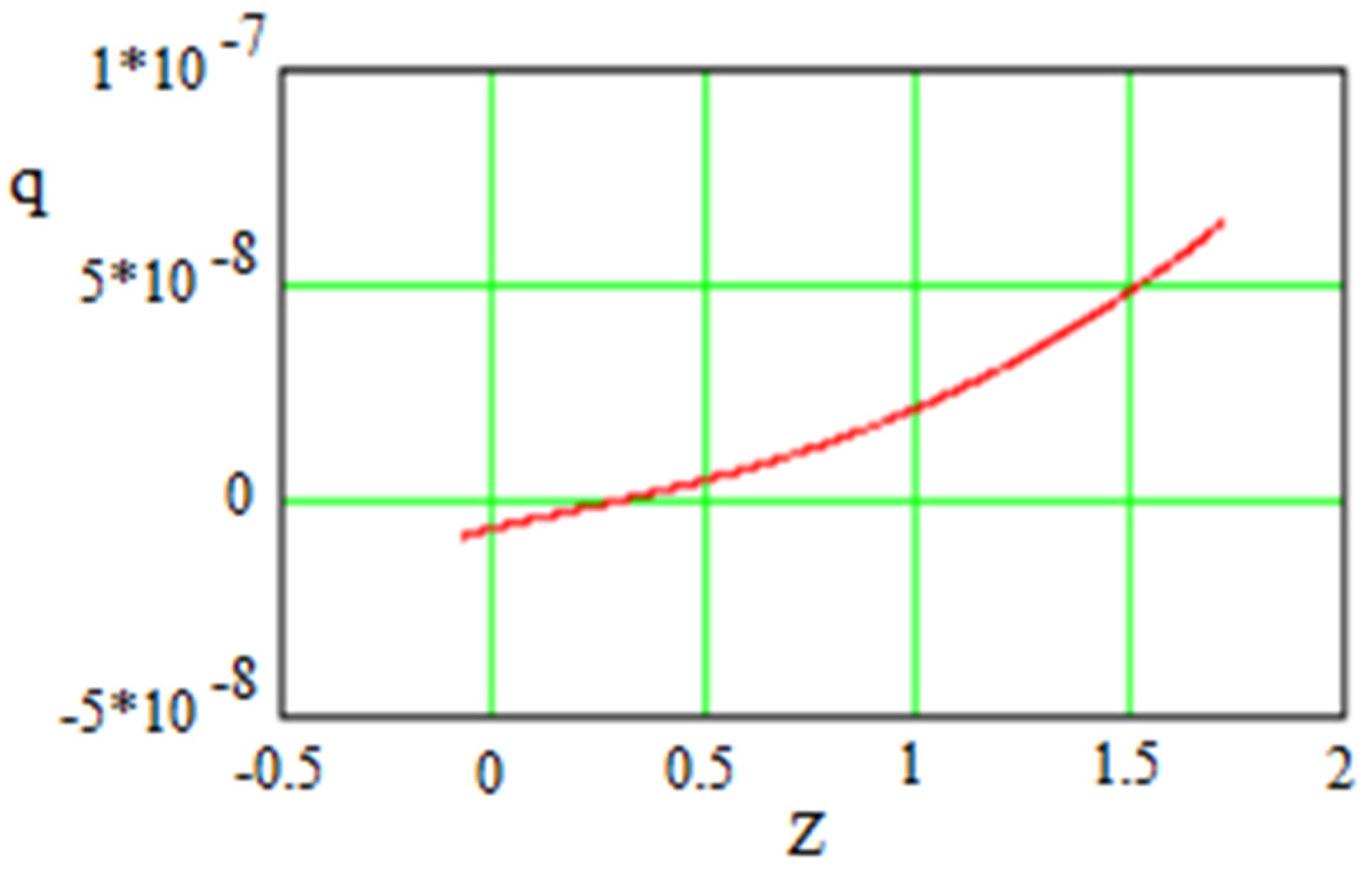
Figure 16.
The same as Figure 15 but for . One can see that .
Direct measurements of the transition point parameter were made by several authors (see below). All these works must be divided into two categories. The first group of authors directly used the ΛCDM model in their studies. The second group of authors considered the model-independent approach. As expected, the first group have obtained close to numbers following from [45] ; [46] found 0.82 0.08; [47] ; [48] ; [49] ; [50] ; [51] . The second group of authors (model-independent results) found that is much closer to our numbers; they are [52] ; [53] ; [42] ; [54] ; [55] (99.9% confidence level).
The observational determination of transition redshifts is an ill-defined problem due to the necessity to measure the second derivative of scale factor . Such a procedure produces significant errors that can be seen from the above references. Nevertheless, the increase in accuracy with the model-independent approach to measuring transition redshifts can help to make a choice between these models.
7. Conclusions
The GCDM model of graviton dark energy is consistent with the supernova observational data with the same accuracy as the ΛCDM model. The graviton DE naturally explains the reason why the DE appears during the matter dominated era. The transition redshifts that follow from graviton theory are consistent with the model independent transition redshifts found from observational data. The way to find out which of the models (GCDM or ΛCDM) better fits the observational data lies in the need to abandon the practically standard assumption that and consider when analyzing observational data. Another prospect for evaluating the GCDM model and comparison with ΛCDM lies in increasing the accuracy of transition redshifts measurements.
Author Contributions
Conceptualization, L.S.M.; Software, D.A.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All supported data are obtained from open sources as listed in the References section.
Acknowledgments
We would like to express our deep appreciation to Ethan Vishniac for the critical comments and invaluable advice in the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Outline of Graviton Theory of Cosmological Acceleration
We operate in the framework of one-loop quantum gravity because the theory cannot be renormalized in higher loops; however, the effect of condensation of gravitons is created by general properties of gravitational field (conformal non-invariance and zero rest mass of gravitons) 5. The results of one-loop theory in which only a gravitational field is considered, are mathematically robust due to the finiteness of one-loop quantum gravity. In our case, the finiteness is provided by the compensation of diverged contributions of gravitons and ghosts to observable quantities [27].
Our original model of the empty Universe consists of the background and gravitons only 6. In the self-consistent theory of gravitons, the macroscopic metric is described by regular Einstein equations
The energy momentum tensor (EMT) of gravitons and ghosts should be obtained by solving operator equations of motion and averaging over a quantum ensemble . Note that the average EMT of nontrivial ghost fields interacting with gravity must appear in the right-hand side Equation (A1) because there are no gauges that eliminate the diffeomorphism group degeneracy in the General Relativity. Our gauge selection was based on two principles. First, both background and gravitons should be considered in the same reference frame. Second, the gauge should provide automatically the one-loop finiteness. We found the only gauge that satisfies both conditions come from the set of synchronic gauges.
Our calculations were done in the frame of one-loop approximation over quantum fields. In the flat isotropic Universe, Equation (A1) read
where is the Hubble function and is the scale factor. Here and are moments of the spectral distribution function of gravitons that is renormalized by ghosts. The moments are:
Here and later, the dots are time derivatives. Heisenberg’s equations for Fourier components of the transverse 3-tensor graviton field and Grassman ghost field are:
Considering of normalization of fields in accordance with Equations (A2) and (A3), canonical commutation relations for gravitons and anticommutation relations for ghosts read
Equations (A2)–(A4) and quantization rules Equation (A5) have been obtained by the path integral [56,57]; they have been obtained from the class of synchronic gauges that automatically provide one-loop finiteness of observables. One-loop effects of vacuum polarization and particle creation by background field are contained in Equation (A4) for gravitons and ghosts; these equations are linear in quantum fields, but their coefficients depend on the non-stationary background metric. Correspondingly, in the background Equation (A2) we keep the average values of bilinear forms of quantum fields only. In this model, quantum particles interact through a common self-consistent field only.
In this work, we are examining self-consistent theory of gravitons and ghosts with the wavelengths of the order of distance to the horizon, i.e.,
Here is the Hubble function, is a scale factor, and upper dotes denote time derivatives. When describing modes Equation (A6), one should keep in mind two things. First, in the area of the spectrum Equation (A6), there are no reasonable approximations, which could be used to solve Friedmannian equations, if the law of cosmological expansion , is not known in advance. Second, the quantum gravity processes of vacuum polarization, spontaneous graviton creation by self-consistent field and graviton–ghost condensation are the most intensive in this region of spectrum. From Equation (A6) it is also obvious that the threshold for quantum gravitational processes involving zero rest mass gravitons and ghosts is absent; these processes at the scale of horizon occur at any stage of evolution of the Universe, including the modern Universe. The theory that allows quantitatively describe such quantum gravitational effects is constructed by creation of the Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy (BBGKY-chain). Now, the BBGKY chain can be created for the moments of spectral function .
Appendix B. Bogoliubov–Born-Green–Kirkwood–Yvon Hierarchy (BBGKY Chain)
In the presence of non-relativistic matter M it reads [27,28]
where M is mass of the non-relativistic matter in the Universe. Equations (A7) and (A8) form the BBGKY chain; each equation of this chain connects the neighboring moments. Equations (A7) and (A8) must be solved jointly with the Einstein Equation (A2). The set of Equations (A2), (A7) and (A8) (to which the definition is added) can be solved numerically with initial conditions determined by the scale factor, moments of the spectral function and their derivatives
The initial condition for the Hubble function is calculated via the equation of the constraint following from Equations (A7) and (A8)
As follows from Formula (A9), in a general case we must have an infinite array of initial conditions to solve the BBGKY chain. We can, however, use one of the exact solutions (see below) which allows us to reduce the problem of initial conditions to just one parameter which is initial value for the energy density of DE (Section 5). For the empty space (M = 0), the BBGKY chain has three exact solutions, which are the attractors [27]. One of these attractors is the exact de Sitter solution to Equations (A7) and (A8) for the empty (M = 0) space; it reads
where .
The substitution of Equation (A12) to Equations (A7) and (A8) leads to the equation of state of GCDM model, which reads
The explicit form of the equation of state reads [27]
Here is the number of gravitons in the modern Universe 7. Note also that as was stated above we deal with the horizon size wavelengths. From Equation (A12) we get Equation (A15) below (see the details in [27])
The important consequences follow from Equation (A14). The equation of state (A14) is invariant with respect to Wick rotation ; it follows from the fact that RHS of Equation (A14) depends on the fourth degree of Hubble constant and the equation of state is the invariant with respect to the transition from Lorentzian space of our space-time to the Euclidian spacetime and vice versa; this invariance underlies the instanton theory of dark energy [57].
Appendix C. Integration of BBGKY Chain
As was shown by [27], the virtual gravitons produce the de Sitter expansion of the empty (with no matter) space (see also Appendix A). To investigate the model of the Universe filled with the matter we have to numerically integrate the BBGKY chain (Appendix B).
When the BBGKY chain is numerically integrated, we face two problems. The first is that the chain is infinite (i.e., in Equations (A7) and (A8) ), so we should cut the BBGKY chain at some . The second problem is that the initial conditions needed to integrate Equations (A7) and (A8) are unknown, so here we inevitably face the challenge of having to make a physical hypothesis about the initial conditions. When the BBGKY chain, Equations (A7) and (A8), is numerically integrated we need define the initial conditions at t = 0, which comes to 3 N + 1 free parameters (the set of differential Equations (A7) and (A8) requires 3 N + 1 initial conditions). Even with N = 5 (our choice for the cutoff), it is an exceptionally large space to explore to find the best fit with observations. We decided to solve the problem of the large number of initial conditions by utilizing the exact de Sitter solution for the empty space, Equation (A12), for which the BBGKY chain has only one free parameter ΩEDE due to the recurrence in Equation (A12). As we will see further the EDE number is the only one initial condition that the computational program use for integration of Equations (A7) and (A8). We modified the BBGKY for the empty space, introducing a matter component as it can be seen from Equation (A8). We do not know the exact solution of the BBGKY chain with the matter component included, but we can integrate the chain numerically and see the result. The computer calculation shows that the model with the matter included still produces de Sitter-like behavior at small z, regardless of the small variations in initial matter component; thus, the de Sitter behavior acts as an attractor, and this result is understandable, because the end state is a state where the matter is no longer a significant player.
Regarding the choice of the number of terms in BBGKY chain, we found that the calculation of the N = 5 is no longer much different from the calculation for the N = 6 (the difference is about 2–3% which is much less than observational errors). That is why we’re cutting off the integration chain on the N = 5. We start calculations at the moment t = 0 and take the initial scale factor . As we mentioned above, we continue the calculation until the calculated value of dimensionless energy density of DE, Ω(z), becomes equal to the current observational value of the energy density of DE Ω(z = 0) = Ω0. In what follows we omit the DE index, so that by the letter Ω0, we denote the dimensionless content of DE at the end point of given calculation, and Ω(z) denotes the dimensionless content of DE at the current point z. Respectively, the energy density of nonrelativistic matter today is . In accordance with Equation (A13), the energy density of DE is defined by the value of . So, variations of are in fact variations of . So that variations in EDE are the variations in the initial conditions for the integration of the set of differential Equations (A7) and (A8). As it can be seen from Section 4, the initial value of providing the best fit for the supernova observations for all cases of interest corresponds to such value of the EDE which is consistent with CMB anisotropy and located in the vicinity of SLS. The time in formulas above is defined in the time unit of the Hubble constant. We used time step of 4 years in the numerical integration, comprising about 3 billion steps.
Appendix D. Why Now? Why the Dark Energy of Graviton Origin Should Appear in the Matter-Dominated Era?
The answer to the question “Why Now?” follows directly from the unique features of gravitational field, conformal non-invariance and zero rest mass of graviton ([45]).
We first need to go back to Equation (A4a), which must be rewritten in terms of proper time . In the terms of proper time, Equation (A4a) takes the form
Prime symbol defines and for simplicity indexes operator signs were omitted in and . There exist only two states of substances filling the Universe, the difference between which is not “felt” by the graviton. The first substance is the modern matter, the equation of state of which is and its expansion law is . The second substance is the dark energy with the equation of state and expansion law . Only in these two substances are the same: in both cases they are ; this means the graviton Equation (A16) is the same for both and substances. The two solutions form the basis of all solutions for the second order differential Equation (A16); this fact might explain why DE of graviton origin with the equation of state “prefers” to appear in the modern universe filled with a matter with the equation of state . Only from the present state of the universe with the equation of state do gravitons “freely pass” into the state of the de Sitter expansion with the equation of state , without “feeling” the difference between the regimes.
Note that the term is a consequence of conformal non-invariance of gravitational field.
As it was described by [58,59], the Hubble tension “might be explained by the presence of an exotic dark-energy density in the early Universe of the type that might arise in some of these ax verse scenarios”. Note that the graviton dark energy can appear exactly at the “right time” when “the exotic dark energy” must appear to solve the Hubble tension problem. Therefore, for now, our choice is to limit ourselves to the EDE estimates based on the limit.
Appendix E. About Early Dark Energy
The cosmological history of the Universe is well-known. In accordance, e.g., to [31], the Universe has gone through three distinct eras: radiation dominated, ; matter-dominated and dark energy dominated . In terms of z, this means that the appearance of the “pure” matter-dominated era one can expects by . In other words, the birth of DE takes place in the modern era of the evolution of the Universe and probably near ; however, there is nothing to prevent the DE from appearing anywhere in between (at , the change in the sign of deceleration to acceleration ceases to satisfy the observational data, see Section 6). The following idea may serve as some argument in favor of the appearance of DE in the region . There is no reason why DE should not appear at the first opportunity, i.e., in the area of ; moreover, note that is a special place because the surface of the last scattering (SLS) is situated at the same place [37]. Thus, we can expect of the appearance of graviton DE in the vicinity of SLS; it is here the appearance of a noticeable amount of DE should be observable due to appearance of anisotropy in CMB. The following citation is from [32]: “The presence or absence of dark energy at the epoch of last scattering is the dominant effect on the CMB anisotropies”. Such early dark energy was named by EDE (see [60]). The analysis of CMB anisotropies produces the most precise bounds on EDE [61,62,63,64,65,66]. As noted by [32], the upper limit on the EDE is (95%; Plank + WP + highL). Obviously, the initial value of DE that we use in our calculations corresponds in its meaning to the concept of early dark energy (EDE) introduced hypothetically in the listed above works. Therefore, we start our calculation assuming that the initial condition for DE at the start is below of 0.009. We start our numerical integration with the initial scale factor . As calculation progresses, the scale factor is increasing. The computer “stops” when DE is equal to its present value . At this moment, the scale factor is equal to its modern value , and this means that the initial is equal to . While taking the estimation of from different groups of observers [32,33,34], we found that the initial are always grouped near the region of SLS (see Table 1 in Section 4).
Notes
| 1 | Quoted from [67]. |
| 2 | In fact, the history of the cosmological constant from its inception in 1917 to the present day is an exciting “astronomical adventure novel,” detailed in a beautifully written historical and astronomical study [67]. |
| 3 | It worth to note that even big enough at the point leads to a picture similar to Figure 4. |
| 4 | The tension between numerical value of Hubble constant H was a subject for intense discussion between two research groups [68,69]. The last publication of Freedman [43] shows that the last measurement of h gives H0 = 69.8 ± 0.6 (stat) ± 1.6 (sys) km/s/Mpc. Note that we obtained h = 0.71 as a number minimizing the statistical sums for the cosmological constant for all three cases, which is closed to Freedman’s h = 0.698. |
| 5 | Hypotheses on the possibility of graviton condensate formation in the Universe was proposed in [70,71] in a general form. A description of these effects by an adequate mathematical formalism is the problem at the present time. |
| 6 | In our current paper, we added the non-relativistic matter with the equation of state p = 0 (see below). |
| 7 | This equation of state is superficially similar to what comes from conformal anomalies. As was shown in [72], quantum corrections to the Einstein equations due to zero oscillations can provide a self-consistent de Sitter solution in the vicinity Planck’s value curvature (see also [73]). |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. LambdaCDM epoch reconstruction from F (R, G) and modified Gauss-Bonnet gravities. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.; Bertolami, O.; Sen, A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Copeland, S.E.G.; Sami, M.; Tsujikawa. Dynamics of dark energy. S. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Chernin, A.D. Dark energy and universal antigravitation. Phys. Uspekhi 2008, 51, 253–282. [Google Scholar] [CrossRef]
- Yoo, J.; Watanabe, Y. Theoretical models of dark energy. Int. J. Mod. Phys. D 2012, 21, 1230002. [Google Scholar] [CrossRef]
- Heisenberg, L. A systematic approach to generalisations of General Relativity and their cosmological implications. arXiv 2018, arXiv:1807.01725v1. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 1988, 302, 668. [Google Scholar] [CrossRef]
- Caldwell, R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Caldwell, R.; Linder, E.V. Limits of quintessence. Phys. Rev. Lett. 2005, 95, 1401. [Google Scholar] [CrossRef]
- Verlinde, E. Emergent gravity and the dark universe. SciPost Phys. 2017, 2, 016. [Google Scholar] [CrossRef]
- Alexander, S.; Cortês, M.; Liddle, A.R.; Magueijo, J.; Sims, R.; Smolin, L. Cosmology of minimal varying Lambda theories. Phys. Rev. D 2019, 100, 083507. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. The cosmological constant and the theory of elementary particles. Sov. Phys. Usp. 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Hoyle, F.; Burbidge, G. Relation between the Red-shifts of Quasi-stellar Objects and their Radio Magnitudes. Nature 1966, 212, 1334. [Google Scholar] [CrossRef]
- Longair, M.; Scheuer, P.A.G. Red-shift magnitude relation for quasi-stellar objects. Nature 1967, 215, 919–922. [Google Scholar] [CrossRef]
- Burbidge, G.; Burbidge, E. Absorption lines in quasi-stellar objects. Nature 1967, 216, 1092–1093. [Google Scholar] [CrossRef]
- Petrosian, V.; Salpeter, E.; Szekeres, P. Quasi-stellar objects in universes with non-zero cosmological constant. Astrophys. J. 1967, 147, 1222–1226. [Google Scholar] [CrossRef]
- Shklovsky, J. On the nature of" standard" absorption spectrum of the quasi-stellar objects. Astrophys. J. 1967, 150, L1–L3. [Google Scholar] [CrossRef]
- Kardashev, N. LemaItre’s Universe and Observations. Astrophys. J. 1967, 150, L135–L139. [Google Scholar] [CrossRef]
- Rowan-Robinson, M. On cosmological models with an antipole. Mon. Not. R. Astron. Soc. 1968, 141, 445–458. [Google Scholar] [CrossRef][Green Version]
- Petrosian, V.; Salpeter, E. Lemaître models and the cosmological constant. Comm. Astrophys. Sp. Phys. 1970, 2, 109–115. [Google Scholar]
- Petrosian, V. Confrontation of Lemaître models and the cosmological constant with observations. Symp.-Int. Astron. Union 1974, 63, 31–46. [Google Scholar] [CrossRef]
- Marochnik, L.; Usikov, D.; Vereshkov, G. Graviton, ghost and instanton condensation on horizon scale of the Universe. Dark energy as a macroscopic effect of quantum gravity. Found. Phys. 2008, 38, 546–555. [Google Scholar] [CrossRef]
- Marochnik, L.; Usikov, D.; Vereshkov, G. Macroscopic effect of quantum gravity: Graviton, ghost and instanton condensation on horizon scale of the Universe. arXiv 2013, arXiv:1306.6172. [Google Scholar] [CrossRef]
- Vereshkov, G.; Marochnik, L. Quantum gravity in Heisenberg representation and self-consistent theory of gravitons in macroscopic spacetime. J. Mod. Phys. 2013, 4, 285. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2020, 20, 083C01. [Google Scholar]
- Frieman, J.; Turner, M.; Huterer, D. Dark energy and the accelerating universe. Ann. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 517, A16. [Google Scholar]
- Bennett, C.; Larson, D.; Weiland, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. Astrophys. J. 2012, 208, 20. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 Results: Cosmological Constraints from Galaxy Clustering and Weak Lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope cluster supernova survey. V. Improving the dark-energy constraints above z> 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and Hubble Space Telescope light curves of six type Ia supernovae at 0.511 < z < 1.12 and the Union2 compilation. Astrophys. J. 2010, 716, 712. [Google Scholar]
- Hadzhiyska, B.; Spergel, D. Measuring the duration of last scattering. Phys. Rev. D 2019, 99, 043537. [Google Scholar] [CrossRef]
- Seber, G.; Lee, A. Linear Regression Analysis, 2nd ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Faraway, J. Practical Regression and Anova Using R; University of Bath: Bath, UK, 2003. [Google Scholar]
- Andrae, R.; Schulze-Hartung, T.; Melchior, P. Dos and don’ts of reduced chi-squared. arXiv 2010, arXiv:1012.3754v1. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. 2021, 908, L6. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the Expansion History of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar]
- Busca, N.G.; Delubac, T.; Rich, J.; Bailey, S.; Front-Ribera, A.; Kirkby, D.; Le Goff, J.-M.; Pieri, M.M.; Slosar, A.; Aubourg, É.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS quasars. Astron. Astrophy. 2013, 552, A96. [Google Scholar] [CrossRef]
- Farooq, O.; Ratra, B. Binned Hubble parameter measurements and the cosmological deceleration–acceleration transition. Astrophys. J. 2013, 766, L7. [Google Scholar] [CrossRef]
- Sutherland, W.; Rothnie, P. On the luminosity distance and the epoch of acceleration. Mon. Not. R. Astron. Soc. 2015, 446, 3863. [Google Scholar] [CrossRef]
- Rana, A.; Jain, D.; Mahajan, S.; Mukherjee, A. Bounds on graviton mass using weak lensing and SZ effect in galaxy clusters. Phys. Lett. B 2018, 781, 220–226. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Penna-Lima, M. A general reconstruction of the recent expansion history of the universe. J. Cosmol. Astropart. Phys. 2015, 9, 045. [Google Scholar] [CrossRef]
- Daly, R.A.; Djorgovski, S.G.; Freeman, K.A.; Mory, M.P.; O’dea, C.P.; Kharb, P.; Baum, S. Improved constraints on the acceleration history of the universe and the properties of the dark energy. Astrophys. J. 2008, 677, 1. [Google Scholar] [CrossRef]
- Daly, R.A.; Djorgovski, S.G. The Acceleration History of the Universe and the Properties of the Dark Energy. AIP Conf. Proc. 2007, 937, 298–302. [Google Scholar]
- Wang, F.-Y.; Dai, Z.-G. Constraining Dark Energy and Cosmological Transition Redshift with Type Ia Supernovae. Chin. J. Astron. Astrophys. 2006, 6, 561–571. [Google Scholar] [CrossRef]
- Shapiro, C.; Turner, M. What do we really know about cosmic acceleration? Astrophys. J. 2006, 649, 563–569. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D.J. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. Cosmol. Astropart. Phys. 2016, 5, 014. [Google Scholar] [CrossRef]
- Faddeev, L.; Popov, V. Feynman diagrams for the Yang-Mills field. Phys. Lett. B 1967, 25, 29. [Google Scholar] [CrossRef]
- Marochnik, L. Dark Energy and Inflation from Gravitational Waves. Universe 2017, 3, 72. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Early dark energy, the Hubble-parameter tension, and the string axiverse. arXiv 2017, arXiv:1608.01309v2. [Google Scholar]
- Poulin, V.; Smith, T.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Sievers, J.L.; Hlozek, R.A.; Nolta, M.R.; Acquaviva, V.; Addison, G.E.; Ade, P.A.R.; Aguirre, P.; Amiri, M.; Appel, J.W.; Felipe Barrientos, L.; et al. The Atacama Cosmology Telescope: Cosmological parameters from three seasons of data. J. Cosmol. Astropart. Phys. 2013, 10, 060. [Google Scholar] [CrossRef]
- Doran, M.; Schwindt, J.-M.; Wetterich. Structure formation and the time dependence of quintessence. Phys. Rev. D 2001, 64, 123520. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Doran, M.; Müller, C.M.; Schäfer, G.; Wetterich, C. Early quintessence in light of the Wilkinson Microwave Anisotropy Probe. Astrophys. J. 2003, 591, L75–L78. [Google Scholar] [CrossRef]
- Calabrese, E.; Putter, R.; Huterer, D.; Linder, E.V.; Melchiorri, A. Future CMB constraints on early, cold, or stressed dark energy. Phys. Rev. D 2011, 83, 023011. [Google Scholar] [CrossRef]
- Reichardt, C.; Putter, R.; Zahn, O.; Hou, Z. New limits on early dark energy from the south pole telescope. Astrophys. J. 2012, 749, L9. [Google Scholar] [CrossRef]
- Hou, Z.; Reichardt, C.L.; Story, K.T.; Follin, B.; Keisler, R.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Carlstorm, J.E.; Chang, C.L.; et al. Constraints on Cosmology from the Cosmic Microwave Background Power Spectrum of the 2500 SPT-SZ Survey. Astrophys. J. 2014, 782, 74. [Google Scholar] [CrossRef]
- Pettorino, V.; Amendola, L.; Wetterich, C. How early is early dark energy? Phys. Rev. D 2013, 87, 083009. [Google Scholar] [CrossRef]
- O’Raifeartaigh, C.; O’Keeffe, M.; Nahm, W.; Mitton, S. One Hundred Years of Cosmological Constant: From ‘Superfluous Stunt’ to Dark Energy. arXiv 2017, arXiv:1711.06890. [Google Scholar] [CrossRef]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D.M. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Redetermination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Hu, B. General Relativity as Geometro-Hydrodynamics. Int. J. Theor. Phys. 2005, 44, 1785–1806. [Google Scholar] [CrossRef]
- Antoniadis, I.; Mazur, P.; Mottola, E. Cosmological dark energy: Prospects for a dynamical theory. New. J. Phys. 2007, 9, 11. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Starobinsky, A.A. Particle production and vacuum polarization in an anisotropic gravitational field. Sov. J. Exp. Theor. Phys. 1972, 34, 1159. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).