Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole
Abstract
:1. Introduction
2. Magnetized Regular Black Hole (MRBH)
3. Weak Deflection Angle for MRBH in Non-Plasma Medium
4. Graphical Representation for Non-Plasma of MRBH
4.1. Angle of Deflection versus Impact Parameter b
4.2. Deflection Angle versus BH Charge q
5. Effect of Plasma on Weak Deflection Angle for MRBH
6. Graphical Analysis for Plasma Medium
6.1. Deflection Angle with Impact Parameter b
6.2. Deflection Angle with BH Charge q
7. Derivation of Greybody Factor of MRBH
8. Graphical Study of the Greybody Bound for MRBH
Rigorous Bound in Connection with Omega
9. Conclusions
9.1. Bending Angle
- (i)
- Non-plasma Medium:The deflection angle obtained in Equation (19) for non-plasma medium depends on m of the BH, q, b, G, and l. We observe that in the attain deflection angle, the first term is the well-known result for the Schwarzschild black hole, when we put , , and .
- (ii)
- Plasma Medium:In case the of the plasma medium, the deflection angle in Equation (28) depends on m of the BH, q, b, G, and l and on the plasma term. The bending angle obtained in the plasma medium increases with the parameter , which shows that the lower the photon frequency observed by a static spectator at infinity, the greater the deflection angle of it for the fixed electron plasma frequency. We also observe that, when we take the , , and , the deflection angle obtained in the plasma medium reduces to the deflection angle of the Schwarzschild BH in plasma medium. We also found that the deflection angle obtained in the plasma medium reduces to the deflection angle that we obtained in case of non-plasma, when we take .
9.2. Greybody Factor Bounds T
9.3. Graphical Behaviour
- (i)
- For MRBH:
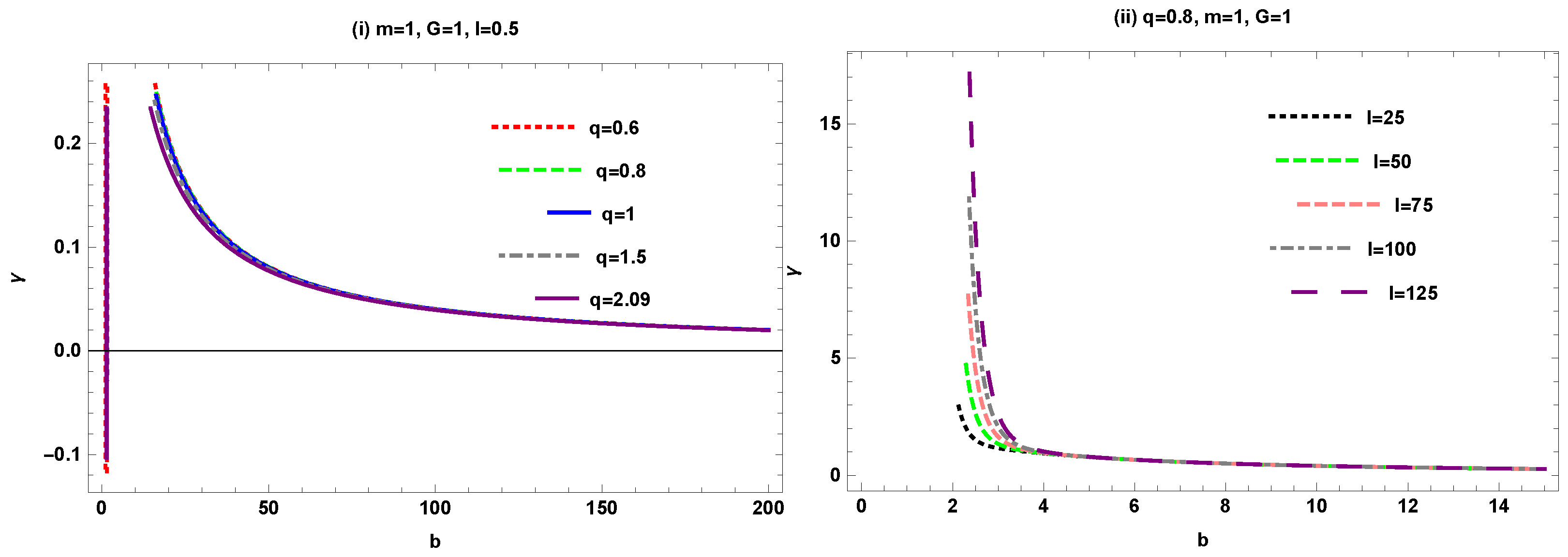
- The bending angle versus impact parameter b: The graphical behaviour shows that, when we fix the value of , , and , and give variation to q, the deflection angle shows positive behaviour for and shows negative behaviour at and . Similarly, we observed that the deflection angle is decreasing and eventually goes to infinity for large values of l, and by fixing , , and Newton’s constant .
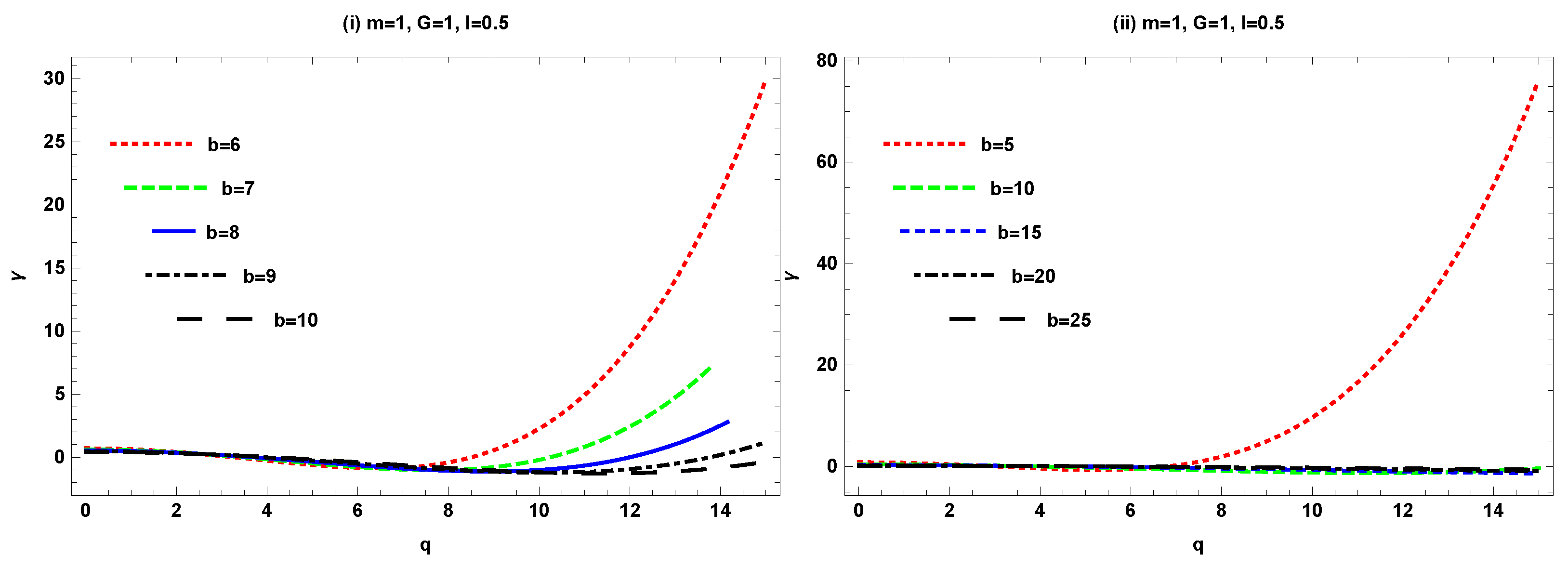
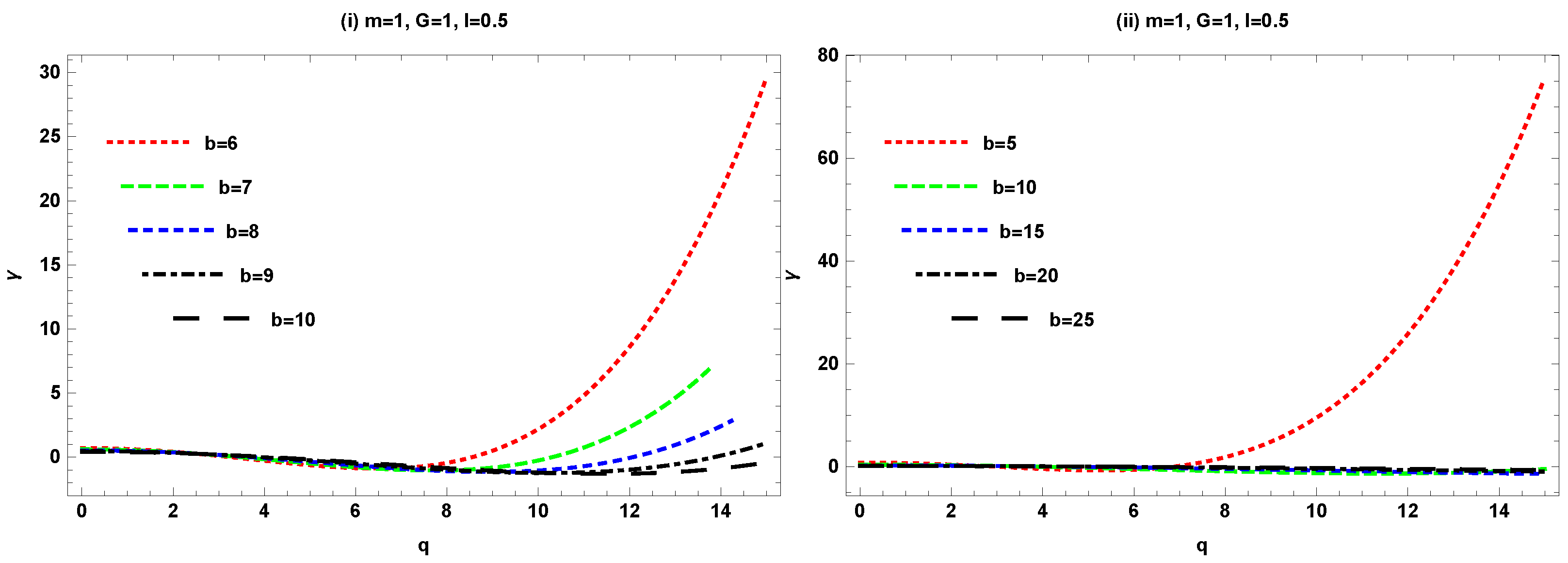
- Bending angle versus magnetic charge q: For the fixed values of , , and , the angle first increases for small values of b, but for large values of b, the deflection angle decreases.
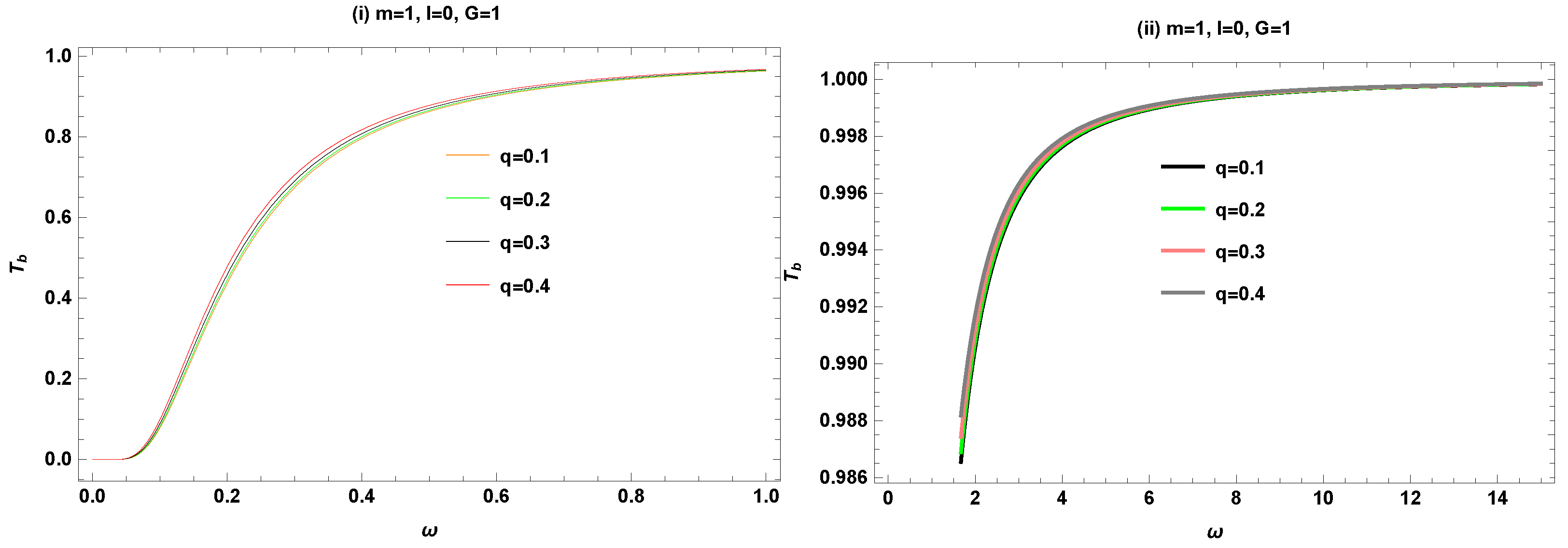
9.4. Graphical Analysis of Greybody Bound
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Einstein, A. Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field. Science 1936, 84, 506–507. [Google Scholar] [CrossRef] [Green Version]
- Herdeiro, C.A.R.; Lemos, J.P.S. The black hole fifty years after: Genesis of the name. arXiv 2018, arXiv:1811.06587. [Google Scholar]
- Ricon, A.; Panotopoulous, G. Quasinormal modes of an improved Schwarzschild black hole. Phys. Dark Univ. 2020, 30, 100639. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: The Advanced LIGO Detectors in the Era of First Discoveries. Phys. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.S.; Mao, S.; Zhao, Y.; Lu, Y. Gravitational lensing of gravitational waves: A statistical perspective. Mon. Not. Roy. Astron. Soc. 2018, 476, 2220–2229. [Google Scholar] [CrossRef]
- Bartelmann, M.; Schneider, P. Weak gravitational lensing. Phys. Rep. 2001, 340, 291–472. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Relativ. Gravit. 2018, 50, 42. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Romero, G.E.; Torres, D.F. Reissner-Nordstrom black hole lensing. Phys. Rev. D 2002, 66, 024010. [Google Scholar] [CrossRef] [Green Version]
- Keeton, C.R.; Kochanek, C.S.; Falco, E.E. The Optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution. Astrophys. J. 1998, 509, 561–578. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Iftikhar, S. Equatorial gravitational lensing by accelerating and rotating black hole with NUT parameter. Astrophys. Space Sci. 2016, 361, 36. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R.; Kocherlakota, P.; Narayan, R.; Joshi, P.S. Shadows of spherically symmetric black holes and naked singularities. Mon. Not. Roy. Astron. Soc. 2019, 482, 52–64. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, R.; Ghosh, S.G. Gravitational lensing by black holes in the 4D Einstein–Gauss–Bonnet gravity. JCAP 2020, 09, 030. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G.; Wang, A. Gravitational deflection of light and shadow cast by rotating Kalb-Ramond black holes. Phys. Rev. D 2020, 101, 104001. [Google Scholar] [CrossRef]
- Manna, T.; Rahaman, F.; Molla, S.; Bhadra, J.; Shah, H.H. Strong Lensing of a Regular Black Hole with an Electrodynamics Source. Gen. Relativ. Gravit. 2018, 50, 54. [Google Scholar] [CrossRef] [Green Version]
- Kuhfittig, P.K.F. Gravitational lensing of wormholes in the galactic halo region. Eur. Phys. J. C 2014, 74, 2818. [Google Scholar] [CrossRef] [Green Version]
- Rahaman, F.; Kalam, M.; Chakraborty, S. Gravitational lensing by stable C-field wormhole. Chin. J. Phys. 2007, 45, 518. [Google Scholar]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quant. Grav. 2008, 25, 235009. [Google Scholar] [CrossRef]
- Werner, M.C. Gravitational lensing in the Kerr-Randers optical geometry. Gen. Relativ. Gravit. 2012, 44, 3047–3057. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Kitamura, T.; Asada, H. Gravitational bending angle of light for finite distance and the Gauss–Bonnet theorem. Phys. Rev. D 2016, 94, 084015. [Google Scholar] [CrossRef] [Green Version]
- Crisnejo, G.; Gallo, E. Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss–Bonnet theorem. A unified treatment. Phys. Rev. D 2018, 97, 124016. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Asada, H. Finite-distance corrections to the gravitational bending angle of light in the strong deflection limit. Phys. Rev. D 2017, 95, 044017. [Google Scholar] [CrossRef] [Green Version]
- Övgün, A. Weak field deflection angle by regular black holes with cosmic strings using the Gauss–Bonnet theorem. Phys. Rev. D 2019, 99, 104075. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K.; Övgün, A. Gravitational Lensing by Rotating Wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef] [Green Version]
- Jafarzade, K.; Zangeneh, M.K.; Lobo, F.S.N. Shadow, deflection angle and quasinormal modes of Born-Infeld charged black holes. JCAP 2021, 04, 008. [Google Scholar] [CrossRef]
- Kumaran, Y.; Övgün, A. Deriving weak deflection angle by black holes or wormholes using Gauss-Bonnet theorem. Turk. J. Phys. 2021, 45, 247–267. [Google Scholar]
- Okyay, M.; Övgün, A. Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. JCAP 2022, 01, 009. [Google Scholar] [CrossRef]
- Fu, Q.M.; Zhao, L.; Liu, Y.X. Weak deflection angle by electrically and magnetically charged black holes from nonlinear electrodynamics. Phys. Rev. D 2021, 104, 024033. [Google Scholar] [CrossRef]
- Javed, W.; Hamza, A.; Övgün, A. Effect of nonlinear electrodynamics on the weak field deflection angle by a black hole. Phys. Rev. D 2020, 101, 103521. [Google Scholar] [CrossRef]
- Hensh, S.; Abdujabbarov, A.; Schee, J.; Stuchlík, Z. Gravitational lensing around Kehagias–Sfetsos compact objects surrounded by plasma. Eur. Phys. J. C 2019, 79, 533. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Fernando, S. Greybody factors of charged dilaton black holes in 2 + 1 dimensions. Gen. Relativ. Gravit. 2005, 37, 461–481. [Google Scholar] [CrossRef] [Green Version]
- Panotopoulos, G.; Rincón, A. Greybody factors for a minimally coupled scalar field in three-dimensional Einstein-power-Maxwell black hole background. Phys. Rev. D 2018, 97, 085014. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Zinhailo, A.F. Grey-body factors and Hawking radiation of black holes in 4D Einstein–Gauss–Bonnet gravity. Phys. Lett. B 2020, 810, 135793. [Google Scholar] [CrossRef]
- Boonserm, P.; Visser, M. Bounding the Bogoliubov coefficients. Ann. Phys. 2008, 323, 2779–2798. [Google Scholar] [CrossRef] [Green Version]
- Boonserm, P. Rigorous bounds on Transmission, Reflection, and Bogoliubov coefficients. arXiv 2009, arXiv:0907.0045. [Google Scholar]
- Boonserm, P.; Visser, M. Bounding the greybody factors for Schwarzschild black holes. Phys. Rev. D 2008, 78, 101502. [Google Scholar] [CrossRef] [Green Version]
- Boonserm, P.; Chatrabhuti, A.; Ngampitipan, T.; Visser, M. Greybody factors for Myers–Perry black holes. J. Math. Phys. 2014, 55, 112502. [Google Scholar] [CrossRef] [Green Version]
- Otalora, G.; Övgün, A.; Saavedra, J.; Videla, N. Inflation from a nonlinear magnetic monopole field nonminimally coupled to curvature. JCAP 2018, 06, 003. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. Roy. Soc. Lond. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Frolov, V. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef] [Green Version]
- Kruglov, S.I. Regular model of magnetized black hole with rational nonlinear electrodynamics. Int. J. Mod. Phys. A 2021, 36, 2150158. [Google Scholar] [CrossRef]

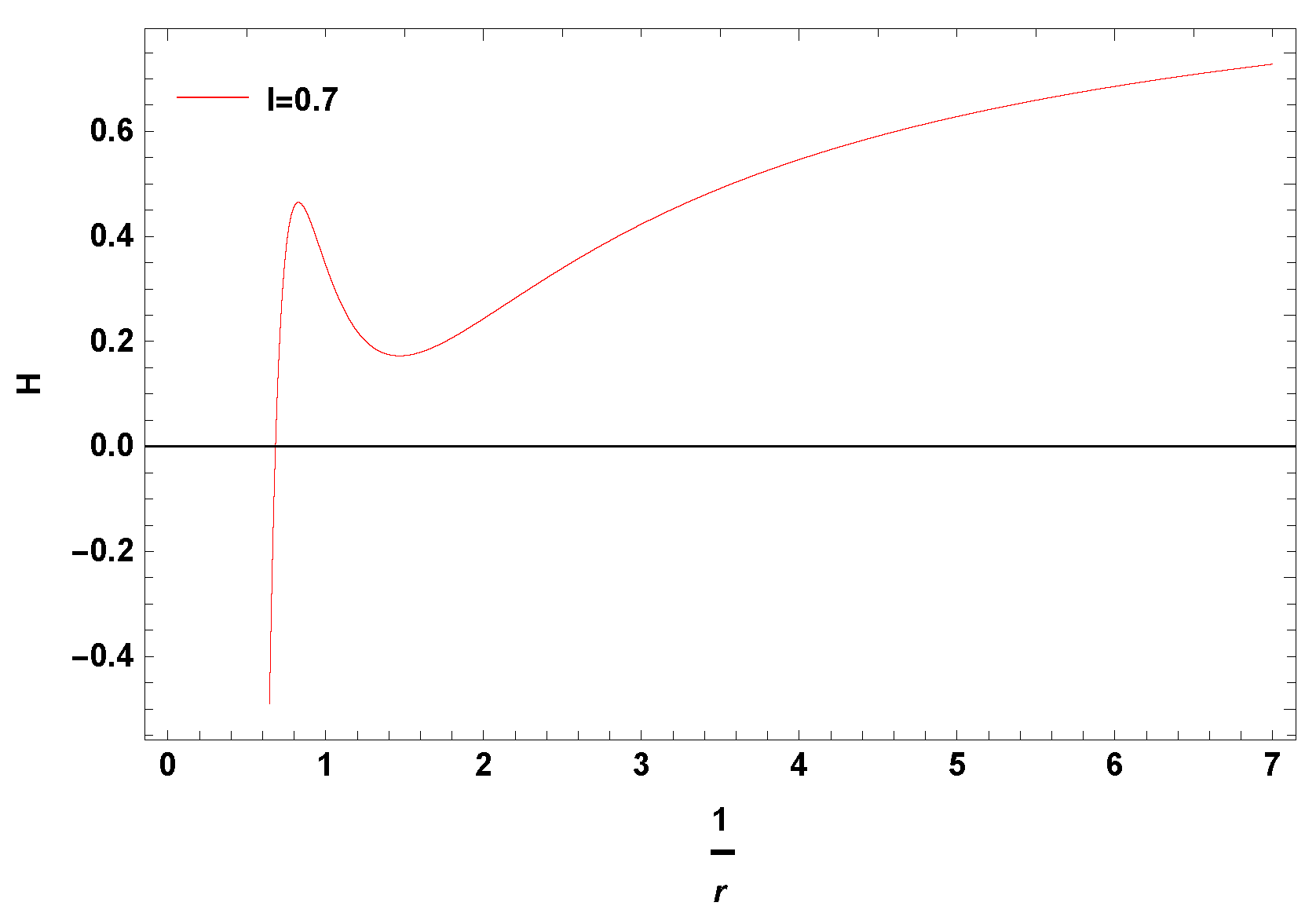
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, W.; Riaz, S.; Övgün, A. Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole. Universe 2022, 8, 262. https://doi.org/10.3390/universe8050262
Javed W, Riaz S, Övgün A. Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole. Universe. 2022; 8(5):262. https://doi.org/10.3390/universe8050262
Chicago/Turabian StyleJaved, Wajiha, Sibgha Riaz, and Ali Övgün. 2022. "Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole" Universe 8, no. 5: 262. https://doi.org/10.3390/universe8050262
APA StyleJaved, W., Riaz, S., & Övgün, A. (2022). Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole. Universe, 8(5), 262. https://doi.org/10.3390/universe8050262






