Is the Hubble Crisis Connected with the Extinction of Dinosaurs?
Abstract
:1. Introduction
- The sound horizon scale is properly calibrated by the CMB anisotropy spectrum and/or BBN in the context of standard prerecombination physics.
- The form of is consistent with (1) as constrained by low z distance probes which are independent of any type of calibration.
- The calibration of SnIa implemented e.g., via Cepheid stars at remains valid at where the Hubble flow is probed.
1.1. Gravitational Transition as a Proposed Solution to the Hubble Crisis
- They have the same good quality of fit as the standard CDM for geometric cosmological data that probe the Hubble expansion rate while being consistent with local calibrators (e.g., Cepheid stars) of the SnIa absolute magnitude [20].
- They have better quality of fit than standard CDM for dynamical cosmological data that probe the growth rate of cosmological perturbations (weak lensing [52,53,54], redshift space distortions [55,56,57] and cluster count data [58,59,60,61,62,63]). These data suggest weaker growth than that implied by CDM in the context of general relativity [64,65,66,67]. This weaker growth is naturally provided in the context of the gravitational transition to weaker gravity (lower ) at early times assumed in this class of models [19].
- The sudden gravitational transition hypothesis has several profound observational consequences that make it testable by a wide range of data on scales starting from geological and solar system scales up to astrophysical and cosmological scales. Surprisingly, current data can not rule out such gravitational transition because only the time derivative of is strongly constrained while constraints on a transition are much weaker (see Table 1). Instead, hints have recently been found for such a transition in Tully–Fisher data [30] and also in Cepheid-SnIa calibrator data [50].
1.2. Observational Constraints on the Gravitational Transition
1.3. Effects of a Gravitational Transition on the Solar System Chronology
2. The Oort Cloud and Long Period Comets
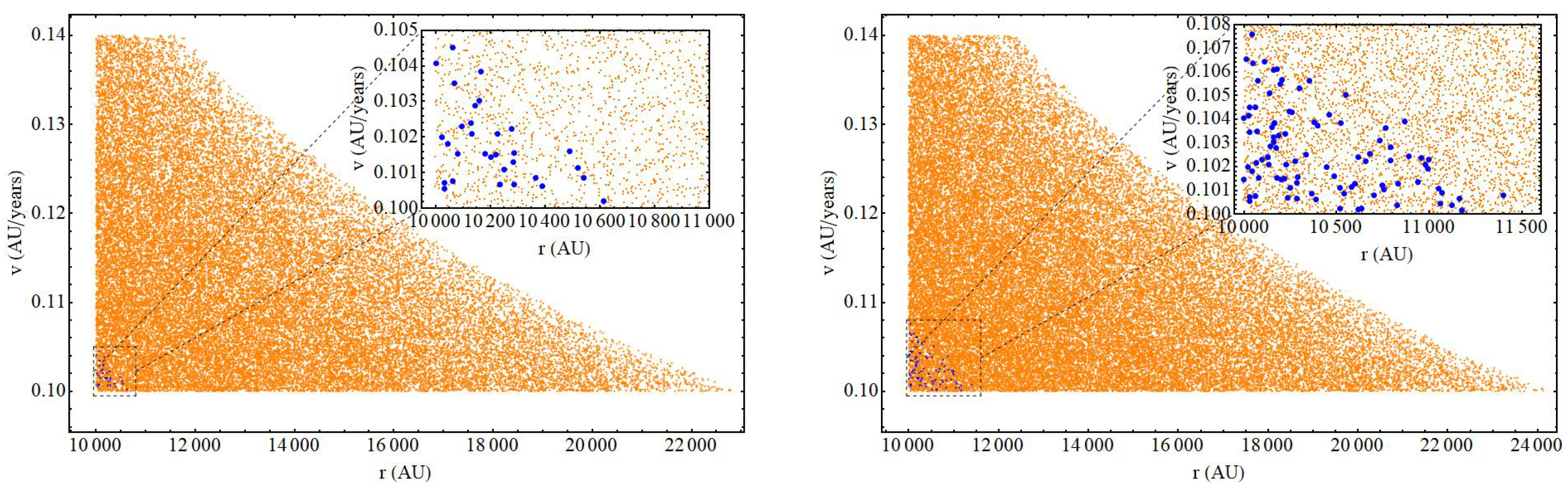
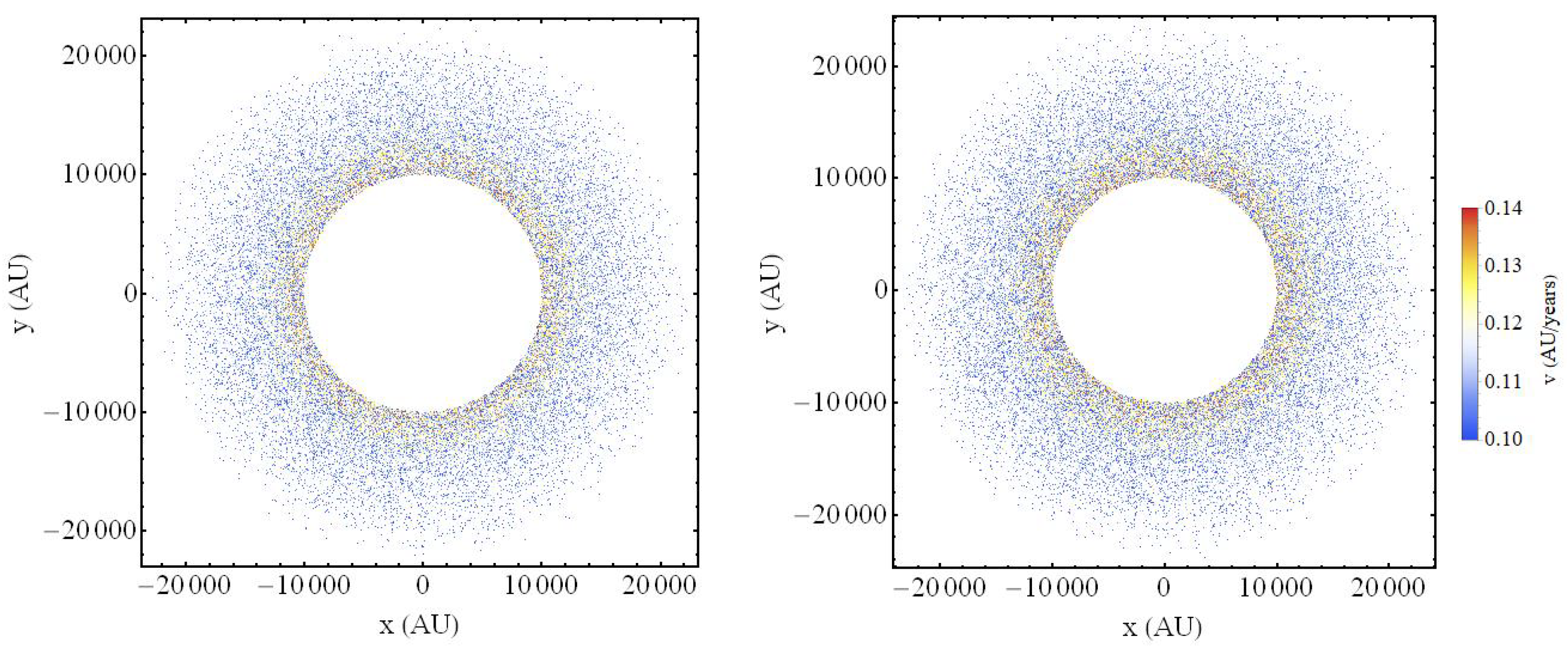
3. Effects of a Gravitational Transition on the LPC Flux: A Monte Carlo Approach
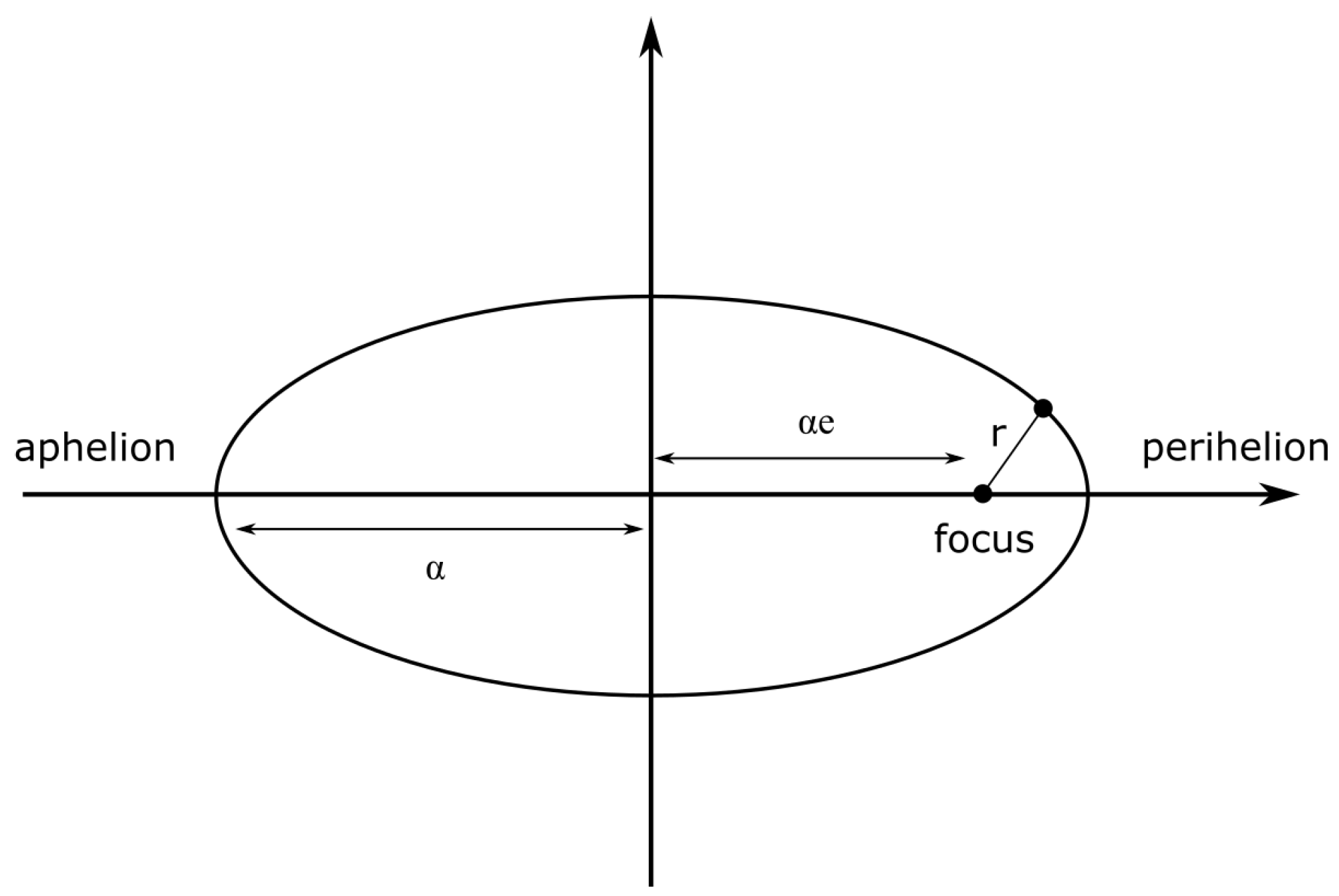
- We consider a sample of points (LPCs) with random initial radial coordinate distances from the primary focus of the ellipse ranging from to , with initial velocity corresponding to circular orbits perturbed by a random velocity perturbation, and with random magnitude ranging from 0 to AU/yr and direction . The corresponding unperturbed circular velocities range from AU/yr to AU/yr. Thus, the considered velocity perturbations are of the same order as the unperturbed initial circular velocities and are assumed to be induced by stellar encounters and/or by galactic tidal effects.
- The total initial velocities of each simulated comet in polar coordinates are obtained from a superposition of the unperturbed initial circular velocity plus a random velocity perturbation,where corresponds to the magnitudes of the initial random comet velocity perturbations, is the initial comet distances from the primary focus and the random angular position of each comet is . The random selection of the velocity perturbation is performed using a uniform probability distribution for both the magnitude of the velocity and its direction in the plane of motion.
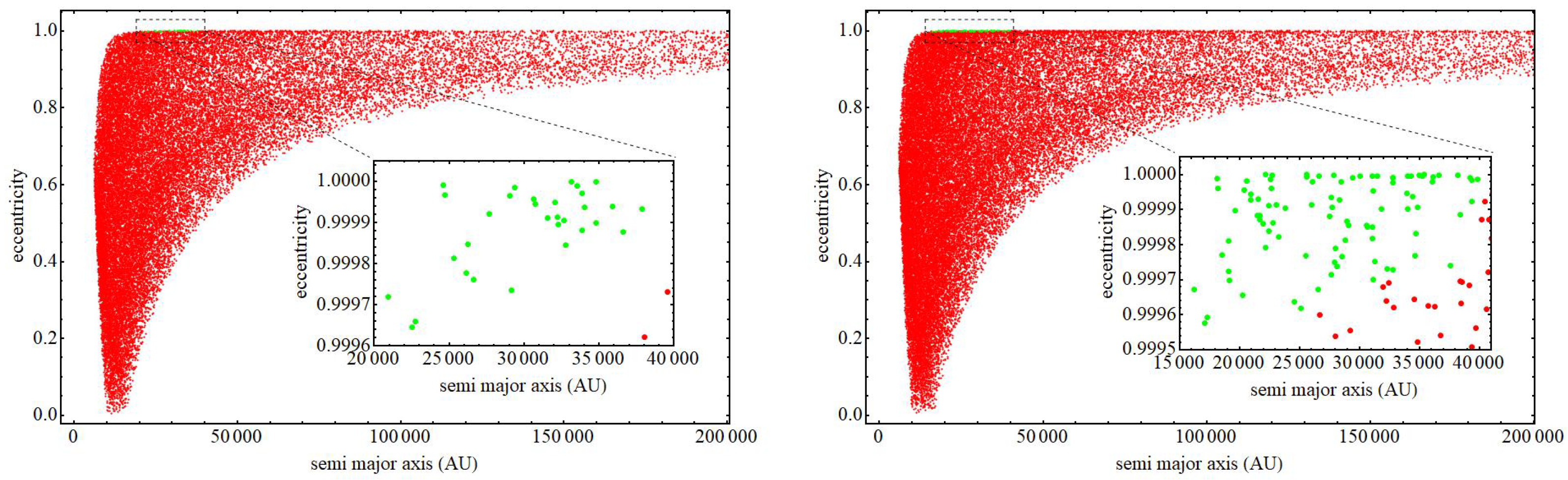
- From comets with the randomly perturbed velocities, we then select those that have the following properties: a. their semi-major axis as obtained from (10) is in the range and b. their eccentricity after the perturbation is inside the loss cone, namely they have a perihelion p less than (approximately Saturn’s distance from the Sun). This condition corresponds to eccentricities in the range [83]. This implies that these perturbed comets will enter the solar system and suffer stronger perturbations by the solar system planets, which could thus further disrupt their orbits, leading to possible impacts with planets or satellites in the solar system. The percentage of comets that enter the planetary region is thus recorded for various ranges of the velocity perturbation magnitude .
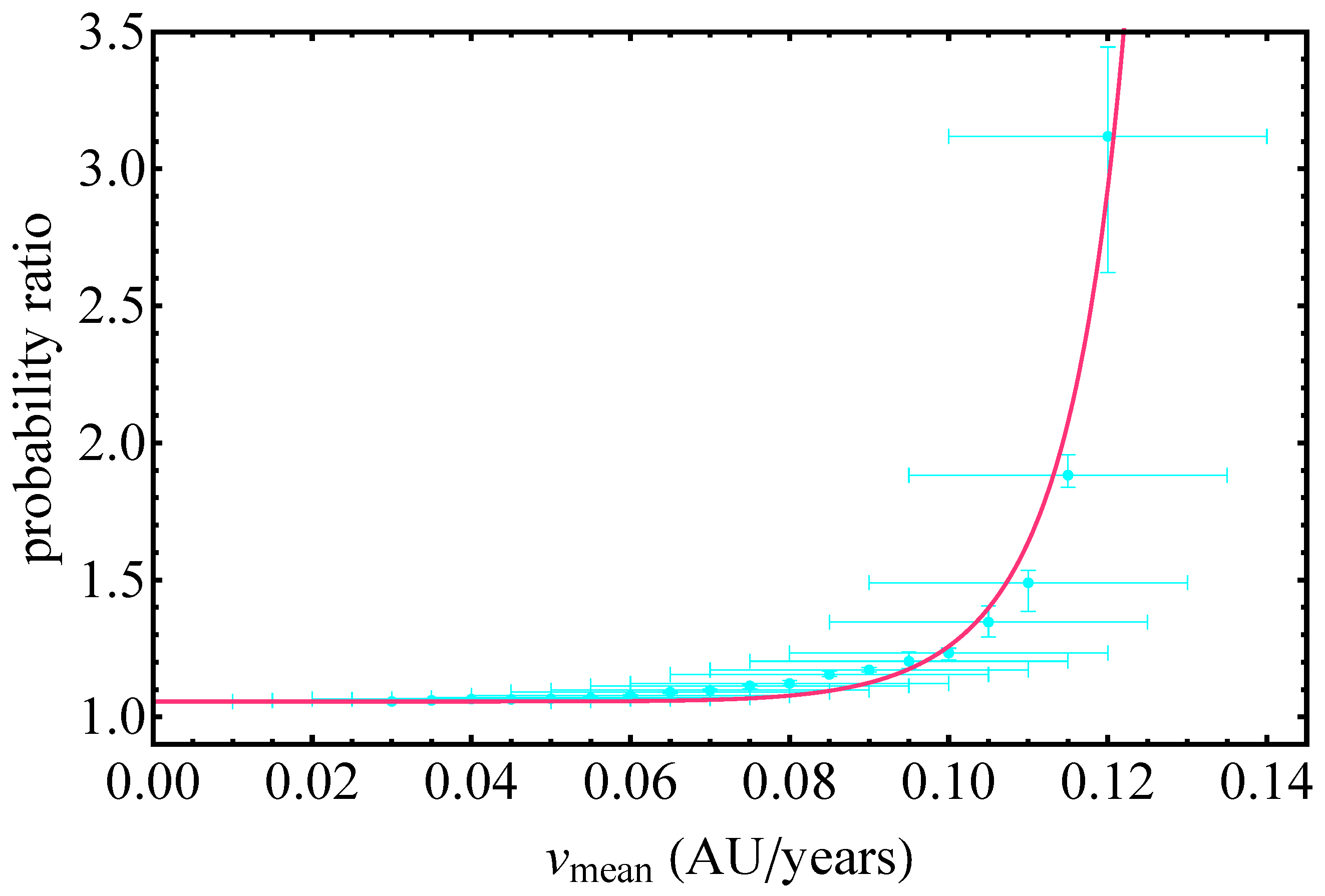
- The above Monte Carlo simulation is repeated for a increased value of Newton’s constant , which corresponds to increasing the value of (or the value by which is replaced in the AU-yr units) by the same percentage. The new fraction of comets that enter the loss cone (planetary region) is thus recorded, and its ratio is taken over the corresponding fraction obtained with the standard value of (). This ratio provides the excess probability that the comet will enter the loss cone after the gravitational transition to stronger gravity.
4. Conclusions
- The new extended Pantheon + dataset [2] of Cepheid + SnIa data provides the opportunity for a comprehensive analysis of the unified Cepheid+SnIa data in the redshift range in a self-consistent and unified manner. Such an analysis which may be implemented once the full Pantheon+ dataset becomes publicly available will allow the more detailed search for signatures of a transition for redshifts , extending the analysis of [50]. Even in the current analysis of the Pantheon + dataset [2], hints for a transition are evident in Figure 10 of [2], where it is shown that the more distant Cepheids in SnIa hosts tend to have a higher value of the period luminosity parameter than the Cepheids in the closeby anchor galaxies (Figure 7). This effect is significantly amplified if the outliers are taken into account (red points).
- As implied by Equation (5), the temperature of Earth strongly depends on the value of (see Equation (5)) [70] and so does the solar luminosity . Thus, an increase in would lead to a similar increase in the Earth temperature. Thus, a careful search of unaccounted for temperature variations of Earth during the past could either impose strong constraints on the gravitational transition hypothesis, or could reveal possible signatures of such an event.
- The search for physically motivated models and mechanisms that could generically predict the presence of such a gravitational transition realized either spatially through the nucleation of true vacuum bubbles [50] or as a transition in time involving, e.g., a pressure singularity [68], is also an interesting extension of this analysis.
- The study of the stability of the whole solar system under a gravitational transition is also an interesting extension of the present analysis. The Lyapunov time of the chaotic solar system is of O (100 Myrs). Therefore, it is highly nontrivial to conclude that the solar system is stable or unstable under a finite transition of on the timescale of the Lyapunov time. The question to address in this context is ‘What is the maximum abrupt fractional change of such that the solar system survives the transition?’. For a two body Sun–Earth system, it is easy to show via a simple simulation that the orbit of the Earth gets slightly deformed by an abrupt change in the gravitational strength, but this cannot be generalized to the much more complex full solar system dynamics.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | It has been shown by [18] that gravitational transitions with high are unable to resolve the cosmological tensions. |
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. arXiv 2021, arXiv:2112.04510. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Efstathiou, G. A Lockdown Perspective on the Hubble Tension (with comments from the SH0ES team). arXiv 2020, arXiv:2007.10716. [Google Scholar]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Bites the Dust: Sensitivity of the Hubble Constant Determination to Cepheid Color Calibration. arXiv 2021, arXiv:2105.11461. [Google Scholar]
- Kazantzidis, L.; Perivolaropoulos, L. Hints of a Local Matter Underdensity or Modified Gravity in the Low z Pantheon data. Phys. Rev. D 2020, 102, 023520. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Koo, H.; Nesseris, S.; Perivolaropoulos, L.; Shafieloo, A. Hints for possible low redshift oscillation around the best-fitting ΛCDM model in the expansion history of the Universe. Mon. Not. R. Astron. Soc. 2021, 501, 3421–3426. [Google Scholar] [CrossRef]
- Sapone, D.; Nesseris, S.; Bengaly, C.A.P. Is there any measurable redshift dependence on the SN Ia absolute magnitude? Phys. Dark Univ. 2021, 32, 100814. [Google Scholar] [CrossRef]
- Dainotti, M.G.; de Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [Green Version]
- Niedermann, F.; Sloth, M.S. New early dark energy. Phys. Rev. D 2021, 103, L041303. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; de Laurentis, M.; Olmo, G.J.; Akrami, Y.; Bahamonde, S.; et al. Modified Gravity and Cosmology: An Update by the CANTATA Network. arXiv 2021, arXiv:2105.12582. [Google Scholar]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 tension, phantom dark energy, and cosmological parameter degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L. Late-time approaches to the Hubble tension deforming H(z), worsen the growth tension. Mon. Not. R. Astron. Soc. 2021, 504, 3956–3962. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L.; Zhao, G.B. Why reducing the cosmic sound horizon alone can not fully resolve the Hubble tension. Commun. Phys. 2021, 4, 123. [Google Scholar] [CrossRef]
- Sakr, Z.; Sapone, D. Can varying the gravitational constant alleviate the tensions? J. Cosmol. Astropart. Phys. 2022, 3, 034. [Google Scholar] [CrossRef]
- Marra, V.; Perivolaropoulos, L. Rapid transition of Geff at zt ≃ 0.01 as a possible solution of the Hubble and growth tensions. Phys. Rev. D 2021, 104, L021303. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. w-M phantom transition at zt < 0.1 as a resolution of the Hubble tension. Phys. Rev. D 2021, 103, 083517. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. An Ultra-Late Gravitational Transition as a Resolution of the Hubble Tension. 2022. Available online: https://www.youtube.com/watch?v=TGOQ3i_sz_s (accessed on 22 January 2022).
- Esposito-Farese, G.; Polarski, D. Scalar tensor gravity in an accelerating universe. Phys. Rev. D 2001, 63, 063504. [Google Scholar] [CrossRef] [Green Version]
- Ashoorioon, A.; van de Bruck, C.; Millington, P.; Vu, S. Effect of transitions in the Planck mass during inflation on primordial power spectra. Phys. Rev. D 2014, 90, 103515. [Google Scholar] [CrossRef] [Green Version]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Hassan Puttasiddappa, P. Difficulties in reconciling non-negligible differences between the local and cosmological values of the gravitational coupling in extended Brans-Dicke theories. J. Cosmol. Astropart. Phys. 2021, 9, 040. [Google Scholar] [CrossRef]
- Uzan, J.P. The Fundamental Constants and Their Variation: Observational Status and Theoretical Motivations. Rev. Mod. Phys. 2003, 75, 403. [Google Scholar] [CrossRef] [Green Version]
- Gaztanaga, E.; Garcia-Berro, E.; Isern, J.; Bravo, E.; Dominguez, I. Bounds on the possible evolution of the gravitational constant from cosmological type Ia supernovae. Phys. Rev. D 2002, 65, 023506. [Google Scholar] [CrossRef] [Green Version]
- Alvey, J.; Sabti, N.; Escudero, M.; Fairbairn, M. Improved BBN Constraints on the Variation of the Gravitational Constant. Eur. Phys. J. 2020, C80, 148. [Google Scholar] [CrossRef]
- Alestas, G.; Camarena, D.; di Valentino, E.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition vs. smooth H(z) deformation models for the resolution of the Hubble crisis. arXiv 2021, arXiv:2110.04336. [Google Scholar]
- Alestas, G.; Antoniou, I.; Perivolaropoulos, L. Hints for a Gravitational Transition in Tully–Fisher Data. Universe 2021, 7, 366. [Google Scholar] [CrossRef]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quant. Grav. 2018, 35, 035015. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P.; Pavlov, D.A.; Turygin, C.C. Estimates of the change rate of solar mass and gravitational constant based on the dynamics of the Solar System. Astron. Astrophys. 2021, 647, A141. [Google Scholar] [CrossRef]
- Deller, A.T.; Verbiest, J.P.W.; Tingay, S.J.; Bailes, M. Extremely high precision VLBI astrometry of PSR J0437-4715 and implications for theories of gravity. Astrophys. J. Lett. 2008, 685, L67. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.W.; Desvignes, G.; Wex, N.; Caballero, R.N.; Champion, D.J.; Demorest, P.B.; Ellis, J.A.; Janssen, G.H.; Kramer, M.; Krieger, A.; et al. Tests of Gravitational Symmetries with Pulsar Binary J1713+0747. Mon. Not. R. Astron. Soc. 2019, 482, 3249–3260. [Google Scholar] [CrossRef] [Green Version]
- Genova, A.; Mazarico, E.; Goossens, S.; Lemoine, F.G.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission. Nat. Commun. 2018, 9, 289. [Google Scholar] [CrossRef] [Green Version]
- Masuda, K.; Suto, Y. Transiting planets as a precision clock to constrain the time variation of the gravitational constant. Publ. Astron. Soc. Jpn. 2016, 68, L5. [Google Scholar] [CrossRef] [Green Version]
- Córsico, A.H.; Althaus, L.G.; García-Berro, E.; Romero, A.D. An independent constraint on the secular rate of variation of the gravitational constant from pulsating white dwarfs. J. Cosmol. Astropart. Phys. 2013, 6, 032. [Google Scholar] [CrossRef]
- Hellings, R.W.; Adams, P.J.; Anderson, J.D.; Keesey, M.S.; Lau, E.L.; Standish, E.M.; Canuto, V.M.; Goldman, I. Experimental Test of the Variability of G Using Viking Lander Ranging Data. Phys. Rev. Lett. 1983, 51, 1609–1612. [Google Scholar] [CrossRef]
- Guenther, D.B.; Krauss, L.M.; Demarque, P. Testing the Constancy of the Gravitational Constant Using Helioseismology. Astrophys. J. 1998, 498, 871–876. [Google Scholar] [CrossRef] [Green Version]
- Bellinger, E.P.; Christensen-Dalsgaard, J. Asteroseismic constraints on the cosmic-time variation of the gravitational constant from an ancient main-sequence star. Astrophys. J. Lett. 2019, 887, L1. [Google Scholar] [CrossRef] [Green Version]
- Vijaykumar, A.; Kapadia, S.J.; Ajith, P. Constraints on the time variation of the gravitational constant using gravitational-wave observations of binary neutron stars. Phys. Rev. Lett. 2021, 126, 141104. [Google Scholar] [CrossRef]
- Degl’Innocenti, S.; Fiorentini, G.; Raffelt, G.G.; Ricci, B.; Weiss, A. Time variation of Newton’s constant and the age of globular clusters. Astron. Astrophys. 1996, 312, 345–352. [Google Scholar]
- Thorsett, S.E. The Gravitational constant, the Chandrasekhar limit, and neutron star masses. Phys. Rev. Lett. 1996, 77, 1432–1435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jofre, P.; Reisenegger, A.; Fernandez, R. Constraining a possible time-variation of the gravitational constant through gravitochemical heating of neutron stars. Phys. Rev. Lett. 2006, 97, 131102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giani, L.; Frion, E. Testing the Equivalence Principle with Strong Lensing Time Delay Variations. J. Cosmol. Astropart. Phys. 2020, 9, 008. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke cosmology with a Λ-term: A possible solution to ΛCDM tensions. Class. Quant. Grav. 2020, 37, 245003. [Google Scholar] [CrossRef]
- Avilez, A.; Skordis, C. Cosmological constraints on Brans-Dicke theory. Phys. Rev. Lett. 2014, 113, 011101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, F.; Chen, X. Cosmic microwave background with Brans-Dicke gravity II: Constraints with the WMAP and SDSS data. Phys. Rev. D 2010, 82, 083003. [Google Scholar] [CrossRef] [Green Version]
- Wright, B.S.; Li, B. Type Ia supernovae, standardizable candles, and gravity. Phys. Rev. D 2018, 97, 083505. [Google Scholar] [CrossRef] [Green Version]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid SnIa calibrator parameters? Phys. Rev. D 2021, 104, 123511. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L.; Tanidis, K. Constraining a late time transition of Geff using low-z galaxy survey data. arXiv 2022, arXiv:2201.05846. [Google Scholar]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef] [Green Version]
- Köhlinger, F.; Viola, M.; Joachimi, B.; Hoekstra, H.; van Uitert, E.; Hildebrandt, H.; Choi, A.; Erben, T.; Heymans, C.; Joudaki, S.; et al. KiDS-450: The tomographic weak lensing power spectrum and constraints on cosmological parameters. Mon. Not. R. Astron. Soc. 2017, 471, 4412–4435. [Google Scholar] [CrossRef]
- Joudaki, S.; Blake, C.; Johnson, A.; Amon, A.; Asgari, M.; Choi, A.; Erben, T.; Glazebrook, K.; Harnois-Déraps, J.; Heymans, C.; et al. KiDS-450 + 2dFLenS: Cosmological parameter constraints from weak gravitational lensing tomography and overlapping redshift-space galaxy clustering. Mon. Not. R. Astron. Soc. 2018, 474, 4894–4924. [Google Scholar] [CrossRef]
- Zhao, G.B.; Wang, Y.; Saito, S.; Gil-Marín, H.; Percival, W.J.; Wang, D.; Chuang, C.H.; Ruggeri, R.; Mueller, E.M.; Zhu, F.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: A tomographic measurement of cosmic structure growth and expansion rate based on optimal redshift weights. Mon. Not. R. Astron. Soc. 2019, 482, 3497–3513. [Google Scholar] [CrossRef] [Green Version]
- Huterer, D.; Shafer, D.; Scolnic, D.; Schmidt, F. Testing ΛCDM at the lowest redshifts with SN Ia and galaxy velocities. J. Cosmol. Astropart. Phys. 2017, 5, 015. [Google Scholar] [CrossRef]
- Samushia, L.; Percival, W.J.; Raccanelli, A. Interpreting large-scale redshift-space distortion measurements. Mon. Not. R. Astron. Soc. 2012, 420, 2102–2119. [Google Scholar] [CrossRef]
- Rapetti, D.; Allen, S.W.; Mantz, A.; Ebeling, H. Constraints on modified gravity from the observed X-ray luminosity function of galaxy clusters. Mon. Not. R. Astron. Soc. 2009, 400, 699. [Google Scholar] [CrossRef] [Green Version]
- Costanzi, M.; Saro, A.; Bocquet, S.; Abbott, T.M.C.; Aguena, M.; Allam, S.; Amara, A.; Annis, J.; Avila, S.; Bacon, D.; et al. Cosmological constraints from DES Y1 cluster abundances and SPT multiwavelength data. Phys. Rev. D 2021, 103, 043522. [Google Scholar] [CrossRef]
- Costanzi, M.; Rozo, E.; Simet, M.; Zhang, Y.; Evrard, A.E.; Mantz, A.; Rykoff, E.S.; Jeltema, T.; Gruen, D.; Allen, S.; et al. Methods for cluster cosmology and application to the SDSS in preparation for DES Year 1 release. Mon. Not. R. Astron. Soc. 2019, 488, 4779–4800. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. Astron. Astrophys. 2016, 594, A24. [Google Scholar] [CrossRef] [Green Version]
- Mantz, A.; Allen, S.W.; Rapetti, D.; Ebeling, H. The Observed Growth of Massive Galaxy Clusters I: Statistical Methods and Cosmological Constraints. Mon. Not. R. Astron. Soc. 2010, 406, 1759–1772. [Google Scholar] [CrossRef] [Green Version]
- Rozo, E.; Wechsler, R.H.; Rykoff, E.S.; Annis, J.T.; Becker, M.R.; Evrard, A.E.; Frieman, J.A.; Hansen, S.M.; Hao, J.; Johnston, D.E.; et al. Cosmological Constraints from the SDSS maxBCG Cluster Catalog. Astrophys. J. 2010, 708, 645–660. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. σ8 Tension. Is Gravity GettingWeaker at Low z? Observational Evidence and Theoretical Implications. In Modified Gravity and Cosmology; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Macaulay, E.; Wehus, I.K.; Eriksen, H.K. Lower Growth Rate from Recent Redshift Space Distortion Measurements than Expected from Planck. Phys. Rev. Lett. 2013, 111, 161301. [Google Scholar] [CrossRef] [PubMed]
- Tsujikawa, S. Possibility of realizing weak gravity in redshift space distortion measurements. Phys. Rev. D 2015, 92, 044029. [Google Scholar] [CrossRef] [Green Version]
- Skara, F.; Perivolaropoulos, L. Tension of the EG statistic and redshift space distortion data with the Planck-ΛCDM model and implications for weakening gravity. Phys. Rev. D 2020, 101, 063521. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Oikonomou, V.K. Did the Universe Experienced a Pressure non-Crushing Type Cosmological Singularity in the Recent Past? Europhys. Lett. 2022, 137, 39001. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Galaxies with Extended Rotation Curves and the Stellar Mass of Rotating Galaxies. Astrophys. J. 2005, 632, 859–871. [Google Scholar] [CrossRef] [Green Version]
- Teller, E. On the Change of Physical Constants. Phys. Rev. 1948, 73, 801–802. [Google Scholar] [CrossRef]
- Bottke, W.; Vokrouhlický, D.; Nesvorný, D. An asteroid breakup 160Myr ago as the probable source of the K/T impactor. Nature 2007, 449, 48–53. [Google Scholar] [CrossRef]
- Shoemaker, E.M. Impact Cratering through Geologic Time. J. R. Astron. Soc. Can. 1998, 92, 297. Available online: https://ui.adsabs.harvard.edu/abs/1998JRASC..92..297S (accessed on 20 March 2022).
- Terada, K.; Morota, T.; Kato, M. Asteroid shower on the Earth-Moon system immediately before the Cryogenian period revealed by KAGUYA. Nat. Commun. 2020, 11, 3453. [Google Scholar] [CrossRef] [PubMed]
- Gehrels, T. Hazards Due to Comets and Asteroids; University of Arizona Press: Tucson, AZ, USA, 1995; Available online: https://ui.adsabs.harvard.edu/abs/1995hdca.book.....G (accessed on 20 March 2022).
- McEwen, A.S.; Moore, J.M.; Shoemaker, E.M. The Phanerozoic impact cratering rate: Evidence from the farside of the Moon. J. Geophys. Res. Planets 2007, 102, 9231–9242. [Google Scholar] [CrossRef]
- Ward, S.; Day, S. Terrestrial crater counts: Evidence of a two to four-fold increase in bolide flux at 125 Ma. Earth Planets Space 2007. Available online: https://websites.pmc.ucsc.edu/~ward/papers/crater-counts(v2.4).pdf (accessed on 20 March 2022).
- Festou, C.M.; Keller, U.H.; Weaver, H.A. Comets II; University of Arizona Press: Tucson, AZ, USA, 2004; ISBN 978-0-8165-2450-1. Available online: https://ui.adsabs.harvard.edu/abs/2004come.book.....F (accessed on 20 March 2022).
- Bridges, J.C.; Changela, H.G.; Nayakshin, S.; Starkey, N.A.; Franchi, I.A. Chondrule fragments from Comet Wild2: Evidence for high temperature processing in the outer Solar System. Earth Planet. Sci. Lett. 2012, 341–344, 186–194. [Google Scholar] [CrossRef] [Green Version]
- Cody, G.D.; Heying, E.; Alexander, C.M.O.; Nittler, L.R.; Kilcoyne, A.L.D.; Sandford, S.A.; Stroud, R.M. Establishing a molecular relationship between chondritic and cometary organic solids. Proc. Natl. Acad. Sci. USA 2011, 108, 19171–19176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zolensky, M.; Nakamura-Messenger, K.; Rietmeijer, F.; Leroux, H.; Mikouchi, T.; Ohsumi, K.; Simon, S.; Grossman, L.; Stephan, T.; Weisberg, M.; et al. Comparing Wild 2 particles to chondrites and IDPs. Meteorit. Planet. Sci. 2008, 43, 261–272. [Google Scholar] [CrossRef]
- Nakamura, T.; Noguchi, T.; Tsuchiyama, A.; Ushikubo, T.; Kita, N.T.; Valley, J.W.; Zolensky, M.E.; Kakazu, Y.; Sakamoto, K.; Mashio, E.; et al. Chondrulelike Objects in Short-Period Comet 81P/Wild 2. Am. Assoc. Adv. Sci. 2008, 321, 1664–1667. [Google Scholar] [CrossRef] [Green Version]
- Dones, L.; Weissman, P.R.; Levison, H.F.; Duncan, M.J. Oort Cloud Formation and Dynamics, Star Formation in the Interstellar Medium: In Honor of David Hollenbach. Astron. Soc. Pac. Conf. Ser. 2004, 323, 371. [Google Scholar]
- Heisler, J. Monte Carlo simulations of the Oort comet cloud. Icarus 1990, 88, 104–121. [Google Scholar] [CrossRef]
- Weissman, P.R. The Oort Cloud, Completing the Inventory of the Solar System. Astron. Soc. Pac. Conf. Ser. 1996, 107, 265–288. [Google Scholar]
- Siraj, A.; Loeb, A. Breakup of a long-period comet as the origin of the dinosaur extinction— Scientific Reports. Nat. Publ. Group 2021, 11, 1–5. [Google Scholar]
- Bottke, W.F.; Morbidelli, A.; Jedicke, R.; Petit, J.M.; Levison, H.F.; Michel, P.; Metcalfe, T.S. Debiased Orbital and Absolute Magnitude Distribution of the Near-Earth Objects. Icarus 2002, 156, 399–433. [Google Scholar] [CrossRef]
- Granvik, M.; Morbidelli, A.; Jedicke, R.; Bolin, B.; Bottke, W.F.; Beshore, E.; Vokrouhlický, D.; Nesvorný, D.; Michel, P. Debiased orbit and absolute-magnitude distributions for near-Earth objects. Icarus 2018, 312, 181–207. [Google Scholar] [CrossRef]
- Hills, J.G. Comet showers and the steady-state infall of comets from the Oort cloud. Astron. J. 1981, 86, 1730–1740. [Google Scholar] [CrossRef]
- Dones, L.; Weissman, P.R.; Levison, H.F.; Duncan, M.J. Oort Cloud Formation and Dynamics, Comets II; University of Arizona Press: Tucson, AZ, USA, 2004; p. 153. Available online: https://adsabs.harvard.edu/full/2004ASPC..323..371D (accessed on 20 March 2022).
- Duncan, M.; Quinn, T.; Tremaine, S. The Formation and Extent of the Solar System Comet Cloud. Astron. J. 1987, 94, 1330. [Google Scholar] [CrossRef]
- De Biasi, A. Tidal Effects on the Oort Cloud Comets and Dynamics of the Sun in the Spiral Arms of the Galaxy. Ph.D Thesis, University of Padova, Padova, Italy, 2014. Available online: https://ui.adsabs.harvard.edu/abs/2014PhDT.......263D (accessed on 20 March 2022).

| Method | () | Time Scale (yr) | References | |
|---|---|---|---|---|
| Lunar ranging | 24 | [31] | ||
| Solar system | 50 | [32] | ||
| Pulsar timing | 1.5 | [33] | ||
| Orbits of binary pulsar | 22 | [34] | ||
| Ephemeris of Mercury | 7 | [35] | ||
| Exoplanetary motion | 4 | [36] | ||
| Hubble diagram SnIa | 0.1 | ∼ | [27] | |
| Pulsating white-dwarfs | 0 | [37] | ||
| Viking lander ranging | 6 | [38] | ||
| Helioseismology | [39] | |||
| Asteroseismology | [40] | |||
| Gravitational waves | 8 | [41] | ||
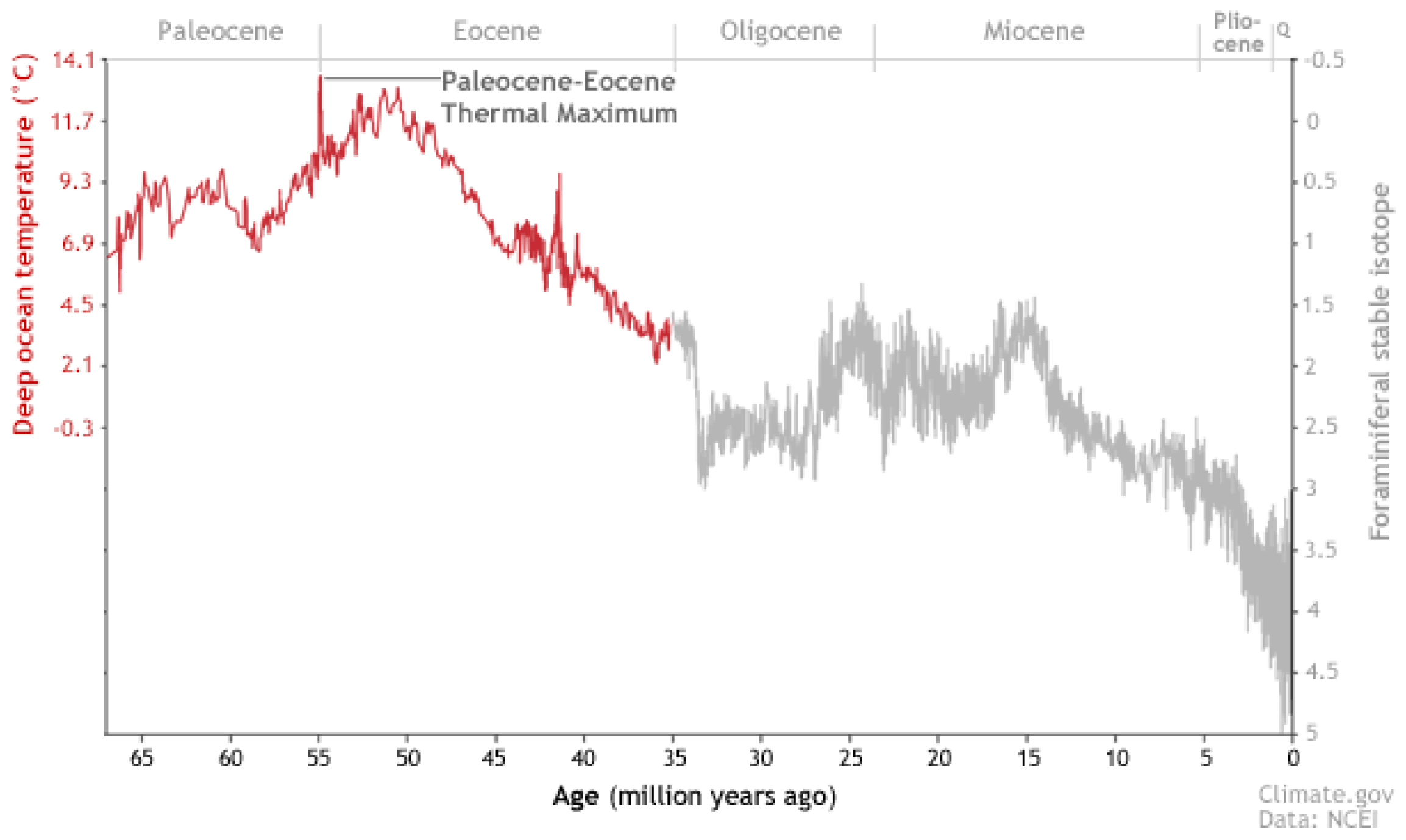
| Paleontology | [26] | |||
| Globular clusters | ∼ | [42] | ||
| Binary pulsar masses | ∼ | [43] | ||
| Gravitochemical heating | ∼ | [44] | ||
| Strong lensing | ∼ | [45] | ||
| Big Bang Nucleosynthesis | [28] | |||
| Anisotropies in CMB | [46,47,48] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perivolaropoulos, L. Is the Hubble Crisis Connected with the Extinction of Dinosaurs? Universe 2022, 8, 263. https://doi.org/10.3390/universe8050263
Perivolaropoulos L. Is the Hubble Crisis Connected with the Extinction of Dinosaurs? Universe. 2022; 8(5):263. https://doi.org/10.3390/universe8050263
Chicago/Turabian StylePerivolaropoulos, Leandros. 2022. "Is the Hubble Crisis Connected with the Extinction of Dinosaurs?" Universe 8, no. 5: 263. https://doi.org/10.3390/universe8050263
APA StylePerivolaropoulos, L. (2022). Is the Hubble Crisis Connected with the Extinction of Dinosaurs? Universe, 8(5), 263. https://doi.org/10.3390/universe8050263






