Constraining MOdified Gravity with the S2 Star

Abstract

We have used publicly available kinematic data for the S2 star to constrain the parameter space of MOdified Gravity. Integrating geodesics and using a Markov Chain Monte Carlo algorithm, we have provided the first constraint on the scales of the Galactic Centre for the parameter $\alpha$ of the theory, which represents the fractional increment of the gravitational constant G with respect to its Newtonian value. Namely, $\alpha \lesssim 0.662$ at 99.7% confidence level (where $\alpha =0$ reduces the theory to General Relativity).

1. Introduction

Scalar-Tensor-Vector Gravity (STVG), also referred to in the literature as MOdified Gravity (MOG), is a theory of gravity firstly proposed in [1] as an alternative to Einstein’s theory of General Relativity (GR). It introduces extra fields in the description of the gravitational interaction, allowing for correct predictions on galactic and extragalactic scales [2,3,4,5,6], without resorting to dark matter [7]. The gravitational action in MOG presents additional terms along the classical Hilbert–Einstein action, depending on the metric tensor $g_{\alpha \beta }$ of spacetime. More specifically, a massive vector field ${\phi }^{\alpha }$ is introduced and its mass, $\mu$, is treated as a scalar field. Furthermore, Newton’s gravitational constant $G_N$ is also elevated to a scalar field G.

The motion of test particles in MOG is affected by the presence of the vector field ${\phi }^{\alpha }$ which acts as a fifth force, whose repulsive character counteracts the increased attraction due to the scalar field nature of G. The fractional increment of G, with respect to its Newtonian value, $G_N$, is given by a new parameter of the theory, $\alpha =(G-G_N)/G_N$. A distinctive feature in the motion of test massive bodies in MOG is that Keplerian orbits in a central potential are characterized by an increased value of the rate of orbital precession [8,9]. This is given by:

$$\mathsf{\Delta }{\omega }_{\mathrm{MOG}}=\mathsf{\Delta }{\omega }_{\mathrm{GR}}\left(1+\frac{5}{6}\alpha \right),$$

(1)

where $\mathsf{\Delta }{\omega }_{\mathrm{GR}}$ is the usual expression of the periastron advance in GR,

$$\mathsf{\Delta }{\omega }_{\mathrm{GR}}=\frac{6\pi G_{N}M}{a{c}^2(1-e^2)},$$

(2)

related to semi-major axis, a, and eccentricity, e, of the orbiting body.

Here, we will summarize the extended work carried out in [8], where we used publicly available data for the S2 star from [10], along with the measurement of its orbital precession from [11] to constrain the parameter space of MOG.

2. MOdified Gravity

In MOG, the gravitational action is written as [1]:

$$\mathcal{S}={\mathcal{S}}_{\mathrm{HE}}+{\mathcal{S}}_m+{\mathcal{S}}_V+{\mathcal{S}}_S.$$

(3)

The first term, ${\mathcal{S}}_{\mathrm{HE}}$, is the classical Hilbert–Einstein action of GR, while $S_m$ is related to the ordinary matter energy-momentum tensor,

$$\begin{array}{cccc}\hfill {\mathcal{S}}_{\mathrm{HE}}& =\frac{1}{16\pi }\int d^{4}x\sqrt{-g}\frac{1}{G}R,\hfill & \hfill T_{\alpha \beta }^m& =-\frac{2}{\sqrt{-g}}\frac{\delta {\mathcal{S}}_m}{\delta g^{\alpha \beta }}.\hfill \end{array}$$

(4)

where $g_{\alpha \beta }$ is the metric tensor of spacetime, g its determinant and R the Ricci scalar. The two extra terms, ${\mathcal{S}}_V$ and ${\mathcal{S}}_S$, on the other hand, are related to the vector and scalar field respectively, and read:

$$\begin{array}{cc}\hfill {\mathcal{S}}_V=& -\int d^{4}x\sqrt{-g}\left(\frac{1}{4}{B}^{\alpha \beta }{B}_{\alpha \beta }-\frac{1}{2}{\mu }^2{\phi }^{\alpha }{\phi }_{\alpha }+V\left(\phi \right)\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathcal{S}}_S=& \int d^{4}x\sqrt{-g}\frac{1}{G^3}\left(\frac{1}{2}{g}^{\alpha \beta }{\nabla }_{\alpha }G{\nabla }_{\beta }G-V\left(G\right)\right)+\int d^{4}x\frac{1}{{\mu }^{2}G}\left(\frac{1}{2}{g}^{\alpha \beta }{\nabla }_{\alpha }\mu {\nabla }_{\beta }\mu -V\left(\mu \right)\right).\hfill \end{array}$$

(6)

With ${\nabla }_{\alpha }$ we have indicated the covariant derivative related to the metric tensor $g_{\alpha \beta }$, and with $B_{\alpha \beta }$ the Faraday tensor associated to the massive vector field ${\phi }_{\alpha }$: $B_{\alpha \beta }={\nabla }_{\alpha }{\phi }_{\beta }-{\nabla }_{\beta }{\phi }_{\alpha }$. $V\left(\phi \right)$, $V\left(G\right)$ and $V\left(\mu \right)$, on the other hand, represent scalar potentials describing the self-interaction of the vector and scalar fields.

In MOG, particles with mass m move according to a modified version of the geodesic equations [12]:

$$\begin{array}{c}\hfill \left(\frac{d^2{x}^{\alpha }}{d{\lambda }^2}+{\Gamma }_{\beta \rho }^{\alpha }\frac{d{x}^{\beta }}{d\lambda }\frac{d{x}^{\rho }}{d\lambda }\right)=\frac{q}{m}{B^{\alpha }}_{\beta }\frac{d{x}^{\beta }}{d\lambda }.\end{array}$$

(7)

The term on the right-hand side represents a fifth force [1,3,12], due to the coupling between massive particles and the vector field ${\phi }^{\alpha }$. The coupling constant, q, is postulated to be positive ($q>0$) so that this force is repulsive [1] and physically stable self-gravitating systems can exist [3]. Additionally, q is taken to be proportional to m, $q=\kappa m$ with $\kappa$ a positive proportionality constant [12], ensuring the validity of Einstein’s Equivalence Principle.

The field equations associated to the MOG action in Equation (3) can be solved exactly assuming that:

• the metric tensor is spherically symmetric;
• the scalar field G can be treated as a constant on the scales of compact objects, ${\partial }_{\nu }G=0$ [13,14]. This means that the aforementioned parameter $\alpha$ can be regarded as a positive dimensionless constant, whose value depends on the mass of the gravitational source [1]:

  $$G=G_N(1+\alpha )=\mathrm{const}.$$

  (8)
• The proportionality constant $\kappa$ defining the fifth-force charge of massive particles is defined by:

  $$\kappa =\sqrt{\alpha G_N}.$$

  (9)
• The mass of the vector field, $\mu$, can be neglected on the scales of compact objects, as its effects are only evident on kpc scales [3,4,15].

Under these assumptions (and by setting the speed of light in vacuum to $c=1$), one obtains [13] the following line element:

$$\begin{array}{cc}\hfill d{s}^2=& \frac{\mathsf{\Delta }}{r^2}d{t}^2-\frac{r^2}{\mathsf{\Delta }}d{r}^2-r^{2}d{\mathsf{\Omega }}^2.\hfill \end{array}$$

(10)

This Schwarzschild-like metric is the most general spherically symmetric static solution in MOG, and it provides an exact description of the gravitational field around a pointlike nonrotating source of mass M (and hence a fifth-force charge $Q=\sqrt{\alpha G_N}M$). It differs from the classical one in GR (to which it reduces when $\alpha =0$) by a different definition of the $\mathsf{\Delta }$ function:

$$\begin{array}{c}\hfill \mathsf{\Delta }=r^2-2G_{N}Mr+\alpha G_{N}M\left((1+\alpha )G_{N}M-2r\right).\end{array}$$

(11)

The solid angle element, on the other hand, has the usual expression $d{\mathsf{\Omega }}^2=d{\theta }^2+{sin}^2\theta d{\varphi }^2$. The vector field ${\phi }^{\alpha }$ associated to the metric tensor in Equation (10) is given by [16]

$${\phi }_{\alpha }=\left(-\frac{\sqrt{\alpha G_N}M}{r},0,0,0\right),$$

(12)

generating a repulsive force directed along the radial direction. As a consequence, the increased value of the gravitational constant G increases the attractive effect of gravity on test particles, while the repulsive effect of the vector field counteracts this effect. As shown in [9], particles around a MOG BH experience an increased orbital precession, whose first-order expression explicitly depends on the parameter $\alpha$ and is given in Equation (1).

3. The Orbit of S2 in MOG

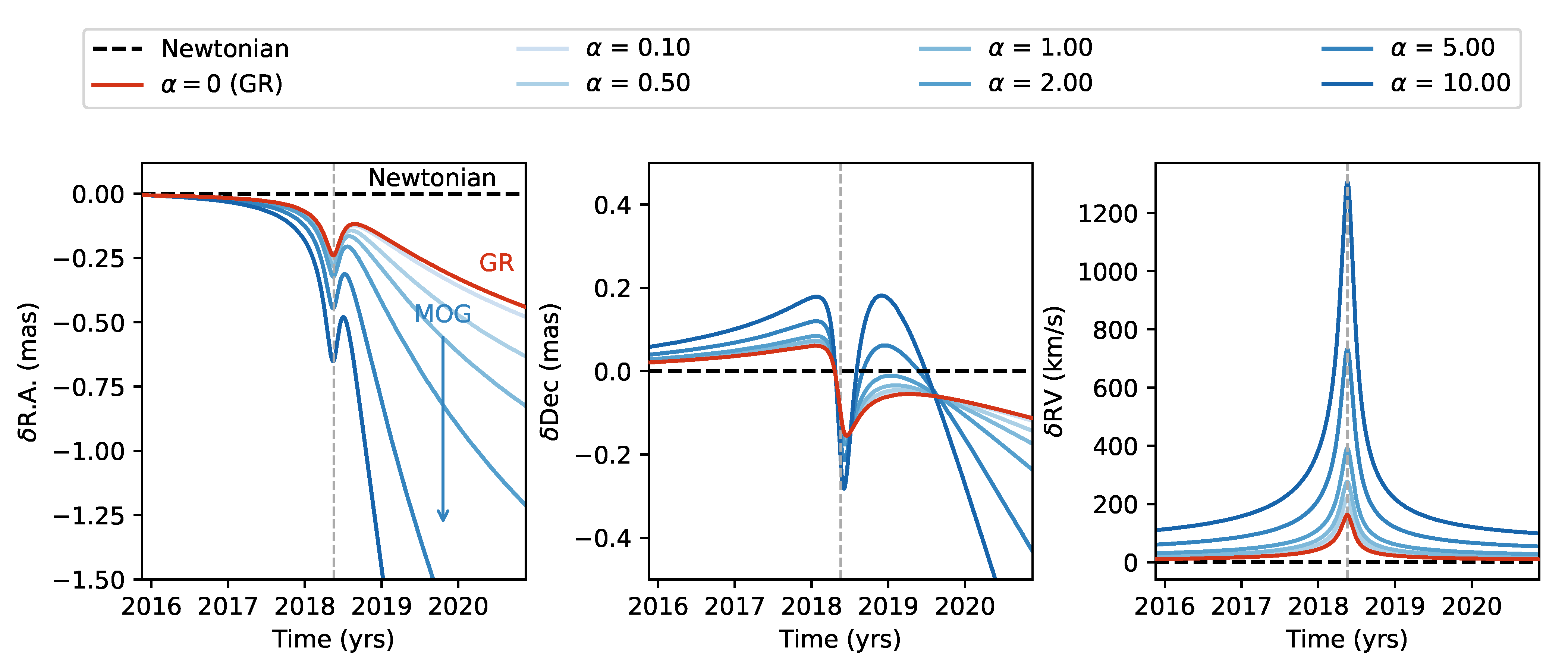
Upon numerically integrating the geodesic equations in Equation (7), we obtain fully relativistic sky-projected orbits for the S2 star in MOG starting from its osculating Keplerian elements at the initial time 1. These parameters are the semimajor axis of the orbit, a, the eccentricity e, the inclination i, the angle of the line of nodes $\mathsf{\Omega }$, the angle from the ascending node to pericentre $\omega$, the orbital period T and the time of the pericentre passage $t_p$. These uniquely assign the initial conditions of the star at a given time, that we set to be the time of passage at apocentre, given by $t_a=t_p-T/2$. Along with these parameters, one needs to fix the mass of the gravitational source, M, its distance from Earth, R, and a possible offset and drift (described by five additional parameters $x_0$, $y_0$, $v_{x,0}$, $v_{y,0}$ and $v_{z,0}$) of this object in the astrometric reference frame of the observer. From the integrated geodesic, the astrometric positions can be obtained via a geometric projection of the spacetime coordinates, through the Thiele-Innes elements [19], and modulating the observation times for the classical Rømer delay. The kinematic line-of-sight velocity of the star is converted into the spectroscopic observable, i.e., its redshift. In doing so we take into account both the special relativistic longitudinal and transverse Doppler effect and the gravitational time dilation, due to the combination of high velocity and high proximity at pericentre. Other effects, such as the gravitational lensing or the Shapiro time delay provide negligible contributions [17,18], and we hence do not take them into account. In Figure 1, we report how much the spectroscopic and the two astrometric observables deviate around pericentre from a Newtonian orbit of the S2 star, for different values of the parameter $\alpha$. As can be seen, measurements performed at and after pericentre of both the astrometric position of the star and its radial velocity carry a signature of the gravitational field produced in MOG.

Figure 1. Numerically integrated sky-projected geodesic trajectories for the S2 star in pre- and post- pericentre (dashed vertical line) phase, for different values of the parameter $\alpha$. In particular, we report the deviation from the Newtonian case (dashed horizontal black line) of the GR orbit ($\alpha =0$, red line) and for increasingly higher values of $\alpha$ (in different shades of blue) on the right ascension direction (left panel), on the declination direction (central panel) and for the radial velocity (right panel).

4. Data and Methodology

S2 is a B-type star in the nuclear star cluster of SgrA*, a compact radio source in the Galactic Centre (GC) of our Galaxy, identified with a supermassive black hole (SMBH) with mass $M\sim 4\times {10}^6{M}_{\odot }$. Throughout its 16-year orbit, both special and general relativistic effects have been detected [11,20,21] confirming predictions from GR on one hand, and opening a new way to test gravity [8,17,18,22] on the other.

We exploit publicly available kinematic data for the S2 star to constrain the 15-dimensional parameter space of our orbital model in MOG, given by (M, R, T, $t_p$, a, e, i, $\mathsf{\Omega }$, $\omega$, $x_0$, $y_0$, $v_{x,0}$, $v_{y,0}$, $v_{z,0}$, $\alpha$). More specifically, we use the astrometric positions and radial velocities of S2 presented in [10] and the measurement of the relativistic orbital precession performed in 2020 by the Gravity Collaboration [11], through precise astrometric observations with the GRAVITY interferometer at VLT (which, however, are not publicly available and we can only rely on the precession measurement itself). In particular, they measured the parameter $f_{\mathrm{SP}}$ in

$$\mathsf{\Delta }\omega =\mathsf{\Delta }{\omega }_{\mathrm{GR}}{f}_{\mathrm{SP}},$$

(13)

where $\mathsf{\Delta }{\omega }_{\mathrm{GR}}$ is given in Equation (2), obtaining $f_{\mathrm{SP}}=1.10\pm 0.19$, thus favoring GR against Newtonian gravity at >5$\sigma$.

In order to fit our orbital model to such data we employ the Markov Chain Monte Carlo (MCMC) sampler in emcee [23], and we evaluate the integrated autocorrelation time of the chains to check the convergence of the algorithm. In particular, we perform two separate analyses:

Ⓐ

We only use astrometric positions and radial velocities up to mid-2016 in [10]. Our dataset, thus, contains no information at all about the 2018 pericentre passage. In this case we use the following log likelihood:

$$log\mathcal{L}=log\mathcal{N}(\mathrm{R}.\mathrm{A}.,{\sigma }_{\mathrm{R}.\mathrm{A}.})+log\mathcal{N}(\mathrm{Dec},{\sigma }_{\mathrm{Dec}})+log\mathcal{N}(\mathrm{RV},{\sigma }_{\mathrm{RV}})$$

(14)

by which we assume that all data points are uncorrelated with each other and that they are normally distributed within their experimental uncertainty, namely:

$$log\mathcal{N}(\mathbf{x},\mathbf{\sigma })=\sum _{i}log\left[\frac{1}{{\sigma }_i\sqrt{2\pi }}exp\left(\frac{{(x_i-{\mu }_i)}^2}{{\sigma }_i^2}\right)\right],$$

(15)

where $x_i$ is the i-th experimental data point, ${\sigma }_i$ its uncertainty and ${\mu }_i$ the corresponding prediction from our model.

Ⓑ

We use the same dataset used in case Ⓐ, but adding as a single measurement the rate of orbital precession obtained in [11]. Since the latter measurement was done using the same astrometric dataset that we use, plus data recorded at pericentre, we need to multiply all our uncertainties by $\sqrt{2}$ to avoid double counting data points. This yields

$$log\mathcal{L}=log\mathcal{N}(\mathrm{R}.\mathrm{A}.,\sqrt{2}{\sigma }_{\mathrm{R}.\mathrm{A}.})+log\mathcal{N}(\mathrm{Dec},\sqrt{2}{\sigma }_{\mathrm{Dec}})+log\mathcal{N}(\mathrm{RV},\sqrt{2}{\sigma }_{\mathrm{RV}})+log\mathcal{N}(f_{\mathrm{SP}},\sqrt{2}{\sigma }_{\mathrm{SP}}).$$

(16)

In both cases we use uniform flat priors for our parameters2 centered on their best-fitting value by [10] and with an amplitude given by 10 times their experimental uncertainty, and we set heuristically $\alpha \in [0,2]$ as uniform interval for the MOG parameter.

5. Results

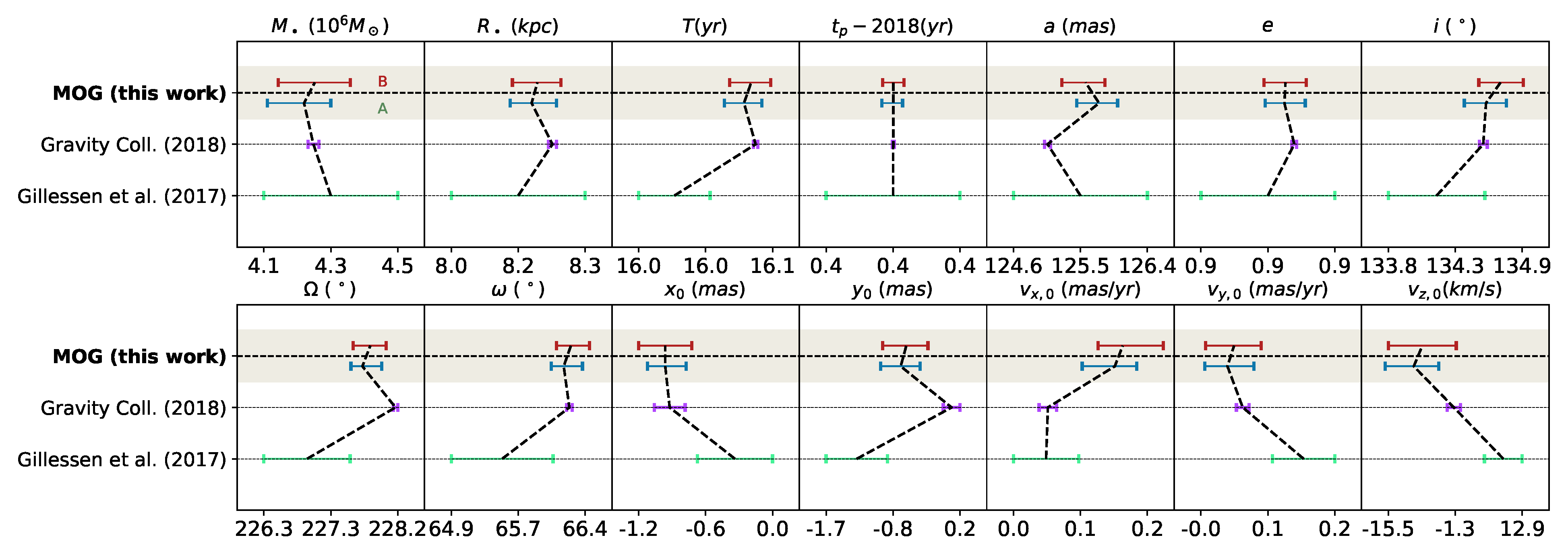
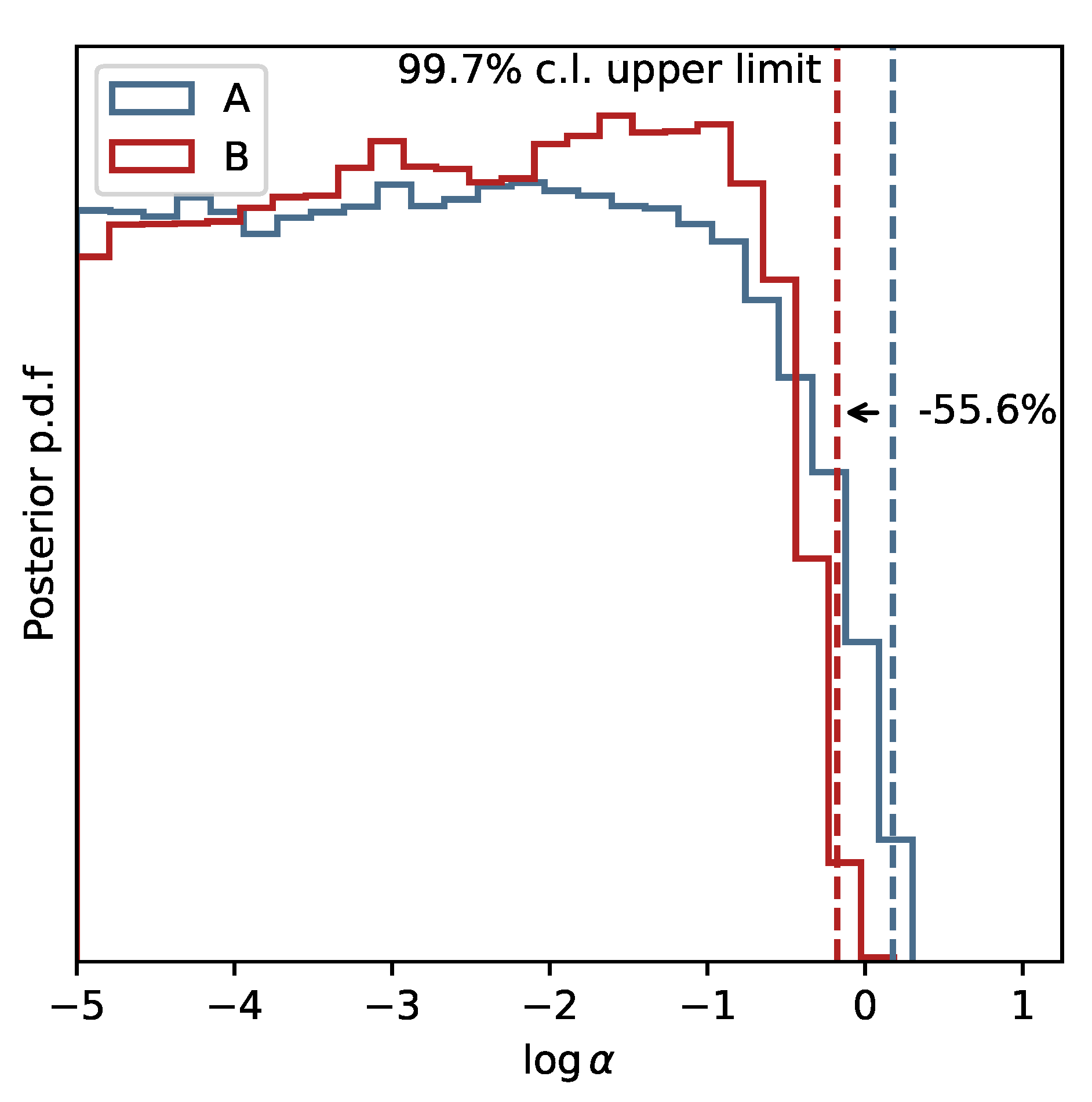
In Figure 2 we report the $1\sigma$ confidence intervals for the orbital parameters in our analyses Ⓐ and Ⓑ, compared with the corresponding $1\sigma$ intervals from [10] (who fitted Keplerian orbits to the data) and [11] (in which a first-order Post-Newtonian orbital model is used). The parameters from our analyses are compatible within their errors with the results from the previous studies. Finally, in Figure 3 we report in logarithmic scale the normalized posterior distributions for the parameter $\alpha$ from the two analysis Ⓐ (in blue) and Ⓑ (in red) along with their 99.7% confidence level (c.l.) upper limit. Our results provide with the first constraint on the MOG theory at the GC, yielding:

$$\begin{array}{cc}\hfill \mathrm{Ⓐ}:& \alpha \lesssim 1.499\mathrm{w}/\mathrm{o}\mathrm{precession}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathrm{Ⓑ}:& \alpha \lesssim 0.662\mathrm{w}/\mathrm{precession}\hfill \end{array}$$

(18)

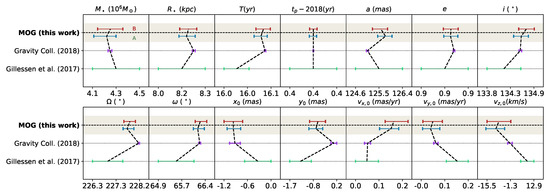
Figure 2. The best fitting values and $1\sigma$ confidence interval for the orbital parameters of the S2 star in our analyses Ⓐ (blue bars) and Ⓑ (red bars), compared with the best-fitting values from previous works in [11] (in which 1-PPN model is fitted to the data) and [10] (using a Keplerian model to describe the orbit of S2).

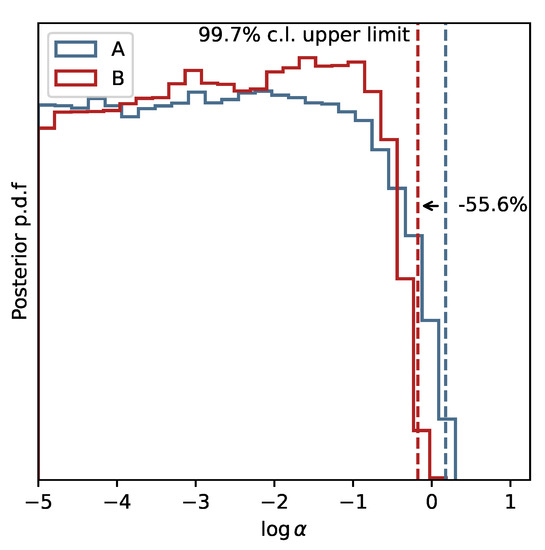
Figure 3. The normalized posterior probability distribution of the parameter $\alpha$ in logarithmic scale for the two analysis Ⓐ (in blue) and Ⓑ (in red). The 99.7% c.l. level upper limit of the parameter is reported as a dashed vertical line in the two cases. The analysis Ⓑ provides a more peaked distribution for $\alpha$ around 0, with the upper limit going down by $55.6\%$ between the two analyses.

While both analyses are compatible with GR, the additional information carried by the single orbital precession data point at pericentre results in a more peaked distribution for $\alpha$ in case Ⓑ, whose upper limit decrease by $55.6\%$ with respect to analysis Ⓐ.

6. Conclusions

Here, we have summarized our results in [8], providing the first constraint on the extra parameter, $\alpha$, of MOG at the GC, obtained by studying the fully relativistic motion of the S2 star around the SMBH SgrA*. In particular, we have numerically solved the geodesic equations for a test particle around a static BH in MOG, described by the metric element in Equation (10), particularizing the kinematic properties of the test particle for the orbital parameters of the S2 star [10,11]. Then, we explored the 15-dimensional parameter space of our model by means of an MCMC algorithm, which allowed us to study the posterior distributions of the parameters, upon comparison with publicly available kinematic data for S2 and the measurement of its rate of orbital precession. In particular, we performed two separate analyses, in which we either excluded–Ⓐ–or included–Ⓑ–the information of the pericentre advance. We demonstrated that the additional information carried by the relativistic orbital precession is able to bring down the 99.7% c.l. upper limit on the parameter $\alpha$ from $\alpha \lesssim 1.499$ in analysis Ⓐ to $\alpha \lesssim 0.662$ in analysis Ⓑ: a significant reduction of $\sim 55.6\%$.