Abstract
This paper investigates the geometry of a gravitational vacuum star (also known as a gravastar) from the perspective of gravity. The gravastar can be treated as a black hole substitute with three domains: (i) the inner domain, (ii) the intrinsic shell, and (iii) the outer domain. We examine these geometries using Kuchowicz ansatz for temporal metric function corresponding to a specific model. We compute a nonsingular radial metric potential for both the interior and intermediate domains. The matching of these domains with exterior Schwarzschild vacuum results in boundary conditions that assist in the evaluation of unknown constants. Finally, we examine various attributes of gravastar domains, such as the equation of state parameter, proper length, energy, and surface redshift. We conclude that the gravastar model is a viable alternative to the black hole in the background of this gravity.
PACS:
04.50.Kd; 04.70.Dy; 97.10.Cv
1. Introduction
Cosmic systems comprised of small- and large-scale structures impact the evolution of the universe and serve as the foundation for cosmological research. Different theories were proposed to study the structure and mechanism of these celestial objects. In this context, Einstein proposed the general theory of relativity (GR) to examine the dynamical interaction between matter, curvature, space, and time, which opened new gateways to cosmology as well as astrophysics. Later on, in 1929, Edwin Hubble proposed that the universe is expanding rapidly as all the galaxies are moving far from us. Many recent observations of the cosmos, such as supernova type 1a, cosmic microwave background radiation, and large-scale structures agree with the rapid expansion of the cosmos [1,2]. An unknown force (termed as dark energy) with large negative pressure is responsible for this cosmic behavior.
One of the leading cosmological models in GR used to describe expansion of cosmos is the CDM model, which includes dark energy (), cold dark matter (CDM), and ordinary matter. However, there are well-known problems in CDM model: cosmic coincidence and fine-tuning hinder the discussion of cosmos in GR. Furthermore, singularities in the high-energy region cannot be explained by GR due to quantum phenomena. To resolve these issues, modified versions of GR were developed to solve the singularity problem as well as the characteristics of enigmatic dark energy. A natural extension of GR called gravity is obtained by incorporating the corresponding function of curvature invariant in the geometric part of the Einstein–Hilbert action. This theory effectively addresses a variety of astrophysical and cosmological challenges [3,4,5].
Harko et al. [6] established gravity as a generalization of theory by introducing a nonminimal coupling between matter and geometry via product of Ricci scalar and trace of the energy–momentum tensor (EMT) T. The particles experience an additional force in nonminimally curvature–matter coupled theories, which shows the violation of conservation law. As a consequence, under the impact of this force, particles follow nongeodesic motion. Nonminimal coupling models yield complex field equations whose solutions are difficult to obtain. Therefore, minimal coupling models are employed to reduce degrees of freedom. In literature, the correlation between accelerated expansion and dark cosmic components was extensively investigated by employing minimal as well as nonminimal coupling between matter and curvature. Furthermore, these interactions provide an efficient description of the rotation curves of galaxies and different cosmic ages.
Many researchers attempted to develop acceptable cosmic models describing the origin, evolution, and transition of the universe through various cosmological eras. In this regard, the Big-Bang model proposed that matter and energy of the universe were confined to a single point (referred to as a singularity), with infinite energy density and temperature. Due to some unknown phenomena, the singularity expanded exponentially leading to the beginning of the universe about 13.8 billion years ago. Despite the wide acceptance of the Big-Bang proposal, researchers put forward other captivating proposals to understand the origin and evolution of the universe. One of them is the bounce theory, which is an alternate approach that describes the evolutionary changes of the universe as a series of bounces (expanding and shrinking repeatedly) with no start or end state. Katirci and Kavuk [7] incorporated the idea of bouncing cosmos in a modification of GR and presented energy–momentum squared gravity (EMSG). In this theory, the Einstein–Hilbert action is modified by incorporating the analytic function of the form . This theory suggests that the universe with maximum energy density and a minimum scale factor in the early times bounces to a phase of expansion [8]. As a result, this proposal overcomes the problem of Big-Bang singularity in nonquantum prescription without influencing the cosmic evolution.
This theory possesses a true sequence of cosmological eras. In the context of the standard cosmological model, the cosmological constant does not play an important role in the early times and becomes important only after the matter-dominated era. In this theory, the repulsive nature of the cosmological constant plays a crucial role at early times in resolving the singularity. The EMSG represents an interesting modified gravity model that can explain the current evolution of the universe and the emergence of accelerated expansion as a geometrical physical effect. The gravity defines the coupling between matter and geometry. On the other hand, gravity is based on the inclusion of analytic function of the form . In contrast to gravity, the EMSG gravity supports bounce theory and is an optimistic approach to study cosmic evolution by resolving the Big-Bang singularity.
Astrophysical and cosmological issues were discussed in the presence of squared matter components in EMSG field equations. Board and Barrow [9] observed that the universe is expanding uniformly in all directions in the context of higher-order matter theories. Nari and Roshan [10] constructed pressureless compact stellar models in the framework of EMSG which were less compact in comparison to that of their GR counterparts. In the perspective of EMSG, Akarsu et al. [11] examined nonminimal couplings for relativistic stellar objects as well as dark matter and obtained appropriate constraints on the CDM model. Bahamonde et al. [12] described the expansion of the universe utilizing various coupling models and concluded that these models are a great fit for understanding the current accelerated expanding behavior of the universe. Sharif and Gul [13,14,15,16,17,18,19,20,21,22] employed Noether symmetries to study the effects of various physical factors on viable astrophysical structures in the background of the same theory. They also investigated the viability and stability of collapsing stellar configurations and observed that gravity correction terms decrease the collapse rate.
Stars composed of hydrogen and helium are the basic building blocks of galaxies arranged systematically in a cosmic web. The star burns its fuel to maintain the equilibrium against the inward directed force of gravity. The outward pressure disappears when a star runs out of fuel within its core. As a consequence, the star experiences gravitational collapse, which results in the formation of new compact objects. One of the compact objects is a completely collapsed structure known as a black hole. Its geometry comprises an event horizon covering the singularity where all laws of physics break down. To address singularity and event horizon issues, Mazur and Motolla [23] proposed a hypothetical compact model (dubbed as a gravitational vacuum star or gravastar) as a replacement for black hole. The most fascinating feature of this hypothetical compact object is its singularity-free structure. The singularity is prevented by using the de Sitter (dS) spacetime in the inner domain, while a layer of baryonic fluid lies between the exterior Schwarzschild and dS spacetimes. The properties of each domain are governed by a particular equation of state (EoS).
Currently, no observable evidence exists in favor of gravastar; however, various studies predict gravastar’s existence and detection in future. In this regard, Sakai et al. [24] proposed a method for detecting gravastar by examining gravastar shadows. Kubo and Sakai [25] found that gravastar could be detected by applying the technique of gravitational lensing (total change in luminosity of nearby or companion stars). They concluded that a gravastar structure having same mass as that of a black hole might have maximal luminosity effect in contrast to a black hole. The occurrence of ringdown signals produced by an object without an event horizon was hinted by the observation of GW150914 using interferometric LIGO detectors [26,27]. A recent study of the images obtained by the First M87 Event Horizon Telescope (EHT) also hinted towards the possibility that these existing shadows may belong to gravastar structure [28].
Many astrophysicists directed their efforts towards investigating the structure and mechanism of gravastars. Visser and Wiltshire [29] explored gravastar’s stability against radial pertubations and found dynamically stable geometries corresponding to different EoS parameter. Carter [30] extended this work by determining the bounds of vacuum energy related to inner and outer domains. Bilić et al. [31] developed gravatar’s core solutions by replacing dS geometry in the interior region by Born–Infeld phantom spacetime and found solutions for a wider range of radii and masses. Ghosh et al. [32] used the singularity-free Kuchowicz metric function to discuss the various aspects of stable gravastar structure in the background of GR. Ghosh and his collaborators [33] obtained a distinct gravastar solution via embedding class 1 technique using Karmarkar condition. They found exact solutions for intrinsic shell and calculated finite nonsingular solutions for the interior region of gravastar.
In the context of theory, Das et al. [34] examined gravastar geometry and discussed its attributes graphically in relation to EoS. To discuss various features of thin-shell gravastar structure in theory (where is the Gauss–Bonnet invariant), Shamir and Ahmad [35] obtained solutions by solving field equations corresponding to a particular minimal coupling model of this gravity. Sharif and Waseem [36] employed conformal motion to explore charged gravastar structure and found that the internal sector acts as an electromagnetic mass model that assists in the creation of singularity-free structure. The same authors [37] considered Kuchowicz metric function in the background of curvature–matter coupled theory to analyze various features of gravastar. Recently, gravastar solutions were discussed through the gravitational decoupling technique [38,39].
In the present work, we examine solutions of gravastars by adopting the Kuchowicz ansatz in the perspective of gravity. We evaluate the radial metric component for the intrinsic shell as well as gravastar’s internal geometry. For a specific model, we also discuss the graphical behavior of different attributes corresponding to the intrinsic shell of gravastar. The following pattern is adopted for presenting this paper. Section 2 provides basic formulation of field equations with Kuchowicz metric function. Section 3 describes three regions of the gravastar model along with corresponding EoS. The graphical analysis of evaluated solutions corresponding to obtained values of unknown constants as well as model parameters are given in Section 4. The concluding remarks are presented in the last section.
2. Basic Formalism of Theory
In this section, we construct field equations of theory by taking isotropic matter configuration. The modified action of this theory is [7]:
where g denotes the determinant of the metric tensor, indicates the matter Lagrangian and is a coupling constant. The corresponding field equations become:
where ,, and is
The EMT defines the correlation between matter distribution and energy. Its nonvanishing components provide physical variables that characterize various dynamical aspects of a self-gravitating systems. Nonconserved EMT in gravity implies the existence of an extra force that determines nongeodesic motion of particles as follows:
We consider perfect matter distribution:
where P, and describes the pressure, energy density, and four-velocity of the fluid, respectively. For matter configuration, there are two choices of , i.e., either or . The choice of matter Lagrangian does not affect the matter distribution in context of minimally coupled theories of gravity [40]. Here, we assume and manipulate Equations (3) and (5) to obtain:
Within the framework of multivariate function and its derivative, the field Equation (2) is complex and nonlinear. Therefore, we consider a particular function that illustrates minimal/nonminimal interactions between geometry and matter components. The field equations corresponding to nonminimal model turns out to be extremely complicated, making their solution more difficult. Therefore, we take a minimal model of the form [7]:
where and is the model parameter. It describes the current cosmic expansion and evolutionary picture of the universe. Inclusion of extends the boundaries of GR farther than and theories. The functional form (6) was used to study various aspects of self-gravitating objects. It solves a number of cosmological issues [41] and corresponds to three key eras of the universe; namely, the dS-dominated, radiation-dominated, and matter-dominated epochs. Plugging this form of in Equation (2), we have:
where is the Einstein tensor.
To investigate the interior region of gravastar, we use static spherically symmetric geometry as:
The corresponding field equations are:
where prime denotes the radial derivative. We assume that the metric function has the form suggested by Kuchowicz [42]. Thus, we have:
where A (having dimension ) and B (having no dimension) are unknown constants, L is the dimension of length. Kuchowicz devised this nonsingular metric function to study celestial configurations. Ghosh et al. [32] used this metric ansatz to investigate characteristics of gravastar in GR. Inserting Equation (12) in (9)–(11), we have:
3. Structure of Gravastar
The interior region of gravastar is enclosed by a thin-shell consisting of ultra-relativistic fluid, while the exterior region is fully vacuum described by the Schwarzschild metric. The entire structure of gravastar is specified by the following three domains:
- (A)
- Interior domain ,
- (B)
- Intrinsic shell ,
- (C)
- Exterior domain ,
where is very small thickness of thin-shell.
3.1. The Inner Geometry
Following Mazur and Mottola’s [23] idea, we adopt the EoS, with being the EoS parameter. We employ the dark energy EoS (for ) to describe the innermost region of gravastar. Consequently, the inward acting gravitational pull on the intrinsic shell is counter balanced by a substantial negative pressure directed outward from the core of the spherical object. This EoS, along with Equation (16), provides (constant), which implies:
This equation illustrates that the pressure and matter density remains constant throughout the inner geometry. Plugging this equation in Equation (13), the radial metric function is acquired as:
where the arbitrary integration constant () is taken to be zero to obtain regular solution at the core () of gravastar. As a consequence, Equation (18) takes the form:
The gravitational mass in the inner region is given by:
3.2. The Intrinsic Shell
The intermediate gravastar thin-shell is assumed to be made up of stiff matter which follows the relation . Zel’dovich [43] introduced this EoS to describe stiff fluid distribution in connection with the cold baryonic universe. In this scenario, it may occur as a result of gravitational quanta at low temperatures or as a result of thermal perturbations with no chemical potential. Several researchers [44,45,46,47,48] utilized this fluid to solve a variety of astrophysical and cosmological issues. Plugging stiff fluid EoS in Equations (13) and (14) yields:
where denotes the integration constant. Inserting Equation (21) along with the stiff fluid EoS and Kuchowicz metric function in Equation (16), the density turns out to be of the form:
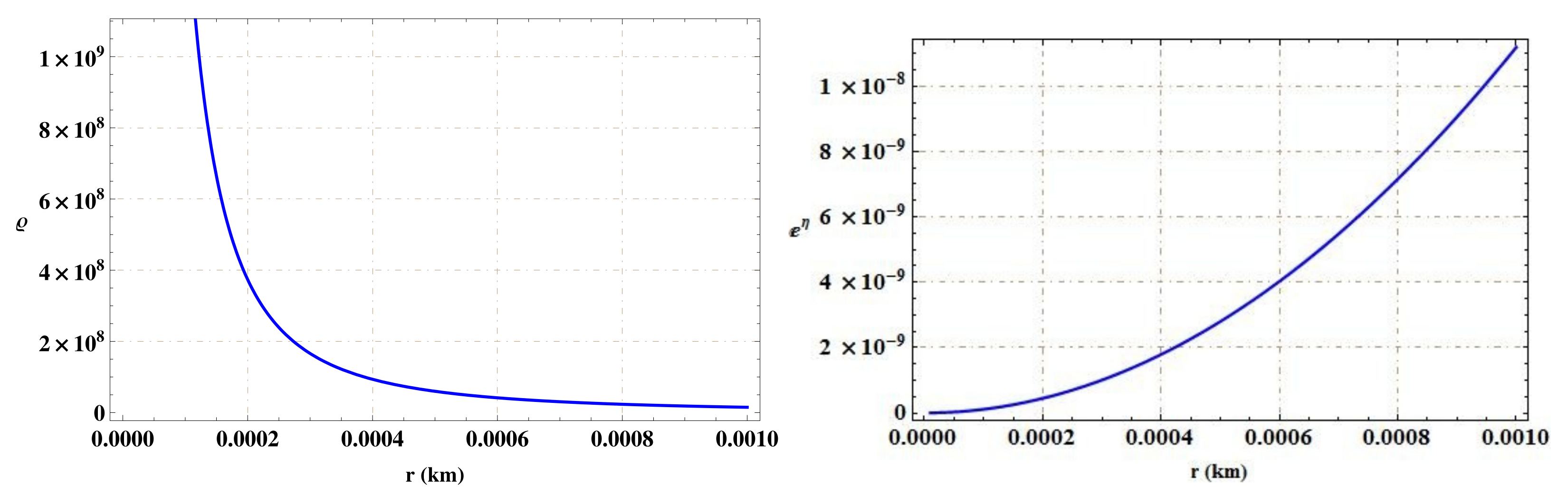
As the shell of gravastar is extremely thin, its thickness therefore ranges between 0 and 1, i.e., . Furthermore, the equations corresponding to this domain are highly nonlinear, which makes it difficult to obtain an exact solution of the field equations. The plot of energy density against the thickness of shell is presented in Figure 1, which shows that it is positive throughout the region.
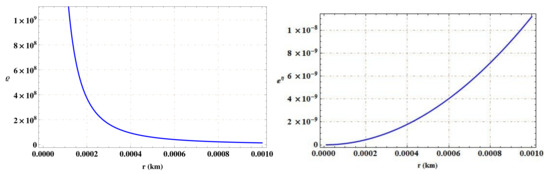
Figure 1.
Behavior of energy density and metric function against thickness of thin-shell for .
3.3. The Exterior Geometry and Darmois–Israel Matching Constraint
This vacuum region is described by the Schwarzschild metric obeying . It is characterized as follows:
where . Gravastar structure has two boundaries, one interlinks the interior domain and thin-shell while thin-shell is connected to external spacetime by other boundary. The continuity of metric potentials at these boundaries must hold for a physically well-behaved system. These metric components are matched at the interface to determine the values of arbitrary constants A, B and as follows:
The obtained values of these constants are km, and km. Figure 1 presents graphical analysis of the metric function as well as density. We observe that the metric function is singularity-free, whereas density and pressure have positive behavior throughout the thin-shell of gravastar and sharply decrease with shell thickness.
It is necessary to acquire the constraints that permit the smooth matching of internal and external geometries. In achieving these constraints, Israel’s formalism plays a vital role in obtaining the appropriate conditions for smooth matching. At the hypersurface (), the continuity of metric coefficients is necessary but their differentials may not be continuous. To determine the surface stress-energy tensor, we utilize the Lanczos equation as follows:
where presents the discontinuity of the extrinsic curvature. Here, + sign corresponds to the external region while − indicates the internal region of gravastar, respectively. The extrinsic curvature components at hypersurface are characterized by:
where denotes the intrinsic shell coordinates and presents the unit normal at which is given as:
For isotropic matter distribution, EMT takes the form , where is the surface energy density and being the surface pressure are given by Lanczos equations as:
Using surface energy density, we evaluate mass of the intermediate shell as:
Ultimately, the total gravastar’s mass is provided as:
4. Attributes of Gravastar Thin-Shell
This section examines certain important gravastar characteristics such as the EoS parameter, length, energy, and surface redshift in relation to thickness of shell.
4.1. The EoS Parameter of Intrinsic Shell
For thin-shell region of gravastar, the EoS parameter is obtained by utilizing Equations (30) and (31) at as:
The positive values of matter variables (density and pressure) provide positive value of . For real value of this parameter, the suitable constraints are and . Furthermore, binomial series is used to expand the square-root entities of Equation (34) along with the constraints , , and taking only the first-order terms, we can obtain:
This mathematical expression provides two choices for , i.e., either turns out to be negative if , or has positive value if .
4.2. Proper Length for Intrinsic Shell
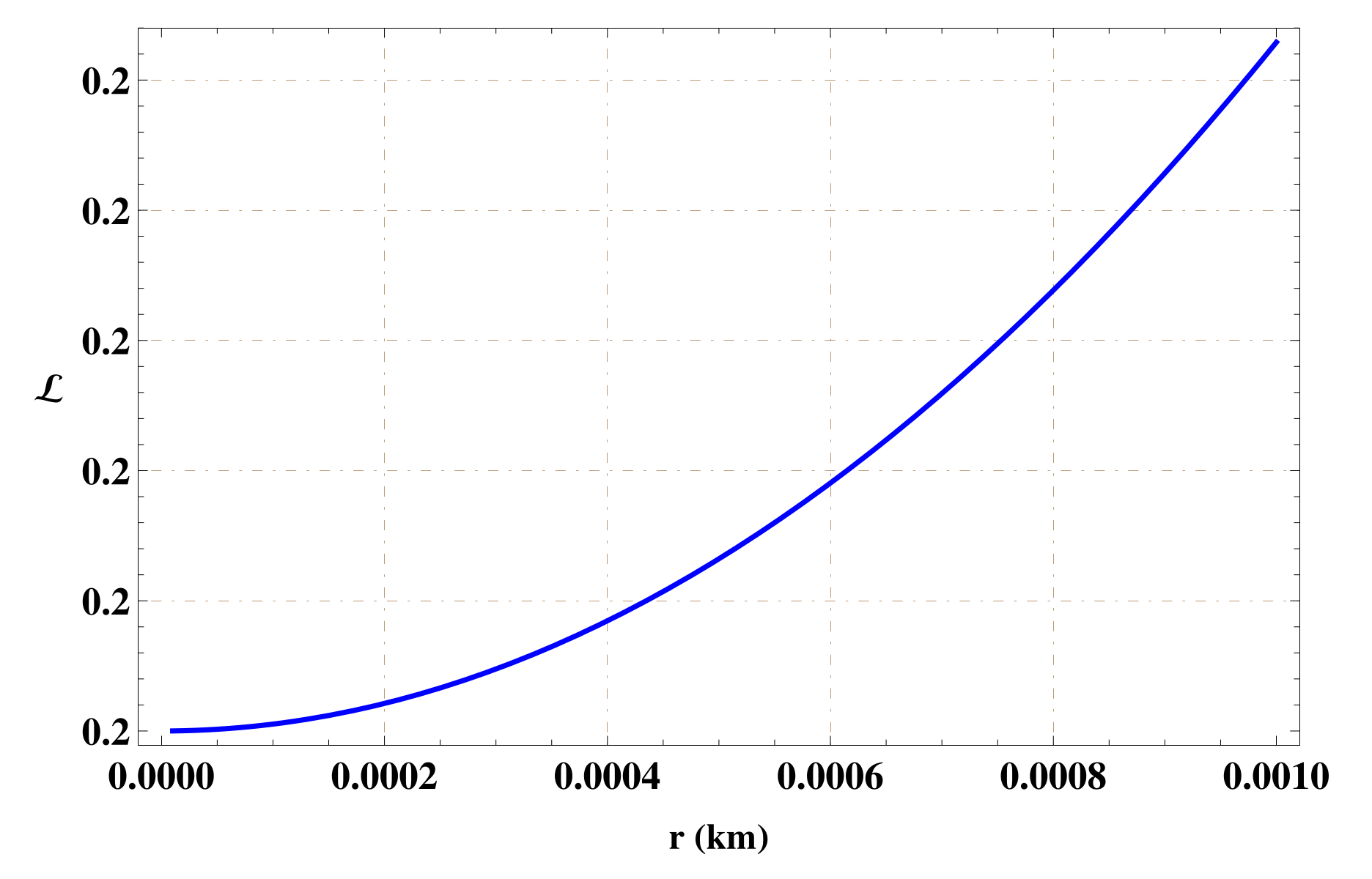
The length of gravastar is determined from the boundary of the inner region to the boundary of intrinsic shell . Thus, we have:
The plot of the proper length against small thickness of intermediate shell gravastar is shown in Figure 2, which describes the increasing profile of length against thickness of intrinsic shell.
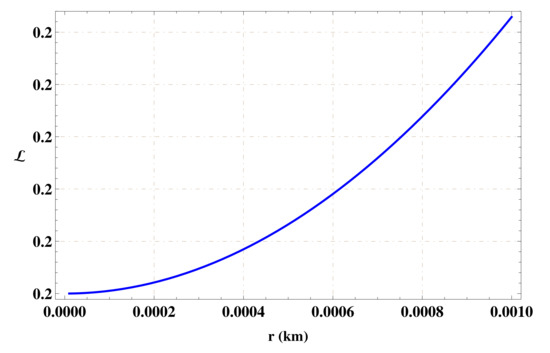
Figure 2.
Behavior of length against thickness of thin-shell for .
4.3. Energy of the Thin-Shell
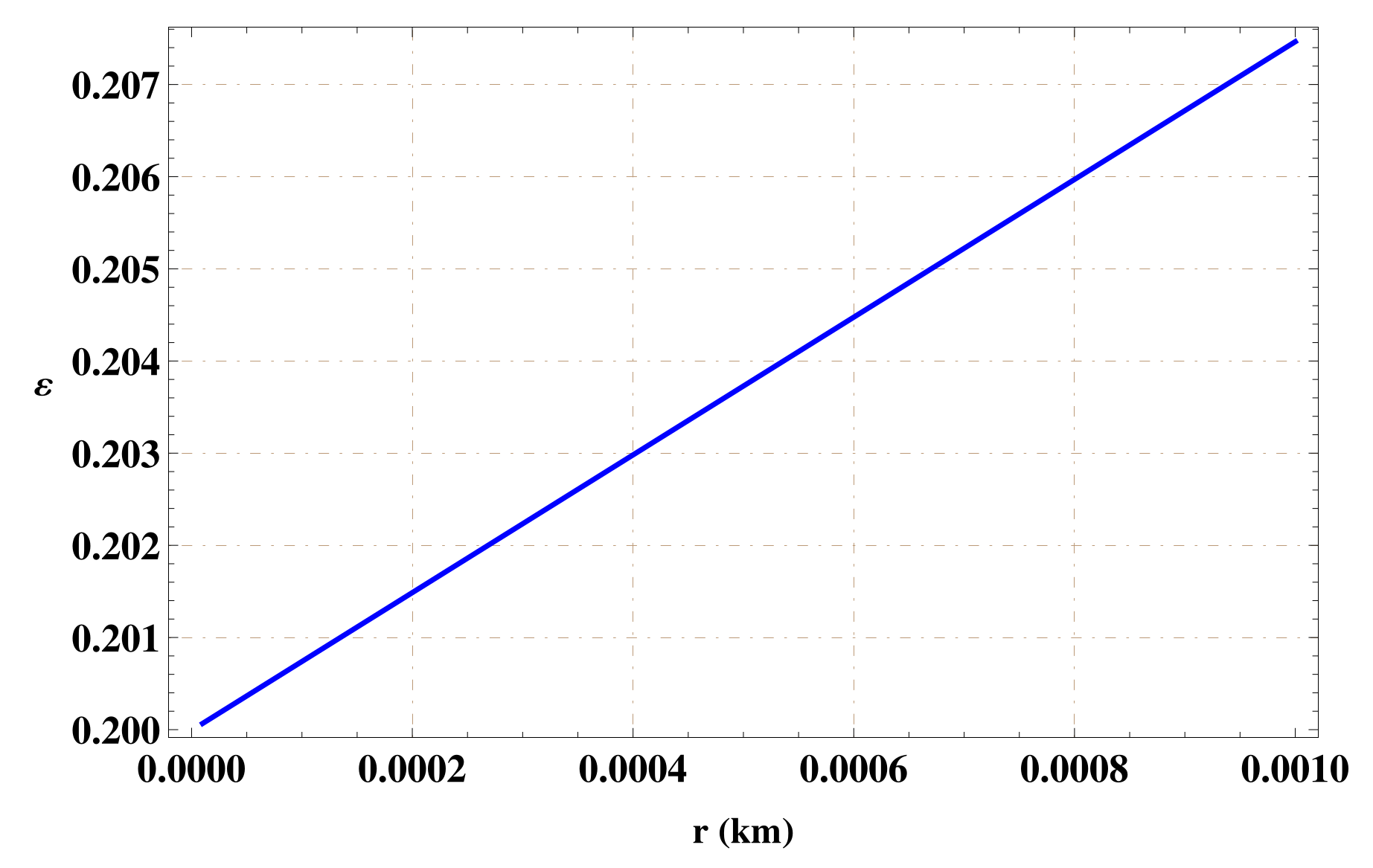
The gravastar’s interior region is occupied by dark energy, resulting in the repulsive behavior. The energy present within intrinsic shell is given as:
The graphical trend of energy against thickness provides the increasing behavior of the energy within the intermediate thin-shell as shown in Figure 3.
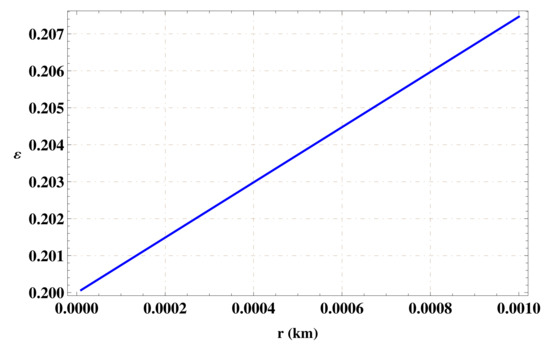
Figure 3.
Energy of intermediate thin-shell for .
4.4. Surface Redshift of Intrinsic Shell
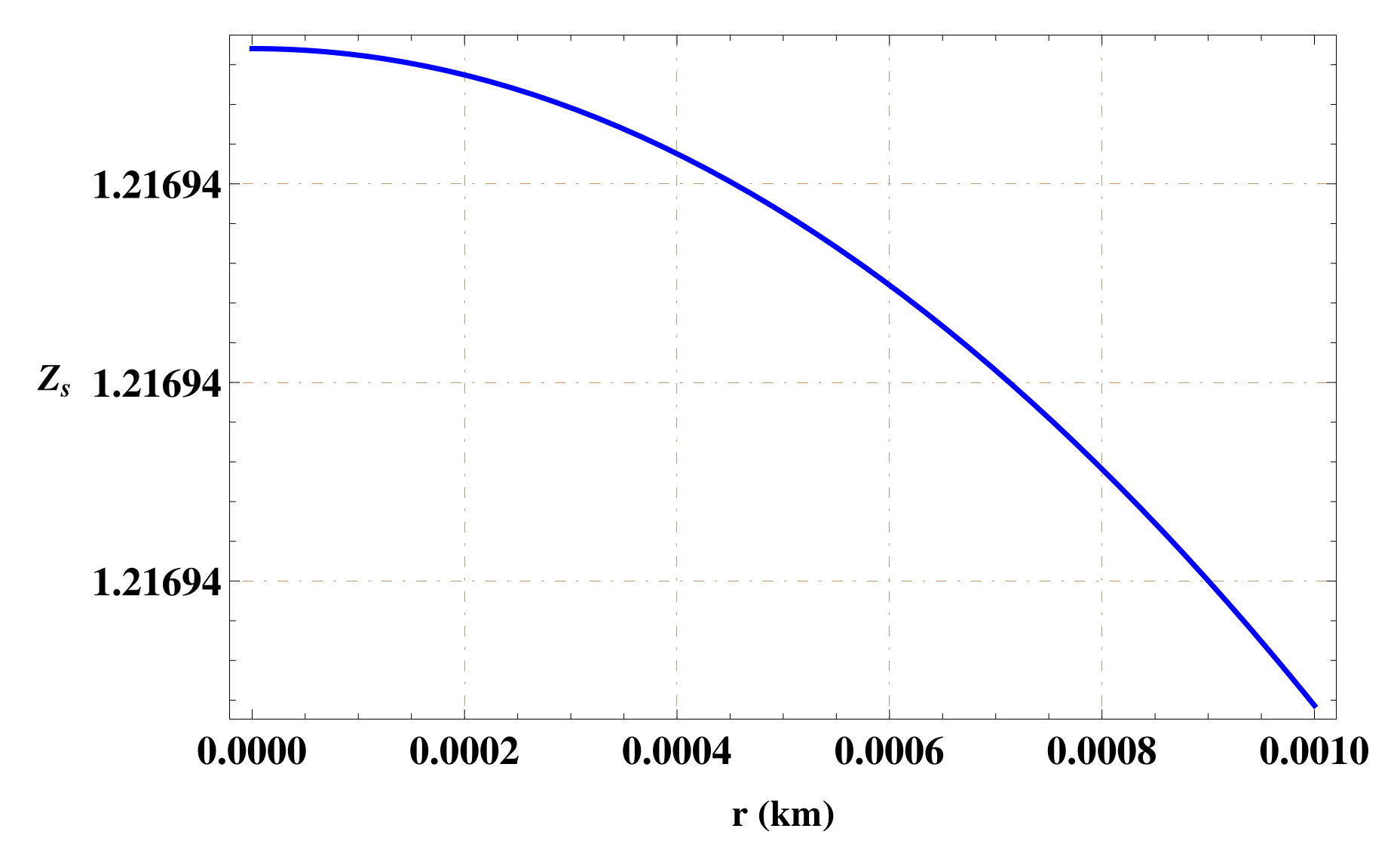
In the structural study of gravastar, the surface redshift is viewed as an essential source of information associated with the detection as well as stability of gravastars. For perfect matter configuration, it is suggested that the maximum value of redshift parameter is 2 [49,50]. The mathematical expression of surface redshift is given as [32]:
The plot of surface redshift (by inserting the numerical values of constants A and B) is shown in Figure 4, which indicates that the value of the redshift parameter does not exceed the bound 2 within the shell of gravastar. Thus, the obtained solutions of gravastar structure are physically consistent and stable.
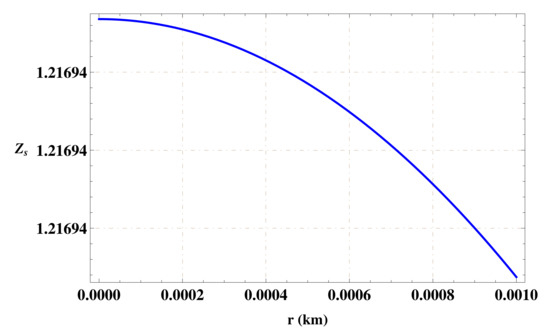
Figure 4.
Surface redshift in relation to thickness of shell for .
5. Concluding Remarks
In this paper, we used the Kuchowicz metric function to calculate a new solution for studying an astrophysical compact object known as gravitational vacuum star (gravastar) in gravity. The Kuchowicz metric potential is employed due to its nonsingular and regular behavior throughout gravastar structure. To investigate various features of gravastar, we constructed solutions for each domain of the specific model . In the inner sector of gravastar, we calculated the metric function as well as energy density. Dark energy EoS was used in the conservation equation to obtain the constant energy density for the innermost region. The gravastar avoids singularity by maintaining constant density throughout the interior region. Consequently, at the center of gravastar, the singularity is eliminated as the behavior of metric function remains finite. Moreover, we calculated the gravitational mass which turned out to be zero at the center and positive within the inner region.
In the intrinsic shell of gravastar, we evaluated the radial metric function by solving the field equations corresponding to ultra-relativistic matter distribution. We used Schwarzschild metric as an exterior domain to determine the unknown constants through boundary conditions. Using Darmois–Israel criterion for smooth matching of spacetimes, density as well as pressure are obtained at the surface. We also analyzed characteristics of gravastar, such as matter density, pressure, EoS parameter, proper length, energy, and surface redshift corresponding to the thickness of the intermediate shell. All these quantities indicate that the obtained structure is stable and physically acceptable in the context of gravity.
Das et al. [34] presented different features of gravastar in framework and obtained a direct relation of physical features corresponding to the thickness of shell. We found that the gravastar features follow similar physical behavior as given in [34]; further, the value of length decreases and the energy increases in our case. Pressure in the interior region is negative and positive in the shell region, while the pressure vanishes in the outermost region, which is completely vacuumed. Thus the pressure in all regions follows a similar trend as given in [51]. We conclude that the formation of a gravastar-like stellar model admitting the Kuchowicz metric potential is physically consistent and viable, similar to GR [32].
Author Contributions
M.S. suggested the research problem and finalized the manuscript while S.N. did the calculations and prepared the initial draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pietrobon, D.; Balbi, A.; Marinucci, D. Integrated Sachs-Wolfe effect from the cross correlation of WMAP 3 year and the NRAO VLA sky survey data: New results and constraints on dark energy. Phys. Rev. D 2006, 74, 043524. [Google Scholar] [CrossRef]
- Astieer, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of ΩM, ΩΛ and w from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef] [Green Version]
- Felice, A.D.; Tsujikawa, S.R. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef] [Green Version]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N. Palatini formulation of modified gravity with a nonminimal curvature-matter coupling. Mod. Phys. Lett. A 2011, 26, 1467–1480. [Google Scholar] [CrossRef]
- Katirci, N.; Kavuk, M. f(,TμνTμν) gravity and Cardassian-like expansion as one of its consequences. Eur. Phys. J. Plus 2014, 129, 163. [Google Scholar] [CrossRef]
- Roshan, M.; Shojai, F. Energy-momentum squared gravity. Phys. Rev. D 2016, 94, 044002. [Google Scholar] [CrossRef] [Green Version]
- Board, C.V.R.; Barrow, J.D. Cosmological models in energy-momentum-squared gravity. Phys. Rev. D 2017, 96, 123517. [Google Scholar] [CrossRef] [Green Version]
- Nari, N.; Roshan, M. Compact stars in energy-momentum squared gravity. Phys. Rev. D 2018, 98, 024031. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Katirci, N.; Kumar, S.; Nunes, R.C.; Sami, M. Cosmological implications of scale-independent energy-momentum squared gravity: Pseudo nonminimal interactions in dark matter and relativistic relics. Phys. Rev. D 2018, 98, 063522. [Google Scholar] [CrossRef] [Green Version]
- Bahamonde, S.; Marciu, M.; Rudra, P. Dynamical system analysis of generalized energy-momentum-squared gravity. Phys. Rev. D 2019, 100, 083511. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Gul, M.Z. Noether symmetry approach in energy-momentum squared gravity. Phys. Scr. 2020, 96, 025002. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Noether symmetries and anisotropic universe in energy-momentum squared gravity. Phys. Scr. 2020, 96, 125007. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of spherical collapse in energy-momentum squared gravity. Int. J. Mod. Phys. A 2021, 36, 2150004. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Compact stars admitting Noether symmetry in energy-momentum squared gravity. Adv. Astron. 2021, 2021, 6663502. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Viable wormhole solutions in energy-momentum squared gravity. Eur. Phys. J. Plus 2021, 136, 503. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamics of charged anisotropic spherical collapse in energy-momentum squared gravity. Chin. J. Phys. 2021, 71, 365–374. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Dynamical analysis of charged dissipative cylindrical collapse in energy-momentum squared gravity. Universe 2021, 7, 154. [Google Scholar]
- Sharif, M.; Gul, M.Z. Stability of the closed Einstein universe in energy-momentum squared gravity. Phys. Scr. 2021, 96, 105001. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Study of stellar structures in f(,TμνTμν) theory. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250012. [Google Scholar] [CrossRef]
- Sharif, M.; Gul, M.Z. Role of energy–momentum squared gravity on the dynamics of charged dissipative plane symmetric collapse. Mod. Phys. Lett. A 2022, 37, 2250005. [Google Scholar] [CrossRef]
- Mazur, P.; Mottola, E. Gravitational vacuum condensate stars. Proc. Natl. Acad. Sci. USA 2004, 101, 9545–9550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakai, N.; Saida, H.; Tamaki, T. Gravastar shadows. Phys. Rev. D 2014, 90, 104013. [Google Scholar] [CrossRef] [Green Version]
- Kubo, T.; Sakai, N. Gravitational lensing by gravastars. Phys. Rev. D 2016, 93, 084051. [Google Scholar] [CrossRef]
- Cardoso, V.; Franzin, E.; Pani, P. Is the gravitational-wave ringdown a probe of the event horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, V.; Franzin, E.; Pani, P. Erratum: Is the gravitational-wave ringdown a probe of the event horizon? [Phys. Rev. Lett. 2016, 171101]. Phys. Rev. Lett. 2016, 117, 089902. [Google Scholar] [CrossRef]
- Akiyama, K.; Albredi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-R.; Ball, D.; Baloković, M.; Barret, J.; Bintley, D.; et al. First M87 event horizon telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 2019, 875, 1. [Google Scholar]
- Visser, M.; Wiltshire, D.L. Stable gravastars—An alternative to black holes? Class. Quantum Grav. 2004, 21, 1135. [Google Scholar] [CrossRef]
- Carter, B.M.N. Stable gravastars with generalized exteriors. Class. Quantum Grav. 2005, 22, 4551. [Google Scholar] [CrossRef] [Green Version]
- Bilić, N.; Tupper, G.B.; Viollier, R.D. Born–Infeld phantom gravastars. J. Cosmol. Astropart. Phys. 2006, 2, 13. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Shee, D.; Ray, S.; Rahaman, F.; Guha, B.K. Gravastars with Kuchowicz metric potential. Res. Phys. 2019, 14, 102473. [Google Scholar] [CrossRef]
- Ghosh, S.; Biswas, S.; Guha, B.K.; Ray, S.; Rahaman, F. Gravastars in (3+1) dimensions admitting Karmarkar condition. Ann. Phys. 2019, 411, 167968. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, S.; Guha, B.K.; Das, A.; Rahaman, F.; Ray, S. Gravastars in f(R,T) gravity. Phys. Rev. D 2017, 95, 124011. [Google Scholar] [CrossRef] [Green Version]
- Shamir, F.; Ahmad, M. Gravastars in f(G,T) gravity. Phys. Rev. D 2018, 97, 104031. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Waseem, A. Charged gravastars with conformal motion in f(R,T) gravity. Astrophys. Space Sci. 2019, 364, 189. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Waseem, A. Impact of Kuchowicz metric function on gravastars in f(R,T) theory. Eur. Phys. J. Plus 2020, 135, 930. [Google Scholar] [CrossRef]
- Ovalle, J.; Posada, C.; Stuchlk, Z. Anisotropic ultracompact Schwarzschild star by gravitational decoupling. Class. Quat. Grav. 2019, 36, 205010. [Google Scholar] [CrossRef] [Green Version]
- Azmat, H.; Zubair, M.; Ahmad, Z. Study of anisotropic and non-uniform gravastars by gravitational decoupling in f(R,T) gravity. Ann. Phys. 2022, 439, 168769. [Google Scholar] [CrossRef]
- Faraoni, V. Lagrangian description of perfect fluids and modified gravity with an extra force. Phys. Rev. D 2009, 80, 124040. [Google Scholar] [CrossRef] [Green Version]
- Akarsu, O.; Katirci, N.; Kumar, S. Cosmic acceleration in dust only universe via energy-momentum powered gravity. Phys. Rev. D 2018, 97, 024011. [Google Scholar] [CrossRef] [Green Version]
- Kuchowicz, B. General relativistic spheres. I. New solutions for spherically symmetric matter distributions. Acta Phys. Pol. 1968, 33, 541–563. [Google Scholar]
- Zel’dovich, Y.B. A hypothesis, unifying the structure and the entropy of the universe. Mon. Not. R. Astron. Soc. 1972, 160, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Wesson, P.S. An exact solution to Einstein’s equations with a stiff equation of state. J. Math. Phys. 1978, 19, 2283–2284. [Google Scholar] [CrossRef]
- Madsen, M.S.; Mimoso, J.P.; Butcher, J.A.; Ellis, G.F. Evolution of the density parameter in inflationary cosmology reexamined. Phys. Rev. D 1992, 46, 1399. [Google Scholar] [CrossRef]
- Braje, T.M.; Romani, R.W. Evidence for a stiff equation of state. Astrophys. J. 2002, 580, 1043. [Google Scholar] [CrossRef]
- Linares, L.P.; Malheiro, M.; Ray, S. The importance of the relativistic corrections in hyperon stars. Int. J. Mod. Phys. D 2004, 13, 1355–1359. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General relativistic fluid spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Barraco, D.E.; Hamity, V.H. Maximum mass of a spherically symmetric isotropic star. Phys. Rev. D 2002, 65, 124028. [Google Scholar] [CrossRef]
- Cattoen, C.; Faber, T.; Visser, M. Gravastars must have anisotropic pressures. Class. Quantum Grav. 2005, 22, 4189. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).