Excitation Function of Kinetic Freeze-Out Parameters at 6.3, 17.3, 31, 900 and 7000 GeV
Abstract
1. Introduction
2. The Methods and Formalisms
3. Results and Discussion
3.1. Comparison with Data
3.2. Tendencies of Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Waqas, M.; Li, B.C. Kinetic freeze-out temperature and transverse flow velocity in Au-Au collisions at RHIC-BES energies. Adv. High Energy Phys. 2020, 2020, 1787183. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.H.; Ma, Y.G.; Zhang, S. Charm hadron azimuthal angular correlations in Au + Au collisions at = 200 GeV from parton scatterings. Nucl. Sci. Tech. 2019, 30, 185. [Google Scholar] [CrossRef]
- Shen, C.; Yan, L. Recent development of hydrodynamic modeling in heavy-ion collisions. Nucl. Sci. Tech. 2020, 31, 122. [Google Scholar] [CrossRef]
- Tawfik, A.N. Out-Of-Equilibrium Transverse Momentum Spectra of Pions at LHC Energies. Adv. High Energy Phys. 2019, 2019, 4604608. [Google Scholar] [CrossRef]
- Yu, H.; Fang, D.Q.; Ma, Y.G. Investigation of the symmetry energy of nuclear matter using isospin-dependent quantum molecular dynamics. Nucl. Sci. Tech. 2020, 31, 61. [Google Scholar] [CrossRef]
- Csanad, M.; Majer, I. Initial temperature and EoS of quark matter from direct photons. Phys. Part. Nucl. Lett. 2011, 8, 1013–1015. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, F.H. Kinetic Freeze-Out Properties from Transverse Momentum Spectra of Pions in High Energy Proton-Proton Collisions. Physics 2020, 2, 277–308. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H. Initial, effective, and kinetic freeze-out temperatures from transverse momentum spectra in high-energy proton(deuteron)–nucleus and nucleus–nucleus collisions. Eur. Phys. J. Plus 2020, 135, 147. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Tsallis Statistics in High Energy Physics: Chemical and Thermal Freeze-Outs. Physics 2020, 2, 654–664. [Google Scholar] [CrossRef]
- Csanad, M.; Majer, I. Equation of state and initial temperature of quark gluon plasma at RHIC. Cent. Eur. J. Phys. 2012, 10, 850–857. [Google Scholar] [CrossRef]
- Adare, A. Enhanced production of direct photons in Au+Au collisions at = 200 GeV and implications for the initial temperature. Phys. Rev. Lett. 2010, 104, 132301. [Google Scholar] [CrossRef] [PubMed]
- Nayak, J.K.; Alam, J.-e.; Sarkar, S.; Sinha, B. Measuring initial temperature through photon to dilepton ratio in heavy ion collision. J. Phys. G 2008, 35, 104161. [Google Scholar] [CrossRef]
- Soltz, R.A.; Garishvili, I.; Cheng, M.; Abelev, B.; Glenn, A.; Newby, J.; Levy, L.A.L.; Pratt, S. Constraining the initial temperature and shear viscosity in a hybrid hydrodynamic model of = 200 GeV Au+Au collisions using pion spectra, elliptic flow, and femtoscopic radii. Phys. Rev. C 2013, 87, 044901. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Ajaz, M.; Ismail, A.A.K.H.; Yang, P.P.; Wazir, Z. Extraction of freezeout parameters and their dependence on collision energy and collision cross-section. arXiv 2021, arXiv:2112.00975. [Google Scholar]
- Waqas, M.; Liu, F.H.; Wazir, Z. Dependence of temperatures and kinetic freeze-out volume on centrality in Au-Au and Pb-Pb collisions at high energy. Adv. High Energy Phys. 2020, 2020, 8198126. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, F.H.; Olimov, K.K. Initial- and final-state temperatures of emission source from differential cross-section in squared momentum transfer in high energy collisions. Adv. High Energy Phys. 2021, 2021, 6677885. [Google Scholar] [CrossRef]
- Tawfik, A.N. Equilibrium statistical-thermal models in high-energy physics. Int. J. Mod. Phys. A 2014, 29, 1430021. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Yassin, H.; Elyazeed, E.R.A. Extensive/nonextensive statistics for pT distributions of various charged particles produced in p+p and A+A collisions in a wide range of energies. arXiv 2020, arXiv:1905.12756. [Google Scholar]
- Yassin, H.; Elyazeed, E.R.A.; Tawfik, A.N. Transverse momentum spectra of strange hadrons within extensive and nonextensive statistics. Phys. Scr. 2020, 95, 7. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H.; Wang, R.Q.; Siddique, I. Energy scan/dependence of kinetic freeze-out scenarios of multi-strange and other identified particles in central nucleus-nucleus collisions. Eur. Phys. J. A 2020, 56, 188. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Wang, R.Q.; Ajaz, M.; Ismail, A.A.K.H. Freezeout properties of different light nuclei at the RHIC beam energy scan. Eur. Phys. J. Plus 2021, 136, 1082. [Google Scholar] [CrossRef]
- Kumar, L. Systematics of Kinetic Freeze-out Properties in High Energy Collisions from STAR. Nucl. Phys. A 2014, 931, 1114–1119. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X. Study of Proton, Deuteron, and Triton at 54.4 GeV. Adv. High Energy Phys. 2021, 2021, 6674470. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Liu, F.H. An evidence of triple kinetic freezeout scenario observed in all centrality intervals in Cu–Cu, Au–Au and Pb–Pb collisions at high energies. J. Phys. G 2021, 48, 075108. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Liu, F.H.; Wazir, Z. Effects of coalescence and isospin symmetry on the freezeout of light nuclei and their anti-particles. Sci. Rep. 2021, 11, 20252. [Google Scholar] [CrossRef]
- Liu, F.H. Unified description of multiplicity distributions of final-state particles produced in collisions at high energies. Nucl. Phys. A 2008, 810, 159–172. [Google Scholar] [CrossRef]
- Hagedorn, R. Multiplicities, pT Distributions and the Expected Hadron → Quark-Gluon Phase Transition. Riv. Nuovo Cim. 1983, 6N10, 1–50. [Google Scholar] [CrossRef]
- Liu, F.H.; Li, J.S. Isotopic production cross section of fragments in Fe-56 + p and Xe-136 (Xe-124) + Pb reactions over an energy range from A-300 to A-1500 MeV. Phys. Rev. C 2008, 78, 044602. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Statist. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Olimov, K.K.; Kanokova, S.Z.; Olimov, A.K.; Umarov, K.I.; Tukhtaev, B.J.; Gulamov, K.G.; Yuldashev, B.S.; Lutpullaev, S.L.; Saidkhanov, N.S.; Olimov, K.; et al. Combined analysis of midrapidity transverse momentum spectra of the charged pions and kaons, protons and antiprotons in p + p and Pb + Pb collisions at (snn)1/2 = 2.76 and 5.02 TeV at the LHC. Mod. Phys. Lett. A 2020, 35, 2050237. [Google Scholar] [CrossRef]
- Ajaz, M.; Waqas, M.; Peng, G.; Yasin, Z.; Younis, H.; Al Karim Haj Ismai L, A. Study of pT spectra of light particles using modified Hagedorn function and cosmic rays Monte Carlo event generators in proton-proton collisions at 900 GeV center of mass energy. arXiv 2021, arXiv:2112.03187. [Google Scholar]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200-A/GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef] [PubMed]
- Abelev, B.I. Identified particle production, azimuthal anisotropy, and interferometry measurements in Au+Au collisions at s(NN)**(1/2) = 9.2-GeV. Phys. Rev. C 2010, 81, 024911. [Google Scholar] [CrossRef]
- Tang, Z.; Yi, L.; Ruan, L.; Shao, M.; Chen, H.; Li, C.; Mohanty, B.; Sorensen, P.; Tang, A.; Xu, Z. Statistical Origin of Constituent-Quark Scaling in the QGP hadronization. Chin. Phys. Lett. 2013, 30, 031201. [Google Scholar] [CrossRef][Green Version]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the Nonextensivity Parameter q in Some Applications of Tsallis Statistics and Lévy Distributions. Phys. Rev. Lett. 2000, 84, 2770. [Google Scholar] [CrossRef]
- Adams, J. Identified particle distributions in pp and Au+Au collisions at s(NN)**(1/2) = 200 GeV. Phys. Rev. Lett. 2004, 92, 112301. [Google Scholar] [CrossRef]
- Adamczyk, L. Bulk Properties of the Medium Produced in Relativistic Heavy-Ion Collisions from the Beam Energy Scan Program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Seifert, E.; Cassing, W. Baryon-antibaryon dynamics in relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 044907. [Google Scholar] [CrossRef]
- Acharya, S. Production of charged pions, kaons, and (anti-)protons in Pb-Pb and inelastic pp collisions at = 5.02 TeV. Phys. Rev. C 2020, 101, 044907. [Google Scholar] [CrossRef]
- Socolowski, O., Jr.; Grassi, F.; Hama, Y.; Kodama, T. Fluctuations of the initial conditions and the continuous emission in hydro description of two-pion interferometry. Phys. Rev. Lett. 2004, 93, 182301. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, Y.; Ruan, L.; van Buren, G.; Wang, F.; Xu, Z. Spectra and radial flow at RHIC with Tsallis statistics in a Blast-Wave description. Phys. Rev. C 2009, 79, 051901. [Google Scholar] [CrossRef]
- Becattini, F.; Heinz, U.W. Thermal hadron production in p p and p anti-p collisions. Z. Phys. C 1997, 76, 269–286, Erratum in Z. Phys. C 1997, 76, 578.. [Google Scholar] [CrossRef]
- Jiang, K.; Zhu, Y.; Liu, W.; Chen, H.; Li, C.; Ruan, L.; Tang, Z.; Xu, Z.; Xu, Z. Onset of radial flow in p + p collisions. Phys. Rev. C 2015, 91, 024910. [Google Scholar] [CrossRef]
- Hove, L.V. Multiplicity Dependence of p(T) Spectrum as a Possible Signal for a Phase Transition in Hadronic Collisions. Phys. Lett. B 1982, 118, 138. [Google Scholar] [CrossRef]
- Levai, P.; Muller, B. Transverse baryon flow as possible evidence for a quark-gluon plasma phase. Phys. Rev. Lett. 1991, 67, 1519–1522. [Google Scholar] [CrossRef]
- Alexopoulos, T.; Anderson, E.W.; Bujak, A.T.; Carmony, D.D.; Erwin, A.R.; Gutay, L.J.; Hirsch, A.S.; Nelson, K.S.; Porile, N.T.; Oh, S.H.; et al. Evidence for Hadronic Deconfinement in -p Collisions at 1.8-TeV. Phys. Lett. B 2002, 528, 43–48. [Google Scholar] [CrossRef]
- Weiner, R.M. Surprises from the search for quark-gluon plasma? When was quark-gluon plasma seen? Int. J. Mod. Phys. E 2006, 15, 37–70. [Google Scholar] [CrossRef]
- Alpgard, K. First Results on Complete Events from p anti-p Collisions at the Center-of-Mass Energy of 540-GeV. Phys. Lett. B 1981, 107, 310–314. [Google Scholar] [CrossRef]
- Arnison, G. Some Observations on the First Events Seen at the CERN Proton-anti-Proton Collider. Phys. Lett. B 1981, 107, 320–324, Erratum in Phys. Lett. B 1982, 109, 510.. [Google Scholar] [CrossRef]
- Becattini, F.; Castorina, P.; Milov, A.; Satz, H. A Comparative analysis of statistical hadron production. Eur. Phys. J. C 2010, 66, 377–386. [Google Scholar] [CrossRef]
- Kraus, I.; Cleymans, J.; Oeschler, H.; Redlich, K. Particle production in p-p collisions and prediction for LHC energy. Phys. Rev. C 2009, 79, 014901. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H.; Fakhraddin, S.; Rahim, M.A. Possible scenarios for single, double, or multiple kinetic freeze-out in high energy collisions. Indian J. Phys. 2019, 93, 1329–1343. [Google Scholar] [CrossRef]
- Abelev, B.; STAR Collaboration. Systematic measurements of identified particle spectra in pp, d+ Au and Au+Au collisions from STAR. Phys. Rev. C 2009, 79, 034909. [Google Scholar] [CrossRef]
- Kolb, P.F.; Heinz, U. Hydrodynamic description of ultrarelativistic heavy-ion collisions. In Quark-Gluon Plasma 3; Hwa, R.C., Wang, X.-N., Eds.; World Scientific: Singapore, 2004. [Google Scholar] [CrossRef]
- Abelev, B.B. Production of Σ(1385)± and Ξ(1530)0 in proton-proton collisions at = 7 TeV. Eur. Phys. J. C 2015, 75, 1. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Wazir, Z.; Lao, H. Analysis of kinetic freeze out temperature and transverse flow velocity in nucleus-nucleus and proton-proton collisions at same center of mass energy. Int. J. Mod. Phys. 2021, 30, 2150061. [Google Scholar] [CrossRef]
- Aduszkiewicz, A. Measurements of π±, K±, p and spectra in proton-proton interactions at 20, 31, 40, 80 and 158 GeV/c with the NA61/SHINE spectrometer at the CERN SPS. Eur. Phys. J. C 2017, 77, 671. [Google Scholar] [CrossRef]
- Alper, B.; Böggild, H.; Booth, P.; Bulos, F.; Carolll, L.J.; Damgaard, G.; Von Dardel, G.; Duff, B.; Hansen, K.H.; Heymann, F.; et al. Production Spectra of pi±, K±, rho± at Large Angles in Proton Proton Collisions in the CERN Intersecting Storage Rings. Nucl. Phys. B 1975, 100, 237–290. [Google Scholar] [CrossRef]
- Aamodt, K. Production of pions, kaons and protons in pp collisions at s=900 GeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1655. [Google Scholar] [CrossRef]
- Adam, J. Measurement of pion, kaon and proton production in proton–proton collisions at s=7 TeV. Eur. Phys. J. C 2015, 75, 226. [Google Scholar] [CrossRef]
- Shao, M.; Yi, L.; Tang, Z.; Chen, H.; Li, C.; Xu, Z. Examine the species and beam-energy dependence of particle spectra using Tsallis Statistics. J. Phys. G 2010, 37, 085104. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic Thermodynamics: Transverse Momentum Distributions in High-Energy Physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Biro, T.S.; Purcsel, G.; Urmossy, K. Non-Extensive Approach to Quark Matter. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar] [CrossRef]
- Avdyushev, V.A. A new method for the statistical simulation of the virtual values of parameters in inverse orbital dynamics problems. Sol. Syst. Res. 2009, 43, 543–551. [Google Scholar] [CrossRef]
- Chatrchyan, S. Study of high-pT charged particle suppression in PbPb compared to pp collisions at = 2.76 TeV. Eur. Phys. J. C 2012, 72, 1945. [Google Scholar] [CrossRef]
- Suleymanov, M. The meaning behind observed pT regions at the LHC energies. Int. J. Mod. Phys. E 2018, 27, 1850008. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys. Rev. D 1983, 27, 140. [Google Scholar] [CrossRef]
- Landau, L.D. On the multiple production of particles in high energy collisions. Izv. Akad. SSSR 1951, 15, 219. [Google Scholar]
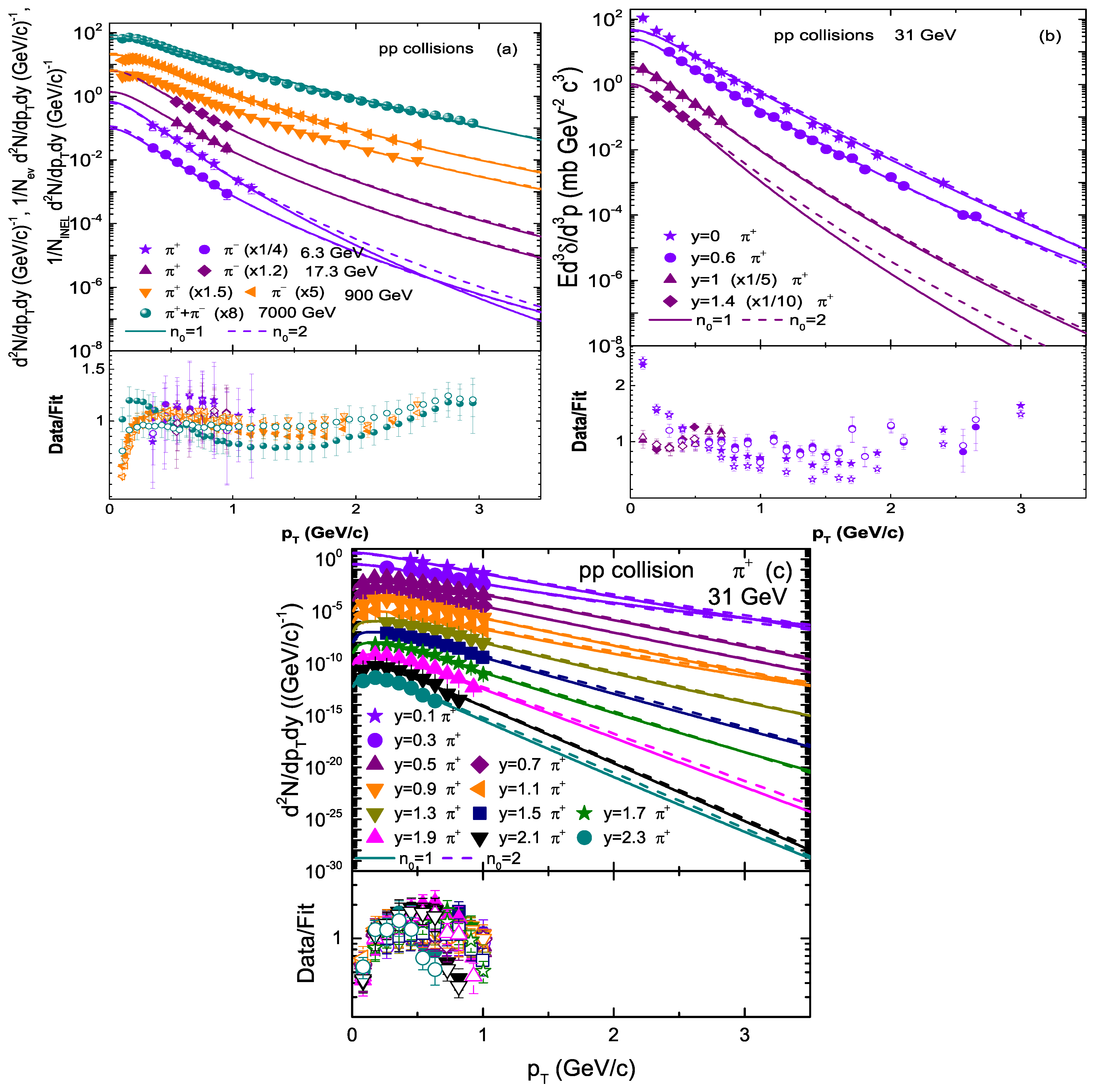

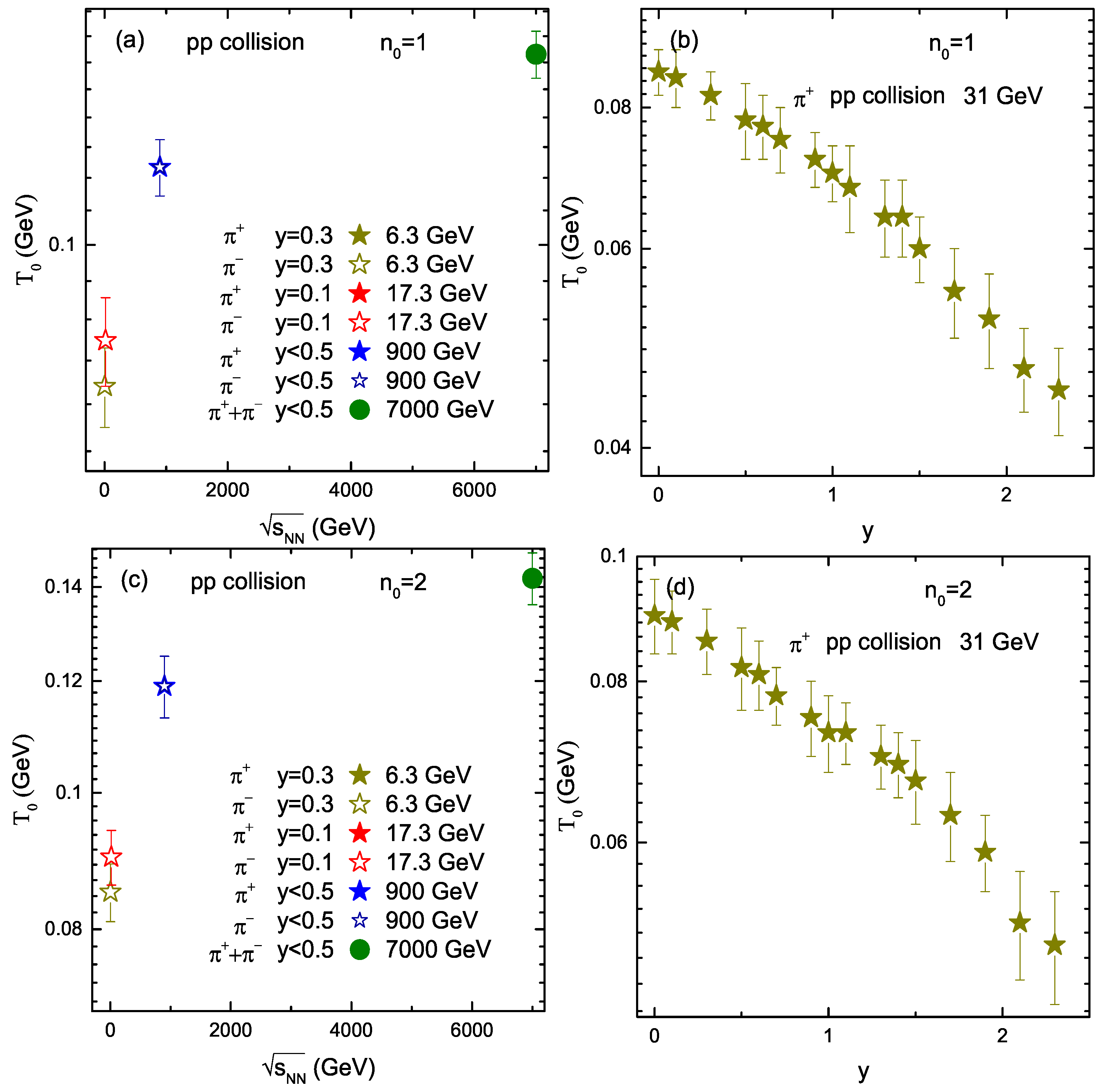
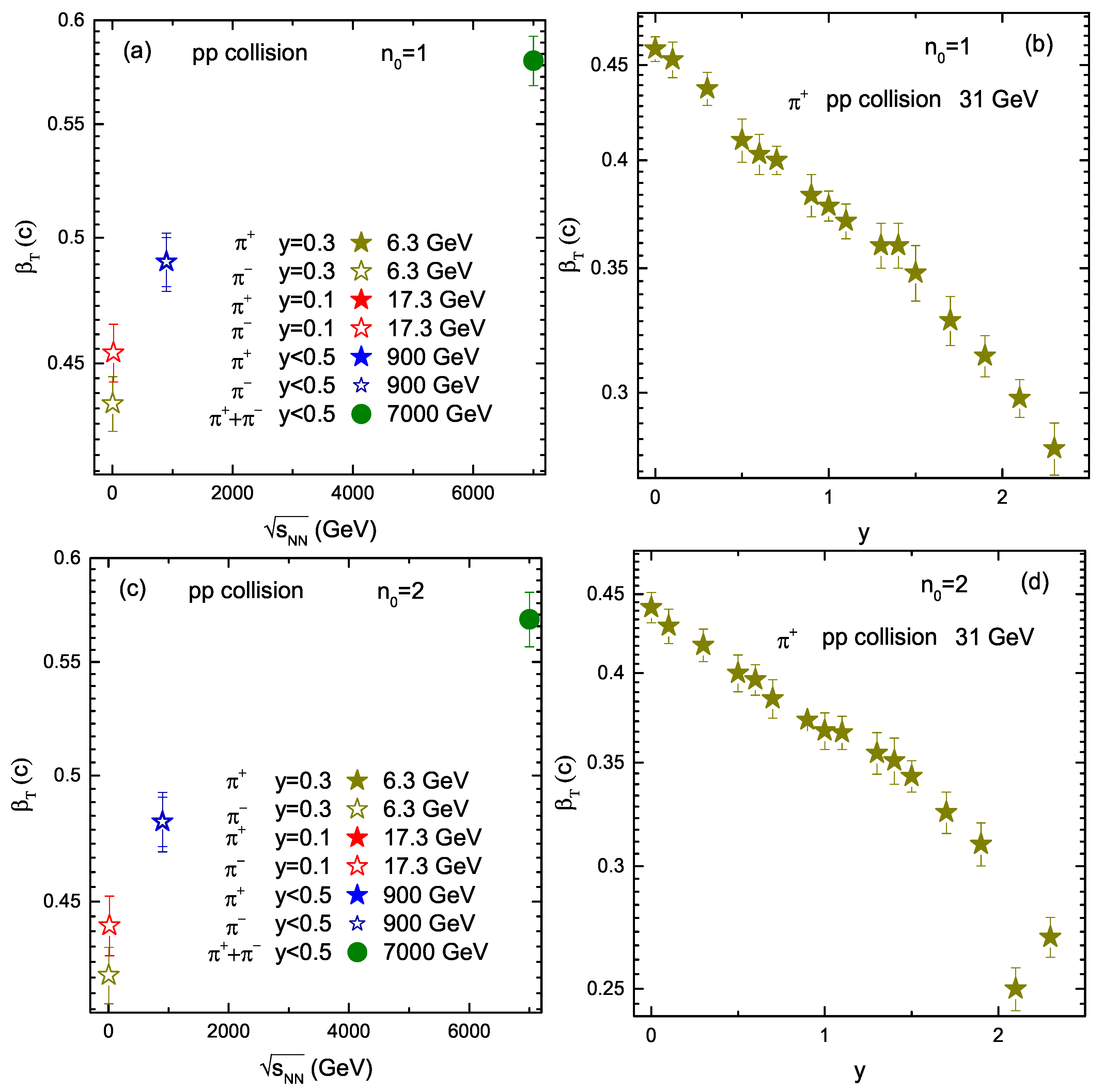
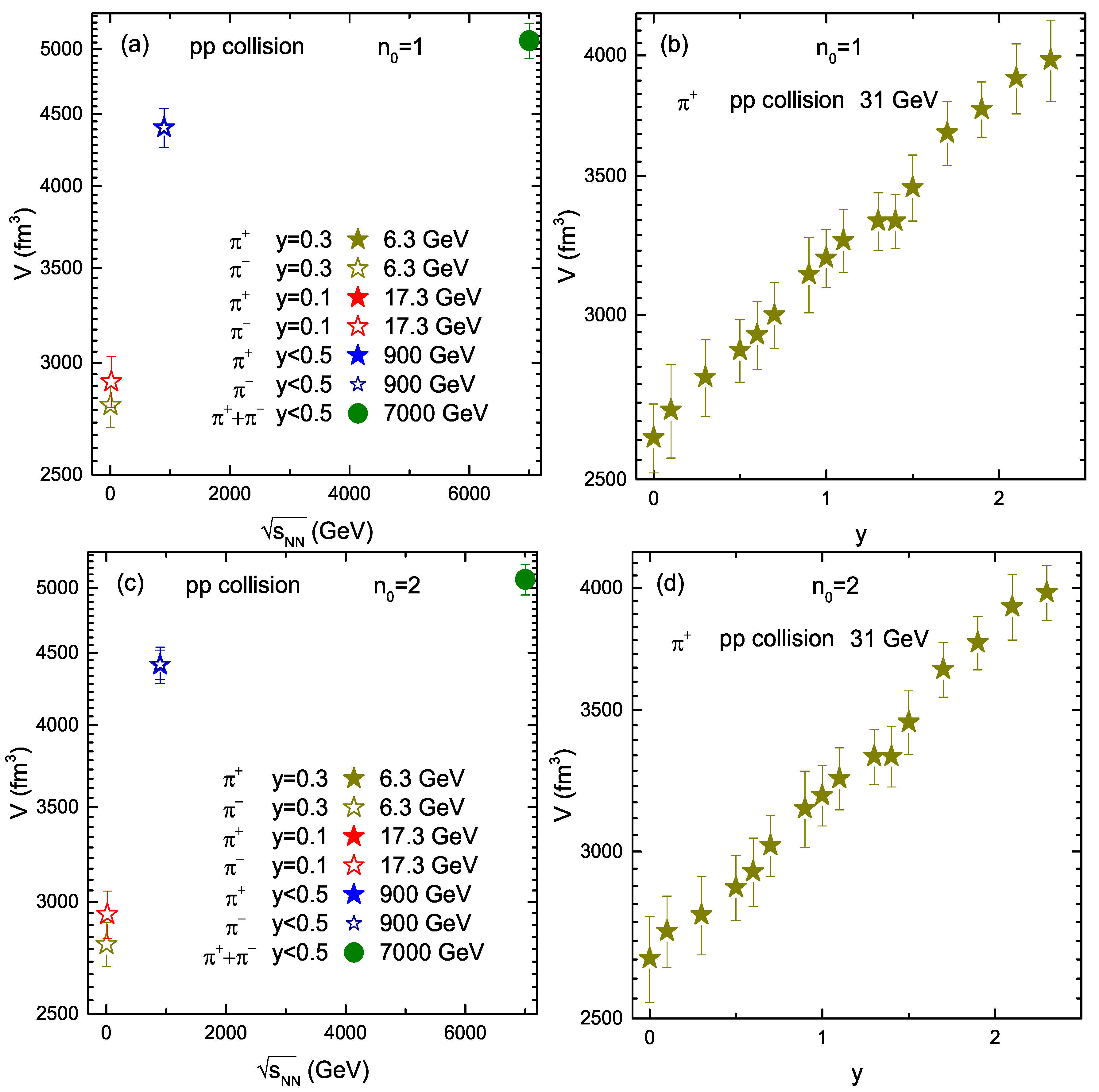
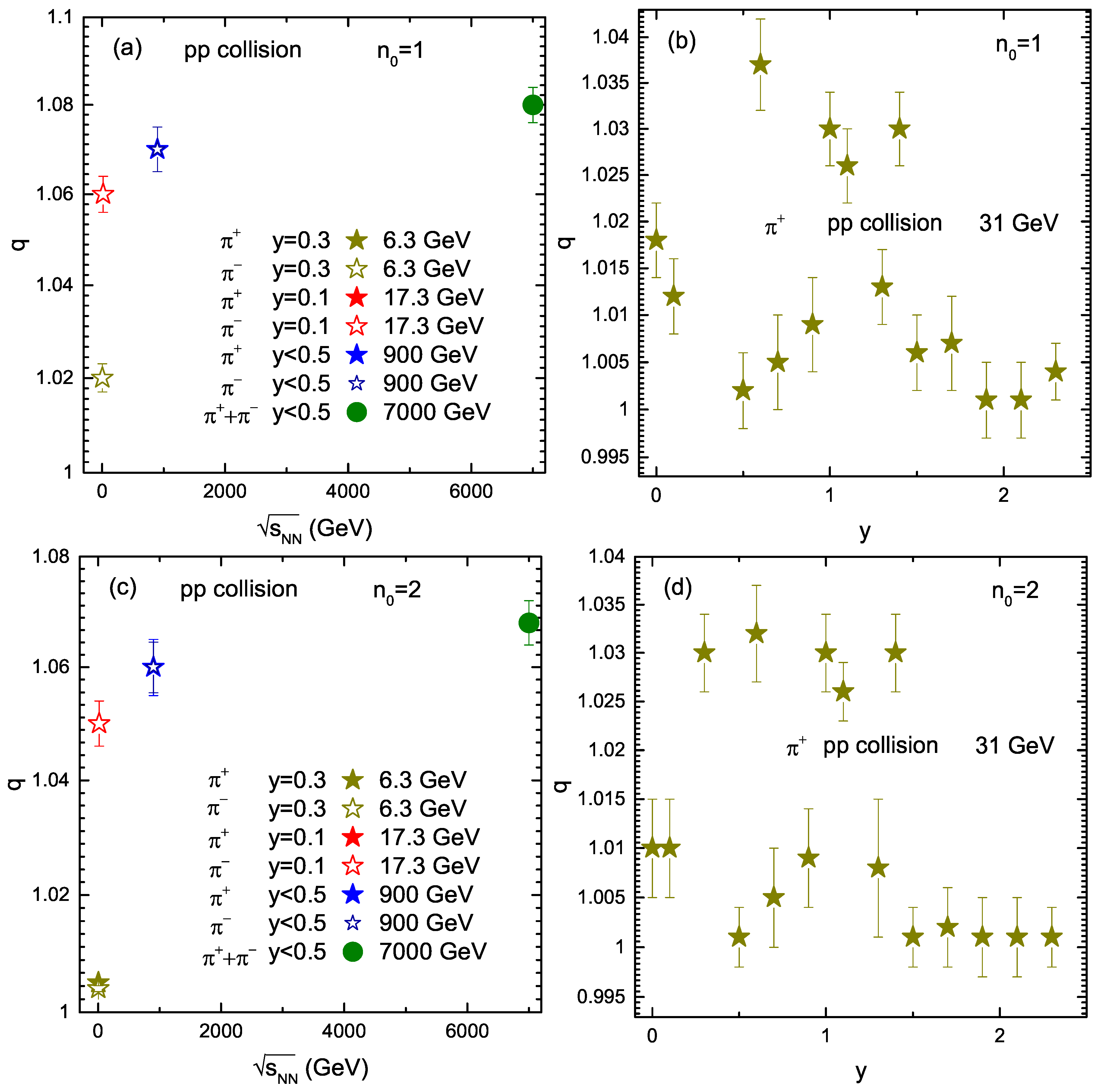
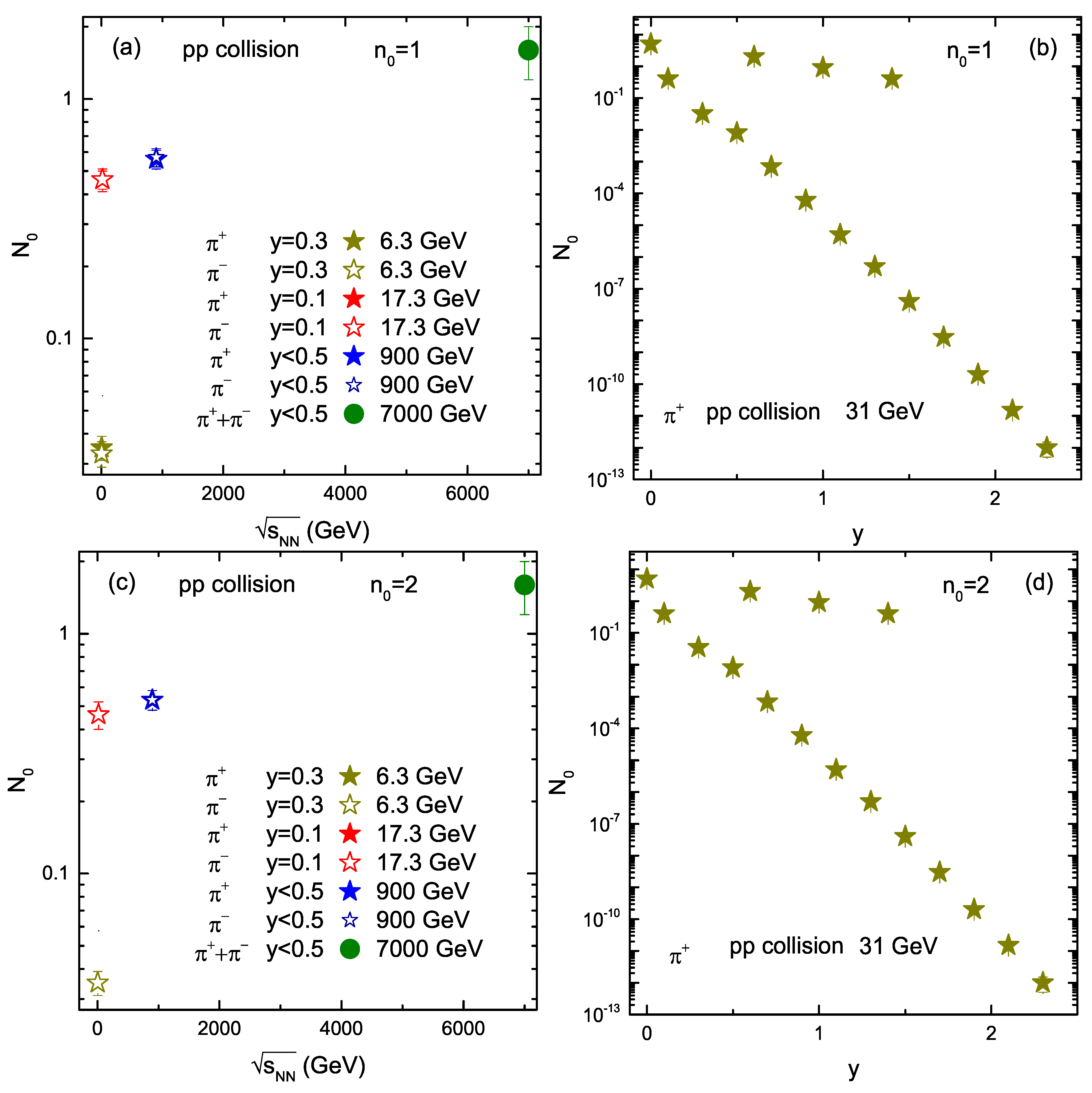
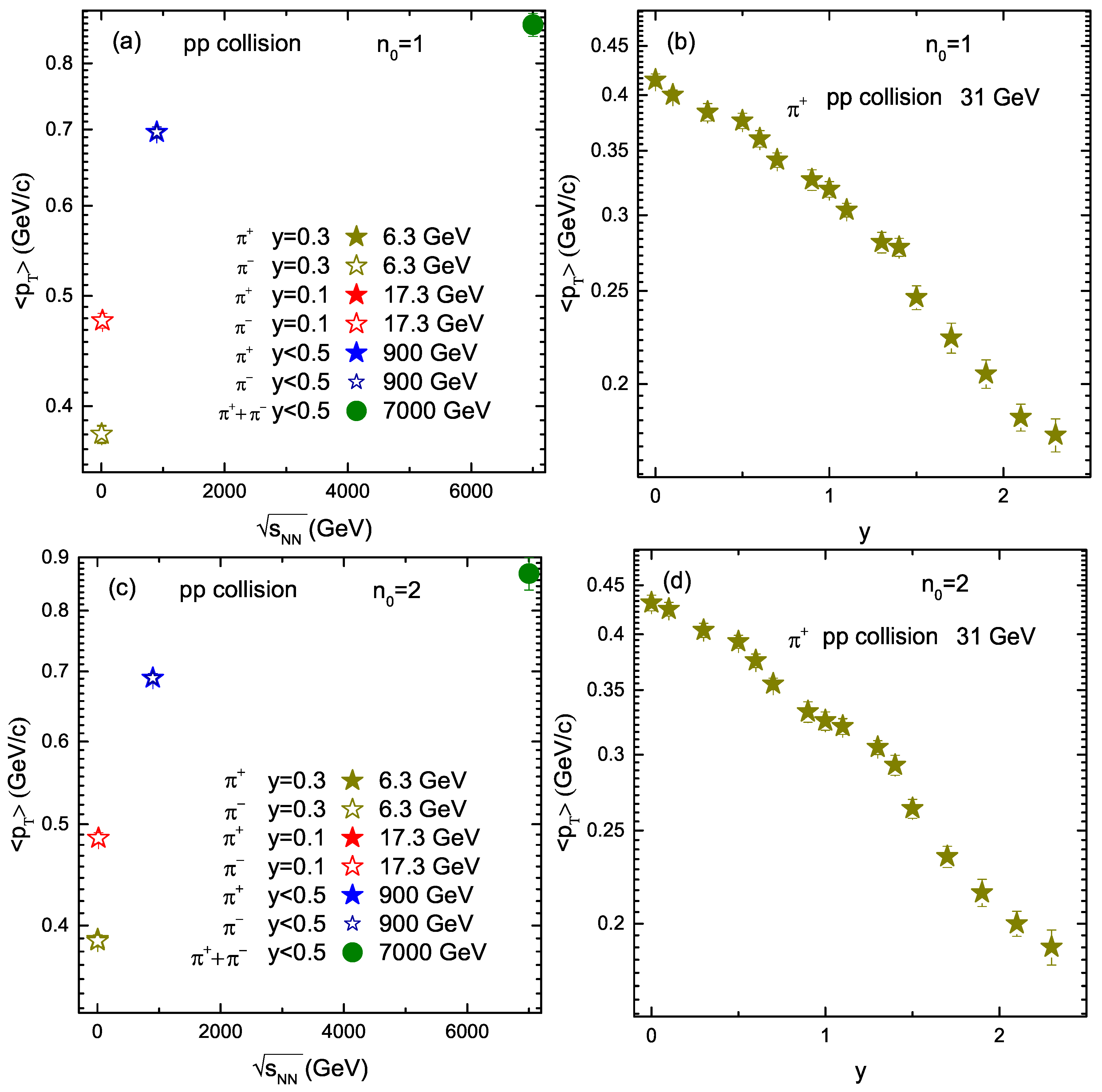
| Energy (GeV) | Rapidity | Particle | (GeV) | (c) | q | /dof | p | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 30.6 GeV | 132/15 | 1 | ||||||||
| 30.6 GeV | 0.4/2 | 0.18 | ||||||||
| 30.6 GeV | 3/5 | 0.3 | ||||||||
| 30.6 GeV | 13/8 | 0.89 | ||||||||
| 30.6 GeV | 29/17 | 0.97 | ||||||||
| 30.6 GeV | 16/8 | 0.98 | ||||||||
| 30.6 GeV | 18/8 | 0.98 | ||||||||
| 30.6 GeV | 7/4 | 0.86 | ||||||||
| 30.6 GeV | 8/7 | 0.67 | ||||||||
| 30.6 GeV | 6/6 | 0.58 | ||||||||
| 30.6 GeV | 17/1 | 0.99 | ||||||||
| 30.6 GeV | 11/6 | 0.91 | ||||||||
| 30.6 GeV | 23/6 | 0.0.99 | ||||||||
| 30.6 GeV | 48/7 | 1 | ||||||||
| 30.6 GeV | 53/6 | 1 | ||||||||
| 30.6 GeV | 22/4 | 0.99 | ||||||||
| 6.3 GeV | 2.3/5 | 0.19 | ||||||||
| 6.3 GeV | 1/4 | 0.09 | ||||||||
| 17.3 GeV | 0.5/2 | 0.22 | ||||||||
| 17.3 GeV | 0.5/2 | 0.22 | ||||||||
| 900 GeV | 22/30 | 0.145 | ||||||||
| 900 GeV | 25/30 | 0.27 | ||||||||
| 7000 GeV | 41/35 | 0.77 |
| Energy (GeV) | Rapidity | Particle | (GeV) | (c) | q | /dof | p | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 30.6 GeV | 143/15 | 1 | ||||||||
| 30.6 GeV | 0.2/2 | 0.95 | ||||||||
| 30.6 GeV | 2/5 | 0.15 | ||||||||
| 30.6 GeV | 13/8 | 0.88 | ||||||||
| 30.6 GeV | 31/17 | 0.98 | ||||||||
| 30.6 GeV | 14/8 | 0.92 | ||||||||
| 30.6 GeV | 15/8 | 0.94 | ||||||||
| 30.6 GeV | 5/4 | 0.71 | ||||||||
| 30.6 GeV | 8/7 | 0.67 | ||||||||
| 30.6 GeV | 4/6 | 0.32 | ||||||||
| 30.6 GeV | 4/1 | 0.95 | ||||||||
| 30.6 GeV | 7/6 | 0.68 | ||||||||
| 30.6 GeV | 28/6 | 0.99 | ||||||||
| 30.6 GeV | 44/7 | 0.99 | ||||||||
| 30.6 GeV | 50/6 | 1 | ||||||||
| 30.6 GeV | 28/4 | 0.99 | ||||||||
| 6.3 GeV | 2.4/5 | 0.208 | ||||||||
| 6.3 GeV | 1.5/4 | 0.173 | ||||||||
| 17.3 GeV | 0.2/2 | 0.095 | ||||||||
| 17.3 GeV | 0.2/2 | 0.095 | ||||||||
| 900 GeV | 27/30 | 0.37 | ||||||||
| 900 GeV | 31/30 | 0.58 | ||||||||
| 7000 GeV | 45/35 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waqas, M.; Haj Ismail, A.A.K.; Ajaz, M.; AbdelKader, A. Excitation Function of Kinetic Freeze-Out Parameters at 6.3, 17.3, 31, 900 and 7000 GeV. Universe 2022, 8, 138. https://doi.org/10.3390/universe8020138
Waqas M, Haj Ismail AAK, Ajaz M, AbdelKader A. Excitation Function of Kinetic Freeze-Out Parameters at 6.3, 17.3, 31, 900 and 7000 GeV. Universe. 2022; 8(2):138. https://doi.org/10.3390/universe8020138
Chicago/Turabian StyleWaqas, Muhammad, Abd Al Karim Haj Ismail, Muhammad Ajaz, and Atef AbdelKader. 2022. "Excitation Function of Kinetic Freeze-Out Parameters at 6.3, 17.3, 31, 900 and 7000 GeV" Universe 8, no. 2: 138. https://doi.org/10.3390/universe8020138
APA StyleWaqas, M., Haj Ismail, A. A. K., Ajaz, M., & AbdelKader, A. (2022). Excitation Function of Kinetic Freeze-Out Parameters at 6.3, 17.3, 31, 900 and 7000 GeV. Universe, 8(2), 138. https://doi.org/10.3390/universe8020138








