Abstract
The lack of space inversion symmetry endows non-centrosymmetric superconducting materials with various interesting parity-breaking phenomena, including the anomalous Josephson effect. Our paper considers a Josephson junction of two non-centrosymmetric superconductors connected by a uniaxial ferromagnet. We show that this “Chiral Magnetic Josephson junction” (CMJ junction) exhibits a direct analog of the Chiral Magnetic Effect, which has already been observed in Weyl and Dirac semimetals. We suggest that the CMJ can serve as an element of a qubit with a Hamiltonian tunable by the ferromagnet’s magnetization. The CMJ junction avoids using an offset magnetic flux in inductively shunted qubits, thus enabling a simpler and more robust architecture. Furthermore, when the uniaxial ferromagnet’s easy axis is directed across the junction, the resulting “chiral magnetic qubit” provides robust protection from the noise caused by magnetization fluctuations.
1. Introduction
The discovery of superconductors lacking spatial inversion symmetry [1,2,3,4,5] has opened the possibility of studying the spontaneous breaking of continuous symmetry in a parity-violating material. In particular, the superconducting order parameter in these non-centrosymmetric superconductors (NCSs) is a parity-odd quantity [4,5], enabling several interesting magnetoelectric phenomena due to the mixing of singlet and triplet superconducting parameters, correlations between supercurrents and spin polarization, the appearance of helical states, and the peculiar structure of Abrikosov vortices (see [6,7] for a review). Notably, in these superconducting materials, vortices can show an inversion of the magnetic field away from the vortex core [8,9] and new compact states that are the superconducting counterparts of the Chandrasekhar–Kendall states in highly conducting plasmas [10].
Parity breaking in NCSs also results in an unconventional Josephson effect, where the junction features a phase-shifted current relation [11,12]:
Here, is the superconducting phase difference across the junction, is the critical Josephson current, and is the parity-breaking phase offset. Nonzero bias results in a nonvanishing current across the junction, even when the phase difference is zero. Since the current is a parity-odd quantity, this signals a parity violation.
Phase-biased junctions (often called “-junctions”) have been suggested to appear in a wide range of systems, including non-centrosymmetric [11,13,14] and multilayered [15] ferromagnetic links between conventional superconductors, topological insulators [16,17], nanowires [18,19], quantum point contacts [20], quantum dots [21,22,23], and Weyl semimetals [24,25]. The first experimental realization of Josephson -junctions has been reported in superconductor–quantum dot structures, where the phase offset is controlled via electrostatic gating [26].
In this article, we introduce the Josephson junction made of two NCSs weakly linked by a uniaxial ferromagnet with an easy axis normal to the interface, i.e., parallel to the electric current (see Figure 1). Unlike in previous proposals [11,27,28], the ferromagnetic exchange field here is directed normally to the NCS/F/NCS interfaces. Parity breaking in NCS couples the magnetization to the supercurrent , resulting in a term · in the Ginzburg–Landau free-energy functional describing crystal structures with O point group symmetry. As derived below, this results in a nonzero current even in the absence of phase gradients across the junction. This current, directed along the magnetic field, stems from the breaking of parity in a non-equilibrium state and is thus a direct analog of the Chiral Magnetic Effect [29] predicted for systems of chiral fermions and observed in Dirac and Weyl semimetals [30,31,32,33]. This analogy motivates our terminology “Chiral Magnetic Josephson junction” (CMJ junction) to describe the NCS/F/NCS junction displayed in Figure 1. Below, we demonstrate that the current across the CMJ junction is still given by the expression (1), where the magnitude of the bias can be tuned by the ferromagnet’s magnetization.
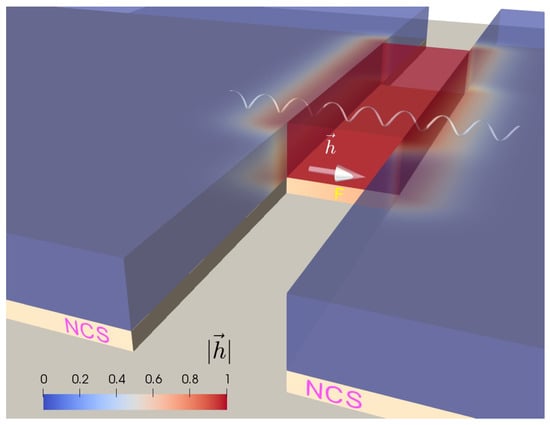
Figure 1.
The Chiral Magnetic Josephson junction: two non-centrosymmetric superconductors (NCSs) are weakly linked by a uniaxial ferromagnet (F). The exchange field of the ferromagnet, oriented across the link, induces an inversion symmetry-breaking component of the supercurrent (represented by the spiral) in the junction.
We propose to use the CMJ junction as a constituent of a superconducting qubit. The junction’s energy associated with the current (1) is
where is the Josephson energy. The total energy of the qubit is the sum of the junction’s energy (2) and a term quadratic in the phase difference . For example, in the case of an inductively shunted junction [34], this quadratic term results from the inductive energy :
Here, the offset plays the role of an offset flux and can be used to control the form of the qubit Hamiltonian. Using the magnetization of the ferromagnetic link should simplify the qubit architecture by avoiding the use of an offset flux and the corresponding source.
Noise in the offset flux is an essential component of qubit decoherence [35,36]. As demonstrated below, the noise in the offset phase results from the fluctuations of the component of the magnetization normal to the interface. In the proposed setup, this direction corresponds to the easy axis of the uniaxial ferromagnet. Thus, only longitudinal magnetization fluctuations contribute to the noise, but these are suppressed by the ratio of the qubit temperature to the Curie temperature of the ferromagnet, which is about . Moreover, the current in the CMJ junction is parallel to magnetization and thus is “force-free”, i.e., not subjected to a Lorentz force. This dramatically reduces the coupling between the current and the magnetization that contributes to the noise.
The offset phase of the CMJ junction can be estimated within the Ginzburg–Landau (GL) framework. The superconducting state in non-centrosymmetric superconductors is commonly believed to be a mixture of singlet and triplet pseudo-spin states [6,7] due to the spin–orbital coupling in the presence of the broken inversion symmetry [37]. Using , the Ginzburg–Landau free energy describing the superconducting state of non-centrosymmetric material reads as [7,38]:
The single-component superconducting order parameter is coupled to the vector potential of the magnetic field via the gauge derivative , while the coefficients b, and are standard phenomenological GL parameters. The parity-odd nature of the non-centrosymmetric superconductor is reflected by the last term (Lifshitz invariant) of the free energy (4), which describes the direct coupling of the magnetic field to the usual, parity-odd component of the supercurrent density:
Note that the exchange field of the ferromagnet plays the role of the background magnetic field . The parity-odd last term in (4) yields an additional parity-even contribution to the total supercurrent :
The GL functional (4) describes NCS materials with O point symmetry, such as LiPtB [5,39] and MoAlC [40,41], and the coupling constant K determines the magnitude of the superconducting magnetoelectric effects following the broken inversion symmetry. Our derivation applies to non-centrosymmetric superconductors with other crystallographic groups with a generic Lifshitz invariant . In this case, when the x-axis is directed across the normal link, the diagonal element should be nonzero. Notice that Lifshitz invariants of the type do not have such a diagonal element and thus cannot satisfy this requirement 1.
As illustrated in Figure 1, we consider a pair of identical non-centrosymmetric superconductors separated by a uniaxial ferromagnetic weak link whose internal exchange field points across the link. We neglect the term quartic in the condensate and disregard inhomogeneities of both the condensate and the exchange field in the transverse -plane. The minimization of the GL free energy (4) with respect to the superconducting order parameter in the background of the ferromagnetic exchange field then yields the equation
that describes the tunneling of the Cooper pairs across the weak link. For the time being, we assume the absence of an external electromagnetic field at the link, . Due to proximity effects, the tunneling of the Cooper pairs between the non-centrosymmetric superconductors through the centrosymmetric weak link will not respect the parity inversion , as can be seen from Equation (7).
The general solution of Equation (7) for the superconducting gap inside the weak link reads as:
where the wavevectors
should have a nonzero real part so that the weak link is in a normal state, thus requiring . The coefficients in Equation (8) are determined by the boundary conditions at the interfaces of the weak ferromagnetic link with the superconductors at . It is customary to make a simplification using rigid boundary conditions [11,42], which assume the absence of a barrier at the interfaces and imply continuity of the superconducting order parameter:
here, is the absolute value of the order parameter at the superconducting leads.
Using the relation Equations (8)–(10) together with the definition of the total current (6) yields the phase-shifted current relation:
which exhibits the offset of the phase difference given by
This offset, corresponding to the parity-breaking phenomenon, is proportional to the strength of the magnetic interaction K in the Ginzburg–Landau free energy (4). In other words, the presence of the nonzero phase bias signals the breaking of the parity-inversion symmetry between leftward and rightward tunneling of the Cooper pairs and leads to a nonzero current in the “steady state” of the junction even if the phase difference between the superconducting leads is zero, .
In a long junction, , the current (11) is an exponentially small quantity due to suppression of the Cooper-pair tunneling between widely separated superconducting leads. The limit of a short junction in the presence of parity breaking should be taken with care. In the thermodynamic equilibrium , the current through the junction is always zero. However, in the steady state with zero phase difference , the electric current does not vanish and is given by the parity-even term (6):
This current plays a crucial role in the dynamics of the chiral magnetic qubit. As mentioned earlier, the current (13) shares a striking similarity with the Chiral Magnetic Effect [29], with and K, respectively, playing the roles of the external magnetic field and the source of the parity breaking.
Some features of the phenomenon that we discuss also appear in usual centrosymmetric s-wave superconductors separated by the Josephson junction made of an NCS-type ferromagnet with tangentially-oriented field . Even though the underlying dynamics are quite different, the latter system is described by an equation similar to (7) [11]. However, in our case, the currents that flow along the magnetic field are force-free and, thus, are not subjected to the noise resulting from the transverse fluctuations of magnetization.
Similar types of Josephson junctions with the ferromagnetic exchange field oriented transversally between two non-centrosymmetric superconductors with the point group (corresponding to interactions of the type ) have been proposed in [27,28]. The Josephson current in a non-ferromagnetic junction between two non-centrosymmetric superconductors does not exhibit the offset in the phase [43]. A finite phase offset for the Josephson current of chiral charge appears, however, for the junction between two Weyl superconductors separated by a Weyl semimetal and for a magnetic field oriented transversally [44].
Notice that an ordinary Josephson junction driven by an external AC electric current possesses an I–V curve with a ladder structure characterized by regions with constant voltage. These regions, known as Shapiro steps, are precisely specified by parameters of the Josephson junction, allowing for accurate frequency–voltage conversion in the experimental setting [45]. For noncentrosymmetric superconductors, the positions of the Shapiro steps should be shifted due to the magnetoelectric effect, which contributes to the voltage drop in the presence of the ferromagnetic exchange field . The phenomenon is similar to the Josephson junctions involving the topological insulator as the weak link sandwiched between two type-2 superconductors. In such a device, the magnetoelectric effect is caused by axion coupling in the topological insulator that breaks the time-reversal symmetry of the system and affects Shapiro steps [46].
We estimate the phase bias (12) numerically as follows:
The length of the ferromagnetic Josephson junction is typically of the order of tens of nanometers ( in [47]). The exchange field h should not exceed the upper critical field , which, for several NCS superconductors, may reach significant values, T. Fields of this order and higher are known to be created by usual ferromagnets [48]. Note that even for magnetic fields larger than , the vortex formation can be avoided by choosing a weak link with a sufficiently small cross-section such that the total magnetic flux entering the superconductor is smaller than the flux quantum . The main uncertainty in our estimate comes from the poorly known parity-odd coupling K. Its value was estimated to be [49,50], where is the penetration depth. Despite this uncertainty, the phase bias may be tuned to take values of order . For a given NCS superconductor, the phase bias can be manipulated by the magnetization of the weak link.
The chiral magnetic Josephson junction sketched in Figure 1 can be inductively shunted, for example, by a series of conventional Josephson junctions, to form a “chiral magnetic qubit" (see Figure 2). Such circuits include, in addition, two mixed Josephson junctions between the conventional and NCS superconductors. These mixed junctions do not generate the electric current across them at zero phase difference [51].
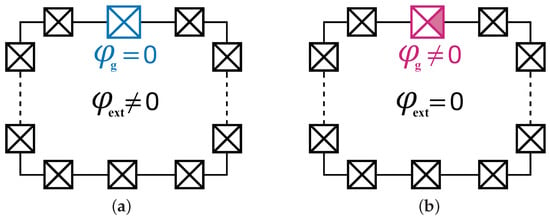
Figure 2.
(a) Fluxonium-type qubit based on conventional Josephson junction inductively shunted by a series of Josephson junctions. The qubit is biased by an external magnetic flux , where is the elementary flux quantum. The gate phase offset for a conventional Josephson junction is absent, . (b) Chiral magnetic qubits based on the Chiral Magnetic Josephson (CMJ) junction are inductively shunted by a series of Josephson junctions. The CMJ junction possesses an internal phase offset eliminating the need for an external magnetic flux .
The Coulomb interactions between the Cooper pairs are described by the kinetic term in the Hamiltonian of the qubit:
where is the Cooper-pair number operator, and the last two terms describe the Josephson tunneling and the induction (3). The Hamiltonian (15) is generic for a family of inductively shunted qubits, including the fluxonium [52,53], one-junction flux qubits, and flux-biased phase qubits [54].
As illustrated in Figure 2a, fluxonium qubits relate the phase offset to the externally applied flux as , where is the flux quantum. These are further characterized by a specific set of model parameters, such as the small inductive energy () and a moderate charging energy (), which give a unique combination of long coherence time and large anharmonicity of the energy levels [55]. Transmon qubits, on the other hand, are characterized by Coulomb charging energy much smaller than the Josephson tunneling energy, , thus reducing noise caused by the offset charge fluctuations [56].
A nonzero phase bias imposes a large anharmonicity on the energy-level structure [34] determined by the Schrödinger equation:
The regime provides maximum level-splitting and the absence of nearly degenerate level pairs [34]. Figure 3 displays the structure of the energy levels corresponding to this Hamiltonian. The transitions between the first excited state and the ground state, , can be substantially suppressed by the barrier separating them. This barrier is almost absent in the typical fluxonium regime ( and ), as the first excited energy level practically coincides with the height of the barrier, Figure 3a. This conclusion is valid to good accuracy for a wide range of values of the phase offset .
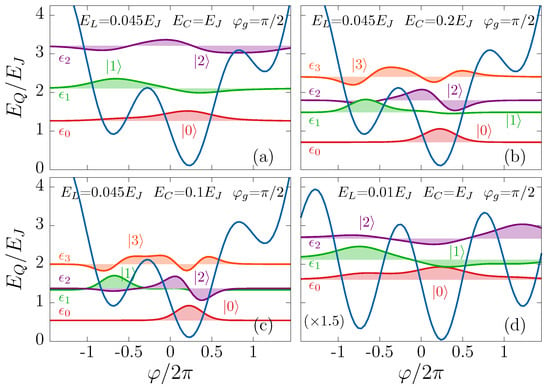
Figure 3.
The potential energy (3) of the chiral magnetic qubit with the chiral magnetic Josephson junction possessing the phase offset for various Coulomb charging energies and inductive energies : (a) , ; (b) , ; (c) , ; and (d) , . Lowest eigenstates with are shown along with the numerically computed energy levels and the corresponding wavefunctions .
Decreasing the Coulomb energy towards the transmon regime leads to the appearance of the prohibitive barrier for transitions between the different wells, Figure 3b. As displayed in Figure 3c, further decreases in the Coulomb energy reduce the energy difference between and states. The lifetime of the first excited level may be enhanced by lowering the inductive energy . Figure 3d shows that at , the barrier is sufficiently high to ensure quasi-classical protection of the first excited level. Related discussions of the energy levels can be found in [55,57] for fluxonium-type qubits.
The conventional way to induce the phase in fluxonium qubits is to apply a background magnetic flux . The noise in magnetic flux is typically of the order of ; overcoming this noise is a central problem in quantum computer design. In our case, the noise in is due to the noise in magnetization. Indeed, Equation (12) yields the noise relation
To reduce the noise in magnetization, we propose to use a highly anisotropic uniaxial ferromagnet, e.g., of magnetoplumbite type. In the case of a uniaxial ferromagnet, the 3D rotational symmetry is explicitly broken by the crystalline lattice’s symmetry. The only surviving symmetry is 2D rotations around the easy symmetry axis of the ferromagnet in the basal plane perpendicular to this axis. In this case, magnetization fluctuations are given by the simplified form of the Landau–Lifshitz–Gilbert equation with no gyroscopic term. They correspond to the rotation of magnetization around the easy axis (which here points along the x axis) with fluctuating components of magnetization and but with a fixed , which is an integral of motion. Since the phase offset (12) depends only on , the transverse fluctuations of magnetization do not induce noise in this quantity.
Unlike the transverse ones, the longitudinal fluctuations of magnetization (i.e., fluctuations of the magnitude of ) induce noise in the offset phase . However, longitudinal magnetization fluctuations are expected to be suppressed compared to the transverse ones by a factor of , where T is temperature, is Curie temperature of the ferromagnet, and c is a constant of order one. Indeed, the transverse fluctuations correspond to gapless Goldstone modes with kinetic energy , while the longitudinal one is massive with energy . Analysis [58,59] of the Landau–Lifshitz–Bloch equation (including both transverse and longitudinal fluctuations of magnetization) indicates that the constant . Therefore, at temperatures of the superconducting qubits, which are on the order of tens of milli-Kelvin, with Curie temperatures on the order of 1000 K, we expect the suppression of longitudinal fluctuations by a factor of . This allows us to expect a suppression in the noise resulting from the offset flux of the CMJ junction as compared to external flux noise by a significant factor of .
The domain structure in uniaxial ferromagnets is known to depend crucially on the anisotropy [60]. In weakly anisotropic ferromagnets (Landau–Lifshitz type), there is branching of domains close to the surface, and the magnetic flux does not leave the ferromagnet. This is not a desirable domain configuration, as the magnetic field has to penetrate the superconductor. On the other hand, in strongly anisotropic ferromagnets (Kittel type), such as magnetoplumbite, the domains do not branch, and thus the magnetic flux does escape the ferromagnet. The superconducting interface may affect the domain structure of a thin ferromagnetic film [61]; this question requires further investigation.
To summarize, we introduced a Josephson junction consisting of two non-centrosymmetric superconductors connected by a uniaxial ferromagnet, and we demonstrated that it exhibits a direct analog of the Chiral Magnetic Effect. We proposed this Chiral Magnetic Josephson junction (CMJ junction) for use as an element of a qubit with parameters tunable by the ferromagnet’s magnetization. The resulting Chiral Magnetic Qubit is protected from noise caused by fluctuations in magnetization and does not require an external magnetic flux, allowing for a simpler and more robust architecture. The main uncertainty stems from the poorly known parity—the odd response of non-centrosymmetric superconductors—and we believe that these materials and the properties of their interfaces deserve further study.
Author Contributions
Conceptualization, D.E.K.; methodology, M.N.C.; software, J.G.; formal analysis, J.G. and M.N.C.; investigation, D.E.K.; writing—original draft preparation, J.G., M.N.C., and D.E.K.; visualization, J.G.; supervision, D.E.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work of D.K. was supported by the U.S. Department of Energy, Office of Nuclear Physics, under contracts DE-FG-88ER40388 and DE-AC02-98CH10886, and by the Office of Basic Energy Science under contract DE-SC-0017662.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CMJ | Chiral Magnetic Josephson |
| CME | Chiral Magnetic Effect |
Note
| 1 | Possible candidates for the NCS superconductors should thus have a crystalline structure with either the point group O (Li2Pt3B, Mo3Al2C), T point group (e.g. LaRhSi, LaIrSi), or (La5B2C6), (UIr), etc. On the other hand, the point groups with n = 2, 3, 4, 6 (possessed, for example, by the compounds MoS2, MoN, GaN, CePt3Si, CeRhSi3, amd CeIrSi3 [7]) correspond to the Lifshitz invariants of the type that do not fit our proposal. |
References
- Bulaevskii, L.N.; Guseinov, A.A.; Rusinov, A.I. Superconductivity in crystals without symmetry centers. Sov. J. Exp. Theor. Phys. 1976, 44, 1243. [Google Scholar]
- Levitov, L.S.; Nazarov, Y.V.; Éliashberg, G.M. Magnetostatics of superconductors without an inversion center. Sov. J. Exp. Theor. Phys. Lett. 1985, 41, 445. [Google Scholar]
- Bauer, E.; Hilscher, G.; Michor, H.; Paul, C.; Scheidt, E.W.; Gribanov, A.; Seropegin, Y.; Noël, H.; Sigrist, M.; Rogl, P. Heavy Fermion Superconductivity and Magnetic Order in Noncentrosymmetric CePt3Si. Phys. Rev. Lett. 2004, 92, 027003. [Google Scholar] [CrossRef] [PubMed]
- Samokhin, K.V.; Zijlstra, E.S.; Bose, S.K. CePt3Si: An unconventional superconductor without inversion center. Phys. Rev. B 2004, 69, 094514. [Google Scholar] [CrossRef]
- Yuan, H.Q.; Agterberg, D.F.; Hayashi, N.; Badica, P.; Vandervelde, D.; Togano, K.; Sigrist, M.; Salamon, M.B. S-Wave Spin-Triplet Order in Superconductors without Inversion Symmetry: Li2Pd3B and Li2Pt3B. Phys. Rev. Lett. 2006, 97, 017006. [Google Scholar] [CrossRef]
- Bauer, E.; Sigrist, M. (Eds.) Non-Centrosymmetric Superconductors: Introduction and Overview; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Smidman, M.; Salamon, M.B.; Yuan, H.Q.; Agterberg, D.F. Superconductivity and spin-orbit coupling in non-centrosymmetric materials: A review. Rep. Progr. Phys. 2017, 80, 036501. [Google Scholar] [CrossRef]
- Garaud, J.; Chernodub, M.N.; Kharzeev, D.E. Vortices with magnetic field inversion in noncentrosymmetric superconductors. Phys. Rev. B 2020, 102, 184516. [Google Scholar] [CrossRef]
- Samoilenka, A.; Babaev, E. Spiral magnetic field and bound states of vortices in noncentrosymmetric superconductors. Phys. Rev. B 2020, 102, 184517. [Google Scholar] [CrossRef]
- Garaud, J.; Korneev, A.; Samoilenka, A.; Molochkov, A.; Babaev, E.; Chernodub, M. Toroflux: A counterpart of the Chandrasekhar-Kendall state in noncentrosymmetric superconductors. arXiv 2022, arXiv:2208.08180. [Google Scholar]
- Buzdin, A. Direct Coupling Between Magnetism and Superconducting Current in the Josephson φ0 Junction. Phys. Rev. Lett. 2008, 101, 107005. [Google Scholar] [CrossRef]
- Konschelle, F.; Buzdin, A. Magnetic Moment Manipulation by a Josephson Current. Phys. Rev. Lett. 2009, 102, 017001. [Google Scholar] [CrossRef] [PubMed]
- Atanasova, P.K.; Panayotova, S.A.; Rahmonov, I.R.; Shukrinov, Y.M.; Zemlyanaya, E.V.; Bashashin, M.V. Periodicity of magnetization reversals in φ0 Josephson junction. arXiv 2019, arXiv:1905.03895. [Google Scholar]
- Shukrinov, Y.M.; Mazanik, A.; Rahmonov, I.R.; Botha, A.E.; Buzdin, A. Re-orientation of the easy axis in φ0-junction. EPL (Europhys. Lett.) 2018, 122, 37001. [Google Scholar] [CrossRef]
- Liu, J.F.; Chan, K.S. Anomalous Josephson current through a ferromagnetic trilayer junction. Phys. Rev. B 2010, 82, 184533. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yokoyama, T.; Nagaosa, N. Manipulation of the Majorana Fermion, Andreev Reflection, and Josephson Current on Topological Insulators. Phys. Rev. Lett. 2009, 103, 107002. [Google Scholar] [CrossRef]
- Dolcini, F.; Houzet, M.; Meyer, J.S. Topological Josephson ϕ0 junctions. Phys. Rev. B 2015, 92, 035428. [Google Scholar] [CrossRef]
- Yokoyama, T.; Eto, M.; Nazarov, Y.V. Anomalous Josephson effect induced by spin-orbit interaction and Zeeman effect in semiconductor nanowires. Phys. Rev. B 2014, 89, 195407. [Google Scholar] [CrossRef]
- Campagnano, G.; Lucignano, P.; Giuliano, D.; Tagliacozzo, A. Spin–orbit coupling and anomalous Josephson effect in nanowires. J. Phys. Condens. Matter 2015, 27, 205301. [Google Scholar] [CrossRef]
- Reynoso, A.A.; Usaj, G.; Balseiro, C.A.; Feinberg, D.; Avignon, M. Anomalous Josephson Current in Junctions with Spin Polarizing Quantum Point Contacts. Phys. Rev. Lett. 2008, 101, 107001. [Google Scholar] [CrossRef]
- Zazunov, A.; Egger, R.; Jonckheere, T.; Martin, T. Anomalous Josephson Current through a Spin-Orbit Coupled Quantum Dot. Phys. Rev. Lett. 2009, 103, 147004. [Google Scholar] [CrossRef]
- Dell’Anna, L.; Zazunov, A.; Egger, R.; Martin, T. Josephson current through a quantum dot with spin-orbit coupling. Phys. Rev. B 2007, 75, 085305. [Google Scholar] [CrossRef]
- Brunetti, A.; Zazunov, A.; Kundu, A.; Egger, R. Anomalous Josephson current, incipient time-reversal symmetry breaking, and Majorana bound states in interacting multilevel dots. Phys. Rev. B 2013, 88, 144515. [Google Scholar] [CrossRef]
- Alidoust, M.; Halterman, K. Evolution of pair correlation symmetries and supercurrent reversal in tilted Weyl semimetals. Phys. Rev. B 2020, 101, 035120. [Google Scholar] [CrossRef]
- Alidoust, M. Self-biased current, magnetic interference response, and superconducting vortices in tilted Weyl semimetals with disorder. Phys. Rev. B 2018, 98, 245418. [Google Scholar] [CrossRef]
- Szombati, D.B.; Nadj-Perge, S.; Car, D.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Josephson Φ0-junction in nanowire quantum dots. Nat. Phys. 2016, 12, 568. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Liu, J.F. Anomalous Josephson effect in noncentrosymmetric superconductors. Appl. Phys. Lett. 2016, 108, 102601. [Google Scholar] [CrossRef]
- Rahnavard, Y.; Manske, D.; Annunziata, G. Magnetic Josephson junctions with noncentrosymmetric superconductors. Phys. Rev. B 2014, 89, 214501. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. Chiral magnetic effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; Warringa, H.J. Chiral magnetic conductivity. Phys. Rev. D 2009, 80, 034028. [Google Scholar] [CrossRef]
- Li, Q.; Kharzeev, D.E.; Zhang, C.; Huang, Y.; Pletikosić, I.; Fedorov, A.; Zhong, R.; Schneeloch, J.; Gu, G.; Valla, T. Chiral magnetic effect in ZrTe5. Nat. Phys. 2016, 12, 550. [Google Scholar] [CrossRef]
- Xiong, J.; Kushwaha, S.K.; Liang, T.; Krizan, J.W.; Hirschberger, M.; Wang, W.; Cava, R.J.; Ong, N.P. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 2015, 350, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhao, L.; Long, Y.; Wang, P.; Chen, D.; Yang, Z.; Liang, H.; Xue, M.; Weng, H.; Fang, Z.; et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031023. [Google Scholar] [CrossRef]
- Girvin, S.M. Chapter 3—Circuit QED: Superconducting qubits coupled to microwave photons. In Quantum Machines: Measurement and Control of Engineered Quantum Systems: Lecture Notes of the Les Houches Summer School: Volume 96, July 2011; Oxford Scholarship Online: Les Houches, France, 2014; Volume 96, pp. 113–256. [Google Scholar] [CrossRef]
- Clerk, A.A.; Devoret, M.H.; Girvin, S.M.; Marquardt, F.; Schoelkopf, R.J. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 2010, 82, 1155–1208. [Google Scholar] [CrossRef]
- Devoret, M.H.; Wallraff, A.; Martinis, J.M. Superconducting Qubits: A Short Review. arXiv 2004, arXiv:0411174. [Google Scholar]
- Gor’kov, L.P.; Rashba, E.I. Superconducting 2D System with Lifted Spin Degeneracy: Mixed Singlet-Triplet State. Phys. Rev. Lett. 2001, 87, 037004. [Google Scholar] [CrossRef]
- Agterberg, D.F. Magnetoelectric Effects, Helical Phases, and FFLO Phases. In Non-Centrosymmetric Superconductors: Introduction and Overview; Bauer, E., Sigrist, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 155–170. [Google Scholar] [CrossRef]
- Badica, P.; Kondo, T.; Togano, K. Superconductivity in a New Pseudo-Binary Li2B(Pd1−xPtx)3 (x=0–1) Boride System. J. Phys. Soc. Jpn. 2005, 74, 1014–1019. [Google Scholar] [CrossRef]
- Karki, A.B.; Xiong, Y.M.; Vekhter, I.; Browne, D.; Adams, P.W.; Young, D.P.; Thomas, K.R.; Chan, J.Y.; Kim, H.; Prozorov, R. Structure and physical properties of the noncentrosymmetric superconductor Mo3Al2C. Phys. Rev. B 2010, 82, 064512. [Google Scholar] [CrossRef]
- Bauer, E.; Rogl, G.; Chen, X.Q.; Khan, R.T.; Michor, H.; Hilscher, G.; Royanian, E.; Kumagai, K.; Li, D.Z.; Li, Y.Y.; et al. Unconventional superconducting phase in the weakly correlated noncentrosymmetric Mo3Al2C compound. Phys. Rev. B 2010, 82, 064511. [Google Scholar] [CrossRef]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef]
- Asano, Y.; Yamano, S. Josephson effect in noncentrosymmetric superconductor junctions. Phys. Rev. B 2011, 84, 064526. [Google Scholar] [CrossRef]
- Zhang, S.B.; Erdmenger, J.; Trauzettel, B. Chirality Josephson Current Due to a Novel Quantum Anomaly in Inversion-Asymmetric Weyl Semimetals. Phys. Rev. Lett. 2018, 121, 226604. [Google Scholar] [CrossRef]
- Shapiro, S. Josephson Currents in Superconducting Tunneling: The Effect of Microwaves and Other Observations. Phys. Rev. Lett. 1963, 11, 80–82. [Google Scholar] [CrossRef]
- Nogueira, F.S.; Nussinov, Z.; van den Brink, J. Josephson Currents Induced by the Witten Effect. Phys. Rev. Lett. 2016, 117, 167002. [Google Scholar] [CrossRef] [PubMed]
- Ryazanov, V.V.; Oboznov, V.A.; Rusanov, A.Y.; Veretennikov, A.V.; Golubov, A.A.; Aarts, J. Coupling of Two Superconductors through a Ferromagnet: Evidence for a π Junction. Phys. Rev. Lett. 2001, 86, 2427–2430. [Google Scholar] [CrossRef] [PubMed]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Lu, C.K.; Yip, S. Transverse Magnetic Field Distribution in the Vortex State of Noncentrosymmetric Superconductor with O Symmetry. J. Low Temp. Phys. 2009, 155, 160–168. [Google Scholar] [CrossRef][Green Version]
- Kashyap, M.K.; Agterberg, D.F. Vortices in cubic noncentrosymmetric superconductors. Phys. Rev. B 2013, 88, 104515. [Google Scholar] [CrossRef]
- Hayashi, N.; Iniotakis, C.; Machida, M.; Sigrist, M. Josephson effect between conventional and non-centrosymmetric superconductors. J. Phys. Chem. Solids 2008, 69, 3225–3227. [Google Scholar] [CrossRef]
- Manucharyan, V.E.; Koch, J.; Glazman, L.I.; Devoret, M.H. Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets. Science 2009, 326, 113–116. [Google Scholar] [CrossRef]
- Pop, I.M.; Geerlings, K.; Catelani, G.; Schoelkopf, R.J.; Glazman, L.I.; Devoret, M.H. Coherent suppression of electromagnetic dissipation due to superconducting quasiparticles. Nature 2014, 508, 369. [Google Scholar] [CrossRef]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Progr. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Nguyen, L.B.; Grabon, N.; San Miguel, J.; Pankratova, N.; Manucharyan, V.E. Demonstration of Protection of a Superconducting Qubit from Energy Decay. Phys. Rev. Lett. 2018, 120, 150503. [Google Scholar] [CrossRef] [PubMed]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef]
- Earnest, N.; Chakram, S.; Lu, Y.; Irons, N.; Naik, R.K.; Leung, N.; Ocola, L.; Czaplewski, D.A.; Baker, B.; Lawrence, J.; et al. Realization of a Λ System with Metastable States of a Capacitively Shunted Fluxonium. Phys. Rev. Lett. 2018, 120, 150504. [Google Scholar] [CrossRef] [PubMed]
- Garanin, D.A.; Ishchenko, V.V.; Panina, L.V. Dynamics of an ensemble of single-domain magnetic particles. Theor. Math. Phys. 1990, 82, 169–179. [Google Scholar] [CrossRef]
- Chubykalo-Fesenko, O.; Nowak, U.; Chantrell, R.W.; Garanin, D. Dynamic approach for micromagnetics close to the Curie temperature. Phys. Rev. B 2006, 74, 094436. [Google Scholar] [CrossRef]
- Kaczér, J. On the domain structure of uniaxial ferromagnets. Sov. J. Exp. Theor. Phys. 1964, 19, 1204. [Google Scholar] [CrossRef]
- Bulaevskii, L.N.; Chudnovsky, E.M. Ferromagnetic film on a superconducting substrate. Phys. Rev. B 2000, 63, 012502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).